格林公式及其应用共35页
合集下载
738-第三节 格林公式及其应用-PPT精选文档

解 用格林公式。 记右半圆域为 D。 A Q P ( )dxdy 原式 x y D D
OA
OA
L
D
3dxdy
D
3 2 1 . 3| D | 0 sinydy cos 2
2
5/23
OA : x 0
D
例2. 求 (2x y4 )dx (3x5y6 )dy , L:
L
(0 ,0 ) 、 (3 ,0 ) 、 (3 ,2 )为 顶 点 的 三 角 形 , 的 顺 边 时针方向。 D。 解 用格林公式。 记 相 应 三 角 域 为
原式
D
Q P ( ) dxdy x y D
L
3) 在 D 上, Pdx Qdy 与路径无 ;
AB
4) 在 D 上, Pdx Qdy 是某个函数的全 ( x, y) ( Qdy 是一个原函 . 数 即 有原函数 (x ,y ) Pdx
0 0
8/23
说明: 积分与路径无关时, 曲线积分可记为
P d xQ d y P dxQ dy AB A
21/23
r
x
Q P d x d y P d x Q d y 格林公式 x y D L
用格林公式易证: xOy 面上有界闭区 D 的面
| D| xdy D ydx
D
1 xdy ydx . 2 D
x a cos 所围面积 : ( 0 2 π) 例如, 椭圆 L y b sin 1 A x d y y d x 2L 2 π 1 2 2 πab ( ab cos ab sin ) d 0 2
格林公式及其应用

L1 L2 L2
Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
113格林公式及其应用共35页文档

D的边界上对坐标的曲线积分的关系,是牛顿-莱布尼茨 公式的推广. (2)格林公式的应用
1)在计算上,可以实现二重积分与曲线积分的
相互转化;
2)在应用上,通过它可以求出曲线积分与路径
无关的条件.(下面的内容)
(3)格林公式成立的条件:
L封闭且取正向
P、Q在D上一阶偏导数连续
9
D ( Q x P y)d x d yL P d x Q d y
3.格林公式的应用
(1) 计算二重积分
例1 计 算 e y 2 d x d y 其 中 D 是 以 O ( 0 ,0 ) ,A ( 1 , 1 ) ,
B ( 1 , 1 ) 为 顶 D 点 的 三 角 形 闭 区 域 . y B
A
解 取 P0,Qxey2, 则
D
利用格林公式 , 有
x e y 2d y
D
1
1
me1m.
4
D的反向边界
14
应用格林公式计算曲线积分添加辅助曲线应注意
(1)一般辅助线取平行坐标轴的直线或折线;
(2)辅助曲线的方向为它能使得封闭曲线构成 正方向.
y
y
4dxdy
0
4
x2
dx
D
8 64 .
3
A O :y 0 ,x :4 0 .
13
例4 计 算 ( 2 x y e x 2 ) d x ( e x 2 m x ) d y 其 中 L 为 由 点 L
O ( 0 ,0 ) 沿 曲 线 y 2 x x 2 到 点 B ( 1 ,1 ) . y
两式相加得: Q P
D ( x y)d x d yL P d x Q d y
7
2) 若D不满足以上条件, 则可通过加辅助线将其分割
高等数学-格林公式及其应用.ppt

l D1
O D2
x
1
2π
d
1 2π
π
20
2
l :4x2 y2 2
法二
l
ydx xdy 4x2 y2
l
ydx
2
xdy
1
2
ydx xd y
l
格林公式
D2是由l 所围区域
4x2 y2 2
所以 I 0 π
π.
1
2
1
2
(1
D2
(2)
π
2
1)dxdy
2
π
25
10.3 格林公式及其应用
Pdx Qdy
L
(L1, L2, L3对D来说为正方向)
8
10.3 格林公式及其应用
(3) 对复连通区域证明:
对若复区连域通不区止域由D一, 格条林闭公曲式线
的右所曲端围线应成积 包.添分 括加,沿且直区边线域界段D的的A方全B向,部CE对边.区界 G D
域则DD来的说边都界是曲正线向由. AB, L2 , BA,
2π 0
格林公式
sin d(
2
(Q P )dxdy D1 x y 0
cos ) cos d(
2
2
0 sin
)
24
10.3 格林公式及其应用
l
ydx xdy 4x2 y2
2π
sin
d(
2
cos
)
2
cos
d(
sin
)
0
2
2 0
π
2
2
sin
2
2
2
2
cos2
d
y L: x2 y2 4
4.1格林公式及其应用

1 U 0 ln r
(r 0),
2
通常称它为二维拉普拉斯方程的基本解。
现在我们介绍三维拉普拉斯方程
u xx u yy u zz 0
的球对称解。 作球坐标变换
x r sin cos ,
r
x2 y2 z2 ,
z x y z
2 2 2
y r sin sin , z r cos ,
其中
n
表示外法向导数。
u(v n)dS
8
(
P Q R )d x y z
( P cos(n, x) Q cos(n, y) R cos(n, z))dS, (3)
设函数 u u( x, y, z) 和 v v( x, y, z )以及它们的所有 一阶偏导数在 上是连续的, 且在 内具有 连续的所有二阶偏导数。 在公式(3)中, 令P u 则得格林第一公式:
(6)
(7)
(8)
1 u(M 0 ) 4
因为函数 v 在点 M 0 处变为无穷大, 故对区域 不能直接应用格林第二公式(6). 但是,如果在 区域 内挖去一个以 M 0 为心,充分小正数 为 半径的球 K M , 则在剩下的区域 K M 中函数 v 就是连续可微的了(如图4.1)。
(6)
(7)
(8)
1 u(M 0 ) 4
1 u ( M ) rMM n 0
0
1 u ( M ) dS. rMM n 0
证
在区域 K M 上对上述的调和函数 u 和
1 v 应用公式(6)得 r
(4’)
在式(4’)中,交换函数 u , v 的位置,得
(r 0),
2
通常称它为二维拉普拉斯方程的基本解。
现在我们介绍三维拉普拉斯方程
u xx u yy u zz 0
的球对称解。 作球坐标变换
x r sin cos ,
r
x2 y2 z2 ,
z x y z
2 2 2
y r sin sin , z r cos ,
其中
n
表示外法向导数。
u(v n)dS
8
(
P Q R )d x y z
( P cos(n, x) Q cos(n, y) R cos(n, z))dS, (3)
设函数 u u( x, y, z) 和 v v( x, y, z )以及它们的所有 一阶偏导数在 上是连续的, 且在 内具有 连续的所有二阶偏导数。 在公式(3)中, 令P u 则得格林第一公式:
(6)
(7)
(8)
1 u(M 0 ) 4
因为函数 v 在点 M 0 处变为无穷大, 故对区域 不能直接应用格林第二公式(6). 但是,如果在 区域 内挖去一个以 M 0 为心,充分小正数 为 半径的球 K M , 则在剩下的区域 K M 中函数 v 就是连续可微的了(如图4.1)。
(6)
(7)
(8)
1 u(M 0 ) 4
1 u ( M ) rMM n 0
0
1 u ( M ) dS. rMM n 0
证
在区域 K M 上对上述的调和函数 u 和
1 v 应用公式(6)得 r
(4’)
在式(4’)中,交换函数 u , v 的位置,得
高等数学Green公式的应用
D
∂Q ∂P )dxdy − ∂x ∂y
的边界正向曲线. 其中 L 为 D 的边界正向曲线.
前一页 后一页
返回
为简单区域, 证明 设 D 为简单区域,即垂直 x 轴(或 y 轴)的 的边界至多只有两个交点, 直线与 D 的边界至多只有两个交点,则 D 可用不 等式表示为: 等式表示为:ϕ1 ( x ) ≤ y ≤ ϕ 2 ( x ) (a ≤ x ≤ b) 或
ψ 1 ( y ) ≤ x ≤ ψ 2 ( y ) ( c ≤ y ≤ d ) 如图 7- 38 ,由二重积分 38,
的计算有
图 7-38
b ϕ 2 ( x ) ∂P b ∂P dxdy = ∫ dx ∫ dy = = ∫ { P[ x , ϕ 2 ( x )] − P[ x , ϕ1 ( x )]} dx ∫∫ ∂y a ϕ1 ( x ) ∂y a D
第 六节
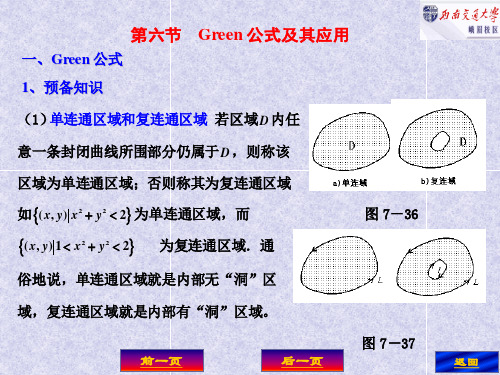
一、Gree n 公式 1、预备知识
Green 公式及其应用
(1 ) 单连通区域和复连通区域 若区域 D 内任 意一条封闭曲线所围部分仍属于 D ,则称该 区域为单连通区域;否则称其为复连通区域 区域为单连通区域; 为单连通区域, 如 {( x , y ) x 2 + y 2 < 2} 为单连通区域,而 图 7-36
2 、Green 公式 定理( 公式) 为光滑(或分段光滑) 定理(Green 公式) 设 D 为光滑(或分段光滑)闭曲线 L 所围平面的闭 : 区域, 上具有连续的一阶偏导, 区域,函数 P ( x , y ) , Q( x , y ) 在 D 上具有连续的一阶偏导,则
∫
L
Pdx + Qdy = ∫∫ (
注 (1 )
∂Q ∂P 上必须连续, , 在 D 上必须连续,这 ∂x ∂y
∂Q ∂P )dxdy − ∂x ∂y
的边界正向曲线. 其中 L 为 D 的边界正向曲线.
前一页 后一页
返回
为简单区域, 证明 设 D 为简单区域,即垂直 x 轴(或 y 轴)的 的边界至多只有两个交点, 直线与 D 的边界至多只有两个交点,则 D 可用不 等式表示为: 等式表示为:ϕ1 ( x ) ≤ y ≤ ϕ 2 ( x ) (a ≤ x ≤ b) 或
ψ 1 ( y ) ≤ x ≤ ψ 2 ( y ) ( c ≤ y ≤ d ) 如图 7- 38 ,由二重积分 38,
的计算有
图 7-38
b ϕ 2 ( x ) ∂P b ∂P dxdy = ∫ dx ∫ dy = = ∫ { P[ x , ϕ 2 ( x )] − P[ x , ϕ1 ( x )]} dx ∫∫ ∂y a ϕ1 ( x ) ∂y a D
第 六节
一、Gree n 公式 1、预备知识
Green 公式及其应用
(1 ) 单连通区域和复连通区域 若区域 D 内任 意一条封闭曲线所围部分仍属于 D ,则称该 区域为单连通区域;否则称其为复连通区域 区域为单连通区域; 为单连通区域, 如 {( x , y ) x 2 + y 2 < 2} 为单连通区域,而 图 7-36
2 、Green 公式 定理( 公式) 为光滑(或分段光滑) 定理(Green 公式) 设 D 为光滑(或分段光滑)闭曲线 L 所围平面的闭 : 区域, 上具有连续的一阶偏导, 区域,函数 P ( x , y ) , Q( x , y ) 在 D 上具有连续的一阶偏导,则
∫
L
Pdx + Qdy = ∫∫ (
注 (1 )
∂Q ∂P 上必须连续, , 在 D 上必须连续,这 ∂x ∂y
《格林公式及其应用》PPT课件

n (cos,cos).
v nds L
(P cos Q cos)ds
L
由格林公式
Pdy Qdx =========
(P Q )d .
L
D y x
(格林公式的另一种形式)
称函数
为平面向量场 v (P(x, y),Q(x, y))
的散度.物理意义:稳定流体通过某一闭曲线的流量,等
于其散度在该闭曲线所的区域上的二重积分之值.
(x y)dx (x y)dy
( L )
x2 y2
0dxdy 0.
D1
首页
上页
返回
下页
结束
铃
这里(L ) 表示多连通区域 D1的正向边界曲线 .这时L按 逆时针方向,而按顺时针方向.因而
(x y)dx (x y)dy
( L )
x2 y2
(x y)dx (x y)dy (x y)dx (x y)dy,
(x y)dx (x y)dy
L
x2 y2
1 r2
2 [r2 (cost sin t)(sin t) r2 (cost sin t)(cost)]dt
0
2
0 1dt 2.
例 4 设函数u(x,y)在有界闭区域D上有连续的二阶
偏导数,L 为D 的边界且逐段光滑.证明:
u
L
u n
ds
y
x
(x2 y)dx (x y2 sin3 y)dy, AO
oA
(x2 y)dx (x y2 sin3 y)dy
AO
0 x2dx 8 .
2
3
首页
上页
返回
下页
结束
铃
当曲线积分 (x2 y)dx (x y2 sin3 y)dy 与路径无 AB
格林公式及其应用-课件

OB
y
(1 )
o
y x2
x y2
B(1,1)
x
A(1,0)
进一步猜测:沿任意分 段光滑的曲线 LOB:
2xydx x2dy ?
LOB
(1 )
问题1
一、Green公式
是否所有二型线积分都 有这样的性质: 积分值只与曲线 L的起点和终点有关
而与曲线 L所走过的路径无关? ( 否 )
B(1,1)
I 1 2 y2 y 2 ydy 1 y4dy o
0
0
x
A(1,0)
5 1 y4dy 1 0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
L
LOAAB 来自12x 0dx
112 dy 1
0
0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
猜一猜:
2xydx x2dy ?
ydx
其中,L是D的正向边界曲线。
G.F .:P 0,Q x
证:xdy
L
Py 0,Qx 1
(1 0)d D
D
同理: ydx d D ydx
L
D
L
例1
4. Green公式举例
求椭圆
x2 a2
y
(1 )
o
y x2
x y2
B(1,1)
x
A(1,0)
进一步猜测:沿任意分 段光滑的曲线 LOB:
2xydx x2dy ?
LOB
(1 )
问题1
一、Green公式
是否所有二型线积分都 有这样的性质: 积分值只与曲线 L的起点和终点有关
而与曲线 L所走过的路径无关? ( 否 )
B(1,1)
I 1 2 y2 y 2 ydy 1 y4dy o
0
0
x
A(1,0)
5 1 y4dy 1 0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
L
LOAAB 来自12x 0dx
112 dy 1
0
0
1. 引例
一、Green公式
引 求I 2xydx x2dy,其中L分别为:1) y2 x;2) y x2;
例
L
1 3)OAB上由O(0,0) B(1,1)一段有向曲线 (如图)。
猜一猜:
2xydx x2dy ?
ydx
其中,L是D的正向边界曲线。
G.F .:P 0,Q x
证:xdy
L
Py 0,Qx 1
(1 0)d D
D
同理: ydx d D ydx
L
D
L
例1
4. Green公式举例
求椭圆
x2 a2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
▪
26、要使整个人生都过得舒适、愉快,这是不可能的,因为人类必须具备一种能应付逆境的态度。——卢梭
▪
27、只有把抱怨环境的心情,化为上进的力量,才是成功的保证。——罗曼·罗兰
▪
28、知之者不如好之者,好之者不如乐之者。——孔子
▪
29、勇猛、大胆和坚定的决心能够抵得上武器的精良。——达·芬奇
格林公式及其应用
11、用道德的示范来造就一个人,显然比用法律来约束他更有价值。—— 希腊
12、法律是无私的,对谁都一视同仁。在每件事上,她都不徇私情。—— 托马斯
13、公正的法律限制不了好的自由,因为好人不会去做法律不允许的事 情。——弗劳德
14、法律是为了保护无辜而制定的。——爱略特 15、像房子一样,法律和法律都是相互依存的。——伯克
பைடு நூலகம்
▪
30、意志是一个强壮的盲人,倚靠在明眼的跛子肩上。——叔本华
谢谢!
35
