(完整word版)数学简易逻辑-知识点归纳+题型
新高考数学题型归纳,第一章 集合与简易逻辑

第一章集合与简易逻辑第一节集合题型1、元素与集合的关系元素与集合的关系:属于和不属于。
常用数集的表示:C —复数集;R —实数集;Q —有理数集;Z —整数集;N —自然数集;N+或N*—正整数集。
1、【多选】下列关系中正确的是()A.{}102,∉-B.(){}2|42x y x =∈,C.R ∈πD.Φ∈02、【2022·全国乙卷】设集合{}54321,,,,=U ,集合M 满足{}31,=M C U ,则()A.M ∈2B.M ∈3C.M ∉4D.M∉53、【2018·北京】已知集合(){}241|≤-+≥-=ay x y ax y x y x A ,>,,,则()A .()A R a ∈∈∀12,,B .()AR a ∉∈∀12,,C .当且仅当0<a 时,()A ∉12,D .当且仅当23≤a 时,()A ∉12,4、若集合{}2024||≤∈=x N x x P ,45=a ,则()A.P a ∈B.{}P a ∈C.{}Pa ⊆D.Pa ∉题型2、集合相等集合元素的特征:确定性、互异性、无序性。
集合相等,集合中元素完全相同,集合中元素之和相等,集合中元素之积相等。
1、若},,0{},,1{2b a a ab a +=,求20242024b a+的值.【答案:1】2、已知集合,,且B A },,0{B },,,{A ==-=y x y x xy x 求实数x 与y 的值.【答案:x=y=-1】3、设R b a ∈,,集合b}ab {0a}b a {1,,,,=+,则=-a b ()【答案:C 】A.1B.-1C.2D.-24、【2014·福建】若}2,1,0{},,{=c b a ,且下列三个关系:①2≠a ;②2=b ;③0≠c 有且只有一个正确,求c b a ++10100的值.5、集合},2,0{a A =,},1{2a B =.若}16,4,210{,,=B A 则a 的值为()【答案:D 】A .0B .1C .2D .4题型3、集合之间的基本关系集合与集合之间的关系:①包含关系,②相等关系,③真子集关系。
高中数学教师备课必备系列(简易逻辑)专题五 四种命题及真假判断 Word版含解析

【基础回顾】
一.命题的概念
在数学中把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题.其中判断为真的语句叫真命题,判断为假的语句叫假命题.
二.四种命题及其关系
.四种命题
即:如果第一个命题的条件是第二个命题的结论,且第一个命题的结论是第二个命题的条件,那么这两个命题叫做互为逆命题;
如果一个命题的条件和结论分别是原命题的条件和结论的否定,那么这两个命题叫做互否命题,这个命题叫做原命题的否命题;
如果一个命题的条件和结论分别是原命题的结论和条件的否定,那么这两个命题叫做互为逆否命题,这个命题叫做原命题的逆否命题。
.四种命题间的逆否关系
.四种命题的真假关系
()两个命题互为逆否命题,它们有相同的真假性;
()两个命题为互逆命题或互否命题,它们的真假性没有关系.
【典型例题】
例.已知是两个命题,若“”是假命题,则()
.都是假命题.都是真命题
.是假命题,是真命题.是真命题,是假命题
【答案】
【解析】
例.给出下列命题:其中正确命题的序号是()
①已知,若,则,
②不存在实数,使
③是函数的一个对称轴中心
④已知函数.
.①②.②④.①③.④
【答案】
【解析】
试题分析:
④因为在锐角三角形中,,所以,;则有
,;又因为函数
在上为减函数,所以.故正确.
考点:向量的线性运算;三角函数的基本关系式;函数的图像和性质.
例.下列说法中正确的是()
()“”是“函数是奇函数”的充要条件。
高考复习课件数学简易逻辑

单击此处添加小标题
对于含有大前提的命题,在改写命 题形式时,大前提不要 动.
题型二 充要条件的判断
指出下列命题中,p是q的什么条件(在“充分不 必要条件”、“必要不充分条件”、“充要条件”、“既 不充分也不必要条件”中选出一种作答). (1)在△ABC中,p:∠A=∠B,q:sinA=sinB (2)对于实数x、y,p:x+y≠8,q:x≠2或y≠6; (3)非空集合A、B中,p:x∈A∪B,q:x∈B (4)已知x、y∈R,p:(x-1)2+(y-2)2=0
§1.2 简易逻辑
要点梳理
1.逻辑联结词 常用的逻辑联结词有 或、 、且 . 非
2.真值表
假. 假.
真. 真
.
真. 真. 真
.假 .
真. 假. 假 .假 .
3.四种命题及关系
用p和q分别表示 原命题的条件和结 论,用┒p和┒ q分 别表
示p和q的否定.
4.充要条件 pq
qp
pq qp
pq
qp
2.(2008·湖南理,2)“|x-1|<2成立”是“x(x-3)<0成立”
的
B
(
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
解析 ∵|x-1|<2
-1<x<3成立,
x(x-3)<0成立 0<x<3成立,
又-1<x<3 0<x<3,0<x<3 -1<x<3,
∴“|x-1|<2成立”是:“x(x-3)<0成立”的必要不充分
一个命题的真假(有时不一定只有一种情况),然后再求
出每个命题是真命题时参数的取值范围,最后根据每个命
数学逻辑知识点总结

数学逻辑知识点总结数学逻辑是数学的一个重要分支,它研究的是数学命题和论证的形式结构。
通过数学逻辑,我们可以建立数学的基础,推导定理,解决问题,拓展数学知识,并且可以应用到现实生活中,如计算机科学、哲学、语言学等方面。
本文将对数学逻辑的基本知识点进行总结,包括命题逻辑、谓词逻辑、集合论和函数论等。
一、命题逻辑1. 命题:在逻辑学中,命题是能够判断真假的陈述句,如“2+2=4”、“地球是圆的”等。
命题可以用P、Q、R等字母表示。
2. 连词和量词:在命题逻辑中,常用的连词包括合取(∧,表示且)、析取(∨,表示或)、蕴涵(→,表示如果……,那么……)和双条件(↔,表示当且仅当);常用的量词包括全称量词(∀,表示所有)和存在量词(∃,表示存在)。
3. 逻辑运算:命题逻辑中的逻辑运算是指对命题进行组合,例如通过合取和析取可以得到新的复合命题,通过蕴涵和双条件可以得到含有条件关系的复合命题。
4. 真值表:真值表是一种描述命题逻辑运算的方法,通过真值表可以对不同的命题组合情况进行分类和分析,从而确定命题的真假。
5. 推理规则:在命题逻辑中,有一些常用的推理规则,如假言推理、析取三段论、排中律和矛盾律等,通过这些规则可以根据已知的真假条件得出新的结论。
6. 归结原理:归结原理是命题逻辑的一个重要理论,在归结原理中,通过归结的方法可以判断一个命题是否可满足,从而进行逻辑推理。
二、谓词逻辑1. 谓词:在谓词逻辑中,谓词是一种对对象进行描述的函数,例如“x>y”、“P(x)”等。
谓词可以分为一元谓词、二元谓词等,分别表示一个对象的性质和两个对象之间的关系。
2. 量词和谓词演算:在谓词逻辑中,引入了量词和谓词演算的概念,量词包括全称量词和存在量词,而谓词演算则是一种形式化的逻辑推理方法,通过对谓词的操作和替换,可以得到新的谓词表达式。
3. 谓词逻辑的语义和语法:谓词逻辑是一种复杂的逻辑系统,它包括语义和语法两个方面,通过语义可以理解谓词的含义和推理规则,通过语法可以对谓词进行形式化的描述和分析。
集合与简易逻辑知识点总结- 高三数学一轮复习

知识点总结1 集合与简易逻辑一、集合(一)元素与集合1.集合的含义某些指定对象的部分或全体构成一个集合.构成集合的元素除了常见的数、点等数学对象外,还可以是其他对象.2.集合元素的特征(1)确定性:集合中的元素必须是确定的,任何一个对象都能明确判断出它是否为该集合中的元素.(2)互异性:集合中任何两个元素都是互不相同的,即相同元素在同一个集合中不能重复出现.(3)无序性:集合与其组成元素的顺序无关.3.元素与集合的关系元素与集合之间的关系包括属于(记作a A ∈)和不属于(记作a A ∉)两种.4.集合的常用表示法集合的常用表示法有列举法、描述法、图示法(韦恩图).5.常用数集的表示 数集 自然数集 正整数集 整数集 有理数集 实数集符号 NN ∗或N + Z Q R (二)集合间的基本关系1.集合A 为集合B 的子集 ,记作A B ⊆(或B A ⊇),读作“A 包含于B ”(或“B 包含A ”).(2)真子集:若A B ⊆,且存在b B ∈,但b A ∉,则集合A 是集合B 的真子集,记作AB (或B A ⊃≠). 读作“A 真包含于B ”或“B 真包含A ”.(3)相等:对于两个集合A 与B ,如果A B ⊆,同时B A ⊆,那么集合A 与B 相等,记作A =B .(4)空集:把不含任何元素的集合叫做空集,记作∅;(三)集合的基本运算(1)交集:由所有属于集合A 且属于集合B 的元素组成的集合,叫做A 与B 的交集,记作A B ⋂, 即{}|A B x x A x B ⋂=∈∈且.(2) 并集:由所有属于集合A 或属于集合B 的元素组成的集合,叫做A 与B 的并集,记作A B ⋃,(3) 即{}|A B x x A x B ⋃=∈∈或.(3)补集:对于一个集合A ,由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集,简称为集合A 的补集,记作U C A ,即{|,}U C A x x U x A =∈∉且.(四)集合的运算性质(1)集合的运算性质:①交换律:A ∪B =B ∪A ;A ∩B =B ∩A ;②结合律:(A ∪B )∪C =A ∪(B ∪C );(A ∩B )∩C =A ∩(B ∩C );③分配律:(A ∩B )∪C =(A ∪C )∩(B ∪C );(A ∪B )∩C =(A ∩C )∪(B ∩C );【集合常用结论】1.子集个数:含有n个元素的有限集合M,其子集个数为2n;其真子集个数为2n-1;其非空子集个数为2n-1;其非空真子集个数为2n-2.2. 是任何集合的子集,是任何非空集合的真子集.3.∁U(A∪B)=(∁U A)∩(∁U B);∁U(A∩B)=(∁U A)∪(∁U B);4.A∪B=A⇔B⊆A;A∩B=B⇔B⊆A.5.集合运算中的常用方法若已知的集合是不等式的解集,用数轴求解;若已知的集合是点集,用数形结合法求解;若已知的集合是抽象集合,用Venn图求解.二、简易逻辑(一).全称命题、特称(存在性)命题及其否定(1)全称命题p:∀x∈M,p(x),其否定为特称(存在性)命题:¬p:∃x0∈M,¬p(x0).(2)特称(存在性)命题p:∃x0∈M,p(x0),其否定为全称命题:¬p:∀x∈M,¬p(x).(二).充分条件与必要条件的判定方法(1)定义法:若p⇒q,则p是q的充分条件(或q是p的必要条件);若p⇒q,且q⇏p,则p是q的充分不必要条件(或q是p的必要不充分条件).(2)集合法:利用集合间的包含关系。
(完整word版)数学简易逻辑-知识点归纳+题型

原命题若p 则q 否命题若┐p 则┐q逆命题若q 则p逆否命题若┐q 则┐p互为逆否互逆否互为逆否互互逆否互文科数学选修1—1 第一章 简易逻辑 一.四种命题及关系1。
命题:__________的语句;2。
分类:①简单命题:不含有逻辑联结词的命题;②复合命题:由_________和逻辑联结词“___”、“___"、“____”构成的命题;构成复合命题的形式:p 或q 记作______;p 且q 记作____;非p 记作_____。
3。
命题的四种形式与相互关系 原命题:若p 则q ; 逆命题:________; 否命题:________; 逆否命题:________.注:①互为_____关系的两个命题同真假.②命题中一些关键词的否定:1、下列说法:①若一个命题的否命题是真命题,则这个命题不一定是真命题;②若一个命题的逆否命题是真命题,则这个命题是真命题;③若一个命题的逆命题是真命题,则这个命题不一定是真命题;④若一个命题的逆命题和否命题都是真命题,则这个命题一定是真命题;其中正确的说法是 ( )A 。
①②B 。
①③④C 。
②③④D 。
①②③2、已知m ,n 是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( ) A 、若α,β垂直于同一个平面,则α//β B 、若m,n 平行于同一个平面,则m//nC 、若α,β不平行,则α内不存在与β平行的直线D 、若m,n 不平行,则m 与n 不可能垂直于同一个平面3.原命题:“设a ,b ,c ∈R ,若a 〉b ,则ac 2〉bc 2",在原命题以及它的逆命题、否命题、逆否命题中,真命题的个数为( )4.有四个命题:①“若0x y +=,则x 、y 互为相反数"的逆命题; ②“全等三角形的面积相等”的否命题;③“若1q ≤,则关于x 的方程220x x q ++=有实根"的逆命题;④“A B B =,则A B ⊇”的逆否命题。
(完整word版)高中数学选修11《常用逻辑用语》知识点讲义
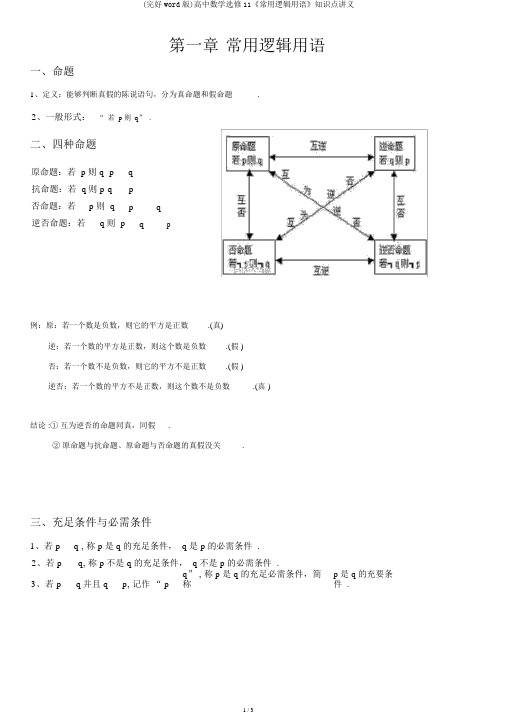
第一章常用逻辑用语一、命题1、定义:能够判断真假的陈说语句,分为真命题和假命题.2、一般形式:“ 若p则q” .二、四种命题原命题:若 p则 q p q抗命题:若 q则 p q p否命题:若p则 q p q逆否命题:若q则 p q p例:原:若一个数是负数,则它的平方是正数.(真)逆:若一个数的平方是正数,则这个数是负数.(假 )否:若一个数不是负数,则它的平方不是正数.(假 )逆否:若一个数的平方不是正数,则这个数不是负数.(真 )结论 :①互为逆否的命题同真,同假.②原命题与抗命题、原命题与否命题的真假没关.三、充足条件与必需条件1、若 p q , 称 p是 q的充足条件, q是 p的必需条件 .2、若 p q, 称 p不是 q的充足条件, q不是 p的必需条件 .3、若 p q并且 q p, 记作“ p q” , 称 p是q的充足必需条件,简称p是 q的充要条件 .注:能够借助会合关系来判断:p q p是 q的充足条件 .p q p是 q的充足不用要条件 .例:“ 福州人” “ 福建人” 会合“ 福州人”“ 福建人” 命题“福州人”是“福建人”的充足条件 .“福建人”是“福州人”的必需条件 .四、复合命题真假的表格.1、2、3、五、全称量词、存在量词1、全称命题 p :x M , P x2、特称命题 p : x0M , P x0它的否认 p :x M , P x0它的否认 p : x M , P x例:“ 四边形都有外接圆”P :四边形ABCD ,都有A、B、C、D共圆.全称命题P : 四边形 A1 B1C1D1此中A1 + C1 =200,此中 A、 B、 C、D不共圆 . 特称命题“存在 x0R,使 x02 +2x020 "P : x0R,使 x02 +2x020P : x R, x2 +2x 20。
高中数学《集合与简易逻辑》知识点
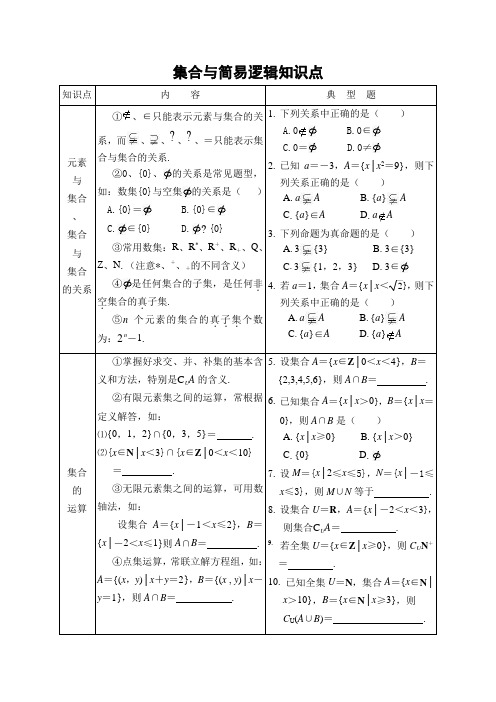
集合与简易逻辑知识点知识点内容典型题元素与集合、集合与集合的关系①、∈只能表示元素与集合的关系,而、、?、?、=只能表示集合与集合的关系.②0、{0}、的关系是常见题型,如:数集{0}与空集的关系是()A.{0}=B.{0}∈C.∈{0}D.?{0}③常用数集:R、R*、R+、R+、Q、Z、N.(注意*、+、+的不同含义)④是任何集合的子集,是任何非.空.集合的真.子集.⑤n个元素的集合的真子..集.个数为:2n-1.1.下列关系中正确的是()A.0B.0∈C.0=D.0≠2.已知a=-3,A={x│x2=9},则下列关系正确的是()A.a AB.{a}AC.{a}∈AD.a A3.下列命题为真命题的是()A.3{3}B. 3∈{3}C.3{1,2,3}D. 3∈4.若a=1,集合A={x│x<2},则下列关系中正确的是()A.a AB.{a}AC.{a}∈AD.{a}A集合的运算①掌握好求交、并、补集的基本含义和方法,特别是C U A的含义.②有限元素集之间的运算,常根据定义解答,如:⑴{0,1,2}∩{0,3,5}=.⑵{x∈N│x<3}∩{x∈Z│0<x<10}=.③无限元素集之间的运算,可用数轴法,如:设集合A={x│-1<x≤2},B={x│-2<x≤1}则A∩B=.④点集运算,常联立解方程组,如:A={(x,y)│x+y=2},B={(x , y)│x-y=1},则A∩B=.5.设集合A={x∈Z│0<x<4},B={2,3,4,5,6},则A∩B=.6.已知集合A={x│x>0},B={x│x=0},则A∩B是()A.{x│x≥0}B.{x│x>0}C.{0}D.7.设M={x│2≤x≤5},N={x│-1≤x≤3},则M∪N等于 .8.设集合U=R,A={x│-2<x<3},则集合C U A=.9.若全集U={x∈Z│x≥0},则C U N+=.10.已知全集U=N,集合A={x∈N│x>10},B={x∈N│x≥3},则C U(A∪B)=.知识点内容典型题逻辑连结词且或p q p∧q1 1 11 0 00 1 00 0 0p q p∨q1 1 11 0 10 1 10 0 011.设命题p:2>3,q:-5是有理数,则命题p∧q的真假是.12.命题p:李明是三好学生,命题q:李明不是优秀班干部,则命题p∧q为 .逻辑连结词非蕴含p p1 00 1p q p→q1 1 11 0 00 1 10 0 113.设命题p:甲乙二人至少有一个击中目标,则p:.14.设命题p:一个实数x,使x2-3=0,则p:.15.命题P :一个实数x,使得2x2-2x+1≤0,则P:.两个结论(p∧q)=p∨q(p∨q)=p∧q16.设命题p:他在学校,q:他在家,则(p∨q):.充分必要条件与充要条件对命题p、q有:p→q(真),则称p是q的充分条件,q是p的必要条件.若p?q(真),且q?p(真),则说p是q的充分且必要条件,简称“充要条件”,记作“p q”.p是q的充要条件,又常说q当且仅当p,或p与q等价. 例如:⑴│x│>a的充要条件是.⑵“ab>0”是“a>0且b>0”的条件.17.x=y是x2=xy的()A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件18.命题p:ab=0,命题q:a=0或b=0,则p是q的()A.充分条件B.必要条件C.充要条件D.既不充分又不必要条件19.x=y是x2=xy的条件.20.x>0是x2>0的条件.简易逻辑常见符号存在()、任意()、使得()、非()、且(∧)、或(∨)、若…则…(→)、推出(?)、等价()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
原命题若p 则q 否命题若┐p 则┐q
逆命题若q 则p
逆否命题若┐q 则┐p
互为逆否互逆否互为逆否
互
互逆
否
互文科数学选修1-1 第一章 简易逻辑 一.四种命题及关系
1.命题:__________的语句;
2.分类:①简单命题:不含有逻辑联结词的命题;
②复合命题:由_________和逻辑联结词“___”、“___”、“____”构成的命题;
构成复合命题的形式:p 或q 记作______;p 且q 记作____;非p 记作_____.
3.命题的四种形式与相互关系 原命题:若p 则q ; 逆命题:________; 否命题:________; 逆否命题:________.
注:
①互为_____关系的两个命题同真假.
②命题中一些关键词的否定:
1、下列说法:①若一个命题的否命题是真命题,则这个命题不一定是真命题;②若一个命
题的逆否命题是真命题,则这个命题是真命题;③若一个命题的逆命题是真命题,则这个命题不一定是真命题;④若一个命题的逆命题和否命题都是真命题,则这个命题一定是真命题;其中正确的说法是 ( ) A.①② B.①③④ C.②③④ D.①②③
2、已知m,n 是两条不同的直线,α,β是两个不同的平面,则下列命题正确的是( ) A 、若α,β垂直于同一个平面,则α//β B 、若m,n 平行于同一个平面,则m//n
C 、若α,β不平行,则α内不存在与β平行的直线
D 、若m,n 不平行,则m 与n 不可能垂直于同一个平面
3.原命题:“设a ,b ,c ∈R ,若a >b ,则ac 2>bc 2
”,在原命题以及它的逆命题、否命题、逆否命题中,真命题的个数为( )
4.有四个命题:①“若0x y +=,则x 、y 互为相反数”的逆命题; ②“全等三角形的面积相等”的否命题;
③“若1q ≤,则关于x 的方程220x x q ++=有实根”的逆命题;
④“A B B =U ,则A B ⊇”的逆否命题.
其中真命题是____________________.
5、写出“平行四边形的对边平行且相等”的逆命题、否命题、逆否命题,并判断真假。
二.充分条件和必要条件
1.命题“若p 则q ”为真,记作“_____”;“若p 则q ”为假,记作“______”
2.条件与结论的关系:①若p ⇒q ,且p ⇐q ,即p q ⇔则p 是q 的________条件; ②若p ⇒q ,且p q ,则p 是q 的__________条件;
③若p q ,且p ⇐q ,则p 是q 的___________条件;
④若p
q ,且p
q ,则p 是q 的___________条件.
注:①解题时要注意条件p 和结论q 分别是什么.
②解题时可先求出范围,小范围_______大范围,但大范围________小范围 练习:
1、(潮州市2015届期末)在C ∆AB 中,“C 0AB⋅A >u u u r u u u r
”是“C ∆AB 为锐角三角形”的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
2、(湛江市2015届高三二模)“11c -<<”是“直线0x y c ++=与圆2
2
1x y +=相交”的( )
A .充分不必要条件
B .必要不充分条件
C .充分必要条件
D .既不充分也不必要条件
3、(佛山市2015届高三上期末)已知()2
f x x x =-,且a ,b ∈R ,则“1a b >>”是
“()()f a f b <”的( )
A. 充分不必要条件
B. 必要不充分条件
C. 充分必要条件
D. 既不充分也不必要条件 4.2x 2-5x -3<0的一个必要不充分条件是 ( )
A .-
2
1
<x <3 B .-
21<x <0 C .-3<x <2
1 D .-1<x <6
5.已知p:2
2
430x ax a -+<,其中0a >,q:|x-3|<1, 若q 是p 的充分不必要条件,求实数a 的取值范围。
三.逻辑联结词
1.“或”、“且”、“非”称为逻辑联结词,
2.“非p ”指的是命题的否定形式,它与否命题的区别:
命题的否定是对___________,它与原命题的真假性______. 否命题是要对________________. 3、“p 或q ”、“p 且q ”、“非p ”形式的复合命题的真假性的判断 ①“非p ”形式复合命题的真假与p 的真假相反(真假相反);
②“p 且q ”形式复合命题当p 与q 同为真时为真,其他情况时为假(一假___假); ③“p 或q ”形式复合命题当p 与q 同为假时为假,其他情况时为真(一真___真).
注:“p 或q ”,“p 且q ”,“非p ”命题中的“p ”、“q ”是两个命题.而原命题,
逆命题,否命题,逆否命题中的“p ”,“q ”是一个命题的条件和结论两个部分. 练习:
1、已知命题p :对任意x ∈R ,总有20x
>;q :“1x >”是“2x >”的充分不必要条件.
则下列命题为真命题的是 ( ) A .p q ∧ B .p q ⌝∧⌝ C .p q ⌝∧ D .p q ∧⌝
2、(2013年全国I 卷)已知命题p :∀x ∈R ,2x
<3x
;命题q :∃x ∈R ,x 3
=1-x 2
,则下列命题中为真命题的是( )
A .p ∧q
B .⌝p∧q
C .p ∧⌝q
D .⌝p∧⌝q 3、(华南师大附中2015届高三三模)已知命题ααπαcos )cos(,:=-∈∃R p ;命题
01,:2>+∈∀x R x q .则下面结论正确的是( )
A .¬q 是真命题
B .p 是假命题
C .p ∧q 是假命题
D .p ∨q 是真命题 4、已知0c >且1c ≠,设p :指数函数(21)x y c =-在实数集R 上为减函数,
q :不等式2(2)1x x c +->的解集为R .若命题p q ∨是真命题, p q ∧是假命题,求c 取值范围.
四.全称量词与存在量词
1.全称量词:__________________________________等;
全称命题p :)(,∈∀x p M x 否定为p ¬: ______________ 2.存在量词:__________________________________等;
存在性命题p :)(,∈∃x p M x 否定为p ¬: ______________
练习:1、“2
000,220x R x x ∃∈++≤” 的否定是________________________________
2、“1,12x x ∀>+>” 的否定是________________________________
3、“所有正方形都是矩形”的否定是_______________________________ 4.若“∀x ∈R ,x 2
-2x -m>0”是真命题,则实数m 的取值范围是____________ 【综合练习】
1、若函数()()(2)f x x a bx a =++,(,)a b R ∈,则“0a =”是“()f x 为偶函数”的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既充分也不必要条件
2、(汕头市2015届高三上期末)下列说法中,正确的是( ) A .命题“若22
am bm <,则a b <”的逆命题是真命题
B .命题“R x ∃∈,2
0x x ->”的否定是“R x ∀∈,2
0x x -≤” C .命题“p 或q ”为真命题,则命题“p ”和命题“q ”均为真命题 D .已知R x ∈,则“1x >”是“2x >”的充分不必要条件
3、(深圳市2015届高三二模)命题0:0p x ∃>,
00
1
2x x +=,则p ⌝为____________________ 4、下列叙述中正确的是( )
A .若a b c R ∈,
,,则“20ax bx c ++≥“的充分条件是”240b ac -≤” B .若a b c R ∈,
,,则“22ab cb >“的充要条件是”a c >” C .命题“对任意x ∈R ,有20x ≥”的否定是“存在x ∈R ,有2
0x ≥”
D .l 是一条直线,αβ,是两个不同的平面,若,l l αβ⊥⊥,则α∥β 5. 已知命题)0(012:;23
1
1:22>≤-+-≤--
m m x x q x p ; 若p ⌝是q ⌝的充分非必要条件,试求实数m 的取值范围.。
