北京市各区2012届高三上学期期中、期末考试分类解析(15)：算法初步

合集下载

北京市9区2012届高三上学期期末考试试题--数学_-_方法AnllPU

丰台区2011—2012学年度第一学期期末练习 2012.1高三数学（理科）第一部分（选择题共40分）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项． 1．设集合A={x ∣x<4}，B={x ∣x2<4}，则(A) A ⊆B(B) B ⊆A(C) A ⊆R Bð(D) B ⊆R Að2．在复平面内，复数2i1+i 对应的点位于(A) 第一象限(B) 第二象限(C) 第三象限(D) 第四象限3．已知命题p ：x R ∃∈，2lg x x ->，命题q ：x R ∀∈，20x >，则(A) 命题p q ∨是假命题 (B) 命题p q ∧是真命题 (C) 命题()p q ∨⌝是假命题(D) 命题()p q ∧⌝是真命题4．若某空间几何体的三视图如右图所示，则该几何体的体积是(A) 23 (B) 43(C) 2 (D)65．预测人口的变化趋势有多种方法，“直接推算法”使用的公式是0(1)(1)nn P P k k =+>-，其中Pn 为预测人口数，P0为初期人口数，k 为预测年内增长率，n 为预测期间隔年数．如果在某一时期有-1<k<0，那么这期间人口数(A) 呈上升趋势 (B) 呈下降趋势 (C) 摆动变化 (D) 不变 6．执行如右图所示的程序框图，输出的S 值为(A) 252(41)3-(B) 262(41)3-(C) 5021-(D) 5121-7．若函数21()log ()f x x a x =+-在区间1(,2)2内有零点，则实数a 的取值范围是(A) 25(log ,1]2--(B)25(1,log )2侧视图正视图(C) 25(0,log )2 (D)25[1,log )28．如图，P 是正方体ABCD —A1B1C1D1对角线AC1上一动点，设AP 的长度为x ，若△PBD 的面积为f(x)，则f(x)的图象大致是(A)(B)(C)(D)第二部分（非选择题共110分）二、填空题共6小题，每小题5分，共30分．9．设Sn 是等差数列{an}的前n 项和，若S5= a8+5，S6= a7+ a9-5，则公差d 等于． 10．若过点A(-2,m)，B(m,4)的直线与直线2x+y+2=0平行，则m 的值为． 11．曲线y=3-3x2与x 轴所围成的封闭图形的面积为．12．已知平面向量(4,3)a =r ，2(2,2)a b -=-r r ，则a r 与b r 的夹角余弦值等于．13．在面积为S 的矩形ABCD 内随机取一点P ，则△PBC 的面积小于4S的概率是．14．函数()f x 的导函数为()f x '，若对于定义域内任意1x ，2x 12()x x ≠，有121212()()()2f x f x x xf x x -+'=-恒成立，则称()f x 为恒均变函数．给出下列函数：①()=23f x x +；②2()23f x x x =-+；③1()=f x x ；④()=xf x e ；⑤()=ln f x x ．其中为恒均变函数的序号是．（写出所有满足条件的函数的序号）1A三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数2()2cos 2xf x x =．（Ⅰ）求函数()f x 的最小正周期和值域；（Ⅱ）若α为第二象限角，且1()33f πα-=，求cos 21cos 2sin 2ααα+-的值．16.（本小题共14分）如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC ，AC=BC=2，AB =CC1=4，M 是棱CC1上一点．（Ⅰ）求证：BC ⊥AM ；（Ⅱ）若M ，N 分别是CC1，AB 的中点，求证：CN //平面AB1M ；（Ⅲ）若132C M =，求二面角A-MB1-C 的大小．17.（本小题共13分）某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在地区附近有A ，B ，C 三家社区医院，并且他们的选择是相互独立的．（Ⅰ）求甲、乙两人都选择A 社区医院的概率；（Ⅱ）求甲、乙两人不选择同一家社区医院的概率；（Ⅲ）设4名参加保险人员中选择A 社区医院的人数为ξ，求ξ的分布列和数学期望．A B CA 1B 1C 1MN18.（本小题共13分）在平面直角坐标系xOy 中，O 为坐标原点，动点P 与两个定点(1,0)M ，(4,0)N 的距离之比为12．（Ⅰ）求动点P 的轨迹W 的方程；（Ⅱ）若直线l ：3y kx =+与曲线W 交于A ，B 两点，在曲线W 上是否存在一点Q ，使得OQ OA OB =+u u u r u u u r u u u r，若存在，求出此时直线l 的斜率；若不存在，说明理由．19.（本小题共14分）设函数x bx a x x f +-=ln )(在1=x 处取得极值．（Ⅰ）求a 与b 满足的关系式；（Ⅱ）若1>a ，求函数)(x f 的单调区间；（Ⅲ）若3>a ，函数3)(22+=x a x g ，若存在1m ，21[,2]2m ∈，使得12()()9f m g m -<成立，求a 的取值范围．20.（本小题共13分）若有穷数列{an}满足：（1）首项a1=1，末项am=k ，（2）an+1= an+1或an+1=2an ，(n=1，2，…，m-1)，则称数列{an}为k 的m 阶数列．（Ⅰ）请写出一个10的6阶数列；（Ⅱ）设数列{bn}是各项为自然数的递增数列，若312222+2(l b b b b k l N =+++∈L ，且2)l ≥，求 m 的最小值．（考生务必将答案答在答题卡上，在试卷上作答无效）丰台区2011—2012学年度第一学期期末练习2012.01 高三数学（理科）答案及评分参考9．510．8- 11．412．2425 13．12 14． ①②（只写出一个给2分）三、解答题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程． 15.（本小题共13分）已知函数2()2cos 2xf x x =．（Ⅰ）求函数()f x 的最小正周期和值域；（Ⅱ）若α为第二象限角，且1()33f πα-=，求cos 21cos 2sin 2ααα+-的值．解：（Ⅰ）因为 ()1cos f x x x =+ ……………………1分12cos()3x π=++， ……………………2分所以函数()f x 的周期为2π，值域为[1,3]-． ……………………4分（Ⅱ）因为1()33f πα-=，所以112cos =3α+，即1cos 3α=-． ……………………5分因为 222cos 2cos sin 1cos 2sin 22cos 2sin cos αααααααα-=+-- ……………………8分 (cos sin )(cos sin )2cos (cos sin )ααααααα+-=-cos sin 2cos ααα+=， ……………………10分又因为α为第二象限角，所以sin 3α=． ……………………11分所以原式1cos sin 13322cos 23ααα-++-===-． ……………………13分16.（本小题共14分）如图，在三棱柱ABC-A1B1C1中，CC1⊥底面ABC ，AC=BC=2，AB =CC1=4，M 是棱CC1上一点．（Ⅰ）求证：BC ⊥AM ；（Ⅱ）若M ，N 分别是CC1，AB 的中点，求证：CN //平面AB1M ；（Ⅲ）若132C M =，求二面角A-MB1-C 的大小．证明：（Ⅰ）因为三棱柱ABC-A1B1C1中CC1⊥平面ABC ，所以CC1⊥BC ． ……………………1分因为AC=BC=2，AB =，所以由勾股定理的逆定理知BC ⊥AC ． ……………………2分因为AC ∩CC1=C ，所以BC ⊥平面ACC1A1． ……………………3分因为AM ⊂平面ACC1A1，所以BC ⊥AM ． ……………………4分（Ⅱ）连结A1B 交AB1于P ． ……………………5分因为三棱柱ABC-A1B1C1，所以P 是A1B 的中点．因为M ，N 分别是CC1，AB 的中点，所以NP // CM ，且NP = CM ，所以四边形MCNP 是平行四边形， ……………………6分所以CN//MP ． ……………………7分因为CN ⊄平面AB1M ，MP ⊂平面AB1M ， ………………8分所以CN //平面AB1M ． ……………………9分（Ⅲ）因为BC ⊥AC ，且CC1⊥平面ABC ，以C 为原点，CA ，CB ，CC1分别为x 轴，y 轴，z 轴建立空间直角坐标系C-xyz ．PN MC 1B 1A 1CBAABCA 1B 1C 1MN因为132C M =，所以C(0,0,0)，A(2,0,0)，B1(0,2,4)，5(0,0,)2M ，5(2,0,)2AM =-u u u r，13(0,2,)2B M =--u u u u r． ……………………10分设平面1AMB 的法向量(,,)n x y z =r ，则0n AM ⋅=r u u u u r，10n B M ⋅=r u u u u r ．即5(2,0,)(,,)=023(0,2,)(,,)=0.2x y z x y z ⎧-⋅⎪⎪⎨⎪--⋅⎪⎩， ……………………11分令5x =，则3,4y z =-=，即(5,3,4)n =-r．又平面MB1C 的一个法向量是=(2,0,0)CA u u u r，所以cos ,>=2||||n CA n CA n CA ⋅<=r u u u rr u u u r r u uu r ． ………………12分由图可知二面角A-MB1-C 为锐角，所以二面角A-MB1-C 的大小为4π． ……………………14分17.（本小题共13分）某市医疗保险实行定点医疗制度，按照“就近就医、方便管理”的原则，参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构．若甲、乙、丙、丁4名参加保险人员所在的地区附近有A ，B ，C 三家社区医院，并且他们对社区医院的选择是相互独立的．（Ⅰ）求甲、乙两人都选择A 社区医院的概率；（Ⅱ）求甲、乙两人不选择同一家社区医院的概率；（Ⅲ）设4名参加保险人员中选择A 社区医院的人数为ξ，求ξ的分布列和数学期望．解：（Ⅰ）设“甲、乙两人都选择A 社区医院”为事件A ，那么 ……………………1分111()339P A =⨯=． ……………………3分所以甲、乙两人都选择A 社区医院的概率为19． ……………………4分（Ⅱ）设“甲、乙两人选择同一个社区医院”为事件B ，那么 ……………………5分111()3333P B =⨯⨯=， ……………………7分zM所以甲、乙两人不选择同一个社区医院的概率是2()1()3P B P B =-=． ……………………8分（Ⅲ）（方法一）随机变量ξ可能取的值为0，1，2，3，4．那么 ……………………9分044216(0)()381P C ξ==⨯=； 1341232(1)()3381P C ξ==⨯⨯=； 22241224(2)()()3381P C ξ==⨯⨯=； 334128(3)()()3381P C ξ==⨯⨯=； 44411(4)()381P C ξ==⨯=．（错三个没分）所以ξ的分布列为……………………12分1632248140123481818181813E ξ=⨯+⨯+⨯+⨯+⨯=． ……………………13分（方法二）依题意1(4,)3B ξ:, ……………………10分所以ξ的分布列为4444122()()()3381k k k k kP k C C ξ--==⨯⨯=⨯，0,1,2,3,4k =．即……………………12分所以14433E ξ=⨯=． ……………………13分 18.（本小题共13分）在平面直角坐标系xOy 中，O 为坐标原点，动点P 与两个定点(1,0)M ，(4,0)N 的距离之比为12．（Ⅰ）求动点P 的轨迹W 的方程；（Ⅱ）若直线l ：3y kx =+与曲线W 交于A ，B 两点，在曲线W 上是否存在一点Q ，使得OQ OA OB =+u u u r u u u r u u u r，若存在，求出此时直线l 的斜率；若不存在，说明理由．解：（Ⅰ）设点P 的坐标为(,)P x y ，依题意，||1||2PM PN =， ……………………1分即= ……………………3分化简得224x y +=．所以动点P 的轨迹W 的方程为224x y +=． ……………………5分（Ⅱ）因为直线l ：3y kx =+与曲线W 相交于A ，B 两点，所以2O l d -=<，所以k >或k <． ……………………7分假设存在点Q ，使得OQ OA OB =+u u u r u u u r u u u r． ……………………8分因为A ，B 在圆上，且OQ OA OB =+u u u r u u u r u u u r，由向量加法的平行四边形法则可知四边形OAQB 为菱形，所以OQ 与AB 互相垂直且平分， ……………………9分所以原点O 到直线l ：3y kx =+的距离为1||12d OQ ==． ……………………10分即1O l d -==，解得28k =，k =±，经验证满足条件． ……………………12分所以存在点Q ，使得OQ OA OB =+u u u r u u u r u u u r． ……………………13分19.（本小题共14分）已知函数x bx a x x f +-=ln )(在1=x 处取得极值．（Ⅰ）求a 与b 满足的关系式；（Ⅱ）若1>a ，求函数)(x f 的单调区间；（Ⅲ）若3>a ，函数3)(22+=x a x g ，若存在1m ，21[,2]2m ∈，使得12()()9f m g m -<成立，求a 的取值范围．解：（Ⅰ）2()1a bf x x x '=--， ……………………2分由(1)0f '= 得 a b -=1． ……………………3分（Ⅱ）函数)(x f 的定义域为),0(+∞， ……………………4分由（Ⅰ）可得22221(1)(1)[(1)]()1a a x ax a x x a f x x x x x -------'=--==．令()0f x '=，则11=x ，12-=a x ． ……………………6分因为1=x 是)(x f 的极值点，所以21x x ≠，即2≠a ． ……………………7分所以当2>a 时，11>-a ，所以单调递增区间为)1,0(，),1(+∞-a ，单调递减区间为)1,1(-a ． ……………………8分当21<<a 时，110<-<a ，所以单调递增区间为)1,0(-a ，),1(+∞，单调递减区间为)1,1(-a ． ……………………9分（Ⅲ）当3>a 时，)(x f 在1[,1)2上为增函数，在(1,2]为减函数，所以)(x f 的最大值为02)1(<-=a f ． ……………………10分因为函数)(x g 在1[,2]2上是单调递增函数，所以)(x g 的最小值为0341)21(2>+=a g ． ……………………11分所以)()(x f x g >在1[,2]2上恒成立． ……………………12分要使存在1m ，21[,2]2m ∈，使得12()()9f m g m -<成立，只需要9)1()21(<-f g ，即9)2(3412<--+a a ，所以48<<-a ． …………………13分又因为3>a ，所以a 的取值范围是(3,4)a ∈． ……………………14分20.（本小题共13分）若有穷数列{an}满足：（1）首项a1=1，末项am=k ，（2）an+1= an+1或an+1=2an ，(n=1，2，…，m-1)，则称数列{an}为k 的m 阶数列．（Ⅰ）请写出一个10的6阶数列；（Ⅱ）设数列{bn}是各项为自然数的递增数列，若312222+2(l b b b b k l N =+++∈L ，且2)l ≥，求m 的最小值．解：（Ⅰ）1，2，3，4，5，10或1，2，4，8，9，10． ……………………2分（Ⅱ）由已知在数列{an}中 an+1= an+1或an+1=2an ，当m a 为偶数时，1(2)2m m m a a a -=≥，或11m m a a -=-．因为12m m a a -≤ (2)m a ≥，所以在数列{an}中 12mi a a ≤≤中i 的个数不多于11j m a a -≤≤中j 的个数，要使项数m 最小，只需 1(2)2m m m a a a -=≥． ……………………5分当am 为奇数时，必然有 11(2)m m m a a a -=-≥，1m a -是偶数，可继续重复上面的操作．所以要使项数m 最小，只需遇到偶数除以2，遇到奇数则减1．因为312222+2l b b b b m a k ==+++L ，且1230l b b b b <<<<L ≤，只需除以1b 次2，得到31121122+2l b b b b b b ---+++L 为奇数；减1，得到3112122+2l b b b b b b ---++L 为偶数，再除以21b b -次2，得到322122l b b b b --+++L ；再减1，得到32222l b b b b --++L 为偶数， …………，最后得到12l l b b --为偶数，除以1l l b b --次2，得到1，即为1a ．所以121321()()+()(1)1l l m b b b b b b b l -=+-+-+-+-+L =l b l +． ……………………13分（若用其他方法解题，请酌情给分）。

北京市各区2012届高三上学期期中、期末考试分类解析(15)：算法初步

十五、算法初步
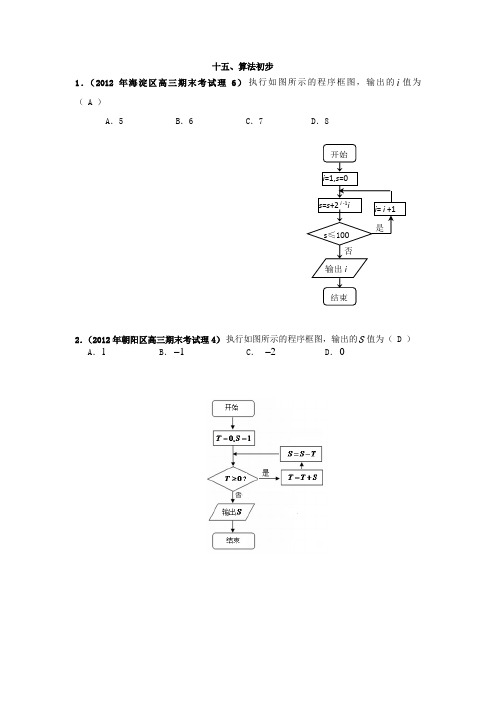
1．（2012年海淀区高三期末考试理6）执行如图所示的程序框图，输出的i 值为（ A ）
A ．5
B ．6
C ．7
D ．8
2．（2012年朝阳区高三期末考试理4）执行如图所示的程序框图，输出的S 值为（ D ） A ．1 B ．1- C ． 2- D ．0
3．（2012年丰台区高三期末考试理6）执行如右图所示的程序框图，输出的S 值为（ A ） A ．
252(41)3- B ．262
(41)3
- C ．5021- D ． 5121-
4．（2012年丰台区高三期末考试文6）执行如右图所示的程序框图，输出的S 值为（ B ）
A ．650
B ．1250
C ．1352
D ．5000
5．（2012年西城区高三期末考试理4）执行如图所示的程序框图，输出的S 值为（ C ）
A ．3
B ．6-
C ．10
D ．15-
6．（顺义区2012届高三尖子生综合素质展示2）某程序的框图如图所示，则运行该程序后输出的B 的值是（ A ）
A ．63
B ．31
C ．15
D ．7
7．（2012年昌平区高三期末考试理12）某程序框图如图所示，则输出的S .
答案：26。

北京市9区2012届高三上学期期末考试试题--数学_-_方法AnllAq

昌平区2011－2012学年第一学期高三年级期末质量抽测数学试卷（理科） 2012 .1考生注意事项：1.本试卷共6页，分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分，满分150分，考试时间 120分钟．2.答题前，考生务必将学校、班级、姓名、考试编号填写清楚．答题卡上第一部分(选择题)必须用2B 铅笔作答，第二部分(非选择题)必须用黑色字迹的签字笔作答，作图时可以使用2B 铅笔．3.修改时，选择题用塑料橡皮擦干净，不得使用涂改液．请保持卡面整洁，不要折叠、折皱、破损．不得在答题卡上作任何标记．4.请按照题号顺序在各题目的答题区域内作答，未在对应的答题区域作答或超出答题区域的作答均不得分．第Ⅰ卷（选择题共40分）一、选择题(本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．)1．已知集合}55|{},53|{>-<=≤<-=x x x N x x M 或， M N U 等于A ．}55|{<<-x xB ．}35|{->-<x x x 或C ．}53|{≤<-x xD ．}53|{>-<x x x 或2. 已知两条直线01:1=-+y x l ，023:2=++ay x l 且21l l ⊥，则a =A. 31-B ．31C ． -3D ．33．设4log , 2 ,3.03.03.02===c b a ，则A. b a c << B ．a b c << C ．c a b << D ．a c b <<4. 若某空间几何体的三视图如图所示，则该几何体的体积是A ．12B ．8C ．6D ．45．从甲、乙等6名同学中挑选3人参加某公益活动，要求甲、乙至少有1人参加，不同的挑选方法共有 A ．16种 B ．20 种 C ． 24 种 D ．120种主视左视图俯视6. 已知α、β是两个不同平面，m 、n 是两条不同直线，下列命题中假命题是 A ．若m ∥n ,m α⊥, 则n α⊥ B ．若m ∥α,n αβ=I , 则m ∥nC ．若m α⊥,m β⊥, 则α∥β D ．若m α⊥,m β⊂, 则α⊥β7. 某类产品按工艺共分10个档次，最低档次产品每件利润为8元.每提高一个档次，每件利润增加2元. 用同样工时，可以生产最低档产品60件，每提高一个档次将少生产3件产品.则获得利润最大时生产产品的档次是A ．第7档次B ．第8档次C ．第9档次D ．第10档次8. 已知定义在R 上的函数)(x f 满足)2(f = 1，)(x f '为)(x f 的导函数.已知)(x f y '=的图象如图所示,若两个正数b a ,满足1)2(>+b a f ，则21--a b 的取值范围是A ．() 1 , 81-B ．), 1 ()81 , (∞+--∞Y C ．) 1 , 8(- D ．) , (1) 8 , (∞+--∞Y 第Ⅱ卷（非选择题共110分）填空题（本大题共6小题，每小题5分，共30分）．9.已知函数 y =x x ωωcos sin 的最小正周期是2π，那么正数.10. 已知向量(1,2)=a ，(,1)k =b ，若向量//a b ，那么k =.11.已知过点()2,3-的直线l 与圆C ：2240xy x ++=相交的弦长为32，则圆C的圆心坐标是___________,直线l 的斜率为.)(x f 'o否S =1, k =1 开始结束k ＞3输出S是 k = k +1 S =2S + k12. 某程序框图如图所示，则输出的S = .13. 已知7722107)(x a x a x a a m x ++++=-Λ的展开式中4x 的系数是35-，则m =；=++++7321a a a a Λ.14. 设函数)(x f 的定义域为R ，若存在与x 无关的正常数M ，使|||)(|x M x f ≤对一切实数x 均成立，则称)(x f 为有界泛函.在函数①x x f 5)(-=，②2)(x x f =，③x x f 2sin )(=，④xx f )21()(=，⑤x x x f cos )(=中，属于有界泛函的有__________(填上所有正确的序号) .三、解答题(本大题共6小题，共80分．解答应写出文字说明，证明过程或演算步骤．) 15．（本小题满分13分）在ABC ∆中，AA A cos cos 2cos 212-=．（I ）求角A 的大小；（II ）若3a =，sin 2sin B C =，求ABCS ∆．16．(每小题满分13分)某人进行射击训练，击中目标的概率是54，且各次射击的结果互不影响.（Ⅰ）假设该人射击5次，求恰有2次击中目标的概率；（Ⅱ）假设该人每射击5发子弹为一组，一旦命中就停止，并进入下一组练习，否则一直打完5发子弹才能进入下一组练习，求：① 在完成连续两组练习后，恰好共使用了4发子弹的概率； ② 一组练习中所使用子弹数ξ的分布列，并求ξ的期望.17.（本小题满分14分）如图在四棱锥P ABCD -中，底面ABCD 是正方形，ABCD PA 底面⊥，垂足为点A ，1==AB PA ,点M ，N 分别是PD ，PB 的中点．（I ）求证:ACM PB 平面// ；（II ）求证:⊥MN 平面PAC ；（III ）若2= ,求平面FMN 与平面ABCD 所成二面角的余弦值. 18．（本小题满分13分）已知数列}{n a 是等差数列,22 , 1063==a a ，数列}{n b 的前n 项和是n T ，且131=+n n b T .（I ）求数列}{n a 的通项公式；（II ）求证：数列}{n b 是等比数列；（III ）记nn n b a c ⋅=，求证：nn c c <+1.19．（本小题满分13分）已知函数21()()axf x x x e a =--（0a >）.（I ）当1=a 时，求函数()f x 的单调区间；（II ）若不等式05)(≥+a x f 对x ∈R 恒成立,求a 的取值范围.20. (本小题满分14分)已知函数)(x f 是奇函数，函数)(x g 与)(x f 的图象关于直线1=x 对称，当2>x 时，3)2()2()(---=x x a x g (a 为常数).（I ）求)(x f 的解析式；（II ）已知当1=x 时，)(x f 取得极值，求证：对任意4|)()(|),1,1(,2121<--∈x f x f x x 恒成立；（III ）若)(x f 是),1[+∞上的单调函数，且当1)(,100≥≥x f x 时，有00))((x x f f =，求证：0)(x x f =.昌平区2011－2012学年第一学期高三年级期末质量抽测数学(理科)试卷参考答案及评分标准 2012.1二、填空题(本大题共6小题，每小题5分，共30分．)9．2 10. 2111.（-2，0）； 2±12. 26 13． 1 ; 1 14. ①③⑤三、解答题(本大题共6小题，共80分) 15.（本小题满分13分）解：（I ）由已知得：AA A cos cos )1cos 2(2122-=-，……2分.21cos =∴A ……4分 π<<A 0Θ，.3π=∴A …………6分（II ）由C c B b sin sin = 可得：2sin sin ==c bC B ………7分 ∴ c b 2= …………8分214942cos 222222=-+=-+=c c c bc a c b A ………10分解得：32b , 3==c ………11分2332333221sin 21=⨯⨯⨯==A bc S . ……13分16.（本小题满分13分）解：（I ）设射击5次，恰有2次击中目标的事件为A .62532)541()54()(3225=-⋅⋅=C A P ……4分（Ⅱ）①完成两组练习后，恰好共耗用4发子弹的事件为B ,则0768.0088.0)8.01(8.0)8.01(8.0)8.01(8.0)8.01(8.0)(22=⋅⋅-+⋅-⋅-+⋅-⋅=B P .……8分②ξ可能取值为1，2，3，4，5. …… 9分8.0)1(==ξP ; 16.08.0)8.01()2(=⋅-==ζP 032.08.0)8.01()3(2=⋅-==ζP0064.08.0)8.01()4(3=⋅-==ζP 0016.08.0)8.01()5(4=⋅-==ζP ……11分2496.1=∴ζE . ……13分17（本小题满分14分）证明：（I ）连接O BD AC MN MO MC AM BD AC =I 且,,,,,,的中点分别是点BD PD M O ,,ΘACM PB PB MO 平面⊄∴,//∴ACM PB 平面//. …… 4分(II) ABCD PA 平面⊥ΘABCD BD 平面⊂BDPA ⊥∴是正方形底面ABCD Θ，BD AC ⊥∴ 又AAC PA =⋂ΘPAC BD 平面⊥∴ …… 7分在中PBD ∆，点M ，N 分别是PD ，PB 的中点．∴BD MN //PAC MN 平面⊥∴ . …… 9分（III ）ABCD PA 平面⊥Θ，是正方形底面ABCD以A 为原点，建立空间直角坐标系由2= 可得)31,32,32(),21,0,21(),21,21,0(),0,0,0(F N M A设平面MNF 的法向量为 n ),,(z y x = 平面ABCD 的法向量为)1,0,0(=)61,32,61(),0,21,21(-=-= …… 11分可得：⎪⎪⎩⎪⎪⎨⎧=-+=+-06326022z y x y x 解得：⎩⎨⎧==x z x y 5 令可得,1=x n )5,1,1(= …… 13分 y27275275, cos =>=<n AP ……14分 18．（本小题满分13分）解：（1）由已知⎩⎨⎧=+=+.225,10211d a d a 解得 .4,21==d a .244)1(2-=⨯-+=∴n n a n ………………4分（2）由于nn b T 311-=， ① 令n =1，得.31111b b -= 解得431=b ，当2≥n 时，11311---=n n b T ② －②得n n n b b b 31311-=- ， 141-=∴n n b b 又0431≠=b , .411=∴-n n b b∴数列}{n b 是以43为首项，41为公比的等比数列.……………………9分（3）由（2）可得.43n n b =……9分 n n n n n b a c 4)24(3-=⋅=……10分.436304)24(34]2)1(4[3111+++-=---+=-n n n n n n n n c c1≥n Θ，故.01<-+n n c c .1n n c c <∴+……………………13分19．（本小题13分）解: 对函数()f x 求导得:()(2)(1)axf x e ax x '=+- ……………2分 (Ⅰ)当1=a 时, )1)(2()(-+='x x e x f 令()0f x '>解得 1x >或2-<x ()0f x '<解得12<<-x所以, ()f x 单调增区间为)2,(--∞和(1,)+∞,()f x 单调减区间为 (-2 ,1) . ……………5分(Ⅱ) 令()0f x '=,即(2)(1)0ax x +-=,解得2x a =-或1x = 6分当0a >时,列表得：……………8分对于2x a <-时，因为220,,0x x a a >->>,所以21x x a -->，∴()f x >0 ……… 10 分对于2x a ≥-时，由表可知函数在1x =时取得最小值1(1)0a f e a =-<所以，当x ∈R 时，min 1()(1)af x f e a ==- …… 11分由题意，不等式05)(≥+a x f 对x ∈R 恒成立，所以得051≥+-a e a a ，解得5ln 0≤<a ……………13分20.（本小题满分14分）解:(Ⅰ) 当0<x 时，必有0>-x ，则,22>-x 而若点),(y x P 在)(x f y =的图象上，则),(y x P 关于1=x 的对称点),2(1y x P-必在)(x g 的图象上，即当0<x 时， 33]2)2[(]2)2[()2()(x ax x x a x g x f y +-=-----=-==由于)(x f 是奇函数，则任取,0>x 有,0<-x 且33])()([)()(x ax x x a x f x f +-=-+---=--=又当0=x 时，由)0()0(f f -=- 必有0)0(=f综上，当R x ∈ 时ax x x f -=3)(. ……5分（Ⅱ）若1=x 时)(x f 取到极值，则必有当1=x 时03)(2=-='a x x f ，即3=a 又由)1)(1(333)(2+-=-='x x x x f 知，当)1,1(-∈x 时，0)(<'x f ，)(x f 为减函数时当]1,1[-∈∴x ，2)1()(2)1(3)1()1()()1(3-=≥≥=---=≥≥-f x f f x f f 时当)1,1(,21-∈∴x x 4|)1()1(||)()(|21=--<-f f x f x f . ……9分（Ⅲ）若)(x f 在),1[+∞ 为减函数，则03)(2<-='a x x f 对任意),1[+∞∈x 皆成立，这样的实数a 不存在若)(x f 为增函数，则可令03)(2>-='a x x f .由于)(x f '在),1[+∞上为增函数，可令03)1(3)(2≥-='≥-='a f a x x f ，即当3≤a 时，)(x f 在),1[+∞上为增函数由1)(,100≥≥x f x ，0))((x x f f =设1)(00≥>x x f ，则)()]([00x f x f f >)(00x f x >∴与所设矛盾若1)(00≥>x f x 则)]([)(00x f f x f >0)(x x f >∴与所设矛盾故必有00)(x x f = ……14分。

2012北京东城普通校高三(上)期中数学文(含答案)

.
3
2
2
1
13. 已知命题 p : x0 R, ax0 x 0
0 . 若命题 p 是假命题，则实数 a 的取值范围
2
是
.
14. 已知函数 f ( x) 的定义域为 A ，若其值域也为 A ，则称区间 A 为 f ( x) 的保值区间．若
f (x) x m ln x的保值区间是 [ e, ) ，则 m 的值为
16 ．（本小题满分 13 分）解：（Ⅰ）∵ 角的终边与单位圆交于点
∴ sin ∴ f( )
4
3
， cos
，
5
5
2 3 sin cos 2sin 2
p(3 , 4) 55
（Ⅱ） f ( x)
2 3 4 3 2 ( 4) 2
55
5
2 3 sin x cos x 2sin 2 x
24 3 32
.
25
∴ a1 d 5,2a1 8d 22
解得 a1 3, d 2 ∴ a n 2n 1 Sn n 2 2n ,
（Ⅱ）∵ f (x)
1 x2
,
1
bn
f ( an )
∴ bn
1
a
2 n
1
∵ an 2n 1
∴
2
an
1
4n(n
1)
∴ bn
1
11 1
(
)
4n(n 1) 4 n n 1
Tn b1 b2 b3
bn
= 1 (1- 1 + 1 - 1 +…＋1 - 1 )
……………… 3 分
（Ⅱ）令 h( x)
f ( x)

北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试数学试卷(文科)含答案

北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试数学试卷（文史类）2012.11（考试时间120分钟满分150分）本试卷分为选择题（共 40分）和非选择题（共 110分）两部分第一部分（选择题共40 分）、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，选出符合题目要求的一项•x y 20 C .C . 3C . 3In f （a n ）为等差数列，则称函数f （x ）为“保比差数列函数”.现有定义在（0,）上的如1.已知全集U1,2,3,4,5,6 ,集合 A 1,3,51,2 ,则AI (e u B )等于C .2.曲线y 2xX 3在x1处的切线方程为 3.已知平面向量a ,b 满足 |a| 1, |b|2，且（a b)则a 与b 的夹角是4.已知数列a n是各项均为正数的等比数列，若a 2 2, 2a 3 a 4 16，则 a n 等于C . 2n 2n5.已知角的终边经过点（3a,4a ）（a0），则sin2等于7A .256.在ABC 中, urn uuU 则 PA (PB12B .25M 是BC 的中点，AMuuuPC)的值为C-Huuu 3，点P 在AM 上，且满足AP24 25uuuu2 PM ,A. B. 2C.2D. 47.函数f(x)3,x ,x0,的图象与函数g （x ） In （x 1）的图象的交点个数是8.已知数列a n 是各项均为正数且公比不等于1的等比数列.对于函数y f （x ），若数列第二部分(非选择题共110分)二、填空题：本大题共 6小题，每小题5分，共30分.把答案填在答题卡上.19. 已知cos( )—,且为第二象限的角，则 sin =_，tan = _.2 _ —10. 已知集合 A {x R |x 2} , B = x R I 12x 8 ,则 AI B =_. 2 —11. 设S n 为等差数列{a n }的前n 项和，若33 34 4代 37 16，则公差dS 9uur umr12. 在 ABC 中，若BA BC 4 , ABC 的面积为2，则角B _________________ .f(x) 1 f(x) 1,ntf(x)' 13.已知函数y f (x)满足:f(1)=a (0a 1)，且 f (x 1)则2f(x),f(x) 1,f (2)=__ (用a 表示)；右 1f (3)=— f(2)则a .14.已知函数f (x)是定义在 R 上的奇函数, 且在定义域上单调递增 .当x 1a,时，不等式f(x 2a) f (x) 0恒成立，则实数a 的取值范围是 _.三、解答题：本大题共 6小题，共80分.解答应写出文字说明，演算步骤或证明过程 .15. (本小题满分13分)1 设厶ABC 的内角A,B,C 所对的边分别为a,b,c ，已知a 2,b 3,cosC -. 3(I)求厶ABC 的面积； (n)求 sin(C A)的值. 16. (本小题满分13分)设数列a n 的前n 项和为S n ，已知41 , a n 1 3S n 1 , n N •(I)写出a 2,a 3的值，并求出数列 a n 的通项公式; (n)求数列 na n 的前n 项和T n .12① f (x)-,② f (x) x ,x则为“保比差数列函数”的所有序号为A .①②B .③④③ f (x) e x , ④ f (x)、、x ,C .①②④D .②③④yA217. (本小题满分13分)函数f(x) Asin( x )(A 0, 0,| | )部分2图象如图所示.(I)求f (x)的最小正周期及解析式；(n)设g(x) f(x) 2cos2x，求函数g(x)在区间[0, _]上的最大值和最小值.218. (本小题满分14分)2函数f(x) 2ax 4x 3 a, a R.(I)当a 1时，求函数f(x)在1,1上的最大值；(n)如果函数f(x)在区间1,1上存在零点，求a的取值范围.19. (本小题满分14分)设函数f (x) x ae x, a R .(I)求函数f (x)单调区间；(n)若x R , f (x) 0成立，求a的取值范围.20. (本小题满分13分)给定一个n项的实数列曰忌丄,a n(n N )，任意选取一个实数c，变换T(c)将数列a1,a2,L ,a n变换为数列|印c|,| a? c|,L ,|务c|，再将得到的数列继续实施这样的变换，这样的变换可以连续进行多次，并且每次所选择的实数c可以不相同，第k(k N )次变换记为T k(q)，其中C k为第k次变换时选择的实数•如果通过k次变换后，数列中的各项均为0,则称「(G) , T2G)，…，T k(c k)为“ k次归零变换”(I)对数列：124,8,分别写出经变换「(2) , T2(3) , T3⑷后得到的数列；(n)对数列：1,3,5,7，给出一个“ k次归零变换”，其中k 4 ；(川)证明：对任意n项数列，都存在“ n次归零变换”.北京市朝阳区2012-2013学年度第一学期高三年级期中练习15. （本小题满分13分）1解：（I ）在厶ABC 中，因为cosC -3因为a b ，所以A 为锐角，所以 sin (C A) si nCgcosA cosCgsi nA2012.11、选择题（共40二、填空题（共30分）1)三、解答题（共80分）所以sin C、.1 cos 2C1 (\2 2'2 ..33所以S VABC1 abgsin C1 2 3 $ 丘 2 & 2 3又由正弦定理得,sin C所以sin Aagsin C c 所以 cos A 1 sin 2 A1 (492)211分2、、2 7 1 4.210、2 八. ........................ 13 分3 9 3 9 2716. （本小题满分13分）解：（I）a2 4 , a3 16. .......................................................... 2 分由题意，a n 1 3S n 1，则当n 2 时，a n 3S n 1 1.两式相减，化简得a n 1 4a n（n 2） . ..................................... 4分a2,又因为a11，a24，- 4，印则数列a n是以1为首项，4为公比的等比数列，所以a n 4n 1( n N ) ................................. 6 分2 n 1(n) T n a1 2a2 3a3 L na n 1 2 4 3 4 L n 4 ,4T n 4 1 2 42 3 43L (n 1) 4n 1 n 4n , ........................ 8 分两式相减得，3T n 1 4 42L 4n 1 n 4n 1— n 4n• ...................... 12 分1 4n 1 1化简整理得，T n 4n(—_) _(n N ). ......................................... 13分17.（本小题满分13分）解: （I）由图可得A2, T2—,所以T .所以2. 2 3 62.................. o................. Z k............. 2 分当x —时，f(x)2，可得2si n(2-)2 ,66因为丨丨-，所以-所以f(x)的解析式为f(x) 2si n(2x ) . ....................................... 5分6(n)g(x) f(x) 2cos2x 2sin(2x 6) 2cos2x2sin 2xcos —62cos 2xs in— 2cos 2x6、、3s in2x cos2x2sin(2 x ) . .............................................. 10 分6因为x [0,—]，所以一2x2 6 6 6当2x ，即x 时，g(x)有最大值，最大值为2 ；.......... 12分6 2 3当2x ，即x 0时，g(x)有最小值，最小值为 1 . ....................... 13分6 618. (本小题满分14分)解：(I)当a 1 时，则f (x) 2x2 4x 42( x22x) 4 2(x 1)2 6 .因为x 1,1 ,所以x 1 时，f(x)max f(1) 2 . .................................. 3分(n)当a 0时，f(x) 4x 3 ,显然在1,1上有零点，所以a 0时成立•……4分当a 0时，令16 8a(3 a) 8(a 1)(a 2) 0,解得a 1, a 2. ........................................... 5分(1)当a 1 时，f(x) 2x2 4x 2 2(x 1)2由f(x) 0,得x 1 [ 1,1];1当a 2 时，f(x) 4x24x 1 4(x -)2.1由f (x) 0 ,得x - [ 1,1],所以当a 0, 1, 2时，y f(x)均恰有一个零点在1,1上. ........... 7分(2)当f ( 1)gf (1) (a 7)(a 1) 0 ,即1 a 7时，y f x在1,1上必有零点. ............................ 9分(3)若y f x在1,1上有两个零点，则a 1 或 a 2..................................................... 14 分19. (本小题满分14分)解：(I) f (x) 1 ae x ............................ 1 分ia 0时，f(x)在区间( ,In a)上是增函数，在区间(In a,)上是减函数 ........... Q由(I)可知：当 a 0时， f (x)0不恒成立................ 9 分又因为当a 0时，f (x)在区间(，In a)上是增函数，在区间 (Ina,)上是减函数，所以f (x)在点x In a 处取最大值，且 f( Ina) Ina ae lna Ina . ........................... 11 分令 Ina，得 a -,e故f(x) 0对x R 恒成立时，a 的取值范围是［―,). ................................................... 14分e20. (本小题满分14分) 解：(I )T 1(2) : 1,0,2,6;T 2(3) : 2,3,1,3; T 3 ⑷：2,1,3,1. .......................................... 3 分a 0,a 0,8(a 1)(a2) 0,8(a 1)(a 2) 0,1 1 1,a或 1- 1,••… a ................. 13分f( 1) 0, f( 1) 0,f(1) 0f(1) 0-解得a 7或a2.综上所述，函数 f(x)在区间1,1上存在极值点，实数 a 的取值范围是当a 0时，令f (x) 0,得xIn a ..................... 4分若x In a 则 f (x) 0 ,从而 f (x)在区间(,In a)上是增函数；若xIn a 则 f (x) 0,从而 f (x)在区间(In a,)上是减函数.综上可知：当a 0时, f (x)在区间(，)上是增函数；当a 0时，f (x) 0 , f (x)在R 上是增函数. 3分（H）方法1: T⑷：3,1,13 T2（2）: 1,1,1,1; T3（1）: 0,0,0,0方法2：T1（2）: 1,1,3,5; T2（2）: 1,1,1,3; T3（2）: 1,1,1,1 ; T^）: 0,0,0,0.（川）记经过T k（c k）变换后，数列为a（k）£,L ,a n k）.1 1取c, -（31 82）,则31（1） aj —|印321，即经T1（q）后，前两项相等；2 2取c抽1）af），则a12） a22） a32） 11 a^ af |，即经T2G）后，前3 项相等;2 2继续做类似的变换，取C k haf1〉a k k J），（k n 1），经T k（cQ后，得到数列的2前k 1项相等.特别地，当k n 1时，各项都相等，最后，取c n aj1〉，经T n（c n）后,数列各项均为0.所以必存在n次“归零变换”.（注：可能存在k次“归零变换”，其中k n）. ...................... 13分。

北京市各区2012届高三上学期期中、期末考试分类解析(5)：三角函数

五、三角函数1．（2012年东城区高三期末考试理6）如图所示，点P 是函数)sin(2ϕω+=x y )0,(>∈ωR x 的图象的最高点，M ，N 是该图象与x 轴的交点，若0=⋅PN PM ，则ω的值为（ B ）A ．8π B ．4π C ．4 D ．82．（2012年东城区高三期末考试文7）函数()sin()f x x =+ωϕ（其中2π<ϕ）的图象如图所示，为了得到()sin g x x =ω的图象，则只要将()f x 的图象（ A ）A ．向右平移6π个单位长度 B ．向右平移12π个单位长度 C ．向左平移6π个单位长度 D ．向左平移12π个单位长度3．（2012年朝阳区高三期末考试理5）已知函数()sin f x x x =+，设()7a f π=，()6b f π=，()3c f π=，则,,a b c 的大小关系是（ B ）A ．a b c <<B ．c a b <<C ．b a c <<D ．b c a <<4．（2012年海淀区高三期末考试理5）函数()sin(2)(,)f x A x A ϕϕ=+ R 的部分图象如图所示，那么(0)f =( C )A ．12- B ．2-．1- D ．-5．（2012年海淀区高三期末考试理7）已知函数2()cos sin f x x x =+，那么下列命题中假命．．题．是 ( B ) A ．()f x 既不是奇函数也不是偶函数 B ．()f x 在[,0]π-上恰有一个零点 C ．()f x 是周期函数 D ．()f x 在(,2π5π)6上是增函数6．（2011年海淀区高三年级第一学期期中练习理5）下列四个函数中，以π为最小正周期，且在区间(,)2ππ上为减函数的是（ D ）A ．sin 2y x =B ．2cos y x =C ．cos2x y = D ．tan()y x =-7．（2011年朝阳区高三年级第一学期期中统一考试理3）已知函数()2sin()f x x ωϕ=+(0,0π)ωϕ><<的图象如图所示，则ω等于( B )A ．13 B ．32C ．1D ．28．（顺义区2012届高三尖子生综合素质展示3）直线3π=x ，2π=x 都是函数) , 0)(sin()(πϕπωϕω≤<->+=x x f 的对称轴，且函数)(x f 在区间]2, 3[ππ上单调递减，则( C )A ．2πϕ= B ．6=ω，2πϕ-=C ． 6=ω，2πϕ=D ．3=ω，2πϕ-=9．（2011年东城区高三示范校高三综合练习(一)文3）将函数sin y x =的图象上所有的点横坐标伸长到原来的2倍（纵坐标不变），再把所得各点向右平行移动10π个单位长度，所得图象的函数解析式是（ B ）A ．sin(2)10y x π=-B ．1sin()220y x π=-C ．sin(2)5y x π=-D ．1sin()210y x π=-10．（2011年海淀区高三年级第一学期期中练习理7）要得到函数sin cos y x x =-的图象，只需将函数cos sin y x x =-的图象（ C ）A ．向左平移4π个单位长度 B ．向右平移2π个单位长度 C ．向右平移π个单位长度 D ．向左平移34π个单位长度11．（2011年东城区高三示范校高三综合练习(一)理2）已知函数R ∈-=x x x x f ,cos sin 3)(，若1)(≥x f ，则x 的取值范围为（ B ）A ．⎭⎬⎫⎩⎨⎧∈π+π≤≤π+πZ k k x k x ,3 B ．⎭⎬⎫⎩⎨⎧∈π+π≤≤π+πZ k k x k x ,232C ．⎭⎬⎫⎩⎨⎧∈π+π≤≤π+πZ k k x k x ,656D ．⎭⎬⎫⎩⎨⎧∈π+π≤≤π+πZ k k x k x ,6526212．（2011年海淀区高三年级第一学期期中练习理13）在A B C ∆中，角,,A B C 的对边分别是,,a b c ，8,10a b ==, A B C ∆的面积为2, 则A B C ∆中最大角的正切值是。

2012-2013学年北京市朝阳区高三年级第一学期期中数学(文科)参考答案

2012-2013学年北京市朝阳区高三年级第一学期期中数学(文科)参考答案北京市朝阳区2012～2013学年度高三年级第一学期期中统一考试数学试卷答案（文史类）2012. 11一、选择题：本大题共8小题，每小题5分，共40分．题号（1）（2）（3）（4）（5）（6）（7）（8）答案D A B C D A C C二、填空题：本大题共6小题，每小题5分，共30分．（注：两空的填空，第一空3分，第一空2分）三、解答题：本大题共6小题，共80分．解答应写出文字说明，演算步骤或证明过程．题号（9）（10）（11）（12）（13）（14）答案 323-[1,2)-2d =4545o2a24或11(,)2-∞15．（本小题满分13分）解：（Ⅰ）在△ABC 中，因为1cos 3C =，所以22122sin 1cos 1()3C C =-=-=． ………………………2分所以1122sin 2322223ABC S ab C ==⨯⨯⨯=V g ． ………………………5分（Ⅱ）由余弦定理可得，2222cos ca b ab C=+-g1492233=+-⨯⨯⨯9=所以3c =． …………………………………………7分又由正弦定理得，sin sin c aC A=，所以222sin 423sin 3a CA c⨯===g ． (9)分因为a b <，所以A 为锐角，所以22427cos 1sin 1()99A A =-=-=． ……………………11分所以sin()sin cos cos sin C A C A C A -=-g g27122393927=-⨯=．……………………13分16．（本小题满分13分）解：（Ⅰ）24a =，316a =． ……………………………………………2分由题意，131n n aS +=+，则当2n ≥时，131nn aS -=+．两式相减，化简得14n na a +=（2n ≥）． ……………………………………4分又因为11a =，24a =，214a a =，则数列{}na 是以1为首项，4为公比的等比数列，所以14n n a -=（n *∈N ） ……………………………………………6分（Ⅱ）2112323124344n nn Ta a a na n -=++++=+⨯+⨯++⋅L L ，2314412434(1)44n nn T n n -=⨯+⨯+⨯++-⋅+⋅L ， ……………………8分两式相减得，2114314444414nn nnn T n n ---=++++-⋅=-⋅-L ．………12分化简整理得，114()399n n n T =-+(n *∈N )． ………………………………13分17．（本小题满分13分）解：（Ⅰ）由图可得2A =，22362T πππ=-=，所以T =π．所以2ω=．…………………………………2分当6x π=时，()2f x =，可得 2sin(2)26ϕπ⋅+=，因为||2ϕπ<，所以6ϕπ=． ……………………………………………4分所以()f x 的解析式为()2sin(2)6f x x π=+． …………………………5分（Ⅱ）()()2cos 22sin(2)2cos 26g x f x x x x π=-=+- 2sin 2cos2cos 2sin 2cos 266x x x ππ=+-32cos 2x x=- ………………………………………8分2sin(2)6x π=-． ………………………………………10分因为[0,]2x π∈，所以2666x ππ5π-≤-≤．当262x ππ-=，即3x π=时，()g x 有最大值，最大值为2； ………………12分当266x ππ-=-，即0x =时，()g x 有最小值，最小值为1-．……………13分18．（本小题满分14分）解：（Ⅰ）当1a =时，则2()244f x x x =+-222(2)42(1)6x x x =+-=+-．因为[]1,1x ∈-，所以1x =时，()(1)2max f x f ==． ………………………3分（Ⅱ）当0a =时，()43f x x =-，显然在[]1,1-上有零点，所以0a =时成立.……4分当0a ≠时，令168(3)8(1)(2)0a a a a ∆=++=++=，解得1,a =-2a =-． ………………………………………5分（1）当1a =-时，22()2422(1)f x xx x =-+-=--．由()0f x =，得1[1,1]x =∈-；当2a =-时，221()4414()2f x xx x =-+-=--．由()0f x =，得1[1,1]2x =∈-，所以当0,1,2a =--时，()y f x =均恰有一个零点在[]1,1-上.………………7分（2）当(1)(1)(7)(1)0f f a a -=-+≤g ，即17a -≤≤时，()y f x =在[]1,1-上必有零点． ………………………………………9分（3）若()y f x =在[]1,1-上有两个零点，则0,8(1)(2)0,111,(1)0,(1)0a a a a f f >⎧⎪∆=++>⎪⎪-<-<⎨⎪-≥⎪⎪≥⎩或0,8(1)(2)0,111,(1)0,(1)0.a a a a f f <⎧⎪∆=++>⎪⎪-<-<⎨⎪-≤⎪⎪≤⎩ …………………13分解得7a ≥或2a <-．综上所述，函数()f x 在区间[]1,1-上存在极值点，实数a 的取值范围是1a ≥-或2a ≤-. ………………………………………14分19．（本小题满分14分）解：（Ⅰ）()1e xf x a '=-． ……………………1分当a ≤时，()0f x '>，()f x 在R上是增函数． ……………………3分当a >时，令()0f x '=，得ln x a=-． ……………………4分若ln x a <-则()0f x '>，从而()f x 在区间(,ln )a -∞-上是增函数；若ln x a >-则()0f x '<，从而()f x 在区间(ln ,)a -+∞上是减函数．综上可知：当0a ≤时，()f x 在区间(,)-∞+∞上是增函数；当0>a 时，()f x 在区间(,ln )a -∞-上是增函数，在区间(ln ,)a -+∞上是减函数．………………………………………9分（Ⅱ）由（Ⅰ）可知：当0a ≤时，()0f x ≤不恒成立．又因为当0a >时，()f x 在区间(,ln )a -∞-上是增函数，在区间(ln ,)a -+∞上是减函数，所以()f x 在点ln x a =-处取最大值，且ln (ln )ln e ln a f a a a a --=--=--1． ……………………………………11分令ln a --10≤，得ea 1≥，故()0f x ≤对x ∈R 恒成立时，a 的取值范围是[,)e+∞1． ………………14分20．（本小题满分14分）解：（Ⅰ）1(2)T ：1,0,2,6;2(3)T ：2,3,1,3;3(4)T ：2,1,3,1.………………………3分（Ⅱ）方法1：1(4)T ：3,1,1,3;2(2)T ：1,1,1,1;3(1)T ：0,0,0,0．方法2：1(2)T ：1,1,3,5;2(2)T ：1,1,1,3;3(2)T ：1,1,1,1；4(1)T ：0,0,0,0．………………………………………6分（Ⅲ）记经过()kkT c 变换后，数列为()()()12,,,k k k naa a L ．取1121()2c a a =+ ,则(1)(1)12121||2aa a a ==-，即经11()T c 后，前两项相等；取(1)(1)2231()2ca a =+，则(2)(2)(2)(1)(1)123231||2aa a a a ===-，即经22()T c 后，前3项相等；继续做类似的变换，取(1)(1)11()2k k kk k ca a --+=+，（1k n ≤-），经()kkT c 后，得到数列的前1k +项数学（文科）参考答案第11页（共5页）相等．特别地，当1k n =-时，各项都相等，最后，取(1)n n n c a -=，经()n n T c 后，数列各项均为0.所以必存在n 次“归零变换”．（注：可能存在k 次“归零变换”，其中k n <）．………………………………13分。

2012北京朝阳高三(上)期中数学理(含答案)

北京市朝阳区2012-2013学年度高三年级第一学期期中统一考试数学试卷（理工类） 2012.11（考试时间120分钟满分150分）本试卷分为选择题（共40分）和非选择题（共110分）两部分第一部分（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，选出符合题目要求的一项. 1. 已知全集{}1,2,3,4,5,6U =, 集合{}1,3,5A =, {}1,2B =, 则A I (U ðB )等于（） A ．∅ B ．{}5 C ．{}3 D ．{}3,52. 已知数列{}n a 是各项均为正数的等比数列，若2342,216a a a =+=，则n a 等于（）A ．22-nB ．32n -C ．12-n D ．n23.已知平面向量a ，b 满足||1=a ，||2=b ，且()+⊥a b a ，则a 与b 的夹角为（）A ．56π B ．23π C ． 3π D ．6π 4.曲线e ()1xf x x =-在0x =处的切线方程为（）A ．10x y --=B ．10x y ++=C ．210x y --=D ．210x y ++=5.在ABC ∆中，M 是BC 的中点，3AM =，点P 在AM 上，且满足2AP PM =u u u r u u u u r，则()PA PB PC ⋅+u u u r u u u r u u u r 的值为（）A ．4-B ．2-C ．2D ．46.函数33,0,(),0x x f x x x --<⎧=⎨≥⎩的图象与函数()ln(1)g x x =+的图象的交点个数是（） A ．1 B ．2 C ．3 D ．47.函数()f x 是定义域为R 的可导函数，且对任意实数x 都有()(2)f x f x =-成立．若当1x ≠时，不等式(1)()0x f x '-⋅<成立，设(0.5)a f =，4()3b f =，(3)c f =，则a ，b ，c 的大小关系是（）A ．B ．C ．D ．8.已知数列{}n a 是各项均为正数且公比不等于1的等比数列.对于函数()y f x =，若数列{}ln ()n f a 为等差数列，则称函数()f x 为“保比差数列函数”.现有定义在(0,)+∞上的如下函数：①1()f x x=， ②2()f x x =， ③()e x f x =， ④()f x x =，则为“保比差数列函数”的所有序号为（）A ．①②B ．③④C ．①②④D ．②③④第二部分（非选择题共110分）b ac >>c b a >>a b c >>b c a >>9.设集合{|2}A x x =∈≤R ，B ={x ∈R ∣}1262x <<,则A B =I . 10.设n S 是等差数列{}n a 的前n 项和．若569108,24a a a a +=+=，则公差d = ，10S = .11.已知角α的终边经过点(3,4)(0)a a a <，则sin α= ，tan(2απ-)= .12. 在ABC ∆中，若4BA BC ⋅=u u u r u u u r，ABC ∆的面积为2，则角B = .13. 已知函数()y f x =满足：(1)=f a （01a <≤），且()1,()1,()(1)2(),()1,f x f x f x f x f x f x -⎧>⎪+=⎨⎪≤⎩则(2)=f （用a 表示），若1(3)=(2)f f ，则a = . 14.已知函数()f x x x =.当[,1]x a a ∈+时，不等式(2)4()f x a f x +>恒成立，则实数a 的取值范围是 .三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15.（本小题满分13分）设△ABC 的内角,,A B C 所对的边分别为,,a b c ，已知12,3,cos 3a b C ===．（Ⅰ）求△ABC 的面积；（Ⅱ）求sin()C A -的值．16.（本小题满分14分）设数列{}n a 的前n 项和为n S .已知11a =，131n n a S +=+，n *∈N . （Ⅰ）写出23,a a 的值，并求数列{}n a 的通项公式；（Ⅱ）记n T 为数列{}n na 的前n 项和，求n T ；（Ⅲ）若数列{}n b 满足10b =，12log (2)n n n b b a n --=≥，求数列{}n b 的通项公式.17.（本小题满分13分）π32π6πo2x2-y（Ⅰ）求函数()f x 的解析式，并写出其单调递增区间；（Ⅱ）设函数()()2cos 2g x f x x =+，求函数()g x 在区间 [,]64ππ-上的最大值和最小值．18.（本小题满分13分）已知函数2()243f x ax x a =+--，a ∈R . （Ⅰ）当1a =时，求函数()f x 在[]1,1-上的最大值；（Ⅱ）如果函数()f x 在区间[]1,1-上存在零点，求a 的取值范围.19.（本小题满分14分）设函数()ln f x a x x1=+，a ∈R ．（Ⅰ）求函数的单调区间；（Ⅱ）当0a >时，若对任意0x >，不等式()2f x a ≥成立，求的取值范围；（Ⅲ）当0a <时，设10x >，20x >，试比较与的大小并说明理由． )(x f a )2(21x x f +2)()(21x f x f +20.（本小题满分13分）给定一个n 项的实数列12,,,(N )n a a a n *∈L ，任意选取一个实数c ，变换()T c 将数列12,,,n a a a L 变换为数列12||,||,,||n a c a c a c ---L ，再将得到的数列继续实施这样的变换，这样的变换可以连续进行多次，并且每次所选择的实数c 可以不相同，第(N )k k *∈次变换记为()k k T c ，其中k c 为第次变换时选择的实数.如果通过k 次变换后，数列中的各项均为0，则称11()T c ， 22()T c ，…，()k k T c 为 “k 次归零变换”.（Ⅰ）对数列：1,3,5,7，给出一个 “k 次归零变换”，其中4k ≤；（Ⅱ）证明：对任意n 项数列，都存在“n 次归零变换”；（Ⅲ）对于数列231,2,3,,nn L ，是否存在“1n -次归零变换”？请说明理由. k北京市朝阳区2012-2013学年度第一学期高三年级期中练习数学试卷答案（理工类） 2012.11一、选择题：题号（1）（2）（3）（4）（5）（6）（7）（8）答案D C BDACAC 二、填空题：题号（9）（10）（11）（12）（13）（14）答案 (1,2]- 2 40 45- 24745︒ 2a24或1 (1,)+∞（注：两空的填空，第一空3分，第一空2分）三、解答题：本大题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 15. （本小题满分13分）解：（Ⅰ）在△ABC 中，因为1cos 3C =，所以22122sin 1cos 1()33C C =-=-=． ………………………2分所以，1122sin 2322223ABC S ab C ==⨯⨯⨯=V g ． ………………………5分（Ⅱ）由余弦定理可得，2222cos c a b ab C =+-g1492233=+-⨯⨯⨯9=所以，3c =． …………………………………………7分又由正弦定理得，sin sin c aC A=，所以，222sin 423sin 39a C A c ⨯===g ． ……………………9分因为a b <，所以A 为锐角,所以，22427cos 1sin 1()99A A =-=-=． ……………………11分所以，sin()sin cos cos sin C A C A C A -=-g g227142102393927=⨯-⨯=． …………………………………13分16. （本小题满分14分）解：（Ⅰ）由已知得，24a =，316a =. ……………………………………………2分由题意，31a S =+，则当2n ≥时，31a S =+.两式相减，得14n n a a +=（2n ≥）. ……………………………………………3分又因为11a =，24a =，214a a =，所以数列{}n a 是以首项为1，公比为4的等比数列，所以数列{}n a 的通项公式是14n n a -=（n *∈N ）. ………………………………5分（Ⅱ）因为2112323124344n n n T a a a na n -=++++=+⨯+⨯++⋅L L ，所以2314412434(1)44n nn T n n -=⨯+⨯+⨯++-⋅+⋅L ， ……………………6分两式相减得，2114314444414nn nn n T n n ---=++++-⋅=-⋅-L ， ………8分整理得，311499n n n T -=⋅+ (n *∈N ). ………………………………9分（Ⅲ）当2n ≥时，依题意得2122log b b a -=,3223log b b a -=,… , 12log n n n b b a --=.相加得，122232log log log n n b b a a a -=+++L . ……………………………12分依题意122log log 42(1)n n a n -==-.因为10b =，所以[]212(1)(1)n b n n n =+++-=-L （2n ≥）. 显然当10b =时，符合.所以(1)n b n n =-(n *∈N ). ……………………………………14分17. （本小题满分13分）解：（Ⅰ）由图可得2A =，22362T πππ=-=，所以T =π，所以2ω=． …………………………………………………………2分当6x π=时，()2f x =，可得 2sin(2)26ϕπ⋅+=，因为||2ϕπ<，所以6ϕπ=． ………………………………………………………4分所以函数()f x 的解析式为()2sin(2)6f x x π=+．………………………………5分函数()f x 的单调递增区间为[,]()36k k k πππ-π+∈Z ．…………………………7分（Ⅱ）因为()()2cos 22sin(2)2cos 26g x f x x x x π=+=++2sin 2cos2cos 2sin 2cos 266x x x ππ=++ …………………………8分 3sin 23cos 2x x =+23sin(2)3x π=+. ………………………10分因为[,]x ππ∈-，所以502x ππ≤+≤．当232x ππ+=，即12x π=时，函数()g x 有最大值为23； ……………12分当203x π+=，即6x π=-时，函数()g x 有最小值0． ………………13分 18. （本小题满分13分）解：（Ⅰ）当1a =时，则2()244f x x x =+-222(2)42(1)6x x x =+-=+-．因为[]1,1x ∈-，所以1x =时，()f x 的最大值(1)2f =．………………………3分（Ⅱ）当0a =时，()43f x x =- ,显然在上有零点, 所以0a =时成立.……4分当0a ≠时，令168(3)8(1)(2)0a a a a ∆=++=++=,解得1,a =-2a =-． ………………………………………5分（1）当1a =-时, 22()2422(1)f x x x x =-+-=-- 由()0f x =，得1[1,1]x =∈-；当 2a =-时,221()4414()2f x x x x =-+-=--．由()0f x =，得1[1,1]2x =∈-，所以当 0,1,2a =--时, ()y f x =均恰有一个零点在上.………………7分（2）当(1)(1)(7)(1)0f f a a -=-+≤g ，即17a -≤≤时，在上必有零点. ………………………………………8分（3）若在上有两个零点, 则0,8(1)(2)0,111,(1)0,(1)0a a a a f f >⎧⎪∆=++>⎪⎪-<-<⎨⎪-≥⎪⎪≥⎩或0,8(1)(2)0,111,(1)0,(1)0.a a a a f f <⎧⎪∆=++>⎪⎪-<-<⎨⎪-≤⎪⎪≤⎩ …………………12分解得7a ≥或2a <-．综上所述，函数()f x 在区间[]1,1-上存在极值点，实数的取值范围是1a ≥-或2a ≤-. ………………………………………13分19. （本小题满分14分）[]1,1-[]1,1-()y f x =[]1,1-()y f x =[]1,1-a（Ⅰ）由题意， ………………………………………2分（1）当0a >时，由得，解得，函数的单调递减区间是；由得，解得，函数的单调递增区间是． …………………………………………4分（2）当0a ≤时，由于0x >，所以21()0a f x x x'=-<恒成立，函数的在区间(0),+∞上单调递减． ……………………………………………………………………………………5分（Ⅱ）因为对于任意正实数x ，不等式()2f x a ≥成立，即恒成立．因为，由（Ⅰ）可知当时，函数()ln f x a x x1=+有最小值．…7分所以，解得10ea <≤．故所求实数的取值范围是1(0,]e． ………………………………………9分（Ⅲ）因为121212()ln 22x x x x f a x x ++2=++， 121212()()1(ln ln )22f x f x a x a x x x +11=+++．1212121212121[ln(]ln 22x x x x a x x a x x x x x x ++=)+=+. ……………………………10分所以12121212121212()()()ln ln 2222x x f x f x x x x x f a a x x x x x x ++++2-=+--+ 1212121212()ln 2()2x x x x a x x x x x x 2+-=-+．（1）显然，当12x x =时，1212()()()22x x f x f x f ++=． ……………………11分（2）当x x ≠时，因为且0a <，21)(,0xx a x f x -='>0)(<'x f 012<-x x a a x 1<)(x f )1,0(a 0)(>'x f 012>-xx a a x 1>)(x f ),1(∞+a)(x f xx a a 1ln 2+≤0>a a x 1=a a a a a a a f ln 1ln )1(-=+=a a a x f a ln )(2min -=≤a 0,0>>x x所以，所以．………………12分又121212()02()x x x x x x 2--<+，所以1212121212()ln02()2x x x x a x x x x x x 2+--<+ 所以，即．综上所述，当12x x =时，1212()()()22x x f x f x f ++=；当12x x ≠时，．……………………………………………………14分 20. （本小题满分13分）解：（Ⅰ）方法1：1(4)T ：3,1,1,3;2(2)T ：1,1,1,1;3(1)T ：0,0,0,0．方法2：1(2)T ：1,1,3,5;2(2)T ：1,1,1,3;3(2)T ：1,1,1,1；4(1)T ：0,0,0,0．．……4分（Ⅱ）经过k 次变换后，数列记为()()()12,,,k k k n a a a L ，1,2,k =L ．取1121)2c a a =(+,则(1)(1)12121||2a a a a ==-，即经11()T c 后，前两项相等；取(1)(1)2231()2c a a =+，则(2)(2)(2)(1)(1)123321||2a a a a a ===-，即经22()T c 后，前3项相等； … …设进行变换()k k T c 时，其中(1)(1)11()2k k k k k c a a --+=+，变换后数列变为 ()()()()()()12312,,,,,,,k k k k k k k k n a a a a a a ++L L ，则()()()()1231k k k k k a a a a +====L ；那么，进行第1k +次变换时，取()()1121()2k k k k k c a a +++=+，则变换后数列变为(1)(1)(1)(1)(1)(1)(1)123123,,,,,,,,k k k k k k k k k k na a a a a a a ++++++++++L L ，显然有(1)(1)(1)(1)(1)12312k k k k k k k a a a a a +++++++=====L ；… …经过1n -次变换后，显然有(1)(1)(1)(1)(1)1231n n n n n n na a a a a ------=====L ；最后，取(1)n n n c a -=，经过变换()n n T c 后，数列各项均为0.所以对任意数列，都存在 “n 次归零变换”． ……………………………………9分（Ⅲ）不存在“1n -次归零变换”. ………………………………………………10分221>+x x 21x x 02ln ,1221212121<+>+x x x x a x x x x 02)()()2(2121<+-+x f x f x x f 2)()()2(2121x f x f x x f +<+2)()()2(2121x f x f x x f +<+11 / 11证明：首先，“归零变换”过程中，若在其中进行某一次变换()j j T c 时，12min{,,,}j n c a a a <L ，那么此变换次数便不是最少.这是因为，这次变换并不是最后的一次变换（因它并未使数列化为全零），设先进行()j j T c 后，再进行11()j j T c ++，由11|||||()|i j j i j j a c c a c c ++--=-+，即等价于一次变换1()j j j T c c ++，同理，进行某一步()j j T c 时，12max{,,,}j n c a a a >L ；此变换步数也不是最小．由以上分析可知，如果某一数列经最少的次数的“归零变换”，每一步所取的i c 满足1212min{,,,}max{,,,}n i n a a a c a a a ≤≤L L ．以下用数学归纳法来证明，对已给数列，不存在“1n -次归零变换”．（1）当2n =时，对于1,4，显然不存在 “一次归零变换” ，结论成立．（由（Ⅱ）可知，存在 “两次归零变换”变换：1253(),()22T T ）（2）假设n k =时成立，即231,2,3,,k k L 不存在“1k -次归零变换”．当1n k =+时，假设2311,2,3,,,(1)k k k k ++L 存在“k 次归零变换”．此时，对231,2,3,,k k L 也显然是“k 次归零变换”，由归纳假设以及前面的讨论不难知231,2,3,,k k L 不存在“1k -次归零变换”，则k 是最少的变换次数，每一次变换i c 一定满足1k i c k ≤≤，1,2,,i k =L ．因为111212|||(1)|||(1)()k k k k k c c c k c c c +++----=+-+++L L L1(1)0k k k k k +≥+->g 所以，1(1)k k ++绝不可能变换为0，与归纳假设矛盾．所以，当1n k =+时不存在“k 次归零变换”．由（1）（2）命题得证． ………………………………………13分。

精品解析：北京市海淀区2012届高三上学期期末考试数学(文)试题解析(教师版)

【试题总体说明】本套试卷严格按照2011年北京卷的高考题进行命制，题目难度适当，创新度较高。

所命试卷呈现以下几个特点：（1）注重对基础知识、基本能力和基本方法的考查，严格控制试题难度。

如选择题2,4；（2）知识点覆盖全面，既注重对传统知识的考查，又注重对新增内容的考查，更注重对主干知识的考查；（3）遵循源于教材、高于教材的原则，部分试题根据教材中的典型例题或习题改编而成；如选择题3,7.（4）深入探究2011高考试题，精选合适的试题进行改编；如填空题9,11.（5）题型新颖，创新度高，部分试题是原创题，有较强的时代特色．如填空题13和解答题20等；（6）在知识网络的交汇处命题，强调知识的整合，突出考查学生综合运用数学知识分析问题、解决问题的能力。

如17题。

一、选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的. （1）复数i(12i)-=（A ）2i -+ （B ）2i + （C ）2i - （D ）2i -- 【答案】B（3）已知数列{}n a 满足：22111, 0, 1(*)n n n a a a a n +=>-=∈N ，那么使5n a <成立的n 的最大值为（）（A ）4 （B ）5 （C ）24 （D ）25【答案】C【解析】22222111,{}1,11(1),n n n n a a a a a n n +-=∴=∴=+-= 是以为公差的等差数列，0,.5,5,25.n n n a a n a n n n >∴=<∴<∴<∴ 的最大值为24，故选C 。

（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D ）既不充分也不必要条件【答案】C【解析】1212121212,11,;,110,.k k l l l l k k k k =≠-∴∴⨯-⨯=∴= ∥∥故为充要条件。

（6）函数()sin(2)(,)f x A x A ϕϕ=+ R 的部分图象如图所示，那么(0)f =（A ）12- （B ）1-（C ）32- （D ）3-【答案】B【解析】由图可知，(,2)3π为函数图象的最高点，2,()2,3A f π∴==2222sin()2,sin()1,2()3332k k Z ππππϕϕϕπ∴+=∴+=∴+=+∈ 12(),(0)2sin 2sin(2)2() 1.662k k Z f k ππϕπϕπ∴=-+∈∴==-+=⨯-=-（7）已知函数()2f x x x x =-，则下列结论正确的是（A ）()f x 是偶函数，递增区间是()0,+（B ）()f x 是偶函数，递减区间是(,1)-（C ）()f x 是奇函数，递减区间是()1,1- （D ）()f x 是奇函数，递增区间是(),0-观察图象可知，函数图象关于原点对称，故函数为奇函数，且在[]1,1- 单调递减。

【精品解析】北京市高考数学最新联考试题分类大汇编(15)算法框图

精品解析：北京市2012年高考数学最新联考试题分类大汇编（15）算法框图试题解析一、选择题：4．(北京市西城区2012年1月高三期末考试理科)执行如图所示的程序框图，输出的S 值为（）（A ）3（B ）6-（C ）10（D ）15-【答案】C【解析】执行程序框图可得：1,1;2,3;3,6;4,10;5,i S i S i S i S i ==-====-===程序结束，输出10.S =（5）（2012年4月北京市海淀区高三一模理科）执行如图所示的程序框图，输出的k 值是（A ）4 （B ）5（C ）6 （D ）7【答案】B2．(北京市西城区2012年4月高三第一次模拟文)执行如图所示的程序框图，若输入3x =，则输出y 的值为（ D ）（A ）5（B ）7（C ）15（D ）31（4）(北京市东城区2012年4月高考一模理科)右图给出的是计算1001...81614121+++++的一个程序框图，其中判断框内应填入的条件是（A ）50<i （B ）50>i （C ）25<i （D ）25>i【答案】B（5）(北京市东城区2012年4月高考一模文科)右图给出的是计算1001...81614121+++++的值的一个程序框图，其中判断框内应填入的条件是（A ） 50>i （B ） 25>i （C ）50<i （D ） 25<i【答案】B5. (2012年4月北京市房山区高三一模理科执行如图所示的程序框图，则输出的n 的值为（ C ）（A ）5（B ）6（C ）7 是（D ）8 否二、填空题：11. (2012年3月北京市朝阳区高三一模文科)执行如图所示的程序框图，若输入k 的值是4，则输出S 的值是 .3413．(2012年3月北京市丰台区高三一模文科)执行如图所示的程序框图，若输出的n 的值为10，则a 0=____．【答案】3。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。