企业诊断-基于PCA的传感器网络的故障诊断分析 精品
基于PCA方法的热泵空调系统传感器故障诊断

基于PCA方法的热泵空调系统传感器故障诊断热泵空调系统是一种利用空气或水等环境能源进行采暖或制冷的系统,它包含了许多传感器用于监测系统的运行状态。
传感器故障可能导致系统工作不稳定或无法正常工作,因此传感器故障诊断对于确保系统的正常运行至关重要。
首先,我们需要收集系统中不同传感器的数据,在正常工作状态下进行监测。
这些数据通常包括温度、湿度、压力等参数的变化。
为了保证准确性,最好在不同工况和环境条件下进行多次数据采集。
然后,需要对传感器数据进行预处理。
预处理包括数据清洗、异常值处理和数据归一化等步骤。
数据清洗可以去除无效或错误的数据,而异常值处理可以修正由传感器故障引起的偏差值。
数据归一化是为了消除因传感器量程不同而引起的数据不一致。
接下来,利用PCA方法对传感器数据进行分析和降维。
PCA方法通过计算协方差矩阵和特征向量,将高维数据投影到低维空间中。
投影后的数据可以被分解为主成分和噪声成分。
主成分包含了原始数据中的主要特征,而噪声成分则包含了数据中的随机变化。
通过分析主成分的贡献率和累积贡献率,我们可以确定主要的故障模式和传感器故障类型。
故障模式是指由于传感器故障引起的数据变化模式,例如温度过高、压力异常等。
传感器故障类型是指导致故障模式的具体传感器故障原因,例如传感器失效、传感器偏移等。
最后,利用机器学习算法对故障模式和传感器故障类型进行分类。
常用的机器学习算法包括决策树、支持向量机和神经网络等。
通过训练模型,我们可以建立故障诊断模型,根据传感器数据预测系统的故障类型,并及时采取相应的维修措施。
综上所述,基于PCA方法的热泵空调系统传感器故障诊断可以通过数据采集、预处理、PCA分析和机器学习算法等步骤实现。
这种方法能够有效地识别故障模式和传感器故障类型,提高系统的可靠性和稳定性,减少能源浪费和维修成本。
因此,它具有重要的研究和应用价值。
PCA故障诊断步骤(分享借鉴)
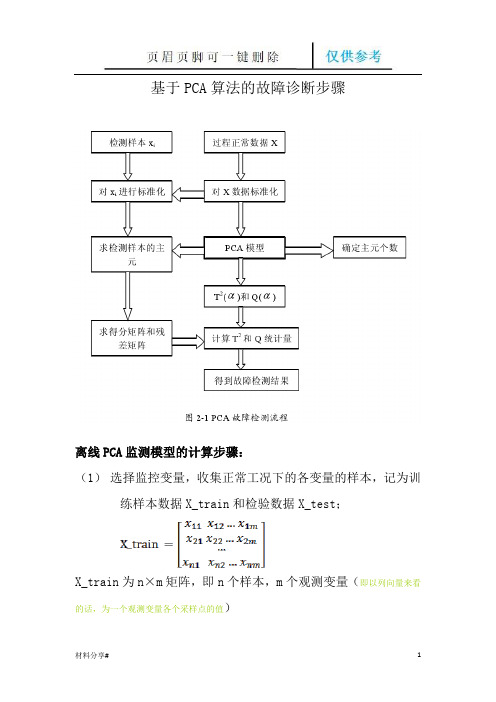
基于PCA算法的故障诊断步骤
离线PCA监测模型的计算步骤:
(1)选择监控变量,收集正常工况下的各变量的样本,记为训练样本数据X_train和检验数据X_test;
X_train为n×m矩阵,即n个样本,m个观测变量(即以列向量来看的话,为一个观测变量各个采样点的值)
对样本数据X_train和检验数据X_test进行中心化和标准化处理
得到和;
中心化处理:按列对X_train减去观测变量的均值
观测变量某一采样点的值减去这一观测变量所有采样点
的平均值
求取一列(即某一观测变量)的平均值
标准化处理:对X_train除以观测变量的标准差(按列(观测变量)进行)
标准差
求出标准化矩阵的协方差矩阵∑;
的协方差矩阵对∑为:
(2)对∑进行特征分解,求得特征值
()及其对应的特征向量
(负荷向量);
(3)确定主元个数, 确定了主元个数k,就得到了k个特征值
,及其对应的特征向量;
A:累计贡献率法:
前k个主元的累积方差贡献率为:
当前k个主元的累积方差贡献率达到85%,则主元个数取k值B:交叉检验估计法:
将采集到的数据分成k个部分,1部分数据用来建立主元模型,剩下的k-1部分用来作为检验数据去检验所建的模型。
如此,建立若干个不同主元个数的模型,并测试所建立的模型,从中选取一个通过检验后误差最小的模型的主元个数作为系统主元个数。
(4)建立PCA主元模型,并进行交叉验证以确定误差最小
按照,求出第i个主元,并依据
求出其主元模型
用带入得到另一主元模型,依据,求出模型误差,确定模型误差最小的那个模型即为主元模型。
(5)计算T2统计量控制限和SPE统计量控制限;。
分析无人机PCA故障检测与诊断技术研究

分析无人机PCA故障检测与诊断技术研究
主成分分析(Principal Component Analysis,PCA)是一种常用的数据降维技术,它可以将高维数据压缩到低维空间,从而提取出数据中的主要特征。
在无人机故障检测与诊
断中,PCA技术可以用于对传感器数据进行降维和特征提取,从而实现对无人机故障的检
测和诊断。
在无人机飞行中,无人机的传感器会收集到大量的数据,包括飞行姿态、加速度、气
压和温度等。
这些数据通过传感器进行采集后,经过预处理和滤波等操作,即可得到用于
故障检测与诊断的数据。
然后,使用PCA技术对数据进行降维处理,保留数据中最具代表
性的主要特征。
具体而言,通过PCA技术,可以将原始数据投影到主成分空间中,从而实现数据的降
维和特征提取。
在该过程中,将数据从高维空间映射到低维空间,并保留尽可能多的信息。
通过分析主成分的方差贡献率,还可以确定主要的故障模式和异常数据。
在无人机故障检测与诊断中,利用PCA技术可以将传感器数据映射到主成分空间中,
并提取出最具代表性的主要特征。
然后,通过比较主成分得分和阈值,可以检测出无人机
是否存在故障。
根据主成分空间中的故障模式和异常数据,可以进一步诊断故障的具体原因。
无人机PCA故障检测与诊断技术的研究为确保无人机的安全运行提供了有力支持。
通
过对传感器数据进行降维和特征提取,利用PCA技术可以检测和诊断无人机的故障,为故
障处理和维修提供指导。
未来,还可以进一步研究和改进无人机故障检测与诊断技术,提
高无人机的可靠性和安全性。
PCA故障诊断步骤剖析
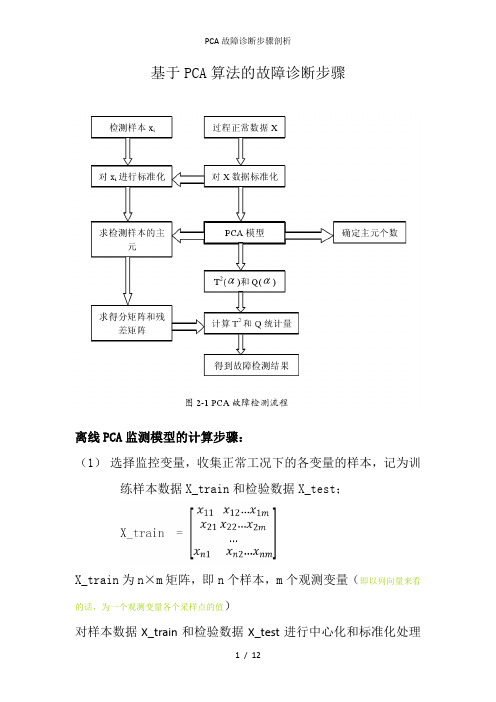
基于PCA算法的故障诊断步骤离线PCA监测模型的计算步骤:(1)选择监控变量,收集正常工况下的各变量的样本,记为训练样本数据X_train和检验数据X_test;X_train为n×m矩阵,即n个样本,m个观测变量(即以列向量来看的话,为一个观测变量各个采样点的值)对样本数据X_train和检验数据X_test进行中心化和标准化处理得到和;中心化处理:按列对X_train减去观测变量的均值观测变量某一采样点的值减去这一观测变量所有采样点的平均值求取一列(即某一观测变量)的平均值标准化处理:对X_train除以观测变量的标准差(按列(观测变量)进行)标准差求出标准化矩阵的协方差矩阵∑;的协方差矩阵对∑为:(2)对∑进行特征分解,求得特征值()及其对应的特征向量(负荷向量);(3)确定主元个数, 确定了主元个数k,就得到了k个特征值,及其对应的特征向量;A:累计贡献率法:前k个主元的累积方差贡献率为:当前k个主元的累积方差贡献率达到85%,则主元个数取k值B:交叉检验估计法:将采集到的数据分成k个部分,1部分数据用来建立主元模型,剩下的k-1部分用来作为检验数据去检验所建的模型。
如此,建立若干个不同主元个数的模型,并测试所建立的模型,从中选取一个通过检验后误差最小的模型的主元个数作为系统主元个数。
(4)建立PCA主元模型,并进行交叉验证以确定误差最小按照,求出第i个主元,并依据求出其主元模型用带入得到另一主元模型,依据,求出模型误差,确定模型误差最小的那个模型即为主元模型。
(5)计算T2统计量控制限和SPE统计量控制限;对于样本个数为n,主元个数为k的过程变量X_train, T2统计量服从自由度为k和n一k的F分布,则置信度为а的T2统计量控制上限为:或检验水平为а的SPE统计量控制上限为:,,,是与(1-)分位点对应的标准差在线过程监测与故障诊断步骤:(1)采集第i时刻的在线实时数据(为1×m矩阵),并进行中心化和标准化处理得到;(2)按照,求出的得分向量,依据,求出PCA模型估计量,这里;(3)计算的T2统计量和SPE统计量,并画出T2统计量和SPE 统计量的控制图;(4)将上述计算结果与T2统计量控制限和SPE统计量控制限比较,以检测过程运行有无异常,当有异常状态发生时,绘制贡献图,找出与故障相关的系统变量:1)检查每个观测值x的标准化得分,并确定造成失控状态的r(r<a)个得分:;2)计算每个变量相对于失控得分的贡献率是:3)当是负时,设它为零;4)计算第j个过程变量的总贡献率:5)把所有m个过程变量的画在一个曲线图上。
分析无人机PCA故障检测与诊断技术研究

分析无人机PCA故障检测与诊断技术研究【摘要】本文主要研究了无人机PCA故障检测与诊断技术,通过分析无人机PCA技术原理、故障检测方法和诊断算法,展示了相关案例分析和实验结果。
研究发现无人机PCA技术在故障检测和诊断方面存在挑战,需要解决问题。
结论部分总结了本文的研究成果,并展望了未来的研究方向和应用前景。
本文旨在为无人机领域的技术进步提供一定的参考和指导。
【关键词】无人机、PCA、故障检测、诊断技术、研究、原理分析、方法研究、算法分析、案例分析、实验结果、问题、挑战、总结、未来展望、应用前景1. 引言1.1 研究背景卫星地图使我们对地球的了解日益深入,并为我们的生活和工作提供了无限可能。
随着无人机技术的不断发展和应用,无人机已经成为获取高分辨率遥感数据的重要工具之一。
无人机在航空摄影测量、农业监测、环境监测等领域的应用越来越广泛。
本研究旨在探讨无人机PCA故障检测与诊断技术,为无人机的飞行安全提供更有效的保障。
通过对无人机PCA技术的原理分析、故障检测方法研究、故障诊断算法分析以及案例分析与实验结果展示,本研究将为该领域的技术研究和实践应用提供有益参考。
1.2 研究目的研究目的是为了探索无人机PCA故障检测与诊断技术的发展趋势,为无人机领域的安全运行提供技术支持。
通过对无人机PCA技术原理、故障检测方法和诊断算法的深入研究,旨在提高无人机系统的可靠性和安全性,降低故障率,提升飞行效率。
通过案例分析与实验结果展示,验证无人机PCA技术在实际应用中的可行性和有效性,为相关研究和应用提供参考依据。
本研究还将分析无人机PCA技术研究存在的问题与挑战,为今后研究工作提供方向和思路。
本研究的目的是探讨无人机PCA故障检测与诊断技术的关键问题,推动无人机领域的技术进步和发展。
1.3 研究意义:无人机在航空领域的应用越来越广泛,无人机的安全性和可靠性成为人们关注的焦点。
PCA技术作为无人机自动控制系统的核心组件,对于无人机的飞行稳定性和性能起着至关重要的作用。
基于PCA的传感器网络的故障诊断分析

基于PCA的传感器网络的故障诊断分析发布者:刘成??发布时间:2006-9-12 10:30:00内容摘要摘要:主成分分析是多元统计方法,正逐步成为控制领域中一种重要的数据处理方法,用于生产监测和质量控制。
本文简要地介绍了PCA中两种常用的图形分析法——Q图和主元得分法,利用统计软件——SPSS对数据进行处理,简化了复杂的运算过程,并对其数据处理过程进行了说明。
最后,通过空压机远程监控系统传感器网络的实例模型,运用SPSS软件,说明了这一数据处理方式的简便、有效性和缺陷。
关键词:主元分析法;故障诊断;空压机;传感器网络正文1.引言在现代化工业控制过程中,通常都运用了大量的测量传感器,如温度,流量,压力传感器等,形成了复杂的传感器网络。
各传感器测量值之间高度相关以及实际生产过程中存在的各种随机因素,使得系统过程变量多且耦合性强,建模困难。
传统的基于机理模型的诊断方法,显然难于满足要求。
统计学中的多元统计方法(如主元分析方法(PCA),偏最小二乘法(PLS)及因子分析),是一种不依赖于过程机理的建模方法,它只需通过对过程数据信息进行建模,然后基于该模型实施过程监控和故障诊断分析。
主元分析(PCA)作为一种多元统计方法,最初是运用在医学、教育、生物,等社会科学领域,由于它不依赖于精确数学模型这一显着优点,使它得到了工控界学者的广泛关注,并逐步发展成为控制领域中一种重要的数据分析处理方法。
其根本思想在于对原有复杂的多变量数据空间进行数据提取,用较少的变量来解释系统数据结构。
它既保留了原有数据的基本信息,又大大降低了数据空间的维数,去掉了一些不必要的耦合,极大地方便了对过程数据的分析。
故障诊断过程主成分分析法进行故障检测和诊断的基本思想就是:根据收集的正常工况下的历史数据,按一定的标准,利用统计方法找出能够表达正常工况下过程各变量之间的因果关系低维主成分,即主元模型,一旦过程的实时测量数据与建立的主元模型不符就可以判断过程中已有故障发生,再通过对测量数据中各变量变化对主元模型的破坏贡献率分析,进一步进行故障诊断。
大作业-基于PCA故障诊断汇总

鉴于主元剖析( PCA)的故障诊疗小构成员 :日期:目录1. 运用 PCA 方法的前提 (2)2. PCA 方法的基本理论 (2)2.1 思路概括 (2)2.2 基本理论 (2)3. 利用 PCA方法进行故障诊疗的步骤 (4)3.1 成立正常工况的主元模型 (4)3.2 在线故障检测与诊疗 (4)4. PCA 的限制性或优弊端 (4)5. 鉴于 TE 过程的故障诊疗 (4)5.1 TE 过程简介 (4)5.2 鉴于 PCA 的故障诊疗 (6)5.2.1 仿真的参数设置 (6)5.2.2 仿真结果 (6)5.3 仿真总结 (12)6. 总结 (12)13 参照文件 ......................................................................................................................14 附录 ..............................................................................................................................1.运用 PCA 方法的前提1、样本观察相对独立2、潜伏变量听从高斯散布2.PCA 方法的基本理论2.1 思路概括PCA 方法是将高维过程数据投影到正交的低维子空间,并保存主要过程信息。
而在几何上,把样本构成的坐标系,经过某种线性组合旋转到新的坐标空间,新的坐标轴代表了具有最大方差的方向[1]。
2.2 基本理论假定 x R m代表一个包括了m个传感器的丈量样本,每个传感器各有n 个独立采样,结构出丈量数据矩阵X R n m,此中每一列代表一个丈量变量,每一行代表一个样本。
( 1)对数据矩阵进行协方差分解,并选择主元的个数X 的协方差矩阵为S X T X,对其进行特点值分解,并且依据特点值的大小降序排序,n 1以下:S X T X VV T [ P P][ P P]Tn 1此中,是一个对角阵,也是 S 的特点值矩阵,并且其对角线上的元素知足1 2 V是 S 的特点向量矩阵,维数为 m x m ,P是V的前 A 列,包括全部主元的信息,余下的 m-A 列,包括非主元信息。
基于PCA神经网络和D-S决策的瓦斯传感器故障辨识

基于PCA神经网络和D-S决策的瓦斯传感器故障辨识黄丹;徐平安;王其军;任玉东;严彬【摘要】针对瓦斯传感器故障诊断时,存在提取的样本数据空间维数大、诊断实时性差、诊断结论的识别能力低和存在不确定性的问题,提出了一种基于主元分析(PCA)-神经网络和D-S证据理论集成的故障诊断策略.使用主元分析方法对高维故障样本空间数据进行降维,再结合神经网络分类器进行故障模式识别.并且运用DS 证据理论对神经网络分类器的故障诊断结果进行数据融合.仿真实验表明:该诊断方法改善了神经网络对瓦斯传感器故障诊断准确率的同时提高了诊断速度,并且降低了故障结论的不确定性以及提高了结论的识别与决策能力.【期刊名称】《仪表技术与传感器》【年(卷),期】2015(000)003【总页数】5页(P99-103)【关键词】瓦斯传感器;故障诊断;主成分分析;神经网络;DS证据理论【作者】黄丹;徐平安;王其军;任玉东;严彬【作者单位】安徽理工大学电气与信息工程学院,安徽淮南 232001;安徽理工大学电气与信息工程学院,安徽淮南 232001;安徽理工大学电气与信息工程学院,安徽淮南 232001;淮南职业技术学院,安徽淮南232001;安徽理工大学电气与信息工程学院,安徽淮南 232001;安徽理工大学电气与信息工程学院,安徽淮南 232001【正文语种】中文【中图分类】TP212瓦斯气体浓度的监测是煤矿安全监测的重要指标之一。
瓦斯传感器也就成了煤矿安全的重要仪器。
目前我国煤矿井下大都使用带有载体催化元件的瓦斯传感器。
但由于井下环境恶劣,导致瓦斯传感器的卡死故障、冲击故障、漂移故障、周期故障等常见故障频发。
因此研究瓦斯传感器的故障诊断方法,对提高煤矿安全监测系统的可靠性有着极其重要的作用[1]。
目前在煤矿安全监测系统中常采用的诊断方法有粗糙集与证据理论的结合,粗糙集与神经网络的结合等。
其中粗糙集在原始故障数据的预处理方面已经得到很好的运用,它在处理冗余数据有其长处,而不足之处在于对噪声的敏感。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于PCA的传感器网络的故障诊断分析发布者:刘成发布时间:20XX-9-12 10:30:00内容摘要摘要:主成分分析是多元统计方法,正逐步成为控制领域中一种重要的数据处理方法,用于生产监测和质量控制。
本文简要地介绍了PCA中两种常用的图形分析法——Q图和主元得分法,利用统计软件——SPSS对数据进行处理,简化了复杂的运算过程,并对其数据处理过程进行了说明。
最后,通过空压机远程监控系统传感器网络的实例模型,运用SPSS软件,说明了这一数据处理方式的简便、有效性和缺陷。
关键词:主元分析法;故障诊断;空压机;传感器网络正文1.引言在现代化工业控制过程中,通常都运用了大量的测量传感器,如温度,流量,压力传感器等,形成了复杂的传感器网络。
各传感器测量值之间高度相关以及实际生产过程中存在的各种随机因素,使得系统过程变量多且耦合性强,建模困难。
传统的基于机理模型的诊断方法,显然难于满足要求。
统计学中的多元统计方法(如主元分析方法(PCA),偏最小二乘法(PLS)及因子分析),是一种不依赖于过程机理的建模方法,它只需通过对过程数据信息进行建模,然后基于该模型实施过程监控和故障诊断分析。
主元分析(PCA)作为一种多元统计方法,最初是运用在医学、教育、生物,等社会科学领域,由于它不依赖于精确数学模型这一显著优点,使它得到了工控界学者的广泛关注,并逐步发展成为控制领域中一种重要的数据分析处理方法。
其根本思想在于对原有复杂的多变量数据空间进行数据提取,用较少的变量来解释系统数据结构。
它既保留了原有数据的基本信息,又大大降低了数据空间的维数,去掉了一些不必要的耦合,极大地方便了对过程数据的分析。
2.PCA故障诊断过程主成分分析法进行故障检测和诊断的基本思想就是:根据收集的正常工况下的历史数据,按一定的标准,利用统计方法找出能够表达正常工况下过程各变量之间的因果关系低维主成分,即主元模型,一旦过程的实时测量数据与建立的主元模型不符就可以判断过程中已有故障发生,再通过对测量数据中各变量变化对主元模型的破坏贡献率分析,进一步进行故障诊断。
2.1 PCA基本定义设原始变量:X1、X2、X3、…、X m主成分:Z1、Z2、Z3、… 、Z m则各因子与原始变量之间的关系可以表示成:写成矩阵形式为:X=BZ+E 。
其中,X为原始变量向量,B为公因子负荷系数矩阵,Z为公因子向量,E为残差向量,忽略E数学模型变为,其中Z中各向量之间彼此不相关。
主成分分析的目的就是要求出系数矩阵B。
2.2主元的提取在数据空间主要信息提取过程中,合理确定主元个数非常重要,主元个数多,其信息准确度高,但系统分析复杂程度也大幅度增加,噪声也难于滤除。
选取过少,则造成数据信息严重丢失,不能反映系统实质,诊断准确度不能保证。
提取主元的步骤具体如下:Step1:对原始数据进行标准化处理,使得样本点集合的重心与坐标原点重合,而压缩处理则可以消除由不同量纲所引起的虚假差异信息,使分析结果更加合理;Step2:计算标准化后的数据矩阵的协方差矩阵,此时,V也是X的相关系数矩阵;Step3:求V的前m个特征值以及他们的特征向量,并将其单位正交化;Step4:计算各成分的贡献率;Step5:前k个成分的累计贡献率;Step6:按贡献率大小列表,选取累计贡献前k个变量作为主成分向量。
2.3 PCA统计分析通过前面步骤得到主成分向量后,运用多变量统计控制图对原有数据空间进行分析,判断系统工作状态。
多元变量统计图有多种,如,主元得分图,平方预测方差图(SPE),HotellingT2图,贡献图等。
其中,SPE图和T2图,可以根据其统计量是否超出控制限来判断系统是否出现异常状况,其过程方便快捷,但不能从图中准确判定故障来源,确定是哪个传感器异常。
与此相反,主元得分图和贡献图稍显繁琐,但可准确确定故障来源。
这里限于篇幅,只简要的介绍其中有代表性的两种——得分图和Q 图。
2.3.1 主元得分图主元得分图是主元模型内部各主元向量的空间分布,各个主元随时间不断变化。
系统正常运行,则各主元向量在一定范围内波动。
若有一段时间有若干点分布在其他区域,则系统发生故障。
假定第j 个得分主元分布发生异常,我们可以利用因子分析找出与第j 个得分主元关系最密切的几个向量,这样就能很快得到故障源位置。
其中,得分主元计算公式为: t j =X P j式中 t j ——得分向量P j ——负荷向量2.3.2 Q 统计图Q 统计图,也叫平方预测方差(SPE )统计图,其实质就是将各采样值的SPE 统计量置一定的可信度,若超出其范围的,即为异常点。
对于第i 个采样点:式中e i ——残差矩阵第i 行I ——单位矩阵P k = {p 1 p 2 … p k }——前k 个得分特征向量检验水平为α时,统计量控制限为:()0h 12002120111h h 2h C Q ⎥⎥⎦⎤⎢⎢⎣⎡+-+=θθθθθαα式中 ()3,2,1i n 1k j i j i ==∑+=λθ 22310321h θθθ-=——X 协方差矩阵的特征值——正态分布置信度为 的统计若 则统计量出现异常,一般采用95%的控制限。
注:以上数据处理过程,如求解特征值,主元向量,载荷向量,多元变量统计控制图都是基于统计软件SPSS 的强大计算功能上的,极大程度简化了计算过程,特别是在过程变量较多时,其具体运用过程,在下面通过实例进行分析。
3.实例故障诊断3.1 空压机监控模型描述空压机远程监控与故障诊断系统,是以PCA检测技术为应用的故障监测与诊断系统。
其采集的信号变量具体分类如下:(1)压力信号分别为1级缸、2级缸及储风缸压力3点;(2)温度信号为1级缸排气温度、2级缸进气温度、2级缸排气温度、油温、曲轴轴承温度2点、电机轴承温度2点以及冷却水出口温度共9点;(3)电量信号为主电机电流1点,及总电源的3相电压共3点。
采集参数总计为(9+3+1)x2+3=29个。
由于变量众多,为了说明方便,选取其中8个典型变量进行实例分析说明,相关变量及其系统结构,如图1所示。
3.2 PCA故障诊断分析选取I、TL、TY、TQ、TP1、TP2、TJ2、TG8等个变量进行监测,显然这些变量都是非线性的,且有些变量(如TP1、TJ2 、TL)之间相关性很强。
采集空压机正常运行和故障阶段300组数据进行PCA分析,采用SPSS软件进行分析,从而得到表1至表3,具体步骤如下:FACTOR/VARIABLES i tp1 tp2 tq tl ty tg tj2/MISSING LISTWISE/ANALYSIS i tp1 tp2tq tl ty tg tj2/PRINT UNIVARIATE INITIAL CORRELATION KMO EXTRACTION ROTATION FSCORE/CRITERIA FACTORS(3) ITERATE(25)/EXTRACTION PC/CRITERIA ITERATE(25)/ROTATION VARIMAX/SAVE REG(ALL)/METHOD=COVARIANCE .由表1可以得到采样数变量均值及方均差。
表2为主元贡献及累积贡献率,它们是选取主元的主要依据,前3个主元的累积贡献率为85.285。
表3为旋转后生成的主成分负荷矩阵,其值绝对值愈大,表明变量与主成分关系愈密切,从表中可以得出:主电机电流、2级缸排气温度和2级缸进气温度与第一主成分,1级缸排气温度、曲轴轴承温度和冷却水温度与第二主成分,机油温度、电机轴承温度与第三主成分关系密切。
此时,只需根据三个主元得分向量的贡献图分析,就可以得到系统故障信息,再根据表2相关矩阵,找出故障源具体位置.由图2可以看到第3主元得分向量分布图在前250组数据分布在两控制限之间,但到了250组之后,有一些数据超出了控制限。
由此可以得知:是与第3主元相关的变量传感器出现了故障,又根据表2相关信息,可以判断故障源是机油或电机轴承温度。
作机油温度控制图,如图3所示,可以看出数据在250组以后,也出现了异常。
由此,验证了前面通过图2和表2得出的故障源是机油温度异常的正确性。
在实际过程中,通过检查空压机机油状况,发现机油泄露,造成机油不足,油温上升。
从而,验证了以上数据分析的有效性。
注:由于空压机故障数据来源是在人为泄露空压机机油,假定机器故障的情况下采集的,采集时间不宜太长,以免造成真正故障,故而故障数据相对较少。
4.结束语本文介绍了PCA分析方法中典型的两种有力的分析工具——Q图和主元图,并利用空压机远程监控系统这一实例,加以验证分析,取得了较好的效果。
该系统在实际运用过程中在上位机中调用了SPSS统计软件,为其数据处理带来了极大方便,但由于系统变量众多(29个),SPSS运行速度较慢,造成系统实时性不好。
在以后的系统改进调试中可以事先对数据进行压缩处理和聚类分组或采用多组PCA并行处理方式,来改善系统反应的实时性。
[1] 熊丽,梁军.基于PCA的系统故障监测方法及其三相异步电动机防真研究,机电工程,20XX年第20卷,第5期.[2] 陈勇,梁军,陆浩.基于PCA的多变量控制系统的故障监测与诊断,工程设计学报,20XX年12月第9卷,第5期.[3] 陈友明,郝小礼,彭建国.空调监测系统的数据恢复方法的研究,湖南大学学报,20XX年6月第30卷,第3期.[4] 卢纹岱.SPSS for Windows统计分析(第3版.电子工业出版,20XX年6月.[5] QIN S J , YUE H Y,DUNIA R. Self2 validating inferential sensors with application to air emission monitoring [J ] . Ind Eng Chem Res , 1997 , 36 : 167521685.[6 ] WACHS A ,L EVIN D R. Improved PCA methods for process distur ibance and failure identification[J ] . AIChE Journal , 1999 , 45 (8) :168821700.[7] 赵望达,鲁五一等. 工控计算机在空压机组监测控制系统中的应用. 压缩机技术,2000,4:16~18。
