化学动力学基础
化学动力学基础知识点总结

化学动力学基础知识点总结
化学动力学是化学的一个分支,主要研究化学反应的速率和机理。
以下是一些化学动力学的基础知识点总结:
1. 反应速率:化学反应速率是指单位时间内反应物或生成物浓度
的变化量,可以用单位时间内反应物或生成物的摩尔数来表示。
2. 反应级数:反应级数是指化学反应速率与反应物浓度的幂次方
之间的关系。
一级反应的速率与反应物浓度的一次方成正比,二级反
应的速率与反应物浓度的二次方成正比,以此类推。
3. 活化能:活化能是指反应物分子从常态转变为能够发生化学反
应的活化态所需的能量。
活化能越高,反应速率越慢。
4. 催化剂:催化剂是一种能够加速化学反应速率而自身在反应过
程中不被消耗的物质。
催化剂通过降低反应的活化能来加速反应速率。
5. 反应机理:反应机理是指化学反应的具体步骤和过程,包括反
应物分子如何相互作用形成过渡态以及过渡态如何转化为生成物。
6. 碰撞理论:碰撞理论认为化学反应是反应物分子之间的碰撞导致的。
只有那些具有足够能量的分子在适当的取向下发生碰撞时,才能发生化学反应。
7. 阿伦尼乌斯方程:阿伦尼乌斯方程是描述反应速率与温度之间关系的经验公式。
它表明反应速率常数与温度成指数关系,活化能越高,温度对反应速率的影响越大。
8. 稳态近似:稳态近似是一种处理快速平衡反应的方法,假设反应中间物的浓度在反应过程中保持恒定。
这些是化学动力学的一些基础知识点,化学动力学在化学研究和实际应用中都有广泛的应用,例如在化学工程、药物研发、环境保护等领域。
第7章 化学动力学基础

例:有一化学反应aA+bB=C在298K时,将AB溶液按
不同浓度混合。得到下列数据。
A的初始浓度 B的初始浓度 1.0 1.0 2.0 1.0 4.0 1.0 1.0 1.0 1.0 2.0 1.0 4.0 求其速率方程? 初始速度(mol/l· s) 1.2×10-2 2.3×10-2 4.9×10-2 1.2×10-2 4.8×10-2 1.9×10-1
( H O ) C (H O ) C (H O ) v t t
2 2 2 2 2 1 2 2
作出H2O2的 c — t 的曲线,得到 0 — 40
min的平均速率:
v 0.20 0.80 0.20 0.80 0.015mol dm 3 min 1 t 40
求该反应的反应级数m+n和速度常数k?
解:由速度方程v=k[CO]m· 2]n [Cl 得:v1=k[CO]m· 2]1n v2=k[CO]m· 2]2n [Cl [Cl
n v1 [Cl 2 ]1 v2 [Cl 2 ]n 2
2 v1 1.2 10 lg lg v2 4.26 10 3 0.45 1.5 n [Cl 2 ]1 0.10 0.30 lg lg [Cl 2 ]2 0.050 v1 1.2 10 2 lg lg v3 6.0 10 3 1 m [CO ]1 0.10 lg lg [CO ]3 0.050
解:由v=k[A]m· n [B] v1=k×1m×1n=k=1.2×10-2
v2=k×2m×1n=k×2m=2.3×10-2
v1 1 1.2 10 2 1 m 2 v2 2 2.3 10 2
v4=k×1m×1n=1.2×10来自2 v5=k×1m×2n=4.8×10-2 ∴k×2n=4.8×10-2 2n=4.8×10-2/k=4=22 ∴n=2
05 第五章 化学动力学基础

(2.1 3.0) rH 2 0.1(mol L-1 s -1 ) 3 3
rNH 3 (0.6 0) 0.1(mol L-1 s -1 ) 3 2
化学与材料科学学院
r kc ( NO)c(O2 )
2
化学与材料科学学院
殷焕顺
2.应用速率方程的注意事项
①反应物是气体时,可用分压代替浓度。
如基元反应:
2 NO( g ) O2 (g) → 2 N O2 (g)
r kc ( NO)c(O2 ) rp k p p ( NO) p(O2 )
2
2
②固体或纯液体不写入速率方程。
mol· -1· -1 L min
化学与材料科学学院
殷焕顺
1.1 平均速率
对任一化学反应:
aA bB
选用产物表示时, 取 + 号;选用反 应物表示时,取 - 号,目的是使 反应速率为正值。
在时间间隔△t内,其平均速率为:
c( A ) rA t c( B ) rB t
化学与材料科学学院
化学与材料科学学院
殷焕顺
1. 速率方程
如任意反应:aA + bB = dD + eE
速率可表示为:
r k c c
x A
y B
k 为反应速率常数;
x、y 分别为反应物A、B的反应级数;
x + y为反应的总级数。
化学与材料科学学院
殷焕顺
质量作用定律-古德贝格(Guldberg)
质量作用定律
描述:在一定温度下,对简单反应(或复合反应中 的基元反应), 化学反应的速率与以反应方程式中 化学计量数为指数的反应物浓度的乘积成正比。
物理化学第9章 化学动力学基础

速率方程必须由实验来确定
四、反应级数 若反应的速率方程可以表示为浓度的幂乘积形式:
r = k[A][B]…
则各浓度项的方次、、…分别称为组分A、B …的
例 1、P165例题
某金属钚的同位素进行β放射,14 d 后,同位
素活性下降了6.85%。试求该同位素的:
(1) 蜕变常数,(2) 半衰期,(3) 分解掉90%所需时间
解:
(1)
k1
=
1 t
ln
a
a
x
=
1 14d
ln
100 100 6.85
=
0.00507d-1
(2) t1/2 = ln 2 / k1 = 136.7d (3) t = 1 ln 1 = 1 ln 1 = 454.2d
例如:
例如,恒容反应器中,氯代甲酸三氯甲酯分解为光气
ClCOOCCl(g) 2COCl2(g)
t = 0 p0
0
t = t p酯
p光气=2( p0 – p酯)
p总 = p酯 + p光气 = 2 p0 –p酯
∴ p酯 = 2p0 – p总
或 p光气 = 2(p总– p0)
三、反应速率 r 的经验表达式
2、适用范围
ln k = Ea B RT
k = AeEa / RT
3、A意义:称指前因子
二、活化能的概念 1、对简单反应:
那些能量高到能发生反应的分子称为“活化分子” 活化能:活化分子的平均能量与反应物分子平 均能量之差值。
北理无机化学第3章-化学动力学基础

基元反应
§3.2 浓度对反应速率的影响
NO2(g)+CO(g) NO(g)+CO2(g)
v=kc(NO2)c(CO)
反应级数 n = 2
基元反应 2NO(g)+O2(g)2NO2(g)
v=kc(NO)2c(O2)
反应级数 n = 3
第三章 化学动力学基础
3.注意
§3.2 浓度对反应速率的影响
或
lg{k}
Ea 2.303RT
lg{k0}
k: 反应速率常数,由反应的性质和温度决定;
Ea:实验活化能,单位为kJ·mol-1,是表示反应特性 的常数;
k0:指数前因子,频率因子,对指定反应为一常数。
第三章 化学动力学基础
§3.3 温度对反应速率的影响
3.3.2 Arrhenius 方程式的应用
vB ΔcB Δt
vC
ΔcC
t
vD ΔcD Δt
浓度的单位:mol·L-1 时间的单位:s(h、min)
第三章 化学动力学基础
例:
起始浓度/(mol·L-1)
§3.1 反应速率的意义
N2 + 3H2 → 2NH3
13
0
2秒后浓度/(mol·L-1)
0.8 2.4 0.4
同一反应,可用不同物质的浓度的变化表示反应速率,其 值可能不同。
vN2
-
(0.8-1) 2
0.1mol
L-1
S-1
vH2
-
(2.4- 3) 2
0.3 mol
L-1
S-1
vNH3
(0.42
0)
0.2 mol
L-1
S-1
第三章 化学动力学基础
物理化学答案——第九章-化学动力学基础
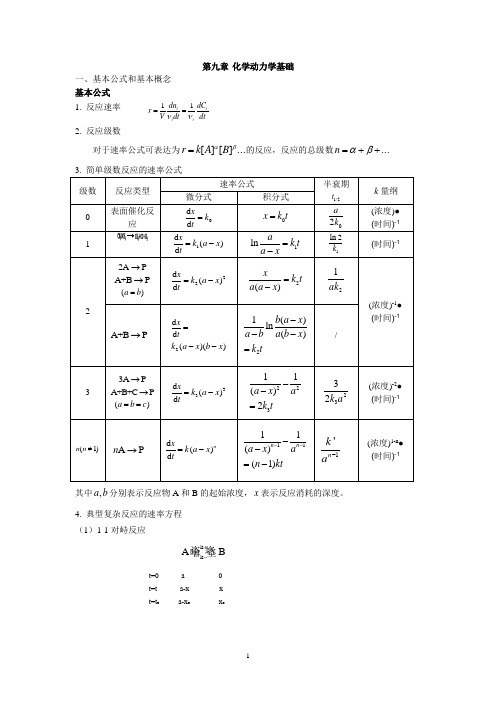
第九章 化学动力学基础一、基本公式和基本概念 基本公式 1. 反应速率 11i ii i dn dC r V dtdtνν==2. 反应级数对于速率公式可表达为...][][βαB A k r =的反应,反应的总级数...++=βαn 3. 简单级数反应的速率公式 级数 反应类型 速率公式半衰期 1/2tk 量纲微分式积分式0 表面催化反应0d d x k t =0x k t = 02a k (浓度)● (时间)-1 11d ()d x k a x t=-1lna k t a x=-1ln 2k(时间)-122A P→A +B P →()a b =22d ()d x k a x t=-2()x k t a a x =-21ak(浓度)-1●(时间)-1A +B P →2d d ()()xtk a x b x =--21()ln()b a x a b a b x k t---=/33A P→A +B +C P→()a b c ==33d ()d x k a x t=-22311()2a x a k t --=2332k a(浓度)-2● (时间)-1(1)n n ≠A P n →d ()d nx k a x t=-1111()(1)n n a x an kt----=-1'n k a-(浓度)1-n ● (时间)-1其中,a b 分别表示反应物A 和B 的起始浓度,x 表示反应消耗的深度。
4. 典型复杂反应的速率方程 (1)1-1对峙反应k k A B +-t=0 a 0 t=t a-x x t=t e a-x e x e速率方程: ()kk te e x x x e +--+-=(2)平行反应最简单的平行反应是由两个一级基元反应组成的平行反应:x=x 1+x 2速率方程:tk k aex a )(21+-=-产物B 和C 的浓度比由竞争反应的速率决定:2121k k x x = (3)连续反应最简单的连续反应是两个单向连续的一级反应:C B A kk −→−−→−21t=0 a 0 0 t=t x y z 速率方程:1k tx ae-=)(21121tk tk eek k a k y ----=]1[21121122tk tk ek k k ek k k a z ---+--=中间产物B 的浓度在反应过程中出现极大值:122)(21k k k m k k a y -=,出现极大值的时间为:2121)ln(k k k k tm-=5. 温度对反应速率的影响 (1)阿累尼乌斯经验公式2ln RTE dTk d a =阿累尼乌斯公式的指数函数式: RTE a Aek -=k 1k 2A a-xCx 2 B x 1(2)阿累尼乌斯活化能基元反应的活化能是活化分子的平均能量与所有分子平均能量之差。
化学动力学

RT
1
k2dA 2BLRT Me
2
eEa
RT
1
A2dA2BLRTMe 2
1
A2dA2BLRM T 2
kkB hTcθ1nexp R Sm θ exp R H Tm θ
适用范围:凝聚相反应
kkB h T R pT 1nexp R Sm θ exp R H Tm θ
Carbon Dioxide Fixation into Chemicals Methyl Formate at High Yields by Surface Coupling over a Pd/Cu/ZnO Nanocatalyst
Gm θRTlnKcθ
G m θRTlnKc
cθ
n1
Gm θ RT
lnKc
cθ
n1
cθ
K n1 c
expRG Tm θ
Kc cθ 1nexpRG Tm θ
k
kBT h
K
c
kkBT h
cθ
1nexpR G Tm θ
G
m
标准摩尔反应活化Gibbs自由能变
G m θ H m θT Sm θ
kkB h Tcθ1nexp R Sm θ exp E aR T R T
kkB hTcθ1nexp R Sm θ exp R T R TE a
kkBTcθ h
1nexp R Sm θexp1R E T a
kkBTecθ h
1nexp R Sm θexp R E Ta
rk2KccAcBC
根据过渡状态理论的假设活化络合物只 进行一次非对称伸缩振动就能断裂发生 反应因此反应速率为
k2
rr K cccAcBC
第六章 化学动力学基础.

第六章 化学动力学基础首 页 习题解析本章练习本章练习答案章后习题答案习题解析 [TOP]例13-1在酸的存在下蔗糖的反应中,偏光计的读数αt 如下: t/(min)0 30 90 150 330 630 ∞ αt46.5741.0030.7522.002.75-10.00-18.75这个反应是一级反应,求反应速率常数。
解1 对一级反应,不仅反应物的浓度本身,如果有和浓度成比例的量,则可以用来代替浓度。
αt是蔗糖溶液的偏振面转过的角度,在t = 0时溶液中只存在蔗糖,在t = ∞时蔗糖应该完全消失,而在公式ln c A =ln c A0-kt 中,和c A0成比例的量是α0-α∞,和c A 成比例的量是αt -α∞,因此可以用ln(αt -α∞)=ln(α0-α∞)-kt 计算各时刻的k 。
min 100.375.1800.4175.1857.46ln min 30131-⨯=++=kmin 101.375.1875.3075.1857.46ln min 90132-⨯=++=kmin 102.375.1800.2275.1857.46ln min 150133-⨯=++=kmin 104.375.1875.275.1857.46ln min 330134-⨯=++=kmin 102.375.1800.1275.1857.46ln min 630135-⨯=+-+=kmin 102.35354321-⨯=++++=k k k k k k解2 采用作图法,以lg(αt -α∞)对t 作图,得一直线,其斜率b = -k /2.303。
t /min3090150330630αt -α∞65.32 59.75 47.50 40.75 21.50 8.75 lg(αt -α∞)1.8151.7761.6771.6101.3320.942则k = -2.303⨯b 又b = - 0.00139,所以 k = 2.303⨯0.00139 = 3.20⨯10-3min -1例13-2尿素的水解反应为CO(NH 2)2 + H 2O −→2NH 3 + CO 225︒C 无酶存在时,反应的活化能为120k J ⋅ mol -1,当有尿素酶存在时,反应的活化能降为46 k J ⋅ mol -1,反应速率为无酶存在时的9.4⨯1012倍,试计算无酶存在时,温度要升到何值才能达到酶催化时的速率?解 浓度一定时,反应速率之比也即速率常数之比KT K T K T T T T T R E 775298298K mol J 1031.8mol J 1204.9ln ln104.922211312112121212=⎪⎪⎭⎫ ⎝⎛⨯-⋅⋅⨯⋅=⨯-=⨯=----解得k k k k k k 12a 10)(例13-3科学工作者已经研制出人造血红细胞。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 对于1级反应: 以 A = G + H 代表1级反应,则 v kc(A ) dc(A ) 微分表达式 k(A )
dt 数学表达式 ln c (A) ln c(A)0 kt
lg c(A ) lg c(A )0
k
2.303
t
0.693 t1 2k 2
一级反应的半衰期与反应物浓度无关。
P是与反应物分子碰撞时的取向有关,叫做取向因子, f为具有发生反应的能量的分子数与总碰撞分子数之比, 叫做能量因子。 活化分子、活化分子组 活化分子百分数
无机
化 学
如用数学形式综合上面两个条件: 则 r = Z×P ×f
Ea RT
能量因子符合玻尔兹曼分布率:
f e
取向因子取值范围10-9~1之间
正 催 化 剂 负 催 化 剂 使v (抑 制 剂 , 使v )
二、催化作用(Catalysis) 原因:改变了反应机理(途径)、使Ea下降, 反应 速率加快.
无机
化 学
催化剂(K)改变反应途径示意图
无机
化 学
7-2 浓度对反应速率的影响
无机
化 学
速率方程
对于
aA bB gG hH
m n
v k[c( A)] [c( B)] k:速率常数;m、n分别为A、B浓度的幂指数。 k、m、n均由实验测得。
无机
化 学
无机
化 学
无机
化 学
v k[c( A)] [c( B)]
m
n
上式中,k为温度函数,与各物质浓度无关。 m+n为反应级数。 反应级数可以为1、2、3等正整数,也可以为0,也可 以是分数。 当反应级数不同时,k值得单位也将不同。
无机
化 学
注意: 对于某一反应,可以用任一反应物或生成物来 表达反应速率。
反应速率不管大小,总取正值 不同反应物表达的反应速率的关系: 速率之比等于计量系数之比。
用方便测量的物质来表达
无机
化 学
注意: 速率数值常随所观察的物种而不同, 为了克 服此不便, IUPAC建议对于反应:
无机
化 学
一、k 与T 的关系 — Arrhenius公式 Ea Arrhenius 提出:
k Ae
RT
式中A — 频率因子,Ea — 实验活化能
Ea ln k ln A RT
Ea lg k lg A 2.303RT
无机
化 学
对Arrhenius方程的进一步分析 1. 在 k k0 exp( Ea / RT ) ,Ea处于方程的 指数项中,对k有显著影响,在室温下, Ea 每增加4kJmol-1,k值降低约80%. 2. 温度升高,k增大,一般反应温度每升高
无机
化 学
7-5 温度对化学反应速率的影响
例:
2 H ( g ) O ( g ) 2 H O( g )
2 2 2
1 m
rG (298K ) 457.18KJ .mol 0
R.T.几乎看不到反应 T = 10 K, v 提高 2-4 倍 点燃,爆炸 : T , k , v
O3 ( g ) NO( g ) NO2 ( g ) O2 ( g )
kc( NO) c(O3 )
发生反应的两个基本前提:
• 发生碰撞的分子应有足够高的能量 • 碰撞的几何方位要适当
无机
化 学
如用数学形式综合上面两个条件:
则
r表示有效碰撞次数,
r = Z×P ×f
Z表示分子总碰撞次数,叫做频率因子,
例:对于上述反应
rH Ea E' a 134 368 234kJ mol1
无机
化 学
优点: (1)可以理论计算一些简单反应的活化能、且与 Arrhenius的实验活化能值相符。 ( 2 )指出了反应速率与微观结构的联系,是一个 正确方向。 ( 3 ) v 不但与 Ea 有关,而且与形成活化配合物过程 G0 有关, 从而建立了动力学与热力学的桥梁。 缺点: (1)确定活化配合物的结构十分困难。 (2) 目前只解决了几个简单反应,应用范围还较小。
无机
化 学Βιβλιοθήκη 了解:1 1 kt c c0 1 t1 kc0 2
对于反应物只有一种的二级反应
对于反应物只有一种的三级反应
1 1 2 2kt 2 c c0
3 t1 2 2 kc 0 2
无机
化 学
7-6 基元反应的速率理论
一 碰撞理论 Lewis提出,以气体分子运动论为基 础,主要用于气相双分子反应。
无机
化 学
化学反应过程中能量变化曲线
Eac Ea(逆)
(正)
Eac
(正)
Ea(逆)
无机
化 学
E(Ⅰ)-反应物(始态)势能 : E(Ⅱ)-生成物(终态)势能
正反应的活化能
逆反应的活化能
Ea(正) =Eac - E(Ⅰ)
Ea(逆) =Eac - E(Ⅱ)
ΔrHm= E(Ⅱ) - E(Ⅰ)= [Eac - Ea(逆)] -[Eac - Ea(正)] ΔrHm= Ea(正) - Ea(逆)
由 Eyring 和 Pelzer 提出,运用了量子力学及统计 力学方法。认为从反应物到生成物之间形成了势 能较高的活化络合物,活化络合物所处的状态叫 过渡态。 要点: 1. 反应物分子—活化配合物(过渡状态) —产物 2. 位能(势能): 始态 过渡状态 终态 3. T一定, Ea ,则活化分子总分子总数的比例 ,反应速率v ;反之, Ea ,反应速率v .
无机
化 学
一般化学反应 若 Ea 40kJ mol 1 若 Ea 400kJ mol1 逆反应活化能 正反应的热效应
Ea 60 ~ 250kJ mol1
v
v
太大,无法测定。 太小。
Ea' E (活化配合物分子) E(产物分子)
H Ea E ' a E
Ea( 正 ) > Ea( 逆 ) , ΔrHm > 0 , 为 吸 热 反 应 Ea(正) <Ea(逆), ΔrHm <0 ,为放热反应
无机
化 学
例:基元反应
CO(g) NO2 (g) CO2 (g) NO(g)
可见:正反应活化能 Ea = E(活化配合物分子) - E(反应物分子)
无机
化 学
有关,即与分子 速率常数与 Z、P、 e 的大小、分子量、活化能、温度、碰撞方位等因
Ea / RT
素有关,从而从理论上论证了阿仑尼乌斯的公式,
阐明了速率常数的物理意义。
该理论直观,但仅限于处理气体双分子反应,
且把分子当作刚性球,忽略了分子的结构。
无机
化 学
二、过渡状态理论(活化配合物理论)
无机
化 学
一、反应速率定义
定义----单位时间内反应物或产物浓度改变的 量的绝对值。
平均速率和瞬间速率
2N2O5 = 4NO2 + O2
测定 O2 ( g ) 的析出量,可计算 N2O5 浓度变化
则反应速率:
V = -[C2(N2O5)-C1(N2O5)]/⊿t
(平均速率)
无机
化 学
绝大多数化学反应的速率是随着反应不断进行 越来越慢,即绝大多数反应速率不是不随时间而 变的“定速”,而是随反应时间而变的“变速” 瞬时速率
无机
化 学
化学动力学基础
化学反应速率 浓度对反应速率的影响 反应级数 反应机理 温度对化学反应速率的影响 基元反应的速率理论 催化剂与催化作用
无机
化 学
7-1 化学反应速率
宏观:热力学、动力学 热力学:过程的能量交换 (H) 、过程的方向 (G)、过程的限度(K) ---可能性。 动力学:反应速率(快慢)、 反应机理(怎样进行)---现实性。
无机
化 学
质量作用定律
在基元反应中,反应速率与物质的量浓度的计量 系数次方的乘积成正比。 即反应速率方程可由方程式直接写出:
例:CO (g) + NO2 (g) = CO2 (g) + NO (g)
V= k(CCO) (CNO2) 质量作用定律只适用于基元反应,对于非基元反 应,反应级数依然需要通过测量。但质量作用定 律适用于复杂反应的基元步骤。 若某反应的反应级数与计量相同,并不能直接说 明反应是否为基元反应。
aA bB dD eE
则瞬时速率为:
dC i v Vi dt
C i v Vi t
平均速率为: 反应速率是有单位的物理量
无机
化 学
二、影响反应速率的因素
不同反应的反应速率不同(取决 于反应物本身的性质) 同一反应 1.浓度; 2.气体反应:压力; 3.温度; 4.使用催化剂。
1 2 1
1
无机
化 学
5. 由Ea计算反应速率常数
例:2N2O5(g)2N2O4 (g) + O2(g) 已知:T1=298.15K, k1=0.469×10-4s-1 T2=318.15K, k2=6.29×10-4s-1 求:Ea及338.15K时的k3
T1T2 k2 解:Ea R ln 102kJ mol-1 T2 T1 k1
10℃,k将增大2~10倍.
无机
化 学
定温度,在高温区值增加较少, 因此对于原本反 应温度不高的反应 ,可采用升温的方法提高反应 速率。 4. 对不同反应,升高相同温度, Ea大的反应 k 增大的倍数多,因此升高温度对反应慢的反应有 明显的加速作用。
k 2 E a T2 T1 3. 根据 ln k1 R T1T2
无机
