函数的单调性定义
函数单调性的概念)

目 录
• 函数单调性的定义 • 判断函数单调性的方法 • 函数单调性的性质 • 函数单调性的应用 • 反例与特殊情况
01 函数单调性的定义
单调增函数
01
02
03
总结词
单调增函数是指函数在某 个区间内,随着自变量的 增加,函数值也单调增加 的函数。
详细描述
单调增函数的定义是,对 于任意两个数$x_1$和 $x_2$($x_1 < x_2$), 如果函数$f(x)$满足 $f(x_1) leq f(x_2)$,则称 $f(x)$在区间$[x_1, x_2]$ 上单调增。
单调函数的连续性是其基本性质之一。在单调递增的函数中,如果函数在某一点的左侧 小于该点的值,那么在该点的右侧也必然小于该点的值,即函数值随着自变量的增大而 增大。同样地,在单调递减的函数中,函数值随着自变量的增大而减小。因此,单调函
数在其定义域内是连续的,不存在间断点。
单调函数的可导性
总结词
单调函数的可导性是指函数在单调区间 内是可导的,即函数的导数在单调区间 内存在且不为零。
数学表达
如果对于所有$x_1 < x_2$, 都有$f(x_1) geq f(x_2)$, 则称$f(x)$为减函数。
严格单调函数
总结词
严格单调函数是指函数在某个区间内,对于任意两个不同的自变量,其函数值也不同的函 数。
详细描述
严格单调函数的定义是,对于任意两个不同的数$x_1$和$x_2$($x_1 < x_2$),如果函数 $f(x)$满足$f(x_1) < f(x_2)$或$f(x_1) > f(x_2)$,则称$f(x)$在区间$[x_1, x_2]$上严格单调。
数学表达
数学函数的单调性

05
单调性的扩展知识
单调性与周期性
总结词
函数的单调性与周期性是两个相对独立的概念,但它 们之间也存在一定的联系。
详细描述
单调性是指函数在某一区间内的增减性,而周期性是指 函数按照一定的时间间隔重复出现的现象。虽然单调性 不直接决定函数的周期性,但它们在某些情况下会相互 影响。例如,一些周期函数可能在某些周期内表现出单 调性,而单调函数可能在不同的单调区间内具有不同的 周期。
总结词
单调性与函数值的大小关系是指,在单调递增的函数中 ,自变量x越大,函数值y也越大;在单调递减的函数中 ,自变量x越大,函数值y越小。
详细描述
单调性是描述函数值随自变量变化趋势的一种特性。对 于单调递增的函数,随着自变量x的增大,函数值y也相 应增大。这意味着在函数的整个定义域内,随着x的增加 ,y的值也持续增加。而对于单调递减的函数,随着x的 增大,y的值反而减小。这种单调性可以通过函数的导数 或微分进行判断。
单调性与不等式
总结词
单调性是解决不等式问题的关键因素之一,通过分析函数的单调性可以解决许多不等式问题。
详细描述
不等式是数学中一类重要的方程,通过分析函数的单调性可以解决许多不等式问题。例如,利用函数的单调递增 性质可以证明不等式,通过构造函数并在特定的区间内证明其单调递增,从而证明不等式的正确性。此外,利用 函数的单调性还可以求解一些不等式问题,例如求解一些函数的极值问题等。
要点二
详细描述
单调性的传递性是数学函数的一个重要性质。如果函数f在某 个区间I内单调增加,并且函数g在另一个区间J内也单调增加, 那么复合函数f○g(即f和g的复合函数)在f和g都有定义的区 间I∩J内也将单调增加。同样地,如果f和g都是单调减少的, 则f○g也将是单调减少的。
单调性定义

单调性定义
函数单调性的定义是:函数的单调性,也叫函数的增减性,可以定性描述在一个指定区间内,函数值变化与自变量变化的关系。
定义
函数的单调性,也叫函数的增减性,可以定性描述在一个指定区间内,函数值变化与自变量变化的关系。
当函数f(x)的自变量在其定义区间内增大(或减小)时,函数值也随着增大(或减小),则称该函数为在该区间上具有单调性(单调增加或单调减少)。
在集合论中,在有序集合之间的函数,如果它们保持给定的次序,是具有单调性的。
如果说明一个函数在某个区间D上具有单调性,则我们将D称作函数的一个单调区间,则可判断出:
D⊆Q(Q是函数的定义域)。
区间D上,对于函数f(x),∀(任取值)x1,x2∈D且
x1>x2,都有f(x1)>f(x2)。
或,∀x1,x2∈D且x1>x2,都有
f(x1)<f(x2)。
函数图像一定是上升或下降的。
该函数在E⊆D上与D上具有相同的单调性。
函数的单调性(定义法)

函数的单调性知识点:1.函数单调性定义(1).定义法,对任意的x1,x2∈D,D⊆I,x1>x2 ,若f(x1)−f(x2)>0则称f(x)在D 内是单增,若f(x1)−f(x2)<0则称f(x)在D内是单减.(2). 对定义在D上的函数f(x),设x1,x2∈D, D⊆I , x1<x2,则有:①f(x1)−f(x2)x1−x2>0⇔f(x)是D上的单调递增函数;②f(x1)−f(x2)x1−x2<0⇔f(x)是D上的单调递减函数.(注意:函数的单调性的局部性(注意:函数的单调性,从定义上来讲,是指函数在定义域的某个子区间上的单调性,是局部的特征,在某个区间上单调,在整个定义域上不一定单调。
求单调区间时,必须先求出函数的定义域;单调区间只能用区间表示,若有多个单调区,应分别写),函数的单调性最值主要涉及初等函数、复合函数、抽象函数、分段函数等情况.)2.复合函数的单调性:3.几种常见函数的单调性:f(x)=ax+bcx+d (abcd≠0,bc≠ad);f(x)=ax +bx(ab≠0)例1.多种方法判断下列函数的单调性:(1).f(x)=x + 1x x∈(0,1)(2).y=x−1xx∈(0,+∞); (3).y=x3x∈R;(4).f(x)=axx²−1,x∈(-1,1)(a≠0)(5).f(x)=x+√1+x2,x∈R例2.(1).已知f(x)=x(x≠a),若a>0且f(x)在(1.+∞)内单调递减,求a的x−a在区间[1,2]上都是减函数,求a的取值取值范围. (2).若f(x)=−x2+2ax,与g(x)=ax+1范围.(3).已知函数f(x)= √3−ax(a≠1)若f(x)在区间(0,1]上是减函数,则a−1实数a的取值范围.(4).已知函数f(x)=√x²+1–ax(a>0)①.证明当a≥1时,函数f(x)在区间[0,+∞)上为单调减函数.②.若函数f(x)在区间[1,+∞)上是增函数,求a的取值范围。
函数的单调性知识点
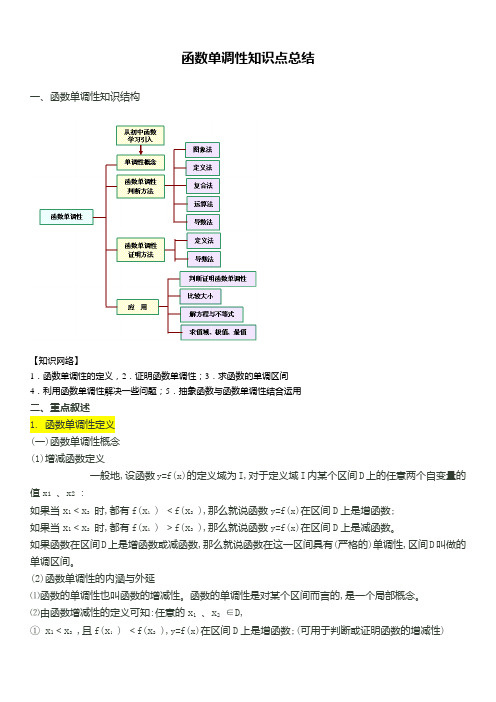
函数单调性知识点总结一、函数单调性知识结构【知识网络】1.函数单调性的定义,2.证明函数单调性;3.求函数的单调区间4.利用函数单调性解决一些问题;5.抽象函数与函数单调性结合运用二、重点叙述1. 函数单调性定义(一)函数单调性概念(1)增减函数定义一般地,设函数y=f(x)的定义域为I,对于定义域I内某个区间D上的任意两个自变量的值x1、x2 :如果当x1<x2时,都有f(x1 ) <f(x2 ),那么就说函数y=f(x)在区间D上是增函数;如果当x1<x2时,都有f(x1 ) >f(x2 ),那么就说函数y=f(x)在区间D上是减函数。
如果函数在区间D上是增函数或减函数,那么就说函数在这一区间具有(严格的)单调性,区间D叫做的单调区间。
(2)函数单调性的内涵与外延⑴函数的单调性也叫函数的增减性。
函数的单调性是对某个区间而言的,是一个局部概念。
⑵由函数增减性的定义可知:任意的x1、x2∈D,① x1<x2 ,且f(x1 ) <f(x2 ),y=f(x)在区间D上是增函数;(可用于判断或证明函数的增减性)② y=f(x)在区间D 上是增函数,且x 1<x 2 , f(x 1) <f(x 2 ) ;(可用于比较函数值的大小) ③ y=f(x)在区间D 上是增函数,且f(x 1) <f(x 2 ), x 1<x 2 。
(可用于比较自变量值的大小) 2. 函数单调性证明方法证明函数单调性的方法有:定义法(即比较法);导数法。
实际上,用导数方法证明一般函数单调性是很便捷的方法,定义法是基本方法,常用来证明解决抽象函数或不易求导的函数的单调性。
(1)定义法:利用增减函数的定义证明。
在证明过程中,把数式的大小比较转化为求差比较(或求商比较)。
⑴转化为求差比较证明程序:①设任意的x 1 、x 2∈D,使x 1<x 2 ; ②求差—变形—判断正负;此为关键步骤,变形大多要“因式分解”。
求差:; 变形:化简、因式分解; 判断:差的符号的正或负。
函数单调性的概念

在[0, )上单调增加; f (0) 0,
当x 0时, x ln(1 x ) 0, 即 x ln(1 x ).
利用单调性证明不等式的步骤: ①将要证的不等式作 恒等变形(通常是移项)使 一端为0另一端即为所作的辅助函数f(x);
②求 f ( x ) 验证f(x)在指定区间上的单调性; ③与区间端点处的函数值或极限值作比较即得证.
/
例3.设f (x) = ax3+x恰有三个单调区间,试确定a的 取值范围,并求其单调区间.
解: f x 3ax 2 1,
若a 0, 则f x 在(-, )恒正, f x 只有一个单调区间,与题意不符.
1 1 1 2 若a<0,则f x 3a x x , 3a x 3a 3a 3a 1 1 a 0时, f x 有三个单调区间,(-,],[ , ) -3a -3a 1 1 为它的减区间, , 为它的增区间. -3a -3a
当 x 1时, f ( x ) 0, 在( ,1]上单调增加; 当1 x 2时,
f ( x ) 0, 在[1,2]上单调减少;
当2 x 时, f ( x ) 0, 在[2, )上单调增加;
单调区间为 ( ,1], [1,2], [2, ).
2
x 0, ln( x 1 x ) ln 1 0
2
x 0时, f ( x) f ( x ) f (0) 0
x 0时,1 x ln( x 1 x ) 1 x .
2 2
例8.设f ( x), g ( x)在[a, b]上可导, 且f ( x) g ( x),
函数的单调性

如果是复合函数,应根据复合函数的单调性的判断方 法, 首先判断两个简单函数的单调性, 再根据“同则增, 异则减”的法则求解函数的单调区间. 3.单调区间的表示 单调区间只能用区间表示,不能用集合或不等式表示; 如有多个单调区间应分别写,不能用并集符号“∪”联 结,也不能用“或”联结.
你能说出你学过的函数的单调区间吗?请举例说明.
失误与防范
1.函数的单调区间是指函数在定义域内的某个区间上单调 递增或单调递减.单调区间要分开写,即使在两个区间 上的单调性相同,也不能用并集表示. 2.两函数 f(x)、g(x)在 x∈(a,b)上都是增(减)函数,则 f(x) 1 +g(x)也为增(减)函数,但 f(x)· g(x), 等的单调性与其 f(x) 正负有关,切不可盲目类比.
一轮复习讲义
函数的单调性
广河中学:马明清
要点梳理
1.函数的单调性 (1)单调函数的定义
忆一忆知识要点
增函数 定义 区间 I 内的任意两个值 x1,x2
减函数
一般地,设函数 f(x)的定义域为 A,区间 I⊆A,如果对于 当 x1<x2 时,都有f(x1)<f(x2),当 x1<x2 时, 都有f(x1)>f(x2) , 那么就说函数 f(x)在区间 I 上是增函数 那么就说函数 f(x)在区间 I 上是减函数
2
1 2
方法与技巧
1.根据函数的单调性的定义,证明(判定)函数 f(x)在其区间 上的单调性,其步骤是 (1)设 x1、x2 是该区间上的任意两个值,且 x1<x2(或 x1>x2); (2)作差 f(x1)-f(x2),然后变形; (3)判定 f(x1)-f(x2)的符号; (4)根据定义得出结论. 2.求函数的单调区间 首先应注意函数的定义域,函数的单调区间都是其定义域的 子集;其次掌握一次函数、二次函数等基本初等函数的单调 区间.常用方法:根据定义,利用图象和单调函数的性质, 或利用导数的性质.
数学人教B必修1第二章213 函数的单调性

2、1、3 函数的单调性1.函数单调性的概念一般地,设函数y=f(x)的定义域为A,区间M⊆A、如果取区间M中的任意两个值x1,x2,改变量Δx=x2-x1>0,则当Δy=f(x2)-f(x1)>0时,就称函数y=f(x)在区间M上是增函数,如下图所示.当Δy=f(x2)-f(x1)<0时,就称函数y=f(x)在区间M上是减函数,如下图所示.如果一个函数在某个区间M上是增函数或是减函数,就说这个函数在这个区间M上具有单调性(区间M称为单调区间)。
谈重点对函数单调性的理解1.函数的单调性是对定义域内某个区间而言的,即单调区间是定义域的子集。
如函数y =x2的定义域为R,当x∈[0,+∞)时是增函数,当x∈(-∞,0)时是减函数。
2.函数单调性定义中的x1,x2有三个特征:一是任意性,即“任意取x1,x2”,“任意”二字决不能丢掉;二是有大小,即x1<x2(x1>x2);三是同属一个单调区间,三者缺一不可。
3.单调性是一个“区间”概念,如果一个函数在定义域的几个区间上都是增(减)函数,但不能说这个函数在其定义域上是增(减)函数.如函数f(x)=错误!在(-∞,0)上是减函数,在(0,+∞)上也是减函数,但不能说f(x)=错误!在(-∞,0)∪(0,+∞)上是减函数.因为当x1=-1,x2=1时有f(x1)=-1<f(x2)=1,不满足减函数的定义。
4.单调区间端点的写法:对于单独的一个点,由于它的函数值是唯一确定的常数,没有增减性变化,所以不存在单调问题,因此在写此单调区间时,包括端点可以,不包括端点也可以,但对于某些无意义的点,单调区间就一定不包括这些点。
【例1-1】下列说法不正确的有()①函数y=x2在(-∞,+∞)上具有单调性,且在(-∞,0)上是减函数;②函数1=yx的定义域为(-∞,0)∪(0,+∞),且在其上是减函数;③函数y=kx+b(k∈R)在(-∞,+∞)上一定具有单调性;④若x1,x2是f(x)的定义域A上的两个值,当x1>x2时,有f(x1)<f(x2),则y=f(x)在A上是增函数.A.1个B.2个C.3个D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数的单调性定义
单调性是数学分析中的一个重要概念,此概念一般表示一个实值
函数的单调性,是一个函数在两个点之间总是增加或总是减少的属性。
它是一种函数的性质,在函数的某个区间内,可以确定函数单调递增、单调递减或者局部单调,因此它可以提供一个有效的方法来分析函数
行为。
许多数学函数均是单调函数,例如函数f(x)=x^2和f(x)=x+2;函数f(x)=\cosx则不属于单调函数,因为其有增大和减小的部分。
单调函数有着一些独特的性质:一个单调函数在某一点,无论其
减小还是增大,只能分别在其有界和没有界点上变化;单调函数的图
象始终向一个方向去改变;单调函数的泰勒展开无法改变其方向。
单调性在很多领域都有广泛的应用,其中有两个典型的例子:
(1)在最优化问题中,我们假设某一函数是单调的,可以将该函
数改写为增函数或减函数,这样就可以使最优化问题切实可行。
(2)在函数分析中,比如在求非线性方程的根的问题中,可以采用Bisection(二分法)和secant(弦截法)等方法,这类方法往往要求所解决问题的函数为单调的函数。
因此,单调性的应用极其广泛,不仅在分析函数行为,改善优化方法以及求解非线性方程等数学分析问题中极为重要,而且还能在应用中博得成就。
