12.3质心运动定理(理论力学课件)
合集下载
质心运动(课堂PPT)

m1l1m2l2(杠杆关系)
m1 x1
l1
xC
l2
m2 x2
x
xC就是m1和m2的质心位置
m 1 (x C x 1) m 2(x 2 x C ) xCm 1 m x1 1 m m 2 2x2m 1x1M m 2x 4 2
二.质心坐标
推广到3维质点系,若n个质点的位矢为
r1,r2, rn,
质点系总质量 Mmi
作用在质点系上的合外力等于质点系 的总质量与质心加速度的乘积
质心的运动状态变化只由系统所受 的合外力决定,与内力无关。
(质心运动定理本身只对惯性系成立!)
10
质心的运动满足: F r合外Marc
质心能作为质点系 整体运动的代表!
11
五.质心动量变化定理
质心运动定理:
F 合 外 d(M dv C t)M a c
2
旋轮线:教材P25习题1.4
• 质点系运动 质心运动+各质点相对于质心的运动3
§6-1 质心动量定理
一. 质心
质心 — 质点系统的质量中心
对质点系, 总有一特殊点,其运动和质点系的所 有质量集中于该处的质点运动相同 质心
以质点系各点质量为权重的系统位置的平均值
以两质点系统为例:
若有一点xC,使
若质心系是非惯性系,则质心系中有:
F 合 F 外 惯 m a '(c质心系中的质心运动定律) 而a 'c0(质 心系中质心的加速度为零)
F 合 外 F 惯 0
在质心非惯性系中惯性力和外力完全抵消,
故系统总动量守恒,且恒为零。
16
§6-2. 质心动能定理
M aCF 合 外
若F合
外 0x,则 a C0
m1 x1
l1
xC
l2
m2 x2
x
xC就是m1和m2的质心位置
m 1 (x C x 1) m 2(x 2 x C ) xCm 1 m x1 1 m m 2 2x2m 1x1M m 2x 4 2
二.质心坐标
推广到3维质点系,若n个质点的位矢为
r1,r2, rn,
质点系总质量 Mmi
作用在质点系上的合外力等于质点系 的总质量与质心加速度的乘积
质心的运动状态变化只由系统所受 的合外力决定,与内力无关。
(质心运动定理本身只对惯性系成立!)
10
质心的运动满足: F r合外Marc
质心能作为质点系 整体运动的代表!
11
五.质心动量变化定理
质心运动定理:
F 合 外 d(M dv C t)M a c
2
旋轮线:教材P25习题1.4
• 质点系运动 质心运动+各质点相对于质心的运动3
§6-1 质心动量定理
一. 质心
质心 — 质点系统的质量中心
对质点系, 总有一特殊点,其运动和质点系的所 有质量集中于该处的质点运动相同 质心
以质点系各点质量为权重的系统位置的平均值
以两质点系统为例:
若有一点xC,使
若质心系是非惯性系,则质心系中有:
F 合 F 外 惯 m a '(c质心系中的质心运动定律) 而a 'c0(质 心系中质心的加速度为零)
F 合 外 F 惯 0
在质心非惯性系中惯性力和外力完全抵消,
故系统总动量守恒,且恒为零。
16
§6-2. 质心动能定理
M aCF 合 外
若F合
外 0x,则 a C0
惯性力 动量定理 质心运动定理精品PPT课件
上页
下页
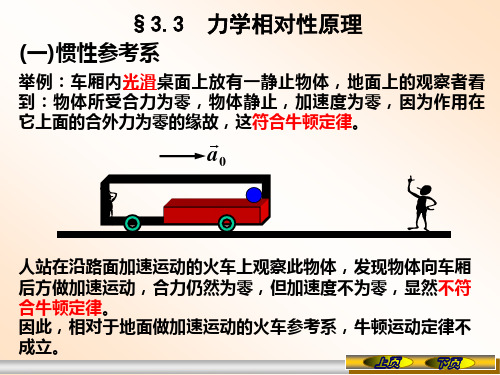
(一)直线加速运动参照系中的惯性力和动力学方程:
1. 惯性力:
F惯 ma0
a0
F惯
惯性力大小等于质点的 质 量与非惯性系加 速度a0 的 乘积,方向与a0方向相反。
注意: 1.惯性力不是真实力,是非惯性系中的观察者假 想出来的力,只有在非惯性系中才能观察得到;
2.惯性力不是物体间的相互作用,不存在惯性力
Fx2
F
2 y
此力与水平方向夹角为
tan Fy
Fx
代值求解得 F 8.1 103 N
300
上页
下页
例2、质量为2.5g的乒乓 球以10m/s的速率飞来, 被板推挡后,又以20m/s 的速率飞出。设两速度在 垂直于板面的同一平面内, 且它们与板面法线的夹角 分别为45o和30o,求: (1)乒乓球得到的冲量; (2)若撞击时间为0.01s, 求板施于球的平均冲力的 大小和方向。
间内合力的冲量。(单位:N·S )
(1)式为质点动量定理的微分形式,表示:
积合分 力的(元1)冲式量:等tt0 于F 质dt点 动P 量 的P0微 分mv。
m
v0
(2)
左侧积分表示在t0 到 t 这段时间
内合外力的冲量,用I 表示
t
I t0 Fdt
上页
下页
(2)式可表示为: I P P0
上页
下页
力学相对性原理:在一切惯性系中,力学定律 具有完全相同的表达形式。
由力学相对性原理可知,在研究力学规律时,所 有的惯性系都是等价的。我们在惯性系中所做的任何 力学实验,都不能确定该惯性系相对于其他惯性系是 否在运动。
力学相对性原理也称为伽利略相对性原理。
§3.4 非惯性系中的动力学
质心运动定理新ppt课件

★ 例题结果讨论 Fx m2e 2 cost
Fy (m1 m2 )g m2e 2 sin t
1) 机座的约束力由两部分组成,一部分由重力(主动力)引起的,称为 静约束力(静反力),另一部分是由于转子质心运动变化引起的,称为附 加动约束力。
2) 附加动约束力的最大值和最小值:
驱动汽车行驶的力
maC Fie F1 F2 Fr
9
★ 质心运动守恒的实例分析 放在光滑板上的电动机的质心运动
10
例题6
电动机的外壳和定子的 总质量为 m1 ,质心C1与转子 转轴 O1 重合 ;转子质量 为 m2 ,质心 O2 与转轴不 重合 ,偏心距 O1O2 = e 。 若转子以等角速度 旋转。
0 时 时
2
Fxmin m2e 2
Fymin (m1 m2)g m2e2
时 Fxmax m2e 2 当Fymin<0时不固定时跳起。
3
2
时
Fymax (m1 m2 )g m2e2
3) 附加动约束力与2成正比,当转子的转速很高时,其数值可以达到静约束
质心完全取决于质点系各质点的质量大小及其位置的分布,而 与所受的力无关,重心只在质点系受重力作用时才存在。 5
2 质心运动定理
由质心公式
rC
mr
M
得:
MC mii
根据质点系的动量定义有:
K mii MC
将上式求导: dK dt
M
dC
dt
M
d 2rc dt 2
力的几倍,甚至几十倍,而且这种约束力是周期性变化的,必然引起机座和基
础的振动,还会引起有关构件内的交变应力。
《理论力学》第10章 质心运动定理

第10章 质心运动定理
26
3、求质心加速度
aC
aB
aCt B
aCnB
4、质心运动定理求约束力,受力分析
ma Cx FixE FA sin450 maCy FiyE FB mg FA cos 450
O
450
1m
A
C
vB
aB
450
B
FA
A
mg
x
FB
C
450
B
★理论力学电子教案
0
px const
★理论力学电子教案
第10章 质心运动定理
18
例题 图示机构,均质杆OA长l,质量为m1,滑块A的质量为m2, 滑道CD的质量为m3。OA杆在一力偶(图中未画出)作用下作 匀角度ω转动。试求O处的水平约束反力(机构位于铅直平面
内,各处摩擦不计)。 C
A
O
E
D
★理论力学电子教案
第10章 质心运动定理
第10章 质心运动定理
27
ma A
第10章 质心运动定理
14
M
C aC mg
FN
F
★理论力学电子教案
第10章 质心运动定理
§2 质点系动量、冲量
质点动量: 质点系动量:
p mv
P mivi mvC
问:刚体系动量?
元冲量:
dI F dt
冲量:
t2 t2
I dI F dt
t1
t1
15
p mv
★理论力学电子教案
第10章 质心运动定理
1
第十章 质心运动定理&动量定理
★理论力学电子教案
第10章 质心运动定理
大学物理-质心质心运动定律

角动量守恒条件
当刚体绕定轴转动时,如果作用于刚体上的外力矩为零,则刚体的 角动量守恒。
角动量守恒应用
利用角动量守恒原理可以解决一些实际问题,如陀螺仪的工作原理、 天体运动中行星轨道的确定等。
角动量不守恒情况
当作用于刚体上的外力矩不为零时,刚体的角动量将发生变化。此时 需要根据外力矩的作用时间和大小来计算角动量的变化量。
适用范围和条件
01
适用范围:质心运动定律适用于任何由多个质点组成的系统,无论这 些质点之间是否存在相互作用力。
02
适用条件:质心运动定律的应用需要满足以下两个条件
03
质点系所受的外力可以视为作用于质心上的合力。
04
质点系内部的相互作用力对质心的运动没有影响,或者其影响可以忽 略不计。
质点系相对于质心参
角动量
描述刚体绕定轴转动时动量的大小 和方向,等于转动惯量与角速度的 乘积。
刚体绕定轴转动时质心位置变化规律
质心位置不变
刚体绕定轴转动时,其质 心位置保持不变,始终位 于转轴上。
质心速度为零
由于质心位于转轴上,因 此质心的速度为零。
质心加速度为零
由于质心速度为零,因此 质心的加速度也为零。
刚体绕定轴转动时角动量守恒原理
02
考系运动
质点系内各点相对于质心参考系位移
01
02
03
定义
质点系内各点相对于质心 的位置矢量称为相对位移。
性质
相对位移是描述质点系内 各点相对于质心位置变化 的物理量,具有矢量性。
计算方法
通过几何方法或解析方法 求出各点相对于质心的位 置矢量。
质点系内各点相对于质心参考系速度
定义
质点系内各点相对于质心的速度称为相对速度。
当刚体绕定轴转动时,如果作用于刚体上的外力矩为零,则刚体的 角动量守恒。
角动量守恒应用
利用角动量守恒原理可以解决一些实际问题,如陀螺仪的工作原理、 天体运动中行星轨道的确定等。
角动量不守恒情况
当作用于刚体上的外力矩不为零时,刚体的角动量将发生变化。此时 需要根据外力矩的作用时间和大小来计算角动量的变化量。
适用范围和条件
01
适用范围:质心运动定律适用于任何由多个质点组成的系统,无论这 些质点之间是否存在相互作用力。
02
适用条件:质心运动定律的应用需要满足以下两个条件
03
质点系所受的外力可以视为作用于质心上的合力。
04
质点系内部的相互作用力对质心的运动没有影响,或者其影响可以忽 略不计。
质点系相对于质心参
角动量
描述刚体绕定轴转动时动量的大小 和方向,等于转动惯量与角速度的 乘积。
刚体绕定轴转动时质心位置变化规律
质心位置不变
刚体绕定轴转动时,其质 心位置保持不变,始终位 于转轴上。
质心速度为零
由于质心位于转轴上,因 此质心的速度为零。
质心加速度为零
由于质心速度为零,因此 质心的加速度也为零。
刚体绕定轴转动时角动量守恒原理
02
考系运动
质点系内各点相对于质心参考系位移
01
02
03
定义
质点系内各点相对于质心 的位置矢量称为相对位移。
性质
相对位移是描述质点系内 各点相对于质心位置变化 的物理量,具有矢量性。
计算方法
通过几何方法或解析方法 求出各点相对于质心的位 置矢量。
质点系内各点相对于质心参考系速度
定义
质点系内各点相对于质心的速度称为相对速度。
《质心运动定理》课件

Байду номын сангаас
表达形式二
质心的速度等于各个质点速度乘以其质量的乘 积之和除以系统总质量。
质心运动定理的推导过程
通过从牛顿第二定律的微分形式出发,我们可以推导出质心运动定理的表达式,详细的推导过程在课件 中进行阐述。
质心运动定理的应用实例
火箭发射
平衡木比赛
通过计算火箭系统的质心位置, 我们可以优化火箭的稳定性及 飞行性能。
《质心运动定理》PPT课 件
探秘质心运动定理
通过本课件,我们将一起深入了解质心运动定理的概念,质心的定义与性质, 以及应用实例,一起探索这个有趣且实用的物理定理。
质心运动定理的概念
质心运动定理描述了一个系统的质心的运动行为。通过计算质心的位置随时间的变化,我们可以了解系 统整体的运动特性。
质心的定义与性质
2
展望
质心运动定理的应用还有待进一步拓展,可以应用于更多领域的研究和实践中。
运动员在平衡木上的动作稳定 性与质心位置密切相关。
摆钟
通过质心运动定理,我们可以 理解摆钟的运动规律及影响因 素。
质心运动定理的意义与局限
意义
质心运动定理为我们理解和研究物体的整体运动提供了重要的理论基础。
局限
质心运动定理仅适用于那些质量分布均匀、不受外力作用的系统。
总结与展望
1
总结
质心运动定理是研究物体整体运动的重要工具,能够揭示系统的运动特性。
1 质心定义
质心是系统的质量分布的平均位置,可以看作是整个系统的重心。
2 质心性质
质心的位置不受系统形状的影响,仅与物体的质量分布有关。
3 质心稳定性
系统的质心总是遵循牛顿第一定律,即以恒定速度直线运动或保持静止。
表达形式二
质心的速度等于各个质点速度乘以其质量的乘 积之和除以系统总质量。
质心运动定理的推导过程
通过从牛顿第二定律的微分形式出发,我们可以推导出质心运动定理的表达式,详细的推导过程在课件 中进行阐述。
质心运动定理的应用实例
火箭发射
平衡木比赛
通过计算火箭系统的质心位置, 我们可以优化火箭的稳定性及 飞行性能。
《质心运动定理》PPT课 件
探秘质心运动定理
通过本课件,我们将一起深入了解质心运动定理的概念,质心的定义与性质, 以及应用实例,一起探索这个有趣且实用的物理定理。
质心运动定理的概念
质心运动定理描述了一个系统的质心的运动行为。通过计算质心的位置随时间的变化,我们可以了解系 统整体的运动特性。
质心的定义与性质
2
展望
质心运动定理的应用还有待进一步拓展,可以应用于更多领域的研究和实践中。
运动员在平衡木上的动作稳定 性与质心位置密切相关。
摆钟
通过质心运动定理,我们可以 理解摆钟的运动规律及影响因 素。
质心运动定理的意义与局限
意义
质心运动定理为我们理解和研究物体的整体运动提供了重要的理论基础。
局限
质心运动定理仅适用于那些质量分布均匀、不受外力作用的系统。
总结与展望
1
总结
质心运动定理是研究物体整体运动的重要工具,能够揭示系统的运动特性。
1 质心定义
质心是系统的质量分布的平均位置,可以看作是整个系统的重心。
2 质心性质
质心的位置不受系统形状的影响,仅与物体的质量分布有关。
3 质心稳定性
系统的质心总是遵循牛顿第一定律,即以恒定速度直线运动或保持静止。
理论力学课件 质心运动定理,,第十章动量矩定理
质心守恒
支承面的法向反力的最小值求得为
2
221min )(ω
e m g m m F y −+=若,则。
因此如电动机无螺栓固定,它将会跳起来。
e
m g
m m 221)(+>ω0min <N F
9.2 质心运动定理
夯体滑动而不跳起的条
件怎样建立?
问题1——运动员质心做什么运动?问题2——运动员手脚运动、肌肉收缩、关节运动是否影响质心运动?抛物线内力不影响质心运动!
跨越式翻滚式背越式
跨越式:人体质心大约在腹部,杆在双腿的下方,质心约在杆上方30cm 翻滚式:人体质心
大约在腹部,杆在
身体的下方,人体
基本上与杆平行,
质心约在杆上方
10cm
背越式:人体质心
不在身体上,可在
背部下方10cm,质
心从杆下方过杆。
1.8m-0.3m=1.5m 1.8m-0.1m=1.7m 1.8m+0.1m=1.9m
第10章动量矩定理
问题:应用动量定理和质心运动定理只能分析出其质心加速度,如何分析猫的转体?
跳水动量矩守恒
跳水运动员为什
么在空中可实现空翻
和转体的转变?
M
A。
质点系动量定理和质心运动定理.pptx
由上式所确定的空间点称质点系的质量中心(质心).
在直角坐标系质心坐标为
xc
mi xi m
yc
mi yi m
zc
mi zi m
对由两个质点组成的质点系,有
xc
m1x1m2x2 m1m2
yc
m1y1m2y2 m1m2
第10页/共19页
x2 xc m1 xc x1 m2
y2 yc m1 yc y1 m2
质心必位于m1与m2的连线上,且质心与各质点距离与质点质量 成反比.
第11页/共19页
[例题3] 一质点系包括三质点,质量为
m2 2单和位
m3
3,单 位置位坐标各为
求质心坐标.
m 1 ( 1 , 2 )m ,2 ( 1 ,1 ) 和 m 3 ( 1 ,2 )
m1 1单位
[解] 质心坐标
xc
m1x1m2x2m3x3 m1m2m3
d p vd tS v
由动量定理
dp vS vF
dt
F表示留在燃烧室内的燃烧物质对排出物质的作用力
Fx Sv2
向下
火箭所受推力,也等于
Sv 2
向上
第5页/共19页
[内例有题质2]量如为图表m0示的传煤送卸带出以,水传平送速带度顶部与将车煤厢卸底入板静v0高止度车差厢为内h。,每开单始位时时车间
第8页/共19页
§3.7.2 质心运动定理
1.质心
质点系动量定理
而
vi
dri dt
i F i d dt(
mivi)
有
i i
F i ddt22(
miri)
F i md dt22(
m iri) m
第二十章质心运动定理动量定理
l
p [
t
W2 W1
W3
x
l W2 l W2 ( W3 ) cos( t )i ( W3 ) sin( t ) j g 2 g 2
g g W3 W2 [ v1 sin( t ) v2 sin( t )] j g g
v1 cos( t )
p z mi viz
e dp Fi dt
e p2 p1 I i
质点系动量的改变量,等于作用于质点系 外力在该时段间内冲量的矢量和。
例5 用动量定理求解例11-1。(电动机重W1,均质杆长l, 重W2,小球重W3的,匀角速度 ,求螺栓和基础作用于电 机的最大总水平力及铅直力。) y 解: W2 W3
dxC vCx 常量 dt
F
e ix
0
vCx 0
则 xC 常量
即质心沿该轴向无位移
例1 电动机重W1,外壳用螺栓固定在基础上。均质杆长l, 重W2,一端连一重W3的小球。电机以匀角速度 转动,求 螺栓和基础作用于电机的最大总水平力及铅直力。
y
解:
aC1x 0 aC 2 x
x
A
y
B
M
AC
xC
M
C
3 AB 9cm 4 AM 3 1 cos AM 90 10 常量 xC AC cos 2 90 cos 2cm 3
AM 3cm
2 2 AM 90 cm 3 3
MM
yM AM sin 90 sin
0
O
D
B
x
5 5 c l sin t( m1 2m2 ) p y my c l cos t( m1 2m2 ) p x mx 2 2
12.3质心运动定理(理论力学课件)
m1g
m2g
c1 c c2 e
t
x
Rx Ry
Rx—— 是螺栓给电动机的水平动反力,它与电动机的角速 度有关,而电动机给螺栓的剪力则与Rx等值反向。
Ry—电动机在铅垂方向上所受的全反力, 当Ry >0时,其方向向上,它来自地面; 当Ry <0时,其方向向下,故知它必来自螺栓拉力,这
时电动机有跳离地面的趋势所以地面未受压而不会给电
m2g
Rx Ry
y
c1 c c2 e
t
x
式中:x1=y1=0,是外壳与定子的质心c1的坐标; x2、y2是转子c2的坐标。
设初瞬时,c2位于x轴上,经过时间t后,转角φ=ωt,
于是有:
x2 e cost y2 esint (2)
xc
m2 x2 m1 m2
;yc
m2 y2 m1 m2
(1)
x2 e cost y2 esint (2)
p = mvc mivi
设其角速度为w,质心C至转轴 的 距 离 为 e , 则 由 式 ( 12.15 ) 可 知 , 此刚体动量的大小为
p = mvc me
显然,当刚体质心位于转轴上时, 则不论转动角速度多大,其动量恒 等于零。
vC
drC dt
mivi p (12.14) mm
p = mvc
①如果 FRe 0 mac 0
则质心作匀速直线运动;
则 vc cont
②若开始静止,则质心位置始终保持不变。
如果作用于质点系的所有外力在某一轴上投影的代数和 恒等于零。则质心沿该轴的坐标保持不变。
以上结论,称为质心运动守恒定律。
③注意:
只有外力才影响质心的运动,内力不影响质心运动, 且没有外力时,质心运动守恒,原为静止的质点系保持静 止。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实际应用时,可采用投影形式。
(12.17 )
质心运动定理在坐标轴上投影:
mm&&yx&&cc
Fxe Fye
m&z&c Fze
(12.18 )
——质点系质量与质心加速度在某一轴上的投影的乘 积等于质点系所受外力的主矢量在同一轴上的投影,
该式称为投影形式的质心运动定理。
三、质心运动守恒 mac miai Fie
质点系外力的矢量和。
同时指出:内力不能改变质心的运动。
形式上,质心运动定理与质点的动力学基本方程完 全相似,因此质心运动定理也可叙述如下:
质点系质心的运动,犹如一个质点的运动,此质点的 质量等于整个质点系的质量,且作用于此质点上的力等 于作用于整个质点系上的外力的矢量和。
mac miai Fie
状况,所以质心的概念是动力学的重要概念之一。
rc ④m质mi r心i 的(1坐2.标10)
计算质心位置时,常用上式在直角坐标系的投影形式,
即
xC
mi xi m
, yC
mi yi m
, zC
mi zi m
(12.13)
式中 mi点为第i个质点的质量,xi、yi、zi,第i个质点的位置坐标,m
。
②若质点系中各质点的质量不相等。则有:
rc
mi m
ri
(12.12 )
ri 的系数表示第 i 个质点的质量在质点系的质量
所占的比例,质心的矢径rc为即为各质点按其质量在质
点系质量中所占的比例的平均位置。
③ 质心的作用
由讨论可见,质心的位置与质点系中的质量分布
状况有关,它在一定程度上反映了质点系的质量分布
y
m1g
m2g
c1 c c2 e
t
x
Rx Ry
作用于质心上的外力有:
重力m1g、m2g; 螺栓的约束反力Rx、Ry。
(2)建立静坐标如图:电动机质心C的方程为:
xc
m1x1 m2 x2 m1 m2
若将上列各式等号右端的分子 与分母同乘以重力加速度g,就 得到质点系的重心坐标公式。
可见物体在重力场中运
动时,重心与质心相重合。
但应当注意,质心与重心是 两个不同的概念。
重心仅在质点系受到重力作用(即在地球表面附近)时才存
在,而质心则与质点系是否受到重力作用无关,它随质点
系的存在而存在。因此,质心概念的适用范围远较重心广
为质点系的质量。
质心是可见,如果把质点系的质量都集中于 质心做为一个质点,那么此质点的 动量就等于质点系的动量,可见质 心运动具有特殊意义。
xC
mi xi , m
yC
mi yi , m
⑤质心与重心的比较:
zC
mi zi m
(12-13 )
2、质心速度
rC
mi ri m
(12.10)
质心C的运动速度可根据式(12.10)导出:
vC
drC dt
mivi p mm
或
mvc mivi
p = mvc mivi
(12.14) (12.15)
式(12.15)为计算质点系动量的简便方法。
由上式可知,不论质点如何运动,在计算质点系的 动量时均可不考虑其中每一质点的速度,而只需知 道质点系的质量和质心的速度就足够了。
§12.3 质心运动定理
一、质量中心
质点系在力的作用下,其运动状 态与各质点的质量及其相互的位 置都有关系,即与质点系的质量 分布状况有关。
1.定义:
rc
mi ri m
(12.10)
由式 (12.10)所定义的质心位置反映出质点系质量分布的一
种
特征质心的概念及其运动在质点系(特别是刚体)动力学 中
p = mvc
3、质心加速度
将式(12.14)对时间求导,得:
aC
dvC dt
dp d(mvC ) d( mivi )
dt dt
dt
mac miai Fie (12.17)
二、质心运动定理
maC miai Fie FRe
(12.17
上式表明,质点系的质量与质心加速度的乘积等)于作用于
例3 设有一电动机用螺旋栓固定在水平地面上, 如图,电动机外壳连同定子的质量为m1,它们的质心为
c1,在转子的轴线上,转子的质量为 m2 。 由于制造不够精确,因而 其质心与转子轴线相距为
e, 试求当电动机以匀角速度 ω转动时,螺旋栓所受的 水平剪力和地面的铅垂反
力。
解:(1)研究整个电动机
看作一个整体,受力分析如图:
2.质r心c 的力mm学i r意i 义
① 若质点系中各质点的质量相等,则:
rc
m
r1 m r2 ...... m m m ...... m
rn
r1 r2 ...... rn
n
1 n ri
1/n 与 i 无关,为公因子。
(12.11 )
式中: ri系数 1/n 表示第 i个质点的质量在质点系质 量中所占的比例,质心的矢径rc即为各质点的平均矢径
例如绕定轴转动的刚体,
p = mvc mivi
设其角速度为w,质心C至转轴 的距离为e,则由式(12.15)可知, 此刚体动量的大小为
p = mvc me
显然,当刚体质心位于转轴上时,
则不论转动角速度多大,其动量恒
等于零。
vC
drC dt
mivi p (12.14) mm
①如果 FRe 0 mac 0
则质心作匀速直线运动;
则 vc cont
②若开始静止,则质心位置始终保持不变。
如果作用于质点系的所有外力在某一轴上投影的代数 和恒等于零。则质心沿该轴的坐标保持不变。 以上结论,称为质心运动守恒定律。
③注意:
只有外力才影响质心的运动,内力不影响质心运 动,且没有外力时,质心运动守恒,原为静止的质点
系保持静止。
如汽车在光滑路面上发动,如果路面没有摩擦 力,则轮子空转不动,即轮心不向前运动,必须要
有外力才能使其运动。
有很多实例都可用来说明质心的运动完全取决于作用 在质点系上的外力而与内力无关。
例如,人在完全没有摩擦的光滑路面上行走是不可能的 ; 汽车开动时,发动机汽缸内的燃气压力对汽车整体 来说是内力,不能使车子前进,只是当燃气推动活塞, 通过传动机构带动主动轮转动,地面对主动轮作用了向 前的摩擦力,而且这个摩擦力大于总的阻力时,汽车才 能前进。
(12.17 )
质心运动定理在坐标轴上投影:
mm&&yx&&cc
Fxe Fye
m&z&c Fze
(12.18 )
——质点系质量与质心加速度在某一轴上的投影的乘 积等于质点系所受外力的主矢量在同一轴上的投影,
该式称为投影形式的质心运动定理。
三、质心运动守恒 mac miai Fie
质点系外力的矢量和。
同时指出:内力不能改变质心的运动。
形式上,质心运动定理与质点的动力学基本方程完 全相似,因此质心运动定理也可叙述如下:
质点系质心的运动,犹如一个质点的运动,此质点的 质量等于整个质点系的质量,且作用于此质点上的力等 于作用于整个质点系上的外力的矢量和。
mac miai Fie
状况,所以质心的概念是动力学的重要概念之一。
rc ④m质mi r心i 的(1坐2.标10)
计算质心位置时,常用上式在直角坐标系的投影形式,
即
xC
mi xi m
, yC
mi yi m
, zC
mi zi m
(12.13)
式中 mi点为第i个质点的质量,xi、yi、zi,第i个质点的位置坐标,m
。
②若质点系中各质点的质量不相等。则有:
rc
mi m
ri
(12.12 )
ri 的系数表示第 i 个质点的质量在质点系的质量
所占的比例,质心的矢径rc为即为各质点按其质量在质
点系质量中所占的比例的平均位置。
③ 质心的作用
由讨论可见,质心的位置与质点系中的质量分布
状况有关,它在一定程度上反映了质点系的质量分布
y
m1g
m2g
c1 c c2 e
t
x
Rx Ry
作用于质心上的外力有:
重力m1g、m2g; 螺栓的约束反力Rx、Ry。
(2)建立静坐标如图:电动机质心C的方程为:
xc
m1x1 m2 x2 m1 m2
若将上列各式等号右端的分子 与分母同乘以重力加速度g,就 得到质点系的重心坐标公式。
可见物体在重力场中运
动时,重心与质心相重合。
但应当注意,质心与重心是 两个不同的概念。
重心仅在质点系受到重力作用(即在地球表面附近)时才存
在,而质心则与质点系是否受到重力作用无关,它随质点
系的存在而存在。因此,质心概念的适用范围远较重心广
为质点系的质量。
质心是可见,如果把质点系的质量都集中于 质心做为一个质点,那么此质点的 动量就等于质点系的动量,可见质 心运动具有特殊意义。
xC
mi xi , m
yC
mi yi , m
⑤质心与重心的比较:
zC
mi zi m
(12-13 )
2、质心速度
rC
mi ri m
(12.10)
质心C的运动速度可根据式(12.10)导出:
vC
drC dt
mivi p mm
或
mvc mivi
p = mvc mivi
(12.14) (12.15)
式(12.15)为计算质点系动量的简便方法。
由上式可知,不论质点如何运动,在计算质点系的 动量时均可不考虑其中每一质点的速度,而只需知 道质点系的质量和质心的速度就足够了。
§12.3 质心运动定理
一、质量中心
质点系在力的作用下,其运动状 态与各质点的质量及其相互的位 置都有关系,即与质点系的质量 分布状况有关。
1.定义:
rc
mi ri m
(12.10)
由式 (12.10)所定义的质心位置反映出质点系质量分布的一
种
特征质心的概念及其运动在质点系(特别是刚体)动力学 中
p = mvc
3、质心加速度
将式(12.14)对时间求导,得:
aC
dvC dt
dp d(mvC ) d( mivi )
dt dt
dt
mac miai Fie (12.17)
二、质心运动定理
maC miai Fie FRe
(12.17
上式表明,质点系的质量与质心加速度的乘积等)于作用于
例3 设有一电动机用螺旋栓固定在水平地面上, 如图,电动机外壳连同定子的质量为m1,它们的质心为
c1,在转子的轴线上,转子的质量为 m2 。 由于制造不够精确,因而 其质心与转子轴线相距为
e, 试求当电动机以匀角速度 ω转动时,螺旋栓所受的 水平剪力和地面的铅垂反
力。
解:(1)研究整个电动机
看作一个整体,受力分析如图:
2.质r心c 的力mm学i r意i 义
① 若质点系中各质点的质量相等,则:
rc
m
r1 m r2 ...... m m m ...... m
rn
r1 r2 ...... rn
n
1 n ri
1/n 与 i 无关,为公因子。
(12.11 )
式中: ri系数 1/n 表示第 i个质点的质量在质点系质 量中所占的比例,质心的矢径rc即为各质点的平均矢径
例如绕定轴转动的刚体,
p = mvc mivi
设其角速度为w,质心C至转轴 的距离为e,则由式(12.15)可知, 此刚体动量的大小为
p = mvc me
显然,当刚体质心位于转轴上时,
则不论转动角速度多大,其动量恒
等于零。
vC
drC dt
mivi p (12.14) mm
①如果 FRe 0 mac 0
则质心作匀速直线运动;
则 vc cont
②若开始静止,则质心位置始终保持不变。
如果作用于质点系的所有外力在某一轴上投影的代数 和恒等于零。则质心沿该轴的坐标保持不变。 以上结论,称为质心运动守恒定律。
③注意:
只有外力才影响质心的运动,内力不影响质心运 动,且没有外力时,质心运动守恒,原为静止的质点
系保持静止。
如汽车在光滑路面上发动,如果路面没有摩擦 力,则轮子空转不动,即轮心不向前运动,必须要
有外力才能使其运动。
有很多实例都可用来说明质心的运动完全取决于作用 在质点系上的外力而与内力无关。
例如,人在完全没有摩擦的光滑路面上行走是不可能的 ; 汽车开动时,发动机汽缸内的燃气压力对汽车整体 来说是内力,不能使车子前进,只是当燃气推动活塞, 通过传动机构带动主动轮转动,地面对主动轮作用了向 前的摩擦力,而且这个摩擦力大于总的阻力时,汽车才 能前进。
