与圆有关的最值问题ppt课件
合集下载
与圆有关的定点定值最值与范围问题
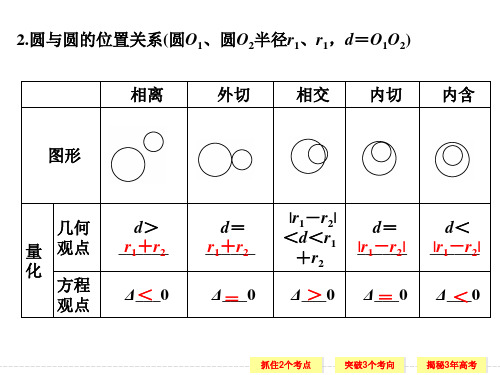
Δ_<__0
抓住2个考点
突破3个考向
揭秘3年高考
【助学·微博】 一个考情分析
与圆有关的综合性问题,其中最重要的类型有定点问题、定值 问题、最值与范围问题. 解这类问题可以通过建立目标函数、利用几何意义、直接求解 或计算求得.
抓住2个考点
突破3个考向
揭秘3年高考
考点自测
1.已知两圆C1:x2+y2-2x+10y-24=0,C2:x2+y2+2x+ 2y-8=0,则经过两圆交点且面积最小的圆的方程为 ________________.
抓住2个考点
突破3个考向
揭秘3年高考
2.若直线 y=x+b 与曲线 y= 1-x2有两个公共点,则 b 的取值
范围是________.
解析 如图,当直线介于 l1 与 l2 之间时满
足题意,即圆心到直线
y=x+b
的距离
2 2
≤ |b|<1,解得 1≤b< 2. 2
答案 [1, 2)
抓住2个考点
突破3个考向
由yx=-02,2-3=0,
得x=2+ y=0
3,
或x=2- y=0.
3,
故以 MN 为直径的圆恒过定点(2+ 3,0)和(2- 3,0).
抓住2个考点
突破3个考向
揭秘3年高考
考向二 与圆有关的定值问题
【例2】 (2013·扬州调研)已知圆C:x2 +y2=9,点A(-5,0),直线l:x-2y =0. (1)求与圆C相切,且与直线l垂直的 直线方程; (2)在直线 OA 上(O 为坐标原点),存在定点 B(不同于点 A), 满足:对于圆 C 上任一点 P,都有PPAB为一常数,试求所有满 足条件的点 B 的坐标.
抓住2个考点
抓住2个考点
突破3个考向
揭秘3年高考
【助学·微博】 一个考情分析
与圆有关的综合性问题,其中最重要的类型有定点问题、定值 问题、最值与范围问题. 解这类问题可以通过建立目标函数、利用几何意义、直接求解 或计算求得.
抓住2个考点
突破3个考向
揭秘3年高考
考点自测
1.已知两圆C1:x2+y2-2x+10y-24=0,C2:x2+y2+2x+ 2y-8=0,则经过两圆交点且面积最小的圆的方程为 ________________.
抓住2个考点
突破3个考向
揭秘3年高考
2.若直线 y=x+b 与曲线 y= 1-x2有两个公共点,则 b 的取值
范围是________.
解析 如图,当直线介于 l1 与 l2 之间时满
足题意,即圆心到直线
y=x+b
的距离
2 2
≤ |b|<1,解得 1≤b< 2. 2
答案 [1, 2)
抓住2个考点
突破3个考向
由yx=-02,2-3=0,
得x=2+ y=0
3,
或x=2- y=0.
3,
故以 MN 为直径的圆恒过定点(2+ 3,0)和(2- 3,0).
抓住2个考点
突破3个考向
揭秘3年高考
考向二 与圆有关的定值问题
【例2】 (2013·扬州调研)已知圆C:x2 +y2=9,点A(-5,0),直线l:x-2y =0. (1)求与圆C相切,且与直线l垂直的 直线方程; (2)在直线 OA 上(O 为坐标原点),存在定点 B(不同于点 A), 满足:对于圆 C 上任一点 P,都有PPAB为一常数,试求所有满 足条件的点 B 的坐标.
抓住2个考点
最新九年级中考数学专题复习: 最值问题-隐圆模型之瓜豆问题 课件

B
C
△BOC是等腰直角三角形,锐角顶点C的轨迹是以点A为圆
心,2为半径的圆,所以O点轨迹也是圆,以AB为斜边构造等
M
腰直角三角形,直角顶点M即为点O轨迹圆圆心.
连接AM并延长与圆M交点即为所求的点O,此时AO最大,
根据AB先求AM,再根据BC与BO的比值可得圆M的半径与圆A
O
半径的比值,得到MO,相加即得AO.
E
MN
AD
B
当堂训练---轨迹之线段篇
3.如图,∠AOB=60º,OA=OB,动点C从点O出发,沿射线OB方向移动,
D
,D是定点,E点满足EO=2,故E点
轨迹是以O为圆心,2为半径的圆.
当DE⊥DF且DE=DF,故作DM⊥DO
且DM=DO,F点轨迹是以点M为圆心
,2为半径的圆.
连接OM,与圆M交点即为F点,此 E
时OF最小.可构造三垂直全等求
线段长,再利用勾股定理求得OM,
减去MF即可得到OF的最小值. B
O
C
M F
接得到M点的轨迹长为P点轨迹长一半,即可解 C
FB
决问题.
当堂训练---轨迹之圆篇
3.如图,正方形ABCD中,AB=2 5,O是BC边的中点,点E是正方形内一
动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90º得DF,连接AE、
CF.求线段OF长的最小值.5 2 - 2
【分析】E是主动点,F是从动点 A
连接DF.DF的最小值是_1___.
A
一个定点----垂线段最短
E
G
D
B
C
F
当堂训练---轨迹之线段篇
2.如图,已知等边三角形ABC的边长为8,点D为AB边上一动点,DE始
新高考数学人教版必修2课件第2章 习题课 与圆有关的最值问题

内容索引
一、与距离有关的最值问题 二、与面积相关的最值问题 三、利用数学式的几何意义解圆的最值问题
随堂演练
课时对点练
一、与距离有关的最值问题
1.圆外一点到圆上任意一点距离的最小值= d-r ,最大 值= d+r .
2.直线与圆相离,圆上任意一点到直线距离的最小值= d-r ,最大值= d+r .
解析 圆C:x2+y2-2y=0的圆心为C(0,1),半径r=1, 由圆的性质可知,四边形的面积S=2S△PBC, 又四边形PACB的最小面积是2, 则 S△PBC 的最小值为 S=1=12r|PB|min=12|PB|min, 则|PB|min=2,因为|PB|= |PC|2-r2= |PC|2-1,
解析 设点A(3,1),易知圆心C(2,2),半径r=2. 当弦过点A(3,1)且与CA垂直时为最短弦, |CA|= 2-32+2-12= 2. ∴半弦长= r2-|CA|2= 4-2= 2. ∴最短弦长为 2 2.
二、与面积相关的最值问题
例2 已知点O(0,0),A(0,2),点M是圆(x-3)2+(y+1)2=4上的动点,则
√C. (-∞,- 3]∪[ 3,+∞) D. [- 3, 3]
解析 将yx看作圆上动点(x,y)与原点 O(0,0)连线的斜率, 如图,可得 k≥ 3或 k≤- 3.
1234
4.已知圆C1:x2+y2+4x-4y=0,动点P在圆C2:x2+y2-4x-12=0上, 则△PC1C2面积的最大值为_4___5_. 解析 因为C1(-2,2),r1=2,C2(2,0),r2=4, 所以|C1C2|= -2-22+22=2 5, 当 PC2⊥C1C2 时,△PC1C2 的面积最大,其最大值为12×2 5×4=4 5.
与圆有关的最值问题课件高二上学期数学人教A版选择性

赋代数式子几何意 义
利用数形结合 思想解决问题
4
例题 已知圆C: x 32 y2 4 ,O为坐标原点;Q是圆C上的一点.
双动点问题
化归
单动点问题
把双动点改为双动直线,就能得到以下的新问题.
例题 已知圆C: x 32 y2 4 ,O为坐标原点;Q是圆C上的一点.
问题(4)若P在直线m: 3x-4y+12=0上,过P作圆C的两条切线,切点 分别为A、B ,则四边形PACB面积的最小值为______ .
问题(3) 若P在直线m: 3x-4y+12=0上,则|PQ|的最小值是____ .
方法一:P固定,Q运动;d为圆心C到直线m的距离.
|PQ|≥|PC|-r=|PC|-2
≥d-2 =
21 2 11.55 Nhomakorabea答案:11 . 5
例题 已知圆C: x 32 y2 4 ,O为坐标原点,Q是圆C上的一点.
由 |3+b| 2, 11
得 b=-3+2 2 或 b=-3-2 2 .
答案: 3 2 2, 3 2 2 .
小结 一般地: (1)形如 k y b 的最值问题,可转化为动直线斜率的最值问题.
xa (2)形如 m ax by 的最值问题,可转化为动直线截距的最值问题.
(3)形如 r2 (x a)2 ( y b)2 的最值问题,可转化为曲线上的点到点(a, b)的距离平方的最值问题.
除距离、面积、角度这些有明显几何意义的问题外,有时也会碰到以 下问题:
例题 已知圆C: x 32 y2 4 ,O为坐标原点;Q是圆C上的一点.
问题(6) 设Q(x,y),则 y 2 的最大值和最小值分别是___,___ .
x2
【高考】二轮复习与圆相关的范围与最值问题ppt课件

分析:由题意圆M的圆心M (2 5cos ,5sin )的轨迹方程为
(x 2)2 y2 25, P是圆M上的动点,PE • PF的最小值 可转化为与PC范围相关的问题
变式:
圆C的方程为(x 2)2 y2 4,圆M的方程为
(x 2 5 cos )2 ( y 5sin )2 1( R).过圆M上
则x 2 y 5 5 cos 2 5 sin 5cos( ) (5 其中 cos 5 ,sin 2 5 )
5
5
所以当 cos( ) 1时,(x 2 y)max 5 5 0,故x 2 y的最大值为 0
总结:
在处理与圆有关的范围和最值问题中,应把握两个“思想”:
几何 与圆相关的范围与最值问题 思想和代数思想。
解:(1)过圆心C作CM EF,CN GH, M , N为垂足
ab 2
设 CM d1, CN d2
a2 b2 2
则EF GH 2(
4 d12
4
d
2 2
),又d12
d22
CA2
1
由: 4 d12
4
d
2 2
8 - (d12 d22 )
81
14
2
2
22
(当且仅当 d1 d2
即
利
用圆
的
参数方
程
(
三角换元), 将所要
求
的
与圆相关的范围与最值问题
范围(最值)问 与圆相关的范围与最值问题
与圆相关的范围与最值问题
题转化
到
三
角函数
求范围(最值)的问题,
与圆相关的范围与最值问题
同时,由于 与圆相关的范围与最值问题
与圆相关的范围与最值问题
(x 2)2 y2 25, P是圆M上的动点,PE • PF的最小值 可转化为与PC范围相关的问题
变式:
圆C的方程为(x 2)2 y2 4,圆M的方程为
(x 2 5 cos )2 ( y 5sin )2 1( R).过圆M上
则x 2 y 5 5 cos 2 5 sin 5cos( ) (5 其中 cos 5 ,sin 2 5 )
5
5
所以当 cos( ) 1时,(x 2 y)max 5 5 0,故x 2 y的最大值为 0
总结:
在处理与圆有关的范围和最值问题中,应把握两个“思想”:
几何 与圆相关的范围与最值问题 思想和代数思想。
解:(1)过圆心C作CM EF,CN GH, M , N为垂足
ab 2
设 CM d1, CN d2
a2 b2 2
则EF GH 2(
4 d12
4
d
2 2
),又d12
d22
CA2
1
由: 4 d12
4
d
2 2
8 - (d12 d22 )
81
14
2
2
22
(当且仅当 d1 d2
即
利
用圆
的
参数方
程
(
三角换元), 将所要
求
的
与圆相关的范围与最值问题
范围(最值)问 与圆相关的范围与最值问题
与圆相关的范围与最值问题
题转化
到
三
角函数
求范围(最值)的问题,
与圆相关的范围与最值问题
同时,由于 与圆相关的范围与最值问题
与圆相关的范围与最值问题
与圆有关的最值问题

“=”当且仅当a b时成立,此时d min
a 2 1 2b2 a 1 a 1 或 r 2 b 1 b 1 a b 2 2 所求圆方程: x 1 y 1 2或( x 1)2 ( y 1)2 2
一、到圆心距离的最值问题; 二、到圆上一点距离的最值问题;
三、与圆上一点的坐标有关的最值问题; 四、与圆半径有关的最值问题.
一、到圆心距离的最值问题:
例1:已知P是直线3x 4 y 8 0上的动点,PA, PB
2 2
是圆x y 2 x 2 y 1 0的两条切线,A, B是切点, C是圆心,求四边形PACB面积的最小值。
2 2
9 12 2 2 易求得P , 时,x y 最小为20 5 5 21 28 2 2 求得P , 时,x y 最大为100 5 5
练习1:求实数x, y满足x ( y 1) 1,
2 2
求下列各式的最值: () 1 3x 4 y
法二:x 2 y 2 ( x 2 y 2 )2 可看作圆 x ( y 1) 1上的点到坐标原点距离
2 2
y
1
的平方的最值,亦可求解
o
x
练习1:求实数x, y满足x ( y 1) 1,
2 2
求下列各式的最值: () 1 3x 4 y (2)x y
2 2
解:(3)法一:由()知 1 : 3 sin k , 得 sin k cos k 3 1 cos
点评:在线性规划中,求形如 x a y b 的
2 2
最值问题,总是转化为求圆 x a y b r
a 2 1 2b2 a 1 a 1 或 r 2 b 1 b 1 a b 2 2 所求圆方程: x 1 y 1 2或( x 1)2 ( y 1)2 2
一、到圆心距离的最值问题; 二、到圆上一点距离的最值问题;
三、与圆上一点的坐标有关的最值问题; 四、与圆半径有关的最值问题.
一、到圆心距离的最值问题:
例1:已知P是直线3x 4 y 8 0上的动点,PA, PB
2 2
是圆x y 2 x 2 y 1 0的两条切线,A, B是切点, C是圆心,求四边形PACB面积的最小值。
2 2
9 12 2 2 易求得P , 时,x y 最小为20 5 5 21 28 2 2 求得P , 时,x y 最大为100 5 5
练习1:求实数x, y满足x ( y 1) 1,
2 2
求下列各式的最值: () 1 3x 4 y
法二:x 2 y 2 ( x 2 y 2 )2 可看作圆 x ( y 1) 1上的点到坐标原点距离
2 2
y
1
的平方的最值,亦可求解
o
x
练习1:求实数x, y满足x ( y 1) 1,
2 2
求下列各式的最值: () 1 3x 4 y (2)x y
2 2
解:(3)法一:由()知 1 : 3 sin k , 得 sin k cos k 3 1 cos
点评:在线性规划中,求形如 x a y b 的
2 2
最值问题,总是转化为求圆 x a y b r
与圆有关的最值问题

( (0, )) 令 2 2 PA PB PA PB cos 2 PA COS 2 APB 2
O B
2
P
r 2 po r (1 2sin ) po 1 1 2( ) po 2 2 2 设po t (t 1) 则PAPB (t 1)(1 t ) t t 3 2 2 3
C O x
3 5. 易得 PM 的最小值为 10
二、利用所求式的几何意义转化为线 性规划问题求最值
例2:若实数x、y满足 x y 2x 4 y 0 求(1)x-2y的最大值.
2 2
y 1 ( 2) x 2
的取值范围。 2 2 ( x 2) ( y 1) 的取值范围。 ( 3) (4) x y 1 的取值范围。
2 2 ( x 2) ( y 1) (3)
表示为圆上任意一点P到点A(2,1)距离的平方
P
因为 所以
PA [CA 5, CA 5]
. C
A(2,1)
PA2 ( x 2)2 ( y 1)2 [50 10 2,50 10 2]
(4) 因为圆上任一点P(x,y)到直线 x y 1 0 的距离
E M A N G C F H O x
解(1)令圆心C到弦EF的距离为 EF+GH 2( 4 d12 4 d 2 2 )
d1,到弦GH的距离为 d2,则
又 d12 d22 CA2 1
4 d12 4 d22 4 d12 4 d22 2 2
(当且仅当 d1 d 2
2 取等号) 2 故EF+GH 2 8 1 14 2
O B
2
P
r 2 po r (1 2sin ) po 1 1 2( ) po 2 2 2 设po t (t 1) 则PAPB (t 1)(1 t ) t t 3 2 2 3
C O x
3 5. 易得 PM 的最小值为 10
二、利用所求式的几何意义转化为线 性规划问题求最值
例2:若实数x、y满足 x y 2x 4 y 0 求(1)x-2y的最大值.
2 2
y 1 ( 2) x 2
的取值范围。 2 2 ( x 2) ( y 1) 的取值范围。 ( 3) (4) x y 1 的取值范围。
2 2 ( x 2) ( y 1) (3)
表示为圆上任意一点P到点A(2,1)距离的平方
P
因为 所以
PA [CA 5, CA 5]
. C
A(2,1)
PA2 ( x 2)2 ( y 1)2 [50 10 2,50 10 2]
(4) 因为圆上任一点P(x,y)到直线 x y 1 0 的距离
E M A N G C F H O x
解(1)令圆心C到弦EF的距离为 EF+GH 2( 4 d12 4 d 2 2 )
d1,到弦GH的距离为 d2,则
又 d12 d22 CA2 1
4 d12 4 d22 4 d12 4 d22 2 2
(当且仅当 d1 d 2
2 取等号) 2 故EF+GH 2 8 1 14 2
27.2.2点与圆的关系(二) ----点圆最值问题

∴ ������������ < ������������ + ������������, 即:������������������ + ������������������ < ������������ + ������������, 又∵ ������������������ = ������������ ∴ 总有 ������������������ < ������������,
点������������和远交点������������,点P到圆上所有点距离中的最小值即 为线段P������������的长,最大值为线段P������������的长.
解:如图,连结OA,可得△OAP 。
∵ 在△OAP中, ������������ > ������������ − ������������
(二)点在圆内 ⇔ 点M到圆心的距离 OM < 半径 R (三)点在圆外 ⇔ 点P到圆心的距离 OP > 半径 R
方法总结:判断点和圆的位置关系,就是判断点到 圆心O的距离与半径的大小关系.
经过已知点的圆
(1)经过已知一点作圆,能作无数个圆。
(2)经过两个点也能作出无数个圆,这些圆的圆心都在线段AB的垂直平分线上。 (3)经过在同一直线上的三点A,B,C无法画圆。
又∵ ������������������ = ������������ 即:������������ + ������������������ > ������������,
∴ ������������������ > ������������, 即:P������������总大于线段PA
A
������������ O
点������������和远交点������������,点P到圆上所有点距离中的最小值即 为线段P������������的长,最大值为线段P������������的长.
解:如图,连结OA,可得△OAP 。
∵ 在△OAP中, ������������ > ������������ − ������������
(二)点在圆内 ⇔ 点M到圆心的距离 OM < 半径 R (三)点在圆外 ⇔ 点P到圆心的距离 OP > 半径 R
方法总结:判断点和圆的位置关系,就是判断点到 圆心O的距离与半径的大小关系.
经过已知点的圆
(1)经过已知一点作圆,能作无数个圆。
(2)经过两个点也能作出无数个圆,这些圆的圆心都在线段AB的垂直平分线上。 (3)经过在同一直线上的三点A,B,C无法画圆。
又∵ ������������������ = ������������ 即:������������ + ������������������ > ������������,
∴ ������������������ > ������������, 即:P������������总大于线段PA
A
������������ O
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
k 2 6
k 2 12
切线方程为y 2 6 x
16
当a b 0时,切线方程可设为 x y 1 ab
即x y a 0 由点到直线的距离公式得:
1 2 a 2
12 12 a 1或a 3
切线方程为x y 1 0或x y 3 0
总之,所求切线方程为y 2 6 x,
解:设P x, y PA 2 PB 2 x 12 y2 x 12 y2
2 x2 y2 1
上式中x2 y2相当于在 x 32 y 42 4
上的点P到原点O的距离的平方。 7
作图不难知道,当O0,0, P x, y,3, 4共线时,
x2 y2有最值。
易求得P
9 5
Y Y=X
解:设 x 12 y 32 r2
则圆心C 1,3,半径为r.
O
X
4x+3y=12
由图观察知,当圆与直线4x 3y 12 0
相切是,半径r最小,即r 2最小。
13
由圆心到直线的距离等于半径,得:
d 4 9 12 1 r 42 32 5
r2 1
x
25
12
y
32
的最小值
解:(2)法一:由(1)知 :
(3)y 2 x 1
x2 y2 cos2 (1 sin )2 2 2sin
x2 y2的最大值为4,最小值为0
y
法二:x2 y2 ( x2 y2 )2可看作圆 x2 ( y 1)2 1上的点到坐标原点距离 的平方的最值,亦可求解
1
ox
10
练习1:求实数x, y满足x2 ( y 1)2 1, 求下列各式的最值:
x
2
3 5
3 2
3 10
P
3 10
,
3 5
18
例5:已知与曲线C:x2 y2 2x 2 y 1 0 相切的直线l交x轴,y轴于A, B两点,O为原点,
M为切点,O为坐标原点,且 PM PO , 求使 PM 最小的点P的坐标。
15
解:1.圆C可化为: x 12 y 22 2
圆心C 1, 2,半径r 2
设圆C的切线在x轴和y轴上的截距分别为a、b
当a b 0时,切线方程可设为y kx
即kx y 0 由点到直线的距离公式得:
k 2
1 25
点评:在线性规划中,求形如 x a2 y b2 的
最值问题,总是转化为求圆 x a2 y b2 r2
半径平方的最值问题。
14
练习2:已知圆C:x2 y2 2x 4 y 3 0
1.若圆C的切线在x轴和y轴上截距相等,
求切线的方程;
2.从圆C外一点P x, y向圆引切线PM,
1
一、到圆心距离的最值问题; 二、到圆上一点距离的最值问题; 三、与圆上一点的坐标有关的最值问题; 四、与圆半径有关的最值问题.
2
一、到圆心距离的最值问题:
例1:已知P是直线3x 4y 8 0上的动点,PA, PB 是圆x2 y2 2x 2y 1 0的两条切线,A, B是切点, C是圆心,求四边形PACB面积的最小值。
x 1
3
11
法二:y 2 y (2) 可看作圆 x 1 x (1)
x2 ( y 1)2 1上的点与P(1, 2)两点的 连线的斜率最值,结合图形可求解
y
1
ox
P( 1,2 )
12
四、与圆半径有关的最值问题:
x0
例4:设x,y满足
yx
求x 12 y 32的最小值。
4x 3y 12
, 12 5
时,x2
y2最小为20
求得P
21 , 5
28 5
时,x2
y2最大为100
8
练习1:求实数x, y满足x2 ( y 1)2 1, 求下列各式的最值:
(1)3x 4 y (2)x2 y2 (3)y 2
解:(1)法一:令
x y
cos
1 sin
,
则
x 1
3x 4 y 3cos 4 4sin 5sin( ) 4
解:已知圆Leabharlann 化为: x 12 y 12 1 圆心C 1,1,半径r 1
Q SPACB 2SPAC PA • AC
PC 2 r2 • r PC 2 1
3
求SPACB的最小值就是求 PC 的最小值, 而 PC 的最小值就是圆心到直线的距离.
348
d
3
32 42
所求面积的最小值为
S 91 2 2
点评:求切线长时总是转化为
到圆心的距离和半径来求解。 4
二、到圆上一点距离的最值问题:
例2:已知P是圆x2 y2 1上一点,Q是直线 l : x 2y 5 0上一点,求 PQ 的最小值。
解:圆心C 0,0,半径r 1,
作 CH l 与H 求圆上一点P到Q的距离可以转化为 圆心C到Q的距离 CQ ,而 CQ 的最小
3x 4 y的最大值为9,最小值为1
法二:设3x 4 y t,直线与圆相切时取最值
于是 3 0 41 t 1, t 4 5,t 9或 1 5
3x 4 y的最大值为9,最小值为1
9
练习1:求实数x, y满足x2 ( y 1)2 1, 求下列各式的最值:
(1)3x 4 y (2)x2 y2
值就是圆心到直线的距离 CH .
5
PQ CQ 1 CH 1
005
1 5 1
12 22
PQ 的最小值为 5-1 点评:到圆上一点距离的最值问题 总是转化为到圆心距离的最值问题。
6
三、与圆上一点的坐标有关的最值问题:
例3:已知定点A1,0, B1,0和圆x 32 y 42 4
上的动点P,求使 PA 2 PB 2 最值时点P的坐标。
x y 1 0或x y 3 0
17
2.连结MC,则 PM 2 PC 2 MC 2
Q PM PO PC 2 MC 2 PO 2
即k x 12 y 22 2 x2 y2
x 2y 3 2
PM PO
x2 y2
2
y
3 2
2
y2
5y2 6y 9 4
当y 6 3时,PM 最小, 10 5
(1)3x 4 y (2)x2 y2
解:(3)法一:由(1)知 :
(3)y 2 x 1
k 3 sin ,得sin k cos k 3 1 cos
即 1 k 2 sin( ) k 3
sin( ) k 3 ,则 k 3 1,k 4
1 k2
1 k2
3
y 2 有最小值为 4,无最大值
