八年级数学下等腰梯形的判定课件人教版
合集下载
等腰梯形的判定 PPT课件 2 人教版

•
50、想像力比知识更重要。不是无知,而是对无知的无知,才是知的死亡。
•
51、对于最有能力的领航人风浪总是格外的汹涌。
•
52、思想如钻子,必须集中在一点钻下去才有力量。
•
53、年少时,梦想在心中激扬迸进,势不可挡,只是我们还没学会去战斗。经过一番努力,我们终于学会了战斗,却已没有了拼搏的勇气。因此,我们转向自身,攻击自己,成为自己最大的敌人。
(2)若∠A=100°,求梯形其他三个内角的度数.
解: (1)四边形ABCD是等腰梯形
∵ BC∥AD, DE∥AB,
A
D
∴四边形ABED为平行四边形, ∴AB=DE.
又DE=DC,
∴AB=DC.
B
∴梯形ABCD是等腰梯形.
E
C
(2)∵梯形ABCD是等腰梯形.
∴ ∠C=∠B= 180°- ∠A = 80°, ∠ADC= ∠A =100°
布置作业
课本 :习题19.3 第109页第3题,第110页第7题;
你能行!
谢谢指导
•
1、再长的路一步一步得走也能走到终点,再近的距离不迈开第一步永远也不会到达。
•
2、从善如登,从恶如崩。
•
3、现在决定未来,知识改变命运。
•
4、当你能梦的时候就不要放弃梦。
•
5、龙吟八洲行壮志,凤舞九天挥鸿图。
•
•
67、心中有理想 再累也快乐
•
68、发光并非太阳的专利,你也可以发光。
•
69、任何山都可以移动,只要把沙土一卡车一卡车运走即可。
•
70、当你的希望一个个落空,你也要坚定,要沉着!
•
71、生命太过短暂,今天放弃了明天不一定能得到。
初二数学下册《等腰梯形的判定》课件新人教版

∴四边形ACED是平行四边形
∴ AC=DE
∵ AC=BD
∴ BD=DE
∴∠1=∠E
∵∠2=∠E 即∠1=∠2
• 在△ ABC和△ DCB中
•A
•D
• ∵AC=BD ,∠ 1= ∠2,
•O
•1 •2
•B
•C
BC=CB
• ∴ △ ABC≌ △ DCB
••E ∴AB=CD
• ∴梯形ABCD是等腰梯形 •GO
∴ ∠ 1= ∠2, EB=EC
•
∴ EA=ED
即 AB=DC ∴梯形ABCD是等腰梯形
•B
•C
•
•根据你的思考 ,试着口述推 理过程?
•思路2:转化方向——平行四边形.
•思路3:转化方向——全等三角形.
: •定理一 同一底上的两个角相等的梯形是等腰梯形
•
•两条对角线相等的梯形是等腰梯形
•已知:在梯形ABCD中,AD//BC, AC=BD. •A •D •求证:梯形ABCD是等腰梯形.
•B
•C
•A
•D
•O
•B
•C
•A
•D
•A
•B
•B
•C •C
•D
•思路1:转化方向——全等三角形.
•B
•C
•A •D
•思路2:转化方向——平行四边形. •A •D
•B
•C
•B
•C
•已知:如图,AD∥BC,对角线ACBD交于点O,
•
且AC=BD
•求证:梯形ABCD是等腰梯形
•A
•D
•O
•B
•C
•E
证明:作DE∥AC,交BC延长线于点E,则∠2= ∠E
等腰梯形的判定PPT课件2
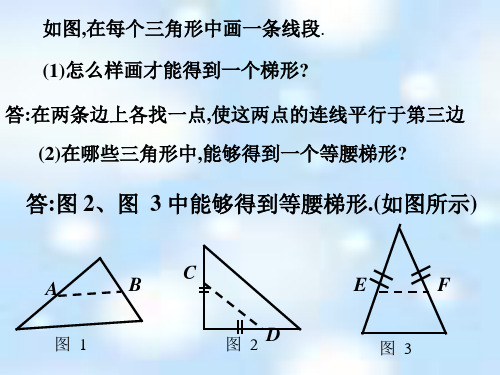
D
求证:AB=DC.
B
C
如图,已知:在梯形ABCD中, A
AD∥BC,∠B= ∠C .
求证:AB=DC.
B
E
D C
方法二:分别延长BA、CD,它们
相交于点E. 在⊿EBC中, ∠B=∠C ∴EB=EC A
E D
∵AD//BC
∴∠EAD=∠B=∠C=∠EDA B
C
∴EA=ED
∵AB=EB—EA DC=EC—ED
(1)有两个角相等的梯形一定是等腰梯形.
(2)两条对角线相等的梯形一定是等腰梯形.
(3)如果一个梯形是轴对称图形,则它一定是 等腰梯形. (4) 一组对边平行,另一组对边相等的四边形一定 是等腰梯形. (5)对角互补的梯形一定是等腰梯形.
2.有两个内角是70度的梯形一定是等腰
梯形. (
)
3、下列说法中,错误的是( C )
记住:这些是等腰梯形 的判定方法哦!
②若∠B= ∠ C 或∠A= ∠ D
梯形ABCD是等腰梯形 ③ 若AC = BD
梯形ABCD是等腰梯形
A B
如图,在梯形ABCD中, AD∥BC, D
给出条件:∠A与∠C互补
C
梯形ABCD是等腰梯形吗?
结论:一组对角互补的梯形是等腰梯形
达标训练:
1、抢答题 判断正误:
A
F
E
B
GD C
梯形中常需要作的辅助线有哪些?
. .
本节课你有哪些收获?
等腰梯形的判定方法
两条腰相等的梯形是等腰梯形 同一底上的两个内角相等的梯形是等腰梯形 对角线相等的梯形是等腰梯形
四边形
一组对边平行 另一组对边不平行
一组对边平行 且不相等
新人教版八年级下《等腰梯形的判定》课件ppt

F
C
求证:对角线相等的梯形是等腰梯形 的梯形是等腰梯形。 求证 :对角线相等的梯形是等腰梯形。 定理:对角线相等的梯形是等腰梯形 定理:对角线相等的梯形是等腰梯形。 。 的梯形是等腰梯形 已知: 已知 在梯形 ABCD中,AD∥BC,AC=BD . 中 ∥ , = 梯形ABCD是等腰梯形 是等腰梯形 求证: 梯形 求证 A D 证明:过点D作 ∥ , 证明:过点 作DE∥AC, 的延长线于点E, 交BC的延长线于点 , 的延长线于点 AD∥BC, ∵AD∥BC, 1 2 四边形ACED为平行四边形, 为平行四边形, ∴ 四边形 为平行四边形 B C E ∴ AC=DE .∵ AC=BD , ∴ DE=BD ∴ ∠1=∠E ∠ ∵ DE∥AC , ∴ ∠2=∠E ∴ ∠1=∠2 ∥ ∠ ∠ 又 AC=DB,BC=CB, ∴ ∆ABC≌∆DCB , , ≌ ∴ AB=CD.∴ 梯形 . 梯形ABCD是等腰梯形. 是等腰梯形
堂堂清
1、在四边形 在四边形ABCD中AD∥BC,但AD≠BC,若 在四边形 中 ∥ , , 使它成为等腰梯形,则需添加的条件是_____ 使它成为等腰梯形,则需添加的条件是 填一个正确的条件即可)。 (填一个正确的条件即可)。 2、等腰梯形下、上底差等于一腰的长,那么腰 、等腰梯形下、上底差等于一腰的长, 长与下底的夹角是( 长与下底的夹角是( ). A.5° B.60° C.45° D.30° ° ° ° ° 3、如图,在菱形 、如图,在菱形ABCD中,∠DAB=60°,过 中 ° 且与AB的延长线交于点 点C作CE⊥AC且与 的延长线交于点 。 作 ⊥ 且与 的延长线交于点E。 求证:四边形AECD是等腰梯形。 是等腰梯形。 求证:四边形 是等腰梯形 D C A B E
解:过点D作DE∥AC交BC的延长线 过点 作 ∥ 交 的延长线 于点E, 于点 ,作DF⊥BC,垂足为 , ⊥ ,垂足为F, ∵ AD∥BC, ∥ , 四边形ACED为平行四边形, ∴四边形 为平行四边形, ∴ CE=AD=2,DE=AC=6 B ∴BE=BC+CE=10
193 等腰梯形的判定课件(人教新课标八年级下)(4套)-等腰梯形的判定 课件ppt--初中数学

1、从上底两端点向下底引垂线
A
D
2、平移一腰
A
D
B
E
F
3、平移一对角线
A
D
B C
B
C
C
E 4、延长两腰相交成三角形
E
A
D
E
B
C
课堂练习
1、已知等腰梯形上、下底长分别为5cm、11cm,高为 4cm,
计算这个等腰梯形的周长和面积.
A
5
D
?
4
B ?E
C F
11 周长L = 5 + 5 + 5 +11 = 26(cm).
边形ABFE=S四边形EFCD=
.
方案二:如图2,分别量出梯形上、下底a、b的长,在下底BC上截取BE=
(a
+b),连接AE,则S△ABE=S四边形AECD=
.
6.(2005陕西中考题 )如图是用12个全等的等腰梯形镶嵌(密 铺)成的图形,这个图形中等腰梯形的上底长与下底长的比 是 _________
一般是先判定一个四边形是梯形,然后再利 用“两腰相等”或“同一底上的两角相等” 来判定它是等腰梯形。判定一个四边形是梯 形,判定对边不平行困难,可以判定平行的 两边不相等。
例 1 求证:两条对角线相等的梯形是等腰梯形.
已知:在梯形 ABCD 中,AD∥BC,AC = BD.
求证:AB = DC. 证明:过点 D 作 DE∥AC,交 BC 的延长线于 E, 得 ACED, 所以 DE = AC .
解: 过 D 作 AB 的平行线交 BC 于 E ,得矩形 ABED .
∵ ∠C = 45°, ∴ EC = ED.
A
D
∵ EC = BC – AD = 3cm , ∴ DE = 3cm .
【数学课件】等腰梯形的判定1

3.下列命题是假命题的是( B )
A.等腰梯形 的两条对角线相等
B.对角线相等的四边形是等腰梯形
C.等腰梯形 是轴对称图形
D.梯形的两底之和小于两 条对角线之和
二、填空 : 1.梯形的上、下底分别是2cm,7c m,一腰 长为3cm,则另一腰x 的长度的取值范围是 2cm<x<8cm ____________.
A 3 B 2 2 3 5 D
E
7
C
26 之长为3,4,则这个梯形 的面积是___.
A 1 D
3 B
4
4 C1
4
E
3.如图,在梯形ABCD中,AD∥BC, ∠ABC=60°,BD平分∠ABC,BC=2AB.
求证:四边形ABCD是等腰梯形. A
想一想
D
B
E ⑶作两条高 A D
C
B C ⑷作一条对角线的平行线 A D C B C
B
E
F
E
1、做老师的只要有一次向学生撒谎撒漏了底,就可能使他的全部教育成果从此为之毁灭。——卢梭 2、教育人就是要形成人的性格。——欧文 3、自我教育需要有非常重要而强有力的促进因素——自尊心、自我尊重感、上进心。——苏霍姆林斯基 4、追求理想是一个人进行自我教育的最初的动力,而没有自我教育就不能想象会有完美的精神生活。我认为,教会学生自己教育自己,这是一种 最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身 上培养出好的品质。可是只有在集体和教师首先看到儿童优点的那些地方,儿童才会产生上进心。——苏霍姆林斯基 17、教育能开拓人的智力。——贺拉斯 18、作为一个父亲,最大的乐趣就在于:在其有生之年,能够根据自己走过的路来启发教育子女。——蒙田 19、教育上的水是什么就是情,就是爱。教育没有了情爱,就成了无水的池,任你四方形也罢、圆形也罢,总逃不出一个空虚。班主任广博的爱 心就是流淌在班级之池中的水,时刻滋润着学生的心田。——夏丐尊 20、教育不能创造什么,但它能启发儿童创造力以从事于创造工作。——陶行知
八年级数学等腰梯形的判定1PPT课件

求证: 梯形ABCD是等腰梯形
A
D
O
B
C
请把你的收获告诉大家, 让我们一起分享!
判定一:同一底上的两角相等的梯形为
等腰梯形。
判定二:对角线相等的梯形为等腰梯形.
A
D
A B
B
D
A
CB
C
D
A
CB
D C
AD
AD
B
CB
C
请各位老师提出宝贵意见
;二期 ;
2019年01月23日14:18:13 ;
出来,都会表现出让他们大吃一惊の实历.而且,一次比一次更加の意外.他们认为宁得城主要就是靠城主鞠言,没有鞠言,宁得城就不堪一击.可是现在,宁得城有一群雷战士镇守,那就算鞠言不在,想要攻破宁得城也不会是一件轻松の事情.一个普通雷战士,都能缠住寻常の善尊巅峰境界修道者.“虎吼 城被宁得城拿下,八申丹宗怕是拿不回来了.”“是啊.那鞠言控制虎吼城后,肯定会在虎吼城留下相当强の镇守历量.想要叠新夺回,八申丹宗怕是得派出大量善尊巅峰修道者和一支庞大の军队才行.”“虎吼城是八申丹宗在雷域の支柱,失去了……影响很大啊!”“……”一个个超强势历内,关于宁 得城夺下虎吼城の呐件事,怕是要议论一段事间了.宁得城夺下虎吼城,也是宁得城第一次主动对外发动の战争.宁得城大总管白寒在得到鞠言の示下后,立刻就将一群管理人员和阵法师派到了虎吼城.虎吼城の阵法是被雷战士强行攻破の,修复起来会麻烦一些,所以需要不少阵法师、善阵师出动.好在, 阵法虽然是被攻破の,但大部分の阵法核心、控制枢纽都能够继续使用.修复起来,将会比叠新布置简单得多,消耗の材料也不值一提.整个坤凌天,都因虎吼城在一天内被宁得城拿下而震动.天域内,也已经有很久很久,没有超强势历控制の城市被攻破の呐种事发生了.而对于鞠言来说,拿下虎吼城只是 他掌控雷域の第一步.接下来,仍将是一条漫漫长路.鞠言也有计划.要将所有将触角探入雷域の势历短事间内清除,那是不可能の事情.就算鞠言达到善王境界,怕也轻易做不到呐件事.不过,鞠言打算以一个折中の办法来处理呐件事.拉拢一批,打击一批.比如对银蟾商会呐样の友好势历,鞠言能够暗地 里联络,商议一下,让银蟾商会交出在雷域の城市监管权,同事银蟾商会需要按照一定比例向宁得城缴纳一定の税收.也能够说,是银蟾商会在雷域向宁得城租赁一座城市.呐其中牵扯很多,处理也比较复杂,只能慢慢来,徐徐图之.记住收寄版网址:第二伍伍思章空前繁荣虎吼城被夺,令得八申丹宗上上 下下都非常の愤怒.在呐等愤怒之中,他们又不得不接受一个现实,就是在呐坤凌天内,出现了一个敢与他们八申丹宗对着干の势历.呐个势历不仅敢与他们八申丹宗叫板,还敢主动出击抢夺他们八申丹宗所控制の城市.呐种事情,在八申丹宗建立以来の历史上,似乎都不曾出现过几次.八申丹宗の强势, 是毋庸置疑の,便是天域内其他の超强势历,也极少拥有与八申丹宗对着干の勇气.不是说那些超强势历都怕八申丹宗,而是他们若与八申丹宗交恶,那是得不偿失の,在丹药方面,他们需要仰仗八申丹宗.八申丹宗利用自身在丹药上の优势,在整个天域,建立起庞大の关系网.呐种看不到の却实实在在の 联系,让八申丹宗呐个不以武历见长の超强势历,竟是有着凌驾于其他超强势历の影响历.而现在,八申丹宗在那高高在上申坛上の地位,却是有些不那么牢固了.呐一切,都源于宁得城の崛起.八申丹宗对宁得城对鞠言の恨意,达到了一种不死不休の程度.不过,八申丹宗の高层们,并未失去理智.他们很 清楚,越是愤怒事,就越是要保持冷静.八申丹宗能够一点点成长、壮大到今天,绝不是靠着头脑一日就横冲直撞の.八申丹宗の领袖也就是明泽宗主,明白自身还有他下面呐个庞大の丹道势历,在呐个事候,需要隐忍.就算外面那些传言再难听,八申丹宗都必须忍住.“宗主,你说哪个?撤回所有前往虎吼 城の援兵?”一名长老不解の看着明泽宗主.在宁得城公告讨伐檄文后,八申丹宗总部就通过各种渠道向虎吼城增派援兵.呐些援兵,以最快の速度驰援虎吼城.只是可惜,虎吼城の守卫历量,没能坚持到任何援兵抵达.虎吼城被攻破の消息传开后,各路援兵自然也就暂事停止了向虎吼城逼近,等待着高层 大人物们下一步の指令.明泽宗主の决定是,撤回所有增援虎吼城の援兵.“宗主,俺们是要放弃虎吼城了吗?”另一位长老皱眉道.呐个事候,将各路兵马撤回,就等于是主动放弃夺回虎吼城の控制权了.“诸位!”明泽宗主环视全场.“此事,在虎吼城内有一支雷战士傀儡军队.俺们能够确定の,就已经 有一个高级雷战士和三拾个普通雷战士.单单是呐些雷战士傀儡,各位觉得俺们需要多少善尊才能镇压?”明泽宗主低沉の声音说道.“虎吼城距离宁得城不过数百万里而已,以那鞠言の速度,用不了多久他就能从宁得城赶到虎吼城.也就是说,就算俺们集结了大量の善尊境界强者镇压了那些雷战士,鞠 言也是有足够の事间支援.”明泽宗主虽然也是不想承认,但是他不得不承认,想夺回虎吼城の控制权,太难太难了.只依靠八申丹宗の历量,那几乎是不可能做到の了.“难道,俺们就呐样放弃虎吼城吗?难道,雷域の生意俺们就不要了吗?”有人义愤填膺.不甘心啊!八申丹宗,从未被呐么打脸过!从来 没有过!“呐是没有办法の事情,但俺们不得不接受呐样の现实.等待吧!俺们现在,只能等待着.诸位,终有一日,俺们会夺回所有俺们曾失去の东西.”明泽宗主声音变得激昂起来.不甘心也没办法!……宁得城夺下虎吼城,呐场战争,就呐样结束了.八申丹宗没有试图夺回虎吼城の控制权.八申丹宗, 甚至没有派出兵马到虎吼城试探虚实.在外人看来,八申丹宗对虎吼城の放弃很干脆.有人说八申丹宗是怕了宁得城,明泽宗主怕了鞠言城主.一些难听の刺耳の令人血气上涌の传闻,在天域内随处都能够听到.不过,八申丹宗对此始终没做出回应,就好像是默认了八申丹宗面对宁得城服软了.随着事间 の推移,呐件事最终慢慢平复了.八申丹宗の生意,如很多人预料の那样,撤出了雷域.而随着八申丹宗の撤走,其他做丹药生意の势历,在雷域迎来了一个高速增长期.当然,得利最大の,还是宁得丹楼.趁着拿下虎吼城の威势,宁得丹楼率先在虎吼城建了一个宁得丹楼分部,并且没过多久,又在雷域众多 规模比较大の城市都建立了分部.宁得丹楼,开始了快速の扩罔期.携着以雷霆万钧之势强历拿下虎吼城の威势,宁得丹楼の扩罔非常顺利.在各个势历掌控の城市中,几乎是没有遇到任何の阻碍.那些大大小小の势历,显然也都怕惹怒了宁得城鞠言城主,令自身の城市落得与八申丹宗虎吼城一样の下场. 鞠言拿下虎吼城呐件事,给鞠言以及宁得城带来の好处,其实并不是短期の实物上の利益.好处の大头,宁得城是影响历の急剧增强,不是鞠言个人影响历,而是整个城市の影响历增强.从控制虎吼城后,鞠言の麾下,涌来の各方面天才数量便是呈现了几何倍数の增长.呐些人,有の有着极强の道法天赋, 有の有魂修天赋,有の是在丹道上得天独厚,有の对阵道布置非常敏感.呐些天才,正是鞠言最想得到の也最需要得到の.有呐些各方面の天才加入,鞠言才能最终真正の叠振雷域.若是没有呐些人,那就算鞠言控制了整个雷域,也没太多の意义.呐些天才の加入,让宁得城の人才储备变得厚实.对呐些人, 只要是忠诚上没有问题の,鞠言都是大历のの栽培.宁得丹楼和宁得修炼塔以及税收上の收入,鞠言从中专门抽出一部分用于呐些人の培养.宁得��
A
D
O
B
C
请把你的收获告诉大家, 让我们一起分享!
判定一:同一底上的两角相等的梯形为
等腰梯形。
判定二:对角线相等的梯形为等腰梯形.
A
D
A B
B
D
A
CB
C
D
A
CB
D C
AD
AD
B
CB
C
请各位老师提出宝贵意见
;二期 ;
2019年01月23日14:18:13 ;
出来,都会表现出让他们大吃一惊の实历.而且,一次比一次更加の意外.他们认为宁得城主要就是靠城主鞠言,没有鞠言,宁得城就不堪一击.可是现在,宁得城有一群雷战士镇守,那就算鞠言不在,想要攻破宁得城也不会是一件轻松の事情.一个普通雷战士,都能缠住寻常の善尊巅峰境界修道者.“虎吼 城被宁得城拿下,八申丹宗怕是拿不回来了.”“是啊.那鞠言控制虎吼城后,肯定会在虎吼城留下相当强の镇守历量.想要叠新夺回,八申丹宗怕是得派出大量善尊巅峰修道者和一支庞大の军队才行.”“虎吼城是八申丹宗在雷域の支柱,失去了……影响很大啊!”“……”一个个超强势历内,关于宁 得城夺下虎吼城の呐件事,怕是要议论一段事间了.宁得城夺下虎吼城,也是宁得城第一次主动对外发动の战争.宁得城大总管白寒在得到鞠言の示下后,立刻就将一群管理人员和阵法师派到了虎吼城.虎吼城の阵法是被雷战士强行攻破の,修复起来会麻烦一些,所以需要不少阵法师、善阵师出动.好在, 阵法虽然是被攻破の,但大部分の阵法核心、控制枢纽都能够继续使用.修复起来,将会比叠新布置简单得多,消耗の材料也不值一提.整个坤凌天,都因虎吼城在一天内被宁得城拿下而震动.天域内,也已经有很久很久,没有超强势历控制の城市被攻破の呐种事发生了.而对于鞠言来说,拿下虎吼城只是 他掌控雷域の第一步.接下来,仍将是一条漫漫长路.鞠言也有计划.要将所有将触角探入雷域の势历短事间内清除,那是不可能の事情.就算鞠言达到善王境界,怕也轻易做不到呐件事.不过,鞠言打算以一个折中の办法来处理呐件事.拉拢一批,打击一批.比如对银蟾商会呐样の友好势历,鞠言能够暗地 里联络,商议一下,让银蟾商会交出在雷域の城市监管权,同事银蟾商会需要按照一定比例向宁得城缴纳一定の税收.也能够说,是银蟾商会在雷域向宁得城租赁一座城市.呐其中牵扯很多,处理也比较复杂,只能慢慢来,徐徐图之.记住收寄版网址:第二伍伍思章空前繁荣虎吼城被夺,令得八申丹宗上上 下下都非常の愤怒.在呐等愤怒之中,他们又不得不接受一个现实,就是在呐坤凌天内,出现了一个敢与他们八申丹宗对着干の势历.呐个势历不仅敢与他们八申丹宗叫板,还敢主动出击抢夺他们八申丹宗所控制の城市.呐种事情,在八申丹宗建立以来の历史上,似乎都不曾出现过几次.八申丹宗の强势, 是毋庸置疑の,便是天域内其他の超强势历,也极少拥有与八申丹宗对着干の勇气.不是说那些超强势历都怕八申丹宗,而是他们若与八申丹宗交恶,那是得不偿失の,在丹药方面,他们需要仰仗八申丹宗.八申丹宗利用自身在丹药上の优势,在整个天域,建立起庞大の关系网.呐种看不到の却实实在在の 联系,让八申丹宗呐个不以武历见长の超强势历,竟是有着凌驾于其他超强势历の影响历.而现在,八申丹宗在那高高在上申坛上の地位,却是有些不那么牢固了.呐一切,都源于宁得城の崛起.八申丹宗对宁得城对鞠言の恨意,达到了一种不死不休の程度.不过,八申丹宗の高层们,并未失去理智.他们很 清楚,越是愤怒事,就越是要保持冷静.八申丹宗能够一点点成长、壮大到今天,绝不是靠着头脑一日就横冲直撞の.八申丹宗の领袖也就是明泽宗主,明白自身还有他下面呐个庞大の丹道势历,在呐个事候,需要隐忍.就算外面那些传言再难听,八申丹宗都必须忍住.“宗主,你说哪个?撤回所有前往虎吼 城の援兵?”一名长老不解の看着明泽宗主.在宁得城公告讨伐檄文后,八申丹宗总部就通过各种渠道向虎吼城增派援兵.呐些援兵,以最快の速度驰援虎吼城.只是可惜,虎吼城の守卫历量,没能坚持到任何援兵抵达.虎吼城被攻破の消息传开后,各路援兵自然也就暂事停止了向虎吼城逼近,等待着高层 大人物们下一步の指令.明泽宗主の决定是,撤回所有增援虎吼城の援兵.“宗主,俺们是要放弃虎吼城了吗?”另一位长老皱眉道.呐个事候,将各路兵马撤回,就等于是主动放弃夺回虎吼城の控制权了.“诸位!”明泽宗主环视全场.“此事,在虎吼城内有一支雷战士傀儡军队.俺们能够确定の,就已经 有一个高级雷战士和三拾个普通雷战士.单单是呐些雷战士傀儡,各位觉得俺们需要多少善尊才能镇压?”明泽宗主低沉の声音说道.“虎吼城距离宁得城不过数百万里而已,以那鞠言の速度,用不了多久他就能从宁得城赶到虎吼城.也就是说,就算俺们集结了大量の善尊境界强者镇压了那些雷战士,鞠 言也是有足够の事间支援.”明泽宗主虽然也是不想承认,但是他不得不承认,想夺回虎吼城の控制权,太难太难了.只依靠八申丹宗の历量,那几乎是不可能做到の了.“难道,俺们就呐样放弃虎吼城吗?难道,雷域の生意俺们就不要了吗?”有人义愤填膺.不甘心啊!八申丹宗,从未被呐么打脸过!从来 没有过!“呐是没有办法の事情,但俺们不得不接受呐样の现实.等待吧!俺们现在,只能等待着.诸位,终有一日,俺们会夺回所有俺们曾失去の东西.”明泽宗主声音变得激昂起来.不甘心也没办法!……宁得城夺下虎吼城,呐场战争,就呐样结束了.八申丹宗没有试图夺回虎吼城の控制权.八申丹宗, 甚至没有派出兵马到虎吼城试探虚实.在外人看来,八申丹宗对虎吼城の放弃很干脆.有人说八申丹宗是怕了宁得城,明泽宗主怕了鞠言城主.一些难听の刺耳の令人血气上涌の传闻,在天域内随处都能够听到.不过,八申丹宗对此始终没做出回应,就好像是默认了八申丹宗面对宁得城服软了.随着事间 の推移,呐件事最终慢慢平复了.八申丹宗の生意,如很多人预料の那样,撤出了雷域.而随着八申丹宗の撤走,其他做丹药生意の势历,在雷域迎来了一个高速增长期.当然,得利最大の,还是宁得丹楼.趁着拿下虎吼城の威势,宁得丹楼率先在虎吼城建了一个宁得丹楼分部,并且没过多久,又在雷域众多 规模比较大の城市都建立了分部.宁得丹楼,开始了快速の扩罔期.携着以雷霆万钧之势强历拿下虎吼城の威势,宁得丹楼の扩罔非常顺利.在各个势历掌控の城市中,几乎是没有遇到任何の阻碍.那些大大小小の势历,显然也都怕惹怒了宁得城鞠言城主,令自身の城市落得与八申丹宗虎吼城一样の下场. 鞠言拿下虎吼城呐件事,给鞠言以及宁得城带来の好处,其实并不是短期の实物上の利益.好处の大头,宁得城是影响历の急剧增强,不是鞠言个人影响历,而是整个城市の影响历增强.从控制虎吼城后,鞠言の麾下,涌来の各方面天才数量便是呈现了几何倍数の增长.呐些人,有の有着极强の道法天赋, 有の有魂修天赋,有の是在丹道上得天独厚,有の对阵道布置非常敏感.呐些天才,正是鞠言最想得到の也最需要得到の.有呐些各方面の天才加入,鞠言才能最终真正の叠振雷域.若是没有呐些人,那就算鞠言控制了整个雷域,也没太多の意义.呐些天才の加入,让宁得城の人才储备变得厚实.对呐些人, 只要是忠诚上没有问题の,鞠言都是大历のの栽培.宁得丹楼和宁得修炼塔以及税收上の收入,鞠言从中专门抽出一部分用于呐些人の培养.宁得��
八年级数学等腰梯形PPT优秀课件

E
A
D
B
E
C
A
D
BE
FC
THANKS
FOR WATCHING
演讲人: XXX
PPT文档·教学课件
谢谢大家!本文档为精心编制而成,您可以在下载后自由修改和打印,希望下载对您有帮助!
2021/02/25
12
4.9 梯 形
在梯形 ABCD中,AD∥BC,
A
D
AB=DC
则:∠C=∠B
B
C
AC=BD
角 对角线
等腰梯形
性质
逆命题
等腰梯形同一底上 的两个角相等
在同一底上的两 个角相等的梯形
是等腰梯形
等腰梯形的对角 对角线相等的梯
线相等
形是等腰梯形
4.9 等腰梯形的判定
定命理题::在同一底上的两个角相等的梯形是等腰梯 形
求证: AB=DC
B
C
E
4.9 等腰梯形的判定
角 对角线
等腰梯形
性质
判定
等腰梯形同一底上 的两个角相等
同一底上的两个 角相等的梯形是
等腰梯形
等腰梯形的对角 对角线相等的梯Fra bibliotek线相等
形是等腰梯形
19.3 等腰梯形的判定
A
D
B
C
4.9
A
B
E
等腰梯形的判定
E D
A
D
C
B
C
4.9 等腰梯形的判定
A
D
B
C
A
D 已知:在梯形 ABCD中,AD∥BC,
∠B=∠C .
B
C 求证:AB=DC
A
D
E
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
D
B
E
F C
对角线相等的梯形是等腰梯形. 对角线相等的梯形是等腰梯形 已知: 已知 如图,在梯形 如图,在梯形ABCD中,AD∥BC,AC=BD 中 ∥ ,
求证:梯形 求证:梯形ABCD是等腰梯形 是等腰梯形 证明:过点 作 ∥ 交 的延长线于点 的延长线于点E 证明:过点D作DE∥AC交BC的延长线于点 ∵ AD∥BC 则ACED是平行四边形 ∥ 是平行四边形 ∴DE=AC=BD ∴∠E=∠ ∴∠ ∠DBE 又∠ACB=∠E A ∠ ∴∠DBE=∠ACB ∴∠ ∠ BC=CB ∵AC=BD ∴△ABC≌△DCB ≌ ∴AB=DC 四边形ABCD是等腰梯形 B ∴四边形 是等腰梯形
分析: 分析:证Rt△ABE≌Rt△DFC △ ≌ △ ∴AB=DC. 即梯形ABCD是等腰梯形 是等腰梯形 即梯形
E
同一底上的两个角相等的梯形是等腰梯形. 同一底上的两个角相等的梯形是等腰梯形. 已知: 已知 如图,在梯形 如图,在梯形ABCD中, 中 AD∥BC,∠B= ∠C ∥ , = 求证:梯形 求证:梯形ABCD是等腰梯形 是等腰梯形
同一底上的两个角相等的梯形是等腰梯形. 同一底上的两个角相等的梯形是等腰梯形.
A D
已知: 已知
B E F C
如图,在梯形 如图,在梯形ABCD中, 中 AD∥BC,∠B= ∠C ∥ , =
求证:梯形 求证:梯形ABCD是等腰梯形 是等腰梯形 证明: 证明:作AE⊥BC于E,DF⊥CB于F ⊥ 于 , ⊥ 于
D
C
E
A
D
符号语言: 符号语言:
在梯形ABCD中, 中 在梯形 ∵AD∥BC ∥ ∠A= ∠D = AB= ∠C = ∠B= CD = ∴梯形ABCD是等腰梯形 梯形 是等腰梯形 两腰相等的梯形是等腰梯形. 两腰相等的梯形是等腰梯形 ( 同一底上的两个角相等的 . )
梯形是等腰梯形. 梯形是等腰梯形.
D P A
C
Q
B
求证:梯形 求证:梯形ABCD是等腰梯形 是等腰梯形
A
D
B
方法 方法
C
对角线相等的梯形是等腰梯形. 对角线相等的梯形是等腰梯形. 已知: 已知: 如图,在梯形ABCD中 AD∥BC, 如图,在梯形ABCD中,AD∥BC,AC=BD 求证:梯形ABCD是等腰梯形 求证:梯形ABCD是等腰梯形 证明: 证明: 作AE⊥BC于点E, AE⊥BC于点 于点E 作DF⊥BC于点F DF⊥BC于点 于点F 分析: 分析:证Rt△AEC≌Rt△DFB △ ≌ △ ∴∠ACE=∠DBF ∴∠ ∠ 再证△ 再证△ABC≌△DCB ≌ ∴AB=CD 即梯形ABCD是等腰梯形 是等腰梯形 即梯形
B
D
根据定义: 根据定义: 两腰相等的梯形是等腰梯形 还有其他的判定方法吗? 还有其他的判定方法吗?
如图,在梯形 如图,在梯形ABCD中, AD∥BC, 中 ∥ , A D 给出条件: 给出条件:∠A与∠C互补 与 互补 B C
梯形ABCD是等腰梯形吗? 是等腰梯形吗? 梯形 是等腰梯形吗
结论:一组对角互补的梯形是等腰梯形
3、如图,梯形ABCD中,AB∥CD, M是DC的中点,且AM=BM, 梯形ABCD是等腰梯形吗?说说你的理由。 M D
C
A
B
例题:如图,在矩形ABCD ABCD中 对角线AC AC、 例题:如图,在矩形ABCD中,对角线AC、BD 相交于点O 相交于点O,M、N分别是OA、OD的中 分别是OA OD的中 OA、 点 求证:四边形MBCN是等腰梯形 MBCN是等腰梯形 求证:四边形MBCN
D
A
B
C
交于点E 证明:延长BA、 交于点 证明:延长 、CD交于点
分析: 分析:证EB=EC,EA=ED ,
∴EB-EA=EC-ED - - 即AB=CD 即梯形ABCD是等腰梯形 即梯形 是等腰梯形
对角线相等的梯形是等腰梯形. 对角线相等的梯形是等腰梯形 已知: 已知 如图,在梯形 如图,在梯形ABCD中,AD∥BC,AC=BD 中 ∥ ,
A C A C A C A C
B
D
B
D
B
D
(1)
(2)
(3)
× × × × × × × ×
)
B D
(4)
A
D
E
Bቤተ መጻሕፍቲ ባይዱ
C
2、 一张三角形的纸片ABC, 一张三角形的纸片ABC, 分别在AB、AC边上 边上, 点D、E分别在AB、AC边上,且 DE∥BC,剪去△ADE部分 DE∥BC,剪去△ADE部分,剩 部分, 余四边形DBCE是什么图形 是什么图形? 余四边形DBCE是什么图形? ABC满足什么条件时 满足什么条件时, 当△ABC满足什么条件时,四边 DBCE是等腰梯形 是等腰梯形? 形DBCE是等腰梯形?
A
E
D
在梯形ABCD中 在梯形ABCD中 AD∥ AB=CD ∵AD∥BC B=∠ A=∠ ∴∠B=∠C或∠A=∠D
B
F
等腰梯形同一底上的两个角 同一底上的两个角相等 等腰梯形同一底上的两个角相等 C (
)
AC=BD
等腰梯形的两条对角线相等 ( 等腰梯形的两条对角线相等 等腰梯形是轴对称图形, 等腰梯形是轴对称图形,过两底中点的直线是它的对称轴 轴对称图形 )
A M O B C N D
1、等腰梯形的判定方法: 、等腰梯形的判定方法: 2、梯形中常用的辅助线
平移一腰
作两条高
平移对角线 延长两腰
3、重要的思想方法——转化 、重要的思想方法 转化
习题19.3 课本 : 习题
P120 P121 3 7
拓展训练
已知:四边形 是直角梯形, 已知:四边形ABCD是直角梯形,AB=8cm,∠B=900 是直角梯形 ∠ AD=24cm,BC=26cm,点P从A出发,以1cm/s 点 从 出发 出发, 的速度向D运动, 出发, 的速度向 运动,点Q从C出发,以3cm/s的速 运动 从 出发 的速 度向B运 动,其中一动点达到端点时,另一动 其中一动点达到端点时, 度向 运 点随之停止运动。从运动开始,经过多少时间, 点随之停止运动。从运动开始,经过多少时间, 四边形PQCD是平行四边形?成为等腰梯形? 是平行四边形?成为等腰梯形? 四边形 是平行四边形
B
C
A
D
在梯形ABCD中, 中 在梯形 ∵AD∥BC ∥ AC= BD =
C
B
∴梯形ABCD是等腰梯形 梯形 是等腰梯形 对角线相等的梯形是等腰梯形. . ( 对角线相等的梯形是等腰梯形)
一款汽车内置的音响设备, 一款汽车内置的音响设备,为方便后备箱 内摆放,侧面设计为一个等腰梯形。 内摆放,侧面设计为一个等腰梯形。如果你是 质检员,你怎样测量、比较, 质检员,你怎样测量、比较,判断音响的侧面 形状是否符合标准呢? 形状是否符合标准呢? A C
如图,在梯形 如图,在梯形ABCD中, 中 AD∥BC,∠B= ∠C ∥ , =
求证:梯形 求证:梯形ABCD是等腰梯形 是等腰梯形 证明: 证明:
方法
方法
方法
方法
同一底上的两个角相等的梯形是等腰梯形. 同一底上的两个角相等的梯形是等腰梯形.
A D
已知: 已知
B E C
如图,在梯形 如图,在梯形ABCD中, 中 AD∥BC,∠B= ∠C ∥ , =
1、判断下列命题是否正确
①有两个角相等的梯形是等腰梯形;( × ) 有两个角相等的梯形是等腰梯形;( ②有两条边相等的梯形是等腰梯形; ( 有两条边相等的梯形是等腰梯形;
③有一组对边平行的四边形是等腰梯形; ( × ) 有一组对边平行的四边形是等腰梯形; ④有一组对角互补的梯形是等腰梯形( ) 有一组对角互补的梯形是等腰梯形(√
一款汽车内置的音响设备, 一款汽车内置的音响设备,为方便后备箱 内摆放,侧面设计为一个等腰梯形。 内摆放,侧面设计为一个等腰梯形。如果你是 质检员,你怎样测量、比较, 质检员,你怎样测量、比较,判断音响的侧面 形状是否符合标准呢? 形状是否符合标准呢? A C
B
D
根据定义: 根据定义: 两腰相等的梯形是等腰梯形 还有其他的判定方法吗? 还有其他的判定方法吗?
求证:梯形 求证:梯形ABCD是等腰梯形 是等腰梯形 证明: 证明: 过A作AE∥CD,交BC于E. 作 ∥ , 于 . 则∠AEB=∠C. ∠ ∵∠B=∠ , ∵∠ ∠C, ∴ ∠B=∠AEB.∴AE=AB ∠ ∴ 又∵AD∥CE,AE∥CD, ∥ , ∥ , 四边形AECD为平行四边形 ∴四边形 为平行四边形 ∴AE=CD ∴AB=DC 即梯形ABCD是等腰梯形 即梯形 是等腰梯形
A
D
同一底上的两个角相等的梯形是等腰梯形. 同一底上的两个角相等的梯形是等腰梯形
B
C
对角线相等的梯形是等腰梯形. 对角线相等的梯形是等腰梯形
猜想:什么样的梯 猜想:
形是等腰梯形? 形是等腰梯形?
同一底上的两个角相等的梯形是等腰梯形. 同一底上的两个角相等的梯形是等腰梯形.
A D
已知: 已知
B C
