8-2安培环路定理
§8-4-磁场的高斯定理和安培环路定理-(2)

由叠加原理,整个电流回路的磁
场中任意闭合曲面的磁通量必定都
等于零,这就是磁场的高斯定理。
S B dS = 0
Idl
B
1
二、安培环路定理(Ampere’s circulation theorem)
1. 安培环路定理的表述:
恒定电流磁场中,磁感应强度沿任意闭合环路
的积分等于此环路所包围的电流代数和的
2π
围绕单根载流导线的任一回路 L:
L2
对L,每个 线元
dl
以过垂直导线平面作参考,分
解为分量dl//和垂直于 该平面的分 量 dl,有
L B dl
L//
B dl//
L
B
dl
dl B 0
B dl
L
L// B dl//
0I
证明步骤同上 4
围绕多根载流导线的任一回路 L:
设
I1,
I
§8-4 磁场的高斯定理和安培环路定理
一、磁场的高斯定理(Gauss’ theorem of magnetic field) 根据毕奥-萨伐尔定律,电流元的磁场以其为轴对
称分布,垂直于电流元的平面内的磁感线是头尾相 接的闭合同心圆,穿入或穿出闭合曲面的磁感应线
的净条数必等于零,任意闭合曲面的都为零。
L
B
dl
L
0I rd
2π r
0I
在围绕单根载流导线的
垂直平面内的任一回路:
Ldl dBFra bibliotekB dl Brd
I
L
B
dl
L
0I rd
2π r
0I
r d
3
闭合路径L不包围电流 ,在垂直平面内的任一回路:
9.4安培环路定理
电流在回路之外
d
I
B1
r1
dl1
B2
dl2
r2
l
B1
0I
2π r1
,
B2
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
3
大学物理学
第九章 恒定磁场 9.4 安培环路定理
多电流情况
I1
I2
I3
l
B B1 B2 B3
Bdl
l
0(I2
I3)
推广:
➢ 安培环路定理
n
B dl 0 Ii
i 1
4
大学物理学
第九章 恒定磁场 9.4 安培环路定理
安培环路定理
n
B dl 0 Ii
i 1
一闭合即路在径真的空积的分稳的恒值磁,场等中于,磁0感乘应以强该度闭合B 路沿径任
所包围的各电流的代数和.
注意
电流 I 正负的规定 :I 与 L 成右螺旋时, I 为正;反之为负.
➢ 分析对称性
电流分布 磁场分布
轴对称
I R
26
大学物理学
l
第九章 恒定磁场 9.4 安培环路定理
B 的方向判断如下:
r
dS1
O
dS2
dB
dB2 dB1
P
27
大学物理学
第九章 恒定磁场 9.4 安培环路定理
➢ 作积分环路并计算环流
如图 r R
B • dl Bdl 2rB
➢
利用安培环路定理求
说 明
B • dl 0 Ii 0 (I2 I3 )
§8-4 稳恒磁场的高斯定理与安培环路定理.

§8-4 稳恒磁场的高斯定理与安培环路定理
一. 稳恒磁场的高斯定理
由磁感应线的闭合性可知,对任意闭合曲面, 穿入的磁感应线条数与穿出的磁感应线条数相同, 因此,通过任何闭合曲面的磁通量为零。
静电场的高斯定理说明静电场为有源场,环 路定理又说明静电场无旋;稳恒磁场的环路 定理反映稳恒磁场有旋,高斯定理又反映稳 恒磁场无源。
安培环路定理
几点注意:
任意形状稳恒电流,安培环路定理都成立。
环流虽然仅与所围电流有关,但磁场却是所 有电流在空间产生磁场的叠加。
安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。
L B (d l d l// )
B
L I d
r
dl
P
B
L
cos
90
dl
B
L
cos
dl//
0 LBr d 2 0 I r d
0 2 r
0I
结果一样!
长直电流的磁场
如果沿同一路径但改变
绕行方向积分:
B dl B cos( ) d l
的所有电流的代数和
安培环路定理
几点注意:
任意形状稳恒电流,安培环路定理都成立。
环流虽然仅与所围电流有关,但磁场却是所 有电流在空间产生磁场的叠加。
安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。
B
毕奥—萨伐尔定律,安培环路定理

长直线
长
内
直
圆
柱外
面
长 直
内
圆
柱 体
外
B 0I 2r
B0
第八章
B 0I 2r
B
0 Ir 2R 2
B 0I 2r
恒定电流的磁场
8-4磁场的安培环路定理
练习:求同轴B的的两分筒布状。导线通有等值反向的电流I,
(1) r R2 , B 0
R2
R1
(2)
R1
r
R2 ,
B
0I 2r
I
rI
(3) r R1, B 0
B • dl 0
第八章 恒定电流的磁场
8-4磁场的安培环路定理
安培环路定理
在稳恒磁场中,磁感应强度
B
在闭合曲线
上的环流,等于该闭合曲线所包围的电流的代
数和与真 空中的磁导率的乘积。即
B • dl 0 Ii
说明:
I4
I1 I2 I3
电流取正时与环路成右旋关系
l
B • dl 0 Ii
.. . . .
R1 R2
.. . .
..r...............
q
v
第八章 恒定电流的磁场
8-4磁场的安培环路定理
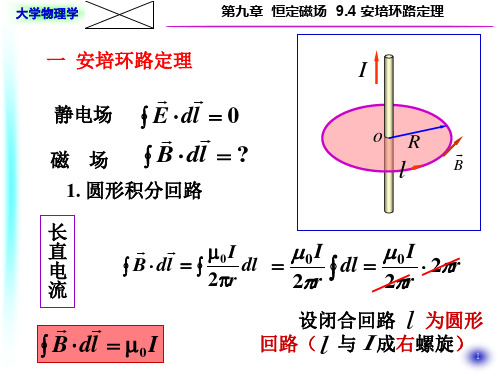
一、 安培环路定理
静电场 E dl 0
l
磁 场 B dl ?
1、圆形积分回路
B
dl
0I 2r
dl
0I
2r
dl
0I 2r
2r
B dl 0I
I
r
B
B
0I
2r
第八章 恒定电流的磁场
8-4磁场的安培环路定理
I
安培环路定理

安培环路定理安培环路定理的严格证明(缩略图)在稳恒磁场中,磁场强度H沿任何闭合路径的线积分,等于这闭合路径所包围的各个电流之代数和。
这个结论称为安培环路定理(Ampere circuital theorem)。
安培环路定理可以由毕奥-萨伐尔定律导出。
它反映了稳恒磁场的磁感应线和载流导线相互套连的性质。
目录按照安培环路定理,环路所包围电流之正负应服从右手螺旋法则。
安培环路定理应用如果闭合路径l包围着两个流向相反的电流I1和I2(如左图所示),这在下式中,按图中选定的闭合路径l 的绕行方向,B矢量沿此闭合路径的环流为如果闭合路径l包围的电流等值反向(如右图所示),或者环路中并没有包围电流,则:安培环路定理的证明(严格证明,大图见参考资料的链接)编辑本段安培环路定理的证明(不完全证明)以长直载流导线产生的磁场为例,证明安培环路定理的正确性。
安培环路定理应用在长直载流导线的周围作三个不同位置,且不同形状的环路,可以证明对磁场中这三个环路,安培环路定理均成立。
取对称环路包围电流在垂直于长直载流导线的平面内,以载流导线为圆心作一条半径为r 的圆形环路l,则在这圆周上任一点的磁感强度H的大小为其方向与圆周相切.取环路的绕行方向为逆时针方向,取线元矢量dl,则H与dl间的夹角,H沿这一环路 l 的环流为式中积分是环路的周长。
于是上式可写成为从上式看到,H沿此圆形环路的环流只与闭合环路所包围的电流I 有关,而与环路的大小、形状无关。
取任意环路包围电流在垂直于长直载流导线的平面内,环绕载流直导线作一条如下图所示的任意环路l,取环路的绕行方向为逆时针方向。
在环路上任取一段线元dl,载流直导线在线元dl处的磁感强度B大小为H与dl的夹角为,则H对dl的线积分为直导线中心向线元的张角为,则有,所以有可见,H对dl的线积分与到直导线的距离无关。
那么B对整个环路的环流值为上述计算再次说明H的环流值与环路的大小、形状无关。
取任意环路不包围电流在垂直于长直载流导线的平面内,在载流直导线的外侧作一条如下图所示的任安培环路定理应用意环路l,取环路的绕行方向为逆时针方向。
安培环路定理例题

安培环路定理例题
一、安培环路定理简介
安培环路定理是电磁学中的一个重要定理,它是由德国物理学家安培(Ampère)提出的。
该定理描述了电流与磁场之间的关系,为我们研究电磁现象提供了有力的理论依据。
二、安培环路定理的数学表达式
安培环路定理的数学表达式为:
∮μJ·dλ = με∮φdλ
其中,μ为真空磁导率,J为电流密度,λ为路径,ε为真空介电常数,φ为磁感应强度。
三、安培环路定理的应用
1.计算磁场强度:利用安培环路定理,我们可以通过测量电流和磁场路径上的磁场强度来计算磁感应强度。
2.分析电磁感应现象:在电磁感应现象中,安培环路定理可以帮助我们理解磁场变化产生的电动势,从而分析电路中的电流分布。
3.求解电磁场问题:安培环路定理在求解电磁场问题时具有重要意义,例如在电磁波传播、电磁感应等领域。
四、安培环路定理的拓展
1.非均匀磁场中的安培环路定理:在非均匀磁场中,安培环路定理仍然适用,但需要对磁场进行积分运算。
2.多维空间中的安培环路定理:在多维空间中,安培环路定理可以扩展为
更高维度的公式,以描述不同维度下的电磁现象。
3.其他相关定理:与安培环路定理密切相关的还有法拉第电磁感应定律、楞次定律等,它们共同构成了电磁学的理论基础。
通过掌握安培环路定理,我们可以更好地理解和分析电磁现象,为实际应用提供理论支持。
安培环路定理

(1)管内:取L矩形回路 abcda
边在轴上,两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证,无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
(安培环路定理)

I4
I1
I3 L
I2
I1为正, I2为负, I3和I4未 被包围
2
③ B 代表空间所有电流(包括不被L包围的电
流)产生的磁感应强度的矢量和.
I1
I2
I4
l
I3
由环路内电流决定
0 Ii 0 (I 2 I3 ) B d l
L
由环路内外电流产生
环路所包围的电流
3
不变
等;
(3)求出环路积分; (4)用右手螺旋定则确定所选定的回路包围电流的 正负,最后由磁
例. 无限长圆柱面电流的磁场分布 设半径为 R ,面上均匀分布的轴向总电流I.
解:分析场结构:有轴对称性 以轴上一点为圆心,取垂直于轴 的平面内半径为 r 的圆为安培环路
abcda a
ab,cd段
a
d B dl B dl 0
b c
b
c
d
11
l
B
a
b
d
c
所以
abcda
a c B dl Bda dl Bbc dl ( Bda Bbc )l 0 d b
Bda Bbc
轴线上的
B 0nI
(证略)
B dl 0 I i
L i
1
二.讨论:
B dl 0 I i
L i
①电流的正负:电流方向与L的绕行方向符合右手 螺旋关系时,电流为正;反之为负。 ② SIint 是环路L所包围的电流的代数和。 对于闭合电流,只有与L相铰链时,才算被L包围.
9
用安培环路定理求解: 一个单位长度上 有 n匝的无限长 直螺线管,由于 是密绕, 所以每 匝视为圆线圈。 由对称性分析场结构 a.只有轴上的分量;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
j----面电流密度矢量的大小, 为通过垂直电流方向 的单位长度上的电流。
返回
B
0 I 2 r
无限长载流密绕直螺线管,细螺绕环
B内 0nI,B外 0
圆电流圈的圆心和轴线上
B中 心 B轴 线
0 I
2R 2 R x
2
0 IS
2 3/ 2
( 不 必 记)
无限大均匀平面电流的磁场,两侧为均匀磁场,方向相 反(右手定则)
B
j
大小为
B
0 j
I1
I内 与L套连的电流
I2
I
i
如图示的 I1
i内
I2
L
dl
电流分布
代数和
与L绕行方向成右螺电流取正 如图示的电流 I 1 取正
I 2取负
选取环路原则
(1)环路要经过所研究的场点。
(2)环路的长度便于计算; 一致.
目的是将:
(3)要求环路上各点 B大小相等,B的方向与环路方向
安培环路定律
法国物理学家
安培
A.M.Ampere (1775-1836)
安培(Andre-Marie Ampere, 1775-1836) 法国物理学家,电动力学的创始人。 12岁学习 了微积分,13岁发表关于螺旋线的论文.在化学方面 ,他最先预见了氯、氟、碘三种物质是元素,还独立 地发现了“阿伏伽德罗定律”.
分布如图示 作闭合环路abcd如图
l
d
c
o
dl ' '
a
b
b c d a B dl B dl B dl B dl B dl
a b c d
Bdl 0 Bdl 0
a c
b
d
Bdl 0 Bdl 0
1820年7月奥斯特发现了电流的磁效应.法国科 学家阿拉果8月在瑞士听到这一消息后,9月初回到 法国立即向法国科学院报告了这一最新发现.善于 接受新的研究成果的安培,怀着极大的兴趣,第二 天就重做了奥斯特的实验,并于9月18日向法国科学 院提交了第一篇论文,报告他的实验成果.接着又 在9月25日、10月9日提出了第二篇和第三篇实验报 告论文.
=B
l
r
B
.2 πr
μoI 2 r =μ o I π = 2 πr
安培环路定律:磁感应场强度矢量沿任 意闭合路径一周的线积分等于真空磁导率乘 以穿过闭合路径所包围面积的电流代数和。
l B . dl =μ Σ I
o
电流和回路绕行方向 构成右旋关系的取正值
电流 I 取负值 I
I
向 行方
向 方 绕 行
绕
I2
I1
l1
I
l2
I
I
l3
(a) (a) (b) (c)
1
(b)
(c)
o
l B . dl = μ l B . dl = 0
2
(I 1 I 2 )
l B . dl = μ
3
o
(I
I )=0
B
空间所有电流共同产生的
I3
L 在场中任取的一闭合线
任意规定一个绕行方向 dl L上的任一线元
L
B dl 0 I
写成
B
0 I
dl
或 B 的方向与环路方向垂直, B dl , cos 0 B dl 0
§ 环路定律的应用 1. 直长通电螺线管内的磁场
. . . . . . . . . . . . . a
d
b
c
B
l B. dl = abB . dl + bc B . dl + cd B . dl+ daB . dl = abB . dl + 0 + 0 + 0 = abB dl cos 0
0
. . . . . . . . . . . . . a b B
d
c
0
l B. dl = abB dl cos 0
= B ab dl
= B ab =μ 0n ab I B =μ 0n I (n:单位长度上的匝数)
2. 环形螺线管的磁场
.
0
. . . l B. dl = l B dl cos 0 .. B . . . = B l dl = B 2 r r π . . R 1 . . ( : ) N 匝数 = 0NI . . R 2 . . . . μ 0NI . . B= . . . . ... B 2 πr
= sδ . dS cos 0
0
dS δ
B
I´ r
2. r > R
I
R
B 2 π r =μ 0 I
μ I B=
2 πr B
0
r
B
r μ I B=
0
2π R 2
O
μ 0I
R
2π R
μ I B=
2 πr
0
r
例. 求无限大载流平面的磁场分布
由俯视图:
I
dB
dB ' dB' '
dl '
p
无限大载流平面的磁场
. . . . .. . .
I
I
0
R1
R2
r
3. 均匀通电直长圆柱体的磁场 设电流 I 均匀分布在整个横截面上。 1. r < R 0 l B .dl = l B dl cos 0 I ´ = sδ . dS
I R
= B 2π r =μ 0 I ´
2 r I I 2 r = δ s dS = π R 2π = R 2 2 ´ r I ( 或: =π 2 ´) I I πR μ 0Ir 得: B= 2π R 2
a c
b
d
2Bab 由安培环路定理 0 j ab
B 1 0 j 2
方向:平行于通电平面。与电流成右手螺旋。
几种典型电流的B分布
一段载流直导线 无限长载流直导线 无限长均匀载流薄圆筒
B
0 I (sin 2 sin 1 ) 4a
0 I 2 r
B
B内 0,B外
在这三篇论文中,包括了电流方向和磁针偏转方 向关系的右手定则;同向直线电流间互相吸引,异 向直线电流间互相排斥;通电螺线管的磁性与磁针 等效,等等.
安培环路定律 Ampere circulation theorem
问题:
l E . dl
=0
l B . dl = ?
I
0
ห้องสมุดไป่ตู้1. 圆形环路
l B . dl = l B dl cos0
