平均变化率
变化率简介

变化率简介变化率是学习导数的前提,它在描述各种变化规律的过程中起着非常重要的作用,速度和加速度就是两个典型例子.新教材人教A 版中,对于变化率主要从以下两个方面介绍:1、平均变化率;2、瞬时变化率.一、平均变化率函数()y f x =在区间00[,]x x x +∆或(00[,]x x x +∆)上的平均变化率是商yx∆∆,其中x ∆是自变量x 在0x 处的改变量,可正可负,但不能为0,y ∆是函数值相应的改变量,即00()()y f x x f x ∆=+∆-(y ∆为正、负、零均可)所以00()()f x x f x y x x+∆-∆=∆∆,下面通过举例来进一步加深对概念的理解。
例1、求332-=x y 在0x 到x x ∆+0之间的平均变化率.解:当自变量从0x 到x x ∆+0之间变化时,函数的平均变化率为:x f∆∆=∆-∆+=x x f x x f )()(00xx x x ∆---∆+=]33[]3)(3[2020 x x xx x x ∆+=∆∆+∆⋅=36)(3602评注:此类题目只需要紧扣定义式,注意运算过程就可以了. 评注:⑴函数平均变化率的求法可分两步:①求y ∆;②求yx∆∆.⑵不论0x 、x ∆中的哪一个变化,都会引起函数平均变化率的变化。
拓展:函数()y f x =的平均变化率的几何意义为其图象上割线的斜率。
即:函数()y f x =的图象为曲线C ,曲线C 上有一点00(,)P x y 及邻近一点00(,)Q x x y y +∆+∆,则割线PQ 的斜率0000y y y yk x x x x+∆-∆==+∆-∆。
利用平均变化率的几何意义,可解决一些实际问题,举例如下:例2、某电视机厂有甲、乙两条生产流水线,产量S (单位:台)与时间t (单位:天)的关系如图所示,问:(1)0t 天内,甲、乙两条生产线的平均日产量哪个大?(2)在接近0t 天时,甲、乙两条生产线谁的日产量大?0,)x y y ∆+∆解析:(1) 0t 天内,甲、乙两条生产线的平均日产量,即函数1()S f t =与2()S f t =在0[0,]t 内的平均变化率,其都为直线OA 的斜率,所以0t 天内,甲、乙两条生产线的平均日产量相同。
平均变化率与瞬时变化率详解课件

定义与计算
瞬时变化率定义
瞬时变化率是指在某一时刻,函数值随自变量变化的快慢程度。通常用导数来 表示函数的瞬时变化率。
瞬时变化率的计算
对于函数$f(x)$,其瞬时变化率可以通过求导数$f'(x)$来计算。即,如果$f(x)$ 在$x=x_0$处的导数为$f'(x_0)$,则$f'(x_0)$即为在$x=x_0$处的瞬时变化率 。
,可以获得股票价格的预测结果,对于投资决策和风险管理具有重要意义。
机械故障预测
总结词
机械故障预测是基于机械设备运行过程中的数据,通 过分析变化率等信息,来预测设备可能出现的故障时 间和类型。
详细描述
机械故障预测是机械工程领域中的一个重要应用案例 。通过对机械设备运行过程中的数据进行分析,可以 提取出设备的运行特征和故障征兆,从而预测设备可 能出现的故障时间和类型。其中,变化率是一个重要 的指标,它可以反映设备的运行状态和磨损程度。通 过对变化率的计算和分析,可以获得机械故障预测结 果,对于提高设备运行效率和安全性具有重要意义。
感谢观看
THANKS
拐点和极值
函数的拐点可能是导函数的零 点,但并非所有导函数的零点
都是函数的拐点。
导数的计算方法
定义法
根据导数的定义计算导 数。
求导公式
利用常见函数的导数公 式进行计算。
复合函数求导
复合函数的导数可以利 用链式法则和乘法法则
进行计算。
高阶导数
高阶导数的计算需要利 用低阶导数的计算方法
,并逐阶求导。
04
瞬时变化率的性质
瞬时变化率非负性
对于单调递增函数,其瞬时变化率大于等于0;对于单调递减函数,其瞬时变化 率小于等于0。
函数的平均变化率课件

实际问题中如何应用函数的平均变化率?
运动学
速度和加速度的变化率都是平均 变化率,可以通过这些平均变化 率来了解运动学中的物理现象。
商业领域
可以通过函数的平均变化率来评 价某一产品或公司的增长速度。
时间管理
可以通过函数的平均变化率来了 解时间利用效率的变化。
平均变化率的图像解释
相邻两点之间的斜率
在图像上,平均变化率可以表示为相邻两条线段的 斜率。
函数的平均变化率的应用举例
1
应用一
在积分计算中,常用平均变化率来近似求解曲线下的面积。
2
应用二
在微分方程的求解中,平均变化率可以用于简单的数值方法计算。
3
应用三
在统计学中,业务活动的整体变化趋势可以通过平均变化率来进行分析。
函数的平均变化率在物理学中的应用
万有引力
质点在单位时间内运动的平均速 度可以用万有引力的平均变化率 来计算。
1 步骤一
首先,要知道函数在哪里发生了断裂,也就 是函数不连续的地方。
2 步骤二
判断函数在不连续点与相邻区间之间的平均 变化率是否存在。
3 步骤三
如果这一区间存在平均变化率,那么新的区 间一定就是函数的定义域。
4 步骤四
如果不存在平均变化率,则需要进一步的讨 论和推导。
如何根据函数的平均变化率推断函数 的值域?
1 步骤一
求出函数的导数。
2 步骤二
根据导数的正负来判断函数的值域。
3 步骤三
如果导数大于零,则函数单调递增;如果导数小于零,则函数单调递减;否则,需要进 一步研究函数。
函数的平均变化率的重要性
平均变化率是微积分的基础概念之一,不仅在学术研究中广泛应用,而且在 日常生活中也具有重要的意义。通过平均变化率可以揭示出事物在不同时间 段内的变化趋势,从而帮助我们做出更好的决策。
文档:解读平均变化率的意义

解读平均变化率的意义变化率问题在生活或学习中经常遇到,这类问题经常借助于函数求解,而对函数平均变化率理解显得尤为重要,下面我们据其定义浅析函数平均变化率的几何意义和物理意义.1.平均变化率的几何意义:如右图:由图可知,设函数()x f y =在处对应函数图象上的两点()()1100,,,y x B y x A ,不妨设10x x <,则此函数在区间[]10,x x 内的平均变化率xy ∆∆()()01010101x x y y x x x f x f --=--=就是经过函数图象上两点()()1100,,,y x B y x A 的割线斜率.注意点:⑴自变量的改变量0≠∆x ,但可正可负; ⑵函数在处有定义,是函数定义域内附近的一点; ⑶xy ∆∆()()01010101x x y y x x x f x f --=--=中自变量的改变量与函数值的改变量,二者差值顺序上对应要一致.如:若01x x x -=∆,则()()01x f x f -,而不是()()10x f x f -; ⑷直线斜率有正有负有零,平均变化率也有正有负有零.例1:分别求函数2x y =在⎥⎦⎤⎢⎣⎡-021,、⎥⎦⎤⎢⎣⎡21,0和⎥⎦⎤⎢⎣⎡1,21的平均变化率,并说明图像的变化情况.分析:根据平均变化率的几何意义可直接求相应割线斜率. 解:设()2x x f y ==,如下图:据平均变化率的几何意义知,函数在⎥⎦⎤⎢⎣⎡-021,内的平均变化率为: ()2121041021021-=--=---⎪⎭⎫⎝⎛-=∆∆f f x y ;y21121-2xyOAB1x0x 0y 1y函数在⎥⎦⎤⎢⎣⎡21,0内的平均变化率为:()2121041021021=-=--⎪⎭⎫⎝⎛=∆∆f f x y ; 函数在⎥⎦⎤⎢⎣⎡1,21内的平均变化率为:()2321411211211=-=-⎪⎭⎫⎝⎛-=∆∆f f x y ; 由上面所求结果可以看出,函数在⎥⎦⎤⎢⎣⎡1,21内的平均变化率大于在⎥⎦⎤⎢⎣⎡21,0内的平均变化率,所以函数图像在⎥⎦⎤⎢⎣⎡1,21内的比在⎥⎦⎤⎢⎣⎡21,0的要陡一些;函数在⎥⎦⎤⎢⎣⎡-021,内与在⎥⎦⎤⎢⎣⎡21,0的平均变化率符号相反,但绝对值相等,函数在这两段内的图像升降变化快慢相同,但平均变化率为正时图像从左向右上升,平均变化率为负时,图像从左向右下降.评注:函数平均变化率的绝对值大,图像相对要陡一些,平均变化率绝对值小,图像相对要平缓,平均变化率能近似刻画图像的升降快慢.在较小范围内,平均变化率为正,图像从左向右上升,反之下降.2.平均变化率的的物理意义设()t s S =表示物体运动路程关于时间的函数,设(),11S t s =()22S t s =,其中210t t <≤,则()t s S =在[]21,t t 内的平均变化率为1212t t S S t S --=∆∆,它表示从到这段时间内,物体的平均速度.说明:平均变化率大,说明物体运动的相对快一些,反之较慢.平均变化率能近似反应物体在某短时间内运动的快慢.例2:自由落体的方程为221gt s =,s m g /10=,一物体从t=1状态下开始自由落下,秒后,物体运动路程的增量为 米,在附近的平均变化率为 ,这秒内物体的平均速度为 .分析:物体运动路程的增量就是函数值的差值,物体秒内的平均速度就是在[]01.01,内的平均变化率;可借助于割线斜率求解.解:⑴因为物体自由落体的方程为221gt s =,s m g /10=,则25t s =,所以时,;01.1=t 时,1005.5=s ,则物体运动路程的增量为1005.051005.5=-.⑵t=1附近的平均变化率为为()10455152+∆-∆=∆-∆+=∆∆tt t t t s ()0≠∆t . ⑶根据平均变化率的物理意义知,这秒内物体的平均速度为:05.1001.01005.0==∆∆t s )/(s m . 评注:路程关于时间的函数的平均变化率是物体在某短时间内的平均速度,掌握这一物理意义,可用于解决一些实际问题.以上是对函数平均变化率的定义及意义的浅析.理解平均变化率的意义,并能熟练应用是后面理解导数的基础.。
平均变化率讲解知识分享
例3 已知函数 f(x ) 2 x 1 ,g (x ) 2 x ,分别计算
在区间[-3,-1],[0,5]上 f ( x )及 g ( x )的平均
变化率。
思考:你从本例中发现一次函数y=kx+b在区间[m,n] 上的平均变化率有什么特点?
等于相应直线的斜率k
例4 已知函数 f (x) x2,分别计算 f ( x )在下列区间
连线的斜率。
(近似的)
2、平均变化率是曲线陡峭程度的“数量化”, 数 数 形 结
曲线陡峭程度是平均变化率的“视觉化”. 形 合
(直观的)
3、" f( x ) 在 [ x 1 ,x 2 ] 上 的 平 均 变 化 率 大 于 0 " 是 " f( x ) 在 [ x 1 ,x 2 ] 递 增 " 的 必要不充分条 件 ;
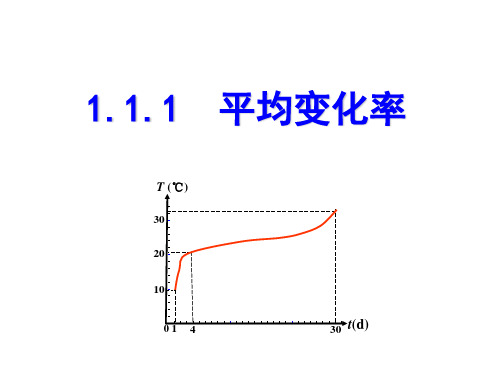
10.2℃ 20.4℃ 30.8℃
温差10.2℃ 温差10.4℃
1、平均变化率
一 般 地 , 函 数 f ( x ) 在 区 间 x 1 , x 2 上 的 平 均 变 化 率 为
f ( x2 ) f ( x1) x2 x1
几何意义:曲线 y f (x)上两点 (x1, f (x1))、(x2, f (x2))
问:在区间
t
,
0
t1
上,哪一个企业
的排污平均变化率大一些?
t1
l1
l2
t
T (℃)
30
20 B 10 A
W
C
甲
标准
乙
01 4
30 t(d)
越陡峭,平均变化率越大
O t0
t1 t
越陡峭,平均变化率越小
(越大)
陡峭 程度
平均变化率的几何意义课件

平均变化率可以反映该段区间 内因变量相对于自变量的平均
变化速度
平均变化率为正表示因变量在 该段区间内呈上升趋势,即正
增长
平均变化率为负表示因变量在 该段区间内呈下降趋势,即负
增长
平均变化率的应用
判断函数单调性
总结词
平均变化率可以用于判断函数的单调性。
详细描述
平均变化率是函数在某区间上的改变量与区间的比值,当这个比值大于0时,函 数在该区间上是单调递增的;当这个比值小于0时,函数在该区间上是单调递减 的。
近似计算
总结词
平均变化率可以用于进行近似计算。
详细描述
在某些情况下,我们可以利用平 均变化率来近似计算函数的值, 这种方法称为微积分中的微分法。
平均变化率的拓展
导数的概念
01
02
03
导数的定义
导数是函数在某一点的变 化率,它描述了函数在该 点的切线斜率。
导数的几何意义
导数在几何上表示函数曲 线在某一点的切线斜率, 即曲线在该点的变化趋势。
曲线的变化趋势
01
曲线的形状代表因变量 随自变量的变化趋势
02
曲线的陡峭程度代表变 化率的绝对值大小
03
曲线向上代表因变量随 自变量增加而增加,即 正相关关系
04
曲线向下代表因变量随 自变量增加而减少,即 负相关关系
平均变化率的几何意义
01
02
0304平均Fra bibliotek化率是曲线在某一段区 间上的平均倾斜程度
平均变化率的几何意义课件
引言
课程背景
01
平均变化率是微积分学中的基本 概念,它描述了一个函数在某区 间上的变化快慢。
02
几何意义是将平均变化率与线段 的长度联系起来,从而在几何空 间中解释函数的变化趋势。
平均变化率的计算公式

平均变化率的计算公式Calculating the average rate of change is an essential concept in mathematics that is used to determine how a quantity changes over a specific interval. This calculation involves analyzing the difference in values of a variable over a given period and then dividing it by the change in time or another independent variable. By understanding the average rate of change, individuals can make informed decisions in various fields, such as economics, physics, and engineering.计算平均变化率是数学中一个重要的概念,用于确定某个数量在特定区间内的变化情况。
这种计算涉及分析一个变量在给定时间内的差异值,然后将其除以时间或其他独立变量的变化。
通过理解平均变化率,个人可以在各个领域做出明智的决策,如经济学、物理学和工程学。
In mathematics, the formula for calculating the average rate of change is (change in y) / (change in x). This formula represents how much the dependent variable y changes for a unit change in the independent variable x. By applying this formula to a set of data points, one can determine the overall trend or direction of the changes occurring in the system.在数学中,计算平均变化率的公式为(y变化)/(x变化)。
第5章5.15.1.1 平均变化率-2024-2025学年新教材数学苏教版选择性必修第一册同步课件

5.1.1 平均变化率
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
1.思考辨析 (正确的打“√”,错误的打“×”)
(1)对于函数 y=f (x),当 x 从 x1 变为 x2 时,x2-x1 一定大于 0.
()
(2)对于函数 y=f (x),当 x 从 x1 变为 x2 时,函数值的变化量为 f (x2)
5.1.1 平均变化率
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
类型 2 实际问题中的平均变化率 【例 2】 (1)圆的半径 r 从 0.1 变化到 0.3 时,圆的面积 S 的平均 变化率为________.
(1)0.4π [∵S=πr2,∴圆的半径 r 从 0.1 变化到 0.3 时, 圆的面积 S 的平均变化率为S(00.3.3)--S0(.10.1)=π×0.320-.2π×0.12= 0.4π.]
5.1.1 平均变化率
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
03
学习效果·课堂评估夯基础
5.1.1 平均变化率
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
1.函数 f (x)=x2+c(c∈R)区间1,3上的平均变化率为( )
5.1.1 平均变化率
1
2
3
4
必备知识·情境导学探新知 关键能力·合作探究释疑难 学习效果·课堂评估夯基础 课时分层作业
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
yC yB k xC xB
y
●B ●A
该比值近似量化B,C之间 这一段曲线的陡峭程度. 称该比值为曲线在B,C之 间这一段平均变化率.
o
x
建构数学理论
平均变化率的定义:
一般地,函数 f (x)在区间 [ x1 , x2 ] 上的平均变化率为
y f ( x2 ) f ( x1 ) x x2 x1
B (32, 18.6) 20
10 A (1, 3.5)
பைடு நூலகம்
2
0 2 10 20 30 34 t(d)
交流与讨论 问题情境4 过山车是一项富有刺激性的娱乐工具。
那种风驰电掣、有惊无险的快感令不少人 着迷。
交流与讨论
容易看出点B,C之间的曲线较 点A,B之间的曲线更加“陡 ●C 峭”. 如何量化陡峭程度呢?
(5)[0.9,1]; 1.9 变题: (6)[0.99,1];1.99 (7)[0.999,1]. 1.999
p
1 3
课后思考:为什么趋近于2呢?2的几何意义是 什么?
x
小结回顾
这节课我的收获是什么?
f ( x1 ) f ( x2 ) y 1.平均变化率的定义: x x1 x2
2.平均变化率的意义: 3.求平均变化率的步骤: 4.思想方法:
说明:(1)平均变化率的实质就是:两点(x1,f(x1)),(x2,f(x2)) 连线的斜率. (以直代曲思想) (2)平均变化率是曲线陡峭程度的“数量化”, 或者说曲线陡峭程度是平均变化率“视觉化” . (数形结合思想) “数离形时难直观,形离数时难入微”——华罗庚
数学应用
例2、已知函数 f(x)=x2,分别计算f(x)在下列 y 区间上的平均变化率: (1)[1,3]; 4 (2)[1,2]; 3 (3)[1,1.1]; 2.1 (4)[1,1.001]. 2.001
问题情境一: 甲和乙投入相同资金经营某商品, 甲用1年时间挣到2万元, 乙用5个月 时间挣到1万元,甲、 乙两人谁的经营 成果更好?
乙的资金增长得更快!
问题情境二:
如右图所示,向高为10cm的杯子等速注水,3 分钟注满。若水深h是关于注水时间t的函数,则下 面两个图象哪一个可以表示上述函数?
h/cm
10
M N 10
h/cm
N
M
O 1
A
3
t/m
O
1
3
B
t/m
开始时,h变化得快,后来h变化得慢。
问题情境3
现有宿迁市某年3月和4月某天日最高气温记载. 时间 日最高气温
T (℃)
3月18日
4月18日 4月20日
3.5℃ 18.6℃ 33.4℃ 温差15.1℃ 温差14.8℃
C (34, 33.4)
30
