全等三角形证明题及答案 ppt课件
合集下载
全等三角形的判定课件ppt

两个三角形只有一组对应元素相等一边对应相等一角对应相等7cm
7cm
不全等
32° 32°
不全等
互动交流 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
互动2:如果两个三角形有两组对应相等的
元素(边或角),这两个三角形全等吗?
任务一:讨论分类
第二组:画一个三角形,要求三角形的两边分别为3cm和5cm;
第三组:画一个三角形,要求三角形的一个内角为60°,一条边
为3cm,且这条长3cm的边是60°角的邻边;
第四组:画一个三角形,要求三角形的一个内角为60°,一
条边为3cm,且这条长3cm的边是60°角的对边;
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
联想?
使△ABC 与△A′B′C′全等的条 件能否再减少一些呢?
A
A′
B
? C B′
? C′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
至少要满足几组元素对应相等,两个 三角形才会全等呢?
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
7cm
不全等
32° 32°
不全等
互动交流 为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
互动2:如果两个三角形有两组对应相等的
元素(边或角),这两个三角形全等吗?
任务一:讨论分类
第二组:画一个三角形,要求三角形的两边分别为3cm和5cm;
第三组:画一个三角形,要求三角形的一个内角为60°,一条边
为3cm,且这条长3cm的边是60°角的邻边;
第四组:画一个三角形,要求三角形的一个内角为60°,一
条边为3cm,且这条长3cm的边是60°角的对边;
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
联想?
使△ABC 与△A′B′C′全等的条 件能否再减少一些呢?
A
A′
B
? C B′
? C′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
至少要满足几组元素对应相等,两个 三角形才会全等呢?
A
A′
C′
B
C B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
全等三角形判定ppt课件

若两个三角形全等,则它们的周长也 相等。
对应角相等
在全等三角形中,任意两个对应 的角都相等。
若两个三角形全等,则它们的内 角和也相等,且均为180度。
可以通过测量两个三角形的三个 内角来判断它们是否全等。
面积相等
若两个三角形全等,则它们的面积也相等。 可以通过计算两个三角形的面积来判断它们是否全等。
1 2
定义
两边和它们的夹角分别相等的两个三角形全等。
图形语言
若a=a',∠B=∠B',b=b',则⊿ABC≌⊿A'B'C'。
3
符号语言
∵a=a',∠B=∠B',b=b',∴⊿ABC≌⊿A'B'C'( SAS)。
角边角判定法(ASA)
01
02
03
定义
两角和它们的夹边分别相 等的两个三角形全等。
图形语言
实例1
证明两个三角形全等并求出未知 边长
实例2
利用全等三角形判定方法证明两个 四边形面积相等
实例3
利用全等三角形判定方法解决一个 实际问题,如测量一个不可直接测 量的距离
06
总结与展望
判定全等三角形的方法总结
三边分别相等的两个三角形全等。这是最基本的判定 方法,通过比较三角形的三边长度来确定两个三角形
证明过程
可以通过AAS(角角边)全等条件进行证明,即 如果两个三角形有两个角和其中一个角的对边分 别相等,则这两个三角形全等。这也是一种常用 的全等三角形判定方法。
实际应用举例
在实际应用中,角角边判定法常用于解决与角度 和边长有关的问题。例如,在建筑设计中,如果 需要确保两个建筑结构的角度和边长完全相等, 就可以利用角角边判定法来进行验证。
1三角形全等的判定(第4课时)PPT课件(华师大版)
当堂检测
1.为班级中每名同学准备了长分别为a、b、c三根木条,所有同学都
用三根木条,首尾顺次拼接组成三角形,这时小陈同学说:“我们所
有人的三角形,形状和大小是完全一样的”小陈同学的说法根据
_______.
SSS
根据:三个木条长度a,b,c,无论怎么摆放,长度不变,利用三
角形全等的判定理由:SSS
当堂检测
(简写为“边边边”或“S.S.S.”)
A
几何语言:
在△ABC和△ DEF中,
AB=DE,
B
C
D
BC=EF,
CA=FD,
∴ △ABC ≌△ DEF(S.S.S.).
E
F
讲授新课
典例精析
【例1】如图,在四边形 ABCD 中,AD = CB,AB = CD.
求证: ∠B = ∠D.
证明:在△ABC 和△CDA 中,
=,
= ,
=.
∴△ABC≌△DFC(SSS).
讲授新课
变式1 若将上题中右边的三角形向左平移(如图),若AB=DF,
AC=DE,BE=CF.问:△ABC和△DFE全等吗?
解:全等.
A
B
E
D
C
F
∵ BE=CF ,
∴BE+EC=CF+EC.
即BC=FE .
在△ABC和△DFE中,
在△ABD和△CDB中,
=(已知),
= (已知),
=(公共边).
∴△ABD≌△CDB(SSS),
∴∠A=∠C.(全等三角形的对应角相等).
②证明:∵ △ABD≌△CDB(已证) ,
∴∠ABD=∠CDB, ∠ADB=∠CBD .
(全等三角形的对应角相等)
人教版《三角形全等的判定》PPT全文课件

知识回顾
问题探究
课堂小结
随堂检测
活动2
0
探究一:探索三角形全等的条件
建立模型,探索发现
只给定一条边相等:
只给定一个角相等:
3cm
3cm
3cm
30°
30°
30°
满足一个条件相等时,两个三角形不一定全等.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
探究一:探索三角形全等的条件
问题:两个三角形满足六个条件中的两个条件,两个三角形全等吗?两个条件有几种情况?
证明:连接AC,
【解题过程】
如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.
∴∠B=∠D.(全等三角形对应角相等)
【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D. 要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.
∥
∵BC=DE, ∴BC+CD=DE+CD. 即BD=CE.
【数学思想】 数形结合思想,分类讨论思想.
∴ ∠ADB=∠FEC,AD=EF (全等三角形对应角相等) ∴AD∥EF(同位角相等,两直线平行)
在△ABD和△FCE中
∴△ABD≌△FCE (SSS).
知识回顾
问题探究
课堂小结
随堂检测
例4
0
探究三:利用三角形全等的判定“SSS”解决问题
△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,请问AD⊥BC吗?请说明理由.
在△ABD和△ADC中,
∴△ABD≌△ACD (SSS).
问题探究
课堂小结
随堂检测
活动2
0
探究一:探索三角形全等的条件
建立模型,探索发现
只给定一条边相等:
只给定一个角相等:
3cm
3cm
3cm
30°
30°
30°
满足一个条件相等时,两个三角形不一定全等.
知识回顾
问题探究
课堂小结
随堂检测
活动3
0
探究一:探索三角形全等的条件
问题:两个三角形满足六个条件中的两个条件,两个三角形全等吗?两个条件有几种情况?
证明:连接AC,
【解题过程】
如图, 在四边形ABCD中, AB=AD, CB=CD, 求证:∠B=∠D.
∴∠B=∠D.(全等三角形对应角相等)
【思路点拨】先连接AC, 由于AB=AD, CB=CD, AC=AC, 利用SSS可证△ABC≌△ADC, 于是∠B=∠D. 要求学生从“形”思维到“质”的思维飞跃, 实现将“文字语言”, “图形语言”转化为“符号语言”.
∥
∵BC=DE, ∴BC+CD=DE+CD. 即BD=CE.
【数学思想】 数形结合思想,分类讨论思想.
∴ ∠ADB=∠FEC,AD=EF (全等三角形对应角相等) ∴AD∥EF(同位角相等,两直线平行)
在△ABD和△FCE中
∴△ABD≌△FCE (SSS).
知识回顾
问题探究
课堂小结
随堂检测
例4
0
探究三:利用三角形全等的判定“SSS”解决问题
△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架,请问AD⊥BC吗?请说明理由.
在△ABD和△ADC中,
∴△ABD≌△ACD (SSS).
三角形全等的判定ppt课件

知4-讲
1. 基本事实:两角和它们的夹边分别相等的两个三角形全 等(可以简写成“角边角”或“ASA”).
感悟新知
2. 书写格式:如图12 . 2-8, 在△ ABC 和△ A′B′C′ 中, ∠ B= ∠ B′, BC=B′C′, ∠ C= ∠ C′, ∴△ ABC ≌△ A′B′C′( ASA).
第十二章 全等三角形
12.2 三角形全等的判定
感悟新知
知识点 1 基本事实“边边边”或“SSS”
知1-讲
1. 基本事实:三边分别相等的两个三角形全等(可以简写成 “边边边”或“SSS”). 这个基本事实告诉我们:当三角形的三边确定后, 其形状、大小也随之确定. 这是说明三角形具有稳定性的 依据.
感悟新知
感悟新知
知5-练
例5 如图12.2-11,AB=AE,∠ 1= ∠ 2,∠ C= ∠ D. 求证:△ ABC ≌△ AED.
感悟新知
思路引导:
知5-练
感悟新知
知5-练
技巧点拨:判定两个三角形全等,可采用执果 索因的方法,即根据结论反推需要的条件. 如本 题还缺少∠ BAC= ∠ EAD,需利用已知条件∠ 1= ∠ 2 进行推导.
感悟新知
知2-练
③以点M′为圆心,以MN 长为半径作弧,在∠ BAC 内 部交②中所画的弧于点N′; ④过点N′作射线DN′交BC 于点E. 若∠ B=52°,∠C=83°,则∠ BDE= ___4_5_°__.
感悟新知
知识点 3 基本事实“边角边”或“SAS”
知3-讲
1. 基本事实:两边和它们的夹角分别相等的两个三角形全 等(可以简写成“边角边”或“SAS”).
感悟新知
解:∵∠BAD=∠EAC, ∴∠BAD+∠CAD=∠EAC+∠CAD, 即∠BAC=∠EAD.
全等三角形的判定H.L.ppt课件
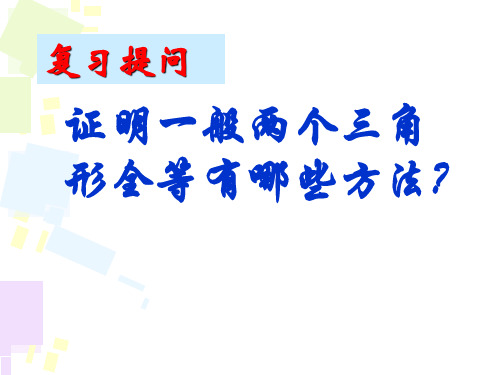
S.S.S S.A.S A.S.A A.A.S H.L S.A.S A.S.A A.A.S
灵活运用各种方法证明直角三角形全等
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
再见
△ABC≌△BAD.
D
C
A
B
例2. 火灾袭来时要迅速疏散逃生,不可蜂拥而出或留恋财物,要当机立断,披上浸湿的衣服或裹上湿毛毯、湿被褥勇敢地冲出去
如图,AC=AD,∠C,∠D
是直角,将上述条件标注在图中,
你能说明BC与BD相等吗?
C A
解:在Rt△ACB和 Rt△ADB 中,有
AB=AB,
B AC=AD.
会不会有自身独特的判定方法呢 ?
动动手 火灾袭来时要迅速疏散逃生,不可蜂拥而出或留恋财物,要当机立断,披上浸湿的衣服或裹上湿毛毯、湿被褥勇敢地冲出去
做一做
画一个Rt△ABC,使得 ∠C=90°,一直角边CA= 8cm,斜边AB=10cm.
B
10cm
A
8cm
C
动动手 火灾袭来时要迅速疏散逃生,不可蜂拥而出或留恋财物,要当机立断,披上浸湿的衣服或裹上湿毛毯、湿被褥勇敢地冲出去
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边” 或“HL”
ห้องสมุดไป่ตู้
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
斜边、直角边公理
(HL)推理格式
∵∠C=∠C′=90° ∴在Rt△ABC和Rt△A´B´C´中
灵活运用各种方法证明直角三角形全等
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
再见
△ABC≌△BAD.
D
C
A
B
例2. 火灾袭来时要迅速疏散逃生,不可蜂拥而出或留恋财物,要当机立断,披上浸湿的衣服或裹上湿毛毯、湿被褥勇敢地冲出去
如图,AC=AD,∠C,∠D
是直角,将上述条件标注在图中,
你能说明BC与BD相等吗?
C A
解:在Rt△ACB和 Rt△ADB 中,有
AB=AB,
B AC=AD.
会不会有自身独特的判定方法呢 ?
动动手 火灾袭来时要迅速疏散逃生,不可蜂拥而出或留恋财物,要当机立断,披上浸湿的衣服或裹上湿毛毯、湿被褥勇敢地冲出去
做一做
画一个Rt△ABC,使得 ∠C=90°,一直角边CA= 8cm,斜边AB=10cm.
B
10cm
A
8cm
C
动动手 火灾袭来时要迅速疏散逃生,不可蜂拥而出或留恋财物,要当机立断,披上浸湿的衣服或裹上湿毛毯、湿被褥勇敢地冲出去
斜边、直角边公理
有斜边和一条直角边对应相等的两个直角三角形全等.
简写成“斜边、直角边” 或“HL”
ห้องสมุดไป่ตู้
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
斜边、直角边公理
(HL)推理格式
∵∠C=∠C′=90° ∴在Rt△ABC和Rt△A´B´C´中
12.2《直角三角形全等的判定》-(共29张PPT)

(2)∵Rt△ABD≌Rt△CDB, ∴∠ADB=∠CBD, ∴AD∥BC.
例2.已知,如图,AC⊥BC,BD⊥AD.
(1)已知∠CAB=∠ DBA,求证:BC=AD.
(2)已知AC=BD,求证:BC=AD.
证明:
D
C
(1)∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°. 在△ABC和△BAD中,
(3)∠DAB = ∠CBA( AAS); D
C
(4)∠DBA = ∠CAB (AAS ).
A
B
四、练习:
1.如图,C是路段AB的中点,两人从C同时出发, 以相同的速度分别沿两条直线行走,并同时到 达D,E两地,DA⊥AB,EB⊥AB,D,E与路段 AB的距离相等吗?为什么?
答: D,E与路段AB的距离相等.
求证:AD=BC.
证明:连接DC. ∵ AD⊥AC,BC⊥BD, ∴∠A=∠B=90°. 在Rt△ADC和Rt△BCD中,
DC=CD, AC=BD, ∴Rt△ADC≌Rt△BCD(HL). ∴AD=BC.
例4.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.
求证:ED⊥AC.
证明:∵AE⊥AB,BC⊥AB, ∴∠EAD=∠ABC=90°. 在Rt△EAD和Rt△ABC中,
AD
AB——DE AC——DF
BC——EF
∠A——∠D
B
E
∠B——∠DEF
C
F ∠ACB——∠F
2:我们已经学过判定全等三角形的方法有哪些?
(SSS)、(SAS)、(ASA)、(AAS)
3、思考:
(1)如图:Rt△ACB、与Rt△A1C1B1中,∠C与∠C1是直 角,用我们已经学过的知识,除了两直角相等以外,你还
例2.已知,如图,AC⊥BC,BD⊥AD.
(1)已知∠CAB=∠ DBA,求证:BC=AD.
(2)已知AC=BD,求证:BC=AD.
证明:
D
C
(1)∵AC⊥BC,BD⊥AD,
∴∠D=∠C=90°. 在△ABC和△BAD中,
(3)∠DAB = ∠CBA( AAS); D
C
(4)∠DBA = ∠CAB (AAS ).
A
B
四、练习:
1.如图,C是路段AB的中点,两人从C同时出发, 以相同的速度分别沿两条直线行走,并同时到 达D,E两地,DA⊥AB,EB⊥AB,D,E与路段 AB的距离相等吗?为什么?
答: D,E与路段AB的距离相等.
求证:AD=BC.
证明:连接DC. ∵ AD⊥AC,BC⊥BD, ∴∠A=∠B=90°. 在Rt△ADC和Rt△BCD中,
DC=CD, AC=BD, ∴Rt△ADC≌Rt△BCD(HL). ∴AD=BC.
例4.已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.
求证:ED⊥AC.
证明:∵AE⊥AB,BC⊥AB, ∴∠EAD=∠ABC=90°. 在Rt△EAD和Rt△ABC中,
AD
AB——DE AC——DF
BC——EF
∠A——∠D
B
E
∠B——∠DEF
C
F ∠ACB——∠F
2:我们已经学过判定全等三角形的方法有哪些?
(SSS)、(SAS)、(ASA)、(AAS)
3、思考:
(1)如图:Rt△ACB、与Rt△A1C1B1中,∠C与∠C1是直 角,用我们已经学过的知识,除了两直角相等以外,你还
《全等三角形的判定》PPT习题课件(多种类型的解法)
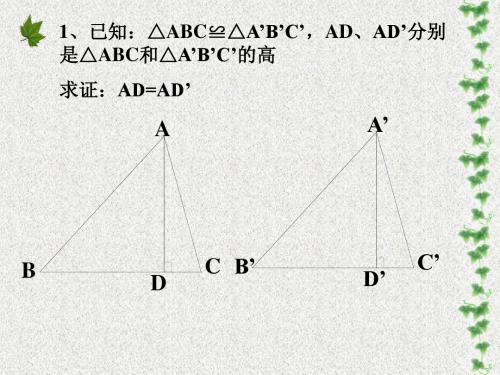
1、已知:△ABC≌△A’B’C’,AD、AD’分别 是△ABC和△A’B’C’的高
求证:AD=AD’
A
A’
B
D
C B’
D’
C’
2、已知:△ABC≌△A’B’C’,AD、AD’分别 是△ABC和△A’B’C’的角平分线
求证:AD=AD’
A
A’
B
D
C
B’
D’
C’
3、已知:△ABC≌△A’B’C’,AD、AD’分别 是△ABC和△A’B’C’的中线
求证:AD=AD’
A
A’
B
D
C B’
D’
C’
A
A’
C
B
C’
B’
如图,已知:Rt△ABC和Rt△A’B’C’,判断下列 条件能否使这两个三角形全等?并说明理由。
1、AB=A’B’,∠A=∠A’ 2、AB=A’B’,∠B=∠B’ 3、BC=B’C’,∠A=∠A’ 4、AC=A’C’,∠B=∠B’ 5、AC=A’C’,BC=B’C’
求证:AD=BC
A B
D
C
证明:延长DA、CB交于点E
已知:在△ABC中,AE=AF,CF⊥AB于F, BE⊥AC于E,BE、CF相交于O
求证: (1)FB=EC (2)FO=EO (3)AO⊥BC
F O B C E A
已知:AP∥BC,∠PAB的平分线与∠CBA的 平分线相交于E,CE的连线交AP于D
思考: AC=A’C’ AB=A’B’
已知:AC平分∠ DAB,E为AC上一点, AD=AB.
求证: ∠CDE=∠CBE .
D E
A
C
多种方法证明
B
已知:AB∥CD,AB=CD,O为AC的中点, 过O的直线交DA、BC的延长线于E、F
求证:AD=AD’
A
A’
B
D
C B’
D’
C’
2、已知:△ABC≌△A’B’C’,AD、AD’分别 是△ABC和△A’B’C’的角平分线
求证:AD=AD’
A
A’
B
D
C
B’
D’
C’
3、已知:△ABC≌△A’B’C’,AD、AD’分别 是△ABC和△A’B’C’的中线
求证:AD=AD’
A
A’
B
D
C B’
D’
C’
A
A’
C
B
C’
B’
如图,已知:Rt△ABC和Rt△A’B’C’,判断下列 条件能否使这两个三角形全等?并说明理由。
1、AB=A’B’,∠A=∠A’ 2、AB=A’B’,∠B=∠B’ 3、BC=B’C’,∠A=∠A’ 4、AC=A’C’,∠B=∠B’ 5、AC=A’C’,BC=B’C’
求证:AD=BC
A B
D
C
证明:延长DA、CB交于点E
已知:在△ABC中,AE=AF,CF⊥AB于F, BE⊥AC于E,BE、CF相交于O
求证: (1)FB=EC (2)FO=EO (3)AO⊥BC
F O B C E A
已知:AP∥BC,∠PAB的平分线与∠CBA的 平分线相交于E,CE的连线交AP于D
思考: AC=A’C’ AB=A’B’
已知:AC平分∠ DAB,E为AC上一点, AD=AB.
求证: ∠CDE=∠CBE .
D E
A
C
多种方法证明
B
已知:AB∥CD,AB=CD,O为AC的中点, 过O的直线交DA、BC的延长线于E、F
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• ∴△ABF≌△DCE,
• ∴CE=BF, ∠AFB=∠DEC,
• ∴CE∥BF,
即CE和BF的数量关系是
CE=BF,位置关系是
CE∥BF.全.等三角形的判定与性质;平行线的性
ppt课件
5
质;平行线的判定与性质.
5.如图,在△ABC中,AB=AC,AD平分∠BAC.求 证:∠DBC=∠DCB.
解:∵AD平分∠BAC, ∴∠BAD=∠CAD. ∴在△ACD和△ABD中 AB=AC ∠BAD=∠CAD AD=AD , ∴△ACD≌△ABD, ∴BD=CD, ∴∠DBC=∠DCB.
全pp等t课件三角形的判定与性质.6
6.已知:如图,点E,A,C在同一直线上,AB∥CD, AB=CE,AC=CD.求证:BC=ED.
证明:∵AB∥CD,
∴∠BAC=∠ECD,
在△BAC和△ECD中
AB=EC ∠BAC=∠ECD
AC=CD ,
∴△BAC≌△ECD(SAS),
ቤተ መጻሕፍቲ ባይዱ
∴CB=ED.
全等三角形的判定与性质.
全等三角形的判定与性质.
ppt课件
11
11.在△ABC中,AB=CB,∠ABC=90°,F为AB延 长线上一点,点E在BC上,且AE=CF. (1)求证:Rt△ABE≌Rt△CBF;
(1)证明:∵∠ABC=90°, ∴∠CBF=∠ABE=90°, 在Rt△ABE和Rt△CBF中, AE=CF AB=BC , ∴Rt△ABE≌Rt△CBF(HL);
ppt课件
7
7.如图,D、E分别是AB、AC上的点,且 AB=AC,AD=AE.求证:∠B=∠C.
在△ABE和△ACD中, ∵ AB=AC ∠A=∠A AE=AD , ∴△ABE≌△ACD(SAS), ∴∠B=∠C.
全ppt等课件 三角形的判定与性质8.
8.已知AC平分∠BAD,AB=AD.求证: △ABC≌△ADC.
2.如图,在△ABC中,∠C=90°,点D是AB边上的 一点,DM⊥AB,且DM=AC,过点M作ME∥BC交
AB于点E.求证:△ABC≌△MED。
证明:∵MD⊥AB, ∴∠MDE=∠C=90°, ∵ME∥BC, ∴∠B=∠MED, 在△ABC与△MED中, ∠B=∠MED ∠C=∠EDM DM=AC , ∴△ABC≌△MED(AAS).
直角三角形全等的判定;ppt课全件 等三角形的性质. 13
如图,△ABC中,AB=AC,∠1=∠2, 求证:AD平分∠BAC.
解:∵AB=AC, ∴∠ABC=∠ACB. ∵∠1=∠2, ∴∠ABD=∠ACD,BD=CD. ∵AB=AC,BD=CD, ∴△ABD≌△ACD. ∴∠BAD=∠CAD. 即AD平分∠BAC.
∵AB=AC.
∴∠ABC=∠ACB
∵BD、CF是角平分线.
∴∠BCF=1 2 ∠ACB,∠CBD=1 2 ∠ABC.
∴∠BCF=∠CBD,
∴ ∠BCF=∠CBD BC=BCpp∠t课件ABC=∠ACB
15
∴△BCF≌△CBD(ASA). 全等三角形的判定.
如图,在△ABC中,D是BC的中点,DE⊥AB, DF⊥AC,垂足分别是E,F,BE=CF. 求证:AD是△ABC的角平分线.
ppt课件
1
1.已知:如图,AB=AE,∠1=∠2,∠B=∠E.求证: BC=ED.
证明:∵∠1=∠2,
∴∠1+∠BAD=∠2+∠BAD,
即:∠EAD=∠BAC,
在△EAD和△BAC中
∠B=∠E AB=AE
∠BAC=∠EAD ,
∴△ABC≌△AED(ASA),
∴BC=ED.
全pp等t课件三角形的判定与性质.2
:∵AC平分∠BAD, ∴∠BAC=∠DAC, 在△ABC和△ADC 中, AB=AD ∠BAC=∠DAC AC=AC , ∴△ABC≌△ADC.
全等三角形的判定.
ppt课件
9
9.如图,已知点E,C在线段BF上,BE=CF, AB∥DE,∠ACB=∠F.求证:△ABC≌△DEF.
证明:∵AB∥DE, ∴∠B=∠DEF. ∵BE=CF, ∴BC=EF. ∵∠ACB=∠F, ∴ ∠B=∠DEF BC=EF∠ACB=∠F , ∴△ABC≌△DEF.
∴△ADE≌△CBF
(SAS).
全等三角形的判定.
ppt课件
4
4.如图,点E、F分别是AD上的两点,AB∥CD, AB=CD,AF=DE.问:线段CE、BF有什么数量关
系和位置关系?并加以证明.
• 证明:∵AB∥CD,
• ∴∠A=∠D,
• ∵在△ABF和△DCE中
• AB=CD ∠A=∠D AF=DE ,
ppt课件 全等三角形的判定. 3
如图,E、F是四边形ABCD的对角线BD上的两点,AE∥CF, AE=CF,BE=DF.求证:△ADE≌△CBF.
证明:∵AE∥CF
∴∠AED=∠CFB,
∵DF=BE,
∴DF+EF=BE+EF,
即DE=BF,
在△ADE和△CBF中,
AE=CF ∠AED=∠CFB
DE=BF ,
全等三角形的判定与性质.
ppt课件
14
如图,△ABC中,AB=AC,过点A作GE∥BC,角平 分线BD、CF相交于点H,它们的延长线分别交GE于
点E、G.试在图中找出3对全等三角形,并对其中 一对全等三角形给出证明.
:△BCF≌△CBD.
△BHF≌△CHD.
△BDA≌△CFA.
证明:在△BCF与△CBD中,
直角三角形全等的判定
ppt课件
12
如图,△ABC中,∠ABC=∠BAC=45°,点 P在AB上,AD⊥CP,BE⊥CP,垂足分别为D, E,已知DC=2,求BE的长.
∵∠ABC=∠BAC=45° ∴∠ACB=90°,AC=BC ∵∠DAC+∠ACD=90°,∠BCE+∠ACD=90° ∴∠DAC=∠BCE 又∵∠ADC=∠CEB ∴△ACD≌△CEB ∴BE=CD=2.
证明:∵DE⊥AB,DF⊥AC, ∴Rt△BDE=Rt△DCF=90°. BD=DC BE=CF , ∴Rt△BDE≌Rt△DCF(HL), ∴DE=DF, 又∵DE⊥AB,DF⊥AC, ∴AD是角平分线.
全等三角ppt课形件 的判定;平行线的性10 质.
10.已知:如图,E、F在AC上,AD∥CB且AD=CB, ∠D=∠B. 求证:AE=CF.
证明:∵AD∥CB, ∴∠A=∠C, 在△ADF和△CBE中, ∠A=∠C AD=CB ∠D=∠B , ∴△ADF≌△CBE(ASA), ∴AF=CE, ∴AF+EF=CE+EF,即AE=CF.
