基于自适应步长的直线生成算法
219336220_基于自适应精度法的硬件在环仿真技术研究

第23卷第3期2023年6月交 通 工 程Vol.23No.3Jun.2023DOI:10.13986/ki.jote.2023.03.006基于自适应精度法的硬件在环仿真技术研究曾琪婷1,王 超1,鲍日湧1,连培昆1,陈 宁2,黄勤钲3(1.福建农林大学交通与土木工程学院,福州 350002;2.北京工业大学北京市交通工程重点实验室,北京 100124;3.福建省建筑科学研究院有限责任公司,福州 350108)摘 要:针对硬件在环仿真技术寻求更短的仿真时间步长与保证仿真实时同步性需求上的矛盾,提出自适应精度法来解决硬件在环仿真的实时同步问题.首先,依托硬件在环仿真系统架构,分析系统运行过程中的软硬件通信延迟;其次,依据仿真时间步长与单步仿真运算时间相匹配原则,提出自适应精度的算法流程;最后,以实际交叉口为例,应用基于自适应精度法的公交优先硬件在环仿真进行实例验证.实验结果表明,所提出的自适应精度法能最大限度地使仿真软件虚拟检测器的工作频率接近现实信号机检测器的工作频率,提高仿真软件与现实信号机的通信频率,减少硬件通信延迟,有利于硬件在环仿真技术的推广与应用.关键词:硬件在环仿真;自适应精度法;仿真精度;仿真步长;交通工程中图分类号:TP 391.9;U 491.17文献标志码:A文章编号:2096⁃3432(2023)03⁃035⁃009收稿日期:2022⁃03⁃04.作者简介:曾琪婷(1998 ),女,硕士研究生,研究方向为智能交通㊁交通控制.E⁃mail:qiting_zeng@.通讯作者:连培昆(1985 ),男,博士,讲师,研究方向为智能交通㊁交通控制.E⁃mail:peikun_lian@.Research on Hardware⁃in⁃the⁃loop Simulation Technology Based on Adaptive Resolution MethodZENG Qiting 1,WANG Chao 1,BAO Riyong 1,LIAN Peikun 1,CHEN Ning 2,HUANG Qinzheng 3(1.College of Transportation and Civil Engineering,Fujian Agriculture and Forestry University,Fuzhou 350002,China;2.Beijing Key Laboratory of Traffic Engineering,Beijing University of Technology,Beijing 100124,China;3.Fujian Academy of Building Research Co.Ltd.,Fuzhou 350108,China)Abstract :Aiming at the contradiction between seeking a shorter simulation time step and ensuring the real⁃time synchronization of simulation in hardware⁃in⁃the⁃loop simulation technology,an adaptive resolution method is proposed to solve the real⁃time synchronization problem of hardware⁃in⁃the⁃loop simulation.First,relying on the hardware⁃in⁃the⁃loop simulation system architecture,the software andhardware communication delays during system operation are analyzed.Secondly,according to the principle of matching the simulation time step with the single⁃step simulation operation time,the algorithm flow of adaptive resolution is proposed.Finally,taking the intersection as an example,the hardware⁃in⁃the⁃loop simulation of bus priority based on the adaptive resolution method is applied to validate the method.The experimental results show that the proposed adaptive resolution method can make the working frequency of the virtual detector of the simulation software approach the working frequency of the real signal detector to the greatest extent,improve the communication frequency between the simulation software and the real signal,and reduce the hardware communication delay.It is beneficialto the popularization and application of hardware⁃in⁃the⁃loop simulation technology.交 通 工 程2023年Key words:hardware⁃in⁃the⁃loop simulation;adaptive resolution method;simulation resolution;simulation time step;traffic engineering0 引言硬件在环仿真近几年被广泛地应用在交通控制领域上[1-4],研究人员利用硬件在环仿真可在实验室环境里安全及便利地测试信号配时方案,它利用现实信号机的控制逻辑来替代仿真软件的虚拟信号控制逻辑[5-6].因此,对于硬件在环仿真,保持仿真软件与现实信号机的实时同步运行将决定着硬件在环仿真系统的准确性与可行性[7].硬件在环仿真的实时同步性要求是指每一个硬件在环单步仿真运算必须在对应的真实时钟时间间隔内完成,影响其实时同步性主要有2个运行过程:一是现实信号机与主机计算机的硬件通信延迟;二是主机里的软件通信延迟,前者往往难以避免,但对输出结果影响较小;而后者则存在较大的不确定性,易对系统运行产生较大干扰.如果主机计算机的某个单步仿真的运算时间超过固定时间步长所能提供的运算时间,这意味着主机无法在固定的仿真时间步长内完成所有规定的仿真任务,将导致随后既定的时间步长所能提供的运算时间被挤占压缩,单步仿真无法在规定时间内完成,软件延迟将会迅速增加,评价指标输出误差将会快速累积,由此直接导致硬件在环仿真运行崩溃与失败.目前已有许多研究尝试减少硬件在环仿真系统的软件延迟,Wells 等[8]指出一台专用的㊁性能优越的主机能保证软件仿真运行比真实时钟时间快;Sanvido等[9]指出1个合适的信号机通信频率能有效地减少仿真软件与现实信号机通信延迟;Johnson等[10]指出可通过预测仿真软件单步仿真运算时间来选择1个合适的时间步长,以确保单步仿真任务能在规定的时间步长内完成;Roe等[11]指出可减少仿真模型里所有车辆的评价指标输出频率,从而使软件仿真运算时间快于真实时钟时间;Engelbrecht等[12]指出在硬件在环仿真运行期间,主机关闭其他软件的运行能使硬件在环仿真运行得更加平稳.随着硬件在环仿真技术的发展,寻求更短的仿真时间步长与保证仿真的实时同步性存在需求上的矛盾.越来越复杂的仿真项目将会导致软件仿真的运算时间急剧增长,如果采用1个较小的仿真时间步长进行硬件在环仿真,即使在1台性能优越的主机里,也难以保证单步仿真的运算时间能满足实时运算要求.此外,每个单步仿真的运算时间均不相同,因此难以选择一个合适的时间步长进行硬件在环仿真.鉴于此,本文提出自适应精度法来解决硬件在环仿真的实时同步问题,该方法通过自适应调整仿真精度值来匹配不同单步仿真的运算时间,如果单步仿真的运算时间与此刻的仿真精度所对应的时间步长的差值大于某个设定的阈值,主机控制软件将会主动降低仿真精度值,以加大仿真时间步长;如果单步仿真的运算时间与此刻的仿真精度所对应的时间步长的差值小于某个设定的阈值,主机控制软件将会主动提高仿真精度值,以缩短仿真时间步长,以此保证硬件在环仿真的准确性与实时性需求.1 自适应精度法设计为了保证硬件通信的准确性,硬件在环仿真的仿真时间步长应足够短,同时需要匹配单步仿真的运算时间.本文所设计的自适应精度法本质上为通过主动调整仿真精度值来控制仿真时间步长,从而使得仿真软件的虚拟检测器能最大限度地接近真实信号机检测器的工作频率.该方法所使用的硬件在环仿真系统采用VISSIM仿真软件与集线器架构进行组织构建[13],(图1)VISSIM仿真软件允许开发人员自由地选择仿真精度值来运行仿真项目,这使得不同仿真精度值的测试成为可能[14];而在集线器架构中,现实交通信号机按照步骤1 2 3 4 5接收VISSIM仿真软件的虚拟检测器信息,而VISSIM仿真软件则按照步骤6 7 8 9 10更新现实交通信号机的灯态信息[15].1.1 基本要求1)硬件在环仿真必须保证实时同步运行,用以保证VISSIM仿真软件与现实信号机的同步性. 2)硬件在环仿真应以相等间隔的仿真时间步长运行.3)VISSIM仿真软件的单步仿真时间必须比真实时钟运行得快,从而保证接口软件完成余下任务的时间充足,能提前等待真实时钟的运行时间重新回到下1个仿真时间步长的起点.4)仿真时间步长要足够短,确保现实信号机接收仿真软件虚拟检测器数据的频率最大限度地接近现实检测器的接收频率.63 第3期曾琪婷,等:基于自适应精度法的硬件在环仿真技术研究图1 硬件在环仿真系统的数据流程自适应精度法在合适的时间点改变仿真精度值,使得单步仿真在每1s 内保持相等间隔的仿真时间步长,这将使硬件在环仿真最大限度地满足基本要求;自适应精度法通过降低仿真精度值来避免仿真软件的超负荷运行,这将使硬件在环仿真能运行得比真实时钟快来满足基本要求;同时,在单步仿真运算时间较短的情况下,自适应精度法可通过提高仿真精度值来缩短仿真时间步长,这将使硬件在环仿真满足基本要求;自适应精度法的上述设置通过在合适的时间点改变仿真精度值,以此来适应不同单步仿真的运算时间波动.图2 自适应精度法变精度点的选择设置1.2 变精度点选择自适应精度法变精度点的选择设置见图2所示,如果硬件在环仿真需要改变精度值,变精度点将出现在每1s 内的最后一个仿真时间步长里.该设置使得仿真时间步长在每1s 内的总长保持一致,因而信号灯态更新㊁仿真结果输出等仿真任务会在整数秒末完成,硬件在环仿真能避免由于变精度而产生的仿真错误,同时有足够的时间去恢复正常的硬件在环仿真状态,这将有利于仿真过程控制.1.3 算法流程自适应精度法有4个关键参数:1)降低仿真精度值的阈值T de (已运行的仿真时间与已消耗的真实时间的差值);2)提升仿真精度值的阈值T in (已运行的仿真时间与已消耗的真实时间的差值);3)降低精度值的过程中,仿真精度值的降低量ΔR de ;4)提升精度值的过程中,仿真精度值的提高量ΔR in .自适应精度法的工作流程参见图3,适配器接口软件依据已运行的仿真时间与已消耗的真实时间的差值ΔT 来改变仿真精度值.ΔT >0意味着部分单步仿真运算时间超过运算时间期限;ΔT <0意味着单步仿真提前完成所有任务.对于ΔT >0,如果ΔT 的数值大于降精度阈值T de ,仿真精度值将会被降低.对于ΔT <0,如果ΔT 的绝对值大于升精度阈值T in ,仿真精度值将会被提升.由上述可知,阈值组合T de 和T in 将会影响仿真精度的平均值与硬件在环仿真的通信准确性;在降低精度值的过程中,仿真精度值的降低量ΔR de 同样会影响仿真精度的平均值与硬件在环仿真的通信准确性.此外,在提升精度值的过程中,仿真精度值的提升量ΔR in 设置为常量,其数值为1.该设置可防止仿真精度值的过快提升,使硬件在环仿真在下一个仿真精度值里更有可能满足运算时间的期限要求.2 案例仿真设计2.1 仿真项目项目选取北京市朝阳路 高碑店北路交叉口为73交 通 工 程2023年图3 自适应精度法的工作流程研究对象,信号控制采用西门子信号机 绿灯延长及红灯早断”的公交优先策略,信号配时第1相位为东西直行相位,第2相位为东西左转相位,第3相位为南进口道直左相位,第4相位为北进口道直左相位,其中第1相位为优先相位,其余相位皆为非优先相位.仿真项目持续时间设置为3794s(现场信号周期长度为193s),仿真速度值为1仿真s/真实s,评价指标的输出时间区间为从193~3794s.同时,为进行自适应精度法的仿真验证,项目设置了4个虚拟检测器组,用于感应公交车辆的到达,参见图4所示.83 第3期曾琪婷,等:基于自适应精度法的硬件在环仿真技术研究图4 朝阳路-高碑店北路交叉口信息设置2.2 实验设计1)实验环境对于仿真软件,影响单步仿真运算时间的主要因素有计算机性能优劣㊁仿真项目复杂程度与仿真运行设置情况[10].为验证自适应精度法在硬件在环仿真实验中的有效性与可靠性,实验环境应搭建在拥有较长的单步仿真运算时间条件下.实验计算机采用处理器为Intel Core i5⁃3210(双核,@2.50GHz),内存为4.00GB,显卡为Intel(R)HD Graphics 4000的笔记本电脑;仿真项目流量选择在项目交叉口晚高峰17:00 19:00时段的高流量状况;仿真界面采用二维视图运行,仿真精度值的变化范围为(1~10)时间步长/仿真s,初始精度值为10时间步长/仿真s [16].2)实验计划针对自适应精度法,设计了3个实验组来测试不同参数组合的应用效果.1)实验组1实验组1用来测试不同的阈值组合T de 和T in 对硬件在环仿真的影响,共设置16个子实验,子实验编号为1~16,具体参见表1所示.此外,实验中有2个特殊的阈值设置,具体介绍见表1. a)降低仿真精度值的阈值:RD i =1/resoluion i (i =10,9, ,2)表1 自适应精度法参数组合设置实验组编号参数组合编号阈值T de /s 阈值T in /s 仿真精度值降低量ΔR de 仿真精度值提升量ΔR in 10.000.001120.050.001130.100.00114RD i0.001150.000.051160.050.051170.100.051118RD i 0.051190.000.1011100.050.1011110.100.101112RD i 0.1011130.00RI i 11140.05RI i 11150.10RI i 1116RD i RI i 11170.000.00[1,2,3]12180.000.05[1,2,3]1190.000.10[1,2,3]1200.00RI i[1,2,3]193交 通 工 程2023年 对于降精度阈值RD i,仿真精度值的变化区间从10时间步长/仿真s逐步递减至2时间步长/仿真s,则降精度阈值RD i的变化区间从0.1s逐步递增至0.5s.当降精度阈值RD i接近0.1s㊁数值较小时,降精度过程较易发生;当降精度阈值RD i接近0.5s㊁数值较大时,降精度过程相对较难发生.阈值RD i试着在降低运算超时率与维持1个相对较高的仿真精度值之间寻求动态平衡.如果单步仿真的运算时间较长,则仿真精度值较容易被快速地降低,这样有利于降低运算超时率;如果仿真精度值相对较小,则阈值RD i的值相对较大,仿真精度值较难被快速地降低,利于仿真精度值维持在1个较高的数值.b)提升仿真精度值的阈值:RI i=1/(resoluion i+1) (i=1,2, ,9)对于升精度阈值RI i,仿真精度值的变化区间从1时间步长/仿真s逐步递增至9时间步长/仿真s,则升精度阈值RI i的变化区间从0.5s逐步递减至0.1s.当升精度阈值RI i接近0.5s㊁数值较大时,升精度值的过程较难发生;当升精度阈值RI i接近0.1s㊁数值较小时,升精度值的过程相对较易发生.阈值RI i试着防止仿真精度值的快速提升,使得硬件在环仿真在下1个仿真精度值里,能满足运算时间期限要求.如果单步仿真的运算时间较长,则仿真精度值较难被快速地提升,这样有利于防止仿真精度值的快速提升,保证硬件在环仿真的稳定运行;如果单步仿真的运算时间相对较短,仿真精度值较易被快速地提升,这样利于仿真精度值维持在1个较高的数值.2)实验组2实验组2用来测试降精度值的过程中,不同的仿真精度值的降低量ΔR de对硬件在环仿真的影响,共设置4个子实验,子实验编号为17~20,具体参见表1所示.在实验组2,设定ΔR de的变化范围为(1~3)时间步长/仿真s,该设定利于高流量状况下硬件在环仿真的稳定运行.若ΔT>ΔT1(ΔT为已运行的仿真时间与已消耗的真实时间的差值),这意味着降低量ΔR de的数值等于1,无法保证硬件在环仿真在下1个仿真精度值里,能满足运算时间期限要求,因而降低量ΔR de的数值等于2将被优先考虑;若ΔT>ΔT2,这意味着降低量ΔR de的数值等于2,无法保证硬件在环仿真在下1个仿真精度值里能满足运算时间期限要求,因而降低量ΔR de的数值等于3将被优先考虑.3 结果分析3.1 全局指标分析在实验组1中,对比仿真精度的最小值,硬件在环仿真采用自适应精度法能得到1个较高的仿真精度平均值.仿真精度平均值取决于升精度阈值T in, T in的数值越小,仿真精度的平均值越大;T in的数值不变时,运算超时率取决于降精度阈值T de;此时, T de的数值越小,运算超时率越低.在实验组2中,对比仿真精度值的降低量ΔR de=1的情形,使用动态的仿真精度降低量能得到更低的运算超时率.因此,从表2的仿真运行过程评价指标的实验结果来看,如果选择维持1个较低的运算超时率进行硬件在环仿真,可选择参数组合13或20;如果选择维持1个较高的仿真精度平均值且同时维持1个较低的运算超时率进行硬件在环仿真,可选择参数组合5或18.3.2 单步仿真运算时间分析图5显示自适应精度法的单步仿真运算时间与仿真精度值的对照图,该图的数据来自表1中的参数组合18的实验结果.由图可看出,当仿真精度值为4时间步长/仿真s时,其单步仿真运算时间期限为250ms;同时,当单步仿真运算时间超过250s时,仿真精度值最终会从4时间步长/仿真s下降到3时间步长/仿真s,自适应精度法通过仿真精度值的变化能适应单步仿真运算时间的上下波动.值得注意的是,当单步仿真运算时间超过250ms 时(参见图5的上半图),部分仿真精度值并未降低到3时间步长/仿真s,这是因为单步仿真并未到达仿真精度值的改变点.同样值得注意的是,当仿真精度值为3时间步长/仿真s时(参见图5的下半图),部分单步仿真的运算时间低于250ms,这是因为在降精度值的过程中,仿真精度值的降低量大于1的结果.3.3 公交车辆检测时间分析在普通硬件在环仿真与自适应精度法下的硬件在环仿真实验条件下,分析公交车辆检测时间的小数部分,参见图6所示.在普通硬件在环仿真条件下,设定仿真精度值为常量,其数值为2时间步长/仿真s.从图6(a)可知,公交车辆检测只发生在0.5s整数倍时间,这将导致VISSIM仿真软件的虚拟检测器的工作频率远低于现实检测器的工作频率,最终将影响硬件在环仿真的准确性.04 第3期曾琪婷,等:基于自适应精度法的硬件在环仿真技术研究表2摇仿真运行过程评价指标参数组合编号降仿真精度升仿真精度仿真精度单步仿真运算超时仿真精度值降低量运算时间次数次数最小值平均值次数平均值/ms次数比例/%平均值/ms 平均值/ms11834183037.1425575451095942.85113221316131247.4626902591711163.601133384984437.5027213732045375.161134464063847.5427405892153978.601134540139636.69245223621338.701129616616246.912533134347913.731130710610446.842524149477218.9111328898746.892527473461418.2611319403645.8321323212891.36112910332945.7821276388924.19113211252145.8321491468443.93112912343045.90216258215026.951131137134.271471019440.301142146044.8617100631160.681135156044.7416706363882.32114016645.0718193614282.351134171364229136.802417038778232.201.681311834246836.70242583816706.881.3812719374135.6820930212291.091.22129207234.271433135530.371.29143 注:运算超时率为单步仿真的运算时间超过仿真时间步长的次数与单步仿真总次数的商.图5 自适应精度法的单步仿真运算时间与仿真精度值的对照图(参数组合18) 在普通硬件在环仿真条件下,设定仿真精度值为常量,其数值为10时间步长/仿真s.从图6(b)可知,公交车辆检测发生在0.1s 整数倍时间,使得VISSIM 仿真软件的虚拟检测器与现实检测器拥有相近的工作频率,这将不会影响硬件在环仿真的准确性.然而,在1个相对复杂的仿真环境里,仿真精度值为10时间步长/仿真s 难以保证硬件在环仿真的实时同步运行;在该状况下,单步仿真的运算时间14交 通 工 程2023年图6 公交车辆检测时间的小数部分较容易超过运算时间期限.在自适应精度法的硬件在环仿真条件下(实验组2参数组合18),设定仿真精度值为变量且其初始数值为10时间步长/仿真s.从图6(c)可知,公交车辆检测的发生时间的小数部分在0.1~1s间变化,相比于图6(b),自适应精度法检测到的发生时间小数部分更加精确,这将使VISSIM仿真软件的虚拟检测器的工作频率最大限度地接近现实检测器的工作频率,使得单步仿真在满足运算时间期限要求的同时,尽可能地提高硬件在环仿真的同步准确性.4摇结束语针对硬件在环仿真技术的实时同步问题,提出了1种通过自适应调整仿真精度值来匹配不同单步仿真运算时间的方法.该方法根据单步仿真的运算时间与此刻仿真精度所对应时间步长的差值,选择在合适的时间点改变仿真精度值,以满足硬件在环仿真的实时性与准确性问题.通过仿真运行过程全局指标分析㊁单步仿真运算时间分析㊁与公交车辆检测时间分析表明:1)自适应精度法能以更短的仿真时间步长运行,能最大限度地使仿真软件虚拟检测器的工作频率接近现实信号机检测器的工作频率,以保证硬件在环仿真系统在运算时间截止期限前完成工作. 2)自适应精度法能适应单步仿真运算时间的上下波动,当仿真项目较为复杂且主机性能不佳时,交通工程人员无需过于担心单步仿真无法满足实时同步要求.3)对于自适应精度法的参数组合,如果选择维持1个较低的运算超时率进行硬件在环仿真,可选择参数组合13或20;如果选择维持1个较高的仿真精度平均值且同时维持1个相对较低的运算超时率进行硬件在环仿真,可选择参数组合5或18.待技术条件成熟,下一步工作可考虑研究自适应精度法对仿真软件驾驶行为的影响.参考文献:[1]王浩,唐棠,王玲,等.交通控制硬件在环仿真综述[J].交通标准化,2013(1):89⁃91.[2]REN Y L,YU G Z,WANG Y P,et al.Hardware⁃in⁃the⁃Loop Simulation System for Multi⁃Intersection Traffic Signal Control[J].2014,8(1):67⁃72.[3]柳祖鹏,何雅琴,杜胜品.基于硬件在环仿真的交通信号控制实验设计[J].实验技术与管理,2017,34(2): 116⁃8+23.[4]唐少虎,刘小明,朱伟,等.基于硬件在环仿真的城市路网交通控制平台[J].重庆交通大学学报(自然科学版),2019,38(4):1⁃8.[5]邹智军.新一代交通仿真技术综述[J].系统仿真学报,2010,22(9):2037⁃42.[6]黄海南,李晓峰,连培昆,等.基于信号配时的公交优先策略触发概率模型[J].计算机应用,2018,38(10): 3025⁃9.[7]SO J,LEE J,PARK B.Evaluation of Manual Traffic⁃Signal Control under Oversaturated Conditions Using Hardware⁃in⁃the⁃Loop Simulation[J].Journal of Transportation Engineering,2013,139(11):1068⁃75.[8]WELLS R B,FISHER J,ZHOU Y,et al.Hardware and software considerations for implementing hardware⁃in⁃the⁃loop traffic simulation;proceedings of the27th Annual Conference of the IEEE Industrial Electronics Society24 第3期曾琪婷,等:基于自适应精度法的硬件在环仿真技术研究IECON’2001,November 29,2001⁃December 2,2001,Denver,CO,United states,F,2001[C ].IEEEComputer Society.[9]SANVIDO M A A.Hardware⁃in⁃the⁃loop simulationframework [D].Swiss Federal Institute of Technology,2002.[10]JOHNSON B,WALL R W,KYTE M,et al.University of Idaho,2011.[11]ROE M.Development of a hardware⁃in⁃the⁃loop analysisframework for advanced its applications [D ].Georgia Institute of Technology,2009.[12]ENGELBRECHT ing hardware⁃in⁃the⁃loop trafficsimulation to evaluate traffic signal controller features;proceedings of the 27th Annual Conference of the IEEE Industrial Electronics Society IECON’2001,November29,2001⁃December 2,2001,Denver,CO,United states,F,2001[C].IEEE Computer Society.[13]陈晨,赵晓华,李振龙,等.公交优先硬件在环测试评估平台设计[J].道路交通与安全,2014,14(3):47⁃51.[14]ISUKAPATI I K,DEMERS A,LIST G F.Hardware⁃In⁃the⁃LoopSimulation:Challengesandsolutions;proceedings of the Traffic and Transportation Studies2010⁃Proceedings of the 7th International Conference on Traffic and Transportation Studies,F,2010[C ].American Society of Civil Engineers (ASCE).[15]柳祖鹏,刘守阳,李思君,等.交通控制硬件在环仿真平台的开发与实现[J].交通信息与安全,2013,31(3):126⁃30.[16]连培昆,李振龙,荣建,等.基于VISSIM 微观交通仿真软件的导流岛机非冲突元胞自动机模型[J].计算机应用,2016,36(6):1745⁃50.(上接第13页)[6]梁对对,崔晓天,谢明隆.绿色交通评价指标体系研究 以深圳为例[C].新型城镇化与交通发展2013年中国城市交通规划年会暨第27次学术研讨会论文集,2014:1085⁃1092.[7]周垠,龙瀛.街道步行指数的大规模评价 方法改进及其成都应用[J].上海城市规划,2017(1):88⁃93.[8]全林花,高国刚,王昊,等.基于多源数据的步行友好性评价方法研究 以长春市典型街道为例[J].城市交通,2021,19(3):112⁃118.[9]孙光华.基于多源大数据的城市街道可步行性评价研究 以南京市中心城区为例[J].现代城市研究,2020(11):34⁃41.[10]李棠迪,雷强胜.城市空间品质视角下的步行系统定量评价 以重庆市渝中半岛为例[C].交通治理与空间重塑 2020年中国城市交通规划年会论文集,2020:71⁃81.[11]许建,张新兰.步行网络评价指标及其应用[J].规划师,2012,28(4):65⁃68.[12]汪培庄.模糊集与随机集落影[M].北京:北京师范大学出版社,1985.[13]李德清,崔红梅,李洪兴.基于层次变权的多因素决策[J].系统工程学报,2004,19(3):258⁃263.[14]李洪兴.因素空间理论与知识表示的数学框架(Ⅷ)[J].模糊系统与数学,1995,9(3):1⁃9.[15]朱勇珍,李洪兴.状态变权的公理化体系和均衡函数的构造[J].系统工程理论与实践,1999(7):117⁃119+132.[16]李德清,李洪兴.状态变权向量的性质与构造[J].北京师范大学学报(自然科学版),2002(4):455⁃461.[17]魏晓云.厦门市步行系统规划研究[J].城市交通,2008,6(6):21⁃26+32.[18]钱林波,叶冬青,曹玮,等.苏南发达地区中小城市步行系统规划体系研究 以江苏省常熟市为例[J].城市交通,2011(5):39⁃50.[19]南京市城市与交通规划设计研究院股份有限公司.南京市慢行(步行与自行车)系统规划[R].南京市规划局,2018.[20]过利超,过秀成,费跃,等.都市区客运走廊主导交通方式选择决策研究[J].交通运输工程与信息学报,2015,13(3):54⁃58.34。
直线生成算法——Bresenham法
直线生成算法——Bresenham法最近的研究涉及在像素图上作直线,自己也不想花时间摸索,于是在网上找到了Bresenham的直线生成算法,有一篇博客讲得清晰明了,但是算法上有些问题,我进行了改进和移植,下面讲解Bresenham的直线生成算法时也是参考这篇博文。
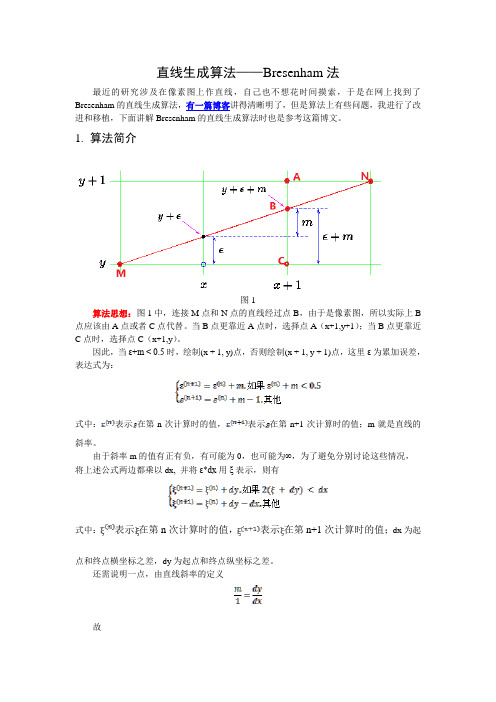
1.算法简介图1算法思想:图1中,连接M点和N点的直线经过点B,由于是像素图,所以实际上B 点应该由A点或者C点代替。
当B点更靠近A点时,选择点A(x+1,y+1);当B点更靠近C点时,选择点C(x+1,y)。
因此,当ε+m < 0.5时,绘制(x + 1, y)点,否则绘制(x + 1, y + 1)点,这里ε为累加误差,表达式为:式中:表示在第n次计算时的值,表示在第n+1次计算时的值;m就是直线的斜率。
由于斜率m的值有正有负,有可能为0,也可能为∞,为了避免分别讨论这些情况,将上述公式两边都乘以dx, 并将ε*dx用ξ表示,则有式中:表示在第n次计算时的值,表示在第n+1次计算时的值;dx为起点和终点横坐标之差,dy为起点和终点纵坐标之差。
还需说明一点,由直线斜率的定义故值得注意的是,现在我们只考虑dx > dy,且x,y的增量均为正的情况,但实际上有8种不同的情况(但是算法思想不变),如图2所示如图22.算法程序前文提到的那篇博文提出了一种方法,能将这8种情况都考虑,很巧妙。
但是实际应用时发现程序运行结果不是完全对,多次检查之后将程序进行了修改。
修改后的算法VB程序如下‘**************************************************************************** Type mypos '自定义数据类型x As Integery As IntegerEnd Type‘**************************************************************************** Function Bresenham(arr() As mypos, x1, y1, x2, y2)Dim x!, y!, dx!, dy!, ux%, uy%, eps!Dim cnt%ReDim arr(100)dx = x2 - x1dy = y2 - y1If dx >= 0 Then ux = 1If dx < 0 Then ux = -1If dy >= 0 Then uy = 1If dy < 0 Then uy = -1x = x1y = y1eps = 0dx = Abs(dx): dy = Abs(dy)cnt = 0If dx >= dy ThenFor x = x1 To x2 Step uxcnt = cnt + 1If 2 * (eps + dy) < dx Theneps = eps + dyarr(cnt).x = xarr(cnt).y = yElseeps = eps + dy - dxIf cnt >= 2 Then y = y + uy 'cnt大于2才执行y = y + uy,即排除起始坐标点,否则造成错误结果arr(cnt).x = xarr(cnt).y = yEnd IfNext xElseFor y = y1 To y2 Step uycnt = cnt + 1If 2 * (eps + dx) < dy Theneps = eps + dxarr(cnt).x = xarr(cnt).y = yElseeps = eps + dx - dyIf cnt >= 2 Then x = x + ux 'cnt大于2才执行x = x + ux,即排除起始坐标点,否则造成错误结果arr(cnt).x = xarr(cnt).y = yEnd IfNext yEnd Ifarr(0).x = cnt’记录元素个数End Function如果大家有不同看法,还希望共同讨论3.程序运行结果(VB+ OpenGL)图3图4绘制y=x,0≤x≤10,图3是原程序运行结果,图4时修改后的程序运行结果,原程序运行得到的起点是(0,1),但实际应该是(0,0)图5图6绘制直线[第1个坐标为起点,第2个坐标为终点](5,5)-(15,15)、(5,10)-(15,15)、(5,15)-(15,15)、(5,20)-(15,15)、(5,25)-(15,15);(25,5)-(15,15)、(25,10)-(15,15)、(25,15)-(15,15)、(25,20)-(15,15)、(25,25)-(15,15);(5,5)-(15,15)、(10,5)-(15,15)、(15,5)-(15,15)、(20,5)-(15,15)、(25,5)-(15,15);(5,25)-(15,15)、(10,25)-(15,15)、(15,25)-(15,15)、(20,25)-(15,15)、(25,25)-(15,15);图5是原程序运行结果,图6是修改后的程序运行结果。
求解常微分方程初值问题的自适应算法

求解常微分方程初值问题的自适应算法常微分方程(ODE)可以用来描述复杂物理系统和运动问题的动态行为,它们在工程、科学以及自然科学等领域都有着广泛的应用。
一般情况下,ODE的解可以通过求解不同的初值问题(IVP)来获得。
由于IVP经常具有复杂的解决方案,因此研究人员和工程师经常会遇到求解IVP的困难问题。
在这种情况下,自适应算法就派上用场,它具有更高的效率和更准确的计算结果,被广泛应用于各行各业。
自适应算法是一种特殊的数值求解方案,它的最终目标是提供较高的求解效率,其特点是在解决IVP时可以自动调整步长大小,从而实现快速求解。
与传统的均匀步长的求解方案相比,自适应算法由于具有较好的步长控制机制,因此可以获得更快的收敛速度和更可靠的计算结果。
自适应算法主要可以分为基于误差估计的和基于步长控制的算法。
基于误差估计的自适应方法首先利用步长控制算法选择步长,然后计算当前步长对解的影响,由此估计误差并自适应地调整步长大小以满足求解要求。
而基于步长控制的算法可以根据当前的误差和相邻两个步的增量之间的关系来调整步长,以最大程度满足求解要求。
此外,自适应算法还可以用来解决常见的IVP,如常微分方程的拟变步求解方案,以及双向非线性ODE的步进求解方案。
虽然传统的步进求解方案也可以用来解决IVP,但是其计算速度很慢,而且往往无法满足精确求解的要求。
同时,自适应方法也可以代替传统步进求解方案,为IVP提供更好的解决方案。
自适应算法的另一个优点是,即使在非精确的初值情况下,它仍然可以提供可靠的计算结果。
由于自适应算法可以有效减少误差,因此可以使得求解过程更稳定。
同时,自适应算法也可以被应用于较复杂的系统,而不必进行大量的预处理工作,从而极大地降低了计算成本。
因此,对于求解常微分方程初值问题,自适应算法是一种有效的解决方案。
它具有较高的求解效率,能够在不精确的初值情况下仍然提供可靠的计算结果,而且可以有效地应用于较复杂的系统中。
直线的Bresenham算法
生成直线的B resenham算法从上面介绍的DDA算法可以看到,由于在循环中涉及实型数据的加减运算,因此直线的生成速度较慢。
在生成直线的算法中,B resenham算法是最有效的算法之一。
B resenham算法是一种基于误差判别式来生成直线的方法。
一、直线Bresenham算法描述:它也是采用递推步进的办法,令每次最大变化方向的坐标步进一个象素,同时另一个方向的坐标依据误差判别式的符号来决定是否也要步进一个象素。
我们首先讨论m=△y/△x,当0≤m≤1且x1<x2时的B resenham算法。
从DDA直线算法可知这些条件成立时,公式(2-2)、(2-3)可写成:x i+1=x i+△x(2-2)y i+1=y i+△y(2-3)x i+1=x i+1 (2-6)y i+1=y i+m(2-7)有两种B resenham算法思想,它们各自从不同角度介绍了B resenham算法思想,得出的误差判别式都是一样的。
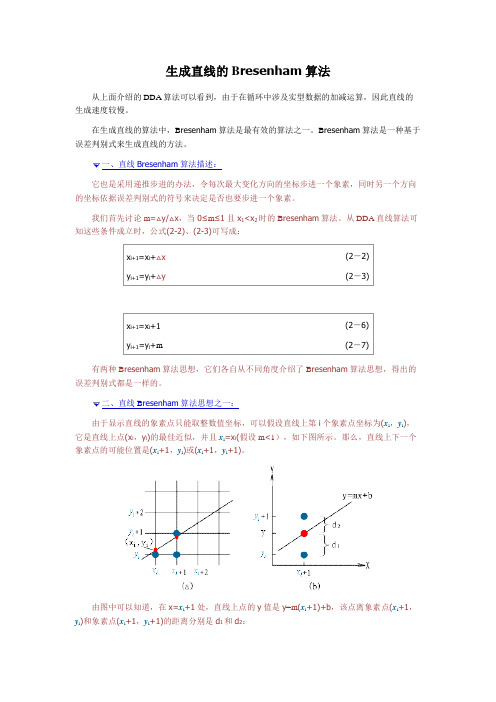
二、直线B resenham算法思想之一:由于显示直线的象素点只能取整数值坐标,可以假设直线上第i个象素点坐标为(x i,y i),它是直线上点(x i,y i)的最佳近似,并且x i=x i(假设m<1),如下图所示。
那么,直线上下一个象素点的可能位置是(x i+1,y i)或(x i+1,y i+1)。
由图中可以知道,在x=x i+1处,直线上点的y值是y=m(x i+1)+b,该点离象素点(x i+1,y i)和象素点(x i+1,y i+1)的距离分别是d1和d2:这两个距离差是我们来分析公式(2-10):(1)当此值为正时,d1>d2,说明直线上理论点离(x i+1,y i+1)象素较近,下一个象素点应取(x i+1,y i+1)。
(2)当此值为负时,d1<d2,说明直线上理论点离(x i+1,y i)象素较近,则下一个象素点应取(x i+1,y i)。
自适应变步长的动量项盲源分离方法

自适应变步长的动量项盲源分离方法马志阳;张天骐;李群;梁先明【摘要】针对传统盲源分离算法采用单一步长而无法同时兼顾收敛速度与稳态性以及动量因子选取的问题,介绍了一种盲源分离优化方法.该方法依据自然梯度算法(Natural Gradient Algorithm,NGA)的收敛条件,通过输出信号建立一种新的表示信号分离程度的度量指标,通过此度量指标构造非线性单调函数,使步长与动量因子参数自适应调节,从而可以合理、准确地选择参数.仿真表明了在平稳和非平稳环境下所提分离指标的正确性,且该指标可有效监测信号分离程度;针对步长及动量因子参数选取所设计的优化策略能够有效地缓解固定值对算法性能的约束,在有无噪声的情况下,均获得了优良的分离效果.【期刊名称】《电讯技术》【年(卷),期】2019(059)003【总页数】7页(P294-300)【关键词】盲源分离;变步长;自然梯度算法(NGA);动量因子【作者】马志阳;张天骐;李群;梁先明【作者单位】重庆邮电大学信号与信息处理重庆市重点实验室,重庆400065;重庆邮电大学信号与信息处理重庆市重点实验室,重庆400065;重庆邮电大学信号与信息处理重庆市重点实验室,重庆400065;中国西南电子技术研究所,成都610036【正文语种】中文【中图分类】TN911.71 引言盲源分离(Blind Source Separation,BSS)是基于源信号统计独立,且源信号和传输信道等先验知识均未知的情况下,仅根据观测的混合信号,将各个源信号从混合信号中分离出来的技术[1]。
盲源分离在盲信号处理领域中起了极大的推动作用,其在无线通信、图像处理、神经网络、语音信号处理上有突出表现[2]。
盲源分离发展至今,已经产生许多成熟的算法,目前较为广泛应用的自适应算法有自然梯度算法(Natural Gradient Algorithm,NGA)、等变自适应(Equivariant Adaptive Separation via Independence,EASI)算法[3]。
自适应变步长MPPT算法

自适应变步长MPPT算法黄舒予;牟龙华;石林【摘要】为减小光伏电池因环境变化造成的功率损失,提高系统的光电转换效率及跟踪响应速度,在传统电导增量法的基础上结合自适应变步长最小均方差LMS(least mean squre)算法,提出了一种自适应变步长最大功率跟踪算法,并在Matlab环境下利用SimPowerSystem功能模块建立了光伏电池的数学模型及自适应变步长算法的控制器模型.仿真结果表明,该算法在光照、温度等系统参数扰动的情况下都能快速找到新的工作点,表现出良好的动态及稳态特性,证实了算法的正确性和有效性.%In order to reduce the power loss caused by changeable environment, and to increase the photoelec tric conversion efficiency as well as tracking speed, a novel adaptive MPPT algorithm based on traditional in crement conductance method and adaptive variable step size LMS algorithm was proposed. By SimPowerSys tem block of Matlab. The simulation model of photovoltaic cell and adaptive variable step size MPPT algorithm controller was built in the paper. Even under the perturbations of illumination and temperature, simulation re sults show that the proposed algorithm can quickly find a new operating point and has a good dynamic and steady-state performance, which confirms the validity of the novel algorithm.【期刊名称】《电力系统及其自动化学报》【年(卷),期】2011(023)005【总页数】5页(P26-30)【关键词】光伏发电;最大功率点跟踪;自适应变步长;电导增量法【作者】黄舒予;牟龙华;石林【作者单位】同济大学电子与信息工程学院,上海201804;同济大学电子与信息工程学院,上海201804;同济大学电子与信息工程学院,上海201804【正文语种】中文【中图分类】TM615光伏电池作为一种典型的非线性电源,其输出功率易受环境温度、光照强度、负载的影响。
步长计算方法范文

步长计算方法范文步长是指在数值计算等领域中,确定迭代过程中每一步的大小。
在计算过程中,步长的合理选择可以提高计算的准确性、稳定性和效率。
1.固定步长:最简单的步长计算方法是固定步长。
在这种方法中,步长是事先确定好的常数,不随迭代过程的进展而变化。
固定步长的优点是简单易懂,计算过程稳定。
然而,如果步长选取不合适,可能会导致计算过程产生震荡或发散。
2.逐步逼近法:逐步逼近法是一种逐步调整步长的方法。
在迭代过程中,根据当前的状态和目标,动态调整步长的大小。
例如,可以根据问题的复杂度和迭代变量的变化幅度来调整步长。
这种方法可以根据问题的特点选择更合适的步长,提高计算效率和准确性。
3.自适应步长:自适应步长是一种根据迭代过程中的反馈信息调整步长的方法。
在每次迭代后,通过评估迭代结果的精度和稳定性,动态调整步长的大小。
如果迭代结果的精度不够高,可以增大步长以提高计算速度;如果迭代结果不稳定,可以减小步长以提高计算的稳定性。
自适应步长可以根据实际情况动态调整步长大小,通常能够在保证计算准确性的同时提高计算效率。
4.弹性步长:弹性步长是一种根据目标函数的局部特点调整步长的方法。
在许多优化算法中,目标函数往往具有不同的局部特征,如平坦区域、陡峭区域等。
在这种情况下,可以采用弹性步长的方法,根据目标函数的局部梯度大小和变化率来动态调整步长的大小。
在陡峭区域可以采用较小的步长以确保收敛性,在平坦区域可以采用较大的步长以提高计算效率。
总之,步长计算方法的选择应根据具体问题和算法的特点来确定。
固定步长适用于简单问题和稳定的计算过程,逐步逼近法适用于复杂问题和变化较大的迭代过程,自适应步长适用于需要动态调整步长的问题,弹性步长适用于具有不同局部特点的目标函数。
同时,根据实际情况选择合适的步长计算方法,可以提高计算的准确性、稳定性和效率。
清华大学学报(自然科学版)

. ! * $ 艳,马正新,等 ( ) : ! " ! # $ $ 荣,张正勇,等 ( ) : ! " ! % " &
! " # ! # * 延时估计误差对间接学习结构预失真器的影响 ………………………………… 李 辉,王德生,陈兆武 ! " # ! # + % , % -系统中有限反馈条件下的低功耗Байду номын сангаас束设计 ………………………………… 李韶华,王有政,周祖成
( ) : ! " ! # . $ 动态门限秘密共享方案 …………………………………………………………… 黄东平,王华勇,黄连生,等 " ! ! " ( 高速网络入侵检测系统负载均衡策略与算法分析 ……………………………… 蒋文保,郝 双,戴一奇,等 ( ) : " ! ! " # ! " ! # . * ( ) : ! " ! # . + 基于随机轮廓匹配的快速图像配准算法 ………………………………………… 李登高,秦开怀 " ! ! ! ! ( ) : ! " ! : . 1 基于角色的可信数字版权安全许可授权模型 …………………………………… 马兆丰,顾 明,孙家广 " ) ’ & ) ( ) : ! " ! : . : 倾转旋翼机模拟平台建模与仿真 ………………………………………………… 余长杰,朱纪洪,胡春华,等 " ) ’ & $ ! " ! : . < 网格环境中分层次哈希表资源发现机制 ………………………………………… 王 ! " ! : . " 多活性级递增叫价组合拍卖方法 ………………………………………………… 金 ,刘卫东,宋佳兴 ,石纯一 勇 ( ) : " ) ’ ) & ( ) : " ) ’ ) % ( ) : " ) ’ ’ ! ( ) : " ) ’ ’ ’ ( ) : " ) ’ ’ $
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ISSN 1000-0054CN 11-2223/N 清华大学学报(自然科学版)J T singh ua Un iv (Sci &Tech ),2006年第46卷第10期2006,V o l.46,N o.1021/401719-1722基于自适应步长的直线生成算法黄斌茂, 张 利(清华大学电子工程系,北京100084)收稿日期:2005-07-13基金项目:国家自然科学基金资助项目(60172027)作者简介:黄斌茂(1981-),男(汉),江西,硕士研究生。
通讯联系人:张利,副教授,E-mail:chin azh angli@mail.tsingh 摘 要:为了改进计算机图形学中画线算法的效率,提出一种基于自适应步长的直线生成算法和一种集成了对称性、最大公约数和自适应步长的集成算法。
由于直线仅包含一种或两种与斜率有关的像素模式,算法利用这一特性,自适应地采用最佳步长,在单次判决中生成多个像素。
通过综合使用直线像素的中点对称性、最大公约数性质以及像素模式的有限性等3种相互独立的特性,集成算法在单次判决中可生成更多像素。
算法的仿真结果表明:新算法生成直线的效率更高、速度更快。
关键词:Bresenham 算法;自适应步长;对称性;最大公约数;像素模式中图分类号:T P 391.4文献标识码:A文章编号:1000-0054(2006)10-1719-04Self -adaptive step straight -line algorithmsHUA NG Binmao ,ZH ANG Li(Department of Electronic Engineering ,T s inghua University ,Beij ing 100084,China )Abstract :Line draw ing algorithm in computer grap hics sys tems is improved w ith a self-adaptive s tep straight-line algor ith m and an oth er integrated algorithm th at combines self-adaptive step algorithm w ith th e s ymmetr y an d greatest com mon divisor (GCD)-based algor ith ms.Th e self-adaptive step algorithm uses the limited pixel patter ns inherent in line s egments to adaptively determine the best step that corres ponds to the line slope an d then gen erates m ulti-pixels in each judgemen t.T he integrated algorithm utilizes the sym metry,GCD,an d limited pixel patterns and gen erates more p ixels in each parisons w ith Bresen ham 's algorithm sh ow th at the integrated algorithms are m ore effective and efficient.Key words :Bresen ham's algorithm ;self-adaptive steps;s ymmetr y;greatest common divisor (GCD);pixel patter n直线段(简称直线)是图形的基本单元,图形渲染的速度很大程度上取决于直线的生成速度。
Br esenham 算法[1]是目前使用最为广泛的直线生成算法,它采用整数加减运算,避免了浮点数操作和乘除运算,从而极大地提高了算法的效率。
在该算法的基础上,研究界提出了多种改进算法。
其改进思路可分为两类:1)将直线分割成多条短线段,采用并行算法生成直线[2];2)通过一次误差判别操作,在一次循环中生成多个像素[312]。
直线上的像素点关于直线中点对称,文[5]利用这一特性,每个循环生成两个像素点。
对端点为S (x s ,y s )及E (x e ,y e )的直线,当 x e -x s 和 y e -y s 的最大公约数r 不为1时,直线上有r 段像素模式相同的线段。
文[4]通过在每个循环内生成r 个像素,加速了直线的生成。
但当r =1时,该算法比Brensenham 算法效率要低。
文[68]采用N 步长(N ≥2)直线生成方法,将八分圆分成多个子区,每个子区有N +1种像素模式,根据直线的斜率可决定其子区归属。
该算法每个循环可生成N 个像素。
其不足是:每个子区中的N +1种像素模式的初始化开销很大;步长固定,不能采用最佳步长。
还有一些研究者结合对称性、多步长、最大公约数提出集成算法[9]。
文[10]简要地提出自适应步长的思想,但未给出推导证明与具体算法;文[11,12]在直线斜率为0< m <0.5时,一次生成多个像素以提高直线的生成效率,但没有注意到直线像素模式关于m =±0.5的对称性。
此外,文[11,12]都没有给出算法的仿真结果。
上述各种改进算法的共同点是在每个循环中生成多个像素,但每次生成的像素个数固定,不能自适应地采用最合适的步长。
本文利用直线在八分圆中像素模式的对称性,以及任一直线只有一种或者两种与斜率相关的像素模式这一特性,提出一种基于自适应步长的直线生成算法,并进一步集成基于对称性及基于GCD 的直线生成算法,给出一种更高效的集成算法。
1 自适应步长直线生成算法本文将“直线”约定如下:起点为S (x s ,y s ),终点为E (x e ,y e ),斜率为m 。
并使用D 、X 表示相邻像素(x i ,y i )和(x i +1,y i +1)处于对角位置或水平位置。
误差判别项为p ,所需的条件测试数为t ,更新p 所需的操作数为i ,更新x 、y 所需的加减法操作数为a 。
整数的加减操作、条件测试、累加操作都分别占用一个单位的运行时间,衡量算法性能的指标TEP(theor etical ev aluation perform ance)[10]可这样计算:TEP =t +a +i 。
直线斜率m 存在4种一般情况:-∞<m <-1,-1<m <0,0<m <1,1<m <∞;5种特殊斜率:m =0,±1,±∞;特殊斜率的直线可直接生成。
不失一般性,本文的讨论约定在0<m <1的八分圆中进行。
1.1 直线的一些性质对起点为S (x s ,y s )、终点为E (x e ,y e )的直线L 1,通过将L 1的起点S (x s ,y s )平移为S 1(0,0),可得到起点为S 1(0,0)、终点为E 1(P ,Q )的直线L 0(其中P =x e -x s ,Q =y e -y s )。
性质1 当0<m <0.5时,对直线L 0:1)L 0可表示为L 0=X n1DX n2D …DXnQ +1;2) i ∈N ,且1≤i ≤Q +1,n i 满足n i ∈N ,n i >0,且当2≤i ≤Q ,n i ∈{A ,A -1},其中A =1/m ;3)n 1、n Q +1满足n 1=n Q +1=1/2m ;4)m =Q Q +∑Q +1i =1ni.证明 初始化x =0、y =0、x end =P ,误差判别项p =m ;p 代表点C (理想直线与网格线的交点)与栅格点B 之间的差值。
显然,若p <0.5,像素点B 比A 的误差要小,反之则应该使用像素点A 逼近理想直线(按图1的情况,应该使用像素A )。
图1 中点判决准则由此可得生成直线像素时的判决准则和误差判别项p 的更新方式为:if(p <0.5){p =p +m ;下一个像素相对位置为X ;}else{p =p -1;下一个像素相对位置为D ;}1)假设存在两个连续的D ,不妨设它们位于X ni之后,设决定第n i 个X 的误差项为p i (-0.5≤p i <0.5);由假设,更新之后有p i +1=p i +m 且0.5≤p i +1<1,p i +2=p i -1+2m 且0.5≤p i +2<1。
由于0<m <0.5,因而p i +2=p i -1+2m <0.5,与上面的推理矛盾!故不可能存在连续的两个D 。
2)假设存在i (2≤i ≤Q )使得n i 有其他取值,即n i <A -1或n i >A 。
设决定n i 个X 之前的D 的误差项为p (0.5≤p <1且p -m <0.5)。
由此可知:决定第n i 个X 的误差项为:p ′=p +n i m -1(-0.5≤p ′<0.5),决定第n i 个X 之后的D 的误差判别项为p ″=p +(n i +1)m -1(0.5≤p ″<0.5+m )。
由于A =1/m ,因而1-m <A m ≤1。
当n i >A 时,n i m ≥(A +1)m >1,由此可得:p ′≥0.5,矛盾!当n i <A -1时,(n i +1)m ≤(A -2+1)m ≤1-m ,因而有:p ″<0.5,矛盾!由此可知,0<m <0.5的直线L 0可表示为:L 0=X n 1DX n 2D …DX n Q +1。
3)由于直线关于中点对称,易得n 1=n Q 。
对于X n 1D ,假设决定D 的误差判别项为p ,此时p =(n 1+1)m ,且有0.5≤p <0.5+m ,由此可得n 1=n Q =1/2m .4)由L 0的表达式易得,证明过程略。
图2显示了起点为S (0,0)、终点为E (14,3)的直线L 0的像素模式。
该直线可表达为X 2DX 3DX 4DX 2。
由性质1易得:A =14/3=4,n 1=n 4=14/6=2。
由图可见:除去端点处的两小段像素X 2,该直线中存在的两种像素模式为DX 3和DX 4。
由于篇幅限制,只能示意短直线的像素模式,对于稍长的直线,像素模式的有限性和重复性将更加明显。
图2 直线像素模式示意图性质2 位于同一个八分圆中的直线关于m =1720清华大学学报(自然科学版)2006,46(10)±0.5具有像素模式的对称性。
