DSP基础知识学习笔记
dsp知识点总结

dsp知识点总结一、DSP基础知识1. 信号的概念信号是指用来传输信息的载体,它可以是声音、图像、视频、数据等各种形式。
信号可以分为模拟信号和数字信号两种形式。
在DSP中,我们主要研究数字信号的处理方法。
2. 采样和量化采样是指将连续的模拟信号转换为离散的数字信号的过程。
量化是指将信号的幅度离散化为一系列离散的取值。
采样和量化是数字信号处理的基础,它们决定了数字信号的质量和准确度。
3. 傅里叶变换傅里叶变换是一种将时域信号转换为频域信号的方法,它可以将信号的频率分量分解出来,从而可以对信号进行频域分析和处理。
傅里叶变换在DSP中有着广泛的应用,比如滤波器设计、频谱分析等。
4. 信号处理系统信号处理系统是指用来处理信号的系统,它包括信号采集、滤波、变换、编解码、存储等各种功能。
DSP技术主要用于设计和实现各种类型的信号处理系统。
二、数字滤波技术1. FIR滤波器FIR滤波器是一种具有有限长冲激响应的滤波器,它的特点是结构简单、稳定性好、易于设计。
FIR滤波器在数字信号处理中有着广泛的应用,比如音频处理、图像处理等。
2. IIR滤波器IIR滤波器是一种具有无限长冲激响应的滤波器,它的特点是频率选择性好、相位延迟小。
IIR滤波器在数字信号处理中也有着重要的应用,比如通信系统、控制系统等。
3. 数字滤波器设计数字滤波器的设计是数字信号处理的重要内容之一,它包括频域设计、时域设计、优化设计等各种方法。
数字滤波器设计的目标是满足给定的频率响应要求,并且具有良好的稳定性和性能。
4. 自适应滤波自适应滤波是指根据输入信号的特性自动调整滤波器参数的一种方法,它可以有效地抑制噪声、增强信号等。
自适应滤波在通信系统、雷达系统等领域有着重要的应用。
三、数字信号处理技术1. 数字信号处理器数字信号处理器(DSP)是一种专门用于数字信号处理的特定硬件,它具有高速运算、低功耗、灵活性好等特点。
DSP广泛应用于通信、音频、图像等领域,是数字信号处理技术的核心。
dsp知识点,复习提纲

1.dsp芯片普遍采用数据总线和程序总线分离的哈佛结构和改进的哈佛结构,有1条程序总线(PB)和3条数据总线(CB、DB、EB)4组地址总线(PAB、CAB、DAB、EAB)。
2.dsp系统的处理过程:①将输入信号x(t)进行抗混叠滤波,滤掉高于折叠频率的分量,以防止信号频谱的混叠②经采样和A/D转换器,将滤波后的信号转换为数字信号x(n)③数字信号处理器对x(n)进行处理,得数字信号y(n)④经D/A转换器,将y(n)转换成模拟信号⑤经低通滤波器,滤除高频分量,得到平滑的模拟信号y(t)。
3.dsp系统的设计过程:①明确设计任务确定设计目标②算法模拟确定性能指标③选择dsp芯片和外围芯片④设计实时的dsp应用系统⑤硬件和软件测试⑥系统集成和测试。
4.双寻址RAM(DARAM):在一个指令周期内,可对其进行两次存取操作,一次读出和一次写入。
单寻址RAM(SARAM): 在一个指令周期内,只能进行一次存取操作。
5.CPU的基本组成:40位算术逻辑运算单元(ALU);2个40累加器(ACCA、ACCB);一个支持-16~31位移位的桶形移位寄存器;乘法器-加法器单元(MAC);比较、选择和存储单元(CSSU);指数编码器;CPU状态和控制寄存器。
6. 乘法器-加法器单元(MAC):具有强大的乘法累加运算功能可在一个流水线周期内完成一次乘法运算和一次加法运算。
7.CPU状态和控制寄存器:状态寄存器0(ST0)、状态寄存器1(ST1)、和处理器工作方式状态寄存器(PMST)。
8.’C54有8个辅助寄存器。
9.流水线操作的原理:将指令分为几个子操作,每个子操作有不同的操作阶段完成,每隔一个机器周期,每个操作阶段就可以进入一条新指令,在同一个机器周期内,在不同的操作阶段可以处理多条指令,相当于并行执行了很多条指令。
T1 T2 T3 T4 T5 T611.中断操作:分为可屏蔽中断和不可屏蔽中断。
12.基本的数据寻址方式:立即寻址、绝对寻址、累加器寻址、直接寻址、间接寻址、存储器映像寄存器寻址、堆栈寻址。
DSP入门必须掌握知识点

1.DSP选型:主要考虑处理速度、功耗、程序存储器和数据存储器的容量、片内的资源,如定时器的数量、I/O 口数量、中断数量、DMA通道数等。
DSP的主要供应商有TI,ADI,Motorola,Lucent和Zilog等,其中TI占有最大的市场份额。
选择DSP可以根据以下几方面决定:1)速度:DSP速度一般用MIPS或FLOPS表示,即百万次/秒钟。
根据您对处理速度的要求选择适合的器件。
一般选择处理速度不要过高,速度高的DSP,系统实现也较困难。
2)精度:DSP芯片分为定点、浮点处理器,对于运算精度要求很高的处理,可选择浮点处理器。
定点处理器也可完成浮点运算,但精度和速度会有影响。
3)寻址空间:不同系列DSP程序、数据、I/O 空间大小不一,与普通MCU不同,DSP在一个指令周期内能完成多个操作,所以DSP的指令效率很高,程序空间一般不会有问题,关键是数据空间是否满足。
数据空间的大小可以通过DMA的帮助,借助程序空间扩大。
4)成本:一般定点DSP的成本会比浮点DSP的要低,速度也较快。
要获得低成本的DSP系统,尽量用定点算法,用定点DSP。
5)实现方便:浮点DSP的结构实现DSP系统较容易,不用考虑寻址空间的问题,指令对C语言支持的效率也较高。
6)内部部件:根据应用要求,选择具有特殊部件的DSP。
如:C2000适合于电机控制;OMAP适合于多媒体等。
1)C5000系列(定点、低功耗):C54X,C54XX,C55X相比其它系列的主要特点是低功耗,所以最适合个人与便携式上网以及无线通信应用,如手机、PDA、GPS等应用。
处理速度在80MIPS--400MIPS之间。
C54XX和C55XX一般只具有McBSP同步串口、HPI并行接口、定时器、DMA等外设。
值得注意的是C55XX提供了EMIF外部存储器扩展接口,可以直接使用SDRAM,而C54XX则不能直接使用。
两个系列的数字IO 都只有两条。
2)C2000系列(定点、控制器):C20X,F20X,F24X,F24XX ,C28x该系芯片具有大量外设资源,如:A/D、定时器、各种串口(同步和异步),WATCHDOG、CAN总线/PWM 发生器、数字IO 脚等。
dsp重点知识点总结

dsp重点知识点总结1. 数字信号处理基础数字信号处理的基础知识包括采样定理、离散时间信号、离散时间系统、Z变换等内容。
采样定理指出,为了保证原始信号的完整性,需要将其进行采样,并且采样频率不能小于其最高频率的两倍。
离散时间信号是指在离散时间点上取得的信号,可以用离散序列表示。
离散时间系统是指输入、输出和状态都是离散时间信号的系统。
Z变换将时域的离散信号转换为Z域的函数,它是离散时间信号处理的数学基础。
2. 时域分析时域分析是对信号在时域上的特性进行分析和描述。
时域分析中常用的方法包括时域图形表示、自相关函数、互相关函数、卷积等。
时域图形表示是通过时域波形来表示信号的特性,包括幅度、相位、频率等。
自相关函数是用来描述信号在时间上的相关性,互相关函数是用来描述不同信号之间的相关性。
卷积是一种将两个信号进行联合的运算方法。
3. 频域分析频域分析是对信号在频域上的特性进行分析和描述。
频域分析中常用的方法包括频谱分析、傅里叶变换、滤波器设计等。
频谱分析是通过信号的频谱来描述信号在频域上的特性,可以得到信号的频率成分和相位信息。
傅里叶变换是将时域信号转换为频域信号的一种数学变换方法,可以将信号的频率成分和相位信息进行分析。
滤波器设计是对信号进行滤波处理,可以剔除不需要的频率成分或增强需要的频率成分。
4. 数字滤波器数字滤波器是数字信号处理中的重要组成部分,通过对信号进行滤波处理,可以实现对信号的增强、降噪、分离等效果。
数字滤波器包括有限冲激响应(FIR)滤波器和无限冲激响应(IIR)滤波器两种类型。
有限冲激响应(FIR)滤波器是一种只有有限个系数的滤波器,它可以实现线性相位和稳定性处理。
无限冲激响应(IIR)滤波器是一种有无限个系数的滤波器,它可以实现非线性相位和较高的滤波效果。
5. 离散傅里叶变换(DFT)和快速傅里叶变换(FFT)离散傅里叶变换(DFT)是将时域离散信号转换为频域离散信号的一种数学变换方法,其计算复杂度为O(N^2)。
DSP课堂笔记总结

1.数字信号处理是利用计算机或专用处理设备,以数字形式对信号进行采集、变换、滤波、估值、增强、压缩、识别等处理,以得到符合人们需要的信号形式。
输入信号可以是语音信号、传真信号,也可以是视频信号,还可以是传感器(如温度传感器)的输出信号。
输入信号经过带限滤波后,通过A/D转换器将模拟信号转换成数字信号。
根据采样定理,采样频率至少是输入带限信号最高频率的2倍,在实际应用中,一般为4倍以上。
数字信号处理一般是用DSP芯片和在其上运行的实时处理软件对输入数字信号按照一定的算法进行处理,然后将处理后的信号输出给D/A转换器,经D/A转换、内插和平滑滤波后得到连续的模拟信号。
3.数字信号处理的实现方法一般有以下几种:(1) 在通用型计算机上用软件实现。
一般采用C语言、MA TLAB语言等编程,主要用于DSP算法的模拟与仿真,验证算法的正确性和性能。
优点是灵活方便,缺点是速度较慢。
(2) 在通用型计算机系统中加上专用的加速处理器实现。
专用性强,应用受到很大的限制,也不便于系统的独立运行。
(3) 在通用型单片机(如MCS-51、MCS-96系列等)上实现。
只适用于简单的DSP算法,可用于实现一些不太复杂的数字信号处理任务,如数字控制。
(4) 用通用型可编程DSP芯片实现。
与单片机相比,DSP芯片具有更加适合于数字信号处理的软件和硬件资源,可用于复杂的数字信号处理算法。
特点是灵活、速度快,可实时处理。
(5) 用专用型DSP芯片实现。
在一些特殊的场合,要求信号处理速度极高,用通用型DSP芯片很难实现,例如专用于FFT、数字滤波、卷积、相关等算法的DSP芯片,这种芯片将相应的信号处理算法在芯片内部用硬件实现,无须进行编程。
处理速度极高,但专用性强,应用受到限制。
在上述几种实现方法中,(1)~(3)和(5)都有使用的限制,只有(4)才使数字信号处理的应用打开了新的局面。
4.DSP系统的特点基于通用DSP芯片的数字信号处理系统与模拟信号处理系统相比,具有以下优点:(1) 精度高,抗干扰能力强,稳定性好。
dsp基础学习总结笔记
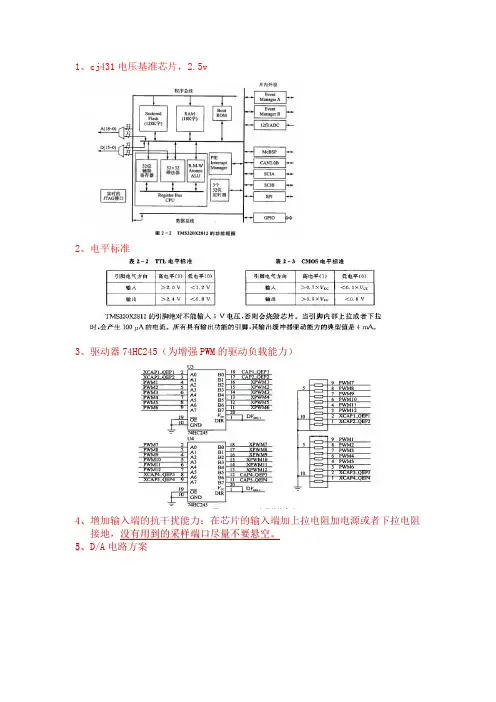
1、cj431电压基准芯片,2.5v2、电平标准3、驱动器74HC245(为增强PWM的驱动负载能力)4、增加输入端的抗干扰能力:在芯片的输入端加上拉电阻加电源或者下拉电阻接地,没有用到的采样端口尽量不要悬空。
5、D/A电路方案通用扩展语言GEL和c相似,但是有所不同。
GEL语言是C语言的一个子集。
与c语言不同的是gel不需要指定函数返回值的类型。
Gel中的while语句和c中的while语句相同,gel不支持标准c的break和continue语句6、一个完整的dsp工程包括头文件(.h),库文件(.lib),源文件(.c),以及配置文件.Cmd使用关键字MENUITEM可以在gel菜单下选择用户自定义的菜单项,然后用hotmenu、dialog或slider等关键字,在这个新的下拉菜单中添加新的菜单项。
7、关于添加文件遇到的问题8、变量查找:edit→find:Ctrl+f9、调试时,添加断点的快捷方法如下点击图上的小手即可10、单步调试第一个的意思是单击一步走一步,第二个的意思是指在单步运行时遇到子函数不进入子函数内部进行而是把它当成一步来执行,第三个的意思是当执行到子函数内部时使用这个按钮就可以执行完剩下的部分返回上一层函数。
如果想在一个窗口内同时看到c和汇编,则有操作View→mixed source/asm 11、观察变量右击变量→add to watch window 可以得到变量的值、类型、地址等。
12、位域定义、结构体以及共同体的知识结构体先定义再声明Union SCIFFCT_REG {Uint16 all;Struct SCIFFCT_BITS bit;};//---------------------------------------------------------------------------// SCI Register File://Struct SCI_REGS {Union SCICCR_REG SCICCR; // Communications control register Union SCICTL1_REG SCICTL1; // Control register 1Uint16 SCIHBAUD; // Baud rate (high) registerUint16 SCILBAUD; // Baud rate (low) registerUnion SCICTL2_REG SCICTL2; // Control register 2Union SCIRXST_REG SCIRXST; // Receive status registerUint16 SCIRXEMU; // Receive emulation buffer registerUnion SCIRXBUF_REG SCIRXBUF; // Receive data bufferUint16 rsvd1; // reservedUint16 SCITXBUF; // Transmit data bufferUnion SCIFFTX_REG SCIFFTX; // FIFO transmit registerUnion SCIFFRX_REG SCIFFRX; // FIFO receive registerUnion SCIFFCT_REG SCIFFCT; // FIFO control registerUint16 rsvd2; // reservedUint16 rsvd3; // reservedUnion SCIPRI_REG SCIPRI; // FIFO Priority control};//---------------------------------------------------------------------------// SCI External References & Function Declarations://Extern volatile struct SCI_REGS SciaRegs;Extern volatile struct SCI_REGS ScibRegs;由于scihbaud和scilbaud定义时为unit16型的,所以不能用.all或者.bit 的方式来访问,只能直接给寄存器整体进行赋值。
DSP各种知识点总结
1 DSP芯片的特点:(1).哈佛结构(程序空间和数据空间分开)(2).多总线结构.(3)流水线结构(取指、译码、译码、寻址、读数、执行)(4)多处理单元. (5)特殊的DSP指令(6).指令周期短. (7)运算精度高.(8)硬件配置强.(9)DSP最重要的特点:特殊的内部结构、强大的信息处理能力及较高的运行速度。
2 三类TMS320:(1)TMS320C2000适用于控制领域(2)TMS320C5000应用于通信领域(3)TMS320C6000应用于图像处理3 DSP总线结构:C54x片内有8条16位主总线:4条程序/数据总线和4条对应的地址总线。
1条程序总线(PB):传送自程序储存器的指令代码和立即操作数。
3条数据总线(CB、DB、EB):CB和EB传送从数据存储器读出的操作数;EB传送写到存储器中的数据。
4条地址总线(PAB、CAB、DAB、EAB)传送相应指令所需要的代码4存储器的分类:64k字的程序存储空间、64K字的数据存储空间和64K字的I/O空间(执行4次存储器操作、1次取指、2次读操作数和一次写操作数。
5存储器空间分配片内存储器的形式有DARAM、SARAM、ROM 。
RAM安排到数据存储空间、ROM构成程序存储空间。
(1)程序空间:MP/MC=1 40000H~FFFFH 片外MP/MC=0 4000H~EDDDH 片外FF00H~FFFFH 片内OVL Y=1 0000H~007FH 保留0080H~007FH 片内OVL Y=0 0000H~3FFFH片外(2)数据空间:DROM=1 F000H~F3FFH 只读空间FF00H~FFFH保留DROM=0 F000H~FEFFH 片外6数据寻址方式(1)立即寻址(2)绝对寻址<两位>(3)累加器寻址(4)直接寻址@<包换数据存储器地址的低7位>优点:每条指令只需一个字(5)间接寻址*按照存放某个辅助寄存器中的16位地址寻址的AR0~AR7(7)储存器映像寄存器寻址(8)堆栈寻址7寻址缩写语Smem:16位单寻址操作数Xmem Ymem 16位双dmad pmad PA16位立即数(0-65535)scr源累加器dst目的累加器lk 16位长立即数8状态寄存器ST0 15~13ARP辅助寄存器指针12TC测试标志位11C进位位10累积起A 的一出标志位OV A 9OVB 8~0DP数据存储器页指针9状态寄存器ST1 CPL:直接寻址编辑方式INTM =0开放全部可屏蔽中断=1关闭C16 双16位算数运算方式10定点DSP 浮点DSP:定点DSP能直接进行浮点运算,一次完成是用硬件完成的,而浮点需要程序辅助。
DSP基础知识简洁版(适合考试用)
一、名词解释1、数字信号处理理论(Digital Signal Processing):频谱分析、数字滤波器设计、自适应信号处理、信号压缩、信号建模……2、数字信号处理器 (Digital Signal Processor) :专门针对数字信号的数学运算需要而设计开发的一类集成电路芯片3、冯·诺依曼结构:也称普林斯顿结构,是一种将程序指令存储器和数据存储器合并在一起的存储器结构。
由于取指令和存取数据要从同一个存储空间存取,经由同一总线传输,因而它们无法重叠执行,只有一个完成后再进行下一个。
4、哈佛结构:是一种将程序指令存储和数据存储分开的存储器结构。
可以减轻程序运行时的访存瓶颈。
5、专用的硬件乘法器:典型的FFT、IIR和FIR等数字信号处理算法中,乘法是DSP运算的重要组成部分;DSP芯片中有专用的硬件乘法器,一次或多次的乘法累加运算可以在一个指令周期内完成。
6、特殊的DSP指令:专门为实现数字信号处理的算法而设置特殊指令;位倒序寻址、循环寻址等特殊指令能够方便快速地实现FFT算法。
7、流水线操作:执行指令的几个阶段在程序执行过程中是重叠的,即几条不同的指令同时处于激活状态,每条指令处于不同的阶段。
8、晶振时钟信号:‘28x DSP片上晶振电路模块允许采用内部振荡器或外部时钟源为CPU内核提供时钟;在使用片上晶振模块的内部振荡器时,应当在X1/XCLKIN和X2两个引脚之间连上一个石英晶振,片上晶振模块输出与石英晶振频率相同的时钟信号,典型的晶振频率是30MHz。
采用外部时钟应把时钟信号直接接到X1/XCLKIN引脚,X2引脚则必须悬空,这时内部振荡器不工作,片上晶振模块输出该外部时钟信号。
二、简答题1.PWM变化PWM输出变化由一个对称/非对称波形发生器和一个相关输出逻辑控制,同时还要依赖于以下几种情况:(1)GPTCONA/B中位的定义;(2)定时器的计数模式;(3)定时器处于连续增/减计数模式下的计数方向。
DSP笔记
R4.3 软件开发语言(1)汇编语言高效指令,代码效率高,底层控制灵活,实时性好;指令集掌握困难,程序可读性,可维护性可移植性差,流程控制困难,开发周期长;适用于运算量大、实时性要求高的场合。
(2)C语言程序可读性、可维护性、可移植性好,修改、升级方便,流程控制容易,开发周期短;某些硬件控制不便,实时性不好;适用于运算量小,实时性要求不高的场合。
(3)汇编与C混合编程。
综合利用两种语言的优越性,用C语言实现流程控制,用汇编语言实现时序或效率要求严格的核心程序。
三者各有所长,技术的发展使得DSP、通用计算机、单片机相互借鉴对方的优点,互相取长补短。
现在,PC机及部分单片机内部都有硬件乘法器;单片机内部也有了通用计算机和DSP内部才有的流水线作业(但规模小些);而DSP内部也有了一定规模的高速缓存。
吸收Intel的嵌入式系统芯片和系统软件的优点。
有的DSP内部集成了高速运行的的DSP内核及控制功能丰富的嵌入式处理器内核。
例如,内部集成有TI公司的C54xCPU内核和ARM公司的ARM7TDMIE内核的DSP,既具有高速的数据处理能力,又有各种类型的外设接口和位控能力,大大拓宽DSP在控制领域的应用。
DSP在注重高速的同时,也在发展自己的低价位控制芯片。
美国Cygnal公司的C8051F020 8位单片机,内部采用流水线结构,大部分指令的完成时间为1或2个时钟周期,峰值处理能力为25MIPS。
片上集成有8通道A/D,两路D/A,两路电压比较器,内置温度传感器、定时器、可编程数字交叉开关和64个通用I/O口、电源监测、看门狗、多种类型的串行总线(两个UART、SPI等)。
DSP工程工程是指编译dsp程序时的结构。
所有第VisualDSP++的开发都出现在工程内,工程文件(.DPJ)存储着程序的编译信息。
工程开发工程开发的步骤一个典型的工程包括模拟、评估、仿真3个阶段。
模拟:在没有真正的硬件支持的条件下也可以编译、编辑和调试DSP程序。
DSP重点知识点总结
DSP重点知识点总结DSP(数字信号处理)是一门涉及数字信号获取、处理和分析的学科。
DSP技术被广泛应用于通信、音频和视频处理、雷达和图像处理等领域。
下面是DSP的重点知识点总结。
1.信号与系统理论:信号可以理解为一种函数或者波形,可以用数学模型表示。
系统是根据输入信号产生输出信号的过程。
信号与系统理论研究信号和系统之间的关系,如卷积、频谱分析等。
2.时域和频域分析:时域分析是指对信号在时间上的特征进行分析,如幅度、相位、周期等。
频域分析则是将信号在频率上进行分析,如频谱、谐波成分等。
3.Z变换和离散时间系统:Z变换是一种离散信号处理的分析工具,它可以将离散时间信号转换成复变量的函数。
离散时间系统是一种对离散时间信号进行处理的系统,可以用系统函数来描述其输入输出关系。
4.数字滤波器设计:数字滤波器是一种对数字信号进行滤波处理的系统。
低通滤波器可以通过去除高频成分来平滑信号,高通滤波器则可以去除低频成分,带通滤波器可以只保留一些频段的信号。
5.快速傅里叶变换(FFT):FFT是一种将时域信号转换成频域信号的算法,它可以高效地计算信号的频谱。
FFT广泛应用于频谱分析、滤波器设计、信号压缩等领域。
6.语音信号处理:语音信号处理是DSP的一个重要应用领域。
它包括语音信号的获取、去噪、压缩、识别等技术。
常用的算法包括线性预测编码(LPC)、梅尔倒谱系数(MFCC)等。
7.图像处理:图像处理是DSP的另一个重要应用领域。
它包括图像的获取、增强、压缩、分割、识别等技术。
常用的算法包括离散余弦变换(DCT)、小波变换等。
8.数字信号处理芯片:数字信号处理芯片是一种集成了数字信号处理功能的专用芯片。
它可以高效地进行信号处理和计算,并广泛应用于通信设备、音频设备等领域。
9.数字信号处理应用:DSP技术在通信、音频、视频、雷达、图像等领域有广泛的应用。
例如,DSP可以用于音频信号的压缩、通信系统的调制解调、雷达信号的处理等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ELCE705 Digital Signal ProcessingSimulation Project Report 1University of MacauYibo Han MB-5-5548-4IntroductionIn this project, I have finished the simulation of discrete signals such as impulse signals, step signals, and discrete-time cosine signals in different time and frequency domains, respectively. Then I did the simulation of average system, plotted the results and made contractive analysis. MATLAB ExercisesProblem 1: Basic discrete sequences(a)The given signal is:x(n)=e jwn, n=1, 2, … 30(1-1-1) The value of w is known as 0.3. So we could use the function real and imag to draw the real part and imaginary part directly. The results will be two discrete curves.The program is shown as follows:n=(1:30);w=0.3;x=exp(j*w*n);subplot(2,1,1);stem(n,real(x));title('Real parts');xlabel('Time index n' );ylabel('Amplitude');subplot(2,1,2);stem(n,imag(x));title('Imaginary parts');xlabel('Time index n' );ylabel('Amplitude');The figure is shown as follows:Fig 1.1.1 The real and imaginary parts of x(n)In MATLAB program, we can use the function abs and angle to provide the magnitude and phase angle of x(n). These two curves are discrete as well since time index n is discrete.The program is shown as follows:n=(1:1:30);w=0.3;x=exp(j*w*n);subplot(2,1,1);stem(n,abs(x));title('Magnitude');xlabel('Time index n' );ylabel('Amplitude');subplot(2,1,2);stem(n,angle(x));title('Phase');xlabel('Time index n' );ylabel('Phase');The figure is shown as follows:Fig 1.1.2 The magnitude and Phase angle of x(n)(b)In order to create unit impulse signal δ[n-8] and unit step signal u[n-10], we could first provide unit impulse signal δ[n] and unit step signal u[n], then move them right side 8 or 10 units on xlabel. In this part, I use the function stem to draw discrete signal results.The program is shown as follows:n=(1:30);n0=1;x1=[(n-n0)-8==0];subplot(2,1,1);stem(n,x1);title('x1[n]=δ[n-8]');xlabel('Time index n' );ylabel('Amplitude');x2=[(n-n0)-10>=0];subplot(2,1,2);stem(n,x2);title('x2[n]=u[n-10]');xlabel('Time index n' );ylabel('Amplitude');The figure is shown as follows:Fig 1.1.3 Figures of unit sig nals δ[n-8] and u[n-10](c)In this part, I used the same way in part (b) to draw the unit stepsignals u[n-5] and u[n-8]. Then I defined a function x2[n]=u[n-5]-u[n-8] in the program and drawn it.The program is shown as follows:n=(0:30);n0=0;x0=[(n-n0)-5>=0];x1=[(n-n0)-8>=0];x2=x0-x1;subplot(3,1,1);stem(n,x0);title('x0[n]=u[n-5]');xlabel('Time index n' );ylabel('Amplitude');subplot(3,1,2);stem(n,x1);title('x1[n]=u[n-8]');xlabel('Time index n' );ylabel('Amplitude');subplot(3,1,3);stem(n,x2);title('x2[n]=u[n-5]-u[n-8]');xlabel('Time index n' );ylabel('Amplitude');The figure is shown as follows:Fig 1.1.4 Procedure for plotting x2[n]=u[n-5]-u[n-8]Problem 2: Discrete sinusoidal sequences(a)In this part, we have a discrete-time cosine sequences. It is shown as: x(t)=A·cos(2πƒn) (1-2-1) A is valued as 1.5, and ƒranged of 4 values as 0, 0.125, 0.25, 0.5. I used the function stem to plot these four figures and put them in one picture to make further comparison.The program is shown as follows:n=(0:1:30);A=1.5;f0=0;x0=A*cos(2*pi*f0*n);subplot(2,2,1);stem(n,x0);title('x(t) (f=0)');xlabel('Time index n' );ylabel('Amplitude'); f1=0.125;x1=A*cos(2*pi*f1*n);subplot(2,2,2);stem(n,x1);title('x(t) (f=0.125)');xlabel('Time index n' );ylabel('Amplitude'); f2=0.25;x2=A*cos(2*pi*f2*n);subplot(2,2,3);stem(n,x2);title('x(t) (f=0.25)');xlabel('Time index n' );ylabel('Amplitude'); f3=0.5;x3=A*cos(2*pi*f3*n);subplot(2,2,4);stem(n,x3);title('x(t) (f=0.5)');xlabel('Time index n' );ylabel('Amplitude'); The figure is shown as follows:Fig 1.2.1 Discrete signals of x(t) with different values of ƒThe figure 1.2.1 shows that as the value of ƒincreased, the period of function x(t)=A·cos(2πƒn) got shorter. When ƒequals to zero, the amplitude of x(t) at every point of time index n will be a fixed value of 1.5, which equals to the value of A. This is because when ƒ=0, x(t)=A·cos(2π·0·n)=A. When ƒincreases, the period of function x(t) gets shorter as the result of follow calculating:T=2π/w=2π/2πƒ=1/ƒ(1-2-2) T refers to the period of Function x(t).(b)When we changes the discrete-time sequences x(t)= A·cos(2πƒn)for n=0 ~ 40, and ƒranges from 0.2 to 1.2, the figure will be generated bythe same method in part (a). I used function stem to draw these figures. The program is shown as follows:n=(0:1:40);A=1.5;f0=0.2;x0=A*cos(2*pi*f0*n);subplot(2,1,1);stem(n,x0);title('x(t) (f=0.2)');xlabel('Time index n' );ylabel('Amplitude');f1=1.2;x1=A*cos(2*pi*f1*n);subplot(2,1,2);stem(n,x1);title('x(t) (f=1.2)');xlabel('Time index n' );ylabel('Amplitude');f2=0.25;The figure is shown as follows:Fig 1.2.2 Figures of x(t) with ƒ=0.2 and ƒ=1.2The figure 1.2.2 shows that when ƒ=0.2 and ƒ=1.2, the two figures just look the same. If we define T0 as the period of x(t) (ƒ=0.2) and T1 as the period of x(t) (ƒ=1.2), we can calculate by using formula (1-2-2) and get the result that T0=5 and T1=5/6, then we can find that T0=6·T1. As we know, periodic function has a quality that if T (T should not be valued as 0) is the period of certain function, then n·T is also the period of this certain function (n should not be valued as 0). So the conclusion is that when ƒ=0.2 and ƒ=1.2, the figures show a same periodic function x(t). Problem 3: Average system(a)In this part, we need to get an understanding of how average system works. The given function is a two-point average algorithm y[n]=1/2(x[n]+x[n-1]). I used the given program to generate the figure of results.The program is shown as follows:r=51;d=0.8*(rand(r,1)-0.5);m=0:r-1;s=2*m.*(0.8.^m);x=s+d';subplot(2,1,1)plot(m,d','r', m, s, 'g', m,x, 'b');xlabel('Time index n'); ylabel('Amplitude');legend('d[n]', 's[n]', 'x[n]');x1=[0 x]; x2=[x 0];y=(x1+x2)/2;subplot(2,1,2);plot(m, y(1:r), 'r', m, s,'b');xlabel('Time index n'); ylabel('Amplitude');legend('y[n]', 's[n]');The figure is shown as follows:Fig 1.3.1 Figures of y[n]=1/2(x[n]+x[n-1])(b)In this part, the given function is changed as y[n]=1/3(x[n]+x[n-1]+x[n-2]), and all the other function values remain unchanged as in part 1. In part 1, we used row vector to indicate x[n] and x[n-1]. We can put an 0 unit in front of the row vector x[n] and change itto row vector x[n-1]. In contrast, we also need to put an 0 unit after the row vector x[n] to make the two row vectors to add together with a same number of digit units, and this operation will not change the value of x[n]. To indicate x[n-2], we can put two 0 units in front of row vector x[n]. In order to keep these row vectors with a same number of digit units, we need to put two 0 units after row vector x[n] to indicate x[n], and put one 0 unit on both left and right side of row vector x[n] to indicate x[n-1]. In the program, I used orders [0 0 x], [0 x 0]and [x 0 0]to realize this calculation.The program is shown as follows:r=51;d=0.8*(rand(r,1)-0.5);m=0:r-1;s=2*m.*(0.8.^m);x=s+d';subplot(2,1,1)plot(m,d','r', m, s, 'g', m,x, 'b');xlabel('Time index n'); ylabel('Amplitude');legend('d[n]', 's[n]', 'x[n]');x1=[0 0 x]; x2=[0 x 0];x3=[x 0 0]y=(x1+x2+x3)/3;subplot(2,1,2);plot(m, y(1:r), 'r', m, s,'b');xlabel('Time index n'); ylabel('Amplitude');legend('y[n]', 's[n]');The figure is shown as follows:Fig 1.3.2 Figures of y[n]=1/3(x[n]+x[n-1]+x[n-2])The figure 1.3.2 shows the calculation result of the three signals’ (x[n], x[n-1] and x[n-2]) average value.ConclusionThrough finishing this project, I have been more familiar with the discrete signals. Moreover, I have understood the unit discrete signals and periodic function signals in the time and frequency domain better. At last, through simulating the average system, I could learn about the procedure and the effect of this useful system clearly, and understand the program better in operating it.。
