小学几何之蝴蝶定理大全
实用文库汇编之小学奥数之几何蝴蝶定理问题

作者: 方升座作品编号: 58001984419960354 创作日期:2020年12月20日实用文库汇编之几何之蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2)AO ∶OC = (S 1+S 2)∶(S 4+S 3)梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2CFEADB上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4)S 的对应份数为(a+b )2定理4:相似三角形性质1)HhC c B b A a ===2) S 1 ∶S 2 = a 2 ∶A 2定理5:燕尾定理S △ABE ∶ S △AEC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △ADC ∶ S △DCB = S △ADG ∶ S △DGB = AD ∶DB二、 例题例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?CBE FDA例2、有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3、如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4 如图,ABCD 是直角梯形,求阴影部分的面积和。
小学奥数之几何蝴蝶定理问题精编版

EFG的面积大6平方厘米。
ABC的面积是多少平方厘米?
A
F
G
BDEC
三、练习题
1、如图,四边形ABCD中,AC和BD订交于O点,三角形ADO的面积=5,三角形DOC的面积=4,三角形AOB的面积=15,求三角形BOC的面积是多少?
2、以下图,BD,CF将长方形ABCD分红4块,△DEF的面积是4 cm2,△CED的面积6cm2。
4
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
例12、
10厘米和12厘米,求暗影部
如图,甲、乙两图形都是正方形,它们的边长分别是
分的面积。
例13、如图,大正方形ABCD的边长为6,依以下条件求三角形BDF的面积。
例14、以下列图,已知D是BC的中点,E是CD的中点,F是AC的中点,且
D
A
O
C
B
例10、左下列图所示的ABCD的边BC长10cm,直角三角形BCE的直角边EC长8cm,已知两块暗影部分的面积和比△EFG的面积大10cm2,求CF的长。
例11、长方形ABCD的面积为36平方厘米,E、F、G分别为边AB、BC、CD的中点,H为AD边上的任一点。求图中暗影部分的面积是多少?
6
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
8、已知ABC中,ABAC12cm,ABC的面积是cm2,P是BC上随意一点,P到
AB,AC的距离是x, y,那么xy;
9、如右图所示,已知三角形ABC面积为1,延伸AB至D,使BD=AB;延伸BC至E,使CE=2BC;延伸CA至F,使AF=3AC,求三角形DEF的面积。
几何中的蝴蝶定理

几何中的蝴蝶定理1. 哎呀,今天咱们来聊一个特别有意思的几何定理,叫蝴蝶定理!说实话,光听这名字就觉得美滋滋的,像是在数学花园里看见了一只翩翩起舞的蝴蝶。
2. 这个定理说的是啥呢?想象一下,在一个圆里面,画了两条相交的弦,就像蝴蝶的两个翅膀一样交叉在一起。
这时候就神奇了!3. 这两条弦交叉的那个点,把每条弦都分成了两段。
要是把这四段线段相乘,你猜怎么着?两组乘积居然完全相等!这就跟变魔术一样神奇。
4. 打个比方啊,假如咱们画了两条弦,一条被分成3厘米和5厘米两段,另一条被分成4厘米和3.75厘米两段。
你用计算器算算:3×5=15,4×3.75=15,这不就神了吗?5. 有的同学可能要问了:这定理咋这么像蝴蝶呢?你仔细看啊,两条相交的弦就像蝴蝶的翅膀,交点就像蝴蝶的身体,这不是活脱脱一只几何蝴蝶嘛!6. 这个定理还有个特别实用的地方。
要是你在做几何题时遇到圆里面有两条相交的弦,立马就能用上这个定理,分分钟解出来!7. 说到证明过程,其实也不难。
就像是把蝴蝶的翅膀折来折去,用相似三角形就能证明。
不过今天咱们主要是理解这个定理的妙处,就不钻牛角尖啦!8. 这个定理还告诉我们一个道理:看似不相关的东西,其实暗藏玄机。
就像蝴蝶翅膀上看似随意的花纹,背后却藏着严谨的数学规律。
9. 在实际应用中,蝴蝶定理经常和其他定理一起使用。
比如说和圆幂定理搭配,简直就是几何题的双保险!解题的时候,就像蝴蝶飞舞一样轻松自如。
10. 有意思的是,这个定理还能推广到更复杂的情况。
要是在圆里面画更多的弦,它们相交的点也会形成一些有趣的规律,就像一群蝴蝶在跳舞。
11. 学习数学最重要的就是找到乐趣。
蝴蝶定理就是个很好的例子,它把枯燥的几何变成了生动的图画,让人感受到数学之美。
12. 所以啊,下次你看到蝴蝶,别光顾着欣赏它的美丽,也想想它身上藏着的数学奥秘。
这不就是数学最迷人的地方吗?它把大自然的美和严谨的逻辑完美地结合在了一起!。
第六讲蝴蝶定理

S 3S 1S 4S 2abO ACBD五年级秋季第六讲——蝴蝶模型——学而思范基程老师【知识点总结】一、来源:蝴蝶模型是几何图形中非常重要的模型之一,分为任意四边形与梯形中的蝴蝶模型,因形似蝴蝶而得名。
二、模型: 1、任意四边形中的蝴蝶定理:① S 1:S 2=S 4:S 3或者S 1×S 3=S 2×S 4②AO:OC =(S 1+S 2):(S 3+S 4) {DO:BO =(S 1+S 4):(S 2+S 3)}2、梯形中的蝴蝶定理: 如果AD:BC=:① S 1:S 3=:② S 2= S 4 ③S 1 : S 3: S 2: S 4=::④ 梯形面积所对应的份数为:3、总结:无论是在任意四边形还是梯形当中的蝴蝶模型,都为我们提供了一种解决四边形或梯形面积的新的方法。
任意四边形当中,将不规则四边形的面积与四边形内的三角形结合了起来;而梯形当中,我们只需要知道梯形上下底之间的比例,就可以得出被对角线所分成的四个三角形的面积之间的比例关系,进而知道每个三角形的面积所对应的份数。
258OACDBF E【例题精讲】(2007年“数学解题能力展示”读者评选高年级组初赛)如图,长方形ABCD 被CE 、DF 分成四块,已知其中三块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为_________平方厘米。
【解析】连结DE 、CF 。
(1)在梯形EFCD 中,根据蝴蝶模型,有三角形EOF 与三角形DOC 的面积比为2:8,所以得到DF :DC=1:2。
那么,三角形EOF 与三角形EOD 的面积比为1:1×2=1:2,所以三角形EOD 的面积为4(平方厘米),三角形COF 的面积也为4(平方厘米)。
因为四边形OEAD 的面积为5(平方厘米),所以,三角形ADE 的面积为1(平方厘米)。
(2)在长方形ABCD 中,三角形ECD 的面积是长方形ABCD 面积的一半,是8+4=12(平方厘米)那么剩下的部分(三角形ADE 与三角形BCE 的面积和也是12),又因为三角形ECF 的面积为2+4=6(平方厘米),所以三角形BCF 的面积为12-1-6=5(平方厘米)。
小学奥数之蝴蝶定理

小学奥数---蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2)AO ∶OC = (S 1+S 2)∶(S 4+S 3)梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4)S 的对应份数为(a+b )2定理4:相似三角形性质CBEFDA1)Hh C c B b A a ===2) S 1 ∶S 2 = a 2 ∶A 2定理5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3、如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4、例1 如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD分割成四个三角形。
蝴蝶定理的八种证明及三种推广

蝴蝶定理的证明定理:设M 为圆内弦PQ 的中点,过M 作弦AB 和CD 。
设AD 和BC 各相交PQ 于点E 和F ,则M 是EF 的中点。
在蝴蝶定理的证明中有各种奇妙的辅助线,同时诞生了各种美妙的思想,蝴蝶定理在这些辅助线的帮助下,翩翩起舞!证法1 如图2,作OU AD OV BC ⊥⊥,,则垂足U V ,分别为AD BC 、的中点,且由于 EUO EMO 90∠=∠=︒ FVO FMO 90∠=∠=︒得M E U O 、、、共圆;M F V O 、、、共圆。
则AUM=EOM MOF MVC ∠∠∠=∠,又MADMCB ,U V 、为AD BC 、的中点,从而MUA MVC ∆∆,AUM MVC ∠=∠ 则 EOM MOF ∠=∠,于是ME=MF 。
证法2 过D 作关于直线OM 的对称点D',如图3所示,则 FMD'EMD MD=MD'∠=∠, ○1 联结D'M 交圆O 于C',则C 与C'关于OM 对称,即PC'CQ =。
又111CFP=QB+PC =QB+CC'+CQ =BC'=BD'C'222∠∠()()故M F B D'、、、四点共圆,即MBF MD'F ∠=∠而 MBF EDM ∠=∠ ○2 由○1、○2知,DME D'MF ∆≅∆,故ME=MF 。
证法 3 如图4,设直线DA 与BC 交于点N 。
对NEF ∆及截线AMB ,NEF ∆及截线CMD 分别应用梅涅劳斯定理,有FM EA NB 1ME AN BF ⋅⋅=,FM ED NC1ME DN CF⋅⋅= 由上述两式相乘,并注意到 NA ND NC NB ⋅=⋅ 得22FM AN ND BF CF BF CF ME AE ED BN CN AE ED⋅=⋅⋅⋅=⋅ ()()()()2222PM MF MQ MF PM MF PM ME MQ+ME PM ME -==-+--化简上式后得ME=MF 。
小学奥数几何之蝴蝶定理

几何之蝴蝶定理一、 基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比 等于对应底边之比。
S 1 : S 2 = a : b定理2:等分点结论( 鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的2034153=⨯定理3:任意四边形中的比例关系( 蝴蝶定理)1) S 1∶S 2 =S 4∶S 3 或 S 1×S 3 = S 2×S 4上、下部分的面积之积等于左、右部分的面积之积2)AO ∶OC = (S 1+S 2)∶(S 4+S 3)梯形中的比例关系( 梯形蝴蝶定理)1)S 1∶S 3 =a 2∶b 2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S 1∶S 3∶S 2∶S 4 =a 2∶b 2 ∶ab ∶ab4)S 的对应份数为(a+b )2定理4:相似三角形性质CFEADBCBEFDA1)HhC c B b A a ===2) S 1 ∶S 2 = a 2 ∶A 2定理5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ECS △BGA ∶ S △BGC = S △AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题例1、如图,AD DB =,AE EF FC ==,已知阴影部分面积为5平方厘米,ABC 的面积是多少平方厘米?例2、有一个三角形ABC 的面积为1,如图,且12AD AB =,13BE BC =,14CF CA =,求三角形DEF 的面积.例3、如图,在三角形ABC 中,,D 为BC 的中点,E 为AB 上的一点,且BE=13AB,已知四边形EDCA 的面积是35,求三角形ABC 的面积.例4、例1 如图,ABCD是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD分割成四个三角形。
小学几何之蝴蝶定理大全
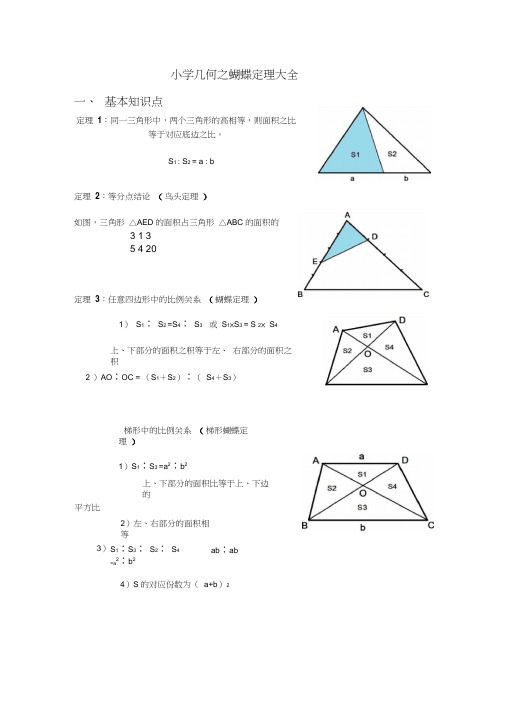
小学几何之蝴蝶定理大全一、基本知识点定理1:同一三角形中,两个三角形的高相等,则面积之比等于对应底边之比。
定理2:等分点结论(鸟头定理)如图,三角形△AED 的面积占三角形△ABC 的面积的3 1 35 4 20定理3:任意四边形中的比例关系(蝴蝶定理)1)S1∶S2 =S4∶S3 或S1×S3 = S 2× S4上、下部分的面积之积等于左、右部分的面积之积2 )AO∶OC = (S1+S2)∶(S4+S3)梯形中的比例关系(梯形蝴蝶定理)1)S1∶S3 =a2∶b2上、下部分的面积比等于上、下边的平方比2)左、右部分的面积相等3)S1∶S3∶S2∶S4=a 2∶b2ab∶abS1 : S2 = a : b4)S 的对应份数为(a+b)2定理 4:相似三角形性质2) S 1 ∶S 2 = a 2 ∶A 2定理 5:燕尾定理S △ABG ∶ S △AGC = S △BGE ∶ S △GEC = BE ∶ ECS △ BGA ∶ S △BGC = S △ AGF ∶ S △GFC = AF ∶FCS △AGC ∶ S △BCG = S △ADG ∶ S △DGB = AD ∶DB二、 例题分析例 1、如图, AD DB , AE EF FC ,已知阴影部分面积为 5 平方厘米, 多少平方厘米?1) BCHABC 的面积是例2、有一个三角形ABC 的面积为1,如图,且AD 1 AB,21ABC中,,D为BC的中点, E 为AB上的一点,且BE= AB,已知四边3形EDCA的面积是35 ,求三角形ABC的面积.例4、例 1 如图,ABCD 是直角梯形,求阴影部分的面积和。
(单位:厘米)例5、两条对角线把梯形ABCD分割成四个三角形。
已知两个三角形的面积(如图所示),求另两个三角形的面积各是多少?(单位:平方厘米)例6、如下图,图中BO=2DO,阴影部分的面积是 4 平方厘米,求梯形ABCD的面积是多少平B三角形DEF 的面积.BE 1BC ,31CF CA ,求4例3、如图,在三角形方厘米?例7、(小数报竞赛活动试题)如图,某公园的外轮廓是四边形ABCD ,被对角线AC、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为 3 平方千米,公园陆地的面积是 6.92 平方千米,求人工湖的面积是多少平方千米?例8、如图:在梯形ABCD 中,三角形AOD 的面积为9 平方厘米,25 平方厘米,求梯形ABCD 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学几何之蝴蝶定理大全
一、基本知识点
定理1:同一三角形中,两个三角形的高相等,则面积之比
等于对应底边之比。
定理2:等分点结论(鸟头定理)
如图,三角形△ AED的面积占三角形△ ABC的面积的
3 1
5 4 20
定理3:任意四边形中的比例关系(蝴蝶定理)
1 )S i:S
2 =S : S
3 或S i X S3 = S 2 x S
上、下部分的面积之积等于左、右部分的面积之积
2 ) AO: OC = (S i+ S2):( S+ S3)
梯形中的比例关系(梯形蝴蝶定理)
A ________ Z_______ 0
1 )S i : S3 =a2:b2
上、下部分的面积比等于上、下边的
平方比
B b C
2)左、右部分的面积相等
2 2
3 ) S : S B : S2: S
4 =a : b : ab : ab
)S的对应份数为(a+b)
定理4:相似三角形性质
a b _c _h
A B C H
2 2
2 ) S i : S = a : A
定理5:燕尾定理
S △ ABG : S △ AGC = S △ BGE : S △ GEC = BE : EC
S△
BGA :
S △ BGC
=
:S △
AGF :
S △
GFC :
=AF:FC
S
△
AGC :
S △ BCG
=
:S △
ADG :
S △
DGB :=AD:DB
二、例题分析
例1、如图,AD DB , AE EF FC,已知阴影部分面积为5平方厘米, 多少平方
厘米
ABC的面积是
例2、有一个三角形ABC的面积为1,如图,且AD - AB,BE
2
1
CF CA,求
4
三角形DEF的面积.
例3、如图,在三角形ABC中,,D为BC的中点,E为AB上的一点,且
1
丄AB,已知四
边
形EDCA勺面积是35,求三角形ABC的面积.
(单位:厘米)
例4、例1如图,ABCD是直角梯形,求阴影部分的面积和。
例5、两条对角线把梯形 ABCD 分割成四个三角形。
已知两个三角形的面积(如图所示) ,求
另两个三角形的面积各是多少(单位:平方厘米)
例6、如下图,图中 B0=2DO 阴影部分的面积是 4平方厘米,求梯形 ABCD 勺面积是多少平 方厘米
例7、(小数报竞赛活动试题)
如图,某公园的外轮廓是四边形
ABCD 被对角线 AC BD 分成四个部分,△ AOB 面
积为1平方千米,△ BOC 面积为2平方千米,△ COD 勺面积为3平方千米,公园陆地的面积
例8、如图:在梯形 ABCD 中,三角形 AOD 的面积为9平方厘米,
平方厘米,求梯形 ABCD 勺面积。
是平方千米,求人工湖的面积是多少平方千米
25
面积为
例9、(2003北京市第十九届小学生“迎春杯”数学竞赛)
四边形ABCD的对角线AC与BD交于点O (如图)所示。
1
如果三角形ABD的面积等于三角形BCD的面积的-,且
3
AO 2,DO 3,那么CO的长度是DO的长度的________________ 倍。
例10、左下图所示的」'ABCD的边BC长10cm,直角三角形BCE的直角边EC长8cm,已知
2
两块阴影部分的面积和比△ EFG的面积大10cm,求CF的长。
例11、长方形ABCD勺面积为36平方厘米,E、F、G分别为边AB BC CD的中点,H为AD 边上的任一点。
求图中阴影部分的面积是多少
例12、如图,甲、乙两图形都是正方形,它们的边长分别是
分的面积。
例13、如图,大正方形 ABCD 勺边长为6,依以下条件求三角形
例14、(右图是一块长方形耕地,它由四个小长方形拼合而成,其中三个小长方形的面积分 别为15、18、30公顷,问图中阴影部分的面积是多少
15 a
IS
•
b 3C
例15、如下图,已知 D 是BC 的中点,E 是CD 的中点,F 是AC 的中点,且 ADG 的面积比
EFG 的面积大6平方厘米。
ABC 的面积是多少平方厘米 ?
三、练习题
1、如图,四边形 ABCD 中, AC 和BD 相交于0点,三角形ADC 的面积=5,三角形DOC 的面积
10厘米和12厘米,求阴影部
BDF 的面积。
=4,三角形AOB勺面积=15,求三角形BOQ的面积是多少
2、如图所示,BD, CF将长方形ABCD分成4块,△ DEF的面积是4 cm 2, △ CED的面积是6cm2。
问:四边形ABEF的面积是多少平方厘米
1 1
3、如右图BE=_BC, CD—AC那么三角形AED的面积是三角形ABC面积的_____________
3 4
4.如图,AKD是1角梯脱皿5蘇,DC=3 &三角形MC的面槪呼方厘米则阴翳分的面积是—平方厘米
5、如图所示,已知 ABCD 是长方形,AE : ED = CF : FD = 1 : 2 ,三角形DEF 的面积是16
6、如右图,ABCD 是梯形,ABED 是平行四边形,己知三角面积如下图所示
(单位:平方
厘米),阴影部分的面积是多少平方厘米。
7、正方形ABFD 的面积为100平方厘米,直角三角形 ABC 的面积,比直角三角形(CDE 的面
8、 已知 ABC 中,AB AC 12cm , ABC 的面积是 cm 2,P 是BC 上任意一点,P 到
AB , AC 的距离是x, y ,那么x y
9、 如右图所示,已知三角形 ABC 面积为1,延长AB 至D,使BD=AB 延长BC 至E ,使CE=2BC 延长CA 至F ,使AF=3AC 求三角形 DEF 的面积。
平方厘米,求三角形 ABE 的面积是多少平方厘米
积大30平方厘米,求DE 的长是多少
E。
