Matlab编程 - 第七章 图与网络分析模型选讲汇编

E(G)= {e1,e2,e3,e4,e5,e6}
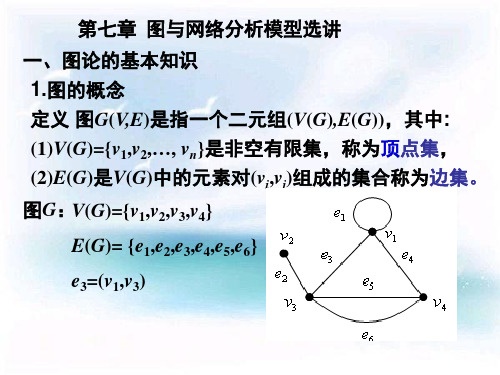
e3=(v1,v3)
若图G是的边是有方向的，称G是有向图，有向图的
边称为有向边或弧。
常用术语
e6
v2
1) 边和它的两端点称为互相关联.
e3
2)与同一条边关联的两个端点称 v4
为相邻的顶点，与同一个顶点
e4
e2 v3
点关联的两条边称为相邻的边.
v5
3)端点重合为一点的边称为环. e5
0 0 3.8 0 0 0 0 5.3 4.5
0 0 0 0 0 3.8 0 0 6.7
v1 2.5
v2 7.1
v3
0 0
0 0
00 00
0 0
0 0
0 0
0 0
7.4 0
5.6
6.1
3.6 3.8 2.4
3.4
4.9
7.2
5.3
v8
v4
v5
5.7
v6 4.5
3.8
7.4
7.4
v9
v7
3
3
有： f (u,v) f (v,w)
uV
wV
vs
7
7
v3
5
vt
v4 7
网络的总流量为从源vs 流出的总流量：
V ( f ) f (vs,w)
wV
流入汇vt 总流量：V ( f ) f (u,vt )
uV
4
vs
7
v1 8
3
7
v3
v2
3
5
vt
v4 7
定义：设网络G(V,E)为相容网络，u,v是G的相邻顶点， G的容量函数为c(u,v)，实际流量函数为f(u,v)，vs 和vt分 别为G(V,E)的源和汇，V(f)为从源vs流出的总流量，
e1 v1
4) 若一对顶点之间有两条以上的边联结，则这些边 称为重边．
5)既没有环也没有重边的图，称为简单图．
6) 若图G的每一条边e 都赋以一个实数w(e)，
称w(e)为边e的权，G连同边上的权称为赋权图 ,
记为：G(V,E,W)， W={w(e)| e∈E}
7) 图G的中顶点的个数，
5
称为图G的阶；图中与某 个顶点相关联的边的数目，
.
u jV
fij
u jV
f
ji
0V, ( V
f (
), i
f ),
i 1 1,9
i9
0F C,
@for(node(i)|i#ne#1#and#i#ne#9:
@sum(node(j):f(i,j))=@sum(node(j):f(j,i)));
@sum(node(j): f(1,j))=flow;
v1 8 v2
4
vs
7
3
7
v3
3
5
vt
v4 7
设u,v网络G(V,E)的相邻顶点，边(u,v)上的函数f(u,v)
称为边(u,v)上的实际流量；
若对网络G(V,E)的任意相邻顶点u,v 均成立：
0≤ f(u,v) ≤ c(u,v) ，
称该网络为相容网络。
v1 8 v2
若v为网络G(V,E)的中间顶点， 4
第七章 图与网络分析模型选讲 一、图论的基本知识 1.图的概念 定义 图G(V,E)是指一个二元组(V(G),E(G))，其中: (1)V(G)={v1,v2,…, vn}是非空有限集，称为顶点集， (2)E(G)是V(G)中的元素对(vi,vj)组成的集合称为边集。 图G：V(G)={v1,v2,v3,v4}
@sum(node(j): f(j,9))=flow;
v1 2.5
5.6
6.1
4.9
v4
5.7 7.4
v7
v2 7.1 v3
3.6 3.8 3.4
2.4
7.2
5.3
v8
v5
v6 4.5
3.8
7.4
v9
6.7
设fij为从vi到vj的实际流量，得一个9阶方阵：F=( fij)
0 2.5 0 5.6 6.1 0 0 0 0 0 0 7.1 0 0 3.6 0 0 0 0 0 0 0 0 0 0 3.4 0 记容量矩阵为C = 0 0 0 0 4.9 0 7.4 0 0 0 2.4 0 0 0 7.2 5.7 0 0
1 0
0 0 0 0
0 5
A
1
0 3
0
4
0
二、最大流问题
定义：设G(V,E)为有向图，若在每条边e上定义一个非 负权c，则称图G为一个网络，称c为边e的容量函数， 记为c(e)。 若在有向图G(V,E)中有两个不同的顶点vs与vt ， 若顶点vs只有出度没有入度，称vs为图G的源， 若顶点vt只有入度没有出度，称为G的汇， 若顶点v 既不是源也不是汇，称为v中ij
f ji 0V, ( f ),
i 1 i 1,9
s.t .u jV
u jV
V ( f ), i 9
0 F C,
sets: node/1..9/; arc(node,node):c,f; Endsets [OBJ]max=flow;
maxV ( f )
s.t
s.t:
v jV
f
(vi
,
v
j
)
v jV
f
(v
j
,
vi
)
V ( f ), 0, vi V ( f ),
vi vs vs ,vt ,vi
v vt
V
0 f (vi , v j ) cij , (vi , v j V )
例7.1分组交换技术在计算机网络中发挥着重要作用，信 息从源节点到目的节点不再需要一条固定的路径，而是 将其分割为几组，通过不同的路径传输到目的节点，目 的节点再重新组合还原文件。现考察如图所示的网络， 图中两节点间的数字表示两交换机间可用的带宽，此时 从节点1到节点9的最大带宽为多少？
无向图G v2
v4
v1
v3
v2
4
5
3
v4
v3 1
v1
邻接矩阵A=(aij)
0 1 1 0
A
1 1
0 1
1 0
1 0
0 1 0 0
0 5 1
A
5 1
0 3
3 0
4
4 0
有向图G v2
v4 v3
v1
v2
4
5
3
v4
v3 1
v1
邻接矩阵A=(aij)
0 1 0 0
A
0 1
0 1
0 0
V ( f ),
若：
f
(v,u)
f
(u,v
)
0,
uV
uV
V ( f ),
则称该网络称为守恒网络。
v vs v vs ,vt
v vt
守恒网络中的流 f 称为可行流。
若存在一个可行流f *，使得对所有可行流 f 都 有V(f *)≥ V(f )成立，则称f *为最大流。
最大流模型：
maxV ( f )
v4
称为该顶点的度。
v2
3 2
v3
v1
8）完全图：若无向图的任 意两个顶点之间都存在着 一条边，称此图为完全图。
2.图的矩阵表示 邻接矩阵: (以下均假设图为简单图).
图G的邻接矩阵是表示顶点之间相邻关系的矩阵： A=(aij)，
其中： aij 10或或权∞，值，若若vvii与与vvjj相不邻相邻