用EXCEL求解最短路径问题
用Excel演示Floyd算法

用Excel演示Floyd算法楼建华【摘要】Floyd算法是计算最短路径长度的基本算法之一,若用Excel实现,算法的核心部分只需填写一个公式,比通常的四重循环结构算法简单、直观.【期刊名称】《兵团教育学院学报》【年(卷),期】2010(020)006【总页数】3页(P50-52)【关键词】Excel;演示;最短路径长度;Floyd算法【作者】楼建华【作者单位】石河子大学信息科学与技术学院,新疆,石河子市,832003【正文语种】中文【中图分类】TP317.3最短路径(长度)是图论、数据结构、运筹学等课程中的典型问题,Floyd算法是解决此类问题的基本算法之一。
Floyd算法的基本原理:如果顶点 vi到顶点 vj的某条最短路径经过顶点 vk,则 vi到vk和 vk到 vj的最短路径共同组成 vi到 vj的一条最短路径。
Floyd算法的基本步骤:对邻接矩阵(aij)n×n重复做下述迭代aij=min{aik+akj|k=1,2,…,n}i,j=1,2,…,n直到迭代前后相同(或迭代次数m满足2m+1≥n)。
Floyd算法的核心部分可用 C语言表述为:实际上,Floyd算法是用已知的顶点数较少的最短路径连接出顶点数较多的最短路径,枚举了所有可能的连接点,运算量很大,时间复杂度为 O (n3log2n)。
例用 Floyd算法求图 1中各顶点间的最短路径长度。
解用 Floyd算法求解过程如图 2、图 3所示,邻接矩阵如表1 中区域B12:F16、B19:F23所示。
相比图 1,图 2新增了 3条路径:v1v2v3,v2v3v4、v3v4v5其中,路径 v1v2v3替换了图 1中较长路径 v1v3。
相比图 2,图 3新增了 3条路径:v1v2v3v4,v2v3v4v5,v1v2v3v4v5它们相应替换了图 2中相应较长路径:v1v4,v2v5,v1v5以下结合图 1给出 Floyd算法的三种演示。
巧用Excel规划求解最短路径

= m i n { d i s t [ j ] , d i s t [ i ] + ma t r i x [ i ] [ j l } ) ; 直到
U= V, 停 止。
/ ¥ D U k s t r a 算法代 码c 语 言实现 : /
据” 选项卡中出现 “ 分 析” 选项组 , 菜 单
从i 到k 的最短路径。 例如, 对于源顶点
V0 , 首先 选 择其 直 接相 邻的顶 点中长
{
蕊衅= M A x ; / / 若_ 不与v O 直
度最 短 的顶 点v i , 那 么通 过 已知 可得
接相邻, 则权值置为无穷大
| 1 4 l l
f 2 0
行 . m a t r i x [ v O I i 0 & 披j ! = v O )
{
蕊噼_ g .  ̄t r Rv O l i ] ; p ( i } = = v O ; / / a p e r 记录最
为了求出最短路径, D i j k s t r a 就提
出了以最 短 路 径 长度 递 增 , 逐 次生 成
f o r t f = l ; i < g 冲
展 帙
/ / 循环扩
抵达地
出发 地 A学校 B学校 C学校 D学校 E学校 F学校 G学校 H学校 I学 校
{
i r r 0 mi n =I N T MAX ;
_
A学校 B学校
C学校 D学校 E学校
从V 0 到V j 顶点的最短距离d i s t [ j ] = mi n { d i s t [ j 】 , d i s t [ i ] + m a t r i x [ i [ j ] } 。 根据这种 思路, 假设存在G = < V, E >, 源顶点为 V 0 , u = { V 0 } , d i s t [ i 】 { 己 录V O 到i 的最短距 离, p a t h [ i ] i  ̄ 录从V 0 到i 路径上的i 前面
运筹学最短路问题excel求解

Microsoft Excel 11.0 运算结果报告工作表 [20103848李园园.xls]Sheet1报告的建立: 2003-1-19 6:23:54目标单元格 (最小值)单元格名字初值终值$E$13V7010可变单元格单元格名字初值终值$D$2V2 路径00$D$3V5 路径01$D$4V7 路径00$D$5V5 路径00$D$6V2 路径00$D$7V6 路径00$D$8V3 路径00$D$9V8 路径00$D$10V6 路径01$D$11V8 路径01$D$12V5 路径00$D$13V7 路径00约束单元格名字单元格值公式状态型数值$G$2V1 网络流1$G$2>=$H$2到达限制值0 $G$3V2 网络流0$G$3=$H$3未到限制值0 $G$4V3 网络流0$G$4=$H$4未到限制值0 $G$5V4 网络流0$G$5=$H$5未到限制值0 $G$6V5 网络流0$G$6=$H$6未到限制值0 $G$7V6 网络流0$G$7=$H$7未到限制值0 $G$8V7 网络流0$G$8=$H$8未到限制值0 $D$2V2 路径0$D$2=二进制到达限制值0 $D$3V5 路径1$D$3=二进制到达限制值0 $D$4V7 路径0$D$4=二进制到达限制值0 $D$5V5 路径0$D$5=二进制到达限制值0 $D$6V2 路径0$D$6=二进制到达限制值0 $D$7V6 路径0$D$7=二进制到达限制值0 $D$8V3 路径0$D$8=二进制到达限制值0 $D$9V8 路径0$D$9=二进制到达限制值0 $D$10V6 路径1$D$10=二进制到达限制值0 $D$11V8 路径1$D$11=二进制到达限制值0 $D$12V5 路径0$D$12=二进制到达限制值0 $D$13V7 路径0$D$13=二进制到达限制值0。
excel最短路问题求解模型
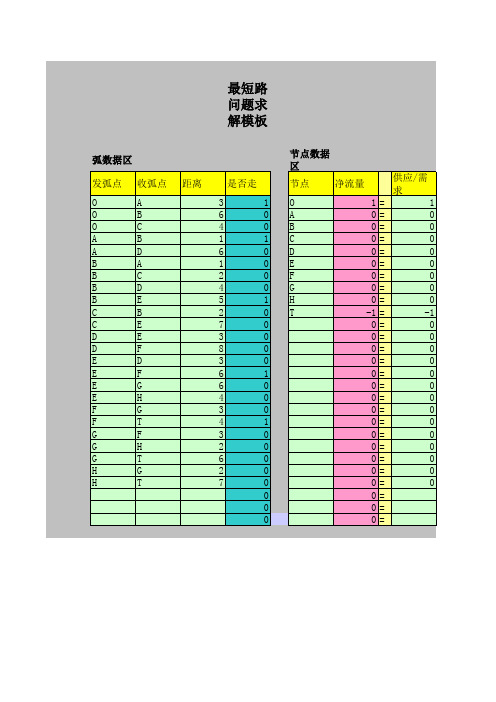
最短路问题求解模板需要对发弧点、收 弧点、距离、节点(节点名称字符随便,但 必须与发弧点和收弧点一致)和供应/需求 栏数据的录入,这里要求供应/需求栏数据 发点为‘1’,收点为“-1”,其余为‘0’。 录完数据,点“工具”→“规划求 解”→“求解”后,在“是否走”栏显示最 优解、“净流量”栏显示相应的约束条件实 际值,最优值显示在N6单元格。 注:使用本模板时,模板中的浅灰色区 域是录入数据的区域;黄色区域是标示区, 尽量不要修改;深浅灰色区域是系统显示最 优解数据的区域,也尽量不要修改;红色区 域中都录有公式,禁止往这些单元格中录入 数据。
最短路问题求解模板
弧数据区 发弧点 O O O A A B B B B C C D D E E E E F F G G G H H 收弧点 A B C B D A C D E B E E F D F G H G T F H T G T 距离 3 6 4 1 6 1 2 4 5 2 7 3 8 3 6 6 4 3 4 3 2 6 2 7 是否走 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 节点数据区 节点 净流量 O 1 A 0 B 0 C 0 D 0 E 0 F 0 G 0 H 0 T -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 = = = = = = = = = = = = = = = = = = = = = = = = = = = 供应/需求 1 0 0 0 0 0 0 0 0 -1 0 0 0 0 0 0 0 0 0 0 0 0 0 0
excel在一列数据中找到最大,最小值要怎么弄

excel在一列数据中找到最大,最小值要怎么弄excel在一列数据中找到最大,最小值要怎么弄假设数据在A列在B1中显示最大值,那么输入公式=MAX(A:A)在B2中显示最小值,那么输入公式=MIN(A:A)怎么在excel的一组数据中找到最大值和最小值如果需要在A列找出最大值和最小值,那么分别输入=MAX(A:A)=MIN(A:A)EXCEL中怎么求一列数据中最大值和最小值的差:jingyan.baidu./article/63acb44afbb82561f17e99.excel如何计算:A列是数据,B列计算=(A列数据-A列数据中最小值)/(A列数据最大值-A列数据中最小值)=(A1-min(A:A))/(max(A:A)-min(A:A))excel vlookup 在多列数据中找到A列相同值用以下公式也可得到你要的效果:=IF(COUNTIF(D:F,A1),A1,"")回车确认后下拉填充。
如何查找一列数据中的最大值和最小值在B1中输入或复制粘贴下列公式=MAX(A:A)在B2中输入或复制粘贴下列公式=MIN(A:A)分别得到A列的最大值和最小值EXCEL中怎么求一列数据中最大值和最小值的差?(用公式计算)EXCEL中怎么求一列数据中最大值和最小值的差?(用公式计算)假设对象是A1:A10=MAX(A1:A10)-MIN(A1:A10)Excel VBA 找一列数据中的最大值和最小值用VBA代码应该怎么写阿Sub test()a = WorksheetFunction.Max("a:a")b = WorksheetFunction.Min("a:a")End Suba是a列最大值b是b列最小值excel怎么求一列中的数据最大值和最小值使用MAX函数求若干数据最大值,使用MIN函数求若干数据最小值。
如何在EXCEL中找到非零最小值求A1:D20区域内非零的最小值,用下面的数组公式;=MIN(IF(A1:D20>0,A1:D20))公式以Ctrl+Shift+Enter结束。
excel 最短路径

excel 最短路径
在Excel中,可以使用Dijkstra算法来求解最短路径问题。
具体步骤如下:
1. 确定起始节点和目标节点,以及它们之间的距离。
2. 创建一个Excel表格,用于存储节点和它们的距离。
在表格中,将起始节点作为第一个节点,将目标节点作为最后一个节点,中间的节点按照顺序排列。
3. 在表格中输入每个节点之间的距离。
如果两个节点之间没有直接的路径,可以输入一个较大的数值。
4. 使用Dijkstra算法来计算最短路径。
具体实现可以参考相关的算法教程或文档。
需要注意的是,Excel本身并没有内置Dijkstra算法的实现,因此需要使用VBA等编程语言或第三方插件来实现该算法。
同时,由于Excel的单元格数量有限,当节点数量过多时,可能会导致计算结果不准确或出现误差。
因此,对于大规模的路径问题,建议使用专业的图论软件或算法库来解决。
Excel表格法求解路径规划问题

实验四: Excel 表格法求解路径规划问题
根据题意及决策变量与目标函数得出本问题的 线性规划模型。
minY=6×X11+3×X12+2×X13+5×X14+7×X21+5×X2 2+8×X23+4×X24+3×X31+2×X32 +9×X33+7×X34
s.t. X11+ X12+ X13+ X14=5(满足A1矿的产量) X21+ X22+ X23+ X24=2(满足A2矿的产量) X31+ X32+ X33+ X34=3(满足A3矿的产量) X11+ X21+ X31 =2(满足B1厂的需求量) X12+ X22 +X32 =3(满足B2矿的需求量) X13+ X23 +X33 =1(满足B3矿的需求量) X14+ X24 +X34 =4(满足B4矿的需求量) Xij >=0(i=1,2,3,j=1,2,3,4)(决策变量非负约束)
执行【工具】→【加载宏】 菜单命令,这时将出现 “加载宏”的对话框,在 “可用加载宏”窗口的 “规划求解”选项上打 “√”。当需要进行规划求 解操作时,直接进行该命 令,就可进入“规划求解 参数”对话框。
实验四: Excel 表格法求解路径规划问题
根据题意,设置本问题的决策变量和目标 函数。 设:Xij为每天从Ai矿运往Bj厂的矿石数量 (百吨),Y为总运费 Y=6×X11+3×X12+2×X13+5×X14+7 ×X21+5×X22+8×X23+4×X24+3×X3 1+2×X32 +9×X33+7×X34 ,则本问题 表格法求解路径规划问题
MBA数据、模型与决策计算题

《数据、模型与决策》1.最短路径问题一辆运桔车从洛杉矶到圣路易斯运送桔子,如图所示。
从洛杉矶出发的运输图图中各分支上的数值表明其连接的两个节点之间的运输时间。
问题:用Excel软件求解从洛杉矶到圣路易斯的最短路径。
要求:(1)要给出线性规划的代数模型,(2)给出线性规划的Excel模型截图,(3)要给出目标函数、某个中间节点和起始节点计算公式的Excel截图,(4)要给出“规划求解”的各项设置条件的截图,(5)最后要给出计算结果的界面截图。
2.AHP法计算题(25分)南方发展公司为其商场选择了三个备选地址:亚特兰大(A)、伯明翰(B)、夏洛特(C)。
具体选择哪个地址的评价涉及如下四个准则:(1)消费者的市场状况(规模和年龄结构),(2)收入水平,(3)基础设施(公共设施和道路状况),(4)交通运输(邻近州际高速以利于供货和消费者)。
在这四个准则下3个方案的比较矩阵和四个准则的比较矩阵如下。
问题:运用AHP方法在Excel上对上述3个方案建模并进行等级排序。
要求:(1)四个准则下3个方案的重要度向量至少给出一个求解过程的Excel 截图,(2)要给出四个准则下3个方案的重要度矩阵的Excel截图,(3)要给出四个准则的重要度向量求解的Excel截图,(4)要给出3个方案的综合重要度向量求解的Excel截图并指出哪个方案为最佳方案,(5)最后要给出一致性检验Excel求解过程的截图。
3.Excel仿真题(30分)“计算机世界”是销售计算机及相关设备的公司,该公司经理拟确定每周该订购的笔记本电脑数量是1台还是2台更好。
决策主要涉及的随机变量是每周销售量(x),根据以往的销售情况x在0~4台之间变化,另外每销售1台笔记本电脑的收益为4300美元,每缺货一台将损失500$,且当供给大于需求时的库存成本为每台50$。
笔记本电脑过去100周的需求销售情况如下表所示。
计算机世界公司笔记本销售情况表问题:假定过去销售情况是稳定的,则根据以上所给的参数,设计Excel仿真模型,并通过仿真100周给出最优的决策方案。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
用EXCEL 求解最短路径问题
例1:求解V1到V8的最短距离。
解:选择“工具”菜单下“加载宏”命令,选择“规划求解”确定即
可,再建立EXCEL S ,如下表所示
3 J J J 亘J L 静此箍V 已* 几1二…丨逸£ •狙il 皿IQQ *
' “亍
]采洁 12 B / U =: 7为文件(T 瞬⑥狈图②插入(I )格式辺工具⑴数据烟雨口⑪帮肋(H ) F12
O licrcfsofl Excel - Book 1 r
血=SUMPRODUCT (C2 :C11
D2 :D14) 起点
4
15 3 3 4
4 5 s 6 6 7 v ^终点 V2 V3 V4 V5 V4 V5 V6 V7 V6 V7 V7 V8 V8
枚数 4 6 E 4 4 7 9 7 5 6 5 4 1
0-1 0 0 0 0 0 节点
71=712+713
V2=V24+V25-V12 V3^V34+V35-V13
V4=V46+V47-V24-V34 V5=V56+V57-V25-V35 V6=V6?+V6S-V46-VS& V7=V78-V47-V57-V67 V8=-V6S-V7S
进出和 0 0 0 0 0 0 0 0 1
0 0
石
0 0 0 -1
16 17 18 19 20 21 22 231
1
< 卜 n \ She^tl /Sheetg/Sheeig/
目标函数
Q
ff
x
心二dui 」丨」2彗ii 廉-m •/ ”…丨疲E •蓟铝 [采萍 12 B Z U 言 乏国1啰書•至既] 活涓土・小氐・*
I 里]文诗(T 碎⑥ 观国凹 插入① 牯式⑪ 工具⑴ 数据型 闽口⑥ 帮助⑩ 隱入窩蚩带舫的可題
C ■icEOSofl Exce] 一 Book 1r £13
F12 "~A A = SUMPRODUCT (C2:C11 D2:D14) C ' D 1 2
3 4 1± 1121
2 3 3 4 4 5 5 6 6 v 77
V2 4 1 V1=V12+V13 1 1
V3 6 0 V2=V24+V25-V12 0 0 V4 E 0 V3^V34+V35-V13 0 0
V5 4 L V4=V46+V47-V24-V34 0 0
网 4 0 V5=V5&+V57-V25-V3E 0 0
V5 7
0 V6=V67+V68-V46-V56 0 0 V6 9 0 V7=V78-V47-V57-V67 0 0 V7 7
0 V3=-V6S-V7S
-1
-1
V& 5 0 V7 6 L
V7 5 0 目标函数
1 15
V8 4 0 V8
1
1
起点 终点 枚数 0-1 | 节点 ________ 进出和 B E F H G 15 16_ 17 18 1? 20 21
IF
23 n
丄」
I I 就结
M \ Sheet 1/ 51)e et2/3 heel 3 /
抚划菠解结果
IX
霜严找劉-解•可满足所希约束超忧蹄⑥
■. •恢量馬谅材
(Q )
运算结果报告 碱感性报告 极限值报告
职消
(保存方案区)二]|帮肋如]
结论:最短距离为15 路线为V1— V2— V5^V7— V8 附 EXCEL
起点终占
—乙八、、权数0-1 节点进出和
V1 V2 4 1 V仁V12+V13 1 1 V1 V3 6 0 V2=V24+V25- 0 0 V2 V4 5 0 V3=V34+V35- 0 0 V2 V5 4 1 V4=V46+V47- 0 0 V3 V4 4 0 V5=V56+V57- 0 0 V3 V5 7 0 V6=V67+V68- 0 0 V4 V6 9 0 V7=V78-V47- 0 0 V4 V7 7 0 V8=-V68-V78 -1 -1 V5 V6 5 0
V5 V7 6 1
V6 V7 5 0 目标函数15
V6 V8 4 0
V7 V8 1 1
例2:
V3 4 V6^'
VI S V7的最短路径。
ffi excel求解,详细过程!!
” 12
” B I II 」諄喜吞虽罟% *菸昶匡事 ”
* A
E3 licEosofl Excel 一 BookE
[目]丈件廈)瞬⑥狈图②插入①格式辺工具⑴数据畑越口⑩帮助⑩ 儀入帝衣粧助的可題
ff X
詁」,弓丄尊牡比亠屯•丿丨勺•-■…丨出E •狙和餾 <)血慕 ・卷H
:衲
Flj
B C D E F
G
H
z
终点 权数 0-1 节点 逬出和
V2 5 0 71=¥12+V13 0 1 V3 2 0 V2^V24+V25-V12 0 0 网 2 0 V3^V34+V36-V13 0 0 V5 7 0 V4=V45+V46-V24-V34 0 0 网 7 0 V5=V56+V57-V25-V4F 0 0 V6 4 0 V6=¥67-V36-V46-V5& 0 0 V5 & 0 V7=-V57-V67 0
-1
V6 2 0 V6 1 0 V7 3 0
V7
6 0 目标函数
A =SUNPRODUCT (C2:C12, D2:D12) 15 16 17 12 1? A
设置目标单元格⑥:豳站国] 零于 二煌大值礎)④星小值(M ) o 值为迪[□ [求解 13
14 2
2 3
3 4 4 5 S 6 V V V 垛划求解参数
20 91
i < b n \ Sheet l /siieetZ/Shget :
t
推测⑥|
约束辿):
JB$2:SD$12 <= 1 $D$2:mi2 二整数 SB$2:mi2 >= 0 $F$2:JF$8 = $G$Z :$G$S
添加鱼)] [更改©] 删除迦]
可变单元格©):
[「关闭)
选顶© [
逢部重设血] 「帮助®「I
F12 ” A =SUNPRODUCT (02:012. D2 :D12)
附 EXCEL
起点
终占 —乙八、、
权数
0-1 节点 进出和
V1 V2 5 0 V 仁 V12+V13 1 1 V1 V3 2 1 V2=V24+V25- 0 0 V2 V4 2 0 V3=V34+V36- 0 0 V2 V5 7 0 V4=V45+V46- 0 0 V3 V4 7 0 V5=V56+V57- 0 0 V3 V6 4 1 V6=V67-V36- 0 0 V4 V5 6 0 V7=-V57-V67 -1
-1
V4 V6 2 0
V5 V6 1 0
V5 V7 3 0
V6
V7 6
1
目标函数
12
J J J
-1 -
/
-蔬E •狙和.齟时皿 ・册I
衲
” 12
I 11」諄
-
F G
H
1
也 Bier os oft E KCC I - Boofcl r
xls 匚]
叵 7旦]
丈件廈)瞬⑥狈图②插入(I )格式辺工具⑴数据畑閒口⑩帮助⑩廉入需衣帮助的冃題 - ff X
2
3 4
2 3 3
4 4
5 S
6 终点 权数 0-1
节点
V2 5
0 71=¥12+V13
V3 2 1 V2^V24+V25-V12 V4 2 0 V3^V34+V36-V13 V5 7 0 西二网5-诃住4-V 刊
V4 7
0 V5=V56+V57-V25-V4E V6 4 1 V6=¥67-V36-V46-V5& V5 & 0 V7=-V57-V67
V6 2 0 V6 1
0 V7 3
V7
6 L
目标函数
逬出和
1 1 0 0 0 0 0 0 0 0 0 0 -1
-1
13 14 15 16 17 1S 19 20 21 | < n n \ Sheetl /siieetZ/Shgeia/ 规划求解找到一解,可满足所有的约束泾最忧
伏况.
报告® '■锲荐规划尹解结臬iv )f
运算菇果报告 诫
感性报吉 _■ i s/is i J />^u>^dj®a^rirr H Q iZr^ y ;*/ i hwirnrairnis inmii r»i i -i ・u ・・r ・・im ・・i
■-・・《■■■・
HE ・w
O
恢复対原值@)
极限值报告
規划求解结果
确定][取消)[保存方案@)一
| I 帮助M
结论:最短距离为 12 路线为 V1— V3— VIV7
Welcome 欢迎您的下载, 资料仅供参考!。
