北师大版八年级数学下册第三章分式测试题及答案
最新北师大版八年级下册分式及分式方程各个章节测试试题以及答案

最新八年级下册分式及分式方程各个章节测试试题(1)分式无意义:B=0。
(2)分式有意义:B ≠0时。
(3)分式的值为0:A=0,B ≠01、在x1、5ab 2、3y x y 7.0+﹣、mnm +、a5cb +-、π2x 3中,是分式的有 个。
2、如果分式1x 3-有意义,那么x 的取值范围是 。
3、下列分式中,不论a 取何值总有意义的是 。
A 、1a 1a 22+-B 、1a 1a 2+-C 、1a 1a 22-+D 、1a 1a 2-+4、若分式1x 1x 2+-的值是0,则x 的值是 。
5、某单位全体员工在植树节义务植树240棵.原计划每小时植树a 棵.实际每小时植树的棵数是原计划的1.2倍,那么实际比原计划提前了______小时完成任务(用含a 的代数式表示).6、若a 、b 都是实数,且04b 16b 2a 22=++-)-(,写3a -b= 。
分式的基本性质:分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值保持不变.1、化简下列分式。
yx 20x y52=abb ab a 22++=22m m 39m --=22112m m m -+-=2、把分式x yy x +中的x 、y 都扩大2倍,那么分式的值 。
A 、扩大2倍B 、不变C 、缩小一半D 、扩大4倍 3、分式x22-可变形为 。
A 、x 22+ B 、x 22+﹣ C 、2x 2- D 、2x 2-﹣4、已知3y1x1=-,则代数式yx y 2x y 2x y 14x 2----= 。
5、对一任意非零实数a 、b ,定义运算“△”如下:a △b=abb a -,计算2△1+3△2+4△3+.......+2024△2023的值。
6、观察下面一列有规律的式子:1x 1x 1x 2+=--1x x 1x 1x 23++=--1x x x 1x 1x 234+++=--1x x x 1x 1x 2345++++=x --.......(1)计算1x 1x n --的结果是(2)根据规律计算:63623222.......2221++++++分式的乘除: 1、计算.(1)2224ab a a b+-÷a 4b a b+-;(2)22(14)41292341y y y y y -++•+-;(3)244x (16x y)()y -÷- (4)222x 6x 92x 69x x 3x-+-÷-+(5)xy x yy x x y x 2--÷+(6))-(-2222y x 4y2x y x y 4x 4÷++2、已知09b 4a =+--,计算22222ba aba b ab a --•+的值。
北师大版八年级数学下册第三章学情评估 附答案 (3)
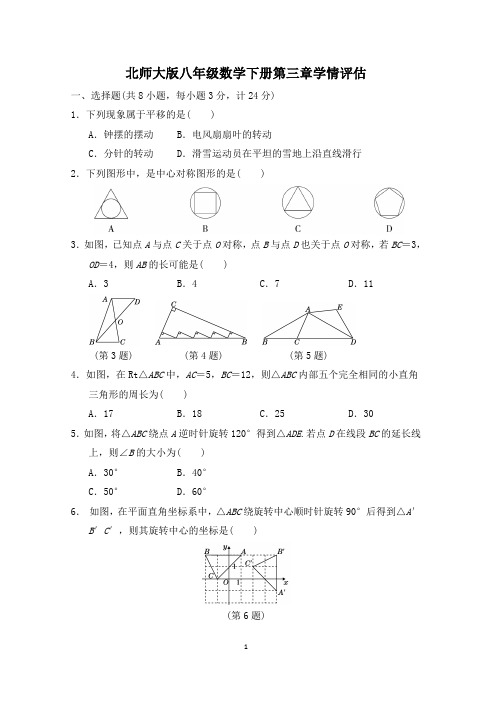
北师大版八年级数学下册第三章学情评估一、选择题(共8小题,每小题3分,计24分)1.下列现象属于平移的是( )A.钟摆的摆动B.电风扇扇叶的转动C.分针的转动D.滑雪运动员在平坦的雪地上沿直线滑行2.下列图形中,是中心对称图形的是( )3.如图,已知点A与点C关于点O对称,点B与点D也关于点O对称,若BC=3,OD=4,则AB的长可能是( )A.3 B.4 C.7 D.11(第3题) (第4题) (第5题)4.如图,在Rt△ABC中,AC=5,BC=12,则△ABC内部五个完全相同的小直角三角形的周长为( )A.17 B.18 C.25 D.305.如图,将△ABC绕点A逆时针旋转120°得到△ADE.若点D在线段BC的延长线上,则∠B的大小为( )A.30°B.40°C.50°D.60°6.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )(第6题)A.(1.5,1.5) B.(1,0)C.(1,-1) D.(1.5,-0.5)7.如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E恰好落在AB 的延长线上,连接AD.下列结论一定正确的是( )A.∠ABD=∠E B.∠CBE=∠CC.AD∥BC D.AD=BC(第7题) (第8题)8.如图,已知点A1的坐标为(1,1),把点A1先向上平移1个单位长度,再向右平移2个单位长度得到点A2;把点A2先向上平移2个单位长度,再向右平移4个单位长度得到点A3;把点A3先向上平移4个单位长度,再向右平移8个单位长度得到点A4,…,则点A2 023的横坐标为( )A.22 022-1 B.22 023-1C.22 024-1 D.22 025-1二、填空题(共5小题,每小题3分,计15分)9.在平面直角坐标系中,点(-2,3)关于原点对称的点的坐标是 ________.10.△DEF是由△ABC平移得到的,点A(-1,-4)的对应点为点D(1,-1),点B(1,1)的对应点为点E,点C(-1,4)的对应点为点F,则点E,F的坐标分别为________.11.数学课上,老师要求同学们利用所学知识在正方形纸上设计一个图案,小明的设计方案为:(1)将正方形均分为八等份后画出一个四边形(如图①);(2)画出四边形关于正方形对角线的交点成________的四边形(如图②);(3)将图②中的图形绕正方形对角线的交点至少顺时针旋转________得到完整图形(如图③).(第11题) (第12题)12.如图,将等边三角形ABC沿BC方向平移得到△A1B1C1.若BC=3,S△PB1C=3,则BB1=________.13.如图,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB绕点A顺时针旋转得到△A1O1B1,将△A1O1B1绕点B1顺时针旋转得到△A2O2B2,将△A2O2B2绕点O2顺时针旋转得到△A3O3B3,…,则点O9的坐标为________.(第13题)三、解答题(共13小题,计81分)14.(5分)如图,在▱ABCD中,BC=a,AF=h,从平移角度说明S▱ABCD=ah.(第14题)15.(5分)如图,在Rt△ABC中,∠BAC=90°,将Rt△ABC绕点A旋转一定的角度得到Rt△ADE,且点E恰好落在边BC上.(1)求证:EA平分∠CED;(2)连接BD,求证:∠DBC=90°.(第15题)16.(5分)如图,已知线段AB和点A′.尺规作图:作出由线段AB平移得到的线段A′B′,其中点A的对应点为A′.(不写作法,保留作图痕迹)(第16题)17.(5分)如图②是两个4×4的正方形网格,每个小正方形的边长都为1,请用图①作为基本图案,通过平移、轴对称、旋转变换,设计两个不同的精美图案,使它们满足:(1)既是轴对称图形,又是中心对称图形;(2)所作图案用阴影标识,且阴影部分的面积为4.(第17题)18.(5分)如图,将△ABC沿BC方向平移得到△DEF.(1)若∠B=74°,∠F=26°,求∠A的度数;(2)若BC=3 cm,EC=2 cm,求△ABC平移的距离.(第18题)19.(5分)如图是一块边长为8米的正方形土地,其中有三条宽度都是1米的小路,其余部分种植各种花草.(1)请利用平移的知识求种植花草的面积;(2)若种植花草共花费4 620元,则平均每平方米土地种植花草的费用是多少元?(第19题)20.(5分)如图,将△ABC沿BC方向平移得到△A′B′C′,其中点B′和点C重合,连接AC′交A′C于点D,△ABC的面积为36.(1)求证:A′D=CD;(2)求△C′DC的面积.(第20题)21.(6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(5,0),B( -3,2),C(-1,-3).(1)请在图中作出△ABC关于原点对称的△A′B′C′,并写出△A′B′C′各顶点的坐标;(2)求△A′B′C′的面积.(第21题)22.(7分)如图,D是△ABC的边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.(1)图中哪两个三角形成中心对称?(2)若△ADC的面积为4,则△ABE的面积为________;(3)若AB=5,AC=3,求AD的取值范围.(第22题)23.(7分)如图,在△ABC中,点E在BC边上,AE=AB,将线段AC绕点A旋转到AF的位置,使得∠CAF=∠BAE,连接EF,与AC交于点G.(第23题)(1)求证:EF=BC;(2)若∠B=65°,∠C=28°,求∠FGC的度数.24.(8分)如图,将△ABC绕点B逆时针旋转60°得到△DBE,DE的延长线与AC 相交于点F,连接DA、BF,BF=AF.(1)求证:DA∥BC;(2)判断DF与AF的数量关系,并证明.(第24题)25.(8分)如图,在△ABC中,∠BAC=120°,以BC为边作等边三角形BCD,把△ABD绕点D按顺时针方向旋转60°到△ECD的位置.(1)求∠BAD的度数;(2)若AB=2,AC=3,求AD的长.(第25题)26.(10分)(1)如图①,在△ABC中,∠C=90°,AC=BC,D是边BC上一点(点D 不与点B、C重合),连接AD,将AD绕着点D逆时针旋转90°得到ED,连接BE,则∠ABE为______;(2)如图②,在△ABC中,∠C=α(0°<α<90°),AC=BC,D是边BC上一点(点D不与点B、C重合),连接AD,将AD绕着点D逆时针旋转α得到ED,连接BE,求证:∠ABE=α;(3)若(2)中的α=60°,AC=BC=3,其他条件不变,连接AE,当∠BAE=30°时,求△ABE的面积.(第26题)答案一、1.D 2.B 3.C 4.D 5.A 6.C 7.C 8.B二、9.(2,-3) 10.(3,4),(1,7)11.中心对称; 90°12.113.(36,0)三、14.解:如图,将△ABF沿BC方向平移AD的长度可以得到△DCE,∴S△ABF=S△DCE,∴易得S▱ABCD=S矩形ADEF=ah.(第14题)15.证明:(1)由旋转性质可知AE=AC,∠AED=∠C,∴∠AEC=∠C,∴∠AED=∠AEC.∴EA平分∠CED.(2)由旋转性质可知AD=AB,∠DAB=∠EAC.∴易得∠DAB=180°-2∠ABD.又∵∠EAC=180°-2∠C,∴∠ABD=∠C.∵∠ABC+∠C=90°,∴∠ABC+∠ABD=90°,即∠DBC=90°.16.解:如图,线段A′B′即为所求.(画法不唯一)(第16题)17.解:如图所示.(答案不唯一)(第17题)18.解:(1)由平移可知∠ACB=∠F=26°,∴∠A=180°-∠B-∠ACB=180°-74°-26°=80°.(2)∵BC=3 cm,EC=2 cm,∴BE=BC-EC=3-2=1(cm),即△ABC平移的距离为1 cm.19.解:(1)由平移的知识可知,种植花草的土地可看成是一块长为8-1=7(米),宽为8-2=6(米)的矩形土地.6×7=42 (平方米).答:种植花草的面积为42平方米.(2)4 620÷42=110(元).答:平均每平方米土地种植花草的费用是110元.20.(1)证明:∵△ABC沿BC方向平移得到△A′B′C′,∴AC∥A′C′,AC=A′C′,∴∠ACD=∠C′A′D.又∵∠ADC=∠C′DA′,∴△ACD≌△C′A′D,∴A′D=CD.(2)解:∵△ABC沿BC方向平移得到△A′B′C′,∴△ABC≌△A′B′C′,∴S△ABC=S△A′B′C′=36.∵A′D=CD,∴易得S△C′DC=12S△A′B′C′=18.21.解:(1)画图略.点A′的坐标为(-5,0);点B′的坐标为(3,-2);点C′的坐标为(1,3).(2)S△A′B′C′=8×5-12×2×5-12×6×3-12×8×2=18.22.解:(1)图中△ADC 和△EDB 成中心对称.(2)8(第22题)(3)连接EC ,如图. 在△ABD 和△ECD 中,⎩⎨⎧AD =ED ,∠ADB =∠EDC ,BD =CD ,∴△ABD ≌△ECD (SAS), ∴AB =EC =5.∵EC -AC <AE <AC +EC , ∴2<AE <8, ∴1<AD <4.23.(1)证明:∵∠CAF =∠BAE ,∴∠BAC =∠EAF .∵将线段AC 绕A 点旋转到AF 的位置, ∴AC =AF .在△ABC 与△AEF 中,⎩⎨⎧AB =AE ,∠BAC =∠EAF ,AC =AF ,∴△ABC ≌△AEF (SAS), ∴EF =BC .(2)解:∵AB =AE ,∠B =65°, ∴易得∠BAE =180°-65°×2=50°, ∴∠FAG =∠BAE =50°. ∵△ABC ≌△AEF ,∴∠F =∠C =28°,∴∠FGC =∠FAG +∠F =50°+28°=78°.24.(1)证明:∵△ABC 绕点B 逆时针旋转60°得到△DBE ,∴AB =BD ,∠ABD =∠ABC =60°,∴△ABD 是等边三角形, ∴∠DAB =60°=∠ABC . ∴AD ∥BC . (2)解:DF =2AF .证明:∵△ABD 是等边三角形, ∴AD =BD ,∠ADB =60°. 在△ADF 和△BDF 中,⎩⎨⎧AD =BD ,AF =BF ,DF =DF ,∴△ADF ≌△BDF (SSS),∴∠ADF =∠BDF =12∠ADB =30°,∴∠DEB =90°. ∴∠C =90°. ∵AD ∥BC ,∴∠DAF =180°-∠C =90°. 又∵∠ADF =30°, ∴DF =2AF .25.解:(1)∵△BCD 是等边三角形,∴∠BDC =60°. 又∵∠BAC =120°,∴∠ABD +∠ACD =360°-120°-60°=180°. 由旋转可知∠DCE =∠ABD , ∴∠DCE +∠ACD =180°, ∴A 、C 、E 三点共线.由旋转可知∠ADE =60°,AD =DE , ∴△ADE 是等边三角形,∴∠EAD =60°, ∴∠BAD =120°-60°=60°. (2)由旋转可知AB =CE =2, 又∵AC =3, ∴AE =AC +CE =5,∵△ADE 是等边三角形,∴AD =AE =5. 26.(1)90°(2)证明:(第26题)如图,过点D 作DF ∥AC 交AB 于点F , 则∠DFB =∠CAB ,∠C =∠FDB =α. ∵CA =CB , ∴∠CAB =∠CBA , ∴∠DFB =∠CBA , ∴DF =DB .由旋转可知,DA =DE ,∠ADE =α=∠FDB , ∴∠ADF =∠EDB , 在△ADF 和△EDB 中,⎩⎨⎧DA =DE ,∠ADF =∠EDB ,DF =DB ,∴△ADF ≌△EDB (SAS),∴∠DBE =∠AFD ,∴∠DBF +∠ABE =∠FBD +∠FDB . ∴∠ABE =∠FDB =α.(3)解:∵∠C =α=60°,CA =CB ,∴△ABC是等边三角形,∴BA=AC=3.由(2)易知∠ABE=60°.又∵∠BAE=30°,∴∠AEB=90°,∴BE=12AB=32,∴AE=332.∴S△ABE=12AE·BE=12×332×32=938.北师大版八年级数学下册期末学情评估一、选择题(共8小题,每小题3分,计24分)1.下列美丽的图案中,既是轴对称图形又是中心对称图形的个数是( )(第1题)A.1个B.2个C.3个D.4个2.若a>b,则下列不等式一定成立的是( )A.ac2>bc2B.a+c>b+cC.ab>b2 D.a 2 < b 23.下列等式中,从左到右的变形是因式分解的是( )A.x2-4x+1=x(x-4)+1B.(y-1)(y-2)=y2-3y+2C.18x3y2=3x3y2·6D.xy2+2xy=xy(y+2)4.如图,若一次函数y1=mx+n与y2=-x+a的交点坐标为(3,2a-8),则mx +n<-x+a的解集为( )A.x<3 B.x<1C.x>3 D.0<x<3(第4题) (第5题)5.如图,△ABC 是等边三角形,D 是AC 的中点,DE ⊥BC ,CE =3,则△ABC 的周长为( ) A .12 B .24 C .36 D .486.若分式方程x -1x +4=mx +4有增根,则m 为( ) A .1B .0C .-4D .-57.如图,▱ABCD 的周长为16,AC ,BD 相交于点O ,OE ⊥AC 交AD 于点E ,则△DCE的周长为( ) A .4B .6C .8D .10(第7题) (第8题) (第13题)8.如图,在Rt △ABC 中,AC =BC ,∠C =90°,D 为AB 的中点,∠GDH =90°,∠GDH 绕点D 旋转,DG ,DH 分别与边AC ,BC 交于点E ,F .下列结论:①AE +BF =AC ;②AE 2+BF 2=EF 2;③S 四边形CEDF =12S △ABC ;④△DEF 始终为等腰直角三角形.其中正确的是( ) A .①②③④B .①②③C .①④D .②③二、填空题(共5小题,每小题3分,计15分)9.小明把自己的左手手印与右手手印按在同一张白纸上,左手手印________(填“能”或“不能”)通过平移与右手手印完全重合在一起.10.已知一个正多边形的内角和为1 440°,则它的一个外角的度数为______. 11.某玩具厂生产一种玩具,甲车间计划生产500个,乙车间计划生产400个,甲车间每天比乙车间多生产10个,两车间同时开始生产且同时完成任务.设乙车间每天生产x 个,可列方程为________________.12.关于x 的不等式组⎩⎨⎧x -b >2a ,x -a <2b 的解集为-3<x <3,则a ,b 的值分别为________.13.如图,在△ABC 中,AB =35,AC =45,点F 在AC 上,AE 平分∠BAC ,AE⊥BF 于点E .若D 为BC 的中点,则DE 的长为________. 三、解答题(共13小题,计81分) 14.(5分)将下列各式因式分解: (1)4x 2y -9y ; (2)(a 2+4)2-16a 2.15.(5分)如图,在边长为1的小正方形组成的网格中,给出了格点△ABC (顶点为网格线的交点).(1)将△ABC 先向下平移3个单位长度,再向右平移4个单位长度得到△A 1B 1C 1,画出平移后的图形;(2)将△ABC 绕点A 1顺时针旋转90°后得到△A 2B 2C 2,画出旋转后的图形; (3)借助网格,利用无刻度直尺画出△A 1B 1C 1的中线A 1D 1(画图中要体现找关键点的方法).(第15题)16.(5分)(1)解不等式:x 3-x -12≥1;(2)解不等式组:⎩⎨⎧1-2x ≤3,①x +43>3x -72-1,②并在数轴上表示其解集.17.(5分)解下列分式方程: (1)xx -2-1=6x 2-4; (2)2-x x -3=13-x -2.18.(5分)先化简:11-x ÷x 2+2x x 2-2x +1+1x +2,再选择一个你喜欢的x 值代入求值.19.(5分)若关于x ,y 的方程组⎩⎨⎧x +y =30-k ,3x +y =50+k 的解都是非负数.(1)求k 的取值范围;(2)若M =3x +4y ,求M 的取值范围.20.(5分)如图,在△ABC 中,∠C =90°, AD 平分∠BAC, DE ⊥AB 于点E ,点F在AC 上,且BD =DF . (1)求证: CF =EB ;(2)请你判断AE ,AF 与BE 之间的数量关系,并说明理由.(第20题)21.(6分)第5代移动通信技术简称5G,某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小明和小强分别用5G与4G下载一部600兆的公益片,小明比小强所用的时间快140秒,求该地4G与5G的下载速度分别是每秒多少兆.22.(7分)某社区计划购进A,B两种健身器材若干件,已知购进B种健身器材的单价是A种健身器材的3倍,用3 850元购进A种健身器材比用4 950元购进B种健身器材多4件.(1)A,B两种健身器材的单价分别是多少元?(2)若购进A,B两种健身器材共20件,且购进A,B两种健身器材的总费用不超过20 000元,求至少购进A种健身器材多少件.23.(7分)如图所示,在△ABC中,AB=BC,D是BC上一点,DE⊥AB于点E,DF⊥BC,交AC于点F.(1)若∠AFD=155°,求∠EDF的度数;(2)若F是AC的中点,求证:∠CFD=12∠B.(第23题)24.(8分)如图,在▱ABCD中,对角线AC与BD相交于点O,点E,F分别在BD和DB的延长线上,且DE=BF,连接AE,CF.(1)求证:△ADE≌△CBF;(2)连接AF,CE,四边形AFCE是平行四边形吗?请说明理由.(第24题)25.(8分)如图①,△ABC和△CEF是两个大小不等的等边三角形,且有一个公共顶点C,连接AF和BE.(1)线段AF和BE有怎样的大小关系?请证明你的结论;(2)将图①中的△CEF绕点C旋转一定的角度,得到图②,(1)中的结论还成立吗?作出判断并说明理由.(第25题)26.(10分)如图,在平面直角坐标系中,直线y=-43x+4与x轴、y轴分别相交于点A、B.点C的坐标为(0,-2),过点A,C作直线.(1)求直线AC的表达式;(2)若P是直线AB上的动点,Q是直线AC上的动点,当以点O,A,P,Q为顶点的四边形是平行四边形时,求点P的坐标.(第26题)答案一、1.C 2.B 3.D 4.A 5.C 6.D 7.C 8.A二、9.不能10.36°11.400x=500x+1012.-3,3 13.52三、14.解:(1)原式=y(4x2-9)=y(2x+3)(2x-3).(2)原式=(a2+4-4a)(a2+4+4a)=(a-2)2(a+2)2.15.解:(1)如图,△A1B1C1即为所求.(2)如图,△A2B2C2即为所求.(3)如图,线段A1D1即为所求.(第15题)16.解:(1)去分母,得2x-3(x-1)≥6,去括号,得2x-3x+3≥6,移项,得2x-3x≥6-3,合并同类项,得-x≥3,系数化为1,得x≤-3.(2)解不等式①,得x≥-1,解不等式②,得x<5,所以不等式组的解集为-1≤x<5.将解集表示在数轴上如图.(第16题)17.解:(1)xx-2-1=6x2-4,x x-2-1 =6(x-2)(x+2),x(x+2)-(x+2)(x-2) =6,x2+2x-x2+4 =6,2x=2,x=1.经检验:x=1是原方程的解,所以原方程的解是x=1.(2)2-xx-3=13-x-2,2-x x-3=-1x-3-2,2-x=-1-2(x-3),2-x=-1-2x+6,-x+2x=-1+6-2,x=3.经检验:x=3是原方程的增根,所以原方程无解.18.解:原式=11-x ·(x-1)2x(x+2)+1x+2=1-xx(x+2)+1x+2=1-x+x x(x+2)=1x2+2x.因为1-x≠0,x(x+2)≠0,所以x≠1,0,-2,当x=-1时,原式=1(-1)2+2×(-1)=-1.(x取值不唯一)19.解:(1)解方程组⎩⎨⎧x +y =30-k ,3x +y =50+k ,得⎩⎨⎧x =k +10,y =-2k +20,因为方程组的解都是非负数,所以⎩⎨⎧k +10≥0,-2k +20≥0,解得-10≤k ≤10.(2)M =3x +4y =3(k +10)+4(-2k +20)=-5k +110,因为-10≤k ≤10,所以-50≤-5k ≤50,所以60≤-5k +110≤160,即60≤M ≤160.20.(1)证明: ∵AD 平分∠BAC, DE ⊥AB ,∠C =90°,∴DC =DE .在Rt △DCF 和Rt △DEB 中,⎩⎨⎧ DC =DE ,DF =DB , ∴Rt △DCF ≌Rt △DEB (HL),∴CF =EB .(2)解:AF +BE =AE .理由如下:∵DC =DE ,DA =DA ,∴Rt △DCA ≌Rt △DEA ,∴AC =AE ,∴AF +FC =AE ,即AF +BE =AE .21.解:设该地4G 的下载速度是每秒x 兆,则该地5G 的下载速度是每秒15x 兆,由题意得600x -60015x=140, 解得x =4,经检验:x =4是原分式方程的解,且符合题意.15x=15×4=60.答:该地4G的下载速度是每秒4兆,5G的下载速度是每秒60兆.22.解:(1)设A种健身器材的单价为x元,则B种健身器材的单价为3x元,根据题意,得3 850x-4 9503x=4,解得x=550,经检验x=550是原方程的解,且符合题意,3×550=1 650(元).答:A,B两种健身器材的单价分别是550元,1 650元.(2)设购进A种健身器材m件,则购进B种健身器材(20-m)件.根据题意,得550m+1 650(20-m)≤20 000,解得m≥119 11 .答:至少购进A种健身器材12件.23.(1)解:∵∠AFD=155°,∴∠DFC=25°.∵DF⊥BC,DE⊥AB,∴∠FDC=∠AED=90°.∴∠C=180°-90°-25°=65°.∵AB=BC,∴∠C=∠A=65°,∴∠EDF=360°-65°-155°-90°=50°.(2)证明:连接BF.∵AB=BC,且F是AC的中点,∴BF⊥AC,∠ABF=∠CBF=12∠ABC,∴∠CFD+∠BFD=90°. ∵DF⊥BC,∴∠CBF+∠BFD=90°,∴∠CFD =∠CBF ,∴∠CFD =12∠ABC . 24.(1)证明:∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∴∠ADB =∠CBD ,∴∠ADE =∠CBF ,在△ADE 和△CBF 中,⎩⎨⎧AD =CB ,∠ADE =∠CBF ,DE =BF ,∴△ADE ≌△CBF (SAS).(2)解:四边形AFCE 是平行四边形,理由如下:∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD .∵DE =BF ,∴OD +DE =OB +BF ,即OE =OF ,∴四边形AFCE 是平行四边形.25.解:(1)AF =BE .证明如下:∵△ABC 和△CEF 是等边三角形,∴AC =BC ,CF =CE ,∠ACF =∠BCE =60°,在△AFC 与△BEC 中,⎩⎨⎧AC =BC ,∠ACF =∠BCE ,CF =CE ,∴△AFC ≌△BEC (SAS),∴AF =BE .(2)成立.理由:∵△ABC 和△CEF 是等边三角形,∴AC =BC ,CF =CE ,∠ACB =∠FCE =60°,∴∠ACB -∠FCB =∠FCE -∠FCB ,即∠ACF =∠BCE ,在△AFC 与△BEC 中,⎩⎨⎧AC =BC ,∠ACF =∠BCE ,CF =CE ,∴△AFC ≌△BEC (SAS),∴AF =BE .26.解:(1)在y =-43x +4中,令y =0,得x =3, ∴点A 的坐标为(3,0),设直线AC 的表达式为y =kx +b ,将A (3,0),C (0,-2)的坐标代入,得⎩⎨⎧0=3k +b ,-2=b ,解得⎩⎨⎧k =23,b =-2,∴直线AC 的表达式为y =23x -2. (2)设P ⎝ ⎛⎭⎪⎫m ,-43m +4,Q ⎝ ⎛⎭⎪⎫n ,23n -2,而A (3,0),O (0,0), ①以PQ ,AO 为对角线,则PQ ,AO 的中点重合,∴⎩⎪⎨⎪⎧m +n 2=3+02,-43m +4+23n -22=0+02,解得⎩⎨⎧m =2,n =1, ∴点P 的坐标为⎝⎛⎭⎪⎫2,43; ②以PA ,QO 为对角线,则PA ,QO 的中点重合,∴⎩⎪⎨⎪⎧m +32=n +02,-43m +4+02=23n -2+02,解得⎩⎨⎧m =2,n =5, ∴点P 的坐标为⎝⎛⎭⎪⎫2,43; ③以PO ,QA 为对角线,则PO ,QA 的中点重合,∴⎩⎪⎨⎪⎧m +02=n +32,-43m +4+02=23n -2+02,解得⎩⎨⎧m =4,n =1, ∴点P 的坐标为⎝⎛⎭⎪⎫4,-43. 综上所述,点P 的坐标为⎝⎛⎭⎪⎫2,43或⎝ ⎛⎭⎪⎫4,-43.。
最新北师大版八年级数学下册5.1.认识分式同步习题

《认识分式》1.不改变分式地值,使下列各组里第二个分式地分母和第一个分式地分母相同.(1)2613x x x ++-,2453x x x -+--+ (2)()()a a b b c --,()()a b a b c -- 2.下列等式地右边是怎样由左边得到地.(1)213(3)26x x x x x -=≠+-- (2)211454x x xx -=--+3.下列各式正确地是( )A .c c a b a b -=-++B .c c a b b a -=-+-C .c c a b a b -=-++D .c ca b a b-=-+- 4.不改变分式地值,分式22923a a a ---可变形为( )A .31a a ++B .31a a --C .31a a +-D .31a a -+ 5.不改变分式地值,把分式23427431a a a a a a -++--+-中地分子和分母按a 地升幂排列,是其中最高项系数为正,正确地变形是( ) A .23437431a a a a a a -++-+- B .23347413a a a a a a -+--++C .23434731a a a a a a +-+--+-D .23347413a a a a a a -++--++6.已知y -2x =0求代数式22222222()()()()x y x xy y x xy y x y --+++-地值?7.已知34y x =,求2222352235x xy y x xy y -++-地值.28.不改变分式地值,使下列分式地分子、分母均不含“-”号. (1)-22()(4)x y -- (2)237(2)m n ----9.下列各式正确地是( )A .x y x y x y x y -+-=--+B .x y x y x y x y -+--=---C .x y x y x y x y -++=-+-D .x y x yx y x y-+-=---+ 10.下列各式正确地是( )A .a m a b m b +=+B .0a b a b +=+C .1111ab b ac c --=-- D .221x y x yx y -=+-1.不改变分式地值,使23323x y x y +-地分子与分母中各项系数都化为整数,其结果为_____.2.已知23a b =,求a bb+地值. 3.已知0345x y m ==≠,求x y m x y m +++-地值. 4.将分式22x x x +化简得1x x +,则x 必须满足______. 5.()22(0)x yx y x y x y-=-≠+-6.()2(0)a ab a bab ab --=≠7.约分.(1)32262789x x x x x ----;(2)322121x x x x x --+-+;(3)2239n nn nx y x y +-;(4)42426923x x x x -+--.8.求下列各式地值. (1)2232712a a a a +--+,其中a=﹣2. (2)222231856x xy y x xy y ----,其中x=﹣3,y=1.9.将分式3325x y x y -+地分子、分母地各项系数都化为整数应为( )A .353x y x y -+;B .10301518x y x y -+;C .1030156x y x y -+;D .1010156x yx y-+.。
专题5.16 分式与分式方程(全章复习与巩固)(知识讲解)八年级数学下册基础知识专项讲练(北师大版)

专题5.16分式与分式方程(全章复习与巩固)(知识讲解)【学习目标】1.理解分式的概念,能求出使分式有意义、分式无意义、分式值为0的条件.2.了解分式的基本性质,掌握分式的约分和通分法则.3.掌握分式的四则运算.4.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相互联系的知识体系.5.结合分析和解决实际问题,讨论可以化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想.【要点梳理】要点一、分式的有关概念及性质1.分式一般地,如果A、B表示两个整式,并且B中含有字母,那么式子AB叫做分式.其中A叫做分子,B叫做分母.特别说明:分式中的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式AB才有意义.2.分式的基本性质(M为不等于0的整式).3.最简分式分子与分母没有公因式的分式叫做最简分式.如果分子分母有公因式,要进行约分化简.要点二、分式的运算1.约分利用分式的基本性质,把一个分式的分子和分母的公因式约去,不改变分式的值,这样的分式变形叫做分式的约分.2.通分利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把异分母的分式化为同分母的分式,这样的分式变形叫做分式的通分.3.基本运算法则分式的运算法则与分数的运算法则类似,具体运算法则如下:(1)加减运算a b a b c c c±±=;同分母的分式相加减,分母不变,把分子相加减.;异分母的分式相加减,先通分,变为同分母的分式,再加减.(2)乘法运算a c acb d bd⋅=,其中a b c d 、、、是整式,0bd ≠.两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.(3)除法运算a c a d adb d bc bc÷=⋅=,其中a b c d 、、、是整式,0bcd ≠.两个分式相除,把除式的分子和分母颠倒位置后,与被除式相乘.(4)乘方运算分式的乘方,把分子、分母分别乘方.4.分式的混合运算顺序先算乘方,再算乘除,最后加减,有括号先算括号里面的.要点三、分式方程1.分式方程的概念分母中含有未知数的方程叫做分式方程.2.分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程.3.分式方程的增根问题增根的产生:分式方程本身隐含着分母不为0的条件,当把分式方程转化为整式方程后,方程中未知数允许取值的范围扩大了,如果转化后的整式方程的根恰好使原方程中分母的值为0,那么就会出现不适合原方程的根---增根.特别说明:因为解分式方程可能出现增根,所以解分式方程必须验根.验根的方法是将所得的根带入到最简公分母中,看它是否为0,如果为0,即为增根,不为0,就是原方程的解.要点四、分式方程的应用列分式方程解应用题与列一元一次方程解应用题类似,但要稍复杂一些.解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节,从而正确列出方程,并进行求解.【典型例题】类型一、分式➽➼分式的意义✭✭分式的基本性质1.已知分式2x nx m+-(m ,n 为常数)满足表格中的信息,则下列结论中错误..的是()x 的取值-22pq分式的值无意义012A .2n =B .2m =-C .6p =D .q 的值不存在【答案】A【分析】根据分式有意义的条件可得m ,n 的值,进而可知p ,q 的值,选出符合要求的选项即可.解:∵x 为﹣2时方程无意义,∴x -m =0,解得:m =﹣2,故B 正确,故分式为:22x n x ++,当x =2时,分式的值为0,故2×2+n =0,n =﹣4,故A 错误,故分式为:242x x -+,当分式值为1时,2x -4=x +2,解得:x =6,故6p =,故C 正确,当2422x x -=+时,2x -4=2x +4,此等式不成立,则q 的值不存在,故D 正确,故选:A .【点拨】本题考查分式有意义的条件,方程思想,能够熟练掌握分式有意义的条件时解决本题的关键.举一反三:【变式1】若不论x 取何实数时,分式22ax x a-+总有意义,则a 的取值范围是()A .1a ≥B .1a >且0a ≠C .1a >D .1a <【答案】C 【分析】分式22ax x a-+总有意义,则分母永远不等于0,即22x x a -+的最小值大于0,据此解题即可.解:∵分式22ax x a-+总有意义,∴()22211x x a x a -+=-+-的最小值10a ->,解得1a >.【点拨】本题主要考查分式有意义的条件及二次函数的最值问题,能够熟练利用条件列不等式是解题关键.【变式2】若分式||3(3)(2)a a a --+的值为0,则a 满足的条件是()A .3a =B .3a =-C .3a =±D .3a =或2a =-【答案】B【分析】由分式的值为0的条件可得:()()30320a a a ì-=ïí-+¹ïî①②,再解方程与不等式即可.解:∵分式||3(3)(2)a a a --+的值为0,()()30320a a a ì-=ï\í-+¹ïî①②由①得:3,a =±由②得:3a ≠且2,a ≠-∴ 3.a =-故选B【点拨】本题考查的是分式的值为0的条件,掌握“分式的值为0,则分子为0,而分母不为0”是解本题的关键.2.不改变分式的值,下列各式变形正确的是()A .11x x y y +=+B .1x yx y-+=--C .22x y x y x y-=++D .22233x x y y ⎛⎫= ⎪⎝⎭【答案】B【分析】根据分式的基本性质即可一一判定.解:A.11x x y y ++≠,故该选项错误,不符合题意;B.()1x y x y x y x y---+==---,故该选项正确,符合题意;C.22x y x y x y-=-+,故该选项错误,不符合题意;D.22239x x y y ⎛⎫= ⎪⎝⎭,故该选项错误,不符合题意;【点拨】本题考查了分式的基本性质,解题的关键是熟练运用分式的基本性质.举一反三:【变式1】下列各式从左边到右边的变形正确的是()A .22x y y xx y x y--=++B .a b a bc c-+-=-C .0.220.22a b a ba b a b++=++D .1x yx y--=+【答案】B【分析】根据分式的基本性质作答.解:A 、22x y y xx y x y--=-++,此选项变形错误;B 、a b a bc c -+-=-,此选项变形正确;C 、0.22100.2102a b a ba b a b++=++,此选项变形错误;D 、1x yx y--=-+,此选项变形错误;故选B .【点拨】本题主要考查了分式的变形,解答此类题一定要熟练掌握分式的基本性质.【变式2】如果把分式xyx y+中的x 和y 都扩大10倍,则分式的值()A .扩大20倍B .扩大10倍C .不变D .缩小10倍【答案】B【分析】根据分式的基本性质即可求出答案;解:()x y xy xyx y x y x y==+++101010010101010 故选:B .【点拨】本题考查了分式的基本性质;解题的关键是熟练运用分式的基本性质进行化简比较.类型二、分式➽➼相关概念➽➼最简分式✭✭约分✭✭最简公分母✭✭通分3.分式122m +与11m +的最简公分母是()A .22m +B .2m +C .1m +D .21m -【答案】A【分析】根据最简公分母的概念,求解即可.通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母,这样的公分母叫做最简公分母.解:分式122m +与11m +的最简公分母22m +,故选:A【点拨】此题考查了最简公分母的概念,解题的关键是熟练掌握最简公分母的概念.举一反三:【变式】分式212x y 和216xy 的最简公分母是()A .2xyB .222x y C .226x y D .336x y 【答案】C【分析】根据最简公分母的确定方法解答即可.解:分式212x y 和216xy的最简公分母是226x y .故选:C .【点拨】本题主要考查了最简公分母的确定方法,确定最简公分母的一般方法:(1)取各分母系数的最小公倍数;(2)凡单独出现的字母连同它的指数作为最简公分母的一个因式;(3)同底数幂取次数最高的,得到的因式的积就是最简公分母.4.下列分式中,属于最简分式的是()A .2xB .22x x C .42xD .11x x --【答案】A【分析】根据最简分式的定义逐一判断即可.解:A.2x,是最简分式,符合题意;B.22x x =12x,不是最简分式,不合题意;C.422x x=,不是最简分式,不合题意;D.111xx -=--,不是最简分式,不合题意,故选:A .【点拨】本题考查最简分式的定义,一个分式的分子与分母没有非零次的公因式时(即分子与分母互素)叫最简分式.举一反三:【变式】下列分式中是最简分式的是()A .224x x B .22x y x y++C .2211x x x +++D .242x x -+【答案】B【分析】分子分母不含公因式的分式叫做最简分式,对四个选项逐一检查是否还能化简即可求得结果.解:A 选项22142x x x=,故不是最简分式;B 选项不能再化简,故是最简分式;C 选项()22121111x x x x x x +++==+++,故不是最简分式;D 选项()()2224222x x x x x x +--==-++,故不是最简分式.故选:B .【点拨】本题考查了分式的约分,解决本题的关键是找到分子分母中的公因式.类型三、解分式方程➽➼根的情况➽➼增根✭✭无解5.(1)通分:()22xyx y +和22x x y -;(2)约分:22416m mm --.【答案】(1)()()()()2222xy x y xyx y x y x y -=++-,()()()222x x y x x y x y x y +=-+-;(2)4m m +【分析】(1)找出两分母的最简公分母,通分即可;(2)原式变形后,约分即可得到结果.解:(1)()()()()2222xy x y xyx y x y x y -=++-,()()()222x x y xx y x y x y +=-+-;(2)()()()224416444m m m m m m m m m --==-+-+.【点拨】此题考查了通分及约分,通分的关键是找出各分母的最简公分母,约分的关键是找出分子分母的公因式.举一反三:【变式】(1)约分:236a bab;(2)通分:223b a 与abc 【答案】(1)2a ;(2)2223b c a bc 与3233a a bc【分析】(1)直接利用分式的性质化简,进而得出答案;(2)首先得出最简公分母,进而得出答案.解:(1)2336322a b ab a aab ab ⨯==⨯;(2)223b a与abc 最简公分母为:23a bc ,则:2222222333b b bc b ca a bc a bc ⨯==⨯,23223333a a a a bc bc a a bc⨯==⨯.【点拨】本题主要考查了通分与约分,正确掌握分式的性质是解题关键.6.若分式方程1x aa x -=+有增根,则a 的值为________.【答案】1-【分析】增根是化为整式方程后产生的不适合分式方程的根.所以应先确定增根的可能值,让最简公分母10x +=,得到=1x -,然后代入整式方程算出a 的值即可.解:方程两边同时乘以1x +得,()1x a a x -=+,∵方程有增根,∴10x +=,解得=1x -.∴10a --=,解得1a =-.故答案为:1-.【点拨】本题考查了分式方程的增根,先根据增根的定义得出x 的值是解答此题的关键.举一反三:【变式】如果关于x 的方程2133mx x =---有增根,那么m 的值为________.【答案】2-【分析】先将分式方程去分母转化为整式方程,再由分式方程有增根,得到最简公分母为0求出x 的值,最后代入整式方程求出k 的值即可.解:分式方程去分母得:23x m =--,由分式方程有增根,得到30x -=,即3x =,把3x =代入整式方程得:2m =-.故答案为:2-.【点拨】本题主要考查了分式方程的增根,增根确定后可按如下步骤进行:①化分式方程为整式方程;②把增根代入整式方程即可求得相关字母的值.类型四、解分式方程➽➼根的情况➽➼正(负)数解✭✭非负(正)数解7.若关于x的不等式组341227x xa x+⎧-≥⎪⎨⎪->⎩无解,且关于y的分式方程3122y a yy y+=---的解为非负整数,则符合条件的所有整数a的和为______.【答案】16【分析】首先根据不等式组无解求得a的取值范围,再解分式方程,根据分式方程的解为非负整数得出a为整数,23a+为非负整数,然后确定出符合条件的所有整数a,即可得出答案.解:341227x xa x+⎧-≥⎪⎨⎪->⎩①②,解不等式①得:3x≥,解不等式②得:7x a<-,∵不等式组341227x xa x+⎧-≥⎪⎨⎪->⎩无解,∴73a-≤,∴10a≤,分式方程3122y a yy y+=---去分母,得32y y a y-=---,∴23ay+=,∵分式方程3122y a yy y+=---的解为非负整数,∴0y≥且20y-≠,∴203a+≥且4a≠,∵a为整数,23a+为非负整数,∴2a=-,1,7,10,∴整数a的和为2171016-+++=.故答案为:16.【点拨】此题考查的是解分式方程、解一元一次不等式组,掌握分式方程、一元一次不等式组的解法是解决此题关键.举一反三:【变式】若关于x 的方程301ax x+=-无解,则a 的值为______.【答案】0或-3【分析】先去分母化为整式方程,根据分式方程无解得到x =0或x =1或3+a =0,将解代入整式方程求出a 即可.解:去分母,得3x +a (x -1)=0,∴(3+a )x-a =0,∵原分式方程无解,∴x =0或x =1或3+a =0,当x =0时,a =0;当x =1时,3+0=0,无解;∴a =0,当3+a =0时,解得a =-3,故答案为:0或-3.【点拨】此题考查了根据分式方程解的情况求参数,正确掌握解分式方程的解法是解题的关键.8.若关于x 的分式方程3121m x +=-的解为非负数,则m 的取值范围是____.【答案】4m ≥-且3m ≠-【分析】先解关于x 的分式方程,求得x 的值,然后再依据“解是非负数”建立不等式求m 的取值范围.解:去分母得,m +3=2x ﹣1,∴x =42+m ,∵方程的解是非负数,∴m +4≥0即m ≥﹣4,又因为2x ﹣1≠0,∴x ≠12,∴42+m ≠12,∴m ≠-3,则m 的取值范围是m ≥﹣4且m ≠-3.故答案为:m ≥﹣4且m ≠-3.【点拨】本题考查了分式方程的解及分式有意义的条件,理解题意得出相应不等式求解即可.举一反三:【变式】关于x 的方程1233x m x x -=+--有正数解,则m 取值范围是______.【答案】5m <且2m ≠【分析】先解分式方程求出方程的解,再根据这个方程有正数解和3x ≠建立不等式,由此即可得.解:1233x m x x -=+--,方程两边同乘以()3x -,得()123x m x -=+-,去括号,得126x m x -=+-,移项、合并同类项,得5x m -=-,系数化为1,得5=-+x m ,关于x 的方程1233x m x x -=+--有正数解,50m ∴-+>,且53m -+≠,解得:5m <且2m ≠,故答案为:5m <且2m ≠.【点拨】本题考查了解分式方程,熟练掌握方程的解法是解题关键,需注意的是,分式方程有正数解隐含方程不能有增根.类型五、分式➽➼化简✭✭求值9.关于x 的分式方程334111ax x x x +-+=--的解为正整数,则满足条件的整数a 的值为____________.【答案】-3【分析】求得分式方程的解,利用方程的解的特征确定整数a 的值.解:分式方程334111ax x x x +-+=--的解为:24x a =+,∵分式方程有可能产生增根1,又∵关于x 的分式方程334111ax x x x +-+=--的解为正整数,且24x a =+≠1,∴满足条件的所有整数a 的值为:-3,∴a 的值为:-3,故答案为:-3.【点拨】本题主要考查了分式方程的解,方程的整数解,考虑分式方程可能产生增根的情况是解题的关键.举一反三:【变式】对于关于x 的分式方程()2141111k k x x x +=≠-+--①若k =1,则方程的解为________;②若方程有增根且无解,则k 的值为________;③若方程的解为负数,请你写出符合条件的且互为相反数的两个k 的值________.【答案】2x =k =2|k|>5即可,如6±【分析】①若k =1,得到分式方程为2114111x x x +=+--,解分式方程即可求解;②根据方程有增根且无解,可得x =±1,然后把x 的值代入整式方程中进行计算即可解答;③根据题意可得51k x k -=+,利用方程的解为负数求出k 的取值范围,再求出互为相反的两个k 值.解:①若k =1,得到分式方程为2114111x x x +=+--,去分母得114x x -++=,解得2x =.故答案为:2x =;②将()2141111k k x x x +=≠-+--去分母得()114x k x -++=,解得51k x k-=+.∵方程有增根且无解,∴210x -=,解得1x =±,当x =1时,511k k-=+,解得:2k =,当x =-1时,511k k -=-+无解,∴k 的值为2.故答案为:2k =;③∵方程的解为负数,∴x <0且x ≠±1,∴501k k-<+且511k k -≠±+,解得5k <-或5k >,∴符合条件的且互为相反数的两个k 的值可以是±6.故答案为:5k <-或5k >,如±6.【点拨】本题考查了分式方程的增根,分式方程的解法,根据题意求出x 的值后,代入整式方程中进行计算是解题的关键.10.计算:(1)211a a a ---;(2)4222⎛⎫⎛⎫+-÷ ⎪ ⎪--⎝⎭⎝⎭a a a a 【答案】(1)11a -(2)a 【分析】(1)先对原式通分变为同分母的分式,再相减即可解答本题;(2)先将括号内的进行计算,再将除法转换为乘法后,再约分即可得到答案.解:(1)211a a a ---=2(1)(1)11a a a a a +----=2(1)(1)1a a a a -+--=22(1)1a a a ---=22+11a a a --=11a -(2)4222⎛⎫⎛⎫+-÷ ⎪ ⎪--⎝⎭⎝⎭a a a a =4222a a a a ⎛⎫⎛⎫++÷ ⎪ ⎪--⎝⎭⎝⎭=24422a a a a -+⎛⎫÷ ⎪--⎝⎭=222a a a a-⨯-=a【点拨】本题主要考查了分式的混合运算,解题的关键是明确分式混合运算的计算方法.举一反三:【变式】计算:(1)22122x x x x-+÷;(2)2126339x x x x --++--.(3)22241123x x x x x ---÷+--.(4)2443111m m m m m -+⎛⎫÷-- ⎪--⎝⎭.【答案】(1)12x -;(2)2239x x --;(3)52x +;(4)22m m --+.【分析】(1)根据分式的加减运算以及乘除运算法则进行计算;(2)根据分式的加减运算以及乘除运算法则进行计算;(3)根据分式的加减运算以及乘除运算法则进行计算;(4)根据分式的加减运算以及乘除运算法则进行计算.解:(1)22122x x x x-+÷解:原式()()()1121x x x x x +-=⋅+12x -=;(2)2126339x x x x --++--解:原式()()1263333x x x x x -=+++-+-()()()()()()()()2336333333x x x x x x x x x -+-=+++--++-()()236633x x x x x -++-+=+-22239x x x +-=-()()()()3133x x x x +-=+-13x x -=-;(3)22241123x x x x x ---÷+--解:原式()()()()3121122x x x x x x -+-=-⋅+-+2322x x x x +-=-++()232x x x +--=++(4)2443111m m m m m -+⎛⎫÷-- ⎪--⎝⎭解:原式()()()22113111m m m m m m -+-⎡⎤=÷-⎢⎥---⎣⎦()()2231211m m m m ⎡⎤---⎢⎥=÷--⎢⎥⎣⎦()222411m m m m -⎡⎤-=-÷⎢⎥--⎣⎦()()()221122m m m m m --=-⋅--+22m m -=-+.【点拨】本题考查分式的混合运算,解题的关键是熟练运用分式的加减运算以及乘除运算法则,本题属于基础题型.类型五、解分式方程➽➼运算✭✭化简✭✭求值11.先化简,再求值:2224124421x x x x x x x x ⎛⎫-+-÷--- ⎪-+--⎝⎭,然后从1-,0,1,2中选择一个合适的数作为x 的值代入求值.【答案】21--x x,1x =-时,12-【分析】先根据分式的运算法则把所给代数式化简,然后从所给数中取一个使分式有意义的数代入计算.解:原式()()()22222412212x x x x x x x x x ⎛⎫+--+-=÷- ⎪----⎝⎭()22224412212x x x x x x x x ⎛⎫-+--=÷-- ⎪----⎝⎭()2222441212x x x x x x x -+--+=÷----12121x x x x -=⋅---111x x =---21x x =--20x -≠ ,且10x -≠,且0x ≠2x ∴≠,且1x ≠,且0x ≠取=1x -时,原式12=-【点拨】本题考查了分式的计算和化简,解决这类题目关键是把握好通分与约分;关键是掌握分式加减的本质是通分,乘除的本质是约分,同时注意在进行运算前要尽量保证每个分式最简.举一反三:【变式】先化简22424422x x x x x x x ⎛⎫--+÷ ⎪-++-⎝⎭,从不等式组()3421213212x x x x ⎧-≤-⎪⎪⎨+⎪-<⎪⎩的整数解中,选取一个你最喜欢的x 的值代入求值.【答案】82x +,1x =时,83【分析】根据分式的乘除法法则和约分法则把原式化简,根据解一元一次不等式组的步骤解出不等式组,从解集中选取使分式有意义的值代入计算即可.解:22424422x x x x x x x ⎛⎫--+÷ ⎪-++-⎝⎭22(2)22(2)(2)x x x x x x x ⎡⎤-=+÷⎢⎥-⎣⎦-++-22(2)(2)(2)(2)(2)2(2)x x x x x x x x ⎡⎤-=-÷⎢⎥-+-+-⎣⎦+2428x x x x =÷--2482x x x x -=⋅-82x =+,由()34212x x -≤-,2863x x -≤-,解得:54x ≥-;由13212x x +-<,4132x x --<,解得:3x <,故不等式组的解集为:534x -≤<,0,2,2x ≠- 当1x =时,原式83=.【点拨】本题考查的是分式的化简求值和一元一次不等式组的解法,掌握分式的乘除法法则和约分法则是解题的关键.12.解分式方程.(1)33122x x x-+=--;(2)214111x x x -+=+-【答案】(1)1x =(2)无解【分析】(1)分式方程两边同乘以(2)x -去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解;(2)分式方程两边同乘以(1)(1)x x +-去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.解:(1)33122x x x-+=--323x x -+-=-3+23x x +=-22x =解得,1x =经检验,1x =是原方程的解,所以,原方程的解为:1x =(2)214111x x x-+=+-2(1)4(1)(1)x x x --=+-222141x x x -+-=-22x -==1x -经检验,=1x -是增根,原方程无解.【点拨】此题主要考查了解分式方程,正确找出分式方程的最简公分母是解答本题的关键.举一反三:【变式】解分式方程(1)432x x =+;(2)217133x x x+=---【答案】(1)6x =(2)无解【分析】(1)等号两边同时乘以(2)x x +将原方程转换为整式方程,然后求解验根即可;(2)等号两边同时乘以(3)x -将原方程转换为整式方程,然后求解验根即可.(1)解:432x x=+,去分母得:43(2)x x =+,解得:6x =,经检验6x =是原方程的解;(2)217133x x x+=---去分母得:2137x x +=-+,解得:3x =,经检验3x =是原方程的增根,故原方程无解.【点拨】本题考查了解分式方程,熟练掌握解分式方程的一般步骤是解本题的关键,注意解分式方程需要验根.类型五、分式方程的应用➽➼列方程✭✭解方程✭✭求值13.(1)解方程:411233x x x -=+--;(2)先化简,再求值:222(2)5242x x x x x x ++-÷---+,其中x 从2-,2和3中选一个合适的值.【答案】(1)2x =-(2)72x +,75【分析】(1)将分式方程化为整式方程,再解整式方程,最检验整式方程的解是不是分式方程的解即可;(2)根据分式的运算法则化简,再代入一个使原方式有意义的值求解即可.(1)解:411233x x x -=+--,方程两边同乘3x -,得()41231x x -=-+,解得2x =-,检验:当2x =-时,30x -≠,∴原分式方程的解是2x =-;(2)解:222(2)5242x x x x x x ++-÷---+()()222252(2)2x x x x x x x +-+-=⋅--++512x x -=-+252x x x +-+=+72x =+,2x =- 或2时,原分式无意义,3x ∴=,当3x =时,原式77325==+.【点拨】本题考查了解分式方程,分式的化简求值,分式有意义的条件,熟练掌握知识点是解题的关键.举一反三:【变式】解方程:(1)2232122x x x x x --+=--(2)()32011x x x x +-=--【答案】(1)1x =(2)无解【分析】(1)根据解分式方程的步骤求解即可;(2)根据解分式方程的步骤求解即可.解:(1)2232122x x x x x--+=--去分母,得()22322x x x x ---=-,解得1x =,经检验,1x =是原方程的根,∴原方程的解为:1x =;(2)()32011x x x x +-=--去分母,得()320x x -+=,解得1x =,经检验,1x =是原方程的增根,∴原方程无解.【点拨】本题考查了解分式方程,熟练掌握解分式方程的步骤是解题的关键,注意验根.14.小状元书店决定用不多于20000元购进甲乙两种图书共1200本进行销售.甲、乙两种图书的进价分别为每本20元、15元,甲种图书每本的售价是乙种图书每本售价的1.5倍,若用1800元在该店可购买甲种图书的本数比用1400元购买乙种图书的本数少10本.(1)甲乙两种图书的售价分别为每本多少元?(2)书店为了让利读者,决定甲种图书售价每本降低3元,乙种图书售价每本降低2元,问书店应如何进货才能获得最大利润?(假设购进的两种图书全部销售完)【答案】(1)甲种图书售价每本30元,乙种图书售价每本20元(2)甲种图书进货400本,乙种图书进货800本时利润最大【分析】(1)根据题意,列出分式方程即可;(2)先用进货量表示获得的利润,求函数最大值即可.(1)解:设乙种图书售价每本x 元,则甲种图书售价为每本1.5x 元,,由题意得:14001800101.5x x-=,解得:20x =,经检验,20x =是原方程的解,∴甲种图书售价为每本1.52030⨯=元,答:甲种图书售价每本30元,乙种图书售价每本20元;(2)设甲种图书进货a 本,总利润W 元,则(30203)(20152)(1200)48400W a a a =--+---=+∵2015(1200)20000a a +⨯-≤,解得400a ≤,∵W 随a 的增大而增大,∴当a 最大时W 最大,∴当400a =本时,W 最大,此时,乙种图书进货本数为1200400800-=(本),答:甲种图书进货400本,乙种图书进货800本时利润最大.【点拨】本题分别考查了分式方程和一次函数最值问题,注意研究利润最大分成两个部分,先表示利润再根据函数性质求出函数最大值.举一反三:【变式1】为做好新冠疫情的防控工作,某单位需购买甲、乙两种消毒液,经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多5元,该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液,(1)求甲、乙两种消毒液的零售价分别是每桶多少元?(2)由于疫情防控进入常态化,该单位需再次购买两种消毒液共100桶,且甲种消毒液的桶数不少于乙种消毒液桶数的12,由于是第二次购买,商家给予八折优惠.求甲种消毒液购买多少桶时,所需资金总额最少最少总金额是多少元?【答案】(1)甲种消毒液的零售价为25元/桶,乙种消毒液的零售价为20元/桶(2)当甲种消毒液购买34桶时,所需资金总额最少,最少总金额是1736元【分析】(1)设乙种消毒液的零售价为x 元/桶,则甲种消毒液的零售价为()+5x 元/桶,结合该单位分别用900元和720元采购相同桶数的甲、乙两种消毒液,即可列出关于x 的分式方程,进而求解即可.(2)设购买甲种消毒液m 桶,则购买乙种消毒液为()100m -桶,根据甲种消毒液的桶数不少于乙种消毒液的桶数的12,即可得出关于m 的一元一次不等式,解得m 的取值范围,然后设所需资金总额为w 元,根据题意列出函数关系式,再利用函数性质即可解决最值.(1)解:设乙种消毒液的零售价为x 元/桶,则甲种消毒液的零售价为()5+x 元/桶,依题意得:9007205x x =+,解得:=20x ,经检验,=20x 是原方程的解,且符合题意,525x ∴+=.答:甲种消毒液的零售价为25元/桶,乙种消毒液的零售价为20元/桶:(2)解:设购买甲种消毒液m 桶,则购买乙种消毒液()100m -桶,依题意得:()11002m m ≥-,解得:1003m ≥,设所需资金总额为w 元,则()250.8201000.841600w m m m =+-=+ ,40> ,w ∴随m 的增大而增大,∴当34m =时,w 取得最小值,最小值43416001736=⨯+=,答:当甲种消毒液购买34桶时,所需资金总额最少,最少总金额是1736元.【点拨】此题考查了分式方程的运用、一元一次不等式以及一次函数运用,解题关键是找准等量关系,正确列出方程.【变式2】某水果店一次购进了若干箱水蜜桃和李子,已知购进水蜜桃花费800元,购进李子花费1680元,所购李子比水蜜桃多10箱,李子每箱的进价是水蜜桃每箱进价的1.4倍.(1)水蜜桃和李子每箱进价分别为多少元?水蜜桃和李子各多少箱?(2)根据市场情况,每箱李子可以比每箱水蜜桃的利润多5元,这批水果全部售完后,店家若想获得不少于800元的利润,应该如何确定每箱水蜜桃和李子的售价?【答案】(1)水蜜桃和李子每箱进价分别为40元和56元,各20箱和30箱(2)每箱水蜜桃和李子的售价分别不少于53元和74元【分析】(1)设水蜜桃每箱x 元,则李子每箱1.4x 元,由题意列出分式方程,解之,再根据进货费用算出多少箱即可;(2)设水蜜桃每箱利润y 元,则李子每箱利润(5)y +元,由题意列出不等式,解不等式即可.(1)解:设水蜜桃每箱x 元,则李子每箱1.4x 元,根据题意得:1680800101.4x x -=,解得:40x =,经检验40x =是原方程的解,则1.4 1.44056x =⨯=,8004020÷=,16805630÷=,答:水蜜桃和李子每箱进价分别为40元和56元,各20箱和30箱;(2)设水蜜桃每箱利润y 元,则李子每箱利润(5)y +元,根据题意得:8001680(5)8004056y y ++≥,解得:13y ≥,134053+=,1355674++=,答:每箱水蜜桃和李子的售价分别不少于53元和74元.【点拨】本题考查了分式方程的应用以及一元一次不等式的应用;理解题意,列出分式方程和一元一次不等式是解题的关键.【变式3】为预防新冠疫情的反弹,桐君阁大药房派采购员到厂家去购买了一批A 、B 两种品牌的医用外科口罩.已知每个B 品牌口罩的进价比A 品牌口罩的进价多0.7元,采购员用7200元购进A 品牌口罩的数量为用5000元购进B 品牌数量的2倍.(1)求A 、B 两种品牌每个口罩的进价分别为多少元?(2)若B 品牌口罩的售价是A 品牌口罩的售价的1.5倍,要使桐君阁大药房销售这批A 、B 两种品牌口罩的利润不低于8800元,则A 品牌口罩每个的售价至少定为多少元?【答案】(1)A 品牌每个口罩的进价为1.8元,则B 品牌每个口罩的进价为2.5元(2)3元【分析】(1)设A 品牌每个口罩的进价为x 元,则B 品牌每个口罩的进价为()0.7x +元,根据用7200元购进A 品牌口罩的数量为用5000元购进B 品牌数量的2倍列分式方程解答;(2)先求出两种品牌口罩购买的数量,设每个A 品牌口罩的售价定为y 元,则每个B 品牌口罩的定价为1.5y 元,列不等式求解即可.(1)解:设A 品牌每个口罩的进价为x 元,则B 品牌每个口罩的进价为()0.7x +元,720050020.7x x =⨯+,解得 1.8x =,经检验, 1.8x =是原方程的解,且符合题意,∴0.7 2.5x +=,答:A 品牌每个口罩的进价为1.8元,则B 品牌每个口罩的进价为2.5元;(2)购进B 品牌口罩的数量为5000 2.52000÷=(个),购进A 品牌口罩的数量为200024000⨯=(个),设每个A 品牌口罩的售价定为y 元,则每个B 品牌口罩的定价为1.5y 元,依题意得:()()4000 1.82000 1.5 2.58800y y ⨯-+⨯-≥,解得3y ≥,答:A 品牌口罩每个的售价至少定为3元.【点拨】此题考查了分式方程的应用,一元一次不等式的应用,正确理解题意列得方程或不等式是解题的关键.。
八年级数学下册 第三章 3.4分式方程学案(2)(无答案) 北师大版

课题: §3.4 分式方程 (2)【学习目标】1、掌握解分式方程的一般步骤. 熟练掌握分式方程的解法2、理解解分式方程验根的必要性. 【学习重点】解分式方程的一般步骤;分式方程验根的必要性 【学前准备】1、 什么是方程,什么是分式方程?2、 解一元一次方程有哪些步骤?3、 分式有意义的条件。
【师生探究,合作交流】 一、 解分式方程 例1 、213-x =2-624-x 解方程:21-x =x3例2:解方程:x300-x2480=4解:去分母,方程两边同乘以小结:解分式方程与解整式方程的区别、联系二、 想一想,答一答1、 分式方程化为整式方程时,根据__________________,方程左右两边各项需同时乘以_________________________;2、 如何确定最简公分母?最简公分母即分母的最小______________.3、 为什么解完分式方程后一定要检验?4、 怎样检验以确定分式方程的根.5、 产生增根的原因是什么?你用了______分钟完成预习!【小试牛刀】 1、 找错误 解方程:32--x x =x-31-2小亮同学的解法: 小颖同学的解法:解:方程两边同乘以x -3, 解:方程两边同乘以(x -3)(3-x ) 得:2-x =-1-2(x -3) 得:(2-x)(3-x )=1-2(x -3)(3-x ) 解这个方程,得x =3. 无法解这个方程2、解方程(1)13-x =x4 (2)1210-x +x215-=2.【小结】1、解分式方程的步骤:一、去分母,化分式方程为整式方程;二、解整式方程;三、验根;四、写出结论.2、“转化思想” -------------将分式方程转化为整式方程; 【作业】1、 解方程:(1)32-x x +x235-=4 (2)16-x =)1(5-+x x x (3)122--x x +1=x215.1-(4) 3-x x =24-+x x (5)21-x +3=21--x x ★122-x x +2-x x =2P90----------习题3.7问题解决【拓展延伸】 ★分式方程12-+x a x = 1 的解为x=3,求a 值★若关于x 的方程31--x x =932-x m有增根,求m 的值。
八年级数学北师大版下册5.2分式的乘除法同步测试题

5.2 分式的乘除法同步测试题班级:_____________姓名:_____________ 一、选择题(本题共计9 小题,每题3 分,共计27分,)1. 计算(−2ab2)3×(2ba)2÷(−2ba)2的结果是()A.−8ab6B.−8a3b6C.16a2b6D.−16a2b62. 化简16−a2a2+4a+4÷a−42a+4⋅a+2a+4,其结果是()A.−2B.2C.−2(a+2)2D.2(a+2)23. 计算−10x3y ⋅6y25x3,结果是()A.−4x2yB.−4yx2C.−4yxD.−15yx24. 化简分式5ab3c ⋅12c25ab2的结果是()A.43B.4cbC.4a3bD.45bac5. 计算(−ab2)2的结果是()A.a2b2B.−a2b2C.a2b4D.−a2b46. 下列各式中,计算正确的是()A.m−n⋅m=mB.m÷n×1n=mC.1m ÷m⋅m÷1m=1 D.m3÷1m÷m2=17. 当m<0时,|m3|−m2m÷|m|的结果是()A.−m+1B.−m−1C.m+1D.m−18. 计算a−1a−b ⋅b2−a21−a的结果是()A.a+bB.−a+bC.a−bD.−a−b9. 若3x=2y,则2x23y2等于()A.49B.278C.827D.94二、填空题(本题共计9 小题,每题3 分,共计27分,)10. 计算:4a2b÷(2ab )2⋅ab3=________.11. 计算:a2b ⋅4b2a=________.12. (−x)2÷y⋅1y=________.13. 化简:a−1a ÷a−1a2=________.14. 化简a4−a2b2(a−b)2÷a(a+b)b2⋅b2a的结果是________.15. 计算:m2n2x2y ⋅(−2xmn)2=________.16. 计算:(xy−x2)xyx−y=__________.17. −3x2y÷3x24y=________.18. 计算:(−2ab2)3⋅(2ba)2÷(−2ba)=________.三、解答题(本题共计8 小题,共计66分,)19. 计算:(pq2r )2÷2pr2+12q.20. 计算:3ab2÷a3b.21. 4x2y÷(−2xy)2.22. 计算:(1)(a2−b3)4;(2)(a2b−cd3)3÷2ad3⋅(c2a)2.23. 计算:a2−6a+94−b2÷3−a2+b⋅a23a−9.24. 计算x2−y2x2−2xy+y2÷x2y+xy2x−y.25. (1)a4−a2b2(a−b)2÷a(a+b)b2⋅b2a(2)m−m 2m2−1÷mm−1•(m+1m−1)2.26. 计算:bc a ⋅2ab c;b a2−9⋅a+3b2−b;a−b a+b ⋅a4−a2b2a2−ab;4x2−4xy+y22x+y÷(4x2−y2).归纳总结:1.计算分式的乘除法时,分子和分母能因式分解的先进行________,能约分的________;2.运算结果通常要化成________.。
北师大版八年级下册数学第三章分式综合评价

北师大版八年级下册数学第三章分式综合评价一、选择题(每小题3分,共30分)1、在3a 2 π,x 22a,34 a+b ,1a ,-m 2,a m 中,是分式的有:( ) A 、2个 B 、3个 C 、4个 D 、5个2、若m-n n = 34 ,则m n 等于:( )A 、74B 、43C 、 47D 、 343、与分式-a+b -a-b 的值相等的是:( )A 、a+b a-bB 、a-b a+bC 、-a+b a-bD 、-a-b a+b4、在分式a+b ab (a ,b 为正数)中,若字母a ,b 的值分别扩大为原来的2倍,则分式的值:( )A 、扩大为原来的2倍B 、缩小为原来的12C 、不变D 、缩小为原来的145、若分式x 2-42x-4 的值为零,则x 等于:( )A 、2B 、—2C 、±2D 、06、化简x-1x ÷(x -1x)的结果是:( ) A 、1x-1 B 、1 C 、1x+1D 、-1 7、要使分式5a-1 与4a-2的值相等,则a 的值是:( ) A 、6 B 、5 C 、4 D 、18、下列分式方程中,无解的是:( )A 、1x-1 =1x 2-1B 、3x x 2-1 =1x+1C 、x x+1 =12D 、1x+1 =1x-19、某工地调来72人参加挖土和运土,已知3人挖出的土1人恰好一次能全部运走,怎样调配劳动力才能使挖出的土能及时运走且不窝工?解决此问题,可设派x 人挖土,其他人运土,列方程为①72-x x =13 ;②72-x=x 3 ;③x+3x=72;④x 72-x =3,所列方程中正确的有:( )A 、1个B 、2个C 、3个D 、4个10、若xy=b,1x 2 +1y 2 =a ,则(x+y)2等于:( )A 、(a+2b)2B 、a 2+b 2C 、b(ab+2)D 、ab(b+2)二、填空题(每小题3分,共30分)11、已知当x=-2时,分式x-b x-a无意义,当x=4时,此分式的值为0,则a+b=_____________ 12、若12x-1 与13(x+4)互为倒数,则x=________________ 13、化简分式x 2-y 2x+y的结果是__________________ 14、当x=_________时,分式2x-1无意义 15、已知x=2010,y=2011,则(x+y)·(x 2+y 2x 4-y 4 )=_________________ 16、计算x x-y +y y-x=_____________________ 17、若分式方程x x-4 =2+a x-4有增根,则a=__________________ 18、计算9xy 5a÷12x 2y=____________________ 19、当x___________时,分式4x+2的值为正数 20、汛期将至,我军机械化工兵连的官兵为驻地群众办实事,计划加固驻地附近20千米的河堤。
北京市八年级数学下册 分式课后练习二 (新版)北师大版

分式课后练习(二)在代数式m 1,41,xyy x 22,y x +2,32a a +中,分式的个数是( ) A .2 B .3 C .4 D .5当x _____时,分式)2)(1(--x x x 有意义. 设A , B 都是整式,若A B 表示分式,则( ) A .A ,B 都必须含有字母B .A 必须含有字母C .B 必须含有字母D .A ,B 都不必须含有字母下列各式中,不论字母x 取何值时分式都有意义的是( )A .121+x B .15.01+x C .231x x - D .12352++x xm 取什么整数时,分式271m m +-的值为正整数? 若分式12x x -+的值为正数,则x 的取值范围是:的值为 .分式课后练习参考答案B . 详解:在m 1、xyy x 22、y x +2中,分母含有字母,所以是分式.故选B .x ≠1且x ≠2.详解:分式有意义必须其分母不等于0,即(x)(x ,即x ≠1且x ≠2.C . 详解:如果一个式子是分式,那么该式子的分母必须含有字母,可据此进行判断.若A B表示分式,则B 必须含有字母.故选C .D . 详解:A .当分母2x +1≠0即x ≠21-时,分式121+x 有意义.B .当分母0.5x +1≠0即x 时,分式15.01+x 有意义.C .当分母x 2≠0即x ≠0时,分式231xx -有意义.D .因为x 2≥0,所以2x 2+1≥1,所以不论x 取何值,分母2x 2+1≠0,所以不论字母x 取何值时,分式12352++x x 都有意义. m 的值是,2,4或10. 详解:∵分式271m m +-的值为正整数, ∴271m m +-=2+91m -, ∴91m ->,且m -1是9的约数, ∴m 的值是,2,4或10. x >1或x <. 详解:∵分式12x x -+的值为正数, ∴x −1>0,x +2>0或x −1<0, x +2<0,解不等式组得x >1或x <.1-.,所以a ,b -1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章分式综合测试题
一、选择题(每题3分,共30分)
1.代数式4-x 1
是( )
A.单项式
B.多项式
C.分式
D.不能确定
2.有理式x 2,31(x+y),3-ππ,x a -5,42y
x -中分式有( )个.
A.1
B.2
C.3
D.4
3.若分式21
22-+-x x x 的值为0,则x 的值是( ).
A.1或-1
B.1
C.-1
D.-2
4.下列分式a bc 1215,a b b a --2
)(3,)(222b a b a ++,b a b a +-22中最简分式的个数是( ).
A.1
B.2
C.3
D.4
5.如果x =a -b ,y =a +b ,计算-
xy x y 2
)(-的值为( ) A .222b a b
- B .-222b a b - C .-2224b a b - D .2224b a b - 6.将b a b a --|
|约分,正确的结果是( )
A .1
B .2
C .±1
D .无法确定
7.下列运算正确的个数是( ) ①m÷n·n 1
=m÷1=m ②x·y÷x·y=xy÷xy=1 ③11111=⋅⋅⋅=÷⋅÷a a a a a a a a ④22224)2(y x x y
x x +=+ A .2 B .1 C .3 D .4
8.如果x <32,那么23|
32|--x x 的值是( )
A .-1
B .0
C .1
D .32
9.若a -b =2ab ,则
b a 11-的值为( ) A .21 B .-21
C .-2
D .2
10.若a 1+a =4,则(a 1
-a )2的值是( )
A .16
B .9
C .15
D .12
二、填空题(每题3分,共30分)
1.已知代数式:3,x 1,3+x 1,
222y x -,π1(x+y),y 1(z+x),11
+x ,x x 212+,32122+++x x x 整式有: 分式有:
2. 已知分式12
2--x x ,当x 时分式值为0. 3.如果32=
b a ,且a ≠2,那么51-++-b a b a =
4.某厂每天能生产甲种零件a 个或乙种零件b 个,且a ∶b=2∶3.甲、乙两种零件各一个配成一套产品,30天内能生产的产品的最多套数为
5.已知y =
32)1(6
126-+-x x x ,x 取 时,y 的值为正整数. 6.计算:______)2()32(232
32---÷-a b a b
7.把分式))((11)(3b a b a b a -+-约分得)(113
b a +时,a 、b 必须满足的条件为_______。
8.已知分式方程12-+x a
x =1的解为非负数,则a 的取值范围_______。
9.如果方程2-x a +3=x x
--21有增根,那么a 的值是__________.
10.当x __________时,x x
---13112的值与x +15的值互为相反数.
三、解答题(共48分)
1.解方程(每题5分,共10分)
(1)32651222-=+----x x x x x x x
(2)114112=---+x x x
2.(8分)先化简后求值:
5
21043242)()(])([y xy x y x x xy y y x xy -÷⋅-⋅--,其中y =-1.
3. (10分)请你先化简,再选一个使原式有意义,而你又喜爱的数代入求值: )142(282232++⋅-÷++-+x x x x x
x x x x。
