交流电桥实验报告
交流电桥实验报告

大学物理实验报告(交流电桥)一、实验目的:1 .了解交流桥路的特点和调节平衡的方法2 .学会使用交流电桥测量电容3 .学会使用交流电桥测量电感二、实验原理:图4-13-1是交流电桥的原理线路。
它与直流单臂电桥原理相似。
在交流电桥中,四个桥臂一般是由交流电路元件如电阻、电感、电容组成;电桥的电源通常是正弦交流电源;交流平衡指示仪的种类很多,适用于不同频率范围。
频率为200Hz 以下时可采用谐振式检流计;音电子指零仪器;也有用电子示波器或交流毫伏表作为平衡指示器的。
本实验采用高灵敏度的电子放大式指零仪,具有足够的灵敏度。
指示器指零时,电桥达到平衡。
一、交流电桥的平衡条件我们在正弦稳态的条件下讨论交流电桥的基本原理。
在交流电桥中电桥的一个对角线cd 上接入交流指零仪,另一对角线ab 上接入交流电源。
Z Z ==•ZxZ 34当其他桥臂的参数已知时,就可决定被测阻抗Z x 的值。
二、交流电桥平衡的分析x下面我们对电桥的平衡条件作进一步的分析。
在正弦交流情况下,桥臂阻抗可以写成复数的形式Z =R +jX =Ze2若将电桥的平衡条件用复数的指数形式表示,则可得Ze j q-Ze j 93=Ze j 92♦Ze j 匕当调节电桥参数,这时有 使交流指零仪中无电流通过时(即I 0=0),cd 两点的电位相等,电桥达到平衡, 即: U =U acad IZ =IZ U 二U cb (两式相除有: 44 IZ 4^~4IZ33 dbI 2Z2=I 3Z3 当电桥平衡时所以 I =0, 0 由此可得: ZZ =ZZ 1324I =I, 12I =I 34 (4-13-1) 上式就是交流电桥的平衡条件,它说明:当交流电桥达到平衡时,相对桥臂的阻抗的乘积相等。
由图4-13-1可知,若第一桥臂由被测阻抗Z 构成,则:x 频范围内可采用耳机作为平衡指示器; 频或更高的频率时也可采用 四个桥臂由阻抗元件组成,在 图4-13-1交流电桥原理Z •Ze j (*+中3)=Z •Ze j (中2+中4)根据复数相等的条件,等式两端的幅模和幅角必须分别相等,故有「ZZ =ZZ上面就是平衡条件的另一种表现形式,可见交流电桥的平衡必须满足两个条件:一是相对桥臂上阻抗幅模的乘积相等;二是相对桥臂上阻抗幅角之和相等。
交流电桥实验报告

交流电桥实验报告实验目的,通过交流电桥实验,了解电桥的原理和应用,掌握交流电桥的测量方法。
实验仪器和材料,交流电桥仪器、电阻箱、电感箱、电容箱、示波器、交流电源等。
实验原理,电桥是一种用来测量电阻、电感和电容的仪器。
当电桥平衡时,电桥两端电压为零,此时电桥的两侧电路中的电阻、电感、电容之间满足一定的关系。
利用电桥平衡条件,可以测量未知电阻、电感和电容值。
实验步骤:1. 搭建交流电桥电路,连接好示波器和交流电源。
2. 调节电阻箱、电感箱、电容箱的数值,使得电桥平衡。
3. 记录下电阻箱、电感箱、电容箱的数值,以及示波器上显示的波形。
4. 重复多次实验,取平均值作为最终结果。
实验结果,通过实验测得未知电阻、电感和电容的数值,并且观察到了示波器上的波形。
根据实验结果计算出了电阻、电感和电容的数值,与理论值基本吻合。
实验分析,通过实验,我们深入了解了交流电桥的原理和应用。
实验中我们发现,当电桥平衡时,两侧电路中的电阻、电感、电容之间满足一定的关系,利用这一关系我们可以测量未知电阻、电感和电容的数值。
同时,通过观察示波器上的波形,我们可以直观地了解电路中的变化。
实验总结,交流电桥实验是一项重要的电路实验,通过实验我们不仅掌握了电桥的测量方法,还加深了对电阻、电感和电容的理解。
实验中我们需要仔细调节电路,确保电桥平衡,同时还要注意观察示波器上的波形,以获得更准确的实验结果。
实验存在的问题,在实验过程中,我们发现电路的连接和调节需要一定的技巧,有时候可能会出现误差。
因此,在今后的实验中,我们需要更加细心地操作,以确保实验结果的准确性。
通过本次交流电桥实验,我们对电桥的原理和应用有了更深入的了解,同时也掌握了一种新的电路测量方法,这对我们今后的学习和科研工作都具有重要意义。
交流电桥实验报告完整

交流电桥实验报告完整交流电桥实验报告完整引言:交流电桥是一种用于测量电阻、电感和电容的电路。
它是由德国物理学家威廉·韦伯于1843年发明的。
交流电桥实验通过比较未知电阻与已知电阻之间的电压差异来确定未知电阻的值。
本实验旨在通过交流电桥实验,了解电阻、电感和电容的基本原理,并学习使用交流电桥进行测量。
实验仪器和材料:- 交流电桥- 变压器- 电阻箱- 电感线圈- 电容器- 示波器- 电源实验步骤:1. 连接电路:首先,将交流电源接入交流电桥,将示波器连接到交流电桥的输出端,以便观察电路中的交流信号。
然后,将未知电阻与已知电阻连接在一起,形成一个电桥电路。
最后,将变压器接入电路,用于调节交流电压的大小。
2. 调节电桥平衡:通过调节已知电阻箱的阻值,使得电桥电路中的交流信号尽可能接近于零。
当电桥平衡时,表示已知电阻和未知电阻之间的电压差为零,即两者阻值相等。
3. 测量未知电阻:当电桥平衡时,记录已知电阻箱的阻值。
然后,通过调节未知电阻箱的阻值,使得电桥再次平衡。
此时,记录未知电阻箱的阻值。
通过对比已知电阻和未知电阻的阻值,可以确定未知电阻的值。
4. 测量电感和电容:将电感线圈和电容器分别连接到电桥电路中,重复步骤2和步骤3,可以测量电感和电容的值。
实验结果和分析:通过交流电桥实验,我们成功测量了未知电阻、电感和电容的值。
在实验中,我们发现调节电桥平衡时,需要小心调节已知电阻箱的阻值,以确保电桥电路中的交流信号尽可能接近于零。
这样可以提高测量的准确性。
在测量未知电阻时,我们发现通过调节未知电阻箱的阻值,使得电桥再次平衡时,可以确定未知电阻的值。
这是因为当电桥平衡时,表示已知电阻和未知电阻之间的电压差为零,即两者阻值相等。
因此,通过比较已知电阻和未知电阻的阻值,我们可以确定未知电阻的值。
类似地,通过测量电感和电容,我们可以使用交流电桥确定它们的值。
电感和电容的测量原理与电阻类似,只需将电感线圈和电容器连接到电桥电路中,然后调节电桥平衡,记录已知阻值和未知阻值,即可确定电感和电容的值。
交流电桥 大学物理实验

交流电桥一.引言直流电桥是精测直流电阻的仪器,本实验所研究的交流电桥则是用来测量交流电路中各种元件参数的仪器。
除可测量交流电阻、电感、电容外,还可测量与电感、电容有关的其他物理量,如互感、介电常数、导磁率等。
可见交流电桥在交流测量方面的用途十分广泛。
交流电桥因测量任务的不同而有各种不同的形式,但只要掌握了它的基本原理和测量方法,对于各种形式的交流电桥都比较容易掌握。
本实验通过几种常用交流电桥电路来测量电感、电容等参数,以加深了解交流电桥的平衡原理、掌握调节交流电桥平衡的方法。
二.目的要求1.掌握交流电桥的平衡条件和测量原理。
2.掌握交流电桥平衡的调节方法。
3.学会使用LCR数字电桥测量电感、电容等元件参数。
三.原理需要了解以下内容:1.电感、电容元件的等效电路及有关参数2.交流电桥及其平衡条件3.常用的交流电桥电路(1)电感电桥(2)麦克斯韦(Maxwell)电桥y 电桥(3)海氏(Ha s)(4)电容电桥4.交流电桥平衡的调节四.仪器用具无感电阻箱三个(其中一个固定置放1000Ω,0.1级),标准电感一个(0.1H,0.1级),标准电容一个(0.1μF,0.2级),信号发生器一台,交流毫伏表一台,待测电感(约0.12H),待测电容(约0.1μF),LCR数字电桥。
五.实验内容1.按本实验所述三种测量电感电桥中任选一种且自组,测量待测电感线圈的电感量L X、损耗电阻r X及品质因数Q,测量频率为1KHz。
2.测量待测电容器的电容量C X、损耗电阻r X及损耗因数tanδ,测量频率为1KHz。
3.用LCR数字电桥分别测量待测电感的电感量L X、损耗电阻r X、品质因数Q和待测电容的电容量C X、损耗电阻r X及损耗因数tanδ。
4.将数字电桥与自组桥测得的结果相比较。
六.注意事项1.仪器用具较多,位置摆放要适当,避免因导线纵横交错而干扰指示器的正常工作。
2.接线时,各仪器的接线柱不可拧得过死;调节时,各仪器旋钮不可过力旋转,以免将它们损坏或将其内部接线扭断。
交流电桥2

交流电桥 实验报告 4+原始数据:(参考值:13.0x L mH 、10.0L R Ω ) ⑵测量电容的数据: (参考值:0.68x C F μ 、0.65x R Ω ) 注:试验用10号机器1500f Hz =已知公式:测电感:23x s L R R C =231R R R R ⋅=x R R R '=-2xxxxL L Q R R ωπγ==测电容:21x s R C C R =12x x R R R R =tan 2Q CR CR δωπγ===数据处理: ⒈测电感:平均值:0.01636x L H ≈、37.1x R ≈Ω测量误差偏大品质因数: 4.16Q ≈⒉测电容:平均值:76.3410x C F -≈⨯、0.2x R ≈Ω√品质因数:31.2110Q -=⨯√试验总结:本实验的误差主要在于实验者的耳朵对声音的不敏感程度,由于耳朵长时间听同一个频率的声波,听到最后都不能分辨到底有没有声音了,而且需要测量的数据中有的很小,而测量仪器的量程很大,因此也增加了很大的误差,这导致我最后的时间结果和理论值差得比较远。
本实验的难点在于同时调节两个可变参量来寻找平衡电路,这是一个漫长过程,根据给出的参考值反推回去,并不停的调节两个参数,寻找平衡点。
实验的操作并不复杂,而且有助教老师的耐心辅导,使得我的实验得以顺利的完成。
√ 思考题:⒈利用图2.2.4-7、图2.2.4-8(见书P91,图略)求出x L 及x R 的有关公式,此电路在调平衡时是否方便?为什么?答:⑴对图2.2.4-7,有:()()1122123334s x x x x sZ R Z R R R j L R R R j L Z R R j L Z R j L ωωωω⎧=⎪=⎪⇒+=++⎨=++⎪⎪=+⎩实部虚部分别相等,整理后,得:()1312321122x x s x x s R R R R R R R R R R R R L R L L LR ⎧=-⎪=+⎧⎪⎪⇒⎨⎨=⎪⎩⎪=⎪⎩√ ⑵对图2.2.4-8,有:()11123123132411x x x xZ R j C Z R R R j L R R j C Z RZ R j L ωωωω⎧=+⎪⎪⎛⎫⎪=⇒++=⎨ ⎪⎝⎭⎪=⎪⎪=+⎩时部虚部分别相等,整理后,得:2212311232221112311222111101x x x x x xL R R R C R R R R R C R C R R R C R j L L j C R C ωωωωω⎧⎧+==⎪⎪+⎪⎪⇒⎨⎨⎪⎪+==⎪⎪+⎩⎩√以上两个电路在调节平衡的时候都不方便,因为最终数据的计算式都含有两个可变电阻阻值,因此在调节这两个可变电阻时,他们会彼此干扰。
交流电桥实验报告
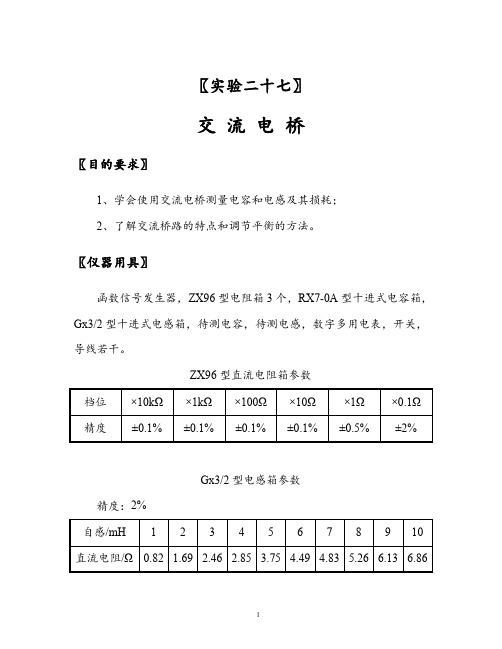
〖实验二十七〗交流电桥〖目的要求〗1、学会使用交流电桥测量电容和电感及其损耗;2、了解交流桥路的特点和调节平衡的方法。
〖仪器用具〗函数信号发生器,ZX96型电阻箱3个,RX7-0A型十进式电容箱,Gx3/2型十进式电感箱,待测电容,待测电感,数字多用电表,开关,导线若干。
ZX96型直流电阻箱参数档位×10kΩ×1kΩ×100Ω×10Ω×1Ω×0.1Ω精度±0.1%±0.1%±0.1%±0.1%±0.5%±2%Gx3/2型电感箱参数精度:2%自感/mH12345678910直流电阻/Ω0.82 1.69 2.46 2.85 3.75 4.49 4.83 5.26 6.13 6.86RX7-0A 型电容箱参数工作电压:250V AC ,零容量:C 12+C 20=72pF 档位×0.1μF ×0.01μF×0.001μF ×0.0001μF 精度±0.5%±0.65%±2%±5%〖实验原理〗1、交流电桥及其平衡条件交流电桥的原理电路如图所示,Z 1、Z 2、Z 3、Z 4、分别为4个桥臂的复阻抗。
调节各臂阻抗,使电桥达到平衡,即A 和B 两点间的电位差为零,此时有:3124Z Z Z Z 这就是交流电桥的平衡条件。
将它用复指数形式表示,可化为:31241234Z Z Z Z ϕϕϕϕ=-=-由此可见,交流电桥平衡时,除了阻抗大小满足比例关系式外,阻抗的相角还要满足一定关系,这是它和直流电桥的主要差别。
为了配置简单,很多交流电桥常用纯电阻作为其中的两个臂。
由相位关系,如果纯电阻作为相邻的两个臂,则其他两个臂必须都是电感性的或都是电容性的阻抗。
如果相对两个臂是纯电阻,则其他两个臂必须一个是电感性的,另一个是电容性的阻抗。
交流电桥实验报告

交流电桥实验报告导言:交流电桥是一种重要的电路检测仪器,用于测量电阻、电感和电容等元件的物理特性。
通过调节电桥的参数,我们可以准确地测量元件的阻抗、频率响应等参数。
本实验旨在研究交流电桥的基本原理和工作原理,并利用实验数据进行分析和讨论。
实验装置:本实验使用的交流电桥由稳流电桥和平衡电桥组成。
稳流电桥负责产生稳定的交流电压,平衡电桥则用于测量被测元件的阻抗值。
实验装置还包括电感和电容箱,用于提供被测元件的替代电路。
实验步骤:1. 首先,将稳流电桥和平衡电桥正确地连接起来,并确保所有电路接线正常。
注意避免触碰电路部件,防止触电危险。
2. 接下来,调节稳流电桥的参数,使电桥产生所需的交流电压。
可以使用示波器等仪器确认输出电压的波形和频率。
3. 将被测元件连接到平衡电桥的测试端口,并通过调节电桥的参数寻找阻抗平衡点。
此时,电桥两侧电压相等,不会流过探测电流。
4. 记录平衡点的参数,包括电桥电流、电压和被测元件的阻抗值。
5. 重复以上步骤多次,以获得更准确的实验数据。
实验结果与讨论:我们通过实验获得了多组数据,并利用这些数据展开了进一步的讨论。
首先,我们观察到在稳流电桥的输出电压不变的情况下,当被测元件的阻抗发生变化时,平衡电桥的电桥电流也随之变化。
通过这种变化,我们可以间接地获取到被测元件的阻抗信息。
其次,我们讨论了电感和电容对交流电桥实验的影响。
实验中,我们选择了不同的电感和电容值,并观察了在不同参数下的平衡电桥状态。
我们发现,当电感或电容值较大时,平衡电桥的调节参数范围更大,调节相对容易;而当电感或电容值较小时,平衡点的调节相对困难。
此外,我们还讨论了交流电桥的精确性和误差来源。
实际操作中,我们发现在寻找平衡点时存在一些难以排除的误差,例如误读仪器数据或电路中的接触问题。
这些误差会对实验结果产生一定的影响。
因此,我们需要在实验中注意操作的准确性,并尽可能减小误差。
结论:通过本次交流电桥实验,我们加深了对交流电桥的理解,并初步认识了如何正确操作该设备。
电桥特性实验报告

一、实验目的1. 理解并掌握电桥的基本原理和测量方法。
2. 熟悉不同类型电桥(如惠斯通电桥、双臂电桥、交流电桥)的特性和应用。
3. 学习如何通过调节电桥参数来达到平衡状态,并利用电桥测量电阻、电容和电感等参数。
4. 分析实验数据,评估电桥的测量精度和误差来源。
二、实验原理电桥是一种测量电阻、电容和电感等参数的电路。
它由四个桥臂组成,通过调节桥臂参数使电桥达到平衡状态,从而实现参数的测量。
1. 惠斯通电桥:由四个电阻组成,用于测量未知电阻值。
当电桥平衡时,电桥对角线上的电位相等,通过测量已知电阻和未知电阻的比值,可以计算出未知电阻的值。
2. 双臂电桥:由四个电阻和一个电流源组成,用于测量低电阻值。
通过采用四端接法,可以消除接触电阻的影响,提高测量精度。
3. 交流电桥:由电阻、电容和电感等元件组成,用于测量电容、电感和品质因数等参数。
通过调节电桥参数,使电桥达到平衡状态,可以计算出待测元件的参数。
三、实验仪器与设备1. 惠斯通电桥实验仪2. 双臂电桥实验仪3. 交流电桥实验仪4. 待测电阻、电容和电感5. 检流计6. 交流电源7. 导线8. 计算器四、实验内容与步骤1. 惠斯通电桥实验:(1) 按照电路图连接惠斯通电桥实验仪。
(2) 调节已知电阻和未知电阻的比值,使电桥达到平衡状态。
(3) 记录已知电阻和未知电阻的值,计算未知电阻的测量结果。
2. 双臂电桥实验:(1) 按照电路图连接双臂电桥实验仪。
(2) 调节已知电阻和未知电阻的比值,使电桥达到平衡状态。
(3) 记录已知电阻和未知电阻的值,计算未知电阻的测量结果。
3. 交流电桥实验:(1) 按照电路图连接交流电桥实验仪。
(2) 调节电桥参数,使电桥达到平衡状态。
(3) 记录待测元件的参数,计算电容、电感和品质因数的测量结果。
五、实验数据与处理1. 记录实验数据,包括已知电阻、未知电阻、电容、电感等参数的测量值。
2. 分析实验数据,计算测量结果的平均值和标准偏差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
〖实验二十七〗交流电桥〖目的要求〗1、学会使用交流电桥测量电容和电感及其损耗;2、了解交流桥路的特点和调节平衡的方法。
〖仪器用具〗函数信号发生器,ZX96型电阻箱3个,RX7-0A型十进式电容箱,Gx3/2型十进式电感箱,待测电容,待测电感,数字多用电表,开关,导线若干。
ZX96型直流电阻箱参数档位×10kΩ×1kΩ×100Ω×10Ω×1Ω×0.1Ω精度±0.1%±0.1%±0.1%±0.1%±0.5%±2%Gx3/2型电感箱参数精度:2%自感/mH12345678910直流电阻/Ω0.82 1.69 2.46 2.85 3.75 4.49 4.83 5.26 6.13 6.86RX7-0A 型电容箱参数工作电压:250V AC ,零容量:C 12+C 20=72pF 档位×0.1μF ×0.01μF×0.001μF ×0.0001μF 精度±0.5%±0.65%±2%±5%〖实验原理〗1、交流电桥及其平衡条件交流电桥的原理电路如图所示,Z 1、Z 2、Z 3、Z 4、分别为4个桥臂的复阻抗。
调节各臂阻抗,使电桥达到平衡,即A 和B 两点间的电位差为零,此时有:3124Z Z Z Z 这就是交流电桥的平衡条件。
将它用复指数形式表示,可化为:31241234Z Z Z Z ϕϕϕϕ=-=-由此可见,交流电桥平衡时,除了阻抗大小满足比例关系式外,阻抗的相角还要满足一定关系,这是它和直流电桥的主要差别。
为了配置简单,很多交流电桥常用纯电阻作为其中的两个臂。
由相位关系,如果纯电阻作为相邻的两个臂,则其他两个臂必须都是电感性的或都是电容性的阻抗。
如果相对两个臂是纯电阻,则其他两个臂必须一个是电感性的,另一个是电容性的阻抗。
2、测量实际电容的电桥实际电容的介质不是理想的介质,在电路中要损耗一部分能量,故其等效电路可看做是一个纯电容C x 和损耗电阻R C 的串联或并联。
实验中是看成二者串联。
由于有损耗存在,所以正弦交流电通过它时,电容两端的电压与通过的电流之间的相位差φ不是90而是90ϕδ=︒-。
φ是电容器端电压与电流之间的相位差,δ称为电容器的损耗角,它随损耗电阻R C 的增加而变大,是衡量电容质量优劣的参数。
为了方便,用损耗角正切来表示,称为损耗,tan C R Cδω=测量电路如图,C 为标准电容,它的损耗电阻在低频时实际近于零;为了与R C 相平衡,又串联了电阻R 0。
根据平衡条件:102011C x R R j R R j C C ωω⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭令其两端实部虚部分别相等:21001200,tan x C C x R RC C R R R R R C R C δωω====反复调节C 0和R 0的数值,直到交流电桥示零器示数达到最小。
为了提高精度,使得R 1和R 2相等,此时C x 和C 0也相等。
该电桥适合测量损耗小的电容。
3、测量电感的电桥:麦克斯韦—维恩电桥这是一种测量电感最常用的电桥,电路如图所示:由平衡条件得:01212x L L C R R R R R R ==平衡时,被测线圈的Q 值为:00xLL Q C R R ωω==式中:C 0和R 0为独立变量,反复调节可以使电桥很快达到平衡。
此电桥只适合测量低Q 值的线圈。
4、交流电桥的收敛性要使交流电桥达到平衡,至少需要选择两个调节参量,经反复调节,使电桥逐步趋于平衡。
但是,不是任选两个参量调节都能使电桥达到平衡;而选择的调节参量不同,使电桥趋于平衡的快慢也不一样。
用电桥收敛性来表示能否通过调节使电桥逐步达到平衡,而收敛性的好坏则反映电桥达到平衡的快慢。
对测量电感L 的麦克斯韦桥,如上图,由平衡条件可得:()12102x L L R L L R R R R R R ==+这里可调参量较多,有R 1、R 2、C 0、L 0和R 0,选择哪两个作为可调参量,电桥的收敛性较好呢?将交流毫伏表的内阻近似为正无穷,可得:()()23141234AB Z Z Z Z u uZ Z Z Z -=++当电桥接近平衡时,表达式的分子接近于0,分母却比较大;此时若微调各参量,分母的相对改变量很小,几乎不变,u AB 的大小几乎正比于表达式的分子的大小。
如果在复数平面上以横坐标轴代表Z 的实部Re Z ,纵轴代表Z 的虚部Im Z ,令:()()023214100L x L A Z Z R R j L B Z Z R R R j L N A Bωω==+==++=-在复数平面上作A 和B ,当所选的调节参量使A 和B 两个矢量之差N 为零时,零示器指零,电桥达到平衡。
下面分析调节各个参量A 或B矢端变化的轨迹,参见下图:(1)调节R 1:调R 1使矢量B 的斜率不变,只是长度改变,B 的矢端轨迹为Oa 线[见图a];(2)调节R 2:调R 2使矢量A 的斜率不变,只是长度改变,A 的矢端轨迹为Ob 线[见图a];(3)调节L0:调L0使B的实数部分不改变,只是虚数部分改变,B 的矢端轨迹为cd线[见图a];(4)调节R0:调R0使B的虚数部分不变,只是实数部分改变,B的矢端轨迹为ef线[见图a]。
由图b可见,如果选择L0和R0为调节参量,只需调节R0使B到g1点,再调节L0,B与A重合,电桥达到平衡。
或先调节L0到g2点,再调R0,同样只经过两次调节,电桥就达到平衡。
在实验中,R0用六钮电阻箱,可认为数值是连续变化的,而L0用一钮十进式电感箱,不是连续可调,所以测电感时只能将L0放在与L x 接近的数值后,调节R0使B沿eb线移至"1"[见图c],再选择调R2使A 沿Ob线移至"2",每调节一次只能使N在该情况下达到最小,如此反复调节R0和R2,最后便A和B的矢端均达到b点,此时N=0,电桥调节达到平衡。
从平衡条件式中也能看出,两个平衡条件中都含有R2,因此R2的每一次改变对两个平衡条件都有影响,互相牵制,必须反复调节。
因此,在实际工作中很少选择R2这样的参量来调节电桥平衡。
而在上文中所介绍的前两种电桥,由于两个互相独立的变量C0和R0均可视为连续变化的,故收敛性均较好,是比较实用的电桥。
〖实验内容〗用函数信号发生器提供频率约为1kHz、电压为4V的正弦交变电压。
用数字多用电表的交流毫伏挡作零示器。
1、测电容测量一个纸质电容器及一个电解电容器的电容及损耗电阻,并计算它的损耗,电路图实验原理中对应的图,其中R1、R2、R0均用电阻箱,R1和R2选用几百欧姆为宜。
标准电容C0用十进式电容箱,它的损耗电阻在低频时很小。
2、测电感用麦克斯韦桥和麦克斯韦—维恩电桥分别测量同一无铁芯电感器的电感L x和损耗电阻R L并计算电感线圈的Q值,并比较两桥的收敛性。
〖数据记录〗使用⑨号盒子中的元件进行测量。
1、纸质电容R1=R2=500Ω;C0=0.2353μF,R0=2.8Ω;U min=0.16mV,f=0.9991kHz。
2、电解电容R1=1kΩ,R2=10kΩ;C0=0.6576μF,R0=44.8Ω;U min=0.00mV,f=998.13Hz。
3、麦克斯韦—维恩桥测电感取R1=R2=150Ω,f=997.88Hz;先取R0=2250Ωi R0/ΩC0/μF U ab/mV12250.4352722215.80.435 1.073215.80.43630.004、麦克斯韦桥测电感取R1=2kΩ,首先调节L0到10mH,其直流电阻为6.86Ω;先取R0=100Ω。
i R0/ΩR2/ΩU ab/mV11002045.0 4.20299.42045.0 2.25399.42041.2 1.67499.32041.2 1.45599.32038.9 1.31699.22038.9 1.01799.22037.80.95899.12037.80.76999.12036.40.601099.02035.20.231199.0(98+0.1*10)2034.90.221299.0(98+0.1*10)2034.80.18〖数据处理及结果〗(使用⑨号盒子中的元件)1、纸质电容()()()()1200500.00.6,500.00.6;0.2350.003, 2.800.04.R R C F R =±Ω=±Ω=±=±Ω()()012012201222120102222120000.235 1.483%0.0030.2350.0032.80 1.453%0.042.800.04tan 4.1xCC x CC R R x C x C RR R R C R C R C C FR C R R C FC F R R R R R R R R R R C μσσσσσμμσσσσσδω==⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈∴=±==Ω⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈Ω∴=±Ω==()003222tan 003tan 330610 2.06%tan 0.08510tan 4.130.0810R C f R C f δδσσσσδσδ---⨯⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈⨯∴=±⨯2、电解电容()()()()()12001.0000.006,10.0000.006;0.6580.003,44.80.1;998.130.01.R k R k C F R f Hz μ=±Ω=±Ω=±=±Ω=±()()01201220122212010222212000 6.580.7835%0.056.580.054.480.6349%0.02844.480.03tan 0.1xCC x CC R R x C x C RR R R C R C R C C F R C R R C FC F R R R R R R R R R R C μσσσσσμμσσσσσδω==⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈∴=±==Ω⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈Ω∴=±Ω==0222tan 003tan 84870.5860%tan 1.0810tan 0.1850.001R C f R C f δδσσσσδσδ-⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈⨯∴=±3、麦克斯韦—维恩桥测电感()()()()()1200150.00.6,150.00.6;0.4360.003,215.80.6;997.880.01.R R C F R f Hz μ=±Ω=±Ω=±=±Ω=±()()0120120122221201202221209.81000.963%0.0949.810.09104.2630.630%0.657104.30.7xx LC x LC R R x L x L R RR R L R C xLL C R R mHL R R C FL mH R R R R R R R R R L Q C R σσσσσμσσσσσωω==⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈∴=±==Ω⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈Ω∴=±Ω==0000222000.589920.742%0.00440.5900.004R C Qf Q R Q R C f Q σσσσσ=⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈∴=±4、麦克斯韦桥测电感()()()()()012002.0000.006, 2.0350.006;10.00.1mH,R 6.86;99.00.1;997.880.01.L R k R k L R f Hz =±Ω=±Ω=±=Ω=±Ω=±()()012000120122221201022221209.828 1.0849%0.1069.80.1104.03930.4311%0.4485104.xx L L L x LL R R x L x L L R R R R R L L R C R L L mH R L R R L FL mH R R R R R R R R R R R σσσσσμσσσσσσ==⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∴≈∴=±=+=Ω+⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭∴≈Ω∴=()00000002220000.40.5922791.004%0.0059490.5920.006L xLL R R L Qf L Q L L Q R R R Q L R R f Q ωωσσσσσσ±Ω===++⎛⎫⎛⎫⎛⎫=++= ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭∴≈∴=±〖思考与讨论〗1、麦克斯韦—维恩桥测电感时,电桥达到平衡的过程图对麦克斯韦—维恩图,按实验原理中图,有:()()()()112003421212124000012341234124012031241,;1,.11111111L x L x L xABL x Z R Z j C R Z R j L Z R R j L R j L R R R R Z Z Z j C j C R R u u u Z Z Z Z Z Z Z Z Z Z Z R j L j C R R R u Z Z Z Z ωωωωωωωω==+=+=⎛⎫⎪++ ⎪-- ⎪++ ⎪⎝⎭=⨯=⨯++++⎛⎫+-+ ⎪⎝⎭=⨯⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭快达到平衡时,分子趋于零;分母变化极小,而且它的值相对于分子比较大。
