电路分析第四章习题参考答案(供参考)
数电第四章参考答案

第四章 组合逻辑电路 作业 参考答案【题4-1】 分析图示组合逻辑电路,列出真值表,写出输出Y 1、Y 2与输入的逻辑函数式,说明整个电路所实现的逻辑功能(不是单个输出与输入的关系,而是把2个输出与3个输入综合起来看)。
解:该电路的逻辑功能为全加器,Y 1是和,Y 2是进位。
【题4-2】某汽车驾驶员培训班进行结业考试,有三名评判员,其中A 为主评判员,B 和C 为副评判员。
在评判时,按照少数服从多数的原则通过,但主评判员认为合格,方可通过。
请填写真值表,写出逻辑表达式,并用一片74LS00(内含四个2输入端与非门)或一片74LS02(内含四个2输入端或非门)这2种方法实现此评判规定。
解:设评判员评判合格为“1”,反之为“0”; 考试通过,F 为“1”,反之为“0”。
根据题意,列真值表如下。
据此可得:ABC12ABCC B A C B A C B A AC BC AB C B A ABC Y +++=+++++=)()(1AC BC AB Y ++=2ACAB AC AB F =+=CB AC B A F ++=+=)(FB CA FB CA【题4-3】设计一个“4输入1输出”的组合逻辑电路,实现“五舍六入”的功能:即当输入的四位8421BCD 码不大于5时,输出0;否则输出1。
要求: (1) 画出卡诺图、化简逻辑函数;(2) 用1片CD4001(内含四个2输入端或非门)实现该逻辑功能(标出管脚号)。
【题4-4】设计一个代码转换电路,输入为3位二进制代码、输出为3位格雷码(见下表),要求从CD4011、CD4001、CD4030中选用1个最合适的芯片实现逻辑功能。
解:CDAB Y 00X X 0X 011001X XXCA B A C A B A BC A Y +++=++=+=))((FB CA21313546121101000111XABC00011011YABC0010111ZABCAX =BA B A B A Y ⊕=+=CB C B C B Z ⊕=+=B CAYZX【题4-5】用一片74HC138(3-8译码器)辅以“4输入与非门”实现“1位全减”。
《电路第五版课后习题答案

答案及解析115答案第一章电路模型和电路定律【题1】:由U A B 5 V 可得:IA C 2.5 A:U DB 0 :U S 125. V。
【题2】:D。
【题3】:300;-100。
【题4】:D。
【题5】: a i i 1 i 2 ; b u u1 u2 ; c u u S i i S R S ; d i iS1RSu u S 。
【题6】:3;-5;-8。
【题7】:D。
【题8】:PU S 1 50 W ;P U S 2 6 W ;P U S3 0 ;P I S 1 15 W ;P I S2 14 W ;P I S 3 15 W 。
【题9】:C。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
1【题14】:3 I 1 2 3 ;IA 。
3【题15】:I 4 3 A;I 2 3 A;I 3 1A;I 5 4 A。
【题16】:I 7 A;U 35 V;X 元件吸收的功率为P U I 245 W。
【题17】:由图可得U E B 4 V;流过 2 电阻的电流I E B 2 A;由回路ADEBCA 列KVL 得U A C 2 3I ;又由节点 D 列KCL 得I C D 4 I ;由回路CDEC 列KVL 解得;I 3 ;代入上式,得U A C 7 V。
【题18】:P1 P2 2 II212222 ;故I I122;I 1 I 2 ;⑴KCL:43I I ;I 11 12858A;U I 1 I 1 V 或 1.6 V;或I 1 I2 。
S 2 15⑵KCL:43I I ;I1 121 8 A;U S 24V。
第二章电阻电路的等效变换【题1】:[解答]I9 47 3ab 9 4 8.5 V;A =0 .5 A ;U II 1 U 6ab . A ;P 6 1.2 5 W = 7 .5 W ;吸1 252收功率7.5W。
【题2】:[解答]【题3】:[解答] C。
第四章(习题答案)

§4-3 戴维宁定理和诺顿定理
(一)戴维宁定理的证明
设流过端口以外的电路中的电流为 i,则据替代定 ,则据替代定 理,外电路可以用一个电流为 i的电流源 iS替代,如图(a)所 替代,如图(a) (a)所 示;则又据 叠加定理,得其相应的分电路 (b),(c): 示;则又据叠加定理 ,得其相应的分电路(b) (c): 叠加定理,得其相应的分电路 (b),
:在线性 线性电路中,任一支路的电流或电 叠加定理 :在 线性 电路中,任一支路的电流或电 压是电路中各个独立电源(激励) 单独作用 时在 压是电路中各个独立电源(激励)单独作用 单独作用时在 该支路中产生的电流或电压的 代数和. 该支路中产生的电流或电压的代数和 代数和.
§4-1 叠加定理
也就是说,只要电路存在唯一解,线性电路中 的任一结点电压,支路电压或支路电流均可表示为 以下形式: y = H 1uS1 + H 2 uS 2 + + H m uSm + K 1 iS1 + K 2 iS 2 + + K n iSn ——表示电路中独立 其中:uSk 表示电路中独立电压源的电压 独立电压源的电压
+ Req + u RL
uS1
NS
uS2
RL
口 含一 源 端
1
戴维宁定理
- -
uoc
维 宁 等 效 电 路
1' i1
RL
isc
1'
1'
u R Geq L
-
+
诺顿定理
诺 顿 等 效 电 路
1'
§4-3 戴维宁定理和诺顿定理
对外电路而言,"含源一端口NS"可以用一条含源支路 对外电路而言," 含源一端口N 可以用一条含源支路 等效替代 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机 戴维宁等效电路和诺顿等效电路称为一端口的等效发电机
《电路分析基础》第一章~第四章练习题

1、电路;2、理想器件;3、电路模型;4、电路模型;5、集总参数元件;6、几何尺寸;7、用来描述电路性能;8、i u q ψ;9、正电荷;10、参考方向;11、电位差;12、电流参考方向与电压降的选择一致;13、P(t)=dW(t)/ dt;14、吸收功率产生功率;15、能量传输;16、任意选取;17、任意选取;18、一条支路;19、支路电压;20、支路电流;21、节点;22、回路;23、网孔;24、网络;25、拓扑约束;26、元件约束;27、拓扑约束元件约束;28代数和;29、支路电流;30、电压降;31、路径;32、线性;33、原点;34、电导;35、线性电阻非线性电阻;36、P=UI;37电源;38、外电路;39、外电路;40、串联;41、并联;42、分压;43、分流;44、控制受控;45、控制量;46、n-1 b-n+1;47、线性电路;48、线性含源;49、完备性独立性;50、假设;51、网孔分析法;52、KVL;53、独立节点;54、单口网络;55、端口电压与电流的伏安关系等效电路;56、外接电压源外接电流源;57、外接电路;58、非线性电路;59、伏安特性曲线;60、网络内部;61、理想电压源;62、理想电流源;63、一个理想电压源uS;64、一个理想电流源iS;65、大小相等且极性一致;66、大小相等且方向一致;67、线性含源单口网络;68、uOC/iSC;69、外加电源法开路短路法;70、负载RL应与戴维南等效
三、计算分析题
1、电路如图1所示,已知us 12V,试求u2和等效电阻Rin。
2、电路如图2所示,试求电流i和电压u。
3、电路如图3所示,试用叠加定理求电压U和电流I。
4、电路如图4所示,试用叠加定理求电压U。
5、电路如图5所示,试用叠加定理求电压U和电流I。
电路与电子技术基础第四章习题答案
解:本题是求零输入响应,即在开关处于 a 时,主要是电感储能,当开关投向 b 后, 讨论由电感的储能所引起的响应。所以对图(a)t≥0 时的电路可列出 di L L + Ri L = 0 t≥0 dt 及 iL(0)=i(t)=10(mA) 其解为: i L (t ) = 10e
而
t≥0
i R (t ) = −i L (t ) = −10e −10 t (mA)
7
t≥0
其波形图见图(b)、图(c)所示。 4-5 电路如题图 4-4 所示,开关接在 a 端为时已久,在 t=0 时开关投向 b 端,求 3Ω电 1Ω a b 阻中的电流。 i (t ) 解:因为 u c (0) = 3 × 2 = 6(V ) (注意:当稳态以后电容为开路,所以流过 1 3A Ω和电容串联支路的电流为零, 因此电容两端的电 压就是并联支路 2Ω支路两端的电压) 当开关投向 b 时电流的初始值为
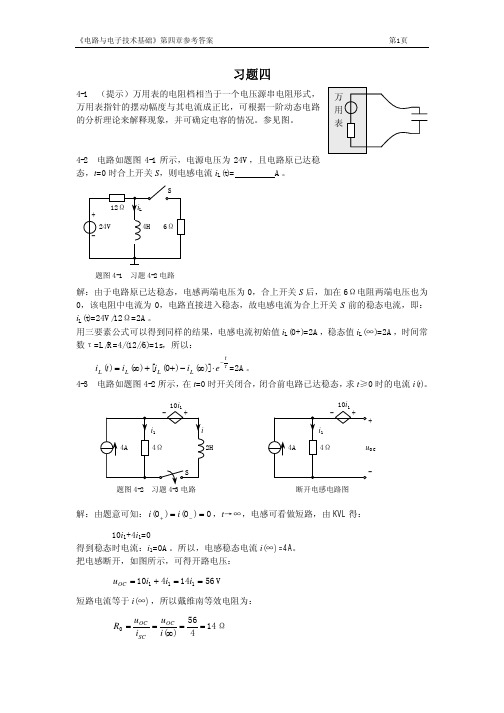
S 12Ω + 24V iL 4H 6Ω
题图 4-1
习题 4-2 电路
解:由于电路原已达稳态,电感两端电压为 0,合上开关 S 后,加在 6Ω电阻两端电压也为 0,该电阻中电流为 0,电路直接进入稳态,故电感电流为合上开关 S 前的稳态电流,即: iL(t)=24V/12Ω=2A。 用三要素公式可以得到同样的结果,电感电流初始值 iL(0+)=2A,稳态值 iL(∞)=2A,时间常 数τ=L/R=4/(12//6)=1s,所以:
当 t=0 时,开关打开,由于电感电流、电容电压均不跃变,有: i L (0 + ) = i L (0 − ) = 0.03( A) 1k u c (0 + ) = u c (0 − ) = 120(V ) 当 t≥0 时,根据基尔霍夫定律有
电路分析基础答案周围版第四章汇编

解:( 1)由电压波形图写出电容端电压的表达式:
10t
0μst 1μs
10
1μst 3μs
u(t )
10t 40 3μst 4μs
依据换路定理: u1 0 u1 0 10V , u2 0 u2 0 0 ,
t0
10
10 K
i2 t
10V u1 C13μF u2 C22μF
i2 0
u1 0 u2 0
10V 0 1A
10
10
4-19 .电路如图所示,设开关 K 在时间 t 0 时断开。开
关 K 断开前一瞬间,电容端电压为 6V。试求: t 0 时,
i0 i0
20 5 2A ; u 0 20 30
10 i 0 20V
更多精品文档
学习 ----- 好资料 4-15.电路如左图所示。换路前电路处于稳态。
t 0 时电路换路。
求换路后瞬间 u1 0 、 u2 0 、 i2 0 。设 u2 0 0 。
解:换路前,电路处于稳态,故: u1 0 10V 。
t 0 时电路换路,求换路后瞬间 u 0 、 i 0 。
t0
30
K 20
ut 5A 10
it
8H
20
5A
30
30
i0Βιβλιοθήκη i 0 10 u t8H
解:换路前,电路处于稳态,故:
uL 0
L diL 0 ,电路简化为中图所示电路。依据分流公式有: dt
i0
20 5 2A
20 30
电路第4章作业答案
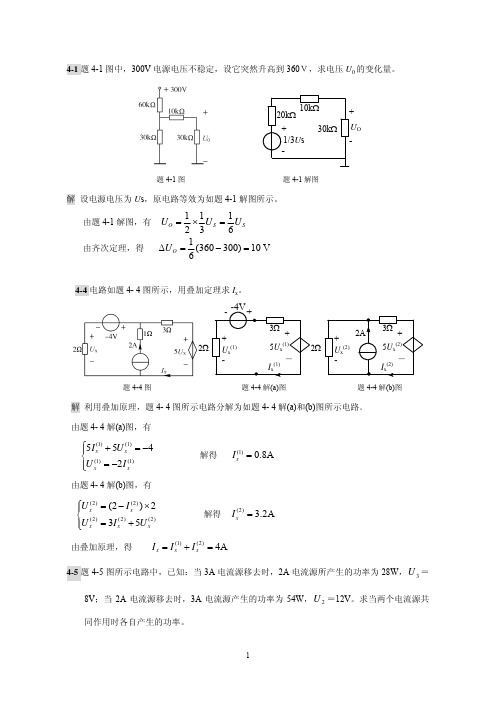
(1) 利用 Req 求 gm,电压源 Us 置零,如题 4-19 解(b)图所示。 采用外加电源法,得
Req =
RS 1 + g m RS
从而,得
所以,有
0.5 =
1 1 + gm
gm = 1
(2) 利用 Uoc 求 Us,将 RL 断开
8
U S = RS g mU OC + U OC = 2U OC = ±1V
Req = 12 // 4 + 6 = 9Ω
+
12Ω 6Ω 4Ω
+ 6V
ቤተ መጻሕፍቲ ባይዱ
-
8V
9Ω
16Ω
题 4-11 解(a)图
题 4-11 解(b)图
题 4-11 解(c)图
(3) 等效电路如题 4-11 解(b)图所示。 (b)解 (1)求开路电压,如题 4-11(b)图所示,有
U OC = U ab = −9 + 6 × 2 + 3 = 6 V
(2) 求等效电阻 Req,将题 4-11(b)图所示电路中独立电源置零,得
Req = 6 + 10 = 16Ω
(3) 等效电路如题 4-11 解(c)图所示。 (c)解 (1)求开路电压,如题 4-11(c)图所示,有
U OC = 2 I1 − 2 I1 = 0 V
(2) 采用外加电源法求等效电阻 Req,如题 4-11 解(d)图所示,有
200 I1 + 200 I1 = 40
求得 I1=0.1A UOC=10V
所以,有
4I1 50Ω 50Ω
a I1 100Ω b 50V RL 5Ω
+
200I1 50Ω
数字电路第四章习题答案

第四章习题4.4 由两个与非门构成的基本RS 触发器的输入如图P4.4所示,画出Q 和Q 端的波形。
图 P4.44.5 由两个或非门构成的基本RS 触发器的输入波形如图P4.5所示,画出输出Q 和Q 的波形。
图 P4.54.6 图P4.6是一个防抖动输出的开关电路。
当拨动开关S 时,由于开关触点接通瞬间发生振颤。
D S 和D R 的电压波形如图中所示,试画出Q 、Q 端对应的电压波形。
图P4.64.7 在同步RS触发器中,若CP、S、R的电压波形如图P4.7所示。
画出Q和Q端的波形。
设触发器的初始状态为Q=0。
图 P4.74.10 主从型JK触发器输入波形如图P4.10所示,画出输出端Q和Q的波形。
设触发器初始状态Q=0。
4.11 主从型JK 触发器组成图P4.11(a )所示电路,输入波形如图P4.11(b )所示,画出各触发器Q 端的波形。
(a )解:AB J 1 ,先画出J 的波形,然后画Q.。
4.12 主从型RS 触发器的CP 、S 、R 、DR各输入的电压波形如图P4.12所示,画出端Q 和Q 端对应的电压波形。
图 P4.124.14 维持阻塞D触发器构成图P4.14所示的电路,输入波形如图P4.14(b)所示。
画出各触发器Q段的波形。
触发器的初态均为0。
(b)图 P4.144.16 上升沿触发的维持阻塞型D触发器74LS74组成图(a)所示电路,输入波形如图(b)所示,画出Q1和Q2的波形,设Q初态为0。
4.20 画出图P4.20电路在图中所示CP、R信号作用下Q1、Q2、Q3的输出电压波形,并说明DQ1、Q2、Q3输出信号的频率与CP信号频率之间的关系。
CP1/21/4QQQ频率的、1/8。
、和的频率分别是、132。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4-2 试用外施电源法求图题4-2 所示含源单口网络VCR,并绘出伏安特性曲线。
解:图中u 可认为是外加电压源的电压。 根据图中u所示的参考方向。可列出
(3)(6)(5)20(9)50uiiAVAiV
4-5试设法利用置换定理求解图题4-5所示电路中的电压0u。何处划分为好?置
换时用电压源还是电流源为好?
解:试从下图虚线处将电路划分成两部分,对网路N1有(节点法)
1
1
1
1967(11)uuuui
整理得:
1511714ui
对网络2N有
25
1133uiii
解得3iA,用3A电流源置换N1较为方便,置换后利用分流关系,可得:
1
21031V1Vu
4-9 求图题4-7所示电路的输入电阻Ri,已知0.99
解: 施加电源tu于输入端可列出网孔方程:
12335121(25100)100 (1)100(100100101010)100.990(2)t
iiuiii
将(2)代入(1)得135tiuRi
4-14求图题4-10所示各电路的等效电路。
解
解: 图(a):因电压的计算与路径无关,所以
[5(1)]4(13)4adaccdadabbduuuVVuuuVV
图(b): 流出a点的电流(521)8aiA,流入b点多的电流(541)8biA。
所以ab之间的等效电路为8A的电流源,电流从b 端流出。
图(c):导线短接。
4-23 电路如图题4-15 所示,已知非线性元件A的VCR为2ui。试求u,i,i1.
解: 断开A,求得等效内阻:1oR
开路电压au所满足的方程:
(11)12111/21cacauuuu
求得2auV,最后将A接到等效电源上,如上图所示。
写出KVL:220ii12AiA或
当1iA时,1uV,21120.5,[2(0.5)1]1.52iAAiA
当2iA时,4uV,21421,[212]32iAAiA
4-25 试求图题4-17所示电路中流过两电压源的电流。
解:
4-25(1)
4-25(2)
用分解方法求解
(1) 将电路划分为两部分,如图4-25(1)(a)所示。
(2) 分别将两部分等效化简成4-25(1)(b)所示电路。
(3) 将两部分连接求出i和u。
(4) 用2.736A电流源置换右侧电路后计算15V电压源的电流i1,如图4-25(2)(c)所
示。列节点1的方程
1
1
1
2
11516.58
516881624.4752.4348uuVuiA
4-30 电路如图题4-22所示。
(1) 求R获得最大功率时的数值;
(2) 求在此情况下,R获得的功率;
(3) 求100V电源对电路提供的功率;
(4) 求受控源的功率;
(5) R所得功率占电路内电源产生功率的百分比。
解:(1) 断开R,求出戴维南等效电路,如下图所示。在该图中,令控制量u1=1V
则:
111141,2,(21)320.5,143cbcdacacabab
ac
ab
oab
iiAiAuVuVuuiAiiiAuRRi
即R=3ohm 时可获得最大功率。
(2) 求开路电压,对上图(b)列网孔方程:
12
121
11
(44)4100204(444)4iiiiuui
,解得1215,10iAiA。由求得的Uoc=(4*10+15*6+20)
=120和Ro可构成戴维南等效电路,并由最大功率传递定理可知3R时,可获
得最大功率。故得2120/2331200RPW
(3) 设网孔电流为123,,iii,其中3i即为流过R的电流,即320iA
12
121
113
(44)4100204(444)4()iiiiuuii
12
30,20iAiA
,解得P100V=-3000W
(4)1214(20)20800PuiiW受控源
(5) 201320()20(3020)200VPiiW,1200(3000800)31.58%
4-32 试利用T变换求解图题4-24所示电路中10V电压源的电流i。
解 T型电阻网络化为型电路后的到如下图所示电路。
图中121051055,1891818VVVimAimAkk,所以
12
5
6
iiimA
