3.6 动量和动量守恒定律
第六章-第1讲 动量和动量定理
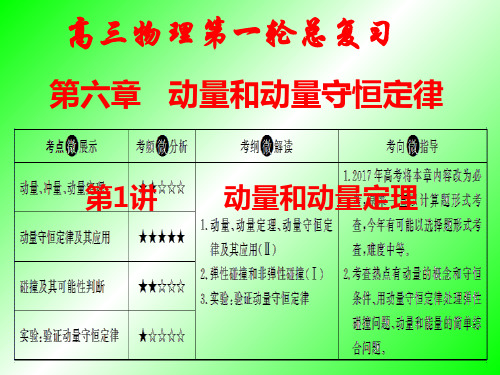
__相__同_______。
3.冲量
(1)定义:力 F 与力的作用时间 t 的乘积 .
(2)定义式:I=Ft .
(3)单位:N·s . (4)方向:恒力作用时,与力的方向相同.
(5)物理意义:是一个过程量,表示力在时间上积累的作用效果.
(F2-mg)t=0-mv(矢量式)
F2=-0.5×0.0-14.0 N+0.5×10 N=205 N, 方向竖直向上。 由牛顿第三定律知,此时铁锤钉钉子的作用力为 205 N,方向竖直向下。 (3)比较 F1 与 F2,其相对误差为|F2-F1F1|×100% =2.5% ,可见本题中重力 的影响可忽略。 答案 (1)200 N,方向竖直向下 (2)205 N,方向竖直向下 (3)见解析
的方向为正方向,根据动量定理(忽略水的重力),有 F′·Δt=Δp=-ρv2SΔt,
即 F′=-ρSv2。
根 据 牛 顿 第 三 定 律 知 F = - F′ = ρSv2 , 式 中 S = π d2 , 代 入 数 值 得
4 F≈1.77×105 N。
答案 1.77×105 N
子题微练
1.为估算池中睡莲叶面承受雨滴撞击产生的平均压强,小明在 雨天将一圆柱形水杯置于露台,测得 1 小时内杯中水面上升了
4.动量定理
(1)内容:物体所受合力的冲量等于物体的动量变化.
(2)表达式:
Ft=mv2-mv1
I=Δp
二、对点微练
1.(动量的理解)(多选)下列关于动量的说法,正确的是(CD )
A.质量大的物体,动量一定大 B.质量和速率都相同的物体,动量一定相同 C.一个物体的速率改变,它的动量一定改变 D.一个物体的运动状态改变,它的动量一定改变 2.(冲量)(多选)恒力 F 作用在质量为 m 的物体上,如图所示, 由于地面对物体的摩擦力较大,物体没有被拉动,则经时间 t,
高中物理选必一第一章动量守恒定律(1动量2动量定理)

第一章动量守恒定律第1节动量知识点一、动量(1)定义:物体质量和速度的乘积,用字母p 表示,p =m v .(2)动量的矢量性:动量既有大小,又有方向,是矢量.动量的方向与速度的方向一致,运算遵循矢量运算法则.(3)单位:国际单位是千克·米每秒,符号是kg·m/s.(4)动量具有相对性:选取不同的参考系,同一物体的速度可能不同,物体的动量也就不同,即动量具有相对性.通常在不说明参考系的情况下,物体的动量是指相对地面的动量.知识点二、动量与速度、动能的区别和联系动量与速度动量与动能区别①动量在描述物体运动方面更进一步,更能体现运动物体的作用效果②速度描述物体运动的快慢和方向①动量是矢量,从运动物体的作用效果方面描述物体的状态②动能是标量,从能量的角度描述物体的状态联系①动量和速度都是描述物体运动状态的物理量,都是矢量,动量的方向与速度方向相同,且p =mv ②动量和动能都是描述物体运动状态的物理量,且p =2mE k 或E k =p 22m知识点三、动量的变化量(1)定义:物体在某段时间内末动量与初动量的矢量差,即Δp =p ′-p(2)动量的变化量Δp 也是矢量,其方向与速度的改变量Δv 相同.(3)因为p =m v 是矢量,只要m 的大小、v 的大小和v 的方向三者中任何一个发生了变化,动量p 就发生变化.(4)动量变化量Δp 的计算①当物体做直线运动时,只需选定正方向,与正方向相同的动量取正,反之取负.若Δp 是正值,就说明Δp 的方向与所选正方向相同;若Δp 是负值,则说明Δp 的方向与所选正方向相反.②当初、末状态动量不在一条直线上时,可按平行四边形定则求Δp 的大小和方向.典例分析一、对动量和动量增量的理解例1关于动量变化,下列说法正确的是()A .做直线运动的物体速度增大时,动量的增量Δp 的方向与运动方向相同B .做直线运动的物体,速度减小时,动量增量Δp 的方向与运动方向相反C .物体的速度大小不变时,动量的增量Δp 为零D .物体做平抛运动时,动量的增量一定不为零二、动量变化量的计算例2羽毛球是速度最快的球类运动之一,林丹扣杀羽毛球的速度可达到342km/h,假设球飞来的速度为90km/h,林丹将球以342km/h的速度反向击回.设羽毛球质量为5g,试求:(1)林丹击球过程中羽毛球的动量变化量.(2)在林丹的这次扣杀中,羽毛球的速度变化、动能变化各是多少?专题一对动量及动量变化的理解例3关于动量的变化,下列说法正确的是()A.做直线运动的物体速度增大时,动量的增量Δp的方向与运动方向相同B.做直线运动的物体速度减小时,动量的增量Δp的方向与运动方向相反C.物体的速度大小不变时,动量的增量Δp为零D.物体做曲线运动时,动量的增量一定不为零专题二对动量及动量变化的计算例4羽毛球是速度较快的球类运动之一,运动员扣杀羽毛球的速度可达到342km/h,假设球飞来的速度为90km/h,运动员将球以342km/h的速度反向击回.设羽毛球的质量为5g,试求(1)运动员击球过程中羽毛球的动量变化量.(2)在运动员的这次扣杀中,羽毛球的速度变化、动能变化各是多少?专题三碰撞中的动量变化例5质量为0.1kg的小球从1.25m高处自由落下,与地面碰撞后反弹回0.8m高处.取竖直向下为正方向,且g =10m/s2.求:(1)小球与地面碰前瞬间的动量;(2)球与地面碰撞过程中动量的变化.第2节动量定理知识点一、冲量(1)概念:力与力的作用时间的乘积叫做力的冲量.(2)定义式:I=Ft.(3)物理意义:冲量是反映力的作用对时间的累积效应的物理量,力越大,作用时间越长,冲量就越大.(4)单位:在国际单位制中,冲量的单位是牛·秒,符号为N·s.知识点二、冲量的理解(1)冲量的绝对性.由于力和时间均与参考系无关,所以力的冲量也与参考系的选择无关.(2)冲量是矢量.冲量的运算服从平行四边形定则,合冲量等于各外力的冲量的矢量和,若整个过程中,不同阶段受力不同,则合冲量为各阶段冲量的矢量和.(3)冲量是过程量,它是力在一段时间内的积累,它取决于力和时间这两个因素.所以求冲量时一定要明确所求的是哪一个力在哪一段时间内的冲量.知识点三、冲量的计算(1)恒力的冲量:公式I=Ft适用于计算某个恒力的冲量,这时冲量的数值等于力与作用时间的乘积,冲量的方向与恒力方向一致.若力为同一方向均匀变化的力,该力的冲量可以用平均力计算,若力为一般变力则不能直接计算冲量.(2)变力的冲量①变力的冲量通常可利用动量定理I=Δp求解.②可用图象法计算如图所示变力冲量,若某一力方向恒定不变,那么在F-t图象中,图中阴影部分的面积就表示力在时间Δt=t2-t1内的冲量.知识点四、冲量与功(1)联系:冲量和功都是力作用过程的积累,是过程量.(2)区别:冲量是矢量,是力在时间上的积累,具有绝对性;功是标量,是力在位移上的积累,有相对性.知识点四、动量定理1.内容:物体在一个过程始末的动量变化量等于它在这个过程中所受力的冲量.这个关系叫做动量定理.2.表达式:I=Δp或Ft=m v′-m v.3.对动量定理的理解(1)动量定理反映了合外力的冲量是动量变化的原因.(2)动量定理的表达式是矢量式,它说明合外力的冲量跟物体动量变化量不仅大小相等,而且方向相同.(3)动量的变化率和动量的变化量由动量定理可得出F=p′-pt,它说明动量的变化率决定于物体所受的合外力.而由动量定理I=Δp可知动量的变化量取决于合外力的冲量,它不仅与物体的受力有关,还与力的作用时间有关.(4)动量定理具有普遍性,即不论物体的运动轨迹是直线还是曲线,不论作用力是恒力还是变力,不论几个力的作用时间是相同还是不同都适用.4.动量定理的应用(1)定性分析有关现象由F=Δpt可知:①Δp一定时,t越小,F越大;t越大,F越小.②Δp越大,而t越小,F越大.③Δp越小,而t越大,F越小.(2)应用动量定理解决问题的一般步骤①审题,确定研究对象:对谁、对哪一个过程.②对物体进行受力分析,分析力在过程中的冲量,或合力在过程中的冲量.③抓住过程的初、末状态,选定参考方向,对初、末状态的动量大小、方向进行描述.④根据动量定理,列出动量定理的数学表达式.⑤写清各物理量之间关系的补充表达式.⑥求解方程组,并分析作答.典例分析一、冲量的理解例1如图所示,质量为m的小球由高为H的光滑固定斜面顶端无初速滑到底端过程中,重力、弹力的冲量各是多大?二、平均冲量的计算例2如图所示,质量为m=1kg的小球由高h1=0.45m处自由下落,落到水平地面后,反弹的最大高度为h2=0.2m,从小球下落到反弹到最高点经历的时间为Δt=0.6s,g取10m/s2.求:小球撞击地面过程中,球对地面的平均压力F的大小.三、合力冲量的计算例3质量为1.0kg的小球从20m高处自由下落到软垫上,反弹后上升的最大高度为5.0m,小球与软垫接触时2)()间为1.0s,在接触时间内小球受到的合力的冲量大小为(空气阻力不计,g=10m/sA.10N·s B.20N·s C.30N·s D.40N·s四、冲量的综合应用例4用0.5kg的铁锤把钉子钉进木头里,打击时铁锤的速度v=4.0m/s,如果打击后铁锤的速度变为0,打击的作用时间是0.01s,那么:(1)不计铁锤受的重力,铁锤钉钉子的平均作用力是多大?(2)考虑铁锤受的重力,铁锤钉钉子的平均作用力又是多大?(g取10m/s2)(3)比较(1)和(2),讨论是否要计铁锤的重力。
动量与动量守恒

动量与动量守恒动量是物体运动状态的量度,它是质量与速度的乘积。
动量守恒定律是物理学中的基本定律之一,其表达了封闭系统内物体总动量的守恒性质。
在本文中,我们将探讨动量和动量守恒的概念、定律以及其在实际中的应用。
一、动量的概念和计算动量(Momentum)是描述物体运动状态的物理量,它是质量(m)与速度(v)的乘积,可以用数学公式表示为 M = m × v。
动量的单位是千克·米/秒(kg·m/s)。
动量具有矢量性质,方向与速度方向相同。
当物体的质量或速度发生变化时,动量也会相应变化。
比如,一个运动中的汽车与静止的汽车相比,前者的动量更大。
同样是一个速度为10米/秒的小球,与一个速度为5米/秒的小球相比,前者的动量更大。
二、动量守恒定律动量守恒定律是指在一个封闭系统中,当没有外力作用于系统时,系统内物体的总动量保持不变。
即使在碰撞或其他相互作用过程中,物体的动量也不会改变。
这个定律可以用公式表示为:m₁v₁ + m₂v₂ = m₁v₁' + m₂v₂'其中,m₁、m₂分别代表两个物体的质量,v₁、v₂代表它们的初始速度,v₁'、v₂'代表它们的最终速度。
动量守恒定律可以应用于各种不同的物理现象,例如弹性碰撞和非弹性碰撞。
在弹性碰撞中,物体之间相互碰撞后能量守恒,动量守恒,且物体之间的相对速度在碰撞前后保持不变。
而在非弹性碰撞中,物体之间的碰撞会导致能量损失,且物体之间的相对速度发生变化。
三、动量守恒的应用动量守恒定律在实际中有广泛的应用,例如交通安全、火箭推进和运动项目等。
在交通安全中,动量守恒定律告诉我们,在车辆碰撞时,如果速度越大,撞击力就会越大。
因此,减少车辆速度可以降低事故发生的危险性。
火箭推进中,动量守恒定律解释了为什么火箭可以向上升空。
燃料喷出的速度越大,火箭所受的向下的冲量就越大,从而使火箭向上运动。
在运动项目中,动量守恒定律也起着重要的作用。
动量和角动量守恒定律

动量和角动量守恒定律动量和角动量守恒定律是物理学中两个重要的守恒定律,它们在描述物体运动过程中起到了关键作用。
本文将对动量和角动量守恒定律的概念、原理以及应用进行详细的讲解。
一、动量守恒定律动量是物体运动的核心概念,它定义为物体质量与其速度的乘积。
动量的守恒定律表明,在一个系统中,如果没有外力作用,系统的总动量将保持恒定不变。
动量守恒定律可以用数学公式表示为:Σmv = 常数,其中Σ表示对系统中所有物体的动量求和,m为物体的质量,v为物体的速度。
例如,考虑一个闭合系统,系统中有两个物体A和B,它们分别具有动量m₁v₁和m₂v₂。
根据动量守恒定律,如果没有外力作用,则系统的总动量为m₁v₁ + m₂v₂,即系统动量守恒。
动量守恒定律的应用非常广泛。
在交通事故中,当两车相撞后,虽然车辆的速度和方向可能发生了改变,但整个系统的总动量保持不变,这可以解释为车辆之间的动量传递。
二、角动量守恒定律角动量是描述物体旋转运动的重要物理量,它定义为物体的转动惯量与其角速度的乘积。
角动量的守恒定律表明,在一个系统中,如果没有外力矩作用,系统的总角动量将保持恒定不变。
角动量守恒定律可以用数学公式表示为:ΣIω = 常数,其中Σ表示对系统中所有物体的角动量求和,I为物体的转动惯量,ω为物体的角速度。
例如,考虑一个旋转的物体系统,系统中有多个物体,它们分别具有角动量I₁ω₁、I₂ω₂等。
根据角动量守恒定律,如果没有外力矩作用,则系统的总角动量为I₁ω₁ + I₂ω₂,即系统角动量守恒。
角动量守恒定律的应用也非常广泛。
例如,在天体运动中,行星绕太阳旋转的过程中,由于没有外力矩作用,它们的角动量保持不变。
三、动量和角动量守恒定律的应用动量和角动量守恒定律在解决物体运动问题时具有广泛的应用。
1. 弹性碰撞在弹性碰撞中,两个物体在碰撞过程中会发生能量和动量的交换,但整个系统的动量守恒。
通过运用动量守恒定律,可以计算出碰撞前后物体的速度和动量的变化。
质点系的动量定理 动量守恒定律

m(vx V ) MV = 0
解得
பைடு நூலகம்
vx =
m+M V m
设m在弧形槽上运动的时间为t,而m相对于M在水平方向移动距离为R, 故有 t M+m t R = ∫ vx dt = Vdt 0 m ∫0 于是滑槽在水平面上移动的距离
S = ∫ Vdt =
0 t
m R M+m
§3.动量守恒定律 / 二、注意几点及举例 动量守恒定律
若x方向 ∑ Fx = 0 , 则∑ mivi 0 x = ∑ mivix 方向 若y方向 ∑ Fy = 0 ,则∑ mivi 0 y = ∑ miviy 方向 4.自然界中不受外力的物体是没有的,但 自然界中不受外力的物体是没有的, 自然界中不受外力的物体是没有的 如果系统的内力 外力, 内力>>外力 如果系统的内力 外力,可近似认为动量 守恒。 守恒。 如打夯、 如打夯、火箭发 射过程可认为内力 内力>> 射过程可认为内力 外力, 外力,系统的动量守 恒。
Fdt=(m+dm)v-(mv+dm0)=vdm=kdt v
则
F = kv = 200 × 4 = 8 ×102 N
一、动量守恒 由质点系的动量定理: 由质点系的动量定理:
∫ ( ∑ Fi外 )dt = P P0 = P
t t0
动量守恒条件: 动量守恒条件:
P P0 = 0
当 ∑ Fi外 = 0 时
第四节 质点系的动 量定理
一、质点系的动量定理 两个质点组成的质点系, 两个质点组成的质点系, 对两个质点分别应用 质点的动量定理: 质点的动量定理: t ∫t ( F1 + f12 )dt = m1v1 m1v10
0
动量守恒定律 (共30张PPT)

碰撞 系统Leabharlann 重力势能属于地面附近 的物体与地球组成的系统。
弹簧具有的弹性势能 属于构成它的许多小小 的物质单元(这些物质单 元之间有弹力的作用)组 成的系统。
研究炸弹的爆炸时,它的 所有碎片及产生的燃气也要作 为一个系统来。
2、内力:属于同一个系统内,它们之间的力。 系统以外的物体施加的力,叫做外力。
解得:v共=88.2m/s正值,方向不变。
解: ①以子弹木块系统为研究对象,取右为正方向。
②碰撞前子弹的动量P子=mv,木块的动量P2=0
碰撞后不粘一起,P'子=mv',P'木=Mv'木
③列表带入公式:系统初动量=系统末动量
碰撞前
碰撞后
物块1 物块2 = 物块1 物块2
mv 0
mv' Mv'木
所以:mv=mv'+Mv'木
解:动量问题只与初末状态有关。
①以第一节车厢和把剩余车厢看为整体的系统为研究
对象,取右为正方向。
②碰撞前的动量P=mv,剩余车厢的动量P余=0
碰撞后粘一起,P共=(m+15m)v共
③列表带入公式:系统初动量=系统末动量
碰撞前
碰撞后
物块1 物块2 = 物块1 物块2
mv 0
(m+15m) v共
所以:mv=(m+15m)v共
解得:v'B=7.4m/s
带数据得:5×9+4×6=5v'1+4×10 正值,方向不变。
3、质量是10g的子弹,以300m/s的速度射入质量是24g、静止在光滑水平桌面上的木 块,并留在木块中。子弹留在木块中以后,木块运动的速度是多大?如果子弹把木块 打穿,子弹穿过后的速度为100ms,这时木块的速度又是多大?
动量守恒定律知识点总结
1、动量守恒定律的条件:系统所受的总冲量为零(不受力、所受外力的矢量和为零或外力的作用远小于系统内物体间的相互作用力),即系统所受外力的矢量和为零。
(碰撞、爆炸、反冲)注意:内力的冲量对系统动量是否守恒没有影响,但可改变系统内物体的动量。
内力的冲量是系统内物体间动量传递的原因,而外力的冲量是改变系统总动量的原因。
2、动量守恒定律的表达式m1v1+m2v2=m1v1/+m2v2/(规定正方向)△p1=—△p2/3、某一方向动量守恒的条件:系统所受外力矢量和不为零,但在某一方向上的力为零,则系统在这个方向上的动量守恒。
必须注意区别总动量守恒与某一方向动量守恒。
4、碰撞(1)完全非弹性碰撞:获得共同速度,动能损失最多动量守恒;(2)弹性碰撞:动量守恒,碰撞前后动能相等;动量守恒,;动能守恒;5、人船模型——两个原来静止的物体(人和船)发生相互作用时,不受其它外力,对这两个物体组成的系统来说,动量守恒,且任一时刻的总动量均为零,由动量守恒定律,有mv=MV(注意:几何关系)动量守恒定律解题技巧例1:质量m1=10g的小球在光滑的水平桌面上以v1=30cm/s的速率向右运动,恰好遇上在同一条直线上向左运动的另一个小球。
第二个小球的质量为m2=50g,速率v2=10cm/s。
碰撞后,小球m2恰好停止。
那么,碰撞后小球m1的速度是多大,方向如何?分析:取相互作用的.两个小球为研究的系统。
由于桌面光滑,在水平方向上系统不受外力。
在竖直方向上,系统受重力和桌面的弹力,其合力为零。
故两球碰撞的过程动量守恒。
解:设向右的方向为正方向,则各速度的正、负号分别为 v1=30cm/s,v2=10cm/s,v'2=0。
据动量守恒定律有mlvl+m2v2=m1v'1+m2v'2。
解得v'1=—20cm/s。
即碰撞后球m1的速度大小为20cm/s,方向向左。
通过此例总结运用动量守恒定律解题的要点如下:(1)确定研究对象。
高中物理-动量守恒定律
动量守恒定律与系统的能量守恒类似,系统的动量也存在守恒的情况。
动量什么情况下才守恒呢?动量守恒定律又是通过什么实验来验证的呢?我们下面就来研究动量守恒定律的内容。
动量守恒定律的内容如果一个系统不受外界力或所受外界的力的矢量和为零,那么这个系统的总动量保持不变,这个结论叫做动量守恒定律。
还可以表述为,当没有外界的力作用时,系统内部不同物体间动量相互交换,但总动量之和为固定值。
动量守恒定律是自然界中最重要最普遍的守恒定律之一,它既适用于宏观物体,也适用于微观粒子;既适用于低速运动物体,也适用于高速运动物体。
提醒同学们,动量也是矢量。
如静止的铀核发生α衰变,反冲核和α粒子的动量的动量变化大小相同,方向相反,动量变化的矢量和是零,但两个动量在数量上都增大了。
动量守恒定律的公式基本公式:m1v1+m2v2=m1v1′+m2v2′;此公式为两个物体动量守恒的表达式,多个物体碰撞可以写成:m1v1+m2v2+……=m1v1′+m2v2′+……公式还可以写成p1+p2=p1′+p2′,或者Δp1+Δp2=0,Δp1=-Δp2(动量变化量守恒)下面,我们来探究动量守恒定律的条件是什么?动量守恒定律的条件用一句话来说动量守恒的前提条件:在规定的方向上,系统不受“外界的力”。
这句话共有三个要素:1方向;2系统;3外力。
(1)关于方向的说明:在探究动量是否守恒的时候,要首先明确方向,一般规定碰撞或运动所在的直线对应的方向(正负两个方向均可)。
(2)对“外力”的理解:这个“外力”指的是“外界的力”,与研究系统内部的力无关,什么是内部的力呢?举个例子,比如两个人在理想冰面互推的“推力”,等等。
而外力呢?对于这两个人来说,墙给某个人的力就是(这个系统)外界的力。
(3)系统的说明:使用动量守恒定律,必须是两个或两个以上的物体构成的系统,或者爆破为两个物体的整体。
总之一句话,我们研究动量的对象是多个物体组成的系统。
(4)需要记忆的动量守恒定律模型:总结:“光滑面两球相撞”、“冰面互推”、“两个弹簧链接的物体”、“斜面上滑动小物块”、“子弹射入木块”、“火箭发射”、“人在船面上走动”、“二起脚空中爆破”、“粒子裂变”等。
物理动量知识点
物理动量知识点物理动量知识点8篇在平时的学习中,是不是经常追着老师要知识点?知识点在教育实践中,是指对某一个知识的泛称。
为了帮助大家更高效的学习,以下是店铺收集整理的物理动量知识点,仅供参考,希望能够帮助到大家。
物理动量知识点1冲量与动量(物体的受力与动量的变化)1.动量:p=v {p:动量(g/s),:质量(g),v:速度(/s),方向与速度方向相同}3.冲量:I=Ft {I:冲量(N?s),F:恒力(N),t:力的作用时间(s),方向由F决定}4.动量定理:I=Δp或Ft=vt–v {Δp:动量变化Δp=vt–v,是矢量式}5.动量守恒定律:p前总=p后总或p=p’′也可以是1v1+2v2=1v1′+2v2′6.弹性碰撞:Δp=0;ΔE=0 {即系统的动量和动能均守恒}7.非弹性碰撞Δp=0;0<ΔE<ΔE {ΔE:损失的动能,E:损失的最大动能}8.完全非弹性碰撞Δp=0;ΔE=ΔE {碰后连在一起成一整体}9.物体1以v1初速度与静止的物体2发生弹性正碰:v1′=(1-2)v1/(1+2) v2′=21v1/(1+2)10.由9得的推论-----等质量弹性正碰时二者交换速度(动能守恒、动量守恒)11.子弹水平速度v射入静止置于水平光滑地面的长木块M,并嵌入其中一起运动时的机械能损失E损=v2/2-(M+)vt2/2=fs相对 {vt:共同速度,f:阻力,s相对子弹相对长木块的位移}物理动量知识点21、动量是矢量其方向与速度方向相同,大小等于物体质量和速度的乘积,即P=mv。
2、冲量也是矢量它是力在时间上的积累。
冲量的方向和作用力的方向相同,大小等于作用力的大小和力作用时间的乘积。
在计算冲量时,不需要考虑被作用的物体是否运动,作用力是何种性质的力,也不要考虑作用力是否做功。
在应用公式I=Ft进行计算时,F应是恒力,对于变力,则要取力在时间上的平均值,若力是随时间线性变化的,则平均值为3、动量定理:动量定理是描述力的时间积累效果的,其表示式为I=ΔP=mv-mv0式中I表示物体受到所有作用力的冲量的矢量和,或等于合外力的冲量;ΔP是动量的增量,在力F作用这段时间内末动量和初动量的矢量差,方向与冲量的方向一致。
动量定理及动量守恒定律
4、一枚在空中飞行的导弹,质量为m,在某点的速度为 ,方向水平。 、一枚在空中飞行的导弹,质量为 ,在某点的速度为v,方向水平。 导弹在该点突然炸裂成两块,其中质量为 的一块沿着与v相反的 导弹在该点突然炸裂成两块,其中质量为m1的一块沿着与 相反的 方向飞去,速度为v1。求炸裂后另一块的速度 2。 求炸裂后另一块的速度v 方向飞去,速度为
动量守恒定律的理解及应用要点
矢量性:动量守恒定律方程是一个矢量方程。 矢量性:动量守恒定律方程是一个矢量方程。对于作用前后物体的运动方向 都在同一直线上的问题,应选取统一的正方向。若方向未知, 都在同一直线上的问题,应选取统一的正方向。若方向未知,可以 设的正方向为标准列动量守恒方程,通过所得结果的正负, 设的正方向为标准列动量守恒方程,通过所得结果的正负,判定未 知量的方向 瞬时性:动量是一个瞬时量,动量守恒指的是系统任一瞬时的动量和恒定, 瞬时性:动量是一个瞬时量,动量守恒指的是系统任一瞬时的动量和恒定, 不是同一时刻的动量不能相加 相对性: 相对性:应用动量守恒定律时各物体的速度必须是相对同一惯性系的速度 普适性:只要系统所受的合外力为零, 普适性:只要系统所受的合外力为零,不论系统内部物体之间的相互作用力 性质如何,不论系统内各物体是否具有相同运动方向, 性质如何,不论系统内各物体是否具有相同运动方向,不论物体相 互作用时是否直接接触, 互作用时是否直接接触,也不论相互作用后粘合在一起还是分裂成 碎片,动量守恒定律均适用。 碎片,动量守恒定律均适用。动量守恒定律不仅适用于低速宏观物 体,而且适用于接近光速运动的微观粒子。 而且适用于接近光速运动的微观粒子。
A
等于碰撞前的总动能 ③ 碰撞后同向运动时后一
A、 PA=6kg.m/s, PB=6kg.m/s 、 , B、 PA=3kg.m/s, PB=9kg.m/s 、 , C、 PA=-2kg.m/s, PB=14kg.m/s 、 - , D、 PA=-5kg.m/s, PB=17kg.m/s 、 - , 物体速度不大于前一物 体速度
