洛伦兹力在现代科技中的应用 修改版
洛伦兹力在现代科技上的应用(正式)

B. a 处离子浓度大于b 处离子浓度
C. 溶液的上表面电势高于下表面电势 D. 溶液的上表面处 离子浓度大于下表面处 的离子浓度 c
N Z
y
B b d x
I
a
磁流体发电机
M v
电磁流量计
B b c
霍尔效应
N
a
ε=Ed=Bvd
(空心导体-
Ub U 1 IBd 1 IB Q vS H nq S nq b B
U U Bvq q v c Bc
B
Q 公式:
Ub Q vS B
c a
b
四、霍尔效应
1、定义:当通电的导体处在垂直于电流方向的 磁场中时,在导体的上、下表面产生电压 金属导体
I f
v
d
f
qE
E
2、哪一面电势高,与导电粒子的种类有关。
3、霍尔电压的计算式:
霍尔电压:UH=Bvd.
B d
直线加速器
最大直线加速器:
斯坦福大学
直线加速器
2英里长直线加速管
(2)、回旋加速器
直线加速器缺点: 体积大,占地大。
1932年美国科学家劳伦斯发明了回旋加速 器,1939年获得了诺贝尔物理学奖。
美国费米加速器实验室
北京正负电子对撞 机:能量达到3GeV
欧洲大型强子对撞机(LHC)是最大的粒子加速器,
故总时间==磁场时间。
3、匀速圆周运动的最大半径=D形盒的半径。 4、在粒子的质量、电荷量确定的情节下,粒子的最
大动能只与D形盒的半径R和磁感应强度B有关,与加
速电压U无关。
(1).直线加速器
+
+
洛伦兹力在现代科技上的应用

力和洛伦兹力 平衡 时,a、b间有稳定的电势
差U,则液体的流速为
液体的流量
为
。
.
14
例5.医生做某些特殊手术时,利用电磁血流计来监测通过动脉的血流速
度.电磁血流计由一对电极a和b以及一对磁极N和S构成,磁极间的磁
场是均匀的.使用时,两电极a、b均与血管壁接触,两触点的连线、磁
场方向和血流速度方向两两垂直.如图所示.由于血液中的正负离子随
qvB qE2•
照相底片
... s2
p
-
1
... ... ...
p2
+
................. s3
................ .............
.........
质谱仪的示意图
qU1
1 2
mv02
利用磁场分离 (B2)
6、测出条纹到狭缝S3
的距离L,则粒子的荷
质比是多少?
q m
电动势U=BdV
R中电流I=
E
BdV
.R+r
=
R+ ρ
d S
BdVS = RS+ ρ1d1
四、霍尔(E.C.Hall)效应P98(教材)
在一个通有电流的导体板上,垂直于板面施加 一磁场,则平行磁场的两面出现一个电势差,这 一现象是1879年美国物理学家霍耳发现的,称为 霍耳效应。该电势差称为霍耳电势差 。
由O′射出.不计重力作用.可能达到上述目的的办法是( A.使a板的电势高于b板,磁场方向垂直纸面向里
AD)
B.使a板的电势低于b板,磁场方向垂直纸面向里
C.使a板的电势高于b板,磁场方向垂直纸面向外
D.使a板的电势低于b板,磁场方向垂直纸面向外
洛伦兹力在现代科技中的应用-修改版

ASCS 1S 2S 3S 4Vr PF BD B 0VU M N 洛伦兹力在现代科技中的应用一.速度选择器原理:其功能是选择出某种速度的带电粒子 1.结构:如图所示(1)平行金属板M、N,将M 接电源正极,N 板接电源负极,M、N 间形成匀强电场,设场强为E;(2)在两板之间的空间加上垂直纸面向里的匀强磁场,设磁感应强度为B; (3)在极板两端加垂直极板的档板,档板中心开孔S 1、S 2,孔S 1、S 2水平正对。
2.原理设一束质量、电性、带电量、速度均不同的粒子束(重力不计),从S 1孔垂直磁场和电场方向进入两板间,当带电粒子进入电场和磁场共存空间时,同时受到电场力和洛伦兹力作用Bq FEq F 洛电,若洛电FFBq Eq v E B0 。
当粒子的速度v EB0 时,粒子匀速运动,不发生偏转,可以从S 2孔飞出。
由此可见,尽管有一束速度不同的粒子从S 1孔进入,但能从S 2孔飞出的粒子只有一种速度,而与粒子的质量、电性、电量无关3。
粒子匀速通过速度选择器的条件——带电粒子从小孔S 1水平射入, 匀速通过叠加场, 并从小孔S 2水平射出,电场力与洛仑兹力平衡, 即 Bq Eq ;即v E B; 当粒子进入速度选择器时速度v EB0 , 粒子将因侧移而不能通过选择器. 如图, 设在电场方向侧移 d 后粒子速度为v ,(1) 当BEv 0时: 粒子向洛伦兹力f 方向侧移 电场力F 做负功,粒子动能 减少, 电势能增加, 有2202121mv d qE mv(2) 当BEv 0时:粒子向电场力F 方向侧移,F 做正功,粒子动能增加, 电势能减少, 有1212022mv qE d mv二.质谱仪 主要用于分析同位素, 测定其质量, 荷质比和含量比, 1.质谱仪的结构原理(1)离子发生器O(发射出电量q、质量m 的粒子从A 中小孔S 飘出时速度大小不计) (2)静电加速器C:静电加速器两极板M 和N 的中心分别开有小孔S 1、S 2,粒子从S 1进入后,经电压为U 的电场加速后,从S 2孔以速度v 飞出;(3)速度选择器D:由正交的匀强电场E 0和匀强磁场B 0构成,调整E 0和B 0的大小可以选择度为v 0=E 0/B 0的粒子通过速度选择器,从S 3孔射出; (4)偏转磁场B:粒子从速度选择器小孔S 3射出后,从偏转磁场边界挡板上的小孔S 4进入,做半径为r 的匀速圆周运动;(5)感光片F:粒子在偏转磁场中做半圆运动后,打在感光胶片的P 点被记录,可以测得PS 4间的距离L。
洛伦兹力知识在现代科技中的应用
首页 结束 上一页 下一页
解:
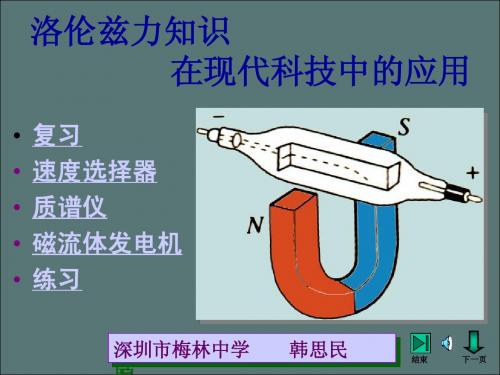
(1)当等离子体喷 d v R 入磁场后, 入磁场后,在洛伦兹 力的作用下, 力的作用下,正、负 离子分别向下极板和 上极板偏转, 上极板偏转,两极板因积累正负电荷而产生静电 场。这时离子同时受到方向相反的洛伦兹力f和电 的作用。 离子继续偏转, 场力F的作用。当f>F时,离子继续偏转,两板电 势差随即增大; 离子匀速穿过磁场, 势差随即增大;当f=F时,离子匀速穿过磁场,两 极电势差达到最大,即为电源电动势。 极电势差达到最大,即为电源电动势。 (2)由qvB=qE和E=ε /d得: ε=Bdv
首页 结束 上一页 下一页
结束
首页 结束 上一页 下一页
专题: 专题:洛伦兹力知识在现代科技中的应用
1.速度选择器:如图所示的平行板器件中, 1.速度选择器:如图所示的平行板器件中, 速度选择器 电场强度E和磁感应强度B相互垂直。 电场强度E和磁感应强度B相互垂直。有某一水 平速度v 平速度v的带电粒子将沿虚线穿过两板间的空间 而不发生偏转, 而不发生偏转,具有其他速度的带电粒子将发 生偏转,这种器件叫速度选择器。 生偏转,这种器件叫速度选择器。
首页 结束 上一页 下一页
3.磁流体发电机:A、B组成一对平行电极,两 3.磁流体发电机 磁流体发电机: 组成一对平行电极, 极间距为d 内有磁感应强度为B的匀强磁场, 极间距为d,内有磁感应强度为B的匀强磁场,一 束等离子体不断地以速度v垂直喷射入磁场, 束等离子体不断地以速度v垂直喷射入磁场,两板 间会产生电势差 并达到一稳定值, 并达到一稳定值, 即电源的电动势。 即电源的电动势。 (1)分析磁流体 发电机的工作原 理。 (2)求发电机的 电动势多大? 电动势多大?
洛伦兹力知识 在现代科技中的应用
第五节洛仑兹力在现代技术中的运用

要点·疑点·考点
五、加速器
回旋加速器的主要特征.
①带电粒子在两D形盒中回旋周期等于两盒狭缝之间 高频电场的变化周期,与带电粒子的速度无关;②将 带电粒子在两盒狭缝之间的运动首尾连起来是一个初 速为0的匀加速直线运动;③带电粒子每经电场加速 一次,回旋半径就增大一次,所有经过半径之比为
经过匀强电场和磁场,只有其运动速度刚好满足f洛 =F电的粒子运动轨迹不发生偏转,从第二块挡板上小 孔中射出。改变匀强电场或匀强磁场的大小,就可以
得到不同速度的带电粒子。这个装置就叫做速度选择
器 (v=E/B)
问:若将一个能通过某速度选择器的正电荷换成 一个电量相等速度不变的负电荷,它还能通过该速度 选择器吗?为什么?
1∶ 2 ∶ 3 ∶……(这可由学生自己证明),对于同一
回旋加速器,其粒子回旋的最大半径是相同的,解题 时务必引起注意.
【例1】何为速度选择器,其工作原理如何,并列举 几个物理模型与速度选择器相似的应用实例。
解析:带电粒子垂直射入正交的匀强电
场和匀强磁场的复合空间,所受电场力 和洛伦兹力方向相反,大小相等。
设B为磁感应强度,d为两板间距,v为喷射速度,最大电势差Um,
则:
Um q Bqv d
Um Bdv
电磁流量计:
如图:是用来测定导电液体在导管中流动时流量 的仪器,设导管直径为d,用非磁性材料制成,磁感 应强度为B,a、b间测出电势差为U
则流量 Q Sv d 2 U dU
即eBv=eE v=E/B=2×105m/s (2)粒子进入磁场B′后做圆周运动,洛伦兹力提 供向心力.
北京市第九十四中学洛伦兹力在现代科技中应用

朝阳区特级教师工作室骨干教师风度展现课洛伦兹力在现代科技中的应用---实例分析指导教师:特级教师---刘敏做课教师:刘敏特级教师工作室核心成员朝阳区骨干教师北京第九十四中学---邓华讲课对象——朝阳区东方德才中学高三学生(讲课时刻:2020、11、25)【教学目标】(一)知识与技术1. 会综合运用电场和磁场知识研究带电粒子在两场中的受力与运动问题。
2. 在原高二知何学习的基础上,深化明白得速度选择器、质谱仪,回旋加速器等科技应用原理。
(二)进程与方式1. 在新的问题情景中,在试探、探讨活动中,体会、感悟用大体物理知识解决科学研究中问题的方式。
2. 通过在速度选择器、质谱仪、回旋加速器等背景下研究带电粒子在场中的运动,强化电场加速、磁场偏转的意义及相关仪器的设计思路。
(三)情感、态度与价值观1.通过创设真实的、有研究意义的问题情境,激发学生探讨问题的热情。
2.在解决问题的进程中,使学生进一步体验解决问题的大体分析方式。
3.通过对放射性物质的研究,使学生领会研究带电粒子在场中运动的实际意义,了解现代科技研究的进展现状。
【教学重点】带电粒子在电场和磁场的受力与运动分析与现代科技应用的联系。
【教学难点】将实际问题转化为物理模型的研究方式。
【教学方式】探讨讨论、分析讲解、归纳运用。
【教学资源】教材、PPT课件、有关视频资料。
【教学进程】第一环节:通过对居里夫人获诺贝尔物理学奖原由的讨论,创设问题情境,激发学生对带电粒子研究的关注。
居里夫人因为研究什么而取得诺贝尔物理学奖?放射性物质放出的是什么?放出的粒子的质量、电量、速度多大?利用什么技术手腕能测出粒子的质量、电量、速度?(那个地址,学生能够说出居里夫人其人、其事,不明白放射性是什么。
放出的是什么粒子,从而产生强烈的好奇心)。
第二环节:通过对〖问题1〗的探讨和讨论,体会速度选择器选择的是粒子的速度——而且提供了侧未知粒子速度的手腕,但不选粒子的质量、电量。
洛伦兹力应用

二、磁流体发电机
离子平衡E场q = qvB
E场 = Bv
l 电源内阻r = ρ S
电动势
E =U = E场l = Blv
E Blv BlvS ∴R 电 I = 中 流 = = R+r R+ ρ l RS + ρl S
三、霍尔效应
B
VH fLm f B
fe Fe
I
v
E E
b
d
由于电荷的积累,形成静电场- 由于电荷的积累,形成静电场-霍尔电场 载流子平衡时 形成的霍尔电压
测定带电粒子的质量和分析同位素
五、、回旋加速器 、、回旋加速器
a、原理: 、原理: 磁场什么作用? 使粒子在D形盒内 形盒内________。 磁场什么作用? 使粒子在 形盒内 。 电场什么作用?重复多次对粒子______. 电场什么作用?重复多次对粒子 最终速度取决于什么量? 最终速度取决于什么量?______. b、条件: 、条件: 交变电压的周期等于粒子圆周运动的周期 交变电压频率=粒子回旋频率 交变电压频率 粒子回旋频率 c、若D型盒半径为 ,粒子质 、 型盒半径为R, 型盒半径为 量m,电量 ,匀强磁场场强为 ,电量q, B,加速电场电压 ,计算最大速 加速电场电压U 计算最大速 加速电场电压 度和运动时间? 度和运动时间?
qEH = qυB
UH = EHb=υBb
四、质谱仪
1、质谱仪的工作原理是什么? 质谱仪的工作原理是什么? 粒子加速 速度选择(过滤) 速度选择(过滤) 粒子偏转(分开) 粒子偏转(分开)
2、加速电场电压时U,偏转匀强磁场磁感应强度是B, 加速电场电压时U 偏转匀强磁场磁感应强度是B 偏转圆轨迹半径是R 求粒子的比荷。 偏转圆轨迹半径是R,求粒子的比荷。
洛伦兹力在现代科技上的应用

汇报人:
01
03
05
02
04
洛伦兹力是磁场 对带电粒子的作 用力
大小与带电粒子的 电荷量、速度和磁 感应强度有关
方向与带电粒子 的运动方向和磁 场方向垂直
在现代科技中洛伦 兹力常用于粒子加 速器、磁悬浮列车 等领域
公式:F=qv×B 解释:F为洛伦兹力q为电荷量v为速度B为磁感应强度 说明:洛伦兹力的大小与电荷量、速度和磁感应强度均成正比 应用:在粒子加速器、回旋加速器等现代科技设备中广泛应用
磁场调控:通过调控洛伦兹力实现对微观粒子的精确操控有望应用于量子计算和纳米科技领 域。
磁场干扰:洛伦兹力对 磁场敏感容易受到外部 磁场干扰影响设备的稳 定性和精度。
能量损耗:由于洛伦兹 力的存在能量会在运动 过程中产生损耗影响设 备的效率和寿命。
技术难度:由于洛伦 兹力的复杂性和不确 定性相关技术的应用 需要高超的技术水平 和深入的理论研究。
磁场驱动的微纳操 作:利用洛伦兹力 对微纳尺度物体进 行精确操控有望在 微电子制造、纳米 光子学等领域发挥
重要作用。
掌握应对洛伦兹力的技术手 段
了解洛伦兹力对现代科技的 影响
探索洛伦兹力在现代科技中 的新应用
加强国际合作与交流共同应 对挑战与机遇
汇报人:
洛伦兹力在磁共振成像技术中的应用实例:如医学诊断、地质勘探等。
洛伦兹力在磁共振成像技术中的未来发展:随着科技的不断进步洛伦兹力在磁共振 成像技术中的应用将更加广泛和深入。
粒子加速器:利用电场对带电粒子进行加速的装置 洛伦兹力:运动电荷在磁场中所受到的力
应用:在粒子加速器中洛伦兹力起到关键作用通过改变磁场和电场实现对粒子的加速和聚焦 重要性:洛伦兹力在粒子加速器中扮演着至关重要的角色是现代科技领域中的重要应用之一
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A S C S 1S 2S 3S 4Vr P F B D B 0V U M N 洛伦兹力在现代科技中的应用一.速度选择器原理:其功能是选择出某种速度的带电粒子1.结构:如图所示(1)平行金属板M 、N ,将M 接电源正极,N 板接电源负极,M 、N 间形成匀强电场,设场强为E ;(2)在两板之间的空间加上垂直纸面向里的匀强磁场,设磁感应强度为B ;(3)在极板两端加垂直极板的档板,档板中心开孔S 1、S 2,孔S 1、S 2水平正对。
2.原理设一束质量、电性、带电量、速度均不同的粒子束(重力不计),从S 1孔垂直磁场和电场方向进入两板间,当带电粒子进入电场和磁场共存空间时,同时受到电场力和洛伦兹力作用υBq F Eq F ==洛电, 若洛电F F = υBq Eq = v E B 0=。
当粒子的速度v E B0=时,粒子匀速运动,不发生偏转,可以从S 2孔飞出。
由此可见,尽管有一束速度不同的粒子从S 1孔进入,但能从S 2孔飞出的粒子只有一种速度,而与粒子的质量、电性、电量无关3. 粒子匀速通过速度选择器的条件——带电粒子从小孔S 1水平射入, 匀速通过叠加场, 并从小孔S 2水平射出,电场力与洛仑兹力平衡, 即υBq Eq =;即v E B 0=; 当粒子进入速度选择器时速度v E B0≠, 粒子将因侧移而不能通过选择器。
如图, 设在电场方向侧移∆d 后粒子速度为v , (1) 当BE v >0时: 粒子向洛伦兹力f 方向侧移 电场力F 做负功,粒子动能 减少, 电势能增加, 有2202121mv d qE mv +∆= (2) 当B E v <0时:粒子向电场力F 方向侧移,F 做正功,粒子动能增加, 电势 能减少, 有1212022mv qE d mv +=∆ 二.质谱仪 主要用于分析同位素, 测定其质量, 荷质比和含量比,1.质谱仪的结构原理(1)离子发生器O (发射出电量q 、质量m 的粒子从A 中小孔S 飘出时速度大小不计)(2)静电加速器C :静电加速器两极板M 和N 的中心分别开有小孔S 1、S 2,粒子从S 1进入后,经电压为U 的电场加速后,从S 2孔以速度v 飞出;(3)速度选择器D :由正交的匀强电场E 0和匀强磁场B 0构成,调整E 0和B 0的大小可以选择度为v 0=E 0/B 0的粒子通过速度选择器,从S 3孔射出;(4)偏转磁场B :粒子从速度选择器小孔S 3射出后,从偏转磁场边界挡板上的小孔S 4进入,做半径为r 的匀速圆周运动;(5)感光片F :粒子在偏转磁场中做半圆运动后,打在感光胶片的P 点 被记录,可以测得PS 4间的距离L 。
装置中S 、S 1、S 2、S 3、S 4五个小孔在同一条直线上2.问题讨论:质量m 和比荷的两种表达形式表达式一:设粒子的质量为m 、带电量为q (重力不计),粒子经电场加速由动能定理有:221υm qU = ①; 粒子在偏转磁场中作圆周运动有:Bq m L υ2= ②; 联立①②得:U L qB m 822= ,比荷228LB U m q = 表达式二:同位素荷质比和质量的测定: 粒子通过加速电场,通过速度选择器, 根据匀速运动的条件: 0B E v =。
若测出粒子在偏转磁场的轨道直径为L , 则Bq B mE Bq mv R L 0222===, 所以同位素的荷质比和质量分别为EBqL B m BL B E m q 2;200==。
三.磁流体发电机磁流体发电就是利用等离子体来发电。
1.等离子体的产生:在高温条件下(例如2000K )气体发生电离,电离后的气体中含有离子、电子和部分未电离的中性粒子,因为正负电荷的密度几乎相等,从整体看呈电中性,这种高度电离的气体就称为等离子体,也有人称它为“物质的第四态”。
2.工作原理:磁流体发电机结构原理如图(1)所示,其平面图如图(2)所示。
M 、N 为平行板电极,极板间有垂直于纸面向里的匀强磁场,让等离子体平行于极板从左向右高速射入极板间,由于洛伦兹力的作用,正离子将向M 板偏转,负离子将向N 板偏转,于是在M 板上积累正电荷,在N 板上积累负电荷。
这样在两极板间就产生电势差,形成了电场,场强方向从M 指向N ,以后进入极板间的带电粒子除受到洛伦兹力洛F 之外,还受到电场力电F 的作用,只要电洛F F >,带电粒子就继续偏转,极板上就继续积累电荷,使极板间的场强增加,直到带电粒子所受的电场力电F 与洛伦兹力洛F 大小相等为止。
此后带电粒子进入极板间不再偏转,极板上也就不再积累电荷而形成稳定的电势差3.电动势的计算: 设两极板间距为d , 根据两极电势差达到最大值的条件电洛F F =, 即dBB E v ε==, 则磁流体发电机的电动势ε=Bdv 。
四.回旋加速器1932年美国物理学家劳伦斯发明的回旋加速器,是磁场和电场对运动电荷的作用规律在科学技术中的应用典例,回旋加速器是用来加速带电粒子使之获得高能量的装置。
1.回旋加速器的结构。
回旋加速器的核心部分是两个D 形金属扁盒(如图所示),在两盒之间留有一条窄缝,在窄缝中心附近放有粒子源O 。
D 形盒装在真空容器中,整个装置放在巨大的电磁铁的两极之间,匀强磁场方向垂直于D 形盒的底面。
把两个D 形盒分别接到高频电源的两极上。
2.回旋加速器的工作原理。
如图所示,从粒子源O 放射出的带电粒子,经两D 形OB盒间的电场加速后,垂直磁场方向进入某一D 形盒内,在洛伦兹力的作用下做匀速圆周运动,经磁场偏转半个周期后又回到窄缝。
此时窄缝间的电场方向恰好改变,带电粒子在窄缝中再一次被加速,以更大的速度进入另一D 形盒做匀速圆周运动……,这样,带电粒子不断被加速,直至它在D 形盒内沿螺线轨道运动逐渐趋于盒的边缘,当粒子达到预期的速率后,用特殊装置将其引出。
3.问题讨论。
(1)高频电源的频率电f 。
带电粒子在匀强磁场中运动的周期Bq m π2T =,带电粒子运动时,每次经过窄缝都被电场加速,运动速度不断增加,在磁场中运动半径不断增大,但粒子在磁场中每运动半周的时间qB m T t π==2不变。
由于窄缝宽度很小,粒子通过电场窄缝的时间很短,可以忽略不计,粒子运动的总时间只考虑它在磁场中运动的时间。
因此,要使粒子每次经过窄缝时都能被加速的条件是:高频电源的周期与带电粒子运动的周期相等(同步),即高频电源的频率为mqB f π2=电,才能实现回旋加速。
(2)粒子加速后的最大动能E km 由于D 形盒的半径R 一定,粒子在D 形盒中加速的最后半周的半径为R ,由R m Bq 2υυ=可知mBqR =υ,所以带电粒子的最大动能mR q B m E km 222222==υ。
虽然洛伦兹力对带电粒子不做功,但E km 却与B 有关; 由于km E m nqU ==22υ,由此可知,加速电压的高低只会影响带电粒子加速的总次数,并不影响回旋加速后的最大动能。
(3)能否无限制地回旋加速。
由于相对论效应,当带电粒子速率接近光速时,带电粒子的质量将显著增加,从而带电粒子做圆周运动的周期将随带电粒子质量的增加而加长。
如果加在D 形盒两极的交变电场的周期不变的话,带电粒子由于每次“迟到”一点,就不能保证粒子每次经过窄缝时总被加速。
因此,同步条件被破坏,也就不能再提高带电粒子的速率了(4)粒子在加速器中运动的时间:设加速电压为U ,质量为m 、带电量为q 的粒子共被加速了n 次,若不计在电场中运动的时间,有: m R q B E nqU km 2222==所以mUqR B n 222= 又因为在一个周期内带电粒子被加速两次,所以粒子在磁场中运动的时间U BR T n t 222π==磁若计上粒子在电场中运动的时间,则粒子在两D 形盒间的运动可视为初速度为零的匀加速直线运动,设间隙为d ,有:221电t md qU nd ⋅= 所以UBdR qU m nd t ==22电 故粒子在回旋加速器中运动的总时间为:U R d BR t t t 2)2(π+=+=磁电 因为d R >>,所以电磁t t >>,故粒子在电场中运动的时间可以忽略【例题】有一回旋加速器,两个D 形盒的半径为R ,两D 形盒之间的高频电压为U ,偏转磁场的磁感强度为B 。
如果一个α粒子和一个质子,都从加速器的中心开始被加速,试求它们从D 形盒飞出时的速度之比。
错解:当带电粒子在D 形盒内做圆周运动时,速率不变。
当带电粒子通过两个D 形盒之间的缝隙时,电场力对带电粒子做功,使带电粒子的速度增大。
设带电粒子的质量为m ,电荷为q ,在回旋加速器中被加速的次数为n ,从D 形盒飞出时的速度为V ,根据动能定理有:221mV nqU =,解得mnqU V 2=。
由上式可知,带电粒子从D 形盒飞出时的速度与带电粒子的荷质比的平方根成正比,所以21=H V V α。
分析纠错:上法中认为α粒子和质子在回旋加速器内被加速的次数相同的,是造成错解的原因。
因带电粒子在D 形盒内做匀速圆周运动的向心力是由洛仑兹力提供的,对带电粒子飞出回旋加速器前的最后半周,根据牛顿第二定律有:R V m qBV 2=解得mq BR V =。
因为B 、R 为定值,所以带电粒子从D 形盒飞出时的速度与带电粒子的荷质比成正比。
因α粒子的质量是质子质量的4倍,α粒子的电荷量是质子电荷量的4倍,故有:21=H V V α 五.霍尔效应1.霍尔效应。
金属导体板放在垂直于它的匀强磁场中,当导体板中通过电流时,在平行于磁场且平行于电流的两个侧面间会产生电势差,这种现象叫霍尔效应。
2.霍尔效应的解释。
如图,截面为矩形的金属导体,在x方向通以电流I,在z方向加磁场B,导体中自由电子逆着电流方向运动。
由左手定则可以判断,运动的电子在洛伦兹力作用下向下表面聚集,在导体的上表面A 就会出现多余的正电荷,形成上表面电势高,下表面电势低的电势差,导体内部出现电场,电场方向由A 指向A ’,以后运动的电子将同时受洛伦兹力洛F 和电场力电F 作用,随着表面电荷聚集,电场强度增加,电F 也增加,最终会使运动的电子达到受力平衡(电洛F F =)而匀速运动,此时导体上下两表面间就出现稳定的电势差。
3.霍尔效应中的结论。
设导体板厚度为h(y 轴方向)、宽度为d 、通入的电流为I ,匀强磁场的磁感应强度为B ,导体中单位体积内自由电子数为n ,电子的电量为e ,定向移动速度大小为v ,上下表面间的电势差为U ;(1)由h Uq Bq =υ⇒υBh U =①。
(2)实验研究表明,U 、I 、B 的关系还可表达为d IB kU =②,k 为霍尔系数。
又由电流的微观表达式有:υυnehd nes I ==③。
