一元一次不等式组1--浙教版
初二数学最新课件-一元一次不等式组3浙教版 精品

例1:解一元一次不等式组 3X+2>X ①
分析:
1 X≤2 ②
3
根据一元一次不等式组解的意义, 只要求出各
不等式的解的公共部分即可.
解: 解不等式①,得X>-1
解不等式②,得X≤6
把①, ②两不等式的解表示在数轴上(如图)
-3 -2 -1 0 1 2 3 4 5 6
所以原不等式组的解是 -1<X≤6
X≤2
X>-1
X <2
X >1
各个一元一次不等式组中,两个不等式里X的值,
有公共部分的是:
①② ③
;
没有公共部分的是:
④
.
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
定义: 组成不等式组的各个不等式的解的公共部分就
是不等式组的解.
注: 当它们没有公共部分时,则称这个不等式组无解.
探索研究
解由两个一元一次不等式组成的不等式组, 有几 种不同情况?
若m<n,你能说出下列四种情况1) x> m (2) x> m (3) x< m (4) x<m
x<n
x >n
x<n
m<x<n ; x>n ; x<m
x>n
; 无解
大小小大, 取两数之间
墨水笔
90
34. 元
圆珠笔
90
44. 元
44.9X+34.9(15-X) <580 44.9X+34.9(15-X) >570 定义: 一般地,由几个同一未知数的一元一次不等 式所组成的一组不等式,叫做一元一次不等式组.
实际生活还有这样的例子吗?
议一议: (用数轴来解释)
在① X>-1 ② X>-2 ③ X<1 ④ X <-1
一元一次不等式组4浙教版

最优化问题
最优化问题的定义
最优化问题是一类在一定条件下寻求目标函数最优值的问题,通常可以转化为一元一次不等式组 进行求解。
最优化问题的求解步骤
首先根据问题的约束条件列出不等式组,然后利用数轴或平面直角坐标系表示不等式组的解集, 最后通过目标函数在解集上的取值情况确定最优解。
最优化问题的应用举例
例如成本最小化、收益最大化、时间最短化等,这些问题都可以通过构建一元一次不等式组模型 ,转化为最优化问题进行求解。
区间数问题的定义
区间数问题是一类涉及区间运算和区 间比较的问题,通常可以转化为一元 一次不等式组进行求解。
区间数问题的应用举例
例如误差分析、数据处理、金融投资等, 这些问题都可以通过构建一元一次不等式 组模型,转化为区间数问题进行求解。
区间数问题的求解步骤
首先根据问题的条件列出区间不等式组, 然后利用数轴表示不等式组的解集,最后 通过比较区间端点的大小确定解的范围。
注意事项
在求解绝对值一元一次不等式组时,需要特别注意绝对值符号的性质, 以及转化后的不等式组的解集与原不等式组解集的关系。
分式一元一次不等式组
分式一元一次不等式组的定义
分母中含有未知数的一元一次不等式组,其解集需考虑分式的性质。
分式一元一次不等式组的解法
首先确定分母的取值范围,然后根据分式的性质将原不等式组转化为整式不等式组,接着 求解整式不等式组得出解集,最后根据分母的取值范围对解集进行筛选得出最终解集。
同向正数可乘性
如果$a > b > 0$且$c > 0$,则 $ac > bc$。
特殊性质
当$a > b > 0$时,$frac{1}{a} < frac{1}{b}$;当$a < b < 0$时,
浙教版八年级竞赛培优训练第9讲 一元一次不等式组
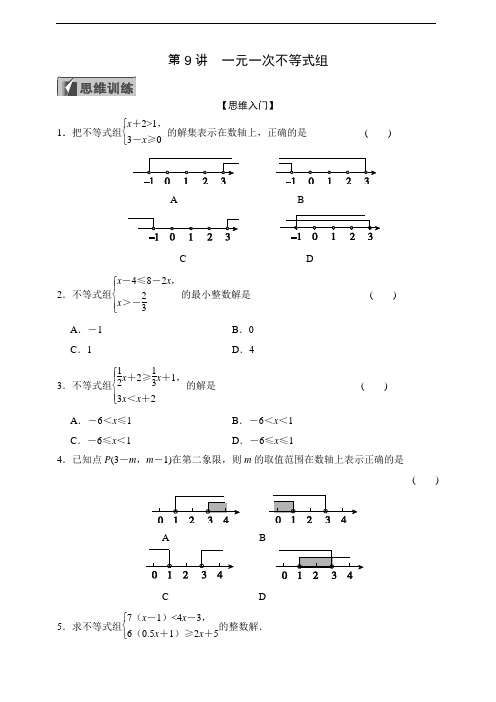
第9讲 一元一次不等式组【思维入门】1.把不等式组⎩⎨⎧x +2>1,3-x ≥0的解集表示在数轴上,正确的是( )A BC D2.不等式组⎩⎪⎨⎪⎧x -4≤8-2x ,x >-23的最小整数解是 ( )A .-1B .0C .1D .43.不等式组⎩⎪⎨⎪⎧12x +2≥13x +1,3x <x +2的解是 ( )A .-6<x ≤1B .-6<x <1C .-6≤x <1D .-6≤x ≤14.已知点P (3-m ,m -1)在第二象限,则m 的取值范围在数轴上表示正确的是( )A BC D5.求不等式组⎩⎨⎧7(x -1)<4x -3,6(0.5x +1)≥2x +5的整数解.6.解不等式组⎩⎪⎨⎪⎧23x +5>1-x ,x -1<34x -18,并写出它的非负整数解.【思维拓展】7.若关于x 的不等式组⎩⎨⎧5-2x >-1,x -a >0无实数解,则a 的取值范围是____.8.对非负数x 四舍五入到个位的值记为〈x 〉,即当n 为非负整数时,若n -12≤x <n +12,则〈x 〉=n .如〈0.46〉=0,〈3.67〉=4. 给出下列关于〈x 〉的结论: ①〈1.493〉=1; ②〈2x 〉=2〈x 〉;③若〈12x -1〉=4,则实数x 的取值范围是9≤x <11;④当x ≥0,m 为非负整数时,有〈m +2 013x 〉=m +〈2 013x 〉; ⑤〈x +y 〉=〈x 〉+〈y 〉.其中,正确的结论有____(填写所有正确的序号).9.定义新运算:对于任意实数a ,b 都有a △b =ab -a -b +1,等式右边是通常的加法、减法及乘法运算,例如:2△4=2×4-2-4+1=8-6+1=3,请根据上述知识解决问题:若3△x 的值大于5而小于9,求x 的取值范围.10.已知实数a 是不等于3的常数,解不等式组⎩⎪⎨⎪⎧-2x +3≥-3,12(x -2a )+12x <0,并依据a 的取值情况写出其解集.11.已知关于x ,y 的方程组⎩⎨⎧5x +2y =11a +18,2x -3y =12a -8的解满足x >0,y >0,求实数a 的取值范围.【思维升华】12.若关于x 的不等式组⎩⎨⎧2-3x ≥0,2x +m >0没有实数解,则实数m 的取值范围是( )A .m <-43B .m ≤-43C .m >-43D .m ≥-4313.已知a 是实数,关于x ,y 的二元一次方程组⎩⎨⎧2x -3y =5a ,x +2y =1-2a 的解不可能出现的情况是( )A .x ,y 都是正数B .x ,y 都是负数C .x 是正数,y 是负数D .x 是负数,y 是正数14.已知方程组⎩⎨⎧x +my =11,x +3=2y 的解都是正整数,则整数m 的值为____.15.已知a +b +c =0,a ≥b ≥c ,a ≠0,则ca 的最大值是 ____,最小值是____. 16.已知关于x 的不等式组⎩⎨⎧x <a +1,2x -2>a 的解集中的整数恰好有2个,求实数a 的取值范围.第9讲 一元一次不等式组【思维入门】1.把不等式组⎩⎨⎧x +2>1,3-x ≥0的解集表示在数轴上,正确的是( D )A BC D2.不等式组⎩⎪⎨⎪⎧x -4≤8-2x ,x >-23的最小整数解是 ( B )A .-1B .0C .1D .43.不等式组⎩⎪⎨⎪⎧12x +2≥13x +1,3x <x +2的解是 ( C )A .-6<x ≤1B .-6<x <1C .-6≤x <1D .-6≤x ≤14.已知点P (3-m ,m -1)在第二象限,则m 的取值范围在数轴上表示正确的是( A )A BC D5.求不等式组⎩⎨⎧7(x -1)<4x -3,6(0.5x +1)≥2x +5的整数解.解:⎩⎪⎨⎪⎧7(x -1)<4x -3,①6(0.5x +1)≥2x +5,②解不等式①,得x <43,解不等式②,得x ≥-1, ∴不等式组的解集为-1≤x <43, ∴不等式组的整数解为-1,0,1.6.解不等式组⎩⎪⎨⎪⎧23x +5>1-x ,x -1<34x -18,并写出它的非负整数解.解:⎩⎪⎨⎪⎧23x +5>1-x ,①x -1<34x -18,②解不等式①,得x >-125, 解不等式②,得x <72, ∴不等式组的解集为-125<x <72. ∴它的非负整数解为0,1,2,3.【思维拓展】7.若关于x 的不等式组⎩⎨⎧5-2x >-1,x -a >0无实数解,则a 的取值范围是__a ≥3__.【解析】 解关于x 的不等式组⎩⎪⎨⎪⎧5-2x >-1,x -a >0,得⎩⎪⎨⎪⎧x <3,x >a , ∵不等式组无解,∴a ≥3.8.对非负数x 四舍五入到个位的值记为〈x 〉,即当n 为非负整数时,若n -12≤x <n +12,则〈x 〉=n .如〈0.46〉=0,〈3.67〉=4. 给出下列关于〈x 〉的结论: ①〈1.493〉=1; ②〈2x 〉=2〈x 〉;③若〈12x -1〉=4,则实数x 的取值范围是9≤x <11;④当x ≥0,m 为非负整数时,有〈m +2 013x 〉=m +〈2 013x 〉; ⑤〈x +y 〉=〈x 〉+〈y 〉.其中,正确的结论有__①③④__(填写所有正确的序号). 【解析】 ①〈1.493〉=1,正确;②〈2x 〉≠2〈x 〉,例如当x =0.3时,〈2x 〉=1,2〈x 〉=0,故②错误; ③若〈12x -1〉=4,则4-12≤12x -1<4+12,解得9≤x <11,故③正确; ④m 为整数,不影响四舍五入,故〈m +2 013x 〉=m +〈2 013x 〉,④正确; ⑤〈x +y 〉≠〈x 〉+〈y 〉,例如x =0.3,y =0.4时,〈x +y 〉=1,〈x 〉+〈y 〉=0,故⑤错误. 综上可得①③④正确.9.定义新运算:对于任意实数a ,b 都有a △b =ab -a -b +1,等式右边是通常的加法、减法及乘法运算,例如:2△4=2×4-2-4+1=8-6+1=3,请根据上述知识解决问题:若3△x 的值大于5而小于9,求x 的取值范围.解:∵3△x =3x -3-x +1=2x -2,且3△x 的值大于5而小于9, ∴5<2x -2<9,即72<x <112.10.已知实数a 是不等于3的常数,解不等式组⎩⎪⎨⎪⎧-2x +3≥-3,12(x -2a )+12x <0,并依据a 的取值情况写出其解集.解:⎩⎨⎧-2x +3≥-3,①12(x -2a )+12x <0,②解①得x ≤3,解②得x <a , ∵ a 是不等于3的常数,∴ 当a >3时,不等式组的解集为x ≤3; 当a <3时,不等式组的解集为x <a .11.已知关于x ,y 的方程组⎩⎨⎧5x +2y =11a +18,2x -3y =12a -8的解满足x >0,y >0,求实数a 的取值范围.解:解方程组⎩⎪⎨⎪⎧5x +2y =11a +18,①2x -3y =12a -8,②①×3得15x +6y =33a +54③, ②×2得4x -6y =24a -16④,③+④得19x =57a +38,解得x =3a +2, 把x =3a +2代入①,得5(3a +2)+2y =11a +18, 解得y =-2a +4,∴方程组的解是⎩⎪⎨⎪⎧x =3a +2,y =-2a +4,∵x >0,y >0,∴⎩⎪⎨⎪⎧3a +2>0,-2a +4>0,解得⎩⎨⎧a >-23,a <2, ∴a 的取值范围是-23<a <2.【思维升华】12.若关于x 的不等式组⎩⎨⎧2-3x ≥0,2x +m >0没有实数解,则实数m 的取值范围是( B )A .m <-43 B .m ≤-43 C .m >-43D .m ≥-4313.已知a 是实数,关于x ,y 的二元一次方程组⎩⎨⎧2x -3y =5a ,x +2y =1-2a 的解不可能出现的情况是( B )A .x ,y 都是正数B .x ,y 都是负数C .x 是正数,y 是负数D .x 是负数,y 是正数【解析】 ⎩⎪⎨⎪⎧2x -3y =5a ,①x +2y =1-2a ,②②×2-①得7y =2-9a ,y =2-9a7③,③代入②,得x =1-2a -2y =1-2a -2×2-9a 7=4a +37.A.⎩⎨⎧2-9a7>0,4a +37>0,解得-34<a <29;B.⎩⎨⎧2-9a 7<0,4a +37<0,解得a >29,a <-34,无解;C.⎩⎨⎧2-9a7>0,4a +37<0,解得a <-34;D.⎩⎨⎧2-9a7<0,4a +37>0,解得a >29,故选B.14.已知方程组⎩⎨⎧x +my =11,x +3=2y 的解都是正整数,则整数m 的值为__-1,0或5__.【解析】 方程组⎩⎪⎨⎪⎧x +my =11,x +3=2y ,∴x +my -x -3=11-2y , 解得(m +2)y =14,y =14m +2.∵方程组有正整数解,∴m +2>0,m >-2,又x =22-3mm +2,故22-3m >0,解得m <223,故-2<m <223,整数m 只能取-1,0,1,2,3,4,5,6,7. 又x ,y 均为正整数,∴只有m =-1或0或5符合题意.15.已知a +b +c =0,a ≥b ≥c ,a ≠0,则c a 的最大值是 __-12__,最小值是__-2__. 【解析】 已知a +b +c =0,即c =-a -b , 因为a ≥b ≥c ,必有a >0,c <0,c a =-a -b a =-1-b a , 可知当b 与a 同号时,即b >0. 式子-1-ba 才可能取最小值.因为a ≥b ,故ba ≤1,故当b a =1时,式子-1-ba 取最小值为-2. 同理:当b 与a 异号时,即b <0, 式子-1-ba 才可能取最大值, a +b +c =0,a =-(b +c ). 因为0≥b ≥c ,即|b |≤|c |.式子-1-b a =-1+b b +c =-1+|b ||b |+|c |,当|b ||b |+|c |取最大值时,整个式子有最大值,|b ||b |+|c |≤|b ||b |+|b |=12. 故式子-1-b a ≤-1+12=-12,此为最大值.16.已知关于x 的不等式组⎩⎨⎧x <a +1,2x -2>a 的解集中的整数恰好有2个,求实数a 的取值范围.解:原不等式组可化为⎩⎪⎨⎪⎧x <a +1,x >a +22,根据题意,有a +22<x <a +1.满足原不等式组解集中的整数恰好有2个,只需 ⎩⎪⎨⎪⎧k ≤a +22<k +1,k +2<a +1≤k +3,(k 为整数) 即⎩⎪⎨⎪⎧2k -2≤a <2k ,k +1<a ≤k +2.(k 为整数)(*) 关于整数k 的不等式组⎩⎪⎨⎪⎧k +1<2k ,2k -2≤k +2有解.解得1<k ≤4,得k 可以取2,3,4.当k =2时,代入(*)式,有⎩⎪⎨⎪⎧2≤a <4,3<a ≤4,解得3<a <4;当k =3时,代入(*)式,有⎩⎪⎨⎪⎧4≤a <6,4<a ≤5,解得4<a ≤5;当k =4时,代入(*)式,有⎩⎪⎨⎪⎧6≤a <8,5<a ≤6,解得a =6.所以,3<a <4或4<a ≤5或a =6即为所求.。
部编版一元一次不等式实用课件浙教版2

3、在依据不等式的性质探究一元一次不等式解法过程中,加深对化归思想的体会。
探究二 一元一次不等式的解法
已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
问题3:像这样的不等式叫一元一次不等式,你能依据一元一次方程的概念说出什么叫一元一次不等式吗?
巩固练习2,
已知方程ax+12=0的解是x=3,求关于x不等式(a+2)x>-6 的解集,并在数轴上表示出来,其中正整数解有哪些?
去括号,得2x+2≥6x-15+12, 去括号
课堂小结 探 解究下点列: 不一 等元 式一 ,次 并不 在等 数式轴的 上概 表念 示解集:
归(纳3):y解与一1的元差一不次大不于等2式y与和3解的一差元;一次方程 这1、个了不解等一式元的一解次集不在等数式轴的上概的念表。示 这合个并不 同等类式项的解集在数轴上的表示 合并同类项
这个不等式的解集在数轴上的表示
移项,合并同类项,得-4x≥-5,
2、掌握一元一次不等式的解法,并能在数轴上表示出解集。
(2) 2(x+5)≤3(x-5);
问题3:像这样的不等式叫一元一次不等式,你能依据一元一次方程的概念说出什么叫一元一次不等式吗?
探究二 一元一次不等式的解法
问题3:像这样的不等式叫一元一次不等式,你能依据一元一次方程的概念说出什么叫一元一次不等式吗?
问题13:上像述这不样等的式不中等各 式含叫有一几元个一未次知不数等?式未,知你数能的依次据数一都元是一几次次方?程的概念说出什么叫一元一次不等式吗?
1、你学到了什么? 3一、元在一依次据方不程等式的性质探究一元一一元次一不次等不式等解式法过程中,加深对化归思想的体会。
一元一次不等式组教案

一元一次不等式组教案【篇一:《一元一次不等式组》教学设计】一元一次不等式组一、课表解读在初中数学课程标准,第三学段数与代数对一元一次不等式组部分是这样描述的:1.充分感受生活中存在着大量的不等式关系,了解不等式组的意义;2.会解简单的一元一次不等式组,并会用数轴确定解集。
二、教材分析1、教材的地位和作用《一元一次不等式组》的主要内容是一元一次不等式组的解法及其简单应用。
是在学习了有理数的大小比较、等式及其性质、一元一次方程的基础上,开始学习简单的数量之间的不等关系,进一步探究现实世界数量关系的重要内容,是继一元一次方程和二元一次方程组之后,又一次数学建模思想的学习,也是后继学习一元二次方程、函数及进一步学习不等式的重要基础,具有承前启后的重要作用。
《一元一次不等式组》是本章的最后一节,是一元一次不等式知识的综合运用和拓展延伸,是进一步刻画现实世界数量关系的数学模型,是下一节利用一元一次不等式组解决实际问题的关键。
2、教学目标设计依据《课程标准》对7—9年级《不等式》学段的目标要求和本班学生实际情况,特确定如下目标:1.通过实例体会一元一次不等式组是研究量与量之间关系的重要模型之一。
2.了解一元一次不等式组及解集的概念。
3.会利用数轴解较简单的一元一次不等式组。
4.培养学生分析、解决实际问题的能力。
5.通过实际问题的解决,体会数学知识在生活中的应用,激发学生的学习兴趣。
培养学生认真倾听,大胆回答,勤于思考、善于反思的良好学习习惯。
3、教学重点、难点:重点:理解一元一次不等式组的有关概念,会解简单的一元一次不等式组;难点:正确理解一元一次不等式组的解集。
三、学情分析1、学生特点从学生学习的心理基础和认知特点来说,学生已经学习了一元一次不等式,并能较熟练地解一元一次不等式,能将简单的实际问题抽象为数学模型,有一定的数学化能力。
但学生将两个一元一次不等式的解集在同一数轴上表示会产生一定的困惑。
这个年龄段的学生,以感性认识为主,并向理性认知过渡,所以,我对本节课的设计是通过两个学生所熟悉的问题情境,让学生独立思考,合作交流,从而引导其自主学习。
第一章 一元一次不等式和一元一次不等式组

第一章一元一次不等式和一元一次不等式组第一节不等关系一、生活中的不等关系1.不等关系在现实生活中并不少见,大家肯定接触过不少,能举出例子吗?那么,如何用式子表示不等关系呢?请看例题:如图,用两根长度均为l cm的绳子,分别围成一个正方形和圆.1)如果要使正方形的面积不大于25 cm2,那么绳长l应满足怎样的关系式?2)如果要使圆的面积不小于100 cm2,那么绳长l应满足怎样的关系式?3)当l=8时,正方形和圆的面积哪个大?l=12呢?4)你能得到什么猜想?改变l的取值,再试一试.本题中大家首先要弄明白两个问题,一个是正方形和圆的面积计算公式,另一个是了解“不大于”“大于”等词的含意.圆的面积是πR2,其中R是圆的半径.两数比较有大于、等于、小于三种情况,“不大于”就是等于或小于.一般地,用符号“<”(或“≤”),“>”(或“≥”)连接的式子叫做不等式(inequality).列不等式:不等式表示代数式之间的不等关系,与方程表示的相等关系相对应。
列不等式表示不等关系的方法步骤:(1)分析题意,重点找出题中的各种量;(2)寻找各种量之间的不等关系;(3)用代数式表示各种量(4)用适当的不等号将不等关系连接起来。
例1.用不等式表示(1)a是正数;(2)a是负数;(3)a与6的和小于5;(4)x与2的差小于-1;例2.根据下面的数量关系列不等式试比较3x2-2x+7与4x2-2x+7的大小例3.数形结合题型a,b两个实数在数轴上的对应点如图所示:用“<”或“>”号填空:(1)a______b;(2)|a|______|b|;(3)a+b_________0;(4)a-b_______0;(5)a+b_______a-b;(6)ab______a.练一练:(1)x 的32与5的差不小于1; (2)x 与6的和小于等于9;(3)8与y 的2倍的和是正数; (4)a 的3倍与7的差是非负数;(5)x 的4倍大于x 的3倍与7的差;(6)x 的54与1的和小于-2;(7)x 与8的差的32不大于0. (8)m 与1差的绝对值是非负数。
部编版一元一次不等式实用课件浙教版7
0
1
2
3
4
5
❖的解集是-1<x<2,则m=____, n=____.
❖(4)你能利用数轴分别确定上面所得的一元一次不等式组的解集吗?
❖不等式组中X的取值范围呢?
x 0, ❖不等式组中X的取值范围呢?
(1 6) ❖不等式组叫做一元一次不等式组。
x 4. - ❖例1:如果不等式组
知数
m+n≤ x < ( 2n+m+1 )÷2
又因为
3≤x<5
所以
2nm2mn13 5
所以 n/m=4
解得
n 4 m 1
2x 3a 7b 练习2:如果不等式组 6b 3x 5a
的解是5<x<22,求a,b的值
题型2:已知不等式的整数解的个数,求 待定字母的取值范围
例 4、已知关于 x 的不等式组 x-m≥0 的整数 5-2x>1
❖解1:原不.一等式组元的解一集为次不等式组的概念
❖的取值范围__________
❖(2)利用数轴,找出这些不等式解集的 公共部分;
(1)“一元”指的是什么? ❖已知关于x,y的方程组 x+y=2a+7
❖的取值范围__________
指不等式组中只含有一个未知数。 ❖例1:如果不等式组
有解,则m
❖你能说出不等式组中X的取值范围吗?
X >b X<a
a
b
X <b X>a
ab
X <b X<a
a
b
X >b
a
b
不等式组的解集 规律(口诀)
X>b
两大取大
X<a
两小取小
a<X<b 无解
大小小大 中间找
第10讲 一元一次不等式(组)
合并同类项,得-x>-2,
系数化为1,得x<2, 所以原不等式的解集是x<2.
一元一次不等式组的解法
◆中考指数:★★★★★ 1.解一元一次不等式组的三个步骤 (1)分别求出不等式组中各个不等式的解集; (2)在数轴上把各个不等式的解集表示出来; (3)在数轴上找出满足所有不等式的解集的公共部分,就 是这个不等式组的解集.若各个不等式的解集没有公共部 分,则该不等式组无解. 2.求不等式组的解集时要注意题目对特殊解的要求,如求 正整数解,非负整数解等.
x 2 3,
x 3 4.
【解析】解不等式x+2≥3得:x≥1.
解不等式x-3≤4得:x≤7.
所以不等式组的解集为:1≤x≤7.
x 3 0, 10.(2012·梅州中考)解不等式组 并判断-1, 2 1 2 x- 3 3x,
这两个数是否为该不等式组的解.
【教你解题】
解不等式①
x+1>0
x>-1
2x+10≥6x-6 2x-6x≥-6-10 -4x≥-16 x≤4 -1<x≤4 在数轴上表示这个解集
解不等式②
确定解集 表示解集
【对点训练】
7.(2012·益阳中考)如图,数轴上表示的是下列哪个不等式组
的解集(
)
(A) (C)
x 5 x> 3 x<5
C:∵ 1 <0, 根据不等式的性质3,不等式的两边都乘以一个负
2
数,不等号的方向需要改变,所以正确;
D:∵c<0,∴根据不等式的性质3,不等号的方向需要改变,
即 > .
a c b c
【对点训练】
1.(2011·凉山州中考)下列不等式变形正确的是( (A)由a>b,得ac>bc (C)由a>b,得-a>-b (B)由a>b,得-2a<-2b (D)由a>b,得a-2<b-2 )
一元一次不等式ppt2 浙教版
例1:解下列不等式,并把解集在数轴上表示出来:
(1) 4x10 (2) 3 x 1.2
5
解:两边同除以4,
解:两边同除以
得x 5 2
注意:不等式 的两边同乘 (或除以)同
得 x≤-2
3 5
,
一个负数,不
等号要改变方
向。
1 0 1 2 5 3
3 2 1 0 1
2
例2:已知不等式7x-2≤9x+3,
•
3、在比夜更深的地方,一定有比夜更黑的眼睛。
•
4、一切伟大的行动和思想,都有一个微不足道的开始。
•
5、从来不跌倒不算光彩,每次跌倒后能再站起来,才是最大的荣耀。
•
6、这个世界到处充满着不公平,我们能做的不仅仅是接受,还要试着做一些反抗。
•
7、一个最困苦、最卑贱、最为命运所屈辱的人,只要还抱有希望,便无所怨惧。
不等号
1个 一次
定义:
不等号的两边都是整式,而且只含有一个 未知数,未知数的最高次数是一次,这样的不 等式叫做一元一次不等式。
特点: (1)不等号的两边都是整式
(2)只含有一个未知数 (3)未知数的次数是1
练一练:下列不等式中哪些是一元一次不等 式?
(1) 2x33y1 (2) x21016
•
13、不管从什么时候开始,重要的是开始以后不要停止;不管在什么时候结束,重要的是结束以后不要后悔。
•
14、当你决定坚持一件事情,全世界都会为你让路。
•
15、只有在开水里,茶叶才能展开生命浓郁的香气。
•
16、别想一下造出大海,必须先由小河川开始。
•
17、不要让未来的你,讨厌现在的自己,困惑谁都有,但成功只配得上勇敢的行动派。
一元一次不等式ppt 浙教版
例1:交洋振兴玩具厂投资5万元建一个简易厂房,生产某 种出口木凳。这种木凳每个的人工和木料成本共是6元, 出售价是10元,应付的税款和其他费用是销售收入的10%。 问至少需要生产、销售多少个这种木凳,才能使所获利润 (利润=毛利润减去税款和其他费用)超过投资建造厂房的 费用?
每本笔记本4元2角。她买了两本笔记本后,还可买几支铅笔?
设还可买x支铅笔,根据题意,得
2x4.22 .21
生活生产中的不等式
(3) 已知一种卡车每辆至多能载3吨货物,现在100吨黄豆,
若要一次运这批黄豆,至少需要这种卡车多少辆?设需要
这种卡车x辆,根据题意得
3x100 .
生活生产中的不等式
人跑到完全地区的时间不超过导火索燃烧的时间
请你举一个身边涉及不等关系的实际问题, 列出一元一次不等式,并求解.
李宁鞋专卖店与迪欧达以同样价格出售一批 同样的鞋,国庆期间各自推出不同的优惠方案:
大甩卖
8折
通通8折
庆国庆,答谢新老顾客
凡本店购满50元,超过部
分一律7折
购票决策
白鹤山庄浏览券每位学生票价10元,经联系对40人 以上的团体可以购买团体票,团体票价8元,但参加本 次活动的人数不足40人,你能否根据人数的多少做出决 策?
(2) 解:设他们每次搬运重物x箱, 由题意,得 60+80+50x≤1000 解得 x≤17.2 答:他们每次最多只能搬运重物17箱.
(1)审题:分析题目中已知什么求什么?明确各量之间 的关系,包括题目中的等量关系与不等量关系.
