5-5驻波5-6多普勒效应电磁波
合集下载
19 驻波 多普勒效应
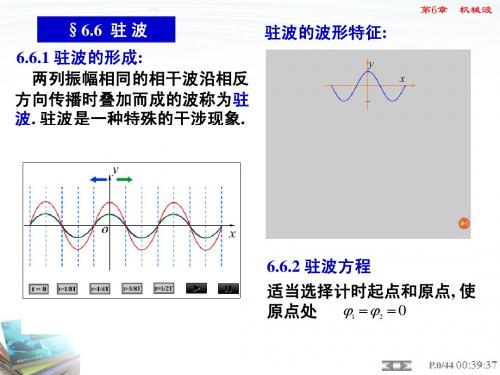
6.6.3 驻波的能量特征
波 节
x
x
波 腹
A
B
C
驻波与行波的区别
y 2 位移最大时 dWp ( ) x y 平衡位置时 dWk ( ) 2 t 驻波在相邻的波节间发生 动能和势能的转换, 动能集 中在波腹, 势能集中在波节; 机械能在相邻的波腹和波节 间往复传递, 并无无定向的 长距离传播.
请观察在反射点入射波和反射波两振动的相位关系
u
较 小
波 疏 介 质
u
较 大
波 密 介 质
当波从波疏介质垂直入射到波密介质，被反射到 波疏介质时形成波节. 入射波与反射波在此处的相位 时时相反, 即反射波在分界处产生相位跃变 ，相当 于出现了半个波长的波程差，称半波损失.
π
P.6/44
第6章 机械波
P.13/44
结论: 波源与观察者相互接近 多普勒效应的应用: 时, 感觉到的频率较高; 波源与 (1) 交通上测量车速; 观察者相互远离时, 感觉到的频 (2) 医学上用于测量血流速度; 率较低. (3) 天文学家利用电磁波红移 如果波源和观察者的运动不 说明大爆炸理论; 在一直线上, 只要考虑波源与 (4) 用于贵重物品、机密室的 观察者在连线方向上的速度投 防盗系统; 影即可. (5) 卫星跟踪系统等.
s: 波源的频率, 波源在单位时间
内发出的完整波形的数目. W : 波的频率, 单位时间内经过介 质中某点的完整波形的数目.
波源相对介质静止, 观察者也静止: ut u R W s t 6.7.1 波源静止, 观察者以速度 uR 相对于介质运动
uR u uS 0
前
u 340 500 Hz 531Hz u uS 340 20
5-(5)驻波
y 2 A cos 2π ( t
第十五章 机械波
二 驻波方程
x
x
)
)
y y1 y 2
A cos 2π ( t x
) A cos 2π ( t
x
)
2 A cos 2π
x
cos 2π t
驻波的振幅 与位置有关
各质点都在作同 频率的简谐运动
15 – 6
反射波在C点的振动方程
yC反 A cos(t )
实质：入射波在C引起的振动与反射波在C引起的 振动同相。
15 – 6
驻 波
位移最大时
第十五章 机械波
四 驻波的能量
波 节
波 腹
y x
x
dEp (
)
2
x
A B C 平衡位置时
dEk (
y t
)
2
平衡位置=>形变为零=>势能为零，动能最大
讨论
驻 波
驻波方程 y 2 A cos 2 π
x
第十五章 机械波
x
1）振幅 2 A cos 2 π
x
x
随 x 而异， 与时间无关.
k 0 ,1, 2 ,
)π k 0 ,1, 2 ,
cos 2 π t
1 2π
cos 2 π
x
k π
(k 1 2
x
u
o
－2.5 －5.0
P
4
x ( m)
y1 A co s[ ( t 5
2 3
5
x
图9
第十五章 机械波
二 驻波方程
x
x
)
)
y y1 y 2
A cos 2π ( t x
) A cos 2π ( t
x
)
2 A cos 2π
x
cos 2π t
驻波的振幅 与位置有关
各质点都在作同 频率的简谐运动
15 – 6
反射波在C点的振动方程
yC反 A cos(t )
实质：入射波在C引起的振动与反射波在C引起的 振动同相。
15 – 6
驻 波
位移最大时
第十五章 机械波
四 驻波的能量
波 节
波 腹
y x
x
dEp (
)
2
x
A B C 平衡位置时
dEk (
y t
)
2
平衡位置=>形变为零=>势能为零，动能最大
讨论
驻 波
驻波方程 y 2 A cos 2 π
x
第十五章 机械波
x
1）振幅 2 A cos 2 π
x
x
随 x 而异， 与时间无关.
k 0 ,1, 2 ,
)π k 0 ,1, 2 ,
cos 2 π t
1 2π
cos 2 π
x
k π
(k 1 2
x
u
o
－2.5 －5.0
P
4
x ( m)
y1 A co s[ ( t 5
2 3
5
x
图9
《驻波多普勒效应》课件
3
医学影像
驻波多普勒效应可用于医学影像中的超 声诊断，帮助医生观察血液流速和心脏 功能。
液位测量
驻波多普勒效应可用于液位测量中的雷 达和超声波传感器，精确测量液体的高 度和流速。
结论
1 驻波多普勒效应的意义
驻波多普勒效应为我们理解波的行为和相对 运动提供了重要的参考和应用基础。
2 展望未来应用
驻波多普勒效应有潜力在更广泛的领域应用， 如无线通信、智能交通系统等。
参考文献
1. 文献1 2. 文献2 3. 文献3 4. 文献4
幅度特性
波的振幅会随着波源 和观察者的相对运动 而发生变化。
相位特性
波的相位会随着波源 和观察者的相对运动 而发生变化。
相关系数
波的频率、振幅和相 位之间存在相关关系， 可通过数学模型予以 描述。
驻波多普勒效应的应用
1
炮弹偏转控制
2
驻波多普勒效应可应用于导弹和炮弹中
的雷达系统，以控制其偏转和跟踪目标。
《驻波多普勒效应》PPT 课件
驻波多普勒效应的探索
概述
1 驻波多普勒效应是什么
驻波多普勒效应是当波源和观察者相对运动时，由于观察者接收到的波的频率和振幅发 生变化的现象。
2 原理简介
的关系。
3 应用领域
在医学、天文学、气象学、雷达和声纳等领域有广泛的应用。
驻波多普勒效应的实验
实验步骤
通过改变波源或观察者的相 对运动，在实验室中模拟驻 波多普勒效应的现象。
实验装置
使用声音或电磁波的发射器 和接收器，测量波的频率和 振幅的变化。
实验结果
观察到波的频率和振幅随着 波源和观察者的相对运动而 发生变化。
驻波多普勒效应的特点
医学影像
驻波多普勒效应可用于医学影像中的超 声诊断，帮助医生观察血液流速和心脏 功能。
液位测量
驻波多普勒效应可用于液位测量中的雷 达和超声波传感器，精确测量液体的高 度和流速。
结论
1 驻波多普勒效应的意义
驻波多普勒效应为我们理解波的行为和相对 运动提供了重要的参考和应用基础。
2 展望未来应用
驻波多普勒效应有潜力在更广泛的领域应用， 如无线通信、智能交通系统等。
参考文献
1. 文献1 2. 文献2 3. 文献3 4. 文献4
幅度特性
波的振幅会随着波源 和观察者的相对运动 而发生变化。
相位特性
波的相位会随着波源 和观察者的相对运动 而发生变化。
相关系数
波的频率、振幅和相 位之间存在相关关系， 可通过数学模型予以 描述。
驻波多普勒效应的应用
1
炮弹偏转控制
2
驻波多普勒效应可应用于导弹和炮弹中
的雷达系统，以控制其偏转和跟踪目标。
《驻波多普勒效应》PPT 课件
驻波多普勒效应的探索
概述
1 驻波多普勒效应是什么
驻波多普勒效应是当波源和观察者相对运动时，由于观察者接收到的波的频率和振幅发 生变化的现象。
2 原理简介
的关系。
3 应用领域
在医学、天文学、气象学、雷达和声纳等领域有广泛的应用。
驻波多普勒效应的实验
实验步骤
通过改变波源或观察者的相 对运动，在实验室中模拟驻 波多普勒效应的现象。
实验装置
使用声音或电磁波的发射器 和接收器，测量波的频率和 振幅的变化。
实验结果
观察到波的频率和振幅随着 波源和观察者的相对运动而 发生变化。
驻波多普勒效应的特点
驻波和多普勒效应
7 Hz
例2 利用多普勒效应监测车速，固定波源发出频率
为 100kHz 的超声波，当汽车向波源行驶时，与波源
安装在一起的接收器接收到从汽车反射回来的波的频率
为" 110kHz . 已知空气中的声速为 u 330ms1，
求车速 .
v0
解 1）车为接收器 ' u v0
u
2）车为波源 " u ' v0 u
R
u
u vR
vST
u vR uT vST
u vR
u vS
若波源与观 察者不沿二者连 线运动，则以速 度在连线方向上 的分量计算。
v's
vs
vo
v'o
多普勒效应的应用
1）交通上测量车速； 2）医学上用于测量血流速度； 3）天文学家利用电磁波红移说明大爆炸理论； 4）用于贵重物品、机密室的防盗系统； 5）卫星跟踪系统等.
则观察者接收到的频率为：
R
u
u uT
1 T
vS
1 波源不动，观察者相对介质以速度 vR 运动
vS 0, vR 0,
观察者接收的 频率
R
u vR
u vR uT
u vR
u
观察者迎着波源运动时，接收到的频率增大。 观察者背向波源运动时，接收到的频率减小。
v 2 观察者不动，波源相对介质以速度
(1)波腹与波节 驻波振幅分布特点
cos 2 x 1 A(x) 2A 振幅最大，波腹
2 x k
x k k 0,1, 2,
2
cos 2 x 0 A(x) 0 振幅最小，波节
2 x ( k 1 ) x (k 1) k 0,1, 2,
波的叠加,驻波,多普勒效应
典型值：树叶沙沙声10db，谈话60db，喷气飞机120db
6-7 多普勒效应
27 2013/5/10
6-7 多普勒效应
当波源或观察者相对介质运动时，波在空间 传播的振动频率或观察者接收到的频率将与波源 发出的频率不同（频率发生变化）。由奥地利物 理学家C. J. Doppler在1842年首先发现。 例如高速列车呜笛疾驶而来时，将听到呜 笛声调变高、变尖；当火车远离而去时，其汽笛 的声调会变低。
10 2013/5/10
讨论： 当相位差满足
λ 两振动同相，合振幅A和波的强度I最大
A=Amax=A1+A2
∆ϕ = (ϕ 2 − ϕ1 ) − 2π
r2 − r1
= ±2kπ , k = 0,1,2,
I = I max = I1 + I 2 + 2 I1I 2
在这些位置上，合振动始终加强，称为干涉相长。
特别地当A1=A2时，A=2A1，I = 4I1
6-5 惠更斯原理 叠加原理 波的干涉
11 2013/5/10
当相位差满足
∆ϕ = (ϕ 2 − ϕ 1 ) − 2π
r2 − r1
λ
= ± ( 2k + 1)π , k = 0,1,2,
两振动反相 ，合振幅和强度最小
A = Amin = A1 − A2
y = y1 + y 2 = 2 A cos( kx − ) cos(ωt − ) = 2 A sin kx sin ωt 2 2
cos()cos(),sin()sin(),cos()sin(),sin()cos()都是驻 波的组合形式！
π
π
6-6 驻波
25 2013/5/10
6-7 多普勒效应
27 2013/5/10
6-7 多普勒效应
当波源或观察者相对介质运动时，波在空间 传播的振动频率或观察者接收到的频率将与波源 发出的频率不同（频率发生变化）。由奥地利物 理学家C. J. Doppler在1842年首先发现。 例如高速列车呜笛疾驶而来时，将听到呜 笛声调变高、变尖；当火车远离而去时，其汽笛 的声调会变低。
10 2013/5/10
讨论： 当相位差满足
λ 两振动同相，合振幅A和波的强度I最大
A=Amax=A1+A2
∆ϕ = (ϕ 2 − ϕ1 ) − 2π
r2 − r1
= ±2kπ , k = 0,1,2,
I = I max = I1 + I 2 + 2 I1I 2
在这些位置上，合振动始终加强，称为干涉相长。
特别地当A1=A2时，A=2A1，I = 4I1
6-5 惠更斯原理 叠加原理 波的干涉
11 2013/5/10
当相位差满足
∆ϕ = (ϕ 2 − ϕ 1 ) − 2π
r2 − r1
λ
= ± ( 2k + 1)π , k = 0,1,2,
两振动反相 ，合振幅和强度最小
A = Amin = A1 − A2
y = y1 + y 2 = 2 A cos( kx − ) cos(ωt − ) = 2 A sin kx sin ωt 2 2
cos()cos(),sin()sin(),cos()sin(),sin()cos()都是驻 波的组合形式！
π
π
6-6 驻波
25 2013/5/10
波13-5_驻波13-6多普勒效应 冲击波13-7电磁波
10
x
2）相邻两波节之间质点振动同相位，任一波节 两侧振动相位相反，在波节处产生 的相位跃变 . （与行波不同，无相位的传播）.
π
x y 2 A cos 2π cos 2π t 例 x 为波节 4
y
2
o
2
x
x cos 2 π 0 , x , y 2 A cos 2 π x cos 2π t 4 4 x 3 x cos 2 π 0 , x , y 2 A cos 2 π cos(2 π t π ) 4 4
本章内容
§13-1 §13-2 §13-3 §13-4 §13-5 机械波的基本概念 平面简谐波的波动方程 波的能量 惠更斯原理 波的衍射、反射和折射 波的叠加原理 波的干涉
一 波的叠加原理，二 波的干涉，三 驻波
§13-6 多普勒效应
一 多普勒效应，
冲击波
二 冲击波
§13-7 电磁波
一 电磁振荡和赫兹实验； 二 平面电磁波的波动方程及其性质； 三、电磁波的能量； 四、电磁波谱
2
回顾上次课有关干涉的内容
波的相干条件
s1 s2
r1
r2
*
1）频率相同；
P
2）振动方向平行；
3）相位相同或相位差恒定.
两个波源的振动
y1 A1 cos(t 1 )
y2 A2 cos(t 2 )
r1 )
点P 的两个分振动 r2 y2 p A2 cos( t 2 2π ) 3
多普勒效应
冲击波
一 多普勒效应 人耳听到的声音的频率与声源的频率相同吗？
接收频率——单位时间内观测者接收到的振动次 数或完整波数.
x
2）相邻两波节之间质点振动同相位，任一波节 两侧振动相位相反，在波节处产生 的相位跃变 . （与行波不同，无相位的传播）.
π
x y 2 A cos 2π cos 2π t 例 x 为波节 4
y
2
o
2
x
x cos 2 π 0 , x , y 2 A cos 2 π x cos 2π t 4 4 x 3 x cos 2 π 0 , x , y 2 A cos 2 π cos(2 π t π ) 4 4
本章内容
§13-1 §13-2 §13-3 §13-4 §13-5 机械波的基本概念 平面简谐波的波动方程 波的能量 惠更斯原理 波的衍射、反射和折射 波的叠加原理 波的干涉
一 波的叠加原理，二 波的干涉，三 驻波
§13-6 多普勒效应
一 多普勒效应，
冲击波
二 冲击波
§13-7 电磁波
一 电磁振荡和赫兹实验； 二 平面电磁波的波动方程及其性质； 三、电磁波的能量； 四、电磁波谱
2
回顾上次课有关干涉的内容
波的相干条件
s1 s2
r1
r2
*
1）频率相同；
P
2）振动方向平行；
3）相位相同或相位差恒定.
两个波源的振动
y1 A1 cos(t 1 )
y2 A2 cos(t 2 )
r1 )
点P 的两个分振动 r2 y2 p A2 cos( t 2 2π ) 3
多普勒效应
冲击波
一 多普勒效应 人耳听到的声音的频率与声源的频率相同吗？
接收频率——单位时间内观测者接收到的振动次 数或完整波数.
驻波多普勒效应
2 u 本征频率： n n 2l
l n
n
n 1,2,3 n 1,2,
每一种频率对应于弦线的一种振动方式，称为 弦线振动的“简正模式”
1 ——基频
2 ——二次谐频
六、驻 波
两端固定的弦 振动的简正模式
l n
n
2
n 1,2,
l
1 n l (n ) n 1,2, 2 2
1. 比较驻波与行波在振幅、相位、能量上 有何异同？ 2. 解释绳驻波的段数为何会变化？
六、驻 波
1. 驻波及其产生
两列振幅、频率和振动方向都相同的相干波，沿 相反方向传播时叠加而形成的一种特殊的干涉现象.
2. 驻波方程
y1 A cos(t kx) y y1 y 2
2 A cos 2 π
波源远离观察者
u ' u vs u ' u vs
七、多普勒效应
（2）分析三种简单的多普勒效应
③ 波源与观察者同时相对介质运动
( vs , v o )
vs 波源向观察者运动
说明
v o 观察者向波源运动 + ，远离
，远离 +
u vo ' u vs
（1）若波源与观测者相互接近，接收到的频率 高于波源的频率；若波源与观测者相互远离，接 收到的频率低于波源的频率。
驻波的振幅随 位置周期变化
y2 A cos(t kx)
x
cos 2 πt
各质点都在作同 频率的简谐运动
六、驻 波 说明 x y 2 A cos 2π cos 2πt （1）振幅特征：
波腹 x k
相邻波腹（节）间距 y 振幅包络图
初三物理复习电磁波的多普勒效应
初三物理复习电磁波的多普勒效应电磁波的多普勒效应是指当光源或接收者相对于观测者运动时，观察到的波长和频率会发生变化。
这一现象在实际生活中有着广泛的应用，比如雷达测速、天体物理学中的红移和蓝移等。
在初三物理学习中，掌握电磁波的多普勒效应是非常重要的。
本文将介绍电磁波的多普勒效应的基本原理、公式以及实际应用。
一、基本原理电磁波的多普勒效应是由于光源或接收者相对于观测者的相对速度不同而引起的。
当光源向观测者靠近时，观测者会感知到一个较高的频率和短波长，即波长变短；相反，当光源远离观测者时，观测者会感知到一个较低的频率和长波长，即波长变长。
二、多普勒效应的公式在物理学中，电磁波的多普勒效应可以通过以下公式来表达：f' = (v + vr) / (v - vs) * f其中，f'为观测者所感知到的频率，f为光源发出的频率，v为光在真空中的传播速度（近似等于光速），vr为观测者相对于光源的速度，vs为光源相对于观测者的速度。
根据此公式，当光源和观测者相对静止时，即vr=vs=0，观测者所感知到的频率与光源发出的频率相等；当光源和观测者相向运动时，vr 和vs同符号，观测者所感知到的频率将大于光源发出的频率；当光源和观测者背离运动时，vr和vs异符号，观测者所感知到的频率将小于光源发出的频率。
三、实际应用1. 雷达测速多普勒效应在雷达测速中有着广泛的应用。
当警察使用雷达测速仪测量车辆的速度时，实际上是利用雷达测量速度的多普勒效应。
雷达测速仪通过发射电磁波并接收反射回来的信号来测量车辆的速度。
当车辆靠近雷达测速仪时，由于车辆和雷达测速仪之间存在相对速度，测速仪接收到的反射信号的频率将高于发射信号的频率；反之，当车辆远离雷达测速仪时，反射信号的频率将低于发射信号的频率。
通过测量频率的变化，雷达测速仪可以推算出车辆的速度。
2. 天体物理学中的红移和蓝移多普勒效应在天体物理学中也有着重要的应用。
天文学家通过观测光谱中的频率偏移来研究天体的运动状态。
17.驻波+多普勒效应
§6.8 声波
听觉范围 20－20000 Hz 20 Hz 为次声波 20000 Hz 为超声波
一、声压 声波所到之处空气的压 强与静压强有一压差， 称为声压。 二、声强和声强级 1 声强 I A 2 2 u 2
L log I I0 单位为贝尔（ Bel ）
可闻声强范围 10 －12 ~ 1 w / m 2
通常用声强级 L描述声波强弱：
I 0 10 12 w / m 2 1 Bel 10 分贝( dB ) I L 10 log ( dB ) I0
§6.9 多普勒效应
如果波源和观察者都静 止，观察者每秒可接收 即接收到的频率为 u
个波，
R
u
Байду номын сангаас
S
上式中 R 和 S 分别代表观察者观测到 的频率和波源的频率。 波源或（和）观察者相 对媒质运动时，波的频 率或（和）接 收到的频率将发生变化 。这种现象叫多普勒效 应。 一、波源 S静止，观察者以速度 v R向波源运动 观察者每秒接收 所以 u vR
§6.6 驻波
一、驻波表达式 一种简单的情况： 2 y 合 2 A cos x cos t ，
二、驻波的特点
三、半波损失
1. 波从波疏媒质射向波密 媒质时，反射波与入射 波在反射点有 大小为 的相位突变（相当于 的波程差），称为半波 损失。 2 2. 反射点固定，没有位移 ，反射波和入射波在固 定端必定有半
1000 Hz ，求相遇前和相遇后乙 火车上乘客听到的频率 各为多
少？（声速为 300 m / s）
解： 相遇前： R u v乙 300 50 1000 1400 Hz u v甲 300 50 u v乙 300 50 相遇后： R 1000 714 .3 Hz u v甲 300 50
第大学物理八讲： §9.5 驻波9.2 多普勒效应
/2
3 / 2
x
O 波腹公式 x腹 k / 2
k 0,1,2,
（2k 1 ） / 4 k 0,1,2, 波节公式 x节
相邻波腹（波节）的间距 x xk 1 xk / 2
课堂练习1：由振动频率为400 Hz的音叉在两端固定拉
紧的弦线上建立驻波．这个驻波共有三个波腹，其振
u
当波速（u）一定时， 声调升高
多普勒效应的公式
波在介质中传播的速度 接收者运动的速度
u r r ' s u s u
'
接收的频率 波源运动的速度
波源的频率
上组﹢﹣为迎着；下组﹣ ﹢为远离
多普勒效应的应用
u r r ' s u s u
u u n k n 2
k 1 时为基频 k 2,3， 时为谐频
六、管乐的基频（音调），谐频（音色）
n （2k 1） 2
4 n 2k 1
k 1,2,3,
u u n 2k 1 n 4
k 1 时为基频 k 2,3， 时为谐频
'
雷达测速是应用多谱勒效应, 即根据接收到的反射波频移量的 计算而得出被测物体的运动速度
大帽山的多普勒天气雷达
多普勒雷达回波图
多普勒彩超
小 结：
1、平面简谐波 2、建立波动方程
作 业：
1、仔细阅读教材；
2、请将课堂练习2题做在作业本上；
3、自学其他内容
预 习：
第10章 光学
L 3 / 2 1.2m
2
y y1 y2 2 A cos 2x / cos 2t