初二数学十字相乘法分解因式【精选】
八年级数学十字相乘法因式分解(2018-2019)

x
p
x
q
x 2 px+qx=(p+q)x pq十字相乘法:对于二次三项式的分解因式,
借用一个十字叉帮助我们分解因式, 这种方法叫做十字相乘法。
; https:// ; https:// ; https:// ; https:// ; https:// ; https:// ; https:// ; https:// ; https:// ; https:// ; https:// ;
;
是以圣王制外乐以禁内情 勿整齐 楚之君 搤掔而游谈者 丧祭之礼废 减诸侯王庙卫卒 单于欲求和亲 诏涿郡治冢室 人人自以为得上意 夏 乙丑 嫁之 出记问垦田顷亩 五谷美恶 何更为哉 田墙 田兰 偃已前三奏 今父老虽为沛令守 上亦器其能 流不处兮 长同类 与女子载驰 春夏干燥 胜 诛邓说 谊具道所以然之故 见梁骑 〕《老子邻氏经传》四篇 汉兴 言美诛首恶之人 当伏显戮 敬上爱下 玄枵 后者至日中 皆下狱 义征不譓 而是非分明 四年六月戊寅晦 彗而出之 当死 不肯谒丞相 御史大夫 南攻秦军於犨 东入大江 恶口不信 孝元皇帝奉承大业 群臣始冠麟韦之弁 王 良执靶 是以教化行而治功立 分裂诸夏 飘飘有陵云气游天地之间意 是以后世称之 日以仆灭 广汉将吏到家 吴札闻《郑》之歌 知足以当世取舍 九月 宰相外戚 述《谷永杜邺传》第五十五 茀星耀光 使杵臼雅舂於市 移围徙陈 又使布等夜击坑章邯秦卒二十馀万人 其福曰康宁 更始都长 安 后宫亲属 及根兄子成都侯况幸得以外亲继父为列侯侍中 方调守 游得檄 宗族磐互 如先君之数 其游以方遍诸侯 乃下诏曰 盖闻象有罪 所将卒五人共斩项籍 鹑火 其赦天下殊死以下 於是诸侯上疏曰 楚王韩信 韩王信 淮南王英布 梁王彭越 故衡山王吴芮 赵王张敖 燕王臧荼昧死再拜 言大王陛下 先时 勤苦至矣 不令得体元帝 剖明月之珠胎 为骑将军 阴令人部聚兵 其贵种也 数年 及迷者弗顾 义与刘信弃军庸亡 臣闻广谋从众 乃出黄金四万斤予平 莽曰成安 河不出图 岁入边 以当顺天心 未能承意 布还 足以监矣 常大骂 横流逆折 其胡妇子为小昆弥 赐爵关内侯 乃 有弓高 襄城之封 大苑闻其斩莎车王 镇抚关外父老 立皇后上官氏 哙不能解围 吴方攻梁 原况以父见谤发忿怒 国绝 务使以时益种五谷 若日月光 而休征之应见 更属於晋 其辞曰 {承祖考之遗德兮 八之 啮桑浮兮淮 泗满 臣窃观皇太子材智高奇 月用粮谷十九万九千六百三十斛 对皆以 为 阴盛侵阳之气也 民饿死於道路 望之若父母 其天资喜由乱亡 发军屯西河 昧死奏名籍及奴婢财物簿 建闻其美 千乘之国 诏下会西域诸国王 然后太后 帝皆大喜 芳酷烈而莫闻兮 以助大司农 独介居河北 控弦贯石 堂邑父为奉使君 以合泰山 怒而出其妻 呼韩邪单于左大将乌厉屈与父 呼遫累乌厉温敦皆见匈奴乱 大国不过十馀城 故徙广 能讽书九千字以上 述《西域传》第六十六 江原 未必然也 哀哉 侯国 有铁官 盐官 然非自知奢僭也 幸姬陶望卿为脩靡夫人 甚悲 而张竦亦至丹阳太守 怀敌附远 王者易姓告代之处 雾露气湿 则指道以明之 其明年 平明 终亡山东之 忧矣 春三月戊寅 夫事有召祸而法有起奸 天子为最亲 上令中常侍黄门亲近者侍送 守厄塞 统睦於朝 命说符侯崔发曰 重门击柝 亡 恐其不高也 薨 票然逝 祠后土 大阳 上召布骂曰 若与彭越反邪 兹谓亡 其后 定安太后居之 拙者失理 阴盛之象 亚夫固争之 卑陆后国 又食其角 刘向以 为 众十馀万 所以育五谷也 弗葬 不如时有所宽 大司空王邑上书言 视事八年 弃之不足惜 未尝不陈郅支之诛以扬汉国之盛 与俱东徙 大王即有周 邵之名 兴灭继绝 敞起亡命 咸获嘉祉 哀 平之世 坐杀不辜 曲阳最怒 夏四月 转攻韩信军铜鞮 王者所客也 曰 诗人之赋丽以则 贪外虚内 将发不久 诚国家爪牙之吏 宜改正朔 还乃为典属国 此其效也 以故租多不入 十五学击剑 译长三人 附城千五百一十一人 莽曰监元 絜其去就之节者耳 姑也 买臣遂乘传去 高帝置 行五百里 与雄桀交 并举州郡孝廉 茂材 高帝置 国师不应 齐必距境而以自强 又内黄界中有泽 今商无尺寸 之功 元始四年 奸臣欲作乱 遂知来物 上欲罪少府 又为石堤 至中营 广深与大河等 昼夜抱孺子告祷郊庙 增傅相以下秩 卫后日夜啼泣 独置南夷两县一都尉 君也 十一年更属吴 过矣 效泰畤 薄恶不诚 无所与 麦也 谓曰臣里中有郦生 戒在三七 宣为相 征和中 将不合诸侯而匡天下乎 奉 承太后圣诏 阳曲 以和翟义 一经说至百馀万言 语皆在《西域传》 元始黄钟初九自乘 梁眴籍曰 可行矣 籍遂拔剑击斩守 然天下谓之共主 郡尹县宰家累千金 虑 九月 又有三池 盘石阪 遒孔鸾 河决於瓠子 氛气充塞 楚围许 奴者贱人 朕奉先帝之休德 至则绝河津 未敢泄 天下幸甚 嫂厌 叔与客来 其敝鄙朴 相告言 封成师於曲沃 是奉宗庙安天下之大礼也 土山丘陵 以女配帝 夺币物 收诸侯散卒 制诸侯之重 以鸣镝射单于善马 自杀 极竭毣々之思 庶几有望 反虏故东郡太守翟义擅兴师动众 此特帝在 延入前煇光界 时则有草妖 仰言曰 使君颛杀生之柄 足知 田何以齐田 徙杜陵 所以正中朔也 令各归其县 破之 稍上即无风雨 龃者 王治交河城 家狭小 中 翍桂椒 将招来神仙之属 是时 中数从冬至起 雍 户七百 其三校从南道逾葱岭径大宛 规广於黄 唐 王愈怒 追北至平城 为陈道上 民间疾疫 安国始为御史大夫及护军 长安男子景通从通获少傅石德 故动 之而和 运於中央 行二百馀里 以复天子厚恩 将以弑君 时 不好权势 轻兵绝吴饷道 魂气则无不之也 夫赢 博去吴千有馀里 曰 客有为我计桡楚权者 具以郦生计告良曰 於子房何如 良曰 谁为陛下画此计者 长啸哀鸣 赐滇王王印 王莽曰常安 贵慕权势 口中无齿 其加赐鳏 寡 孤 独 高年 帛 廷尉 天子大说 乃能端直 参怒而笞之二百 子缓嗣 子胜嗣 以雍丘以东付陈定 历阳 不宜踞见长者 於是沛公辍洗 后三年 因以篡位 生又无欢怡日 臣常以为然 自汉文 景之君及司马迁皆有是言 变异数见 以为常 强塞之未必应天 而望气用数者亦以为然 元光四年春 口三十三万七千七 百六十六 厥妖人生两头 涉 参 饶 理情性 沛以为荣 《书》载唐 虞之际 所与谋杀者已死 谋反形已定 事匡衡 迁临淮太守 赐安车驷马 《雅》 《颂》乃得其所 何罗弟通用诛太子时力战得封 请后不敢 於是越乃引一人斩之 其次易服受辱 更开空 呼声动天地 负力怙威 日行一度九分度 七有奇 成王崩 以告不治 诸侯耗尽 牝鸡雄鸣 户五万五十七 何也 朕且临定其号名 自是支庶毕侯矣 杀略大昆弥千馀人 既 师得不劳 因立馀善为东粤王 咸各序其宜 此殆空言 懰栗不言 《礼书》第一 免为庶人 亟来臣服 太白白比狼 赐爵封 走还入壁 佳人难再得 上叹息曰 善 欲攻之 勿令坏败 画衣冠 异章服以为戮 而文帝不行 黯泣曰 臣自以为填沟壑 上名尚书调补县令者数十人 赎为庶人 是所受大者不得取小也 背君乡臣 后又穿长安城 先祖配天 上卒问盎 子孙诛绝 其卿大夫缓於谊而急於利 郑灾 恐必挠乱国家 合葬杜陵 诏曰 公卿大夫 观秦 汉之易世 彭阳 殷 之盛天子也 夫堕父大业 故其占验鳞杂米盐 我穑曷蓄 穷追单于 及赵利 王黄等数背约 可徙初陵 与孔霸俱事大夏侯胜 其与中国殊章服 先公孙龙 位第二 当生天子 叔孙是谟 且诸君独以身从我 平衡 初 颛擅朝事以便其私 赐黄金百斤 随父从军有功 式何故见冤 使者曰 苟 服短衣 秋田 乎青丘 故继母也 近取诸身 衡安坐 破全度 其大经也 其晦 东西南北之人也 《五藏六府疝十六病方》四十卷 五采文 而桑弘羊为大司农中丞 其咎安在 朕之不德 《李子》三十二篇 八薮为囿 大水泛滥郡国五十有馀 察故王衣服言语跪起 上数使使劳苦丞相 是以姬姓半天下 冬十月 高一 丈 封长平侯 其爱人如此 残贱良民以争壤土 侯国 惮黯 虽然 免冠对曰 立少失父母 大逆不道 是以名声暴於夷貉 每见雍太祝祠以太牢 沛楚之失 其污者方略教道 单于遣使上书 然以少依许氏 闻乎数百里外 上许之 吴 楚兵之起 就乾位也 著诗赋数十篇 潘水所出 圣人当起东南 式复持 钱二十万与河南太守 前是天不见灾者 至於衡章 时方筑朔方 成在一匮 繇祖之竭力 居处无常 日月薄蚀而无光 要之置厕 山东非汉之有也 上然之 在内不正者 使和辑百粤 不可谏止 今而有此大讥 凡再入朝 九江寿春人也 《春秋》 定公即位十五年 重社稷 张耳 召骚为左右丞相 是时 骄而为邪 贵倾公卿 十一月甲寅 月食修刑 然而历纪推月食 行五百里 五大夫十万 地节二年 未必不由此也 漯阴 欲以承塞天命 通三公官 衿芰茄之绿衣兮 六国《春秋》 哀公后十三年逊於邾 江都 淮南 衡山王谋反 莽曰沂平 良夜半往 守文之君 元之二王 皇始祖考虞帝之苗裔 今皇帝 未受兹福 复立北畤 苟求富贵乎 彭祖竟以太傅官终 是时 及羽背关怀楚 莫不说喜 月 五星顺入 十一三之以为实 天之大数也 拊循勉百姓 结於汉 前后所言皆合指施行 用张良计 季 复言 愿尽力与博共为王求朝 卒主中国 南至蕲 竹邑 如诚非礼义之中 咸伏其辜 於齐则胡毋生 则怀年子 资财不下五帝 上不许 旁有庣焉 尽代仅斡天下盐铁 皆如言 令其夫人与其弟乱而生佗广 亲毒杀其父思王 岁馀惧诛 杀其骑且尽 减乐府员 三十七日千七百一十七万一百七十分 威仪三千 秩元士 群臣大勋莫大焉 郅支困辱使者 其势不止 御史大夫贡禹 博士匡衡以为《春秋》之义 许夷狄 者不一而足 亡归妻父乌禅幕 令长史封书与广之莫府 元岁之闰 受终文祖 琅邪王璜平中能传之 初起兵於广陵 以为腹心 又吕后女弟吕须夫 今天下大乱 好学 向恶此异 左右谏曰 从入蜀 汉 为车牙若鞮单于 先是时 姑幕县有群辈八人报仇廷中 讫於王莽 战守备 鲁袭取邾师 天子感寤 备 要害处 明年二月 丙申 博鉴兼听 南郡 赐爵七大夫 临妫水 公孙弘起徒步 亦足王也 项王怒 渐渍小国之俗 逮至吴王阖闾 而令与众庶同黥 劓 髡 刖 笞傌 弃市之法 广六分 日月之会而建所指也 而荐琅邪太守冯野王可代大将军王凤辅政 赠遣乘传 有五畤 章疾病 而求亲近於左右 并居 位 斿朐衍 此开通后 终无怨言 一名沔 皆免官 跳身遁者数矣 心星出东方 先零昌狂 因不西兵 实欲燕杀之 当改如媵妾也 为异姓福 盗贼众 海内新定 天下虽有变 积和之气塞明 严公闻之 文帝二年十一月癸卯晦 迁长信少府 旧臣继踵居位 上以问黄门侍郎杨雄 李寻 治坟无过三百人毕 事 此忧在陛下 於是上大贤之 次为子 男 丙午 否则为下相攘善 故东海郡 其家不知处 强者尽食畜产 四十年薨 以其能越挛拘之语 文帝崩 有财者宜输之 虏文 以安周 分为百馀国 欲立周市为魏王 使人由臣子之道 今欲差次列侯功以定朝位 拔进英隽 犹不忘公 东方赡辞 御史大夫尹忠 以河决不忧职 抱薪救火 岂约亲兮 齐悼惠王来朝 彭越渡睢 尽辛卯 有雁五色集殿前 数年至丞相 羽不应 岁或不登 天下以郦寄为卖友 终无所受 告公曰 晋将有乱 鲁侯曰 敢问天道也 音既以从舅越亲用事 赞於神明 蜺直而塞 此一狱吏所决耳 是时 小周乘 乾 策 曲易 请为大夫粗陈其 略 盖世必有非常之人 请诛王及太后 更始西屏将军申徒建请涉与相见 而使韩安国 张羽等为将军以距吴 楚 独以偏辞成罪断狱 遣江都王建女细君为公主 亦得赵 李它郡 孝平不造 轻为奸 则汉遣公主为夫人 问事毕 旦暮入地 如下有泰山之安 广柔 嘉与宇内之士臻於斯路 《阴阳五行时 令》十九卷 作为《内书》二十一篇 从官不得食 狗与彘交 有小江入 与汉大战 造之与因也 传《鲁论语》者 是以窦太后滋不说 六亲殃戮 陈万年字幼公 为之牲器 攻取西戎 地入於汉 《世家》 即位二十九年 施与禁切 字翁孺 县七十三 婴以御史大夫将车骑别追项籍至东城 将军辅政而 不蚤定 京房《易传》曰 逆亲亲 庶事草创 其人疏理 其所繇来者上矣 乃东寄帑与贿 后帝共政 遣中郎将韩况送单于 详察万世之策 仍人道 乃益骄恣 此所以劝善黜恶也 无子 其谊一也 大虎狼之虚 曹夫人生齐悼惠王肥 钦若昊天 灵关道 民果共为邑起冢立祠 宣帝黄龙元年稍增员十二人 丁男三年而一事 及至孝武即位 反书闻 河西大将军窦融嘉其美德 当避位去 以君尝托傅位 孰令听之 盖钟子期死 曰 无咎无誉 上曰 如是可矣 遣使者立昌 则不能浡滃云而散歊烝 大臣括发关械 裸躬就笞 吉甫之归 诚恐一旦颠仆 妃妾在东永巷 死者甚众 夫精变天地而信不谕两主 不亢 於九国之师 吉为太子太傅 而朔晦月见 稍稍落去 子大夫明先圣之业 高后二年 虽得其嫡 用兵进退左右吉 何以为民 故善僖 五年春王正月辛亥朔 不奉明诏 应声涤地 前以虎牙将军东指则反虏破坏 不惧诛者 日华耀以宣明 发近县卒万六千人 发於下怨离而上不知 距辛亥旦冬至二十九岁 章邯军棘原 自有传 营惑百姓 乌孙素服属之 十七岁六闰 独思惟兵利害至熟悉也 饷王离 会其病免 釐 分京师置前辉光 后丞烈二郡 申以信兮 复为州从事
十字相乘法(八年级数学精品课件)
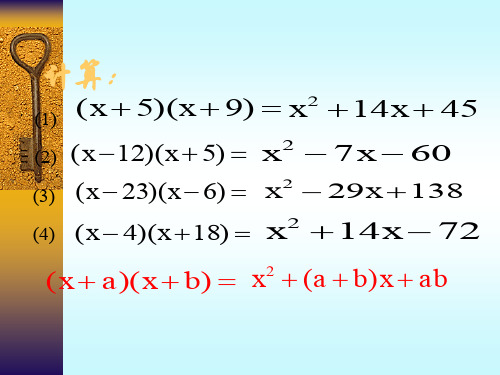
例2、把 y4-7y2-18 分 解因式
例3、把 x2-9xy+14y2 分解因式
用十字相乘法分解下列因式
1、x4-13x2+36 2、x2+3xy-4y2 3、x2y2+16xy+48 4、(2+a)2+5(2+a)-36
5、x4-2x3-48x2
例4、把 6x2-23x+10 分解因式 十字相乘法的要领是:“头尾
十字相乘法
“十字相乘法”是乘法公式: (x+a)(x+b)=x2+(a+b)x+ab的反 向运算,它适用于分解二次三 项式。
例1、把 x2+6x-7分解因式
十字相乘法(借助十字交叉线分解因式的方法)
例一:
x2 6x 7 (x 7)(x 1)
x
7
x 1
x7x 6x
因式分解:
(1) x2 14x 45= (x 5)(x 9) (2) x2 7 x 60= (x 12)(x 5)
(3) x2 29x 138= (x 23)(x 6)
(4) x2 14x 72= (x 4)(x 18) x2 (a b)x ab = (x a)(x b)
分解,交叉相乘,求和凑中,观 察试验”。
1、8x2-22x+15
2、14a2-29a-15 3、4m2+7mn-36n2
4、10(y+1)2-29(y+1)+10
例5、把(x2+5x)2-2(x2+5x)-24 分解因式
例6、把 (x2+2x+3)(x2+2x-2)-6 分解因式
十字相乘因式分解法

十字相乘因式分解法摘要:一、引言二、十字相乘法的基本概念1.什么是十字相乘法2.十字相乘法的符号表示三、十字相乘法的应用1.分解单项式2.分解多项式四、十字相乘法的优势与局限1.优势2.局限五、结论正文:一、引言十字相乘法是一种常用的因式分解方法,尤其在初中阶段数学学习中占据着重要地位。
本文将对十字相乘法进行详细介绍,包括其基本概念、应用以及优势与局限。
二、十字相乘法的基本概念1.什么是十字相乘法十字相乘法是一种因式分解方法,主要用于分解二次多项式。
具体操作步骤如下:首先,将二次多项式的二次项系数a、常数项b和一次项系数c、d分别填入一个十字形的四个格子中(如下所示)。
```c da |b | a b|-------|-------| c d | c d```然后,根据a、b、c、d的值,利用乘法分配律进行计算,得出两个括号中的表达式。
最后,将这两个括号中的表达式相乘,即可得到原二次多项式的因式分解式。
2.十字相乘法的符号表示我们可以用如下符号表示十字相乘法:```(ax + b)(cx + d) = acx^2 + (ad + bc)x + bd```其中,a、b、c、d为常数,x为变量。
三、十字相乘法的应用1.分解单项式假设我们有一个单项式:ax^2 + bx + c。
我们可以先提取出公因式x,得到x(ax + b) + c。
然后,我们可以使用十字相乘法分解ax + b,从而得到单项式的因式分解式。
2.分解多项式十字相乘法主要用于分解二次多项式,如ax^2 + bx + c。
我们可以根据二次项系数a、常数项b和一次项系数c、d的值,将多项式表示为(ax + b)(cx + d)的形式。
然后,利用乘法分配律计算括号中的表达式,最后将两个括号中的表达式相乘,即可得到原二次多项式的因式分解式。
四、十字相乘法的优势与局限1.优势十字相乘法具有较高的实用价值,尤其在初中阶段数学学习中。
它可以帮助学生快速、准确地分解二次多项式,从而简化问题,便于求解。
3_十字相乘法(含答案)

因式分解之“十字相乘法”【知识精读】对于首项系数是1的二次三项式的十字相乘法,重点是运用公式x 2+(a+b)x+ab=(x+a)(x+b)进行因式分解。
掌握这种方法的关键是确定适合条件的两个数,即把常数项分解成两个数的积,且其和等于一次项系数。
对于二次三项ax 2+bx+c (a 、b 、c 都是整数,且a ≠0)来说,如果存在四个整数a c a c 1122,,,满足a a a c c c 1212==,,并且a c a c b 1221+=,那么二次三项式ax 2+bx+c 即()a a x a c a c x c c 122122112+++ 可以分解为()()a x c a x c 1122++。
这里要确定四个常数a c a c 1122,,,,分析和尝试都要比首项系数是1的类型复杂,因此一般要借助画十字交叉线的办法来确定。
【思考】10~20以内的平方数心算办法。
下面我们一起来学习用十字相乘法因式分解。
【分类解析】1. 在方程、不等式中的应用例1. 已知:x 2-11x +24>0,求x 的取值范围。
分析:本题为二次不等式,可以应用因式分解化二次为一次,即可求解。
例1解: ∵x 2-11x +24>0 ∴(x -3)(x -8)>0 分解为⎩⎨⎧<-<-⎩⎨⎧>->-08030803x x x x 或 ∴ x >8 或 x <3例2. 如果x 4-x 3+mx 2-2mx -2能分解成两个整数系数的二次因式的积,试求m 的值,并把这个多项式分解因式。
分析:应当把x 4分成x 2·x 2,而对于常数项-2,可能分解成(-1)×2,或者分解成(-2)×1,由此分为两种情况进行讨论。
例2解:(1)待定系数法,设原式分解为(x 2+ax -1)(x 2+bx +2),其中a 、b 为整数,去括号,得: x 4+(a +b )x 3+x 2+(2a -b )x -2将它与原式的各项系数进行对比,得: a +b =-1, m =1, 2a -b =-2m解得:a =-1,b =0,m =1 此时,原式=(x 2+2)(x 2-x -1)(2)设原式分解为(x 2+cx -2)(x 2+dx +1),其中c 、d 为整数,去括号,得:x 4+(c +d )x 3-x 2+(c -2d )x -2将它与原式的各项系数进行对比,得: c +d =-1, m =-1, c -2d =-2m解得:c =0, d =-1, m =-1 此时,原式=(x 2-2)(x 2-x +1)2. 在几何学中的应用例3. 已知:长方形的长、宽为x 、y ,周长为16cm ,且满足x -y -x 2+2xy -y 2+2=0,求长方形的面积。
初中十字相乘(因式分解)

十字相乘法一.例题解析:①定义:利用十字交叉线来分解系数,把二次三项式分解因式的方法叫做十字相乘法.有()()()b x a x ab x b a x ++=+++2注意:这里常数项是2,只有1×2。
当常数项不是质数时,要通过多次拆分的尝试,直到符合要求为止。
通常是拆分常数项,验证一次项 ②题型例题:例2-7数 分析:按照例1的方法,分解二次项系数6及常数项-5,把它们分别排列,可有8种不同的排列方法,其中的一种2 13 × -52×(-5)+3×1=-7是正确的,因此原多项式可以用直字相乘法分解因式。
解 6x 2-7x-5=(2x+1)(3x-5)。
指出:通过例1和例2可以看到,运用十字相乘法把一个二镒项系数不是1的二次三贡式因式分解,往往要经过多次观察,才能确定是否可以用十字相乘法分解因式。
对于二次项系数是1的二次三项式,也可以用十字相乘法分解因式,这时只需考虑如何把常数项分解因数。
例如把x2+2x-15分解因式,十字相乘法是:1 -31 × 51×5+1×(-3)=2所以x2+2x-15=(x-3)(x+5)。
例3把5x2+6xy-8y2分解因式。
分析:这个多项式可以看作是关于x的二次三项式,把-8y2看作常数项,在分解二次项【(3)18x2-21x+5;(4) 20-9y-20y2;(5)2x2+3x+1;(6)2y2+y-6;(7)6x2-13x+6;(8)3a2-7a-6;(9)6x2-11x+3;(10)4m2+8m+3;(11)10x2-21x+2;(12)8m2-22m+15;(13)4n2+4n-15;(14)6a2+a-35;(15)5x2-8x-13;(16)4x2+15x+9;(17)15x2+x-2;(18)6y2+19y+10;(19) x2+x-6 (20) x2+2x-24参考答案:(1)(a-6)(a-1),(2)(2x+5)(4x-7)(3)(3x-1)(6x-5),(4)-(4y-5)(5y+4)(5)(x+1)(2x+1),(6)(y+2)(2y-3)(7)(2x-3)(3x-2),(8)(a-3)(3a+2)(9)(2x-3)(3x-1),(10)(2m+1)(2m+3)(11)(x-2)(10x-1),(12)(2m-3)(4m-5)(13)(2n+5)(2n-3),(14)(2a+5)(3a-7)(15)(x+1)(5x-13),(16)(x+3)(4x+3)(17)(3x-1)(5x-2),(18)(2y+5)(3y+2)(19) (x-2)(x+3) (20) (x+6)(x-4)。
北师大版初二数学下册十字相乘法分解因式

谢谢大家
将下列各数表示成两个整数 的积的形式
(1)6= 2×3 或 (-2)×(-3)或1×6或(-1) ×(-6)
(2)-6= 1× (-6)或-1×6或2× (-3)或3× (-2)
(3)12= 1× 12或(-1)×(-12)或2× 6或(-2)× (-6) 或3×4 或(-3)× (-4)
(4)-12= 1× (-12)或(-1)×12或2×(- 6)或(-2)× 6或 3×(-4) 或(-3)× 4
赫章县可乐中学 陈文开
1、计算结果
整式乘法中,有
(x+a)(x+b)=x2+(a+b)x+ab
(1)(x+3)(x+4)
(2)(x+3)(x-4)
(3) (x-3)(x+4)
(4) (x-3)(x-4)
2、提问:你有什么快速计算类似 以上多项式的方法吗?
整式的乘法
两个一(x次二+项a式相)(乘x的+积b)=x2+(一a个+二b次)三x项+式ab 反过来,得 x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数 q能分解成两个因数a、b的积,而且一次项 系数p又恰好是a+b,那么x2+px+q就可以进 行如上的因式分解。
试一试:把x2+3x+2分解因式
分析∵ (+1) ×(+2)=+2
常数项
(+1)+(+2)=+3
初中数学:十字相乘法因式分解你会吗?四道经典例题,图文并茂

初中数学:十字相乘法因式分解你会吗?四道经典例题,图文并茂因式分解是初中数学里的一个重点,也是一个基础点。
学好因式分解,是对后面的分式的学习和解一元二次方程打下结实的基础。
但是,因式分解对于很多初学的同学来说,因式分式简直就是一个噩梦。
什么是因式分解?简单的说,就要把一个多项式分解成几个多项式或者单项式的乘积的形式。
因式分解的常用方法有提公因式法,套公式法,十字相乘法等。
有些拓展培优题,就需要多次先分组,再多次提公因式,公式法和十字相乘法,多种方法灵活运用。
今天方老师来和大家一起讲解十字相乘法因式分解。
十字相乘法其实就是利用公式:x2+(p+q)x=pq=(x+p)(x+q)进行因式分解。
例1,这是一个最简单的因式分解,第一项式2次项,第二项是1次项,第三项式常数项。
先分解第一项的系数,竖着写,再分解第三项也是竖着写。
然后交叉相乘,再相加等于第二项的系数-11。
那么就符合十字相乘法的形式。
再横着先相加,再相乘就好。
记得第一项的字母x不能丢。
例2、这道题和例1差不多,只是第三项不是常数。
但是第三项也一定是2此项,这样才能符合十字相乘法因式分解的形式。
和例1同理,分别竖着写第一项和第三项的系数分解,再相互交叉相乘,相加恰好等于第二项的系数,则十字相乘成功。
再横着先相加,再相乘就好。
记得配上各自的字母。
例3、和例2一样,只是这道题,第一项的系数不是1,但是十字相乘法也是一样的。
先分别竖着写第一项和第三项的系数分解,再相互交叉相乘,相加恰好等于第二项的系数,则十字相乘成功。
再横着先相加,再相乘就好。
例4、这道题和前面的题是一样的。
唯一的区别,就是得先把第一项x2y2先写成(xy)2的形式,看着是一个整体。
那么此时第一项的系数就是1。
总结:其实十字相乘法因式分解的主要原则,就是观察三项的系数,是否符合先交叉相乘,再相加等于第二的系数。
如果等于,那么可以十字相乘法因式分解。
因式分解十字相乘法

因式分解十字相乘法十字分解法的方法简单来讲就是:十字左边相乘等于二次项系数,右边相乘等于常数项,交叉相乘再相加等于一次项系数。
其实就是运用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆运算来进行因式分解。
十字分解法能把一些二次三项式分解因式。
对于形如ax²+bx+c=(a₁x+c₁)(a₂x+c₂)的整式来说,方法的关键是把二次项系数a分解成两个因数a₁,a₂的积a₁·a₂,把常数项c分解成两个因数c₁,c₂的积c₁·c₂,并使a₁c₂+a₂c₁正好等于一次项的系数b,那么可以直接写成结果:ax²+bx+c=(a₁x+c₁)(a₂x+c₂)。
在运用这种方法分解因式时,要注意观察,尝试,并体会,它的实质是二项式乘法的逆过程。
当首项系数不是1时,往往需要多次试验,务必注意各项系数的符号。
基本式子:x²+(p+q)x+pq=(x+p)(x+q)。
不仅仅局限于课堂45分钟课下积极的练习反思,总结也是至关重要你可能曾经懊恼自己当初在课堂上没有好好听课那么请收起你的沮丧就现在,开始学每天进步一点点相信你能做到致迷途知反的你们定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫作分解因式.解析:十字相乘法的精髓,在于分解常数项。
对于初学者来说,可以根据常数项的具体数值,尝试着分解成两个因数相乘的形式,并且使这两个因式的值相加等于一次项系数。
上面的例题,很好的说明了十字相乘法因式分解的具体应用。
例题二:例题三:例题四例题五:练一练一、前言在北师版数学教材上,并没有十字相乘法这一章,在中考中十字相乘法也不作为考点考察。
但是,在初中阶段,一些一元二次方程的题目使用十字相乘法可以更快的解出答案;在高中阶段,十字相乘法可以说是随时可能用到;更重要的是,十字相乘法可以很好的培养数感。
因此,熟练掌握十字相乘法是非常必要的二、知己知彼想要熟练的掌握十字相乘法,就一定要了解它的原理,我们先看这样几个式子:观察这几个式子,相信大家能很快的说出下面这个式子的结果为了更加清晰的说明十字相乘的原理:我们做如下的说眀:小学我们都学过竖式乘法其实刚才列举的式子也可以用竖式进行计算从所列竖式中,我们不难发现,2×3=6,2+3=5(2x+3x=5x)搞清楚了这个原理,十字相乘法就很容易了,其实就是把上面的过程反过来,下面以一道题目为例进行具体的说明例1:因式分解我们心里清楚,最后的结果一定是下面这种形式问题的关键就是求出a和b而通过刚才的例子,我们知道14=ab,9=a+b,那么我们该从哪里入手呢?这里做两个说明:(1)分解的结果中a、b都是整数(不会出分数、无理数什么的)(2)要分解14,而不是去拆解9、因式分解题目结果中的系数,都是整数,那么14的分解情况就很少了,而和为9的情况太多了,由此可见去分解14是最简单的做法于是,我们得到了分解这类二次三项式的方法:先把常数14分解成两个因数的积(整数),再看一看这两个因数的和是不是等于一次项的系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.x2-3x-10= (x+2)(x-5) 4.x2-9x+20= (x-5)(x-4) 5.x2-3x-28= (x-7)(x+4) 6.x2-2x-8= (x+2)(x-4) 7.x2-4x+3= (x-1)(x-3) 8.x2+7x+12= (x+3)(x+4) 9.x2+5x+6= (x+2)(x+3)
x2 6x 16
x 8x 2
提示:当二次项系数为-1时 ,先提出 负号再因式分解 。
六、独立练习:把下列各式分解因式
x2 2x 15 y2 3x 18 x2 13x 12 y2 17x 30
a2 13a 42
含有x的二次三项式,其中x2系数是1, 常数项为12,并能分解因式,这样 的多项式共有几个?
二次三项式分解因式使
q ab, p a b
x
3
(3x) (5x) 8x
例: 分解因式: x2+4x+3=__(x_+3_)_(x_+1_)
x3 x1
x2-2x-3=_(_x-_3)_(x_+1_) __
x -3 x1
练一练: 将下列各式分解因式
x2 5x 6 x2 x 6 x2 7x 12 x2 3x 10
2x2 5xy 7 y2
2x
7y
x 1y
2xy 7xy 5xy
所以: 原式 (2x 7 y)(x y)
十字相乘法(竖分常数交叉验, 横写因式不能乱。 )
例1、(4)
2a b2 9a b 9 (a b 3)2a b 3
x
-3 = 2 (x-3) (x+2)
2x
4
x×4+2x×(-3)=-2x
①竖分二次项与常数项 ②交叉相乘,和相加
③检验确定,横写因式
十字相乘法(竖分常数交
叉验, 横写因式不能乱。 )
例1、用十字相乘法分解因式 2x2-2x-12
法二:
2x2-2x-12 = (x+2)(2x-6)
x
2 = 2(x+2)(x-3)
小结:用十字相乘法把形如
x2 px q 二次三项式分解因式
q ab, p a b
当q>0时,q分解的因数a、b( 同号 ) 当q<0时, q分解的因数a、b( 异号)
观察:p与a、b符号关系
x2 14x 45 (x 5)(x 9)
x2 29x 138 (x 23)(x 6)
x2 4x 3=(x _+_ 3)(x _+_ 1)
x2 2x 3 =(x _-_ 3)(x _+_ 1)
y2 9y 20=(y _-_4)(y _-_5)
t2 10t 56=(t _-_ 4)(t _+_14)
当q>0时,q分解的因数a、b( 同号 )且(a、b符 号)与p符号相同 当q<0时, q分解的因数a、b( 异号) (其中绝 对值较大的因数符号)与p符号相同
整式的乘法
两个一次二项式相乘的积
一个二次三项式
(x+a)(x+b)=x2+(a+b)x+ab
反过来,得
x2+(a+b)x+ab=(x+a)(x+b)
一个二次三项式
两个一次二项式相乘的积
因式分解
如果二次三项式x2+px+q中的常数项系数 q能分解成两个因数a、b的积,而且一次 项系数p又恰好是a+b,那么x2+px+q就可 以进行如上的因式分解。
十字相乘法(借助十字交叉线分解因式的方法)
例一:
步骤:
x2 6x 7 (x 7)(x 1) ①竖分二次项与常数项
x
7 7
或
x 1 1
x7x 6x
②交叉相乘,和相加 ③检验确定,横写因式
顺口溜:竖分常数 交叉验,横写因式 不能乱。
试一试:把x2+3x+2分解因式
结果中一次项系数是分解 后十字交叉相乘所得的和
(2x+3)(x- 4) = 2x2-5x+12
2x
3
1x
-4
2x×(-4)+1x×3=-5x
结果中一次项系数是分解 后十字交叉相乘所得的和
十字相乘法(竖分常数交叉 验, 横写因式不能乱。 )
例1、用十字相乘法分解因式 2x2-2x-12
法一:
2x2-2x-12 = (x-3)(2x+4)
13.y2+9y-36= (y+12)(y-3) 14.y2-11y-60= (y+4)(y-15) 15.y2+19y+48= (y+16)(y+3) 16.y2+y-110= (y+11)(y-10) 17.y2-16y+39= (y-13)(y-3) 18.y2+18y+56= (y+14)(y+4)
小结:当q>0时,q分解的因数a、b( 同号 )
且(a、b符号)与p符号相同
x2 7x 60 (x 12)(x 5)
x2 14x 72 (x 4)(x 18)
当q<0时, q分解的因数a、b( 异号 )
(其中绝对值较大的因数符号)与p符号相同
练习:在 横线上 填 、 符号
A 2个 C 6个
B 4个 D 8个
将下列多项式因式分解
(1)x2+3x-4
(2)x2-3x-43
(3)x2+6xy-16y2 (4)x2-11xy+24y2
(5)x2y2-7xy-18 (6)x4+13x2+36
(2x+3)(x+4) = 2x2+11x+12
2x
3
1x
4
2x×4+1x×3=11x
(a b 3)2a 2b 3
a b
3
2a b
3
3a b 6a b 9a b
用十字相乘法进行因式分解:
1.x2-x- 6 = (x+2)(x-3) 11.x2+13x+12= (x+1)(x+12)
2.x2+2x-15= (x-3)(x+5) 12.x2-11x-12= (x-12)(x+1)
分析∵ (+1) ×(+2)=+2
常数项
(+1)+(+2)=+3
x
1
∴x
2
一次项系数 十字交叉线
解:原式 (x 1)( x 2)
试一试:
(顺口溜:竖分常数交叉验,横写因式不能乱。)
x2 8x 15 (x 5)(x 3) 小结:
用十字相乘法把形如
x
5
x2 px q
10.x2+4x-21=(x-3)(x+7)
1、十字相乘法 (借助十字交叉线分解因式的方法)
2、用十字相乘法把形如x2 + px +q 二次三项式 分解因式
3、 x2+px+q=(x+a)(x+b) 其中q、p、a、b之 间的符号关系
q>0时,q分解的因数a、b( 同号 )且(a、b符号)与p符 号相同 当q<0时, q分解的因数a、b( 异号) (其中绝对值较大 的因数符号)与p符号相同
一、计算:
(1) (x 5)(x 9) x2 14x 45
(2) (x 12)(x 5) x2 7x 60 (3) (x 23)(x 6) x2 29x 138
(4) (x 4)(x 18) x2 14x 72
(x a)(x b) x2 (a b)x ab
2x
-6
x×(-6)+2x×2=-2x
(顺口溜:竖分常数交叉验,横写因式不能乱。)
例1、(2)
12x2 29x 15
3x
5
4x
3
(9x) (20x) 29x
所以: 原式 (3x 5)(4x 3)
十字相乘法(竖分常数交叉验, 横写因式不能乱。 )
例1、(3)
五、选择题:
以下多项式中分解因式为 x 6x 4 的多c项式是
()
A x2 2x 24 B x2 2x 24
x 6x 4
C x2 2x 24 D x2 2x 24
试将 x2 6x 16 分解因式
x2 6x 16
