机械原理第十章习题答案
中南大学 机械原理 第十章作业答案

判断题(每2)
9、满足正确啮合条件的一对齿轮一定能连续传动( ) 10、斜齿圆柱齿轮只能实现平行轴传动。( )
11、正传动的一对齿轮必定都是正变位齿轮( )。
12、法向齿距就是基圆齿距( )。 13、两个齿轮的模数、齿数相等,但压力角不等,则此两齿轮的齿廓形状不同 ( )。
14、齿轮上齿厚等于齿槽宽的圆称为分度圆( )。 15、直齿圆柱轮传动中,节圆总是大于分度圆( )。 16、图示中的C、C‘、C“ 为由同一基圆上所生成的几条渐开线。其任意两条渐 开线(不论是同向还是反向)沿公法线方向对应两点之间的距离处处相等(即: A1B1=A2B2;A1C1=A2C2及B1C1=B2C2)。( ) C A2 A1 C' C" B1 C1 B2 C2
分度圆上曲率半径
r sin
r 2 rb2
基圆上曲率半径 齿顶圆上曲率半径 齿厚和齿槽宽:
ρb1 =0
ρb2 =0
ρb1 =55.76
ρb2 =90.6
p S1= S2=e1=e2= =7.85mm 2
30、一对渐开线外啮合直齿圆柱齿轮机构,两轮的分度圆半径分 别为 r1=30mm ,r2=54mm ,α = 20°,试求(12分)
da1=260mm
db1≈234.92mm
db2≈422.86mm
Z1=50
分度圆上压力角 基圆上压力角 α1 =20° αb1 =0° αa1 =25.4° ρ1 =42.75
Z2=90
α2 =20° αb2 =0° αa2 =23.2° ρ 2 =76.95
齿顶圆上压力角
rb a arccos ra
A、一定 B、不一定 C、一定不
机械原理作业参考答案-第10章-孙桓-第8版-A

2)短齿制
* ha 0.8
c * 0 .3
20
则
故,当 当
* 2(ha c* ) 2 (0.8 0.3) z 36.48 1 cos 1 cos 20
z 36 时,基圆直径大于齿根圆直径;
z 37 时,基圆直径小于齿根圆直径;
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
1)正常齿制
c* 0.25
20
* 2(ha c* ) 2 (1 0.25) 41.4543 则 z 1 cos 1 cos20
故,当 z 41 当
时,基圆直径大于齿根圆直径;
z 42 时,基圆直径小于齿根圆直径;
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
《机械原理》(第8版)--孙桓等主编, 高等教育出版社
(4) 蜗杆和蜗轮旋向相同,且蜗杆导程角与蜗轮 螺旋角相等。
z1m 导程角为 arctan d 1
S m / 2 Sb rb 2 rb 2inv rb 2rbinv z r mz / 2
L1 (k 1) pb sb (k 1)m cos rb 2rb inv z m mz cos (k 1)m cos cos 2 inv 2 2 m cos (k 0.5) z inv
2) 两轮分度圆直径
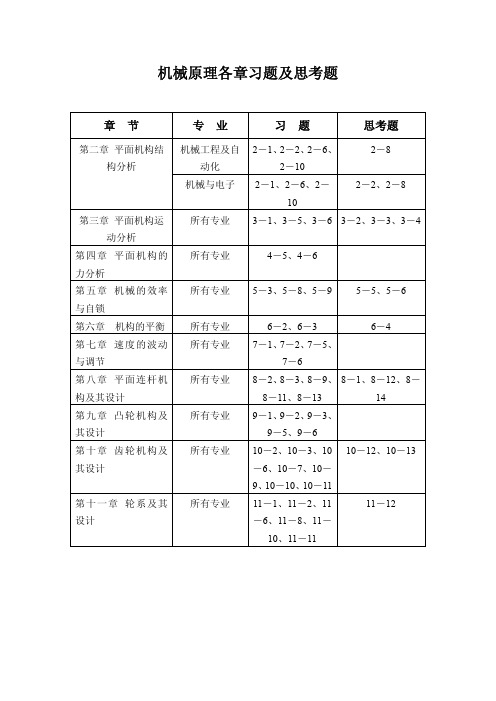
西工大教材-机械原理各章习题及答案
电动机所需的功率为
p = ρ • v /η = 5500 ×1.2 ×10−3 / 0.822 = 8.029(KW )
5-8 在图示斜面机构中,设已知摩擦面间的摩擦系数 f=0.2。求在 G 力作用下(反行程),此斜面 机构的临界自锁条件和在此条件下正行程(在 F 力作用下)的效率。 解 1)反行程的自锁条件 在外行程(图 a),根据滑块的平衡条件:
解 1 ) 取 比 例 尺 μ 1 = 1mm/mm 绘 制 机 构 运 动 简 图 ( 图 b )
(a)
2 )计算该机构的自由度
n=7
pι=9
ph=2(算齿轮副,因为凸轮与齿轮为一体) p’=
F’= F=3n-2pe-ph
=3x7-2x8-2 =1
G7
D 64 C
EF
3
9
B
2
8
A
ω1
b)
2-6 试计算如图所示各机构的自由度。图 a、d 为齿轮一连杆组合机构;图 b 为凸轮一连杆组合 机构(图中在 D 处为铰连在一起的两个滑块);图 c 为一精压机机构。并问在图 d 所示机构中, 齿轮 3 与 5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目是否相同?为什么?
C3 重合点继续求解。
解 1)速度分析(图 b)取重合点 B2 与 B3,有
方向 大小 ?
v vv vB3 = vB2 + vB3B2 ⊥ BD ⊥ AB // CD ω1lAB ?
D
C
3 d3
ω3
4
ω3 90°
2
B(B1、B2、B3)
ω1
A1 ϕ = 90°
机械原理第八版第十章答案

机械原理第八版第十章答案【篇一:机械原理第八版答案与解析】1、如图a所示为一简易冲床的初拟设计方案,设计者的思路是:动力由齿轮1输入,使轴a连续回转;而固装在轴a上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析其是否能实现设计意图?并提出修改方案。
解 1)取比例尺?l绘制其机构运动简图(图b)。
2)分析其是否能实现设计意图。
图 a)由图b可知,n?3,pl?4,ph?1,p??0,f??0 故:f?3n?(2pl?ph?p?)?f??3?3?(2?4?1?0)?0?0因此,此简单冲床根本不能运动(即由构件3、4与机架5和运动副b、c、d组成不能运动的刚性桁架),故需要增加机构的自由度。
图 b)3)提出修改方案(图c)。
为了使此机构能运动,应增加机构的自由度(其方法是:可以在机构的适当位置增加一个活动构件和一个低副,或者用一个高副去代替一个低副,其修改方案很多,图c给出了其中两种方案)。
图 c1)图 c2)2、试画出图示平面机构的运动简图,并计算其自由度。
图a)解:n?3,pl?4,ph?0,f?3n?2pl?ph?1图 b)解:n?4,pl?5,ph?1,f?3n?2pl?ph?13、计算图示平面机构的自由度。
将其中的高副化为低副。
机构中的原动件用圆弧箭头表示。
3-1解3-1:n?7,pl?10,ph?0,f?3n?2pl?ph?1,c、e复合铰链。
3-2解3-2:n?8,pl?11,ph?1,f?3n?2pl?ph?1,局部自由度3-3 解3-3:n?9,pl?12,ph?2,f?3n?2pl?ph?14、试计算图示精压机的自由度解:n?10,pl?15,ph?0解:n?11,pl?17,ph?0p??2pl??p?h?3n??2?5?0?3?3?1p??2pl??p?h?3n??2?10?3?6?2f??0f??0f?3n?(2pl?ph?p?)?f?f?3n?(2pl?ph?p?)?f??3?10?(2?15?0?1)?0?1 ?3?11?(2?17?0?2)?0?1(其中e、d及h均为复合铰链)(其中c、f、k均为复合铰链)5、图示为一内燃机的机构简图,试计算其自由度,并分析组成此机构的基本杆组。
机械原理课后答案第十章作业

由df ≥db ,有: z′≥2(ha*+2 c*) / (1 - cosα) =41.45(不能圆整)
∴ 当齿根圆与基圆重合时,z′=41.45; 当 z ≥ 42时,齿根圆大于基圆。
10-5 已知一对渐开线标准外啮合圆柱齿轮传动,其模数 m=10mm,
解:1)确定传动类型
a = m ( z1+z2 ) /2 = 10 ( 12+12 ) /2 =120 < a′= 130mm 故此传动应为 正 传动。
2)确定两轮变位系数 α′ = arccos(a cosα/ a′) = arccos(120 cos20°/ 130) = 29.83° x1 + x2 = (z1+z2) (invα′-invα) / (2tanα)
10-2 设有一渐开线标准齿轮 z=20,m=8mm,α=20°,ha* =1,试
求:1)其齿廓曲线在分度圆及齿顶圆上的曲率半径ρ、ρa 及齿顶圆压
力角αa ;2)齿顶圆齿厚 s a 及基圆齿厚 s b ;3)若齿顶变尖( s a =0)时,
齿顶圆半径 ra′又应为多少?并完成图示各尺寸的标注。 解:1)求ρ、αa 、ρa d = m z =8×20=160(mm) da= d +2 ha=(z+2ha*)m=(20+2×1)×8= 176(mm) db= d cosα= 160cos20°= 160×0.9397= 150.35(mm) ρ= rb tanα= 75.175 tan20°= 75.175×0.3640= 27.36(mm) αa =arccos( rb/ra )= arccos( 75.175/88 ) = arccos0.8543=31.32° ρa = rb tanαa =75.175tan31.32°= 75.175×0.6085=45.74(mm) 2)求s a 及s b sa=s(ra/r)-2ra(invαa-invα)= 8π/2×88/80-176×(inv31.32°-inv20°)
机械原理课后答案第十章作业解读

法、端面齿距:pn =πmn =25.14(mm)
3)计算重合度
pt =πmn / cosβ =26.19(mm)当
量 齿 数: zv1 = z1 / cos 3β=22.61 zv2 = z2 / cos 3β=45.21 αt =arctan(tanαn / cosβ) = arctan(tan20°/ cos16.26°) =20.764° αat1 = arccos(db1/da1 ) = arccos(155.84/182.67 ) =31.447° αat2 = arccos(db2/da2 ) = arccos(311.69/349.33 ) =26.843° εα= [z1(tanαat1-tanαt )+z2 (tanαat2 – tanαt )] /(2π) =[20(tan31.447°-tan20.764°)+40(tan26.843°–tan20.764°)]/(2π) =1.59 εβ=B sinβ/πmn = 30 sin16.26°/8π=0.332
3)计算几何尺寸 分度圆分离系数:y = (a′-a) / m = 1 齿顶高变动系数:σ= x1 + x2 - y =0.249 齿 顶 高: ha1 = ha2 = ( ha* + x - σ ) m= 13.755(mm) 齿 根 高: hf1 = hf2 = ( ha* + c* - x) m = 6.255(mm) 分 度 圆 直 径: d1 = d2 = m z1 = 120 (mm) 齿 顶 圆 直 径: da1= da2= d1 +2ha1= 147.51 (mm) 齿 根 圆 直 径: df1= df2= d1 - 2hf1= 107.49 (mm) 基 圆 直 径: db1 = db2 = d1 cosα= 112.763(mm) 分 度 圆 齿 厚: s1= s2 = (π/2 + 2 x tanα) m = 20.254 (mm)
机械原理第十章考习题精选全文完整版
可编辑修改精选全文完整版机械原理第十章习题一、单项选择题1.渐开线齿轮的齿廓曲线形状取决于( )A.分度圆B.齿顶圆C.齿根圆D.基圆2.计算蜗杆传动的传动比时,公式( )是错误的。
A. i=ω1/ω2B. i=n1/n2C. i=d2/d1D. i=Z2/Z13.在安装标准直齿轮时若中心距大于标准中心距,则将使( )A.重合度变大B.定角速比无法保证C.啮合角变大D.节圆压力角变小4. 单个渐开线齿轮()A.分度圆等于节圆B.分度圆小于节圆C.分度圆大于节圆D.没有节圆5. 蜗轮的螺旋角β与蜗杆()A.分度圆处的导程角γ大小相等,方向相反B.B.分度圆处的导程角γ大小相等,方向相同C.齿顶圆处的导程角γ1大小相等,方向相反D.齿顶圆处的导程角γ1大小相等,方向相同6.为了减少蜗轮刀具数目,有利于刀具标准化,规定()为标准值。
A.蜗轮齿数B.蜗轮分度圆直径C.蜗杆头数D.蜗杆分度圆直径7. 渐开线齿轮的齿根圆()A.总是小于基圆 B.总是等于基圆C.总是大于基圆 D.有时小于基圆,有时大于基圆8. 为了实现两根相交轴之间的传动,可以采用()A.蜗杆传动B.斜齿圆柱齿轮传动C.直齿锥齿轮传动D.直齿圆柱齿轮传动9. 一对标准齿轮啮合传动时,其啮合角()其分度圆压力角。
A.大于B.等于C.小于D.可能等于也可能大于10.用齿条刀具加工渐开线齿轮时,判断被加工齿轮产生根切的依据是()。
A.刀具的齿顶线通过啮合极限点N1B.刀具的齿顶线超过啮合极限点N1C.刀具的中线超过啮合极限点N1D.刀具的中线不超过啮合极限点N111.在设计计算单个渐开线齿轮的几何尺寸时的基准圆是()A.基圆B.齿根圆C.分度圆D.齿顶圆12. 一对正确啮合的斜齿圆柱齿轮传动的( )均为标准值。
A.法面模数、分度圆上的法面压力角B.端面模数、分度圆上的端面压力角C.端面模数、分度圆上的端面压力角、分度圆上的螺旋角D.法面模数、分度圆上的法面压力角、分度圆上的螺旋角13. 常用来传递空间两交错轴运动的齿轮机构是( )A.直齿圆柱齿轮B.直齿圆锥齿轮C.斜齿圆锥齿轮D.蜗轮蜗杆14.当一对渐开线齿轮制成后,即使两轮的中心距稍有改变,其传动比仍保持不变的原因是()A.压力角不变B.啮合角不变 C.节圆半径不变D.基圆半径不变15.渐开线标准齿轮的根切现象发生在()A.齿数较少时B.模数较小时C.模数较大时D.齿数较多时16.标准直齿圆锥齿轮的标准模数是()A.大端模数B.小端模数C.平均模数D.求出平均模数后圆整所得的模数17.渐开线齿轮的齿廓曲线形状取决于( )A.分度圆B.齿顶圆C.齿根圆D.基圆18.在安装标准直齿轮时若中心距大于标准中心距,则将使( )A.重合度变大B.定角速比无法保证C.啮合角变大D.节圆压力角变小19.单个渐开线齿轮()A.分度圆等于节圆B.分度圆小于节圆C.分度圆大于节圆D.没有节圆20.常用来传递空间两交错轴运动的齿轮机构是( )A.直齿圆柱齿轮B.直齿圆锥齿轮C.斜齿圆锥齿轮D.蜗轮蜗杆二、填空题1. 为了不产生过大的轴向力,在斜齿轮的基本参数中,___________不宜过大。
机械原理总复习题及解答第十章
第十章(附录)常用MATLAB电算编程10.1 连杆机构的电算程序10.1.1 如图10.1所示是一铰链四杆机构,试按以下给定的两连架杆对应位置用解析法编写设计四杆机构的程序:1)对应主动构件转角f的三个位置f1、f2、f3,满足从动件转角的三个对应位置p1、p2、p3 2)对应主动构件转角f的三个位置f1、f2、f3、f4、f5,满足从动件转角的三个对应位置p1、p2、p3、p4、p5图10.1连杆设计(1)图10.2 连杆设计(2)10.1.2 若已知图10.2机构的最大传动角δmax和最小传动角δmin以及尺寸a,d,试编制电算程序求b,c10.1.3 若已知图10.2机构的极位夹角f和曲柄长a以及摇杆的摆角p和长度c,试编制电算程序求连杆长b和机架长d10.1.4 若已知图10.1机构中连杆在三个位置与X轴方向的夹角和连杆上一点m的三个位置坐标,并且已知固定转动副A,D的坐标,试编制电算程序求连杆上B,C点的一组坐标,从而设计出该机构。
10.2 凸轮机构的电算程序10.2.1图10.3是滚子直动从动件盘形凸轮在工作中的一个位置,试根据此图编制电算程序求出凸轮轮廓。
图10.3 滚子直动从动件盘形凸轮13413510.2.2 试编制求凸轮最大压力角的程序 10.3齿轮范成实验演示程序10.3.1编制一个加工齿轮的范成实验演示程序第10章 常用MATLAB 电算编程题解答与分析 10.1 连杆机构的电算程序 10.1.1 解:1)根据教材中的推导,令 ac b d c a R 222221-++=c d R =2 a d R =3 得:)]()cos[()cos()cos(0003021p f p f p p R f f R R -+-=+++- (10-1) 把对应位置的已知条件代入以上算式解方程组即可。
为方便起见取f 0=p 0=0以方便编程。
function linkage3(d,f1,p1,f2,p2,f3,p3) f1=f1*pi/180; f2=f2*pi/180; f3=f3*pi/180; p1=p1*pi/180; p2=p2*pi/180; p3=p3*pi/180;fc='r1-r2*cos(f)+r3*cos(p)=cos(f-p)'; s1=subs(fc,'f',f1); s1=subs(s1,'p',p1); s1=vpa(s1);s2=subs(fc,'f',f2); s2=subs(s2,'p',p2); s2=vpa(s2);s3=subs(fc,'f',f3); s3=subs(s3,'p',p3); s3=vpa(s3);[r1,r2,r3]=solve(s1,s2,s3,'r1','r2','r3'); a=d/(r3) c=d/(r2)b=sqrt(a^2+c^2+d^2-2*a*c*r1)例如:若已知图10.1中d=50,a 杆转角f 为45o 、90o 、135o 对应c 杆转角p 为52o 、82o 、112o可调用:>> linkage3(50,45,52,90,82,135,112) a =27.629285658965426760636076548711 c =41.110355468665232376141549605063 b =57.2362894665213494750616056630382)对于5个位置要求的情况,在程序中我们设定:对应图10.1,已知d ,对应主动件a 的转角f1、f2、f3、f4、f5,从动件有转角p1、p2、p3、p4、p5。
机械原理习题答案第十章
10-1 试求出题10-1图中机构的最小传动角和最大压力角。
解:(a )、4583.01202530sin max =+=+=BC AB l e l α 所以最大压力角︒==28.274583.0arcsin max α 最小传动角︒=︒-︒=-︒=72.6228.279090max min αγ (b )、最大压力角︒=0max α最小传动角︒=︒-︒=-︒=9009090max min αγ10-2 标出题10-2图所示机构在图示位置的传动角。
解:(a)对于该机构,在滑块C处有一传动角c γ,如图所示;在滑块D处也有一传动角D γ,如图所示。
(b)从动件4受到的驱动力是由构件3提供的。
构件4的速度v 很好确定,而构件3作用于构件4的驱动力的方向的确定应当按照下面的步骤进行:①根据构件3上受有三个力、三个力应当汇交于一点可以确定出构件4作用在构件3上的力;②根据作用力和反作用力的关系,确定出构件3作用在构件4上的力的方向。
maxα︒=0αB '题10-1图Fv Dγ)(a DF Dv图示机构在图示位置的传动角γ分别如图中所示。
10-5 标出题10-5图中各个凸轮机构在图示位置时的压力角。
凸轮为主动件。
解:图中各个凸轮机构在图示位置时的压力角α如图所示。
)(b nnn︒=0αααvv vnnnn α题10-5图10-6 在题10-6图中,凸轮为主动件,画出凸轮逆时针转过30º时机构的压力角。
解:利用反转法,即将凸轮固定、机架和从动件沿与凸轮转向相反的方向运动,固定铰链点A 从点A “反转”到点A ’,从动件从AB 运动到A ’B ’,再由点B ’的速度方向和从动件的受力方向确定出凸轮逆时针转过30º时机构的压力角α,如图所示。
原教材6-8 在题6-8图中凸轮为半径为R 的圆盘,凸轮为主动件。
(1) 写出机构的压力角α与凸轮转角之间的关系; (2)讨论如果][αα≥,应采用什么改进设计的措施?解:(1)、当凸轮转动任意角δ时,其压力角α如图所示。
机械原理第十章习题答案
第十章 齿轮机构及其设计习题10-21解:1) 因为7692.06550cos ===K b K r r α, 故压力角452439715.3900'''==K α展角:1375.06932.08307.0tan =-=-==K K K K inv αααθ曲率半径:mm r K b K 535.418307.050tan =⨯==αρ2) 087273.050==K θ,根据渐开线函数表,有 图10-21 ()25434087223.0087273.0087223.0087925.0455*******'''=---+'=K α mm r r K b K 860.6082155.050cos ===α习题10-23 解:分度圆半径:mm mz r 3923262=⨯== 齿顶圆半径:mm mh r r a a 42339*=+=+=基圆半径:mm r r b 648.3620cos 39cos 0=⨯==α 齿廓在齿顶处压力角:0241.2942648.36arccos arccos ===a b a r r α 齿廓在分度圆处曲率半径:mm r 339.1320sin 39sin 0=⨯==αρ齿廓在齿顶处曲率半径:mm tg tg r a b a 516.20241.29648.360=⨯==αρ习题10-25解:基圆节距mm L L p b 914.5512.27426.3356=-=-= 模数mm p m b 003.220cos 1415.3914.5cos 0=⨯==απ 取标准模数mm m 2=。
习题10-26解:中心距()()()5059157001221121112=+⨯=+=⇒+=i m a z mz i a大齿轮齿数:9055091122=⨯==z i z 小、大齿圆分度圆直径为 mm mz d 25055011=⨯==,mm mz d 45059022=⨯==小、大齿轮齿顶圆直径为()mm h z m d aa 2605522*11=⨯=+=,()mm h z m d a a 4605922*22=⨯=+= 小、大齿轮基圆直径为mm d d b 923.23420cos 250cos 01===α,mm d d b 862.42220cos 450cos 02===α 分度圆上齿厚及齿槽宽mm m p s e 854.72514159.322=⨯====π习题10-27 解:齿根圆直径与基圆直径重合时,有()**02220cos c h z m mz a --= 齿数为()46.41229397.015.220cos 122**0**=--=-=-+=c h z m c h z a a 当齿数大于41齿时,齿根圆直径大于基圆直径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十章 齿轮机构及其设计习题10-21解:1) 因为7692.06550cos ===K b K r r α, 故压力角452439715.3900'''==K α展角:1375.06932.08307.0tan =-=-==K K K K inv αααθ曲率半径:mm r K b K 535.418307.050tan =⨯==αρ2) 087273.050==K θ,根据渐开线函数表,有 图10-21 ()25434087223.0087273.0087223.0087925.0455*******'''=---+'=K α mm r r K b K 860.6082155.050cos ===α习题10-23 解:分度圆半径:mm mz r 3923262=⨯== 齿顶圆半径:mm mh r r a a 42339*=+=+=基圆半径:mm r r b 648.3620cos 39cos 0=⨯==α 齿廓在齿顶处压力角:0241.2942648.36arccos arccos ===a b a r r α 齿廓在分度圆处曲率半径:mm r 339.1320sin 39sin 0=⨯==αρ齿廓在齿顶处曲率半径:mm tg tg r a b a 516.20241.29648.360=⨯==αρ习题10-25解:基圆节距mm L L p b 914.5512.27426.3356=-=-= 模数mm p m b 003.220cos 1415.3914.5cos 0=⨯==απ 取标准模数mm m 2=。
习题10-26解:中心距()()()5059157001221121112=+⨯=+=⇒+=i m a z mz i a大齿轮齿数:9055091122=⨯==z i z 小、大齿圆分度圆直径为 mm mz d 25055011=⨯==,mm mz d 45059022=⨯==小、大齿轮齿顶圆直径为()mm h z m d aa 2605522*11=⨯=+=,()mm h z m d a a 4605922*22=⨯=+= 小、大齿轮基圆直径为mm d d b 923.23420cos 250cos 01===α,mm d d b 862.42220cos 450cos 02===α 分度圆上齿厚及齿槽宽mm m p s e 854.72514159.322=⨯====π习题10-27 解:齿根圆直径与基圆直径重合时,有()**02220cos c h z m mz a --= 齿数为()46.41229397.015.220cos 122**0**=--=-=-+=c h z m c h z a a 当齿数大于41齿时,齿根圆直径大于基圆直径。
习题10-29解:标准中心距()()mm z z m a 7002403020211=+=+= 两轮啮合角:00867.2472520cos 700arccos =='α 当03220'='α时,中心距mm a 987.7115.22cos 20cos 70000=='习题10-30解:标准中心距()()mm z z m a 1202121210211=+=+= 啮合角:00841.2913020cos 120arccos =='α 由()αααinv z z x x inv +++='tan 22121,可得:()()()()267.120tan 22401437.005282.0tan 202121=⨯⨯-=+-'=+αααz z inv inv x x 取变位系数6335.021==x x 最小变位系数294.0171217min =-≥x 齿顶高降低系数()267.01267.121=-=-+=∆y x x y齿轮齿顶圆直径()()mm y x h z m d a a 33.147267.02267.1212102221*11=⨯-++⨯=∆-++= 齿轮齿根圆直径()()mm x c h z m d a f 67.107267.15.021*********11=+--⨯=+--= 基圆直径mm d d b 763.11220cos 120cos 011=⨯==α 顶圆压力角0111059.4033.147763.112arccos arccos ===a b a d d α 啮合角00841.2913020cos 120arccos cos arccos =⨯='='a a αα 重合度()[]021.1tan tan 11='-=πααεαt at z 齿厚()()mm m x s s 319.201020tan 6335.025707.1tan 220221=⨯⨯⨯+=+==απ习题10-31解:中心距()()mm z z m a 5.3372118175221=+⨯=+=',可知为标准中心距,可实施高度变位。
206.020tan 5275.0tan 2021=⨯⨯=∆=-=αm s x x 大齿轮分度圆直径mm mz d 590118522=⨯==变位后齿顶圆直径()()mm x h z m d a a 94.597206.022********22=⨯-+⨯=++= 变位后齿顶圆直径()()mm x c h z m d a f 44.575206.025.021*********22=⨯---⨯=+--= 基圆直径mm d d b 42.55420cos 590cos 022=⨯==α齿厚()()mm m x s 1.7520tan 206.025707.1tan 2202=⨯⨯⨯-=+=απ齿槽宽()()mm m x e 61.8520tan 206.025707.1tan 2202=⨯⨯⨯+=-=απ习题10-34解:中心距()()mm z z m a n 466.24815cos 240208cos 2021=⨯+⨯=+=β。
圆整,取mm a 250= 圆整后螺旋角为:()()02126.16250240208arccos 2arccos=⨯+⨯=+=a z z m n β 轴向重合度为3342.081415.326.16sin 30sin 0=⨯⨯==n m B πβεβ 两齿轮端面齿顶圆直径分别为mm h m z m d an n n a 667.1828226.16cos 2082cos 0*11=⨯+⨯=+=β mm h m z m d an n n a 333.3498226.16cos 4082cos 0*22=⨯+⨯=+=β 端面压力角为[][]000763.2026.16cos 20tan arctan cos tan arctan ===βααn t 两齿轮基圆直径分别为 mm z m d t n b 84.155763.20cos 26.16cos 208cos cos 0011=⨯⨯==αβ mm z m d t n a 68.311763.20cos 26.16cos 408cos cos 0022=⨯⨯==αβ 两齿轮齿顶压力角分别为[][]0111445.31667.18284.155arccos arccos===a b at d d α [][]0222847.26333.68.311arccos arccos===a b at d d α 端面重合度为()()[]πααααεα2tan tan tan tan 2211t at t at z z '-+'-=()()[]()14159.32763.20tan 847.26tan 40763.20tan 445.31tan 200000⨯-+-= =1.5484总重合度8826.13342.05484.1=+=+=βαγεεε小、大齿轮的当量齿数为 61.2226.1620cos 03311===βz z v21.4526.16cos 40cos 03322===βz z v习题10-40解:1)蜗杆轴面模数和蜗轮端面模数为mm z d m m x t 5402002212====根据表10-7,可取蜗杆直径为mm d 501=或mm d 901= 则升角为011171.5505arctan arctan =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=d mz γ,或0118.3905arctan =⎪⎭⎫ ⎝⎛=γ 显然,从有利于传动效率来看,取直径为50mm 合适。
2)蜗杆的轴面齿距mm m p x 708.1551415.31=⨯==π导程mm p z l x 708.1511==3)两轮的中心距mm d d a 125220050221=+=+=习题10-37解:小、大齿轮分锥角为0211565.263015arctan arctan ==⎪⎪⎭⎫ ⎝⎛=z z δ,0102435.6390=-=δδ 小、大齿轮的分度圆直径为mm mz d 7515511=⨯==,mm mz d 15030522=⨯== 小、大齿轮的顶圆直径为mm m h d d a a 944.83565.26cos 5275cos 201*11=⨯⨯+=+=δ mm m h d d a a 472.154435.63cos 52150cos 202*22=⨯⨯+=+=δ小、大齿轮的齿根圆直径为()mm m c h d d a f 267.64565.26cos 54.275cos 201**11=⨯⨯-=+-=δ ()mm m c h d d a f 633.144435.63cos 54.2150cos 202**22=⨯⨯-=+-=δ 锥距mm z z m R 853.832301552222221=+⨯=+= 根锥角()()0109.4853.8352.1arctan arctan =⨯==R h f f θ顶锥角00011674.30109.4565.26=+=+=f a θδδ 00022544.67109.4435.63=+=+=f a θδδ 根锥角00011456.22109.4565.26=-=-=f f θδδ 00022326.59109.4435.63=-=-=f f θδδ 小、大齿轮的当量齿数为 77.16565.26cos 15cos 0111===δz z v 08.67435.63cos 30cos 0222===δz z v。
