北师大版八年级数学上册第四章《一次函数》章末复习题含答案解析 (47)
八年级数学上册《第四章 一次函数》单元测试卷及答案-北师大版

八年级数学上册《第四章一次函数》单元测试卷及答案-北师大版学校:___________班级:___________姓名:___________考号:___________一、选择题(本大题共有10个小题,每小题3分,共30分)1.函数y=x-1的图象经过()A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限2.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,观察图象可得()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<0某天小明骑自行车上学,途中因自行车发生故障,修车耽误了一段时间后继续骑行按时赶到了学校.如图描述了他上学的情景,下列说法中错误的是()A.自行车发生故障时离家距离为1000米B.学校离家的距离为2000米C .到达学校时共用时间20分钟D .修车时间为15分钟一次函数2y x m =-+的图象经过点P (2-,3),且与x 轴、y 轴分别交于点A 、B则AOB ∆的面积是( )A .12 B .14 C .4 D .85.一次函数y kx b =+满足0kb <,且y 随x 的增大而减小,则此函数的图像一定不经过() A .第一象限 B .第二象限 C .第三象限 D .第四象限6.一次函数y =kx +b 的图象如图所示,则方程kx +b =0的解为( )A .x =2B .y =2C .x =-1D .y =-17.如图,直线l 是一次函数y=kx+b 的图象,若点A (3,m )在直线l 上,则m 的值是()A .﹣5B .32C .52 D .78.如图,直线AB 对应的函数表达式是( )A .332y x =-+B .332y x =+C .233y x =-+D .233y x =+ 9.同一平面直角坐标系中,函数y ax b =+与y bx a =+的图象大致是( )A. B. C. D.10 .如图,一辆汽车和一辆摩托车分别从A ,B 两地去同一城市l 1 ,l 2分别表示汽车、摩托车离A 地的距离s (km )随时间t (h )变化的图象,则下列结论:①摩托车比汽车晚到1 h ;②A ,B 两地的距离为20 km ;③摩托车的速度为45 km/h ,汽车的速度为60 km/h ;④汽车出发1 h 后与摩托车相遇,此时距离B 地40 km ;⑤相遇前摩托车的速度比汽车的速度快.其中正确的结论有( )A .2个B .3个C .4个D .5个二、填空题(本大题共有8个小题,每小题3分,共24分)11.若函数1(2)n y m x n -=-+是一次函数,则m ,n 应满足的条件是_____________已知油箱中有油25升,每小时耗油5升则剩油量P (升)与耗油时间t (小时)之间的函数关系式为________13.已知一次函数21y x =+的图像经过111(,)P x y ,222(,)Px y 两点 若12x x <,则1y 2y .(填”>”,”<”或”=”)14.一次函数y =(k -2)x +b 的图象如图所示,则k 的取值范围是_______一次函数y kx b =+满足0kb <,且y 随x 的增大而减小则此函数的图像一定不经过_________如图,在平面直角坐标系中,点A 的坐标为(0,6),将△OAB 沿x 轴向左平移得到△O ′A ′B ′点A 的对应点A ′落在直线34y x =-上,则点B 与其对应点B ′间的距离为 .甲、乙两工程队分别同时开挖两条600米长的管道所挖管道长度y (米)与挖掘时间x (天)之间的关系如图所示,则下列说法中:①甲队每天挖100米;②乙队开挖两天后,每天挖50米;③甲队比乙队提前3天完成任务;④当x=2或6时,甲乙两队所挖管道长度都相差100米.正确的有 .(在横线上填写正确的序号)18.正方形111A B C O 、2221A B C C 和3332A B C C …按如图所示的方式放置.点1A 、2A 和3A …和点1C 、2C 和3C …分别在直线1y x =+和x 轴上,则点n B 的坐标是 .(n 为正整数)三、解答题(本大题共有7个小题,共46分)19.已知y 是23x +的正比例函数,且当1x =时5y =-.(1)求y 与x 的函数关系式.(2)若点(,2)a 在该函数的图象上,求a 的值.20.某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租书,租书金额y (元)与租书时间x (天)之间的关系如下图所示.(1)分别写出用租书卡和会员卡租书金额y (元)与租书时间x (天)之间的关系式.(2)两种租书方式每天的收费是多少元?(x <100)21.如图,直线AC 与x 轴的负半轴交于点C ,与y 轴交于点A .直线AB 与x 轴交于点()2,0B ,与y 轴交于点()0,4A .(1)求直线AB 的函数表达式;(2)若7ABC S =△,求点C 的坐标.22.如图,已知一次函数y kx b =+ 的图象经过A (-2,-1),B (1,3)两点并且交x 轴于点C ,交y 轴于点D .(1)求该一次函数的解析式;(2)求△AOB 的面积.23 .在一次蜡烛燃烧实验中乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间的关系如图所示请根据图象所提供的信息解答下列问题:(1)甲、乙两根蜡烛燃烧前的高度分别是__________,从点燃到燃尽所用的时间分别是________;(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;(3)燃烧多长时间,甲、乙两根蜡烛的高度相同?(不考虑都燃尽时的情况)24.如图,已知直线y=-2x+6与x轴交于点A,与y轴交于点B.(1)点A的坐标为________,点B的坐标为________.(2)求△AOB的面积.(3)直线AB上是否存在一点C(点C与点B不重合),使△AOC的面积等于△AOB的面积?若存在,求出点C的坐标;若不存在,请说明理由.如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6)与直线OA相交于点A且点A的纵坐标为2,动点P沿路线O A C→→运动.(1)求直线BC的解析式;(2)在y轴上找一点M,使得△MAB的周长最小,则点M的坐标为______;(请直接写出结果)(3)当△OPC的面积是△OAC的面积的14时,求出这时P的坐标.参考答案一、选择题(本大题共有10个小题,每小题3分,共30分)1D 2A 3D 4B 5C 6C 7C 8A 9B 10B二、填空题(本大题共有8个小题,每小题3分,共24分)11.【答案】m ≠2且n=2 12.【答案】B .P =25-5t 13.【答案】< 14.【答案】k <215.【答案】第三象限 16.【答案】8 17.【答案】①②④ 18.【答案】1(21,2)n n --四、解答题(本大题共有7个小题,共46分)19.解:(1)设(23)y k x =+.∵当1x =时5y =-∴5(213)k -=⨯+∴1k =-∴23y x =--.(2)∵点(,2)a 在23y x =--的图象上∴232a --=.∴ 2.5a =-.20.解:(1)观察图象可知,用租书卡设其函数关系式为y=kx∵函数图象经过点(0,0)和(100,50)∴50=k •100解得k=12,即:函数关系式为y=12x ;用会员卡租书可设其函数关系式为y=ax+b∵图象经过点(0,20)和(100,50)∴2010050b a b =⎧⎨+=⎩解得:31020a b ⎧=⎪⎨⎪=⎩ 即:函数关系式为y=310x+20; (2)用租书卡的方式租书,每天租书的收费为50÷100=0.5元; 用会员卡的方式租书,每天租书的收费为(50-20)÷100=0.3元21.解:(1)设直线AB 的函数表达式为()0y kx b k =+≠ 因为直线AB 经过()0,4A 和()2,0B所以420b k b =⎧⎨+=⎩,所以24k b =-⎧⎨=⎩ 所以直线AB 的函数表达式为24y x =-+.(2)由点C 在x 轴的负半轴上,可设点C 的坐标为(),0a 则OC a a ==-因为()0,4A ,()2,0B 所以4OA =,OB=2因为7ABC S =△,所以172BC OA ⋅= 所以72BC = 所以32OC BC OB =-=,即32a -=,所以32a =- 所以点C 的坐标为3,02⎛⎫- ⎪⎝⎭.22.解:(1)把A (-2,-1),B (1,3)代入y =kx +b ,得 213k b k b -+=-⎧⎨+=⎩解得4353k b ⎧=⎪⎪⎨⎪=⎪⎩∴一次函数解析式为4533y x =+; (2)把x =0代入4533y x =+得53y = 所以D 点坐标为(0,53) 所以△AOB 的面积=S △AOD +S △BOD 1515=2+12323⨯⨯⨯⨯5=2.23 .解:(1)30 cm ,25 cm 2 h ,2.5 h(2)设甲蜡烛燃烧时,y 甲与x 之间的函数关系式为y 甲=k 1x+b 1. 由图可知,函数的图象过点(0,30),(2,0)则b 1=30,2k 1+b 1=0,将b 1=30代入2k1+b 1=0解得k 1=-15.所以y 甲=-15x +30;设乙蜡烛燃烧时,y 乙与x 之间的函数关系式为y 乙=k2x+b2. 由图可知,函数的图象过点(0,25),(2.5,0)则b 2=25,2.5k2+b 2=0,将b2=25代入2.5k2+b2=0解得k2=-10.所以y乙=-10x+25.(3)由题意,得-15x+30=-10x+25,解得x=1,即当蜡烛燃烧1 h,甲、乙两根蜡烛的高度相同.24.解:(1)当y=0时,-2x+6=0解得x=3,则A点的坐标为(3,0);当x=0时,y=-2x+6=6,则B点的坐标为(0,6).(2)S△AOB=12×3×6=9.(3)存在.理由如下:设点C的坐标为(t,-2t+6). 因为△AOC的面积等于△AOB的面积所以12×3×|-2t+6|=9解得t1=6,t2=0(与点B重合,舍去). 所以点C的坐标为(6,-6).25.解:(1)设直线BC的解析式是y=kx+b根据题意得:606bk b ⎧⎨+⎩==解得16k b -⎧⎨⎩== 则直线BC 的解析式是:y=-x+6;(2)如图,作点B (6,0)关于y 轴的对称点B'∴B'(-6,0)连接AB'交y 轴于M ,此时MA+MB 最小,得到△MAB 的周长最小 设直线AB'的解析式为y=mx+n∵A (4,2)∴4260m n m n +⎧⎨-+⎩== ∴1565m n ⎧⎪⎪⎨⎪⎪⎩== ∴直线AB'的解析式为y=1655x + 令x=0∴y=65∴M (0,65) (3)设OA 的解析式是y=ax ,则4a=2解得:a=12则直线的解析式是:y=12x ①当P在OA上时∵当△OPC的面积是△OAC的面积的14时∴P的横坐标是14×4=1在y=12x中,当x=1时,y=12,则P的坐标是(1,12);②当P在AC上时∵△OPC的面积是△OAC的面积的1 4∴CP:AP=1:5∵A(4,2)∴在y=-x+6中,当x=1时,y=5,则P的坐标是(1,5)∴P的坐标是:P1(1,12)或P2(1,5).。
北师大版八年级上册数学第四章 一次函数含答案

北师大版八年级上册数学第四章一次函数含答案一、单选题(共15题,共计45分)1、甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是()A.甲的速度是4km/hB.乙的速度是10km/hC.乙比甲晚出发1h D.甲比乙晚到B地3h2、某种签字笔的单价为2元,购买这种签字笔x支的总价为y元.则y与x之间的函数关系式为()A. B. C.y=-2x D.y=2x3、出生1﹣6个月的婴儿生长发育得非常快,他们的体重y(g)与月龄x(月)间的关系可以用y=a+700x来表示,其中a是婴儿出生时的体重,一个婴儿出生时的体重是3000g,这个婴儿第4个月的体重为( )A.6000gB.5800gC.5000gD.5100g4、如图,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=BC=4,DE⊥BC于点E,且E是BC中点;动点P从点E出发沿路径ED→DA→AB以每秒1个单位长度的速度向终点B运动;设点P的运动时间为t秒,△PBC的面积为S,则下列能反映S与t的函数关系的图象是()A. B. C. D.5、一个有进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分钟的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:min)之间的关系如图所示.则8min时容器内的水量为()A.20 LB.25 LC.27LD.30 L6、已知一次函数的图象,如图所示,当时,的取值范围是()A. B. C. D.7、正比例函数如图所示,则这个函数的解析式为( )A.y=xB.y=-xC.y=-2xD.y=8、弹簧挂上物体后会伸长,测得一弹簧的长度y (cm)与所挂的物体的质量x(kg)之间有下面的关系:x/kg 0 1 2 3 4 5y/cm 10 10.5 11 11.5 12 12.5下列说法不正确的是()A.x与y都是变量,且x是自变量,y是因变量B.弹簧不挂重物时的长度为0 cmC.物体质量每增加1 kg,弹簧长度y增加0.5 cmD.所挂物体质量为7 kg时,弹簧长度为13.5 cm9、如图,点、、、是正方形四条边(不含端点)上的点,设线段的长为,四边形的面积为,则能够反映与之间函数关系的图象大致是()A. B. C. D.10、已知点都在直线上,则大小关系是()A. B. C. D.不能比较11、若函数y=(k+1)x+k2﹣1是正比例函数,则k的值为()A.0B.1C.±1D.-112、如图表示某加工厂今年前5个月每月生产某种产品的产量c(件)与时间t (月)之间的关系,则对这种产品来说,该厂()A.1月至3月每月产量逐月增加,4、5两月产量逐月减小B.1月至3月每月产量逐月增加,4、5两月产量与3月持平C.1月至3月每月产量逐月增加,4、5两月产量均停止生产 D.1月至3月每月产量不变, 4、5两月均停止生产13、某种出租车收费标准是:起步价7元(即行驶距离不超过3千米需付7元车费),超过了3千米以后,每增加1千米加收2.4元(不足1千米按1千米计),某人乘这种出租车从甲地到乙地支付车费19元,设此人从甲地到乙地经过的路程为x千米,则x的最大值是A.11B.8C.7D.514、如图,韩老师早晨出门散步时离家的距离(y)与时间(x)之间的函数图象.若用黑点表示韩老师家的位置,则韩老师散步行走的路线可能是()A. B. C. D.15、直线y=﹣x+1不经过()A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(共10题,共计30分)16、已知是一次函数,则________.17、如图,在平面直角坐标系中,函数和的图象分别为直线,过上的点A1(1,)作x轴的垂线交于点A2,过点A2作y轴的垂线交于点A3,过点A3作x轴的垂线交于点A4…,一次进行下去,则点的横坐标为________ .18、某水果店五一期间开展促销活动,卖出苹果数量x(kg)与售价y(kg/元)的关系如下表:数量x(kg) 1 2 3 4 5 …售价y(kg/元)9 15 21 27 33 …则售价y(kg/元)与数量x(kg)之间的关系式是________.19、正方形,,,…按如图所示的方式放置.点,,,…和点,,,…分别在直线和轴上,则点的坐标是________.20、在直角坐标系xOy中,对于点P(x,y)和Q(x,y′),给出如下定义:若y′=,则称点Q为点P的“可控变点”.例如:点(1,2)的“可控变点”为点(1,2),点(﹣1,3)的“可控变点”为点(﹣1,﹣3).(1)若点(﹣1,﹣2)是一次函数y=x+3图象上点M的“可控变点”,则点M 的坐标为________ .(2)若点P在函数y=﹣x2+16(﹣5≤x≤a)的图象上,其“可控变点”Q的纵坐标y′的取值范围是﹣16<y′≤16,则实数a的取值范围是________ .21、若函数y=2x+b(b为常数)的图象经过点A(0,﹣2),则b=________.22、如图,已知直线y=2x+4与x轴交于点A,与y轴交于点B,以点A为圆心,AB为半径画弧,交x轴正半轴于点C,则点C坐标为________.23、已知一次函数的图象经过点和,那么的值为________.24、直线y=-3x+m经过点A(-1,a)、B(4,b),则a________b(填“>”或“<”)25、已知一次函数的图像经过点,则________.三、解答题(共5题,共计25分)26、如图,直线l是一次函数y=kx+b的图象,求l与两坐标轴所围成的三角形的面积.27、将若干张长为20里面、宽为10里面的长方形白纸,按图所示的方法粘合起来,粘合部分的宽为2厘米.(1)求2张白纸贴合后的总长度;那么3张白纸粘合后的总长度呢?4张呢?(2)设a张白纸粘合后的总长度为b里面,写出b与a之间的关系式,并求当a=100时,b的值.28、某游泳馆每年夏季推出两种游泳付费方式,方式一:先购买会员证,每张会员证100元,只限本人当年使用,凭证游泳每次再付费5元;方式二:不购买会员证,每次游泳付费9元.设小明计划今年夏季游泳次数为x(x为正整数).(I)根据题意,填写下表:(Ⅱ)若小明计划今年夏季游泳的总费用为270元,选择哪种付费方式,他游泳的次数比较多?(Ⅲ)当x>20时,小明选择哪种付费方式更合算?并说明理由.29、某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4kg,乙种材料1kg;生产一件B产品需甲、乙两种材料各3kg.经测算,购买甲、乙两种材料各1kg共需资金60元;购买甲种材料2kg 和乙种材料3kg共需资金155元.(1)甲、乙两种材料每kg分别是多少元?(2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案.30、某工厂以80元/箱的价格购进60箱原材料,准备由甲、乙两车间全部用于生产A产品.甲车间用每箱原材料可生产出A产品12kg,需耗水4吨;乙车间通过节能改造,用每箱原材料可生产出的A产品比甲车间少2kg,但耗水量是甲车间的一半.已知A产品售价为30元/kg,水价为5元/吨.如果要求这两车间生产这批产品的总耗水量不得超过200吨,那么该厂如何分配两车间的生产任务,才能使这次生产所能获取的利润w最大?最大利润是多少?(注:利润=产品总售价﹣购买原材料成本﹣水费)参考答案一、单选题(共15题,共计45分)1、C2、D3、B4、B5、B6、7、B8、B9、A10、C11、B12、B13、B14、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、。
2021-2022学年北师大版八年级数学上册《第4章一次函数》期末复习易错题型专题测试(附答案)

2021-2022学年北师大版八年级数学上册《第4章一次函数》期末复习易错题型专题测试(附答案)一.选择题(共8小题,满分32分)1.将一次函数y=的图象向左平移2个单位得到的新的函数的表达式()A.y=x+1B.y=x+2C.y=x﹣1D.y=x﹣2 2.成都市双流新城公园是亚洲最大的城市湿地公园,周末小李在这个公园里某笔直的道路上骑车游玩,先前进了a千米,休息了一段时间,又原路返回b千米(b<a),再前进c 千米,则他离起点的距离s与时间t的关系的示意图是()A.B.C.D.3.小明从家出发到公园晨练,在公园锻炼一段时间后按原路返回,同时小明爸爸从公园按小明的路线返回家中,如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象,则下列结论中不正确的是()A.公园离小明家1600米B.小明出发分钟后与爸爸第一次相遇C.小明在公园停留的时间为5分钟D.小明与爸爸第二次相遇时,离家的距离是960米4.已知一次函数y=kx+b,函数值y随自变量x的增大而减小,且kb<0,则函数y=kx+b 的图象大致是()A.B.C.D.5.甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲乙两人间距离为s(单位:千米),甲行驶的时间为(单位:小时),s与t之间的函数关系如图所示,有下列结论:①出发1小时时,甲、乙在途中相遇;②乙开车速度是80千米/小时;③出发1.5小时时,乙比甲多行驶了60千米;④出发3小时时,甲乙同时到达终点;其中正确结论的个数是()A.1B.2C.3D.46.宇嘉同学从家出发沿笔直的公路去晨练,他离开家的距离y(米)与时间x(分)的函数关系图象如图所示.下列结论中,不正确的是()A.整个行进过程花了30分钟B.整个行进过程共走了1000米C.在图中停下来休息了5分钟D.返回时速度为100米/分7.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是()A.y1>y2B.y1=y2C.y1<y2D.不能比较8.已知直线y=﹣x+与x轴,y轴分别交于A,B两点,在坐标轴上取一点P,使得△P AB是等腰三角形,则符合条件的点P有()个A.4B.6C.7D.8二.填空题(共10小题,满分40分)9.某市出租车白天的收费起步价为7元,即路程不超过3千米时收费7元,超过部分每千米收费1.2元,如果乘客白天乘坐出租车的路程为x(x>3)千米,乘车费为y元,那么y与x之间的关系为.10.某地出租车行驶里程x(km)与所需费用y(元)的关系如图.若某乘客一次乘坐出租车里程12km,则该乘客需支付车费元.11.我们知道:当x=2时,不论k取何实数,函数y=k(x﹣2)+3的值为3,所以直线y =k(x﹣2)+3一定经过定点(2,3);同样,直线y=(k﹣2)x+3k一定经过的定点为.12.如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位长度后所得直线l′的函数解析式为.13.如图,一次函数y=﹣x+8的图象与x轴、y轴分别交于A、B两点.P是x轴上一个动点,若沿BP将△OBP翻折,点O恰好落在直线AB上的点C处,则点P的坐标是.14.一次函数y=2x﹣6的图象与两坐标轴所围成的三角形面积为.15.如图是表示的是甲、乙两人运动的图象,图中s(米)和t(秒)分别表示运动的路程和时间,根据图象判断,快者的速度比慢者的速度每秒快米.16.若一次函数y=kx+3与x轴、y轴分别交于点A、B,且三角形OAB的面积是6,则k =.17.正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=kx+b(k>0)和x轴上,已知点B1(1,1),B2(3,2),则B n的坐标是.18.直线y=﹣x+4与x轴、y轴分别交于点A、B,M是y轴上一点,若将△ABM沿AM 折叠,点B恰好落在x轴上,则点M的坐标为.三.解答题(共6小题,满分48分)19.如图,在平面直角坐标系xOy中,直线y=﹣x+8分别交x轴、y轴于点A、B,将正比例函数y=2x的图象沿y轴向下平移3个单位长度得到直线l,直线l分别交x轴、y 轴于点C、D,交直线AB于点E.(1)直接写出直线l对应的函数表达式;(2)在直线AB上存在点F(不与点E重合),使BF=BE,求点F的坐标;(3)在x轴上是否存在点P,使∠PDO=2∠PBO?若存在,求点P的坐标;若不存在,请说明理由.20.周末,小明骑电动自行车从家里出发到野外郊游.从家出发0.5小时后到达甲地,游玩一段时间后按原速前往乙地.小明离家1小时20分钟后,妈妈驾车沿相同路线前往乙地.如图是他们离家的路程y(km)与小明离家时间x(h)的函数图象.已知妈妈驾车的速度是小明骑电动自行车速度的3倍.(1)小明骑电动自行车的速度为千米/小时,在甲地游玩的时间为小时;(2)小明从家出发多少小时的时候被妈妈追上?此时离家多远?21.一条笔直的公路上有甲、乙两地相距2400米,王明步行从甲地到乙地,每分钟走96米,李越骑车从乙地到甲地后休息2分钟沿原路原速返回乙地设他们同时出发,运动的时间为t(分),与乙地的距离为s(米),图中线段EF,折线OABD分别表示两人与乙地距离s和运动时间t之间的函数关系图象(1)李越骑车的速度为米/分钟;F点的坐标为;(2)求李越从乙地骑往甲地时,s与t之间的函数表达式;(3)求王明从甲地到乙地时,s与t之间的函数表达式;(4)求李越与王明第二次相遇时t的值.22.已知一次函数y=kx+b的图象经过点(﹣1,﹣5),且与正比例函数y=x的图象相交于点(2,a),求(1)a的值;(2)k,b的值;(3)这两个函数图象与x轴所围成的三角形的面积.23.有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x (单位:分)之间的关系如图所示:(1)求0≤x≤4时y随x变化的函数关系式;(2)当4<x≤12时,求y与x的函数解析式;(3)每分钟进水、出水各是多少升?24.如图,在平面直角坐标系中,直线y=x+2与x轴,y轴分别交于A,B两点,点C(2,m)为直线y=x+2上一点,直线y=﹣x+b过点C.(1)求m和b的值;(2)直线y=﹣x+b与x轴交于点D,动点P从点D开始以每秒1个单位的速度向x 轴负方向运动.设点P的运动时间为t秒.①若点P在线段DA上,且△ACP的面积为10,求t的值;②是否存在t的值,使△ACP为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由.参考答案一.选择题(共8小题)1.解:∵一次函数y=的图象向左平移2个单位,∴平移后所得图象对应的函数关系式为:y=﹣(x+2)+2,即y=﹣x﹣1.故选:C.2.解:由题意,得路程先增加,路程不变,路程减少,路程又增加,故D符合题意;故选:D.3.解:由图可得,公园离小明家1600米,故A选项正确;∵小明从家出发到公园晨练时,速度为1600÷10=160米/分,小明爸爸从公园按小明的路线返回家中的速度为1600÷50=32米/分,∴小明出后与爸爸第一次相遇的时间为1600÷(160+32)=分钟,故B选项正确;由图可得,30分钟后小明与爸爸第二次相遇时,离家的距离是1600﹣30×32=640米,故D选项错误;∵小明在与爸爸第二次相遇后回到家的时间为:40﹣30=10分,∴小明在公园锻炼一段时间后按原路返回的速度为640÷10=64米/分,∴40﹣1600÷64=15分,∴小明在公园停留的时间为15﹣10=5分钟,故C选项正确;故选:D.4.解:∵一次函数y=kx+b,y随着x的增大而减小,∴k<0,∴一次函数y=kx+b的图象经过第二、四象限;∵kb<0,∴b>0,∴图象与y轴的交点在x轴上方,∴一次函数y=kx+b的图象经过第一、二、四象限.故选:C.5.解:由图象可得,当t=1时,s=0,即出发1小时时,甲乙在途中相遇,故①正确,甲的速度是:120÷3=40千米/时,则乙的速度是:120÷1﹣40=80千米/h,故②正确;出发1.5小时时,乙比甲多行驶路程是:1.5×(80﹣40)=60千米,故③正确;在1.5小时时,乙到达终点,甲在3小时时到达终点,故④错误,故选:C.6.解:①∵当y=0时,x=0或x=30,∴整个行进过程花了30分钟,A正确;②观察函数图象可知,y的最大值为1000,∵1000×2=2000(米),∴整个行进过程共走了2000米,B错误;③∵15﹣10=5(分钟),∴在途中停下来休息了5分钟,C正确;④∵1000÷(30﹣20)=100(米/分),∴返回时速度为100米/分,D正确.故选:B.7.解:∵k=﹣<0,∴y随x的增大而减小.∵﹣4<2,∴y1>y2.故选:A.8.解:如图所示,∵直线y=﹣x+与x轴,y轴分别交于A,B两点,∴A(1,0),B(0,),(1)当AB是底边时,作AB的垂直平分线,∵OA≠OB,∴AB的垂直平分线与x轴,y轴都有交点,此时有2个;(2)当AB是腰时,①以A为圆心,以AB为半径画弧,和x轴交于2点,和y轴交于2点(点B除外),即有3个;②以B为圆心,AB为半径画弧,和x轴交于2点(点A除外),和y轴交于2点,即有3个.其中有3个点,即(﹣1,0)重合.共6个.故选:B.二.填空题(共10小题)9.解:依据题意得:y=7+1.2(x﹣3)=1.2x+3.4,故答案为:y=1.2x+3.4,10.解:由图象知,y与x的函数关系为一次函数,并且经过点(2,5)、(4,8),设该一次函数的解析式为y=kx+b,则有:,解得:,∴y=x+2.将x=12代入一次函数解析式,得y=18+2=20,故出租车费为20元.故答案为:20.11.解:根据题意,y=(k﹣2)x+3k可化为:y=(x+3)k﹣2x,∴当x=﹣3时,不论k取何实数,函数y=(x+3)k﹣2x的值为6,∴直线y=(k﹣2)x+3k一定经过的定点为(﹣3,6),故答案为:(﹣3,6).12.解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC 于C,∵正方形的边长为1,∴OB=3,∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,∴两边分别是4,∴三角形ABO面积是5,∴OB•AB=5,∴AB=,∴OC=,由此可知直线l经过(,3),设直线l为y=kx,则3=k,k=,∴直线l解析式为y=x,∴直线l向右平移3个单位长度后所得直线l′的函数解析式为y=(x﹣3),即y=x ﹣,故答案为:y=x﹣.13.解:由一次函数y=﹣x+8的图象与x轴、y轴分别交于A、B两点,可得AO=6,BO=8,AB=10,分两种情况:①当点P在OA上时,由O与C关于PB对称,可得OP=CP,BC=OB=8,设OP=CP=x,则AP=6﹣x,AC=10﹣8=2,在Rt△ACP中,由勾股定理可得x2+22=(6﹣x)2,解得x=,∴P(,0);②当点P在AO延长线上时,由O与C关于PB对称,可得OP=CP,BC=OB=8,设OP=CP=x,则AP=6+x,AC=10+8=18,在Rt△ACP中,由勾股定理可得x2+182=(6+x)2,解得x=24,∴P(﹣24,0);故答案为:(,0)或(﹣24,0).14.解:∵令x=0,则y=﹣6,令y=0,则x=3,∴一次函数y=2x﹣1的图象与两坐标轴的交点分别为(0,﹣6),(3,0),∴一次函数y=2x﹣1的图象与两坐标轴围成三角形的面积=×3×6=9.故答案为:9.15.解:∵慢者8秒走了64﹣12=52米,快者8秒走了64米,∴快者每秒走:64÷8=8m,慢者每秒走:52÷8=6.5m,所以8﹣6.5=1.5m.故答案为:1.5.16.解:(1)当x=0时,y=3,∴B(0,3),∴OB=3.∵•OA•OB=6,∴3OA=12,∴OA=4,∴A(±4,0).∴0=±4k+3,∴k=±,故答案为±17.解:∵点B1(1,1),B2(3,2),∴A1(0,1)A2(1,2)A3(3,4),∴直线y=kx+b(k>0)为y=x+1,∴Bn的横坐标为A n+1的横坐标,纵坐标为An的纵坐标又A n的横坐标数列为An=2n﹣1﹣1,所以纵坐标为2n﹣1,∴Bn的坐标为[A(n+1)的横坐标,An的纵坐标]=(2n﹣1,2n﹣1).故答案为:(2n﹣1,2n﹣1).18.解:如图所示,当点M在y轴正半轴上时,设沿直线AM将△ABM折叠,点B正好落在x轴上的C点,则有AB=AC,由直线y=﹣x+4可得,A(3,0),B(0,4),∴OA=3,OB=4,∴AB=5,∴CO=AC﹣AO=5﹣3=2,∴点C的坐标为(﹣2,0).设M点坐标为(0,b),则OM=b,CM=BM=4﹣b,∵CM2=CO2+OM2,∴(4﹣b)2=22+b2,∴b=,∴M(0,),如图所示,当点M在y轴负半轴上时,OC=OA+AC=3+5=8,设M点坐标为(0,b),则OM=﹣b,CM=BM=4﹣b,∵CM2=CO2+OM2,∴(4﹣b)2=82+b2,∴b=﹣6,∴M点(0,﹣6),故答案为:(0,)或(0,﹣6).三.解答题(共6小题)19.解:(1)∵l是y=2x向下平移3个单位所得,∴l:y=2x﹣3,(2)∵,解得:,∴E(4,5),∵BF=BE,且F不与E重合,∴F在y轴左侧,又∵y=﹣+8,∴当x=0时,y=8,B(0,8),∴BE==5=BF,设F(x0,﹣x0+8),∴BF==5,解得x0=﹣4,∴F(﹣4,11).(3)由图可知,作PG=PD,G在y轴上,∴∠PGO=∠PDO,又∵∠PDO=2∠PBO,∠PGO=∠PBO+∠BPG,∴∠BPG=∠PBG=∠PDO,∴BG=PG=PD,①P在x轴正半轴,∵l:y=2x﹣3,∴当x0时,y=﹣3,即D(0,﹣3),∴OD=3,∴OG=OD=3,则BF=8﹣3=5=PF,∴OP==4,∴P(4,0).②若P在x轴负半轴,与①同理,P(﹣4,0).综上所述P(4,0),(﹣4,0).20.解:(1)由图象得在甲地游玩的时间是1﹣0.5=0.5(h),小明骑车速度:10÷0.5=20(km/h),故答案为:20,0.5.(2)如图,妈妈驾车速度:20×3=60(km/h)设直线OA的解析式为y=kx(k≠0),则10=0.5k,解得:k=20,故直线OA的解析式为:y=20x.∵小明走OA段与走BC段速度不变,∴OA∥BC,设直线BC解析式为y=20x+b1,把点B(1,10)代入得b1=﹣10,∴y=20x﹣10,设直线DE解析式为y=60x+b2,把点D(,0)代入得:b2=﹣80,∴y=60x﹣80,∴,解得:,∴F(1.75,25).答:小明出发1.75小时(105分钟)被妈妈追上,此时离家25km.21.解:(1)由图象可得,李越骑车的速度为:2400÷10=240米/分钟,2400÷96=25,所以F点的坐标为(25,0).故答案为:240;(25,0);(2)设李越从乙地骑往甲地时,s与t之间的函数表达式为s=kt,2400=10k,得k=240,即李越从乙地骑往甲地时,s与t之间的函数表达式为s=240t,故答案为:s=240t;(3)设王明从甲地到乙地时,s与t之间的函数表达式为s=kt+2400,根据题意得,25k+2400=0,解得k=﹣96,所以王明从甲地到乙地时,s与t之间的函数表达式为:s=﹣96t+2400;(4)根据题意得,240(t﹣2)﹣96t=2400,解得t=20.答:李越与王明第二次相遇时t的值为20.22.解:(1)由题知,把(2,a)代入y=x,解得a=1;(2)由题意知,把点(﹣1,﹣5)及点(2,a)代入一次函数解析式得:﹣k+b=﹣5,2k+b=a,又由(1)知a=1,解方程组得:k=2,b=﹣3;(3)由(2)知一次函数解析式为:y=2x﹣3,直线y=2x﹣3与x轴交点坐标为(,0)∴所求三角形面积=×1×=.23.解:设y=kx.∵图象过(4,20),∴4k=20,∴k=5.∴y=5x(0≤x≤4);(2)设y=kx+b.∵图象过(4,20)、(12,30),∴,解得:,∴y=x+15 (4≤x≤12);(3)根据图象,每分钟进水20÷4=5升,设每分钟出水m升,则5×8﹣8m=30﹣20,解得:m=,∴每分钟进水、出水各是5升、升.24.解:(1)把点C(2,m)代入直线y=x+2中得:m=2+2=4,∴点C(2,4),∵直线y=﹣x+b过点C,4=﹣+b,b=5;(2)①由题意得:PD=t,y=x+2中,当y=0时,x+2=0,x=﹣2,∴A(﹣2,0),y=﹣x+5中,当y=0时,﹣x+5=0,x=10,∴D(10,0),∴AD=10+2=12,即0≤t≤12,∵△ACP的面积为10,∴•4=10,t=7,则t的值7秒;②存在,分三种情况:i)当AC=CP时,如图1,过C作CE⊥AD于E,∴PE=AE=4,∴PD=12﹣8=4,即t=4;ii)当AC=AP时,如图2,AC=AP1=AP2==4,∴DP1=t=12﹣4,DP2=t=12+4;iii)当AP=PC时,如图3,∵OA=OB=2∴∠BAO=45°∴∠CAP=∠ACP=45°∴∠APC=90°∴AP=PC=4∴PD=12﹣4=8,即t=8;综上,当t=4秒或(12﹣4)秒或(12+4)秒或8秒时,△ACP为等腰三角形.。
北师大版八年级上册数学第四章 一次函数含答案【参考答案】

北师大版八年级上册数学第四章一次函数含答案一、单选题(共15题,共计45分)1、如图,过点A的一次函数图象与正比例函数y=2x的图象相交于点B,则这个一次函数的关系式是()A.y=2x+3B.y=2x-3C.y=x-3D.y= -x+32、下列平面直角坐标系中的曲线,不能表示y是x的函数的是()A. B. C.D.3、若函数y=(k﹣2)﹣5是关于x的一次函数,则K的值为()A.K=﹣2B.K=2C.K=2或﹣2D.不确定4、已知正比例函数的图像上有两点且,,且x>x2,则y1与y2的大小关系是()1A. B. C. D.不能确定.5、已知汽车油箱内有油40L,每行驶100km耗油10L,则汽车行驶过程中油箱内剩余的油量Q (L)与行驶路程s(km)之间的函数表达式是()A.Q=40+B.Q=40﹣C.Q=40﹣D.Q=40+6、已知一次函数y=(m+3)x-2中,y的值随x的增大而增大,则m的取值范围是()A.m>0B.m<0C.m>-3D.m<-37、如图1,在同一直在线,甲自A点开始追赶等速度前进的乙,图2表示两人距离与所经时间的线型关系。
若乙的速率为每秒1.5公尺,则经过40秒,甲自A点移动多少公尺?()A.60B.61.8C.67.2D.698、已知两个变量x和y,它们之间的3组对应值如表所示,则y与x之间的函数关系式可能是()x ﹣1 1 3y ﹣3 3 1A.y=x﹣2B.y=2x+1C.y=x 2+x﹣6D.y=9、已知正比例函数y=(3k﹣1)x,若y随x的增大而增大,则k的取值范围是()A.k<0B.k>0C.k<D.k>10、反比例函数与正比例函数y=2x在同一坐标系内的大致图象为()A. B. C.D.11、如图所示的函数图象反映的过程是:小徐从家去菜地浇水,又去玉米地除草,然后回家,其中x表示时间,y表示小徐离他家的距离.读图可知菜地离小徐家的距离为()A.1.1千米B.2千米C.15千米D.37千米12、在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是()A.正比例函数B.反比例函数C.图象不经过原点的一次函数D.二次函数13、关于函数y=x ,下列结论正确的是()A.函数图像必经过点(1,2)B.函数图像经过二、四象限C.y随x 的增大而减小D.y随x的增大而增大14、下列图象中,表示y是x的函数的是( )A. B. C. D.15、结合函数y=﹣2x的图象回答,当x<﹣1时,y的取值范围()A.y<2B.y>2C.y≥D.y≤二、填空题(共10题,共计30分)16、在平面直角坐标系中,画一次函数y=-3x+3的图像时,通常过点________和________画一条直线.17、如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l 2,过点(1,0)作x轴的垂线交l2于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l2于点A3,过点A3作y轴的垂线交l2于点A 4,…依次进行下去,则点A2017的坐标为________.18、已知一次函数,随的增大而增大,则________0.(填“>”,“<”或“=”)19、如图,点A的坐标为(﹣5,0),直线y= x+t与坐标轴交于点B,C,连结AC,如果∠ACD=90°,则t=________.20、无论a取什么实数,点P(a﹣1,2a﹣3)都在直线l上.Q(m,n)是直线l上的点,则(2m﹣n+3)2的值等于________.21、一次函数y=3x-1中,y随x的增大而________.22、若正比例函数y=(m﹣2)x的图象经过一、三象限,则m的取值范围是________.23、若点、都在函数的图象上,则和的大小关系是________.24、如图①,在梯形ABCD中,AD∥BC,∠A=60°,动点P从A点出发,以1cm/s的速度沿着A→B→C→D的方向不停移动,直到点P到达点D后才停止.已知△PAD的面积S(单位:cm2)与点P移动的时间t(单位:s)的函数关系式如图②所示,则点P从开始移动到停止移动一共用了________秒(结果保留根号).25、正比例函数y=kx的图象与直线对y=-x+1线交于的点P(a,2),则k的值是________.三、解答题(共5题,共计25分)26、如图所示的折线ABC•表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t•之间的函数关系式.(2)通话2分钟应付通话费多少元?(3)通话7分钟呢?27、如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2。
初中数学北师大版(2024)八年级上册 第四章 一次函数单元测试(含简单答案)
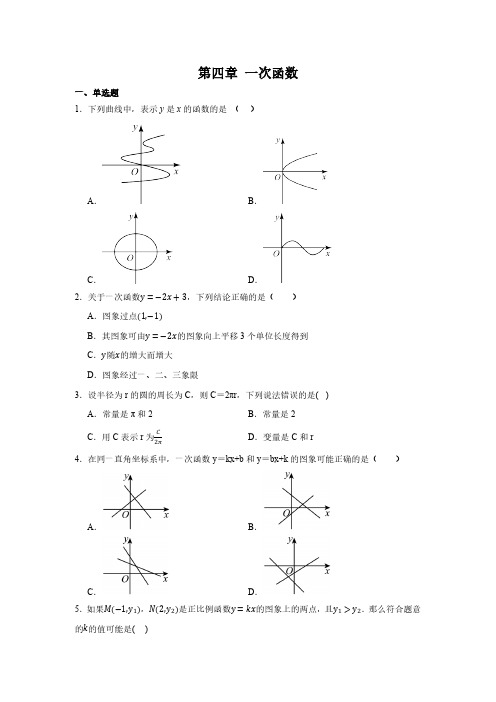
第四章一次函数一、单选题1.下列曲线中,表示y是x的函数的是()A.B.C.D.2.关于一次函数y=−2x+3,下列结论正确的是( )A.图象过点(1,−1)B.其图象可由y=−2x的图象向上平移3个单位长度得到C.y随x的增大而增大D.图象经过一、二、三象限3.设半径为r的圆的周长为C,则C=2πr,下列说法错误的是()A.常量是π和2B.常量是2C.用C表示r为CD.变量是C和r2π4.在同一直角坐标系中,一次函数y=kx+b和y=bx+k的图象可能正确的是( )A.B.C.D.5.如果M(−1,y1),N(2,y2)是正比例函数y=kx的图象上的两点,且y1>y2.那么符合题意的k的值可能是()A.1B.1C.3D.−236.如图所示,已知点C(1,0),直线y=−x+7与两坐标轴分别交于A,B两点,D,E分别是线段AB,OA上的动点,则△CDE的周长的最小值是()A.42B.10C.42+4D.127.函数y=|kx|(k≠0)的图象可能是()A.B.C.D.8.我们把三个数的中位数记作Z{a,b,c}.例如Z{1,3,2}=2.函数y=|2x+b|的图象为C1,函数y=Z{x+1,-x+1,3}的图象为C2.图象C1在图象C2的下方点的横坐标x满足-3<x<1,则b的取值范围为()A.0<b<3B.b>3或b<0C.0≤b≤3D.1<b<39.某电视台“走基层”栏目的一位记者乘汽车赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.若汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,则下列结论正确的是()A.汽车在高速公路上的行驶速度为100km/h B.乡村公路总长为90kmC.汽车在乡村公路上的行驶速度为65km/h D.该记者在出发后5h到达采访地10.如图是一次函数y1=kx+b与y2=x+a的图象,则下列结论:①k<0;②a>0;③b>0:④方程kx+b=x+a的解是x=3,错误的个数是()A.1个B.2个C.3个D.4个二、填空题11.函数y=−3x+6的图象与x轴.y轴围成的三角形面积为.12.如图,购买一种商品,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次性购买50千克这种商品要付款元.13.直线y=kx+b平行于直线y=−2x,且与y轴交于点(0,3),则此函数的解析式y=.14.已知点A(2,y1),B(3,y2)在直线y=﹣3x+1上,则y1与y2的大小关系为:y1y2.(填“>”,“=”或“<”)15.若y=(m−1)x|m|+2是关于x的一次函数,则m等于.16.已知一次函数y1=kx﹣2k(k是常数)和y2=﹣x+1.若无论x取何值,总有y1>y2,则k的值是.17.杭黄高铁开通运营,已知杭州到黄山距离300千米,现有直达高铁往返两城市之间,该高铁每次到达杭州或黄山后,均需停留一小时再重新出发.暑假期间,铁路局计划在同线路上加开一列慢车直达旅游专列,在试运行期间,该旅游专列与高铁同时从杭州出发,在整个小时两车第一次相遇.两车之间的距离y千米运行过程中,两列车均保持匀速行驶,经过103与行驶时间x小时之间的部分函数关系如图所示,当两车第二次相遇时,该旅游专列共行驶了千米.18.如图,在平面直角坐标系中,点A1(1,1)在直线y=x图象上,过A1点作y轴平行线,交直线y=−x于点B1,以线段A1B1为边在右侧作正方形A1B1C1D1,C1D1所在的直线交y=x 的图象于点A2,交y=−x的图象于点B2,再以线段A2B2为边在右侧作正方形A2B2C2D2⋯依此类推,按照图中反映的规律,第2020个正方形的边长是.三、解答题19.父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了表格.距离地面高度(千米)12345温度(℃)201482−4−10根据上表,父亲还给小明出了下面几个问题,你和小明一起回答;(1)如果用ℎ表示距离地面的高度,用t表示温度,写出t与ℎ的关系式;(2)你能计算出距离地面16千米的高空温度是多少吗?x+2和y=2x﹣3的图象分别交y轴与A、B两点,两个一次函数的20.已知一次函数y=﹣12图象相交于点P.(1)求△PAB的面积;(2)求证:∠APB=90°;(3)若在一次函数y=2x﹣3的图象上有一点N,且横坐标为x,连结NA,请直接写出△NAP 的面积关于x的函数关系式,并写出相应x的取值范围.21.已知直线y=-4x+4与x轴和y轴分别交于B、A两点,另一直线经过点B和点D3(11,6).(1)求A、B的坐标;(2)证明:△ABD是直角三角形;(3)在x轴上找点C,使△ACD是以AD为底边的等腰三角形,求出C点坐标.22.如图,l1和l2分别是走私船和我公安快艇航行路程与时间的函数图象,请结合图象解决下列问题:(1)在刚出发时,我公安快艇距走私船多少海里?(2)计算走私船与公安艇的速度分别是多少?(3)求出l1,l2的解析式.(4)问6分钟时,走私船与我公安快艇相距多少海里?23.如图1,某地铁车站在出入口设有上、下行自动扶梯和步行楼梯,甲、乙两人从车站入口同时下行去乘坐地铁,甲乘自动扶梯,乙走步行楼梯,乙离地铁进站入口地面的高度ℎ(单位:m)与下行时间x(单位:s)之间具有函数关系ℎ=−15x+6,甲离地铁进站入口地面的高度y(单位:m)与下行时间x(单位:s)的函数关系如图2所示.(1)求y关于x的函数解析式;(2)请通过计算说明甲、乙两人谁先到达地铁进站入口地面.24.已知直线y=kx+b可变形为:kx−y+b=0,则点P(x0, y0)到直线kx−y+b=0的距离d可用公式d=|kx0−y0+b|1+k2计算.例如:求点P(-2,1)到直线y=x+1的距离.解:因为直线y=x+1可变形为x−y+1=0,其中k=1,b=1.所以点P(-2,1)到直线y=x+1的距离为d=|kx0−y0+b|1+k2=|1×(−2)−1+1|1+12=22=2.根据以上材料求:(1)点P(2,-1)到直线y=2x−1的距离;(2)已知M为直线y=−x+2上的点,且M到直线y=2x−1的距离为35,求M的坐标;(3)已知线段y=kx+3(−1≤x≤2)上的点到直线y=x+1的最小距离为1,求k的值.25.如图,一次函数y=x+1的图象分别与x轴,y轴交于点B与点A,直线AC与x轴正半轴交于点C,且∠BAO=45°,OC=2OB.(1)求直线AC的函数表达式;(2)点D在直线AB上且不与点B重合,点E在直线AC上.若以A,D,E为顶点的三角形与△ABC全等,请直接写出点D的坐标(不必写解答过程);(3)已知平面内一点P(m,n),作点P关于直线AB的对称点P1,作P1关于y轴的对称点P2,若P2恰好落在直线AC上,则m,n应满足怎样的等量关系?说明理由.26.某企业准备为员工采购20000袋医用口罩.经市场调研,准备购买A,B,C三种型号的口罩,这三种型号口罩的价格如下表所示:型号A B C价格/(元/袋)303540已知购买B型号口罩的数量是A型号口罩的2倍,设购买A型号口罩x袋,该企业购买口罩的总费用为y元.(1)请求出y与x之间的函数表达式;(2)因为A型号口罩的数量严重不足,口罩生产厂家能提供的A型号口罩的数量不大于C型号口罩的数量,怎样购买能使该企业购买口罩的总费用最少?请求出费用最少的购买方案,并求出总费用的最小值.参考答案:1.D 2.B 3.B 4.B 5.D 6.B 7.C 8.C 9.D 10.A 11.612.42013.−2x +314.>15.−116.−117.25018.2×3201919.(1)t =20−6ℎ(ℎ≥0)(2)距离地面16千米的高空温度是−76℃20.(1)5;(3)当x >2时,△NAP 的面积S=52(x ﹣2);当x <2时,△NAP 的面积S=52(2﹣x ).21.(1)A (0,4),B (3,0);(3)C (14122,0).22.(1)5海里;(2)走私船:1海里/分;公安快艇:1.5海里/分(3)y 1=t+5 ;y 2=32t ;(4)2海里;23.(1)y =−310x +6;(2)甲先到地铁进站入口地面.24.(1)455;(2)M (6,-4)或M (-4,6);(3)k =−2+3或22x+125.(1)y=−12(2)点D的坐标为(−102,1−102)或(1,2)或(102,1+102);(3)2m+1=n,26.(1)y=−20x+800000(2)当购买A型号口罩5000袋,B型号口罩10000袋,C型号口罩5000袋时,该企业购买口罩的总费用最少,总费用的最小值为700000元。
2024-2025学年北师大版数学八上 第四章 一次函数 单元试卷(含答案)
14.−4
15.<
1
1
16.k=2或−2.
17. = 2 + 10 (−5 < < 0)
18.(1) = 20−2 (2)5 < < 10
19.(1) = 1.5 + 5(0 < < 15);
(2)当弹簧长度为23cm时,所挂物体的质量为 12kg.
20.(1)y1=15x+30(x≥3),y2=12x+60(x≥3);(2)当购买 10 张票时,两种优惠方案付款
.
时,y 随 x 的增大而增大.
14.已知正比例函数 = −2的图象经过点(2,),则 m 的值为
15.已知点(−2,1),(2,2)都在直线 = 2−3上,则1
.
2.(填“<”或“>”或“=”)
16.若直线 ykx2 与坐标轴围成的三角形的面积是 4,则 k 的值为
.
17.已知点(−4,0)及第二象限的动点(,),且− = 5.设的面积为,则关于的
10.已知一次函数 y=kx+b(k,b 为常数,k≠0)的图象经过一、三、四象限,则下列结论
正确的是(
A.kb>0
)
B.kb<0
C.k+b>0
D.k+b<0
二、填空题
11.一次函数 = 2 + 1与轴的交点坐标是
12.请写出一个当 > 1时,随的增大而减小的函数表达式:
13.已知一次函数 = (5−) + 2,当 m
B. = + 1
6.一次函数 = −2−1的图象大致是(
A.
C. = −−2
)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.如图,正方形ABCD的边长为4,点P为正方形边上一动点,若点P从点A出发沿A→D→C→B→A匀速运动一周.设点P走过的路程为x,△ADP的面积为y,则下列图象能大致反映y与x的函数关系的是A.B.C.D.2.下列函数:(1)y=x;(2)y=x4−3;(3)y=4x;(4)y=2x+1,其中一次函数的个数是( )A.1B.2C.3D.43.如图,有一种动画程序,在平面直角坐标系屏幕上,直角三角形是黑色区域(含直角三角形边界),其中A(1,1),B(2,1),C(1,3),用信号枪沿直线y=3x+b发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是( )A.−5≤b≤0B.−5<b≤−3C.−5≤b≤3D.−5≤b≤54.小明和小华是同班同学,也是邻居,某日早晨,小明7:40先出发去学校,走了一段后,在途中停下吃了早餐,后来发现上学时间快到了,就跑步到学校;小华离家后直接乘公共汽车到了学校.如图是他们从家到学校已走的路程s(米)和所用时间t(分)的关系图.则下列说法中正确的是( )①小明家和学校的距离为1200米;②小华乘坐公共汽车的速度是240米/分;③小华在7:50与小明相遇;④小华的出发时间不变,当小华由乘公共汽车变为跑步,且跑步的速度是100米/分时,他们可以同时到达学校.A.①③④B.①②③C.①②④D.①②③④5.若式子√k−1+(k−1)0有意义,则一次函数y=(1−k)x+k−1的图象可能是( )A.B.C.D.6.二次函数y=ax2+bc+c(a,b,c是常数,a≠0)的自变量x与函数值y的部分对应值如表:x⋯−1013⋯y=ax2+bx+c⋯n3m3⋯且当x=32时,与其对应的函数值y<0.有下列结论:① abc<0;② 3是关于x的方程ax2+(b−1)x+c=0的一个根;③ 6<m+ n<263.其中,正确结论的个数是( )A.0B.1C.2D.37.已知一次函数y=kx+b的图象如图所示,则k,b的符号( )A.k>0,b>0B.k>0,b<0C.k<0,b>0D.k<0,b<08.关于一次函数y=2x−b(b为常数),下列说法正确的是( )A.y随x的增大而减小B.当b=4时,图象与坐标轴围成的面积是4C.图象一定过第二、四象限D.与直线y=3−2x一定相交于第四象限内一点9.如图1是一座立交桥的示意图(道路宽度忽略不计),A为入口,F,G为出口,其中直行道为AB,CG,EF,且AB=CG=EF;弯道为以点O为圆心的一段弧,且BC,CD,DE所对的圆心角均为90∘.甲、乙两车由A口同时驶入立交桥,均以10m/s的速度行驶,从不同出口驶出.其间两车到点O的距离y(m)与时间x(s)的对应关系如图2所示.结合题目信息,下列说法错误的是( )A.甲车在立交桥上共行驶8sB.从F口出比从G口出多行驶40mC.甲车从F口出,乙车从G口出D.立交桥总长为150m10.物理实验课上,在室内温度20∘C时,小明把浸有少量酒精的棉花裹在温度计的玻璃泡上,随着酒精的迅速蒸发,温度计的读数T(∘C)与时间t(min)之间的函数关系图象大致是( )A.B.C.D.二、填空题11.如图,长方形AOBC在直角坐标系中,点A在y轴上,点B在x轴上,对角线AB所在直x+4.对角线AB的垂直平分线MN交x轴于点M,则点M的线的函数关系式为:y=−12坐标是.12.一次函数y=−2x+1与x轴交点坐标为;与y轴的交点坐标为.x图象上的一点,且到原点的距离是13,过点A作AB⊥x轴于13.已知A是正比例函数y=125点B,BC⊥OA于点C.若∣OB∣=5,则点B到直线AO的距离是.14.一天学生小明早上从家去学校,已知小明家离学校路程为2280米(小明每次走的路程),小明从家匀速步行了10.5分钟后,爸爸发现小明的一科作业忘带,爸爸立刻拿起小明忘带的作业匀速跑步追赶小明,追上小明后爸爸立即将作业交给小明,小明继续以原速向学校行走(假定爸爸将作业交给小明的时间忽略不计),爸爸将作业带给小明后,原地接了2分钟的电话后,立即以更快的速度匀速返回家中.小明和爸爸两人相距的路程y(米)与小明出发的时间x(分钟)之间的关系如图所示,则爸爸到达家时,小明与学校相距的路程是米.15.如图,直线l1⊥x轴于点(1,0),直线l2⊥x轴于点(2,0),直线l3⊥x轴于点(3,0),⋯,直线l n⊥x轴于点(n,0)(其中n为正整数).函数y=x的图象与直线l1,l2,l3,⋯,l n分别交于点A1,A2,A3,⋯,A n;函数y=2x的图象与直线l1,l2,l3,⋯,l n分别交于点B1,B2,B3,⋯,B n.如果△OA1B1的面积记作S1,四边形A1A2B2B1的面积记作S2,四边形A2A3B3B2的面积记作S3,⋯,四边形A n−1A n B n B n−1的面积记作S n,那么S2015=;S1+S2+S3+L+S n=.16.如图,平面直角坐标系中,A(4,4),B为y轴正半轴上一点,连接AB,在第一象限作AC=AB,∠BAC=90∘,过点C作直线CD⊥x轴于D,直线CD与直线y=x交于点E,且ED= 5EC,则直线BC解析式为.17.函数y=4中,自变量x的取值范围是.x三、解答题x+2与x轴相交于点A,与y轴相交于点18.点O为平面直角坐标系的坐标原点,直线y=−23B.(1) 求点A,点B的坐标.(2) 若∠BAO=∠AOC,求直线OC的函数表达式.(3) 点D是直线x=2上的一点,把线段BD绕点D旋转90∘,点B的对应点为点E.若点E恰好落在直线AB上,则称这样的点D为“好点”,求出所有“好点”D的坐标.19.琳琳通过新闻了解到,近来意大利“新冠肺炎”疫情愈发严重,她决定给意大利的网友Carlo邮寄一批防疫用品.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后走回家.琳琳离家的距离y(km)与时间x(min)之间的关系如图所示,请根据图象解决下列问题:(1) 琳琳家离药店的距离为km.(2) 琳琳邮寄物品用了min.(3) 琳琳两段步行的速度分别是多少?(4) 图中点P的意义是.20.为加强公民的节水意识,合理利用水资源.某市对居民用水实行阶梯水价,居民家庭每月用水量划分为三个阶梯,一、二、三级阶梯用水的单价之比等于1:1.5:2.下图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系.其中线段AB表示第二级阶梯时y与x 之间的函数关系.(1) 写出点B的实际意义.(2) 求线段AB所在直线的表达式.(3) 某户5月份按照阶梯水价应缴水费102元,其相应用水量为多少m3?21.已知一次函数y=■图象过点A(2,4),B(0,3),题目中的矩形部分是一段因墨水污染而无法辨认的文字.(1) 根据信息,求题中的一次函数的解析式;(2) 根据关系式画出这个函数图象.22.在同一直线上有甲乙两地,小明,小红同学分别从甲乙两地同时出发,相向而行,当他们相遇后小明立即以原速返回,且他先到达甲地,小红继续前行到甲地.在整个行进过程中,他们之间的距离y(m)与行进的时间x(min)之间的函数关系如图所示,请结合图象信息解答下列问题.(1) a=,小明速度为m/min,小红速度为m/min.(2) 求小明与小红从第一次相遇到小明到达甲地时,y与x之间的函数表达式.(3) 他们第一次相遇后再过多长时间相距200 m.23.如图,直线y1=x+2与x,y轴分别交于点A,B,直线y2=−2x+m与x,y轴分别交于点C,D,两直线交于点E(1,n).(1) 求m,n的值;(2) 求四边形BOCE的面积;(3) 当y1>y2时,根据图象,直接写出x的取值范围.24.已知直线y=kx−3经过M(−2,1),求此直线与x轴,y轴的交点坐标.25.如图,在数轴上有两个长方形ABCD和EFGH,这两个长方形的宽都是2个单位长度,长方形ABCD的长AD是4个单位长度,长方形EFGH的长EH是8个单位长度,点E在数轴上表示的数是5,且E,D两点之间的距离为12.(1) 填空:点H在数轴上表示的数是,点A在数轴上表示的数是.EH,M以每秒4个单位的速度向(2) 若线段AD的中点为M,线段EH上一点N,EN=14右匀速运动,N以每秒3个单位的速度向左运动,设运动时间为x秒;当x=秒时,原点O恰为线段MN的三等分点.(3) 若长方形ABCD以每秒2个单位的速度向右匀速运动,长方形EFGH固定不动,设长方形ABCD运动的时间为t(t>0)秒,两个长方形重叠部分的面积为S,求S与t的关系式.答案一、选择题1. 【答案】D【解析】由题意可知:当P在AD上时,这时构不成三角形,此时y=0,(x−4)×4=当P在DC上时,△ADP的面积在增大,P与C重合时最大为8,此时y=12 2x−8;当P在CB上时,△ADP的面积不变等于8,此时y=8;×4×(16−x)=32−2x.当P在BA上时,△ADP的面积在减小,此时y=12【知识点】一次函数的解析式2. 【答案】C【知识点】一次函数的概念3. 【答案】A【解析】∵直线y=3x+b中k=3>0,∴此直线必然经过一三象限.∵B(2,1),C(1,3),∴当经过点B时,6+b=1,解得b=−5;当经过点C时,3+b=3,解得b=0,∴−5≤b≤0.【知识点】一次函数的应用4. 【答案】D【解析】由图象可得,小明家和学校的距离为1200米,故①正确;小华乘坐公共汽车的速度是1200÷(13−8)=240米/分,故②正确;480÷240=2(分),8+2=10(分),则小华在7:50与小明相遇,故③正确;小华的出发时间不变,当小华由乘公共汽车变为跑步,且跑步的速度是100米/分时,小华从家到学校所用时间为1200÷100=12(分),则小华到校时间为8:00,易知小明到校时间为8:00,故④正确.【知识点】用函数图象表示实际问题中的函数关系5. 【答案】C【解析】∵式子√k−1+(k−1)0有意义,∴k−1>0,解得k>1,∴1−k<0,k−1>0,∴一次函数y=(1−k)x+k−1的图象过一、二、四象限.【知识点】二次根式有意义的条件、k,b对一次函数图象及性质的影响6. 【答案】C【解析】当x=32时,与其对应的函数值y<0,结合题意可知a>0,当x=0时,c=3,当x=3时,9a+3b+c=3,∴3a+b=0,∴b=−3a,∴b<0,∴abc<0,①正确;ax2+(b−1)x+c=0可以化为ax2+(−3a−1)x+3=0,将x=3代入方程可得9a+3(−3a−1)+3=0,∴3是关于x的方程ax2+(b−1)x+c=0的一个根,②正确;抛物线的解析式为y=ax2−3ax+3,n=a+3a+3=4a+3,m=a−3a+3=−2a+3,m+n=2a+6,∵a>0,∴m+n>6,当x=32时,y=94a−92a+3=−94a+3,∵当x=32时,与其对应的函数值y<0,∴−94a+3<0,∴a>43,∴m+n>263.③错误;故选:C.【知识点】二次函数与不等式、二次函数图象与系数的关系7. 【答案】C【知识点】k,b对一次函数图象及性质的影响8. 【答案】B【解析】k=2>0,y随x的增大而增大,因此选项A不符合题意,当b=4时,函数y=2x−4与x轴、y轴的交点分别为(2,0),(0,−4),因此图象与坐标轴围成的面积是2×4÷2=4,故选项B符合题意,k=2>0,当b>0时,图象过一、三、四象限,当b<0时,图象过一、二、三象限,因此选项C不符合题意,直线y=3−2x过一、二、四象限,与y=2x−b相交可能在一、二、四象限,因此选项D不符合题意.【知识点】k,b对一次函数图象及性质的影响9. 【答案】C【知识点】用函数图象表示实际问题中的函数关系10. 【答案】C【知识点】用函数图象表示实际问题中的函数关系二、填空题11. 【答案】(3,0)【知识点】一次函数的解析式,0);(0,1)12. 【答案】(12【知识点】一次函数与一元一次方程的关系、截距13. 【答案】6013【知识点】正比例函数的图象14. 【答案】270【解析】由题意知,图形的纵坐标表示为两人相距的路程,横坐标表示为小明的出发时间,从0∼10.5分钟时,小明自己走,爸爸还没有出发,∴小明的速度v1=630÷10.5=60米/分钟,从10.5∼21分钟时,爸爸开始从家出发,并在时间t=21分钟时追上小明,∴此时小明的路程为:60×21=1260米,∴爸爸的速度为v2=1260÷(21−10.5)=120米/分钟,设爸爸返回时的速度为v,根据题意得,4v+60×6=920,∴v=140米/分钟,∴等爸爸送完作业返回家时所用时间为21×60÷140=9分钟,∴等爸爸到家小明总用时:21+9+2=32,∴此时小明与学校相距的距离为:2280−32×60=360米.【知识点】用函数图象表示实际问题中的函数关系15. 【答案】2014.5;n22【知识点】一次函数的解析式16. 【答案】y=−15x+10【解析】过A作AM⊥y轴,交y轴于M,交CD于N,则∠BMA=∠ANC=90∘.∵∠BAC=90∘,∴∠BAM+∠CAN=90∘,∠BAM+∠ABM=90∘,∴∠ABM=∠CAN,∵A(4,4),∴OM=DN=4,AM=4,在△ABM和△CAN中,{∠ABM=∠CAN,∠AMB=∠ANC, AB=AC,∴△ABM≌△CAN(AAS),∴AN=BM,CN=AM=4,∵ED=5EC,∴设EC=a,ED=5a,∵A(4,4),∴点A在直线y=x上,∵CN=4a−4,则4a−4=4,∴a=2,即CD=8,ED=10.∵点E在直线y=x上,∴E(10,10),∴MN=10,C(10,8),∴AN=BM=10−4=6,∴B(0,10),设直线BC的解析式是y=kx+10,把C(10,8)代入得:k=−15,即直线BC的解析式是y=−15x+10.【知识点】性质与判定综合(D)、一次函数的解析式17. 【答案】x≠0【知识点】函数自变量的取值范围三、解答题18. 【答案】(1) 当x=0时,y=2,∴点B的坐标为(0,2);当y=0时,x=3,∴点A的坐标为(3,0).(2) 当OC在二、四象限时,OC∥AB,y=−23x;当OC在一、三象限时,OC经过点(3,2),y=23x.(3) 设点D的坐标为(2,m),则E的坐标为(2+2−m,m+2)或(2−2+m,m−2),∴可得:−23(4−m)+2=m+2或−23m+2=m−2,解得:m=8或m=125,∴E的坐标为(2,−8)或(2,125).【知识点】正比例函数的解析式、一次函数与一元一次方程的关系、一次函数图像上点的坐标特征19. 【答案】(1) 2.5(2) 20(3) 从药店步行到邮局的路程为1km,时间为15min,所以速度为115km/min;从邮局步行回家的路程为1.5km,时间为25min,所以速度为 1.525=350(km/min).(4) 离家45min时,琳琳到达邮局,此时她离家的距离为1.5km.【解析】(1) 由图象可知,琳琳家离药店的距离为2.5km.(2) 由图象可知,琳琳邮寄物品用了65−45=20(min).【知识点】用函数图象表示实际问题中的函数关系20. 【答案】(1) 图中B点的实际意义表示当用水25m3时,所交水费为90元.(2) 设第一阶梯用水的单价为p元/m3,则第二阶梯用水的单价为1.5p元/m3,设 A (a,45).根据图示可列方程 {a ⋅p =45,a ⋅p +1.5p (25−a )=90,解之得 {p =3,a =15.则解得 A 点坐标为 (15,45).设线段 AB 所在直线的表达式为 y =kx +b , 则 {45=15k +b,90=25k +b,解得 {k =92,b =−452.∴ 线段 AB 所在直线的表达式为 y =92x −452.(3) 设该户 5 月份用水量为 x m 3(x >25).由上一问知第二阶梯用水的单价为 4.5 元/m 3,第三阶梯用水的单价为 6 元/m 3, 则根据题意得90+6(x −25)=102,解得x =27.答:该用户 5 月份用水量为 27 m 3. 【知识点】一次函数的应用、一次函数与一元一次方程的关系21. 【答案】(1) y =12x +3.(2) 略【知识点】画一次函数图象、一次函数的解析式22. 【答案】(1) 20;60;40(2) 当 x =40 时,y =2000−40×40=400, ∴ 点 C 的坐标为 (40,400),设线段 BC 的函数表达式为 y =k 1x +b 1, 把 B (20,0),C (40,400) 代入,得 {0=20k 1+b 1,400=40k 1+b 1, 解得:{k 1=−40,b 1=−400,∴ 小明与小红从第一次相遇到小明到达甲地时,y 与 x 之间的函数表达式为:y =20x −400(20≤x ≤40).(3) 设线段 CD 的函数表达式为 y =k 2x +b 2, 把 C (40,400),D (50,0) 代入,得 {400=40k 2+b 2,0=50k 2+b 2, 解得:{k 2=−40,b 2=2000,∴线段CD的函数表达式为:y=−40x+2000(40<x≤50),把y=200代入y=20x−400得:200=20x−400,解得:x=30,30−20=10(min),把y=200代入y=−40x+2000得:200=−40x+2000,解得:x=45,45−20=25(min).答:他们第一次相遇后再过10min或25min后相距200 m.【解析】(1) 小红速度为:2000÷50=40(m/min),由图象可知:小明从甲地出发与小红相遇后再返回甲地共用了40min,∴a=40÷2=20(min),∴小明的速度为:(2000−40×20)÷20=60(m/min).【知识点】一次函数的应用、用函数图象表示实际问题中的函数关系23. 【答案】(1) 把E(1,n)代入y1=x+2中得:n=1+2=3,∴E(1,3),把E(1,3)代入y2=−2x+m中得:3=−2×1+m,解得:m=5,∴y2=−2x+5.(2) 在y1=x+2中,令x=0,则y=2,∴B(0,2),∴OB=2.令y=0,则x=−2,∴A(−2,0),∴OA=2.在y2=−2x+5中,令y=0,则x=52,∴C(52,0),∴OC=52.∴S四边形BOCE=S△AEC−S△ABO=12AC⋅∣y E∣−12AO⋅BO=12×92×3−12×2×2=194.(3) x>1【知识点】一次函数与一次不等式的关系、一次函数的解析式24. 【答案】∵y=kx−3过点(−2,1),∴1=−2k−3.∴k=−2.∴y=−2x−3.∵令y=0时,x=−32,∴直线与x轴交点坐标为(−32,0).∵令x=0时,y=−3,∴直线与y轴交点坐标为(0,−3).【知识点】一次函数与一元一次方程的关系25. 【答案】(1) 13;−11(2) 2.2或2.5(3) 由题意知,当0<t<6时,长方形ABCD和EFGH无重叠时,S=0当6≤t≤12时,两个长方形重叠部分的面积为S={2(t−6)×2,6≤t<82×4,8>t≤102(12−t)×2,10<t≤12,即S={4t−24,6≤t<88,8≤t≤10 48−4t,10<t≤12.当t>12时,长方形ABCD和EFGH无重叠,S=0.【解析】(1) ∵长方形EFGH的长EH是8个单位长度,且点E在数轴上表示,∴点H在数轴上表示的数是5+8=13.∵E,D两点之间的距离为12,点D表示的数为5−12=−7,∵长方形ABCD的长AD是4个单位长,∴点A在数轴上表示的数是−7−4=−11.(2) 由题意知,线段AD的中点为M,则M表示的数为−9,线段EH上一点N且EN=14EH,则N表示的数为7;由M以每秒4个单位的速度向右匀速运动,N以每秒3个单位的速度向左运动,则经过x秒后,M点表示的数为4x−9,N点表示的数为7−3x;①当OM=2ON时,则有∣4x−9∣=2∣7−3x∣,解得:x=2.3(经验证,不符合题意,舍去)或x=2.5②当ON=2OM时,则有∣7−3x∣=2∣4x−9∣,解得:x=2.2或x=5(经验证,不符合题意,舍去)综上所述,当x=2.2或x=2.5时,原点O恰为线段MN的三等分点.【知识点】线段的和差、解析式法、绝对值的几何意义、线段中点的概念及计算。
