一次函数章末巩固复习专题
一次函数全章复习与巩固(基础)巩固练习_20210524133742

A..C.D.
二
9. 汇通公司销售人员的个人月收入y(元)与其每月的销售量x(千件)成一次函数关系,其图象如图所示,则此销售人员的月销售量为3500件时的月收入是元.
10.观察下列各正方形图案,每条边上有n(n>2)个圆点,每个图案中圆点的总数是 S.
按 此 规 律 推 断 出 S 与n的 关 系 式 为.
16.(2016•如皋市一模)如图,直线y=3x和y=kx+2相交于点P(a,3),则不等式3x≥kx+2
的解集为.
三
17.如图所示,表示一艘轮船和一艘快艇沿相同路线从甲港出发到乙港行驶过程中路程和时间变化的图象,根据图象回答问题.
(1)分析图象,求出表示轮船和快艇行驶过程的函数解析式;
(2)指出轮船和快艇的行驶速度;
A.y0.05xB.y5xC.y100xD.y0.05x100
3. 下列函数中,自变量的取值范围选取错误的是( ) A.y2x2中,x取全体实数B.y
1
x1
中,x取x≠-1 的实数
C.y
中,x取x≥2的实数D.y
1中,x取x≥-3的实数
4. 若直线 经过点A(2,0)、B(0,2),则 、 的值是 ()
(2)若函数值y的范围是-1≤y≤2,求自变量x的范围.
20.某影碟出租店开设两种租碟方式:一种是零星租碟,每张收费1元;另一种是会员卡租碟,办卡费每月12元,租碟费每张0.4元.小彬经常来该店租碟,若每月租碟数量为张.
(1)写出零星租碟方式应付金额 (元)与租碟数量(张)之间的函数关系式;
(2)写出会员卡租碟方式应付金额 (元 )与租碟数量(张)之间的函数关系式;
7.(2016•商河县二模)如图,经过点B(﹣2,0)的直线y=kx+b与直线y=4x+2相交于点A(﹣1,
人教八年级数学下册-第十九章一次函数章末复习

得:
92k+b=40,
解得:
k= 1 ,
4
100k+b=42,
b=17,
∴y与x之间的函数关系式为y= 1 x+17;
4
号/型 … 170/84 170/88 175/92 175/96 180/100 …
码数 … 38
39
40
41
42
…
(2)若某人的净胸围为108厘米,则该人应买
多大码数的衬衫?
1.一次函数y=(m-2)x+3m-3的图象经过第 一、二、四象限, 求m得取值范围.
∵一次函数y=(m-2)x+3m-3的图象经过第一、 二、四象限,
m-2<0, ∴ 3m-3>0, 解得: 1 <m< 2, ∴m的取值范围是1 <m< 2.
2.直线y=-2x+a经过(3, y1)和(-2, y2)两点, 则y1和y2的大小关系是( )
∴点B的坐标为(0,±2),
设直线解析式为y=kx±2,
∵直线经过点(-4,0),
B.
∴0=-4k±2,解得k=±
1 2
,
.
2
A(-4,0) O
x
∴直线的解析式为y=
1 2
x+2或y=-
1 2
x-2.
2.把直线y=2x-1向上平移2各单位,所得
直线的解析式是:
.
分析: 由“上加下减”的原则可知,直线 y=2x-1向上平移2个单位,所得直线解析 式为y=2x-1+2,即y=2x+1.
y=kx+b
b>0 k>0 b=0
b<0 b>0 k<0 b=0 b<0
图象经过的象限
第六章一次函数章末复习

所以500-185=315(m),
所以男子组追上女子组时,两组队员离终点的路程为315 m.
一次函数的应用
12.(2023济南)学校提倡“低碳环保,绿色出行”,小明和小亮分别选择
步行和骑自行车上学,两人各自从家同时同向出发,沿同一条路匀速前
进.如图所示,l1和l2 分别表示两人到小亮家的距离s(km)和时间t(h)的
A.图象经过第一、三、四象限
B.图象与y轴交于点(0,1)
C.函数值y随自变量x的增大而减小
D.当x>-1时,y<0
6.(2023陕西)在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,
a<0)的图象可能是( D )
A
B
C
D
一次函数的表达式
7.(2023娄底)将直线y=2x+1向右平移2个单位后所得直线对应的函
3.(2023 临沂)对于某个一次函数 y=kx+b(k≠0),根据两位同学的对话
得出的结论,错误的是(
A.k>0
B.kb<0
C.k+b>0
D.k=- b
C )
4.(2023兰州)一次函数y=kx-1的函数值y随x的增大而减小,当x=2时
,y的值可以是( D
A.2
B.1
C.-1
)
D.-2
5.(2023益阳)关于一次函数y=x+1,下列说法正确的是( B )
解:(1)y=1 000(x-50)=1 000x-50 000.
(2)当售价定为60元/件时,该玩具销售火爆,该店继续购进一批该种航
天模型玩具,并从中拿出这两批玩具销售利润的20%用于支持某航模兴
第12章一次函数期末复习一次函数的交点问题PPT课件(沪科版)

则方程组
x-y-3=0 2x-y+2=0
的解是_x_=__-__5 y=-8
.
7.直线y=x+2和直线y=x-3的位置关系是 平行 , 由此可知方程组 x-y=-2解的情况为_无__解___.
x-y=3
8. 如图,在同一平面直角坐标系中,直线
l1:y=
1 4
x+
1 2
与直线l2:
y=kx+3的图象相交
6.把方程x+1=4y+
x 3
化为y=kx+b的情势,
正确的是( C ).
A.
1 3
1 4
B.
1 6
C.
1 6
1 4
D.
1 3
7.已知函数y=-x +m与y= mx-4的图象的交点
在x轴的负半轴上那么m的值为( D ).
A.±2
B.±4 C.2 D.-2
∵图象的交点在x轴上
∴ y=0 ∴ -x +m=0 ∴ x= m
( 2)两个一次函数的图象的交点
3.求一次函数的图象与坐标轴的交点的方法
(1)求一次函数的图象的与x轴交点坐标 设y=0, 变为求方程kx+b=0的解
(2)求一次函数的图象的与y轴交点坐标
设x=0, 变为求代数式kx+b的值
(3)一次函数y=kx+b的图象的与x轴交点
坐标为(
-
b k
,0
)
;
与y轴的交点坐标
C.( -1,-1) D.( -1,5)
12.如果直线y =kx+b平行于直线 y=5x-m, y= kx+b
则方程组 y= 5x- m 的解的情况是( B ).
A.有无数解
B.无解
C.一组解
D.两组解
填空题 1.已知关于x的方程ax-5=7的解为x=1,则一次
最新一次函数全章复习与巩固(提高)知识讲解资料

一次函数单元复习与巩固(提高)【学习目标】1. 了解常量、变量和函数的概念,了解函数的三种表示方法(列表法、解析式法和图像法)能利用图像数形结合地分析简单的函数关系2•理解正比例函数和一次函数的概念,会画它们的图像,能结合图像讨论这些函数的基本性质,能利用这些函数分析和解决简单实际问题3•通过讨论一次函数与方程(组)及不等式的关系,从运动变化的角度,用函数的观点加深对已经学习过的方程(组)及不等式等内容的再认识4.通过讨论选择最佳方案的问题,提高综合运用所学函数知识分析和解决实际问题的能力【知识网络】【要点梳理】要点一、函数的相关概念一般地,在一个变化过程中.如果有两个变量x与y ,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.y是x的函数,如果当x = a时y = b,那么b叫做当自变量为a时的函数值.函数的表示方法有三种:解析式法,列表法,图像法要点二、一次函数的相关概念一次函数的一般形式为y=kx・b,其中k、b是常数,k工0.特别地,当b = 0时,一次函数y=kx,b即y=kx (k丰0),是正比例函数.要点三、一次函数的图像及性质1、函数的图像如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图像.要点诠释:直线kx b可以看作由直线y二kx平移| b |个单位长度而得到(当b > 0时,向上平移;当b v0时,向下平移).说明通过平移,函数y二kx,b与函数y二kx的图像之间可以相互转化.2、一次函数性质及图像特征掌握一次函数的图像及性质(对比正比例函数的图像和性质)理解k、b对一次函数y =kx ■ b的图像和性质的影响:(1)k决定直线y =kx b从左向右的趋势(及倾斜角 :-的大小一一倾斜程度),b决定它与y轴交点的位置,k、b一起决定直线y =kx b经过的象限.(2)两条直线11: y =k-^x b1和l2: y = k2x b2的位置关系可由其系数确定:k i = k2 二l i 与12相交;K =k2,且d =b2= 11与12平行;K *2,且b i =b2 = l i 与12重合;(3)直线与一次函数图像的联系与区别一次函数的图像是一条直线;特殊的直线x =a、直线y二b不是一次函数的图像类型一、函数的概念1、下列说法正确的是:()A .变量x, y满足2x y 3,则y是x的函数;B .变量x, y满足| y x,则y是x的函数;2C .变量x, y满足y = x,则y是x的函数;D .变量x, y满足y2一x2=1,则y是x的函数.【答案】A;【解析】B C D三个选项,对于一个确定的x的值,都有两个y值和它对应,不满足单值对应的条件,所以不是函数•【总结升华】理解函数的概念,关键是函数与自变量之间是单值对应关系,自变量的值确定后,函数值是唯一确定的• 类型二、一次函数的解析式C>2、某出版社出版一种适合中学生阅读的科普读物,若该读物首次出版印刷的印数不少(1)经过对上表中数据的探究,发现这种读物的投入成本(元)是印数x (册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);(2)如果出版社投入成本48000元,那么能印该读物多少册?【思路点拨】待定系数法求函数解析式,根据两点得到两个二元一次方程,组成一个二元次方程组求出解即可•表中信息取两组就可以了【答案与解析】解:(1)设所求一次函数的解析式为y = kx • b ,f5000ft+Z)= 28500,贝叫8000i+i = 36000.解得 k = , b = 16000.2•••所求的函数关系式为 y = x +16000. 2(2)v 48000 = x + 16000.2• x = 12800.答:能印该读物12800册.【总结升华】此类问题主要是考查考生利用待定系数法来求出有关函数一般解析式中的未知 系数,从而确定该函数解析式的能力. 举一反三:该直线的函数解析式.【答案】■鮎4〜.根据方程①和②可以得出 任二2,為=—2,所以「I .所以所求一次函数解析式为 "「〕或r 二_ 类型三、一次函数的图像和性质3、若直线y 二kx • b ( k 工0)不经过第一象限,则 k 、b 的取值范围是()A . k > 0, b v 0B . k > 0, b w 0 c. k < 0, b < 0 D . k < 0, b < 0 【思路点拨】 根据一次函数的图像与系数的关系解答 .图像不经过第一象限,则 k < 0,此时 图像可能过原点,也可能经过二、三、四象限 【答案】D;【解析】当图像过原点时,k < 0, b = 0,当图像经过二、三、四象限时, k < 0且b < 0.【总结升华】图像不经过第一象限包括经过二、三、四象限和过原点两种情况 举一反三:【变式】已知直线“-二一:经过点,且与坐标轴所围成的三角形的面积为「,求4解:因为直线过点?卫,所以0二红+b ,①2又因为直线 '.-二一:与x 轴、yh }轴的交点坐标分别为卫 —,0, BQb )2511再根据:;,所以:丄■-25~A-I j9%整理得亍汕行②.、X【变式】一次函数y=kx-k-2与y 在同一坐标系内的图像可以为( )k【答案】D;提示:分为k V 0;0< k V2; k >2分别画出图像,只有D答案符合要求类型四、一次函数与方程(组)、不等式4、如图,直线y二kx • b经过A (-2,—1)和B (-3, 0)两点,则不等式组1x : kx b . 0的解集为_________________ .【答案】3:: x : -2 ;1【解析】从图像上看,y=kx,b的图像在x轴下方,且在y x上方的图像为画红线的2部分,而这部分的图像自变量x的范围在-3 ::: x ::: -2.【总结升华】也可以先求出y =kx • b的解析式,然后解不等式得出结果举一反三:A. B. C. D.【变式】如图所示,直线y=kx经过点A(—1, —2)和点B( —2, 0),直线y=2x过点A则不等式2 X V kx b V 0的解集为()A. x V- 2 B 2 V x V- 1 C 2V x V 0 D 1 V x V 0【答案】B;提示:由图像可知A(- 1,- 2)是直线y = kx • b与直线y =2x的交点,当x V-1 时2x V kx b,当x >-2 时,kx b V o,所以—2V x V- 1 是不等式2x Vkx b V o的解集类型五、一次函数的应用O b、某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药2h后血液中的含药量最高,达每升6mg,接着逐步衰减,10h后血液中的含药量为每升3 mg,每升血液中的含药量ymg随时间x h的变化情况如图所(1)分别求出x <2和x > 2时,y与x之间的函数关系式;(2)如果每升血液中的含药量为4 mg或4 mg以上时,治疗疾病是有效的,那么这个有效时间是多长?【思路点拨】(1)根据题意由待定系数法求函数的解析式•(2)令y >4,分别求出x的取值范围,便可得出这个药的有效时间.【答案与解析】解:(1)由图知,x < 2时是正比例函数,x > 2时是一次函数.设x < 2 时,y 二kx,把(2,6)代入y = kx,解得k = 3,当0< x w 2 时,y = 3x .设x >2 时,y = kx b,把(2,6),(10,3)代入y =kx b 中,(1)求直线12的解析式;P 是线段BC 上一动点,求使 ON PD 值最小的点P 的坐标.解:(1)由直线 y=X ,4 可得:A( — 4, 0) , B(0, 4)•/ 点A 和点C 关于y 轴对称,• C(4 , 0). 设直线BC 解析式为:y 二kx • b ,则I k "一 _如2k b = 6 …一 得,解得10k b = 3,即3 27 y x84327 当y = 0时,有0 x • •843 •••当 2< x W 18 时,y x —84由于y >4时在治疗疾病是有效的,x =18. 27 3x _44 223 27 ,解得 "x< -3x 勺_4 3 3 8 4 4 22即服药后一h 得到 h 为治病的有效时间,3 322 4 18这段时间为 6(h).3 3 3 分段函数中,自变量在不同的取值范围内函数的解析式也不相同,【总结升华】据自变量或函数的取值确定某段函数来解决问题. 类型六、一次函数综合因此注意根6、如图所示,直线h 与x 轴交于点A ,与y 轴交于点B ,直线12与直线h 关于y 轴对称,且与x 轴交于点C.已知直线11的解析式为y =x .(2)D 为OC 的中点,【答案与解析】【答案】解:⑴ 由直线 y - -X 可得:A(0 , 8) , B(8 , 0).【总结升华】 —b 解得k-1 0 = 4k bb = 4直线BC 解析式为:y = _x ・4.作点D 关于BC 对称点D',连结PD , OD .PD 二 DP ,••• OP + P» PD' + OP••• 当 OP 、D'三点共线时 ON PD 最小.•/ OB = OC • / BCO= 45°/ D CO = 90 ° ,D (4,2),1x2 --x 48 x 二3 4 八3当点P 坐标为i 8,4时,丿ON PD 的值最小.(1)由直线l i 的解析式得到A 、B 点的坐标,进一步得到C 点的坐标,然后利用 B C 两点的坐标利用待定系数法求解析式. 的坐标. 举一反三:(2)利用轴对称性质求出使OP + PD 值最小的点P【变式】如图所示,已知直线y = -x 8交y 轴于点A,交x 轴于点B ,过B 作BD 丄AB 交y轴于D.(1)求直线BD 的解析式;⑵若点C 是x 轴负半轴上一点,过 C 作AC 的垂线与BD 交于点E .请判断线段AC 与 CE 的大小关系?并证明你的结论.OA = OB= 8,Z ABO= 45°.•/ BD 丄AB,/ DBO= 45°,△ ABD为等腰直角三角形..OD = OA= 8, D点坐标为(0,—8).设BD的解析式为y = kx b .过B(8 , 0), D(0,—8),解得k"]b - -8.BD的解析式为y = x 一8(2)AC = CE过点C作CM丄AB于M,作CN丄BD于点N. •/ BC为/ ABD的平分线,.CM = CN/ ACE= 90°,/ MCN=90/ ACM=/ ECN在厶ACM ffiA ECN中AMC "ENC =90°,ICM =CN,ACM "ECN△ ACNm ECN(ASA).AC = CE。
一次函数全章复习与巩固(提高)知识讲解
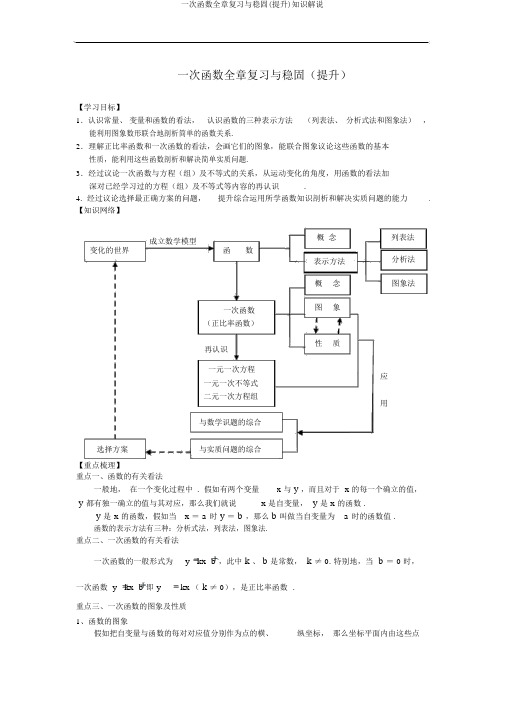
一次函数全章复习与稳固(提升)【学习目标】1.认识常量、变量和函数的看法,认识函数的三种表示方法(列表法、分析式法和图象法),能利用图象数形联合地剖析简单的函数关系.2.理解正比率函数和一次函数的看法,会画它们的图象,能联合图象议论这些函数的基本性质,能利用这些函数剖析和解决简单实质问题.3.经过议论一次函数与方程(组)及不等式的关系,从运动变化的角度,用函数的看法加深对已经学习过的方程(组)及不等式等内容的再认识.4. 经过议论选择最正确方案的问题,提升综合运用所学函数知识剖析和解决实质问题的能力.【知识网络】概念列表法成立数学模型变化的世界函数分析法表示方法概念图象法一次函数图象(正比率函数)性质再认识一元一次方程应一元一次不等式二元一次方程组用与数学识题的综合选择方案与实质问题的综合【重点梳理】重点一、函数的有关看法x 与y,而且对于 x 的每一个确立的值,一般地,在一个变化过程中 . 假如有两个变量y 都有独一确立的值与其对应,那么我们就说x 是自变量,y是 x 的函数.y 是x的函数,假如当x = a 时y=b,那么b叫做当自变量为 a 时的函数值.函数的表示方法有三种:分析式法,列表法,图象法.重点二、一次函数的有关看法一次函数的一般形式为y kx b ,此中k、b是常数,k≠0.特别地,当b=0时,一次函数 y kx b 即 y kx (k≠0),是正比率函数.重点三、一次函数的图象及性质1、函数的图象假如把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点构成的图形,就是这个函数的图象.重点解说:直线y kx b 能够看作由直线y kx 平移|b |个单位长度而获得(当 b >0时,向上平移;当 b <0时,向下平移). 说明经过平移,函数y kx b 与函数y kx的图象之间能够互相转变 .2、一次函数性质及图象特点掌握一次函数的图象及性质(对照正比率函数的图象和性质)重点解说:理解k 、 b 对一次函数y kx b的图象和性质的影响:( 1)k决定直线y kx b 从左向右的趋向(及倾斜角的大小——倾斜程度), b 决定它与y 轴交点的地点,k 、 b 一同决定直线y kx b 经过的象限.( 2)两条直线l1:y k1x b1和 l2:y k2 x b2的地点关系可由其系数确立:k1k2l1与 l 2订交;k1k2,且b1b2l1与 l 2平行;k1k2,且 b1 b2l1与 l 2重合;( 3)直线与一次函数图象的联系与差别一次函数的图象是一条直线;特别的直线x a 、直线 y b 不是一次函数的图象.重点四、用函数的看法看方程、方程组、不等式方程(组)、不等式问题函数问题从“数”的角度看从“形”的角度看求对于x、y的一元一次x 为何值时,函数y ax b的确定直线y ax b 与 x 轴(即直线 y =0)交点的横坐方程 ax b =0(a≠0)值为 0?的解标求对于 x 、y的二元一次x 为何值时,函数y a1x b1与确立直线y a1 x b1与直线方程组y a1 x b1,的解.函数 y a2 x b2的值相等?y a2 x b2的交点的坐标y a2 x b2.求对于x 的一元一次不等x 为何值时,函数y ax b的确定直线 y ax b 在 x 轴式 ax b >0(a≠0)的(即直线y= 0)上方部分的解集值大于 0?全部点的横坐标的范围【典型例题】种类一、函数的看法1、(2014 春?桃城区校级月考)在国内投寄平信对付邮资以下表:信函质量x(克)0<x≤20 0<x≤40 0<x≤60邮资 y(元)0.80 1.60 2.40(1) y 是 x 的函数吗?为何?(2)分别求当 x=5, 10, 30,50 时的函数值.【思路点拨】( 1)依据函数定义:设在一个变化过程中有两个变量确立的值, y 都有独一的值与其对应,那么就说 y 是 x 的函数,数;( 2)依据表格能够直接获得答案.【答案与分析】x 与 y,对于x 是自变量可得x 的每一个y 是 x 的函解:( 1) y 是 x 的函数,当x 取定一个值时,y 都有独一确立的值与其对应;( 2)当 x=5 时, y=0.80 ;当 x=10 时, y=0.80 ;当 x=30 时, y=1.60 ;当 x=50 时, y=2.40 .【总结升华】本题主要考察了函数定义,重点是掌握函数的定义.种类二、一次函数的分析式2、某第一版社第一版一种合适中学生阅读的科普读物,若该读物初次第一版印刷的印数许多于 5000 册时,投入的成本与印数间的相应数据以下:印数 x (册)5000800010000 15000成本y (元)28500360004100053500(1)经过对上表中数据的研究,发现这类读物的投入成本y (元)是印数函数,求这个一次函数的分析式(不要求写出x 的取值范围);(2)假如第一版社投入成本48000 元,那么能印该读物多少册?【思路点拨】待定系数法求函数分析式,依据两点获得两个二元一次方程,次方程组求出解即可.表中信息取两组就能够了.【答案与分析】x (册)的一次构成一个二元一解:( 1)设所求一次函数的分析式为y kx b ,则解得k =, b =16000.∴所求的函数关系式为y =x +16000.( 2)∵ 48000=x +16000.∴x =12800.答:能印该读物 12800 册.【总结升华】此类问题主假如考察考生利用待定系数法来求出有关函数一般分析式中的未知系数,进而确立该函数分析式的能力.贯通融会:【变式】已知直线经过点,且与坐标轴所围成的三角形的面积为,求该直线的函数分析式.【答案】解:因为直线过点,所以,①又因为直线与 x 轴、y轴的交点坐标分别为,再依据,所以整理得②.依据方程①和②能够得出,,所以,.所以所求一次函数分析式为或.种类三、一次函数的图象和性质3、若直线y kx b (k≠0)不经过第一象限,则k、b的取值范围是()A.k >0, b <0B. k> 0, b≤ 0C. k< 0, b< 0D.k <0, b ≤0【思路点拨】依据一次函数的图象与系数的关系解答. 图象不经过第一象限,则k< 0,此时图象可能过原点,也可能经过二、三、四象限.【答案】 D;【分析】当图象过原点时,k <0, b =0,当图象经过二、三、四象限时,k <0且 b <0.【总结升华】图象不经过第一象限包含经过二、三、四象限和过原点两种状况.贯通融会:【变式】一次函数 y kx k 2 与 y x)在同一坐标系内的图象能够为(kA. B. C. D.【答案】 D;提示:分为k <0;0< k <2; k >2分别画出图象,只有 D 答案切合要求.种类四、一次函数与方程(组)、不等式4、如图,直线y kx b 经过A(- 2,- 1)和B(- 3, 0)两点,则不等式组1 xkx b0的解集为.2【答案】 3 x 2;【分析】从图象上看,y kx b 的图象在 x 轴下方,且在y 1x 上方的图象为画红线的x 的范围在 3 x22部分,而这部分的图象自变量.【总结升华】也能够先求出y kx b 的分析式,而后解不等式得出结果.贯通融会:【变式】( 2015 春?东城区期末)已知直线y=kx+b 经过点 A( 5, 0), B( 1,4).(1)求直线 AB的分析式;(2)若直线 y=2x ﹣4 与直线 AB订交于点 C,求点 C的坐标;(3)依据图象,写出对于 x 的不等式 2x﹣ 4> kx+b 的解集.【答案】解:( 1)∵直线y=kx+b 经过点 A( 5, 0), B( 1, 4),∴,解得,∴直线 AB的分析式为:y=﹣x+5;(2)∵若直线y=2x﹣ 4 与直线 AB 订交于点 C,∴.解得,∴点 C( 3, 2);(3)依据图象可得 x>3.种类五、一次函数的应用5、某医药研究所开发了一种新药,在试验药效时发现,假如成人按规定剂量服用,那么服药 2 h后血液中的含药量最高,达每升 6 mg,接着逐渐衰减,10 h后血液中的含药量为每升 3 mg,每升血液中的含药量y mg 随时间x h 的变化状况如图所示.当作人按规定剂量服药后:(1) 分别求出 x ≤2 和 x ≥ 2 时, y 与 x 之间的函数关系式;(2) 假如每升血液中的含药量为4 mg 或 4 mg 以上时,治疗疾病是有效的,那么这个有效时间是多长 ?【思路点拨】 (1)依据题意由待定系数法求函数的分析式. (2)令 y ≥4,分别求出x 的取值范围,即可得出这个药的有效时间. 【答案与分析】解: (1) 由图知, x ≤2 时是正比率函数,x ≥ 2 时是一次函数.设 x ≤ 2 时,ykx ,把 (2 , 6) 代入ykx ,解得k = 3,∴当 0≤x ≤ 2 时,y3x .设 x ≥ 2 时,yk xb ,把 (2 , 6) , (10 , 3) 代入yk x b 中,2k b 6k38,即 y3 27得b,解得x.10k3b27 844当 y =0 时,有 03 x 27 , x 18 .8 4∴ 当 2≤ x ≤ 18 时, y3 x 27 .8 4(2)因为 y ≥ 4 时在治疗疾病是有效的,3x4,解得422 . ∴3 x 27 4x3384即服药后4h 获得22h 为治病的有效时间,33这段时间为224 18 6(h) .33 3【总结升华】 分段函数中, 自变量在不一样的取值范围内函数的分析式也不同样, 所以注意根据自变量或函数的取值确立某段函数来解决问题.种类六、一次函数综合6、以下图,直线l 1 与 x 轴交于点A ,与y 轴交于点B ,直线l 2 与直线l 1 对于 y 轴对称,且与x 轴交于点C .已知直线l 1 的分析式为yx 4 .(1) 求直线 l 2 的分析式;(2)D 为 OC 的中点, P 是线段 BC 上一动点,求使OP +PD 值最小的点 P 的坐标.【答案与分析】解: (1) 由直线 yx 4 可得: A( -4, 0) , B(0, 4)∵点 A 和点 C 对于 y 轴对称,∴ C(4,0) .设直线 BC 分析式为: y kx b ,则4 0 b k 10 4k b解得.b 4∴直线 BC 分析式为: y x 4.(2) 作点 D 对于 BC 对称点 D ′,连接 PD ′, OD ′.∴ PD DP ,∴ OP + PD =PD ′+ OP .∴当 O 、P 、 D ′三点共线时 OP + PD 最小.∵ OB = OC ,∴ ∠BCO =45°,∴∠ D CO =90°,∴ D (4,2) ,∴yOD1x .21 xx 8 由y得 324yx 4y3∴当点 P 坐标为8 , 4 时, OP + PD 的值最小.3 3【总结升华】 (1) 由直线 l 1 的分析式获得A 、B 点的坐标,进一步获得C 点的坐标,而后利用B 、C 两点的坐标利用待定系数法求分析式. (2) 利用轴对称性质求出使OP + PD 值最小的点 P的坐标.贯通融会:【变式】以下图,已知直线y x8 交y轴于点A,交 x 轴于点B,过B作BD⊥AB交y轴于 D.(1)求直线 BD的分析式;(2)若点 C 是x轴负半轴上一点,过 C 作 AC的垂线与 BD交于点 E.请判断线段 AC与CE的大小关系?并证明你的结论.【答案】解: (1) 由直线y x8 可得:A(0,8),B(8,0).∴OA = OB= 8,∠ ABO=45°.∵ BD ⊥AB,∴∠DBO= 45°,△ ABD为等腰直角三角形.∴OD = OA= 8, D 点坐标为 (0 ,- 8) .设 BD的分析式为y kx b .∵过 B(8 ,0) ,D(0,- 8)8k b 0k1∴,解得b .b88∴ BD 的分析式为y x8(2)AC = CE;过点 C 作 CM⊥ AB 于 M,作 CN⊥ BD于点 N.∵BC 为∠ABD的均分线,∴ CM= CN.∵∠ACE=90°,∠MCN=90°∴ ∠ACM=∠ ECN.在△ ACM和△ ECN中AMC ENC 90°,CM CN ,ACM ECN∴△ACM≌△ ECN(ASA).∴AC = CE.。
八年级数学上册第4章一次函数章末整合练新版北师大版

一次函数
章末整合练
CONTENTS
目
录
01
知识梳理
02
核心考点巩固
考点1 函数的概念
1. 下列曲线中不能表示 y 是 x 的函数的是(
A
B
1
2
3
C
4
5
6
7
C
)
D
8
9
10
11
12
13
14
15
16
2. 已知函数 y =(1-3 m ) x + - m2是正比例函数,那么 m
的取值是(
B
解得 x =8;小轮从甲地返回后到追上小辅时,50 x -100=
150( x -10),解得 x =14.
所以小轮出发7 min,8 min或14 min,与小辅相距100 m.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
所以∠ BOE =∠ BEO ,∠ COF =∠ CFO .
所以 BO = BE , CO = CF .
所以△ ABC 的周长= AB + BO + OC + AC = AB + BE
+ CF + AC = AE + AF .
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
因为△ AEF 的周长为8, EF = x ,△ ABC 的周长为 y ,
1
2
3
4
5
6
7
8
一次函数解析式的确定最新版

得 y=-x+7.
(2)依据题意,有 m2-3=1 且 m-1>0,解得 m=2,
∴这个函数的表达式为 y=-x+1.
(3)由题意知,y=kx+4
与坐标轴的交点为(0,4),
4 k
,
0
,
∴y=kx+4 与坐标轴所形成的三角形面积为
S=12×4×
4 k
=8,∴k=±1.
∴原直线的解析式为 y=±x+4.
【例 1】(1)a 为何值时,函数 y=(a-3)x2a-3+(a+5)为一次 函数,并求出表达式;
(2)已知一次函数 y= xm2-3+m-1 的图象经过第一、二、 四象限,求这个一次函数的表达式;
(3)已知直线 y=kx+4 与两坐标轴围成的三角形的面积为 8 ,求该直线的解析式.
解:(1)由定义知,2a-3=1,得 a=2,代入原式,
章末巩固复习考题
专题一 一次函数解析式的确定 在一次函数 y=kx+b(k、b 为常数且 k≠0)中,有两个待定 系数 k 和 b,因此需要两个条件.当 b=0,即为正比例函数时, 有一个待定系数 k,故正比例函数只需要一个条件.常见的求表 达式的题型有如下几种形式:①利用定义求表达式;②已知两 边对应值或图象上两点的坐标求表达式;③利用一次函数性质 确定表达式.
随堂小练 1.已知函数 y=2x+m-1,当 m=____1____时,y 是 x 的 正比例函数;当 m=____2____时,y=xm-1+2 是 y 关于 x 的一次 函数.
2.一次函数 y=kx+b 的图象过点 P(0,3),且与坐标轴围成 的三角形的面积为 3,求其解析式.
解:∵y=kx+b 的图象过点 P(0,3),∴b=3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.一次函数 y=(4m-8)x+5 中,y 随 x 的增大而减小,则 m<2 m 的取值范围是________. 5.星期天,小明从家里出发到图书馆去看书,再回到家. 他离家的距离 y(千米)与时间 t(分钟)的关系如图 2.根据图象回答 下列问题: 3 (1) 小明家离图书馆的距离是_________ 千米; 1 (2)小明在图书馆看书的时间为________ 小时; 图2
15 (3)小明去图书馆时的速度是________千米/时.
6.(2010 年广东)某学校组织 340 名师生进行长途考察活动, 带有行李 170 件,计划租用甲、乙两种型号的汽车共有 10 辆. 经了解,甲车每辆最多能载 40 人和 16 件行李,乙车每辆最多 能载 30 人和 20 件行李. (1)请你帮助学校设计所有可行的租车方案; (2)如果甲车的租金为每辆 2 000 元,乙车的租金为每辆 1 800 元,问哪种可行方案使租车费用最省?
2.下列图象中,以方程 y-x-1=0 的解为坐标的点组成 的图象是( A )
3.如图 1(1),在矩形 ABCD 中,动点 P 从点 B 出发,沿 BC、CD、DA 运动至点 A 停止,设点 P 运动的路程为x,△ABP 的面积为 y,如果 y 关于 x 的函数图象如图 1(2),则△ABC 的面 积是( A )
一次函数章末巩固复习专题
专题一
一次函数的图象与性质
例 1:一次函数 y=2x-1 的图象大致是( B )
思路导引:根据一次函数的图象的性质,结合题意,找出图象. 由题意知,k=2>0,b=-1<0,所以图象经过一、三、四象限, 且 y 随 x 的增大而增大. 【规律总结】对于一次函数 y=kx+b(k≠0)的图象,k 的正负 决定直线从左向右呈上升或下降趋势,b 的值决定直线与 y 轴的交 点位置.
图1 A.10 B.16 C.18 D.20
点拨:P 点由 B 向 C 运动时,△ABP 的面积逐渐增大, P 由 C 向 D 运动时,△ABP 的面积不变,P 点由 D 向 A 运动时, △ABP 的面积逐渐变小.由函数图象知当 0≤x≤4 时,y 逐渐增 大;4≤x≤9 时,y 不变;9≤x 时,y 逐增变小.故知 BC=4,
例 3:为美化深圳市景,园林部门决定利用现有的 3 490 盆甲 种花卉和 2 950 盆乙种花卉搭配 A、B 两种园艺造型共 50 个摆放在 迎宾大道两侧,已知搭配一个 A 种造型需甲种花卉 80 盆,乙种花 卉 40 盆,搭配一个 B 种造型需甲种花卉 50 盆,乙种花卉 90 盆. (1)问符合题意的搭配方案有几种?请你帮助设计出来; (2)若搭配一个 A 种造型的成本是 800 元,搭配一个 B 种造型 的成本是 960 元,试说明(1)中哪种方案成本最低?最低成本是多 少元? 思路导引:根据已知条件,求出自变量的取值范围,根据实际 情况,自变量只能取整数,故可求出搭配方案,在求最低成本时, 应利用一次函数的增减性解题.
方法三:成本为 y=800x+960(50-x)=-160x+48 000(31≤x≤33). 根据一次函数的性质,y 随 x 的增大而减小, 故当 x=33 时,y 取得最小值为 33×800+17×960=42 720(元). 即最低成本是 42 720 元.
1.一次函数 y=3x-4 的图象不经过( B ) A.第一象限 C.第三象限 B.第二象限 D.第四象限
例 2:(2010 年广东清远)正比例函数 y=kx 和一次函数 y=ax+b 的图象都经过点 A(1,2),且一次函数的图象交 x 轴于点 B(4,0).求正 比例函数和一次函数的表达式. 思路导引:用待定系数法,求出 k、a、b 的值,进而求出正比 例函数和一次函数的表达式. 解:因为正比例函数图象经过点(1,2),得 k=2. 所以正比例函数的表达式为 y=2x. 因为一次函数图象经过点(1,2)和(4,0),
则有பைடு நூலகம்
a +b = 2 3 ,解得 . 4a + b = 0 b=8
3
a=−2
2 8 所以一次函数的表达式为 y=-3x+3.
专题二 探求不等关系解一次函数应用题 探求与挖掘一次函数应用题中的不等关系,将自变量限定 在某一数值范围内,是解决与一次函数有关的最值问题和方案 设计问题的利器.
(2)方法一:由于 B 种造型的造价成本高于 A 种造型成本. 所以 B 种造型越少,成本越低,故应选择方案③,成本最低, 最低成本为:33×800+17×960=42 720(元). 方法二: 方案①需成本:31×800+19×960=43 040(元); 方案②需成本:32×800+18×960=42 880(元); 方案③需成本:33×800+17×960=42 720(元). ∴应选择方案③,成本最低,最低成本为 42 720 元.
解:设搭配 A 种造型 x 个,则 B 种造型为(50-x)个,
x ≤ 33 80x + 50(50 − x) ≤ 3 490 ,解得 依题意,得 , x ≥ 31 40x + 90(50 − x) ≤ 2 950
∴31≤x≤33. ∵x 是整数,x 可取 31,32,33, ∴可设计三种搭配方案: ①A 种园艺造型 31 个,B 种园艺造型 19 个; ②A 种园艺造型 32 个,B 种园艺造型 18 个; ③A 种园艺造型 33 个,B 种园艺造型 17 个.
解:(1)设甲种型号的汽车需要 x 辆,则乙种型号的汽车需 要(10-x)辆.
40x + 30(10 − x) ≥ 340 由题意,得 , 16x + 20(10 − x) ≥170
解得 4≤x≤7.5. 又因为 x 取整数,则 x 的值为 4,5,6,7. 因此,有四种可行的租车方案,分别是 方案一:租用甲种型号车 4 辆,乙种型号车 6 辆; 方案二:租用甲种型号车 5 辆,乙种型号车 5 辆; 方案三:租用甲种型号车 6 辆,乙种型号车 4 辆; 方案四:租用甲种型号车 7 辆,乙种型号车 3 辆.
