菱形的性质课件
合集下载
菱形的性质(第一课时)经典完整ppt课件

F D
C
E
A
B 可编辑课件
21
教学反思
▲你对菱形知多少?请你谈一谈.
★从概念上来谈;
●从性质上来谈; ※从计算上来
谈.
可编辑课件
22
从概念上来谈——有一组邻 边相等的平行四边形是菱形.
从性质上来谈—— ①菱形的对边平行且相等,对角相
等,对角 线互相平分.
可编辑课件
23
②菱形的四边都相等;
③菱形的对角线互相垂直,且每一 条对角线平分一组对角。 从计算上来谈——
菱形的面积等于它的对角线长的 乘积的一半。设菱形的两对角线长
分别为a,b,则它的面积S= 1 ab.
2
可编辑课件
24
可编辑课件
25
你能做吗?
如图,菱形ABCD中,∠B=60°,点 E、F分别在AB、AD上,且BE=AF. 求△ECF是等边三角形吗?
AF
D
E
B
C 可编辑课件
26
你能做吗?
如图,矩形ABCD对角 线相交于点O,DE∥AC, D CE∥DB, CE、DE交于 A E,求四边形DOCE是菱形
可编辑课件
10
我们已经知道矩形和菱形是特殊的平行四边形, 因此矩形菱形都是中心对称图形,想一想 矩 形、菱形是不是轴对称图形?如果是轴对称图 形,对称轴各几条?
矩形是轴对称图形,对称轴有两条。
菱形既是轴对称图形又是中心对称图形, 对称轴
有两条,是菱形两条对角线所在的直线.对称中心
是对角线的交点。 可编辑课件
A
⑵求菱形ABCD的面
积.
O
B
D
可编辑课件
C
18
拓展提高
7.菱形ABCD中,点E、F分别是BC、CD 的中点. EF与AC有什么关系?为什么?
19.菱形的性质cfPPT课件(沪科版)
请谈谈你这节课的收获
当堂诊学
(必做题)1.如图,在菱形ABCD中,∠A=60°,AB=4,O为对角 线BD的中点,过O点作OE⊥AB,垂足为E (1)求∠ABD的度数 (2)求线段BE的长
(选做题)2.如图,在菱形ABCD中,E为AB的中点,且DE⊥AB,
AB=a.
(1)求∠ABC的度数
(2)求对角线AC的长
结论:对角线互相垂直的四边形面积都是对角线积的一半
引导探究
5.已知如图,菱形ABCD中,E是AB的中点,且 DE⊥AB,AB=1.
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。D
C
O
A
B
E
目标再现
1、理解菱形的概念及与平行四边形之间的关系 有一组邻边相等的平行四边行叫做菱形 2、掌握菱形的性质并会运用其解决简单的问题
度数为 5° .
B
D
EF
C
引导探究
3、已知菱形的两条对角线长分别为 6a,, b8, 求菱形的面积. 周长呢?
或S菱形=AB× DE
E
结论:菱形的面积是两条对角线积的一半.
4.菱形的两条对角线的长分别是12cm和16cm, 则菱形的面积是_9_6_c_m_2,周长是_4_0_c_m__
引导探究
变式:已知四边形的对角线互相垂直,且两 条对角线长分别为 a,b,求四边形的面积.
2、掌握菱形的性质并会解决简单的问题
独立自学
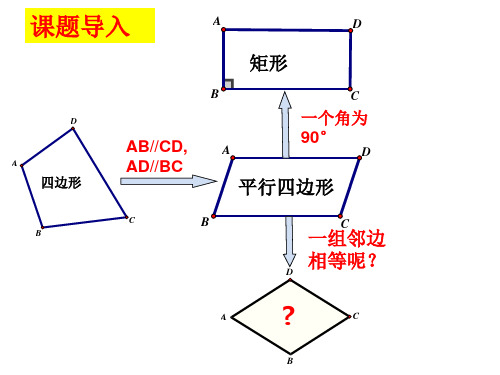
1、在平行四边形中,改变边的长度,能否得到一 个特殊的平行四边形?
D
A
D
平行四边形 (
)
A
菱?形
C
B
C
B
2.什么样的四边形叫做菱形?
当堂诊学
(必做题)1.如图,在菱形ABCD中,∠A=60°,AB=4,O为对角 线BD的中点,过O点作OE⊥AB,垂足为E (1)求∠ABD的度数 (2)求线段BE的长
(选做题)2.如图,在菱形ABCD中,E为AB的中点,且DE⊥AB,
AB=a.
(1)求∠ABC的度数
(2)求对角线AC的长
结论:对角线互相垂直的四边形面积都是对角线积的一半
引导探究
5.已知如图,菱形ABCD中,E是AB的中点,且 DE⊥AB,AB=1.
求(1)∠ABC的度数;
(2)对角线AC、BD的长;
(3)菱形ABCD的面积。D
C
O
A
B
E
目标再现
1、理解菱形的概念及与平行四边形之间的关系 有一组邻边相等的平行四边行叫做菱形 2、掌握菱形的性质并会运用其解决简单的问题
度数为 5° .
B
D
EF
C
引导探究
3、已知菱形的两条对角线长分别为 6a,, b8, 求菱形的面积. 周长呢?
或S菱形=AB× DE
E
结论:菱形的面积是两条对角线积的一半.
4.菱形的两条对角线的长分别是12cm和16cm, 则菱形的面积是_9_6_c_m_2,周长是_4_0_c_m__
引导探究
变式:已知四边形的对角线互相垂直,且两 条对角线长分别为 a,b,求四边形的面积.
2、掌握菱形的性质并会解决简单的问题
独立自学
1、在平行四边形中,改变边的长度,能否得到一 个特殊的平行四边形?
D
A
D
平行四边形 (
)
A
菱?形
C
B
C
B
2.什么样的四边形叫做菱形?
1.菱形的性质与判定第1课时菱形的性质PPT课件(北师大版)

新知导航
2.如图,菱形ABCD的边长为4 cm,对角线AC,BD 交于O,∠BAD=60°.求对角线AC,BD的长.
解:∵四边形ABCD是菱形, ∴AB=AD,∵∠BAD=60°, ∴△ABD是等边三角形, ∴BD=AB=4 cm ∴BO=2 cm,∴AO=2 3 cm,∴AC=4 3 cm
第1课时 菱形的性质
第1课时 菱形的性质
新知导航
知识点3:对角线平分对角
【例3】如图,菱形ABCD中,O是对角线AC上一点,
连接OB,OD,求证:OB=OD.
【例3】证明:∵四边形ABCD是菱形,
∴AD=AB,∠DAO=∠BAO AD=AB
在△ADO和△ABO中, ∠DAO=∠BAO , AO=AO
∴△ADO≌△ABO(SAS),∴OB=OD.
第1课时 菱形的性质
新知导航
(一)基础呈现 菱形的定义:有一组邻边 相等 的 平行四边形 叫做 菱形. 菱形的性质 (1)菱形具有平行四边形的所有性质; (2)菱形不同于一般平行四边形的性质: ①四条边都 相等 ; ②两条对角线 垂直平分 ,并且每条对角线平分对角. ③菱形是轴对称图形,有 2 条对称轴.
(2)平行四边形的对角
相等
.
(3)平行四边形的对角线 互相平分 .
第1课时 菱形的性质
知识回顾
几何语言 ∵四边形ABCD是平行四边形 ∴(边)__如__A__B_=__C_D_________________________; (角)____∠__A__=__∠__C_________________________; (对角线)__O_A__=__O_C_,__O__B_=__O_D__等______________.
第1课时 菱形的性质
1.1.2 菱形的性质与判定 课件

仍无法判定四边形AECF为菱形的是( C )
A. AE=AF
B. EF⊥AC
C. ∠B=60°
D. AC是∠EAF的平分线
课堂练习
3、如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F
.且AD交EF于O,则∠AOF= 90 度.
4、如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的
C
D
归纳总结
四边相等的四边形是菱形.
A
D
A
D
AB=BC=CD=AD
B
C
四边形ABCD
B
菱形ABCD
几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
C
新知讲解
两组对边分别平行或相等
一组对边平行且相等
四边形
两组对角分别相等
对角线相平分
菱形
平行四边形
新知讲解
现在你有哪些证明一个四边形或平行四边形是菱形的判定依据?
1.1.2 菱形的性质与判定
北师版九年级上册
教学目标
1.掌握菱形的判定定理
2.经历菱形判定定理的探究过程
3.会用这些菱形的判定方法进行有关的证明和计算
新知导入
菱形的定义和性质?
定义:有一组邻边相等的平行四边形是菱形.
边:四条边相等,对边平行.
角:对角相等.
对角线:对角线互相垂直平分.
新知导入
根据菱形的定义,可得菱形的第一个判定的方法:
定义 有一组邻边相等的平行四边形是菱形.
定理 对角线互相垂直的平行四边形是菱形.
定理 四边相等的四边形是菱形.
做一做
你能用折纸的办法得到一个菱形吗?动手试一试.
A. AE=AF
B. EF⊥AC
C. ∠B=60°
D. AC是∠EAF的平分线
课堂练习
3、如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F
.且AD交EF于O,则∠AOF= 90 度.
4、如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的
C
D
归纳总结
四边相等的四边形是菱形.
A
D
A
D
AB=BC=CD=AD
B
C
四边形ABCD
B
菱形ABCD
几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,
∴四边形 ABCD是菱形.
C
新知讲解
两组对边分别平行或相等
一组对边平行且相等
四边形
两组对角分别相等
对角线相平分
菱形
平行四边形
新知讲解
现在你有哪些证明一个四边形或平行四边形是菱形的判定依据?
1.1.2 菱形的性质与判定
北师版九年级上册
教学目标
1.掌握菱形的判定定理
2.经历菱形判定定理的探究过程
3.会用这些菱形的判定方法进行有关的证明和计算
新知导入
菱形的定义和性质?
定义:有一组邻边相等的平行四边形是菱形.
边:四条边相等,对边平行.
角:对角相等.
对角线:对角线互相垂直平分.
新知导入
根据菱形的定义,可得菱形的第一个判定的方法:
定义 有一组邻边相等的平行四边形是菱形.
定理 对角线互相垂直的平行四边形是菱形.
定理 四边相等的四边形是菱形.
做一做
你能用折纸的办法得到一个菱形吗?动手试一试.
菱形的性质PPT课件

2
.菱形ABCD中∠ABC=60
度,则∠BAC=_______源自 60度3、菱形的两条对角线长分别 为6cm和8cm,则菱形的边长是 (C ) A.10cm C. 5cm B.7cm D.4cm
4.在菱形ABCD中,AE⊥BC, AF⊥CD,E、F分别为BC,CD 的中点,那么∠EAF的度数是 A ( B )
1.菱形的定义
一组邻边相等的平形四
边形是菱形。
在菱形ABCD中,对角线AC, BD相交于点O.
D A O B C
(1)图中有哪些线段是相等 的?哪些角是相等的?
D A O B C
(2)图中有哪些等腰三角形、 直角三角形?
D A O B C
(3)两条对角线AC,BD有 什么特定的位置关系?
A.75° C.45° B.60° D.30°
B E C F D
随堂练习
1、四边形ABCD是菱形,O 是两条对角线的交点。已知 AB=5cm,AO=4cm,求对角 线BD的长。
今天你学到了什么 定义:有一组邻边相等的平行四边形 叫做菱形
菱形的四条边相等
菱形的对角线互相垂直平分并且每 一条对角线平分一组对角
你知道如何判别菱形吗?
一组邻边相等的平形四边形是菱形。 对角线互相垂直的平行四边形是菱形。 四条边都相等的四边形是菱形。
已知菱形ABCD中,对角线AC、 BD相交于点O,∠BAD=60°, BD=6,求菱形的边长AB和对角 线AC的长。 D
A
B O
C
1.已知菱形的周长是12cm,
3cm 那么它的边长是______.
D A O B C
你知道菱形有哪些性质吗? 边:菱形的四条边相等
角:对角相等,邻角互补
1.1 第1课时 菱形的性质(优质课课件)

例3 如图,E为菱形ABCD边BC上一点,且AB=AE,AE 交BD于O,且∠DAE=2∠BAE,求证:OA=EB.
证明:∵四边形ABCD为菱形, A
D
∴AD∥BC,AD=BA,
∠ABC=∠ADC=2∠ADB ,
O
∴∠DAE=∠AEB,
∵AB=AE,∴∠ABC=∠AEB,
∴∠ABC=∠DAE,
B
EC
∵AB = AD,OB = OD,AO=AO
∴△ABO≌△ADO(SSS)
∴∠DAO=∠BAO,∠AOD=∠AOB= 90°
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,
∠ABD=∠CBD.
二、菱形的性质—总结定理
定理1:菱形的四条边相等。 定理2:菱形的对角线互相垂直且每条对角线平分一组对角。
1.两条对角线互相垂直平分; 2.每一条对角线平分一组对角
有关计算
周长=边长的四倍
作业布置:
1.习题1.1 第1、2、3; 2.《典中点》1、2页.
在等腰三角形ABD中,
∵OB = OD,
∴AO⊥BD,AO平分∠BAD,
即AC⊥BD,∠DAC=∠BAC.
同理可证∠DCA=∠BCA,
∠ADB=∠CDB,
∠ABD=∠CBD.
(2)(3)第二种证明方法
B
∵四边形ABCD是平行四边形,
∴OB = OD
A
O
C
(平行四边形的对角线互相平分).
D
在△ABO和△ADO中,
则菱形的边长是__5_c_m___.
B
O
A
C
D
(4)菱形的一个内角为120°,平分这个内角的对角 线长为11cm,菱形的周长为_4_4_c_m__.
菱形的性质 课件

AC=2OA=8cm
课堂小结: 本节课,你学到了什么?
从定义上来谈——
有一组邻边相等的平行四边
形是 菱形.
从性质上来谈—— ①菱形具有平行四边形的一 切性质;
②菱形是中心对称图形,也 是轴对称图形;
③菱形的四边都相等;
④菱形的对角线互相垂直平分,并
且每条对角线平分一组对角。 从计算上来谈——
菱形的面积等于它的对角线长的
菱形的性质
学习目标:
1.掌握菱形概念,知道菱形与平行 四边形的关系.
2.理解并掌握菱形的性质,会用这些 性质进行有关的论证和计算,会计 算菱形的面积.
菱形就在我们身边
感受生活
你能举出生活中你看到的菱形吗?
感受生活
三菱汽车标志欣赏
自主学习(仔细阅读55页的内容,回 答下列问题) (1)菱形的定义是什么?菱形是平行四
中心对称图形,轴 对称图形
乘积的一半。设菱形的两对角线长
分别为a,b,则它的面积S= 1 ab.
2
比一比,填写下表:
概念 共性
个性
矩形
菱形
有一角为直角的平 行四边形 平行四边形的所有 性质
四个角都是直 角
对角线相等
中心对称图形, 轴对称图形
有一组邻边相等 的平行四边形 平行四边形的所有 性质 四条边是相等
对角线互相垂直, 且每条对角线平分 一组对角
则∠BAD= 角形.
,△为 D
三
A
C
B
3.菱形ABCD中,O是两条对角线的交 点,已知AB=5cm,AO=4cm,求 两对角线AC、BD的长。
D
A
O
C
解:∵四边形ABCD是菱形
∴OA=OC,OB=OD AC⊥BD
菱形的性质与判定分层ppt课件

试一试
对角线互相垂直的平行四边形是菱形吗?
已知:如图1-3,在□ABCD中,对角线AC与
BD交于点O,AC⊥BD.
求证: □ABCD是菱形
证明:
定理
对角线互相垂直的平行四边形是菱形 符号语言:
∵四边形ABCD是平行四边形
AC⊥BD ∴四边形ABCD是菱形
议一议
已知线段AC,你能用尺规作图的方法做一 个菱形ABCD,使AC为菱形的一条对角线吗?
探索新知
根据菱形的定义,邻边相等的平行四边形是菱形. 除此之外,你认为还有什么条件可以判断一个平行四 边形是菱形?先想一想,再与同伴交流.
小明的想法
平行四边形的不少性质定理与判定定理都是互逆 命题.受此启发,我猜想:
四边相等的四边形是菱形,对角线垂直的平行四边 形是菱形.
你是怎么想的?你认为小明的想法如何?与同伴交 流一下.
第一章 特殊平行四边形
1.1.2菱形的性质与判定
教学目标:1.探索证明菱形的两种判定方法,掌握证明的基本要求、 方法及思路.
2.能利用菱形的判定方法进行证明.
复习旧知
1.菱形的定义?性质?
2.如图,已知四边形ABCD是一个平行四边形,则只需
补充
就可以判定它是一个菱形.
3.如图,已知菱形ABCD的对角线AC、BD相交于点O, 并且AC=6cm,BD=8cm,则菱形ABCD的周长为_____ 怎么做的?你认为小刚的作法正确吗?与 同伴交流.
请尝试证明下面的定理
四条边相等的四边形是菱形
已知:如图1-5,四边形ABCD中,AB=BC=CD=DA. 求证: 四边形ABCD是菱形 证明:
定理 四条边相等的四边形是菱形
符号语言:
∵AB=BC=CD=DA ∴四边形ABCD是菱形
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
2
在RtOAB中,AO 1 AB 1 20 10m
2
2
BO AB2 AO2 202 102 300m
花坛的两条小路长
AC 2 AO 20m
BD 2BO 34.64m 花坛的面积
ቤተ መጻሕፍቲ ባይዱ
S菱形ABCD
1 2
AC • BD
346.4m2
运用菱形的性质时注意:
1.利用菱形的性质可证明线段相等、线段垂直、 角相等。 2.由于菱形的对角线互相垂直,所以涉及菱形 的问题都会在直角三角形中得以解决。 3.由于菱形的四条边相等,故常常连接对角线 构造等腰三角形或等边三角形,用等腰三角形 或等边三角形的性质解题。
本题20分
已知菱形的周长为40cm,两对角线的比为3:4, 则两对角线的长分是12cm、16cm 。
本题10分
菱形对角线的平方和等于一边平方的 ( C ) A. 2倍 B. 3倍 C.4倍 D. 5倍
本题20分 已知菱形对角线长分别为12cm和16cm, 求菱形的高。
性质进行简单的计算。
解决自主学习中存在的问题。
感受生活
菱形就在我们身边
感受生活
三菱汽车标志欣赏
例2、如图,菱形花坛ABCD的周长为 20m, ∠ABC=60度,沿着菱形的对角 线修建了两条小路AC和BD,求两条小路 的长和花坛的面积.
解: 花坛ABCD是菱形
AC BD, ABO 1 ABC 1 600 300
S菱形= 对角线乘积的一半
3 个 特:特在“边、对角线、对称性” 性
1
2
3
相信你们是最棒的!
4
5
6
本题10分 菱形两条对角线长为12和16,菱形的边长 为 10 ,面积为 96 。
本题5分
已知菱形的周长是16cm,那么它的边长 是_4c_m__.
本题10分 菱形的面积为24cm2,一条对角线的长为6cm, 则另一条对角线长为8cm;边长为 10cm。
平行四边形的对边平行;
边
平行四
平行四边形的对边相等;
边形的 性质:
对角线 平行四边形的对角线互相平分;
角 平行四边形的对角相等; 平行四边形的邻角互补;
矩形的四个角都是直角。
矩形的性质
矩形的对角线相等。
平行四边形 邻边相等
菱形
19.2特殊的平行四边形
19.2.2菱形
1.了解菱形的概念以及菱形与平行四 边形的关系。 2.掌握菱形的性质,并能运用菱形的
消化性测试参考答案
1、60° 2、A 3、8㎝ 4、16
5.证明:∵四边形ABCD是菱形 ∴ AD=CD=BC=AB ,∠ B= ∠D 又 ∵ E、F分别是BC、CD的中点 ∴DE=BF ∴ △ ADE≌ △ ABF ∴AE=AF
1 个 定 :有一组邻边相等的平行四边形叫菱形 义 2个公式:S菱形=底×高
