(完整版)圆柱的表面积和体积
圆柱、圆锥常用表格面积、体积公式

刘老师圆柱与圆锥圆柱的侧面积=底面圆周长×高字母表示:S侧=C底h 2.底面圆周长 =圆周率×直径 =圆周率×2×半径字母表示:C底=πd=2πr.3求圆柱的表面积三步:(1)圆柱的底面积 =S 底 =πr2=(πd÷2) 2=πd2÷4(2)圆柱侧面积 =S 侧 =h×C底(底面圆周长) =2πrh= πdh(3)圆柱表面积 =S 表 =S侧 +2S 底圆柱体积的公式圆柱的体积 =底面积×高字母表示:V柱=S底h圆锥体积的公式( 1)圆锥的体积等于与它等底等高圆柱体积的1/3V 锥 =V 柱÷3=S底 h÷3(2)已知圆锥底面积( S)和高( h),求体积的公式: V 锥 =S底 h÷3(3)已知圆锥体积( V)和高( h),求底面积的公式: S 底 =3V 锥÷h(4)已知圆锥体积( V)和底面积( S),求高的公式: h=3V 锥÷S底例题精讲圆柱、圆锥常用的表面积、体积公式立体图形表面积体积S圆柱侧面积个底面积2πrh 2 πr2V圆柱πr2h2 hr圆柱hr 圆锥S圆锥侧面积底面积n πl2πr2V圆锥体1πr2 h3603注: l 是母线,即从极点终究面圆上的线段长板块一圆柱与圆锥【例 1】如图,用高都是 1 米,底面半径分别为 1.5 米、1米和 0.5 米的 3 个圆柱组成一个物体.问这个物体的表面积是多少平方米( π取 )1111【例 2】有一个圆柱体的零件,高10 厘米,底面直径是 6 厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是 4 厘米,孔深 5 厘米(见右图).若是将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米)圆柱体的侧面张开,放平,是边长分别为10 厘米和12 厘米的长方形,那【例3】 (第四届希望杯 2 试一试题么这个圆柱体的体积是________立方厘米. (结果用π表示 )(接头处忽略不计),求这【例4】如右图,是一个长方形铁皮,利用图中的阴影部分,恰好能做成一个油桶个油桶的容积.( π )【牢固】如图,有一张长方形铁皮,剪以下图中两个圆及一块长方形,正好可以做成 1 个圆柱体,这个圆柱体的底面半径为10 厘米,那么本来长方形铁皮的面积是多少平方厘米( π 3.14 )10cm【例 5】把一个高是8 厘米的圆柱体,沿水平方向锯去 2 厘米后,剩下的圆柱体的表面积比本来的圆柱体表面积减少平方厘米.本来的圆柱体的体积是多少立方厘米【牢固】一个圆柱体底面周长和高相等.若是高缩短 4 厘米,表面积就减少平方厘米.求这个圆柱体的表面积是多少4cm【例 6】 (2008 年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大2008cm2,则这个圆柱体木棒的侧面积是 ________ cm2. ( π取 )第 2题【牢固】已知圆柱体的高是10 厘米,由底面圆心垂直切开,把圆柱分成相等的两半,表面积增加了40 平方厘米,求圆柱体的体积.( π3 )【例 7】一个圆柱体的体积是立方厘米,底面半径是 2 厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米( π )【例 8】右图是一个零件的直观图.下部是一个棱长为40cm的正方体,上部是圆柱体的一半.求这个零件的表面积和体积.【例 9】输液 100 毫升,每分钟输 2.5 毫升.如图,请你观察第12 分钟时图中的数据,问:整个吊瓶的容积是多少毫升【例 10】(2008 年”希望杯” 五年级第 2 试 )一个拧紧瓶盖的瓶子里面装着一些水(如图 ),由图中的数据可推知瓶子的容积是_______ 立方厘米. ( π取 )10684( 单位:厘米)【牢固】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为π立方厘米.当瓶子正放时,瓶内的酒精的液面高为 6 厘米;瓶子倒放时,空余部分的高为 2 厘米.问:瓶内酒精的体积是多少立方厘米合多少升26【牢固】一个酒瓶里面深30cm ,底面内直径是10cm ,瓶里酒深 15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深 25cm.酒瓶的容积是多少( π取 3)302515【牢固】一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(以以下图所示),请你依照图中注明的数据,计算瓶子的容积是______.7cm5cm4cm【牢固】一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部圆柱体的底面直径和高都是12 厘米.其5 厘米,那么这个容器的容积是多少立方厘米( π 3 )5cm11cm【例 11】(第四届希望杯2)如,底面50 平方厘米的柱形容器中装有水,水面上飘扬着一棱 5 厘米的正方体木,木浮出水面的高度是 2 厘米.若将木沉着器中取出,水面将下降 ________厘米.2厘米【例12】有两个棱8厘米的正方体盒子, A 盒中放入直径8 厘米、高8 厘米的柱体一个,B 盒中放入直径 4 厘米、高8 厘米的柱体 4 个,在 A 盒注水,把 A 盒的水倒入 B 盒,使 B 盒也注水, A 盒余下的水是多少立方厘米【例 13】州来的傅擅做拉面,拉出的面条很很,他每次做拉面的步是的:将一个面先搓成柱形面棍, 1.6 米.尔后折,拉到 1.6 米;再折,拉到 1.6 米⋯⋯照此行下去,最后拉出的面条粗(直径 )有本来面棍的 1 .:最后傅拉出的些面条的64有多少米 (假傅拉面的程中.面条始保持粗平均的柱形,而且没有任何浪)【例14】一个柱形容器内放有一个方形.打开水往容器中灌水. 3 分水面恰好没方体的面.再18 分水灌容器.已知容器的高50 厘米,方体的高20 厘米,求方体底面面与容器底面面之比.【例 15】一只装有水的圆柱形玻璃杯,底面积是80 平方厘米,高是15厘米,水深8 厘米.现将一个底面积是 16 平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米【牢固】一只装有水的圆柱形玻璃杯,底面积是80 平方厘米,高是15厘米,水深 10 厘米.现将一个底面积是 16 平方厘米,高为12 厘米的长方体铁块竖放在水中后.现在水深多少厘米【牢固】一只装有水的圆柱形玻璃杯,底面积是80 平方厘米,高是15厘米,水深 13 厘米.现将一个底面积是 16 平方厘米,高为12 厘米的长方体铁块竖放在水中后.现在水深多少厘米【例 16】一个圆柱形玻璃杯内盛有水,水面高 2.5 厘米,玻璃杯内侧的底面积是72 平方厘米.在这个杯中放进棱长 6 厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米【例 17】一个盛有水的圆柱形容器,底面内半径为 5 厘米,深20 厘米,水深15 厘米.今将一个底面半径为 2 厘米,高为17 厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米【例18】有甲、乙两只圆柱形玻璃杯,其内直径依次是淹没着一铁块,当取出此铁块后,甲杯中的水位下降了的水未外溢.问:这时乙杯中的水位上升了多少厘米10 厘米、 20 厘米,杯中盛有适合的水.甲杯中2 厘米;尔后将铁块淹没于乙杯,且乙杯中【牢固】有一只底面半径是20 厘米的圆柱形水桶,里面有一段半径是 5 厘米的圆柱体钢材浸在水中.钢材从水桶里取出后,桶里的水下降了 6 厘米.这段钢材有多长【例19】一个圆锥形容器高中,水面高多少厘米24 厘米,其中装满水,若是把这些水倒入和圆锥底面直径相等的圆柱形容器【例20】(2009 年”希望杯” 一试六年级)如图,圆锥形容器中装有水50 升,水面高度是圆锥高度的一半,这个容器最多能装水升.r1r2h12h【例 21】如图,甲、乙两容器相同,甲容器中水的高度是锥高的1 ,乙容器中水的高度是锥高的2 ,比33较甲、乙两容器,哪一只容器中盛的水多多的是少的的几倍乙甲【例22】(2008 年仁华考题 )如图,有一卷紧紧围绕在一起的塑料薄膜,薄膜的直径为直径为 8 厘米的卷轴,已知薄膜的厚度为0.04 厘米,则薄膜张开后的面积是20 厘米,中间有一平方米.20cm8cm100cm【牢固】图为一卷紧绕成的牛皮纸,纸卷直径为20 厘米,中间有素来径为 6 厘米的卷轴.已知纸的厚度为毫米,问:这卷纸张开后大体有多长【牢固】如图,厚度为0.25 毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180厘米,内直径是50 厘米.这卷铜版纸的总长是多少米【例23】(人大附中分班考试题目)如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10 厘米,侧面上的洞口是边长为 4 厘米的正方形,上下底面的洞口是直径为 4 厘米的圆,求此立体图形的表面积和体积.板块二旋转问题【例 24】如图,ABC是直角三角形,AB 、 AC 的长分别是 3 和 4.将ABC 绕 AC 旋转一周,求ABC 扫出的立体图形的体积.( π )CB A 【例 25】已知直角三角形的三条边长分别为3cm , 4cm , 5cm ,分别以这三边轴,旋转一周,所形成的立体图形中,体积最小的是多少立方厘米( π取 )【牢固】如图,直角三角形若是以BC 边为轴旋转一周,那么所形成的圆锥的体积为,以AC边为轴旋转16π一周,那么所形成的圆锥的体积为,那么若是以AB 为轴旋转一周,那么所形成的几何体的体积12π是多少BC A【例 26】如图,ABCD是矩形,BC6cm , AB10cm ,对角线 AC 、 BD 订交 O . E 、 F 分别是 AD 与BC 的中点,图中的阴影部分以EF 为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米 ( π取 3)A E DOB FC 【牢固】 (2006 年第十一届华杯赛决赛试题)如图,ABCD是矩形,BC6cm , AB10cm ,对角线 AC 、 BD圆柱、圆锥常用表格面积、体积公式订交 O .图中的阴影部分以CD 为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米A DOB C11 / 11。
圆柱、圆锥常用的表面积、体积公式

刘老师圆柱的侧面积=底面圆周长×高 字母表示:S 侧=C 底h 2. 底面圆周长=圆周率×直径=圆周率×2×半径 字母表示:C 底=πd=2πr 3. 求圆柱的表面积三步:(1)圆柱的底面积=S 底=πr²=π(d÷2)²=πd²÷4(2)圆柱侧面积=S 侧=h×C 底(底面圆周长)=2πrh=πdh (3)圆柱表面积=S 表=S 侧+2S 底圆柱体积的公式 圆柱的体积=底面积×高 字母表示:V 柱=S 底h 圆锥体积的公式(1) 圆锥的体积等于与它等底等高圆柱体积的1/3 V 锥=V 柱÷3=S 底h÷3 (2) 已知圆锥底面积(S )和高(h ),求体积的公式:V 锥=S 底h÷3 (3) 已知圆锥体积(V )和高(h ),求底面积的公式:S 底=3V 锥÷h (4) 已知圆锥体积(V )和底面积(S ),求高的公式:h=3V 锥÷S 底板块一 圆柱与圆锥【例 1】 如图,用高都是1米,底面半径分别为1.5米、1米和0.5米的3个圆柱组成一个物体.问这个物体的表面积是多少平方米?(π取3.14)1110.511.5例题精讲圆柱与圆锥【例 2】有一个圆柱体的零件,高10厘米,底面直径是6厘米,零件的一端有一个圆柱形的圆孔,圆孔的直径是4厘米,孔深5厘米(见右图).如果将这个零件接触空气的部分涂上防锈漆,那么一共要涂多少平方厘米?【例 3】(第四届希望杯2试试题)圆柱体的侧面展开,放平,是边长分别为10厘米和12厘米的长方形,那么这个圆柱体的体积是________立方厘米.(结果用π表示)【例 4】如右图,是一个长方形铁皮,利用图中的阴影部分,刚好能做成一个油桶(接头处忽略不计),求这个油桶的容积.(π 3.14=)【巩固】如图,有一张长方形铁皮,剪下图中两个圆及一块长方形,正好可以做成1个圆柱体,这个圆柱体的底面半径为10厘米,那么原来长方形铁皮的面积是多少平方厘米?(π 3.14=)【例 5】把一个高是8厘米的圆柱体,沿水平方向锯去2厘米后,剩下的圆柱体的表面积比原来的圆柱体表面积减少12.56平方厘米.原来的圆柱体的体积是多少立方厘米?【巩固】一个圆柱体底面周长和高相等.如果高缩短4厘米,表面积就减少50.24平方厘米.求这个圆柱体的表面积是多少?【例 6】(2008年第二届两岸四地”华罗庚金杯”少年数学精英邀请赛)一个圆柱体形状的木棒,沿着底面直径竖直切成两部分.已知这两部分的表面积之和比圆柱体的表面积大22008cm,则这个圆柱体木棒的侧面积是________2cm.(π取3.14)第2题【巩固】已知圆柱体的高是10厘米,由底面圆心垂直切开,把圆柱分成相等的两半,表面积增加了40平方厘米,求圆柱体的体积.(π3=)【例 7】一个圆柱体的体积是50.24立方厘米,底面半径是2厘米.将它的底面平均分成若干个扇形后,再截开拼成一个和它等底等高的长方体,表面积增加了多少平方厘米? (π 3.14=)【例 8】右图是一个零件的直观图.下部是一个棱长为40cm的正方体,上部是圆柱体的一半.求这个零件的表面积和体积.【例 9】输液100毫升,每分钟输2.5毫升.如图,请你观察第12分钟时图中的数据,问:整个吊瓶的容积是多少毫升?【例 10】(2008年”希望杯”五年级第2试)一个拧紧瓶盖的瓶子里面装着一些水(如图),由图中的数据可推知瓶子的容积是_______ 立方厘米.(π取3.14)(单位:厘米)【巩固】一个酒精瓶,它的瓶身呈圆柱形(不包括瓶颈),如图.已知它的容积为26.4π立方厘米.当瓶子正放时,瓶内的酒精的液面高为6厘米;瓶子倒放时,空余部分的高为2厘米.问:瓶内酒精的体积是多少立方厘米?合多少升?【巩固】一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm.把酒瓶塞紧后使其瓶口向下倒立这时酒深25cm.酒瓶的容积是多少?(π取3)253015【巩固】一个盖着瓶盖的瓶子里面装着一些水,瓶底面积为10平方厘米,(如下图所示),请你根据图中标明的数据,计算瓶子的容积是______.【巩固】一个透明的封闭盛水容器,由一个圆柱体和一个圆锥体组成,圆柱体的底面直径和高都是12厘米.其内有一些水,正放时水面离容器顶11厘米,倒放时水面离顶部5厘米,那么这个容器的容积是多少立方厘米?(π3)5cm【例 11】(第四届希望杯2试试题)如图,底面积为50平方厘米的圆柱形容器中装有水,水面上漂浮着一块棱长为5厘米的正方体木块,木块浮出水面的高度是2厘米.若将木块从容器中取出,水面将下降________厘米.【例 12】有两个棱长为8厘米的正方体盒子,A盒中放入直径为8厘米、高为8厘米的圆柱体铁块一个,B盒中放入直径为4厘米、高为8厘米的圆柱体铁块4个,现在A盒注满水,把A盒的水倒入B盒,使B盒也注满水,问A盒余下的水是多少立方厘米?【例 13】兰州来的马师傅擅长做拉面,拉出的面条很细很细,他每次做拉面的步骤是这样的:将一个面团先搓成圆柱形面棍,长1.6米.然后对折,拉长到1.6米;再对折,拉长到1.6米……照此继续进行下去,最后拉出的面条粗细(直径)仅有原先面棍的164.问:最后马师傅拉出的这些细面条的总长有多少米?(假设马师傅拉面的过程中.面条始终保持为粗细均匀的圆柱形,而且没有任何浪费)【例 14】一个圆柱形容器内放有一个长方形铁块.现打开水龙头往容器中灌水.3分钟时水面恰好没过长方体的顶面.再过18分钟水灌满容器.已知容器的高为50厘米,长方体的高为20厘米,求长方体底面面积与容器底面面积之比.【例 15】一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深8厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【巩固】一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深10厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【巩固】一只装有水的圆柱形玻璃杯,底面积是80平方厘米,高是15厘米,水深13厘米.现将一个底面积是16平方厘米,高为12厘米的长方体铁块竖放在水中后.现在水深多少厘米?【例16】一个圆柱形玻璃杯内盛有水,水面高2.5厘米,玻璃杯内侧的底面积是72平方厘米.在这个杯中放进棱长6厘米的正方体铁块后,水面没有淹没铁块.这时水面高多少厘米?【例17】一个盛有水的圆柱形容器,底面内半径为5厘米,深20厘米,水深15厘米.今将一个底面半径为2厘米,高为17厘米的铁圆柱垂直放入容器中.求这时容器的水深是多少厘米?【例18】有甲、乙两只圆柱形玻璃杯,其内直径依次是10厘米、20厘米,杯中盛有适量的水.甲杯中沉没着一铁块,当取出此铁块后,甲杯中的水位下降了2厘米;然后将铁块沉没于乙杯,且乙杯中的水未外溢.问:这时乙杯中的水位上升了多少厘米?【巩固】有一只底面半径是20厘米的圆柱形水桶,里面有一段半径是5厘米的圆柱体钢材浸在水中.钢材从水桶里取出后,桶里的水下降了6厘米.这段钢材有多长?【例19】一个圆锥形容器高24厘米,其中装满水,如果把这些水倒入和圆锥底面直径相等的圆柱形容器中,水面高多少厘米?【例20】(2009年”希望杯”一试六年级)如图,圆锥形容器中装有水50升,水面高度是圆锥高度的一半,这个容器最多能装水升.【例21】如图,甲、乙两容器相同,甲容器中水的高度是锥高的13,乙容器中水的高度是锥高的23,比较甲、乙两容器,哪一只容器中盛的水多?多的是少的的几倍?甲乙【例 22】(2008年仁华考题)如图,有一卷紧紧缠绕在一起的塑料薄膜,薄膜的直径为20厘米,中间有一直径为8厘米的卷轴,已知薄膜的厚度为0.04厘米,则薄膜展开后的面积是平方米.【巩固】图为一卷紧绕成的牛皮纸,纸卷直径为20厘米,中间有一直径为6厘米的卷轴.已知纸的厚度为0.4毫米,问:这卷纸展开后大约有多长?【巩固】如图,厚度为0.25毫米的铜版纸被卷成一个空心圆柱(纸卷得很紧,没有空隙),它的外直径是180厘米,内直径是50厘米.这卷铜版纸的总长是多少米?【例23】(人大附中分班考试题目)如图,在一个正方体的两对侧面的中心各打通一个长方体的洞,在上下底面的中心打通一个圆柱形的洞.已知正方体边长为10厘米,侧面上的洞口是边长为4厘米的正方形,上下底面的洞口是直径为4厘米的圆,求此立体图形的表面积和体积.板块二旋转问题【例 24】如图,ABC是直角三角形,AB、AC的长分别是3和4.将ABC∆∆绕AC旋转一周,求ABC 扫出的立体图形的体积.(π 3.14=)CB A 【例 25】已知直角三角形的三条边长分别为3cm,4cm,5cm,分别以这三边轴,旋转一周,所形成的立体图形中,体积最小的是多少立方厘米?(π取3.14)【巩固】如图,直角三角形如果以BC边为轴旋转一周,那么所形成的圆锥的体积为16π,以AC边为轴旋转一周,那么所形成的圆锥的体积为12π,那么如果以AB为轴旋转一周,那么所形成的几何体的体积是多少?ABC【例 26】 如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD 相交O .E 、F 分别是AD 与BC 的中点,图中的阴影部分以EF 为轴旋转一周,则白色部分扫出的立体图形的体积是多少立方厘米?(π取3)AB【巩固】(2006年第十一届华杯赛决赛试题)如图,ABCD 是矩形,6cm BC =,10cm AB =,对角线AC 、BD相交O .图中的阴影部分以CD 为轴旋转一周,则阴影部分扫出的立体的体积是多少立方厘米?BA。
圆柱体积表面积公式

圆柱体积表面积公式
圆柱体积表面积是一种非常重要的几何体概念,它在日常生活中有着广泛的应用。
圆柱体积表面积公式是一种求解圆柱体表面积的公式,它可以用来求解圆柱体的表面积,也可以用来求解圆柱体的体积。
圆柱体积表面积的公式为:S=2πrh+2πr2,其中S表示圆柱体表面积,r表示半径,h表示高度。
因此,我们可以推导出,当高度h 和半径r都相同时,圆柱体的表面积为2πr2。
圆柱体表面积的计算方法也非常简单,首先,需要确定圆柱体的半径r和高度h,然后,将r和h代入公式,就可以计算出圆柱体表面积。
圆柱体积表面积的应用非常广泛,比如在建筑设计中,我们可以利用这个公式来计算建筑物的表面积,以便计算出需要多少砖块来装饰外墙;在工业生产中,我们可以利用这个公式来计算出某种产品的体积,以便确定生产量;在学术研究中,我们也可以用这个公式来计算出某种物体的表面积,以便更准确地研究其物理性质。
总之,圆柱体积表面积公式是一种非常重要的几何概念,它可以用来求解圆柱体的表面积,也可以用来求解圆柱体的体积,它在日常生活中有着广泛的应用,因此,学习并掌握这个公式对我们来说是
非常有益的。
(完整版)圆柱和圆锥的公式

圆柱和圆锥圆的周长=圆柱和圆锥底面的周长圆的周长=2×圆周率×半径半径=圆的周长÷圆周率÷2c=2∏r r=c÷∏÷2圆的周长=圆周率×直径直径=圆的周长÷圆周率c=∏d d= c÷∏圆的面积=圆柱和圆锥地面的面积=∏×r×r圆的面积=圆周率×半径的平方s底圆柱侧面积原柱侧面积=底面周长×圆柱的高S侧=c×h 因为c=2∏r c=∏d 所以圆柱侧面积还可以写出:s侧=2∏r h 或s侧=∏d h知道圆柱侧面积和圆柱的高,怎么求底面周长、底面直径和底面半径?底面周长=圆柱侧面积÷圆柱的高C=s侧÷h底面直径=圆柱侧面积÷圆柱的高÷圆周率d=s侧÷h÷∏底面半径=圆柱侧面积÷圆柱的高÷圆周率÷2r=s侧÷h÷∏÷2圆柱的表面积表面积:圆柱的表面积=底面周长×高+底面面积×2S表=c×h+ ∏×r×r×2典型情况:做一个油桶需要多少平方米的铁皮。
(需要计算一个侧面积+二个底面面积)特殊情况:一、(1)做无盖的水桶需要多少平方米的铁皮。
(2)圆柱形的游泳池或水池在四周和底部抹水泥或贴瓷砖。
(只要计算一个侧面积+一个底面积)二、(1) 做通风管、落水管、烟囱需要多少铁皮。
(2)压路机前轮压过的路面面积。
(只要计算一个侧面积)圆柱的体积圆柱的体积=底面面积×高V柱=s底×h圆柱底面面积=圆柱体积÷圆柱的高S底=v÷h圆柱的高=圆柱的体积÷圆柱底面面积H= v÷S底圆锥的体积圆锥的体积=圆锥底面积×高V锥=s底×h÷3圆锥的底面积=圆锥的体积×3÷圆锥的高S底=v×3÷h圆锥的高=圆锥的体积×3÷圆锥的底面积h=v×3÷S底圆柱和圆锥面积和体积计算时的注意事项1、看清楚题目中的单位一不一样,最好在所有单位下面画出横线。
(六年级下册)圆柱与圆锥详细题型分类与答案 最终版

一、圆柱的表面积1.例题12.巩固3.拓展4.巩固圆柱与圆锥(一)本节课学习圆柱体表面积的一些运用.解决这些问题,有时需要结合实际,明确所求圆柱体的表面积有几个面;有时需要灵活地利用条件,间接得出所需要的数据进行计算;有时还需要观察图形,在观察与比较中搜索需要的信息.某化工厂有一个烟面,形状为圆柱形,底面半径是厘米,高是米,现在 要将烟囱增高到米.每增加平方米材料需要费用元,一共需要多少费用?808251120一个圆柱体的有盖油桶高分米,它的侧面展开后得到一个长分米的长方形.这个油桶共享了多少平方分米的铁皮?1025.12如图所示,有一块长方形铁皮,把其中的阴影部分剪下制成一个圆柱形油桶,求圆柱形油桶的表面积.如图所示,有一张长方体铁皮,剪下图中两个圆及一块长方形,正好可以做成一个圆柱体,这个圆柱体的底面半径为厘米,那么原来长方形铁皮的面积是多少平方厘米(取).10π 3.142.巩固3.拓展4.巩固把一个正方体削成一个体积最大的圆柱,如果圆柱的侧面积是平方厘米.求正方体的表面积.314把一个横截面是正方形的长方体术料削剪成一个最大的圆柱体,圆柱体的表面积为平方厘米.底面直径与高的比是,原来长方体的表面积是多少?32.971:3已知一个圆柱的底面半径等于一个正方体棱长的一半,高等于这个正方体的棱长,这个正方体的底面积是平方分米.求这个圆柱的表面积.25五、“整体代换”法在求圆柱体表面积或体积时的应用在分数的计算和圆的面积计算中,我们曾经学过“整体代换”的方法,例如:计算一个圆的面积,将圆周率乘半径的平方即可,但是,有的时候我们不知道这个圆的半径是多少,只告诉你,这时就可以直接用乘求得圆的面积.今天,我们学习“整体代换”法在求圆柱体表面积或体积时的应用.=8r 2 3.148圆柱与圆锥(一)(课后作业)圆柱与圆锥(课后作业)1.六年级上学期其它圆柱与圆锥一个圆柱体高厘米,侧面积平方分米,它的底面积是多少平方厘米?8025.122.六年级上学期其它圆柱与圆锥一个圆柱体的侧面展开是一个正方形,圆柱的底面直径是厘米,这个 圆柱体的表面积是多少平方厘米?203.六年级上学期其它圆柱与圆锥一个圆柱体木块,底面直径是分米,高是米,现在将它截成两个圆柱体小木块,那么,表面积增加多少平方分米?107.54.六年级上学期其它圆柱与圆锥一个圆柱体木块,底面周长是厘米,高是厘米,现在将它截成四个圆柱体小木块.那么,这四个圆柱体小木块的表面积为多少平方厘米?25.1265.六年级上学期其它圆柱与圆锥一个圆柱体的表面积和一个长方形的面积相等,长方形的长等于圆柱体的底面周长,已知长方形的面积为平方厘米,圆柱体的高是厘米,圆柱体的底面半径是多少?131.884如图所示,有一个立体图形.下部是一个棱长为厘米的正方体,上部是一个半圆柱体.求这个立体图形的表面积.409.六年级上学期其它圆柱与圆锥将一个正方体木块切削成一个最大的圆柱体,这个圆柱体的体积是立方厘米,问:原来正方体的体积有多大?125610.六年级上学期其它圆柱与圆锥如图所示,一个圆柱体的侧面展开图为正方形,已知它的一个底面面积是平方厘米.求这个圆柱体的表面积.108.六年级上学期其它圆柱与圆锥14.六年级上学期其它圆柱与圆锥如图所示.这是一个底面半径为厘米,高为厘米的圆柱,在它的中间依次向下挖去半径分别为厘米、厘米、厘米,高分别为厘米、厘米、厘米的圆柱.最后得到的立体图形表面积是多少?44321210.515.六年级上学期其它圆柱与圆锥如图所示,在长为厘米的圆筒形管子的横截面上,量出的最长线段为厘米,管子的体积是多少?201013.六年级上学期其它圆柱与圆锥有大、小两种不带盖的圆柱形水桶,它们的表面积的和是平方分米,小桶和大桶的用料面积的比是,小桶的底面周长是分米,大桶的底面周长是分米.求大、小两个桶的侧面积各是多少?54331:262.894.2圆柱与圆锥(奥赛训练)11.六年级上学期其它圆柱与圆锥工人师傅将一张铁皮按图裁剪后,做成一个圆柱形铁皮罐,求这个铁皮罐的表面积(单位:分米).12.六年级上学期其它圆柱与圆锥圆柱形的售报亭的高和底面直径相等,如图所示,开一个边长等于底面半径的正方形售报窗口.窗口处挖去的圆柱部分的面积占圆柱形侧面积的几分之几?所示.表面积增加了多少平方厘米?厘米.那么,它的体积是多少平方二、圆柱的表面积和体积(二)1.例题22.巩固3.巩固4.拓展5.巩固根据圆柱体底面、侧面和表面积的特征,以及它们之间的关系可以解决一些求体积的趣题.下面,我们就开始学习这方面的知识.一个圆柱体的高是厘米,它的侧面展开是一个正方形,求这个圆柱体的体积是多少立方厘米?12.56一个圆柱体的高是厘米,它的侧面展开是一个正方形.求这个圆柱体的体积.31.4一个侧柱体,它的侧面展开是一个长方形(宽为圆柱体的高).已知展开后的长方形的长是宽的倍,且宽是厘米.求这个圆柱体的体积.215.7如图所示,一个圆柱形木块高厘米,若被锯掉厘米后,则表面积减少了平方厘米.求原来圆柱的体积.1208251.2一个圆柱体的高是厘米,若高减少厘米,则表面积比原来减少平方厘米.求原来圆柱体的体积.10394.2平方厘米;如果按如图所示切成24平方厘米;如果按如图所示切成43五、水中浸物1.例题52.巩固3.拓展4.巩固我们知道,酒瓶或饮料瓶的瓶颈处一般都不是规则的圆柱体,如果要求体积等问题,这时该怎么办呢?把一根圆柱体钢材等物体放入一个长方体或圆柱体的容器内,要求水面的高度,必须先判断物体是否全部浸没.通过今天的学习,大家就会明白了.如图所示,有一种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是毫升.现在瓶中装有一些饮料,正放时饮料高度为厘米,倒放时空余部分的高度为厘米.瓶内现有饮料多少毫升?1500205如图所示,某种酒瓶的瓶身呈圆柱形(不包括瓶颈),瓶身内直径为厘米.现在瓶中装有一些酒,正放时酒的高度是厘米,倒放时空余部分的高度是厘米.求这个酒瓶的容积.48123在一个底面积是平方厘米的玻璃杯中装入高厘米的水.现把一个底面半径是厘米、高厘米的圆柱形铁块垂直放入玻璃杯水中,问水面升高了多少厘米?(取)15315π3如图所示,有一个高厘米,容积是毫升的圆柱形容器,里面装满了水.现在把长厘米的圆柱垂直放入,使的底面与的底面接触,这时一部分水从容器中溢出.当把从中拿出来后,中的水高度为厘米.求圆柱的体积.5850A 16B B A B A A 6B 5.巩固一个盛有水的圆柱形容器,底面内半径为厘米,深厘米,水深厘米.现在将一个底面半径为厘米、高为厘米的铁圆柱垂直放入容器中,求这时容器的水深是多少厘米?520152176.小学高年级六年级下学期其它把一个高为分米的圆柱形木块沿底面直径竖直切成相同的两块,表面积增加了平方分米.求这个圆柱体的体积.7.5757.小学高年级六年级下学期其它一个底面半径为厘米的圆柱体容器,放入一个石块后,浸没在水中,水面上升了厘米.求这个石块的体积.528.小学高年级六年级下学期其它在一只底面半径为厘米的圆柱形水桶里有一个直径为厘米的圆柱形钢材浸没在水中,当钢材取出后,桶里的水面下降了厘米,这段钢材长多少厘米?151029.小学高年级六年级下学期其它某种饮料瓶的瓶身呈圆柱形(不包括瓶颈),容积是升.现在瓶中有一些饮料,正放时饮料高度为厘米,倒放时空余部分的高度为厘米,如图所示,瓶内现在有饮料多少升?21052五、专题演练1.例题52.巩固3.巩固4.拓展已知一个圆锥的底面半径和高都等于一个正方体的棱长.这个正方体的体积是立方分米.求这个圆锥的体积.216一个圆柱体,底面积是平方分米,把它削成一个最大的圆锥,削去部分的体积是立方分米.求这个圆柱体的高.56两个正方体的体积之差是立方厘米,如果以每个正方体的一面为底,加工成最大的圆锥,加工成的两个圆锥的体积之差是多少立方厘米?1200一个边长是厘米的正方体玻璃缸中装着水,水中浸没了一个底面直径为厘米、高为厘米的铁质圆锥体和一个底面直径为厘米、高为厘米的铁质圆柱体.当圆锥体、圆柱体都从桶中取出后,桶内水将下降多少厘米?20125855.拓展圆柱与圆锥(三)(课后作业)1.小学高年级六年级下学期其它张大爷去年用长米、宽米的长方体苇席围成容积最大的圆柱形粮囤.今年改用长米、宽米的长方形苇席围成容积最大2132的圆柱形的粮囤.问今年粮囤的容积是去年粮囤容积的多少倍?2.小学高年级六年级下学期其它一个圆柱形的铁块厚厘米,如果把它锻造成底面直径相同的圆锥体,这个圆锥体的高是多少厘米?103.小学高年级六年级下学期其它优秀生培养教程12级第2讲圆柱与圆锥本讲巩固第4题这里有一个圆柱和一个圆锥(如图下图所示),它们的高和底面直径都标在图上,单位是厘米.请问:圆锥体积与圆柱体积的比是多少?4.小学高年级六年级下学期其它把一个长、宽、高分别是厘米、厘米、厘米的铁块和一个棱长为厘米的正方体铁块,熔铸成一个底面直径为厘米的973510圆锥形铁块.求这个圆锥的高是多少厘米?5.小学高年级六年级下学期其它一个立体图形由一个圆柱和一个圆锥组成,如图所示,它们的底面直径都是厘米,高都是厘米.这个立体图形的体积是612圆柱与圆锥(一)答案一、圆柱的表面积1、10248.96元2、351.68平方分米3、131.88平方分米4、828平方厘米二、圆柱的表面积(二)1、401.92平方厘米2、452.16平方厘米3、12.56平方厘米4、12.56平方厘米三、圆柱的表面积(三)1、18cm2、3.5cm3、166.42平方厘米4、124.03平方厘米四、圆柱的表面积(四)1、1331.36平方厘米2、7536平方厘米3、2081.4平方厘米4、385.4平方厘米五、四圆柱的表面积(四)1、8立方厘米2、600平方厘米3、18平方厘米4、117.75平方分米圆柱与圆锥(一)(课后作业)圆柱与圆锥(课后作业)1.【答案】平方厘米78.52.【答案】平方厘米4571.843.【答案】平方分米1574.【答案】平方厘米552.645.【答案】厘米36.【答案】平方厘米251.27.【答案】平方分米94.28.【答案】平方厘米117689.【答案】立方厘米160010.【答案】平方厘米145.614.【答案】平方厘米254.3415.【答案】平方厘米1570圆柱与圆锥(二)答案一、圆柱的表面积和体积(一)1、16平方厘米2、30平方厘米3、75.36平方分米4、62.8立方厘米5、21.98平方分米二、圆柱的表面积和体积(二)1、157.7536cm 32、246.49cm 33、1232.45cm 34、1570cm 35、7.85cm 3三、圆柱的表面积和体积(三)1、314cm 32、351.68cm 33、339.12cm 34、25.12cm 35、54cm 四、圆柱的表面积和体积(四)1、113.04cm 32、56.52cm 33、1413cm 34、32cm5、21.98cm 3五、水中浸物1、400ml2、753.6ml3、0.75cm4、25cm 35、17.72cm 圆柱与圆锥(二)(课后作业)1.【答案】52.【答案】立方厘米197.823.【答案】立方厘米19719.2 4.【答案】升37.68圆柱与圆锥(三)答案一、圆柱的表面积和体积(五)1、1.57m2、 2.5dm3、0.998m 34、339.12cm 3二、圆锥的表面积和体积(一)1、16cm 32、6cm3、64、35、(π≈3)108cm 3135cm 3三、圆锥的表面积和体积(二)1、2.52、72四、圆锥的表面积和体积(三)1、227cm2、4273、225cm4、2升5、32五、专题演练1、216π2、59dm 3、314cm 34、1.256cm 5、112cm 2圆柱与圆锥(三)(课后作业)1.【答案】922.【答案】303.【答案】1/244.【答案】125.【答案】452.166.【答案】平方厘米727.【答案】98.【答案】圆柱:,圆锥:40329.【答案】2410.【答案】3611.【答案】厘米7.2。
圆柱的面积公式和表面积公式

圆柱的面积公式和表面积公式
圆柱的面积公式,表面积公式,体积公式分别如下所示:
1、圆柱表面积:S表=2πR(R+h)(其中R表示圆柱的底面半径,h表示圆柱的高)
2、圆柱体积:V=πR^2h(其中R表示圆柱的底面半径,h表示圆柱的高)
3、圆柱侧面积:S侧=2πRh((其中R表示圆柱的底面半径,h表示圆柱的高)。
扩展资料:
圆柱的体积跟求长方体、正方体一样,都是底面积×高:设一个圆柱底面半径为r,高为h,则体积V:V=πr^2·h 。
如S为底面积,高为h,体积为V:V=Sh。
圆柱体侧面积=底面周长×高(圆的周长(2πr)或(πd))
圆柱体的表面积=2个底面积+1个侧面积。
圆柱、圆锥、圆台的表面积和体积

导学
探索新知
圆台的表面积
S 表面积 S上底面积 S下底面积 S 侧面积
2
2
S上底 =πr ,S下底 =πr .
r O′
l
r
O
(r′、r分别是上、下底面
半径,l是母线长)
圆台的侧面展开图是扇环
导学
圆台的表面积
探索新知
x
2πr
x
2πr
O′ r
l
O
r
(r′、r分别是上、
8.3.2 圆柱、圆锥、圆台表面积和体积
预学
棱柱、棱锥、棱台的表面积:围成它们的各个面的
面积的和,即侧面积+底面积
那你认为圆柱、圆锥、圆台的表面积又是怎样的呢?
S
O'
r O
l
O'
l
r O
r'
l
rO
圆柱、圆锥、圆台的表面积是围成它们的各个面的
面积和,即 S 表 S 底 S 侧
导学
探索新知
1、 圆柱、圆锥、圆台表面积
圆锥的表面积
探索新知
S 表面积 S 底面积 S 侧面积
S底 =πr
S
l
2πr
2
1
扇形的面积公式 : S扇形 = lr
2
(r是扇ห้องสมุดไป่ตู้所在圆半径,l是弧长)
r
O
(r是底面半径,l是
母线长)
S圆锥 =πr +πrl πr (r l )
2
互学
例题讲解
例1、将一个边长分别为4π,8π的矩形卷成一个圆
圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为 (
圆柱、圆锥、圆台、球的表面积和体积
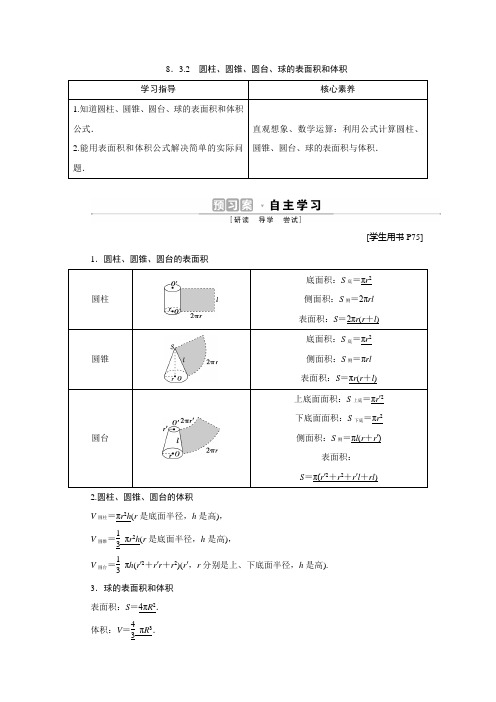
8. 3.2 圆柱、圆锥、圆台、球的表面积和体积 学习指导核心素养1.知道圆柱、圆锥、圆台、球的表面积和体积公式.2.能用表面积和体积公式解决简单的实际问题.直观想象、数学运算:利用公式计算圆柱、圆锥、圆台、球的表面积与体积.[学生用书P75]1.圆柱、圆锥、圆台的表面积圆柱底面积:S 底=πr 2侧面积:S 侧=2πrl 表面积:S =2πr (r +l ) 圆锥底面积:S 底=πr 2侧面积:S 侧=πrl 表面积:S =πr (r +l ) 圆台上底面面积:S 上底=πr ′2 下底面面积:S 下底=πr 2侧面积:S 侧=πl (r +r ′)表面积: S =π(r ′2+r 2+r ′l +rl )2.圆柱、圆锥、圆台的体积 V 圆柱=πr 2h (r 是底面半径,h 是高), V 圆锥=13πr 2h (r 是底面半径,h 是高),V 圆台=13 πh (r ′2+r ′r +r 2)(r ′,r 分别是上、下底面半径,h 是高).3.球的表面积和体积 表面积:S =4πR 2. 体积:V =43πR 3.1.圆柱、圆锥、圆台的侧面积公式之间有什么关系? 提示:S 圆柱侧=2πrl ――→r ′=rS 圆台侧=π(r ′+r )l ――→r ′=0S 圆锥侧=πrl . 2.球面能展开成平面图形吗? 提示:不能展开成平面图形.1.判断正误(正确的打“√”,错误的打“×”) (1)圆柱的侧面面积等于底面面积与高的积.( )(2)圆柱、圆锥、圆台的展开图分别是一个矩形、扇形、扇环.( ) (3)决定球的大小的因素是球的半径.( )(4)球面被经过球心的平面截得的圆的半径等于球的半径.( ) 答案:(1)× (2)× (3)√ (4)√2.若圆锥的底面半径为3 ,高为1,则圆锥的体积为( ) A .π3B .π2C .πD .2π答案:C3.若一个球的直径为 2,则此球的表面积为( ) A .2π B .16π C .8π D .4π解析:选D .因为球的直径为 2,所以球的半径为 1,所以球的表面积 S =4πR 2=4π.4.圆柱的侧面展开图是长 12 cm ,宽 8 cm 的矩形,则这个圆柱的体积为( ) A .288π cm 3B .192πcm 3C .288π cm 3或192π cm 3D .192π cm 3解析:选 C .当圆柱的高为 8 cm 时, V =π×⎝⎛⎭⎫122π 2×8=288π (cm 3),当圆柱的高为 12 cm 时,V =π×⎝⎛⎭⎫82π 2×12=192π(cm 3). [学生用书P75]探究点1 圆柱、圆锥、圆台的表面积 [问题探究]求圆柱、圆锥、圆台的表面积时,关键是什么?探究感悟:求圆柱、圆锥的表面积时,关键是求其母线长与底面的半径;求圆台的表面积时,关键是求其母线长与上、下底面的半径.(1)若圆锥的高为3,底面半径为4,则此圆锥的表面积为( ) A .40π B .36π C .26πD .20π(2)圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为( ) A .81π B .100π C .168πD .169π【解析】 (1)圆锥的母线l =32+42 =5,所以圆锥的表面积为π×42+π×4×5=36π.故选B.(2)圆台的轴截面如图所示,设上底面半径为r ,下底面半径为R ,则它的母线长为l =h 2+(R -r )2 =(4r )2+(3r )2 =5r =10,所以r =2,R =8.故S 侧=π(R +r )l =π×(8+2)×10=100π,S 表=S 侧+πr 2+πR 2=100π+4π+64π=168π.故选C.【答案】 (1)B (2)C圆柱、圆锥、圆台的表面积的求解步骤解决圆柱、圆锥、圆台的表面积问题,要利用好旋转体的轴截面及侧面展开图,借助于平面几何知识,求得所需几何要素,代入公式求解即可,基本步骤如下:(1)得到空间几何体的展开图; (2)依次求出各个平面图形的面积; (3)将各平面图形的面积相加.1.若一个圆柱的轴截面是面积为9的正方形,则这个圆柱的侧面积为( ) A .9π B .12π C .272πD .454π解析:选A.由于圆柱的轴截面是面积为9的正方形,则h =2r =3,所以圆柱的侧面积为2πr ·h =9π.2.如图,已知直角梯形ABCD ,BC ∥AD ,∠ABC =90°,AB =5,BC =16,AD =4,求以BC 所在直线为轴旋转一周所得几何体的表面积.解:以BC 所在直线为轴旋转一周所得几何体是圆柱和圆锥的组合体,如图.其中圆锥的高为16-4=12,圆柱的母线长为AD =4,圆锥的母线长CD =13,故该几何体的表面积为2π×5×4+π×52+π×5×13=130π.探究点2 圆柱、圆椎、圆台的体积(2021·贵州安顺高二期末)若一个圆锥的侧面展开图是半径为3,圆心角为120°的扇形,求该圆锥的体积.【解】 设圆锥底面半径为r ,则由题意得2πr =120180·π·3,解得r =1.所以底面面积为S =πr 2=π. 又圆锥的高h =32-12 =22 ,故圆锥的体积V =13 Sh =13 ×π×22 =223π.求圆柱、圆锥、圆台的体积问题,一是要牢记公式,然后观察空间图形的构成,是单一的旋转体,还是组合体;二是注意旋转体的构成,以及圆柱、圆锥、圆台轴截面的性质,从而找出公式中需要的各个量,代入公式计算.1.圆台上、下底面面积分别是π,4π,侧面积是6π,则这个圆台的体积是( ) A .233 πB .2 3C .736πD .733π解析:选D.S 1=π,S 2=4π,所以r =1,R =2,S 侧=6π=π(r +R )l ,所以l =2,所以h=3 .所以V =13 π(1+4+2)×3 =733π.故选D.2.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积的比值为( )A .1B .12C .32D .34解析:选D.设圆柱底面圆半径为R ,圆锥底面圆半径为r ,高都为h ,由已知得2Rh =rh ,所以r =2R ,所以V 柱∶V 锥=πR 2h ∶13πr 2h =3∶4,故选D.探究点3 球的表面积与体积 [问题探究]用一个平面去截球体,截面是什么形状?该截面的几何量与球的半径之间有什么关系? 探究感悟:用一个平面去截球体,截面是圆面.在不过球心的截面图中,截面圆与球的轴截面的关系如图所示.其关系为R 2=d 2+r 2.用与球心距离为1的平面去截球,所得截面圆的面积为π,则球的表面积为( ) A .8π3B .32π3C .8πD .82π3【解析】 设球的半径为R ,则截面圆的半径为R 2-1 ,所以截面圆的面积为S =π(R 2-1 )2=(R 2-1)π=π,所以R 2=2,所以球的表面积S =4πR 2=8π.故选C. 【答案】 C(1)球的表面积和体积的求解关键因为球的表面积和体积都与球的半径有关,所以在解答这类问题时,设法求出球的半径是解题的关键.(2)球的截面问题的解题技巧①有关球的截面问题,常画出过球心的截面圆,将问题转化为平面中圆的问题. ②解题时要注意借助球半径R 、截面圆半径r 、球心到截面的距离d 构成的直角三角形,即R 2=d 2+r 2.1.(2021·江苏徐州高一期中)一个球的表面积是16π,那么这个球的体积为( ) A .163 πB .323 πC .643πD .2563π解析:选B.设这个球的半径为R ,则4πR 2=16π,解得R =2,所以这个球的体积V =43 πR 3=323π.故选B. 2.两个球的半径相差 1,表面积之差为 28π,则它们的体积之和为________. 解析:设大、小两球半径分别为 R ,r ,则⎩⎪⎨⎪⎧R -r =1,4πR 2-4πr 2=28π,所以⎩⎪⎨⎪⎧R =4,r =3.所以体积之和为 43 πR 3+43 πr 3=364π3 .答案:364π3探究点4 与球有关的切、接问题(1)一个长方体的各个顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为 1,2,3,则此球的表面积为________.(2)如图,在圆柱O 1O 2内有一个球O ,该球与圆柱的上、下底面及母线均相切,记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________.【解析】 (1)长方体外接球直径长等于长方体体对角线长,即 2R =12+22+32 =14 ,所以球的表面积 S =4πR 2=14π.(2)设球O 的半径为r ,则圆柱的底面半径为r ,高为2r ,所以V 1V 2 =πr 2·2r 43πr 3 =32.【答案】 (1)14π (2)32(1)常见几何体与球的切、接问题的解题策略①处理有关几何体外接球或内切球的相关问题时,要注意球心的位置与几何体的关系.一般情况下,由于球的对称性,球心总在特殊位置,比如中心、对角线的中点等.②解决此类问题的实质就是根据几何体的相关数据求球的直径或半径,关键是根据“切点”和“接点”作出轴截面图,把空间问题转化为平面问题来计算.(2)几个常用结论①球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径. ②球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径. ③球与圆柱的底面和侧面均相切,则球的直径等于圆柱的高,也等于圆柱底面圆的直径.将棱长为 2 的正方体木块削成一个体积最大的球,则该球的体积为( )A .4π3B .2π3C .3π2D .π6解析:选A.由题意知,此球是正方体的内切球,根据其几何特征知,此球的直径与正方体的棱长是相等的,故可得球的直径为 2,故半径为 1,其体积是43 ×π×13=4π3.[学生用书P77]1.已知圆柱的底面半径r =1,母线长l 与底面的直径相等,则该圆柱的表面积为( ) A .6π B .8π C .9πD .10π解析:选A.因为圆柱的表面积为2πr 2+2πrl ,r =1,l =2,所以圆柱的表面积为6π.故选A.2.若球的大圆面积扩大为原来的2倍,球的体积扩大为原来的( ) A .8倍 B .4倍 C .22 倍D .2倍解析:选C.球的大圆面积扩大为原来的2倍,则球的半径扩大为原来的2 倍,所以球的体积扩大为原来的22 倍.3.设三棱柱的侧棱垂直于底面,所有棱的长都为 a ,顶点都在一个球面上,则该球的表面积为( )A .πa 2B .73 πa 2C .113πa 2D .5πa 2解析:选B.由题意知,该三棱柱为正三棱柱,且侧棱与底面边长相等,均为 a .如图,P 为三棱柱上底面的中心,O 为球心,易知 AP =23 ×32 a =33 a ,OP =12a ,所以球的半径 R = OA 满足R 2=⎝⎛⎭⎫33a 2 +⎝⎛⎭⎫12a 2=712 a 2,故 S 球=4πR 2=73 πa 2.4.已知圆台上、下底面半径分别为1,2,高为3,则圆台的体积为__________. 解析:由公式知V 圆台=13 π(1+2+4)×3=7π.答案:7π5.如图所示,在边长为4的正三角形ABC 中,E ,F 分别是AB ,AC 的中点,AD ⊥BC ,EH ⊥BC ,FG ⊥BC ,D ,H ,G 为垂足,若将正三角形ABC 绕AD 旋转180°,求阴影部分形成的几何体的体积.解:由题意知,旋转后几何体是一个圆锥,从下面挖去一个圆柱,且圆锥的底面半径为2,高为23 ,圆柱的底面半径为1,高为3 .所求旋转体的体积为大圆锥的体积减去里面小圆柱的体积,即V 旋转体=13 ×π×22×23 -π×12×3 =533 π,故所求旋转体的体积为533π. [学生用书P217(单独成册)][A 基础达标]1.在△ABC 中,AB =4,BC =3,AC =5,现以AB 所在直线为轴旋转一周,则所得几何体的表面积为( )A .24πB .21πC .33πD .39π解析:选A.因为在△ABC 中,AB =4,BC =3,AC =5,所以△ABC 是以∠B 为直角的直角三角形,故以AB 所在直线为轴旋转一周得到的几何体为圆锥,所以圆锥的底面半径为3,母线长为5,所以底面周长为6π,侧面积为12 ×6π×5=15π,所以几何体的表面积为15π+π×32=24π.故选A.2.两个球的体积之比为8∶27,那么这两个球的表面积之比为( ) A .2∶3 B .4∶9 C .2 ∶3D .8 ∶27解析:选B.设两个球的半径分别为r ,R ,则⎝⎛⎭⎫43πr 3 ∶⎝⎛⎭⎫43πR 3 =r 3∶R 3=8∶27, 所以r ∶R =2∶3,所以S 1∶S 2=r 2∶R 2=4∶9.3.(多选)如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R 相等,则下列结论正确的是( )A .圆柱的侧面积为2πR 2B .圆锥的侧面积为2πR 2C .圆柱的侧面积与球面面积相等D .圆柱、圆锥、球的体积之比为3∶1∶2解析:选CD.依题意得球的半径为R ,则圆柱的侧面积为2πR ×2R =4πR 2,所以A 错误;圆锥的侧面积为πR ×5 ·R =5 πR 2,所以B 错误;球面面积为4πR 2,因为圆柱的侧面积为4πR 2,所以C 正确;因为V 圆柱=πR 2·2R =2πR 3,V 圆锥=13 πR 2·2R =23 πR 3,V 球=43 πR 3,所以V 圆柱∶V 圆锥∶V 球=2πR 3∶23 πR 3∶43πR 3=3∶1∶2,所以D 正确.故选CD.4.将半径为R 的半圆卷成一个圆锥,则它的体积是( ) A .524 πR 3 B .58 πR 3 C .324πR 3 D .38πR 3 解析:选C.设圆锥的底面半径为r ,则2πr =πR ,所以r =R2 .所以圆锥的高h =R 2-r 2 =32R . 所以圆锥的体积V =13 πr 2×h =13 π(R 2 )2×32 R =324πR 3.故选C.5.若两球的体积之和是 12π,经过两球球心的截面圆周长之和为 6π,则两球的半径之差为( )A .1B .2C .3D .4解析:选 A .设两球的半径分别为 R ,r (R >r ),则由题意得⎩⎪⎨⎪⎧4π3R 3+4π3r 3=12π,2πR +2πr =6π,解得⎩⎪⎨⎪⎧R =2,r =1.故 R -r =1. 6.一个高为2的圆柱,底面周长为2π,该圆柱的表面积为________.解析:由底面周长为2π可得底面半径为1.S 底=πr 2=π,S 侧=2πr ·h =4π,所以S 表=2S底+S 侧=6π.答案:6π7.表面积为3π的圆锥,它的侧面展开图是一个半圆,则该圆锥的底面直径为________. 解析:设圆锥的母线为l ,圆锥底面半径为r ,由题意可知,πrl +πr 2=3π,且πl =2πr .解得r =1,即圆锥的底面直径为2.答案:28.圆柱形容器内盛有高度为8 cm 的水,若放入三个相同的铁球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的铁球(如图所示),则铁球的半径是________cm.解析:设铁球的半径为x cm ,由题意得πx 2×8=πx 2×6x -43 πx 3×3,解得x =4.答案:49.某组合体的直观图如图所示,它的中间为圆柱形,左右两端均为半球形,若图中r =1,l =3,试求该组合体的表面积和体积.解:该组合体的表面积S =4πr 2+2πrl =4π×12+2π×1×3=10π, 该组合体的体积V =43 πr 3+πr 2l =43 π×13+π×12×3=13π3.10.已知一个圆锥的底面半径为R ,高为H ,在其内部有一个高为x 的内接圆柱. (1)求圆柱的侧面积;(2)x 为何值时,圆柱的侧面积最大?解:(1)作圆锥的轴截面,如图所示.因为rR =H -x H,所以r =R -RH x ,所以S 圆柱侧=2πrx =2πRx -2πR Hx 2(0<x <H ). (2)因为-2πRH<0,所以当x =2πR 4πR H=H2 时,S 圆柱侧最大.故当x =H2时,即圆柱的高为圆锥高的一半时,圆柱的侧面积最大.[B 能力提升]11.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为323 π,那么这个正三棱柱的体积是( )A .963B .163C .243D .483解析:选D.由题意可知正三棱柱的高等于球的直径,从棱柱中间平行棱柱底面截得球的大圆内切于正三角形,正三角形与棱柱底面三角形全等,设三角形边长为a ,球半径为r ,由V 球=43 πr 3=323 π,得r =2.由S 柱底=12 a ×r ×3=34 a 2,得a =23 r =43 ,所以V 柱=S柱底·2r =483 .12.如图,一个盛满溶液的玻璃杯,其形状为一个倒置的圆锥,现放一个球状物体完全浸没于杯中,球面与圆锥侧面相切,且与玻璃杯口所在平面相切,则溢出溶液的体积为( )A .8327 πB .4327 πC .16327πD .32327π解析:选D.由题意,设球的半径为r ,作出玻璃杯的轴截面,可得一个半径为r 的圆内切于一个边长为4的等边三角形,此等边三角形的高h =23 .根据中心(重心)的性质可得,球的半径r =13 h =233 ,所以球的体积V =43 πr 3=43 π×⎝⎛⎭⎫233 3 =32327 π.即溢出溶液的体积为32327π,故选D.13.(多选)如图所示,△ABC 的三边长分别是AC =3,BC =4,AB =5,过点C 作CD ⊥AB ,垂足为D ,下列说法正确的是( )A .以BC 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为15πB .以BC 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为36π C .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为25πD .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为16π解析:选AD.以BC 所在直线为轴旋转时,所得旋转体为底面半径为3,母线长为5,高为4的圆锥,所以侧面积为π×3×5=15π,体积为13 ×π×32×4=12π,所以A 正确,B 错误;以AC 所在直线为轴旋转时,所得旋转体为底面半径为4,母线长为5,高为3的圆锥,侧面积为π×4×5=20π,体积为13×π×42×3=16π,所以C 错误;D 正确.故选AD.14.在长方体ABCD -A 1B 1C 1D 1中,AB =BC =2,过A 1,C 1,B 三点的平面截去长方体的一个角后,得到如图所示的几何体ABCD -A 1C 1D 1,这个几何体的体积为403.(1)求棱AA 1的长;(2)求经过A 1,C 1,B ,D 四点的球的表面积和体积.解:(1)设AA 1=x ,依题意可得403 =2×2·x -13 ×12 ×2×2·x ,解得x =4,故棱AA 1的长为4.(2)依题意可知, 经过A 1,C 1,B ,D 四点的球就是长方体ABCD -A 1B 1C 1D 1的外接球,这个球的直径就是长方体的体对角线,所以球的直径2R =22+22+42 =26 ,解得R =6 .故所求球的表面积为4πR 2=24π,体积为43·πR 3=86 π.[C 拓展探究]15.如图,用一边长为2 的正方形硬纸,按各边中点垂直折起4个小三角形,做成一个“底座”,将体积为4π3 的球放入其中,“底座”形状保持不变,则球的最高点与“底座”底面的距离为( )A .62 +32 B .32C .22 +32D .32 +32解析:选D.由题意,可得“底座”的底面是边长为1的正方形,则经过4个小三角形的顶点截球所得的截面圆的直径为1.因为球的体积为4π3 ,所以球的半径为1,所以球心到截面圆的距离为1-⎝⎛⎭⎫122 =32 ,因为垂直折起的4个小直角三角形斜边上的高为12,所以球的最高点与“底座”底面的距离为32 +1+12 =32 +32.故选D. 16.如图,四边形ABCD 是正方形,BD ︵是以 A 为圆心、AB 为半径的弧,将正方形 ABCD 以 AB 为轴旋转一周,求图中 Ⅰ,Ⅱ,Ⅲ 三部分经旋转所得几何体的体积之比.解:Ⅰ生成圆锥,Ⅱ生成的是半球去掉Ⅰ生成的圆锥,Ⅲ生成的是圆柱去掉扇形 ABD 生成的半球.设正方形的边长为 a ,则Ⅰ,Ⅱ,Ⅲ 三部分经旋转所得几何体的体积分别为 V Ⅰ,V Ⅱ,V Ⅲ,则 V Ⅰ=13 πa 3,V Ⅱ=12 ×43 πa 3-13 πa 3=13 πa 3,V Ⅲ=πa 3-12 ×43 πa 3=13πa 3.所以三部分经旋转所得几何体的体积之比为1∶1∶1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1圆柱的表面积与体积
知识点一:圆柱的认识
(1)底面:圆柱的上下两个面叫做底面,它们是完全相同的两个圆。
(2)侧面:圆柱周围的面是一个曲面,叫做侧面。
(3)高:圆柱两个底面之间的距离叫做高。
注:圆柱有无数条高
(4)侧面展开:圆柱的侧面展开后是一个长方形。
长方形的长是圆柱的底面周长,长方形的
宽是圆柱的高。
知识点二:圆柱的侧面积和表面积
(1)侧面积:圆柱侧面展开后长方形的面积。
(2)侧面积公式:圆柱的侧面积=底面周长×高
(3)表面积:圆柱的侧面积和两个底面的面积之和。
(4)表面积计算公式:圆柱的表面积=圆柱的侧面积+圆柱的两个底面积
知识点三:圆柱的体积
(1)定义:一个圆柱所占空间的大小叫做这个圆柱的体积。
(2)计算公式:圆柱的体积=底面积×高
随堂练习:
一.圆柱的表面积
1.求下面圆柱体的表面积
(1)底面半径是3厘米,高是10厘米。
(2)底面直径是2米,高是底面直径的2.5倍。
(3) 底面周长是6.28cm,高是0.7cm(π取3.14)
2.一个圆柱的底面周长是18.84厘米,高是5厘米,它的表面积是多少平方厘米(π取
3.14)?
3.一个圆柱底面周长是12.56分米,高是6分米,这个圆柱的表面积是多少平方米(π取3.14)?
4.把一段长12分米的圆木锯成3段,表面积增加了37.68平方分米,求原来圆木的表面积?
5.一个圆柱形油桶的底面直径是4分米,高是6分米,做一个这样的油桶(无盖)至少需要多少铁皮?
6.把一段圆柱木料经过底面直径沿高切成两块,它的切面是一个面积为25平方厘米的正方形,原来圆柱体表面积为多少平方厘米(π取3.14)?
二.圆柱的体积
1.求下列圆柱的体积(π取3.14):
(1) 底面直径为5cm,高为10cm:
(2) 底面积是9.42平方厘米,高1.5分米:
(3) 底面直径是10厘米,高是底面直径的
1倍:
2
2. 一个圆柱形粮仓,底面直径是2米,高1.5米,每立方米空间可以装小麦750千克,这个粮仓可以装小麦多少千克(π取
3.14)?
3.一个圆柱形水桶的体积是24立方分米,底面积是6平方分米,桶内装满了水,求水面高是多少分米?
3. 4.把一个圆柱体的高缩短2厘米,底面不变,它的表面积就减少了25.12平方厘米,求这个圆柱原来的体积是多少立方厘米(π取3.14)?。
