解密:粟裕在黄桥战役中做的三道“数学题”
一名将军排兵布阵数学题

一名将军排兵布阵数学题摘要:1.问题背景2.将军排兵布阵的数学问题3.数学问题的解决方法4.将军对解决方案的反应5.问题背后的启示正文:在古代,一名将军为了在战争中取得胜利,需要巧妙地安排兵力,使得每个士兵都能发挥最大的作用。
有一天,这位将军遇到了一个看似简单的数学问题,却让他绞尽脑汁。
这个问题是这样的:假设有一个由100 名士兵组成的方阵,每一行有10 名士兵,总共10 行。
现在需要从方阵中挑选出一些士兵,组成一个新的方阵。
新方阵的要求是:新方阵的每一行都要比原方阵的对应行多2 名士兵。
问最少需要从原方阵中挑选出多少名士兵,才能满足这个条件?将军对这个问题的解决方案非常感兴趣,因为它可以帮助他在战争中更有效地调动兵力。
为了解决这个问题,将军请教了一位聪明的谋士。
谋士告诉将军,解决这个问题需要运用数学中的“最优化理论”。
具体来说,可以通过求解一个线性规划问题来找到最少需要挑选的士兵数量。
线性规划是一种求解最优化问题的方法,它主要涉及四个步骤:1.确定目标函数;2.列出约束条件;3.画出可行域;4.在可行域内找到最优解。
在这个问题中,目标函数是最少挑选士兵数量,约束条件是原方阵和新方阵的行数以及总人数。
通过画出可行域,我们可以找到最优解,即最少需要挑选的士兵数量。
将军听了谋士的解释后,认为这个方法非常巧妙,可以帮助他在战争中更有效地调动兵力。
他感慨道:“战争虽然残酷,但智慧之光始终照耀着人类。
通过运用数学智慧,我们可以更好地保卫家园。
”这个故事告诉我们,无论在古代战争还是现代社会,数学都是解决问题的重要工具。
部编数学八年级上册专题13.2将军饮马(最值模型)专项讲练(解析版)含答案

专题13.2 将军饮马(最值模型) 专项讲练三角形中的最值(将军饮马模型)问题在考试中,无论是解答题,还是选择、填空题,都是学生感觉有困难的地方,也恰是学生能力区分度最重要的地方,主要考查转化与化归等的数学思想。
在各类考试中都以中高档题为主,中考说明中曾多处涉及。
在解决几何最值问题主要依据是:①两点之间,线段最短;②垂线段最短,涉及的基本方法还有:利用轴对称变换化归到“三角形两边之和大于第三边”、“三角形两边之差小于第三边”等。
希望通过本专题的讲解让大家对这类问题有比较清晰的认识。
【解题技巧】题型1: 求两条线段和最小值例1.(2022·广东新丰·八年级期末)如图所示,在ABC V 中,AB AC =,直线EF 是AB 的垂直平分线,D 是BC 的中点,M 是EF 上一个动点,ABC V 的面积为12,4BC =,则BDM V 周长的最小值是______.【答案】8【分析】连接AD ,AM ,由EF 是线段AB 的垂直平分线,得到AM =BM ,则△BDM 的周长=BD +BM +DM =AM +DM +BD ,要想△BDM 的周长最小,即要使AM +DM 的值最小,故当A 、M 、D 三点共线时,AM+DM最小,即为AD,由此再根据三线合一定理求解即可.【详解】解:如图所示,连接AD,AM,∵EF是线段AB的垂直平分线,∴AM=BM,∴△BDM的周长=BD+BM+DM=AM+DM+BD,∴要想△BDM的周长最小,即要使AM+DM的值最小,∴当A、M、D三点共线时,AM+DM最小,即为AD,∵AB=AC,D为BC的中点,∴AD⊥BC,122BD BC==,∴1122ABCS AD BC=×=△,∴AD=6,∴△BDM的周长最小值=AD+BD=8,故答案为:8.【点睛】本题主要考查了线段垂直平分线的性质,三线合一定理,解题的关键在于能够根据题意得到当A、M、D三点共线时,AM+DM最小,即为AD.变式1.(2022·甘肃西峰·八年级期末)如图,在等边△ABC中,E为AC边的中点,AD垂直平分BC,P是AD上的动点.若AD=6,则EP+CP的最小值为_______________.【答案】6【分析】要求EP+CP的最小值,需考虑通过作辅助线转化EP,CP的值,从而找出其最小值求解.【详解】解:作点E关于AD的对称点F,连接CF,∵△ABC是等边三角形,AD是BC边上的中垂线,∴点E关于AD的对应点为点F,∴CF就是EP+CP的最小值.∵△ABC 是等边三角形,E 是AC 边的中点,∴F 是AB 的中点,∴CF =AD =6,即EP +CP 的最小值为6,故答案为6.【点睛】本题考查等边三角形的性质和轴对称等知识,熟练掌握等边三角形和轴对称的性质是本题的关键.变式2.(2021·湖北洪山·八年级期中)如图,将△ABC 沿AD 折叠使得顶点C 恰好落在AB 边上的点M 处,D 在BC 上,点P 在线段AD 上移动,若AC =6,CD =3,BD =7,则△PMB 周长的最小值为 ___.【答案】18【分析】首先明确要使得△PMB 周长最小,即使得PM +PB 最小,再根据翻折的性质可知PM =PC ,从而可得满足PC +PB 最小即可,根据两点之间线段最短确定BC 即为最小值,从而求解即可.【详解】解:由翻折的性质可知,AM =AC ,PM =PC ,∴M 点为AB 上一个固定点,则BM 长度固定,∵△PMB 周长=PM +PB +BM ,∴要使得△PMB 周长最小,即使得PM +PB 最小,∵PM =PC ,∴满足PC +PB 最小即可,显然,当P 、B 、C 三点共线时,满足PC +PB 最小,如图所示,此时,P 点与D 点重合,PC +PB =BC ,∴△PMB 周长最小值即为BC +BM ,此时,作DS ⊥AB 于S 点,DT ⊥AC 延长线于T 点,AQ ⊥BC 延长线于Q 点,由题意,AD 为∠BAC 的角平分线,∴DS =DT ,∵1122ACD S AC DT CD AQ ==V g g ,1122ABD S AB DS BD AQ ==V g g ,∴11221122ABDACD AB DS BD AQ S S AC DT CD AQ ==V V g g g g ,即:AB BD AC CD =,∴763AB =,解得:AB =14,∵AM =AC =6,∴BM =14-6=8,∴△PMB 周长最小值为BC +BM =3+7+8=18,故答案为:18.【点睛】本题考查翻折的性质,以及最短路径问题等,掌握翻折的基本性质,利用角平分线的性质进行推理求解,理解并熟练运用两点之间线段最短是解题关键.变式3.(2022·河南濮阳·八年级期末)如图,等边三角形ABC 的边长为5,A 、B 、1A 三点在一条直线上,且11ABC A BC V V ≌.若D 为线段1BC 上一动点,则AD CD +的最小值是________.【答案】10【分析】连接CA 1交BC 1于点E ,C 、A 1关于直线BC 1对称,推出当点D 与B 重合时,AD +CD 的值最小,最小值为线段AA 1的长=10.【详解】解:连接CA 1交BC 1于点E ,过点B 作直线l ⊥AB ,如图,∵△ABC 是等边三角形,11ABC A BC V V ≌∴11A BC V 是等边三角形,AB =A 1B =5∵A 、B 、1A 三点在一条直线上,∴ △ABC 与△A 1BC 1关于直线l 对称,∵∠ABC =∠A 1BC 1=60°,∴∠CBC 1=60°,∴∠C 1BA 1=∠C 1BC ,∵BA 1=BC ,∴BD ⊥CA 1,CD =DA 1,∴C 、A 1关于直线BC 1对称,∴当点D 与B 重合时,AD +CD 的值最小,最小值为线段AA 1的长=10,故答案为:10.【点睛】本题考查轴对称﹣最短问题,等边三角形的性质等知识,解题的关键是学会找对称点,形成两点之间的线段来解决最短问题,属于中考常考题型.变式4.(2022•西湖区月考)如图直线l 1,l 2表示一条河的两岸,且l 1∥l 2,现要在这条河上建一座桥.桥建在何处才能使从村庄A 经过河到村庄B 的路线最短?画出示意图,并说明理由.【分析】先确定AA ′与河等宽,且AA ′⊥河岸,连接BA ′,与河岸的交点就是点C ,过点C 作CD 垂直河岸,交另一河岸于点D ,即可得出答案.【答案】解:如图,先确定AA ′与河等宽,且AA ′⊥河岸,连接BA ′,与河岸的交点就是点C ,过点C 作CD 垂直河岸,交另一河岸于点D ,CD 就是所求的桥的位置.理由:由作图过程可知,四边形ACDA ′为平行四边形,AD 平移至A ′C 即可得到线段A ′B ,两点之间,线段最短,由于河宽不变,CD 即为桥.【点睛】本题考查的是作图﹣平移变换以及利用轴对称解决最短路径问题,熟知图形平移不变性的性质是解答此题的关键.题型2: 求两条线段差最大值例2.(2022·绵阳市·八年级专题练习)如图,5AB AC ==,110BAC Ð=°,AD 是∠BAC 内的一条射线,且25BAD Ð=°,P 为AD 上一动点,则PB PC -的最大值是______.作点B 关于射线AD 的对称点B ¢,连接则AB AB ¢=,PB PB ¢=,B AD BAD Ð=Т∵ 5AB AC ==,∴5AB AC ¢==,∴ AB C ¢V 是等边三角形,∴5B C ¢=,在PB C ¢V 中,PB PC B C -¢£¢,变式1.(2022·福建福州·八年级期中)如图,在等边ABC V 中,E 是AC 边的中点,P 是ABC V 的中线AD 上的动点,且6AB =,则BP PE -的最大值是________.【答案】3【分析】连接PC ,则BP =CP ,BP PE -=CP-PE ,当点P 与点A 重合时,CP -PE =CE ,进而即可求解.【详解】解:连接PC ,∵在等边ABC V 中,6AB =,P 是ABC V 的中线AD 上的动点,∴AD 是BC 的中垂线,∴BP =CP ,∴BP PE -=CP-PE ,∵在CPE △中,CP -PE <CE ,∴当点P 与点A 重合时,CP -PE =CE ,∵E 是AC 边的中点,∴BP PE -的最大值=6÷2=3.故答案是:3.【点睛】本题主要考查等边三角形的性质,三角形三边长关系,连接CP ,得到BP PE -=CP-PE ,是解题的关键.题型3: 求三条(周长)最小值(双动点问题)【模型图示】要求:点P 位定点,在直线1l ,2l 上分别找点M ,N ,使PMN △周长(即MN PN PM ++)最小操作:分别作点P 关于直线1l ,2l 的对称点’P 和”P ,连结”’P P 与直线1l ,2l 的交点为M ,N ,()”’最小值△P P C PMN =求”’P P 长度通法:如上图,一般会给一个特殊角(15°,30°,45°,60°,75°)A ,连结’AP ,AP ,”AP ,由对称性可求A AP P Ð=Ð2”’也为特殊角(30°,60°,90°,120°,150°),”’AP AP AP ==,可得特殊等腰”’△P AP ,利用三边关系求出”’P P 要求:点P ,Q 为定点,直线1l ,2l 上分别找M ,N ,使PQMN 周长(即MN PN PM PQ +++)小操作:分别作点P ,Q 关于直线1l ,2l 的对称点’P 和’Q ,连结’’Q P 与直线1l ,2l 的交点为M ,N ,()’’最小值四边形Q P PQ C PQMN +=例3.(2022·上虞市初二月考)如图,点P 是∠AOB 内任意一点,OP =6cm ,点M 和点N 分别是射线OA 和射线OB 上的动点,若△PMN 周长的最小值是6 cm ,则∠AOB 的度数是( )A .15B .30C .45D .60【答案】B 【分析】分别作点P 关于OA 、OB 的对称点C 、D ,连接CD ,分别交OA 、OB 于点M 、N ,连接OC 、OD 、PM 、PN 、MN ,由对称的性质得出PM=DM ,OP=OC ,∠COA=∠POA ;PN=DN ,OP=OD ,∠DOB=∠POB,得出∠AOB=12∠COD,证出△OCD是等边三角形,得出∠COD=60°,即可得出结果.【解析】分别作点P关于OA、OB的对称点C、D,连接CD,分别交OA、OB于点M、N,连接OC、OD、PM、PN、MN,如图所示:∵点P关于OA的对称点为D,关于OB的对称点为C,∴PM=DM,OP=OD,∠DOA=∠POA;∵点P关于OB的对称点为C,∴PN=CN,OP=OC,∠COB=∠POB,∴OC=OP=OD,∠AOB=12∠COD,∵△PMN周长的最小值是6cm,∴PM+PN+MN=6,∴DM+CN+MN=6,即CD=6=OP,∴OC=OD=CD,即△OCD是等边三角形,∴∠COD=60°,∴∠AOB=30°,故选:B.【点睛】此题考查轴对称的性质,最短路线问题,等边三角形的判定与性质,熟练掌握轴对称的性质,证明三角形是等边三角形是解题的关键.变式1.(2022·安徽安庆·八年级期末)如图,在四边形ABCD中,∠BCD=50°,∠B=∠D=90°,在BC、CD上分别取一点M、N,使△AMN的周长最小,则∠MAN=_____°.【答案】80【分析】作点A关于BC、CD的对称点A1、A2,根据轴对称确定最短路线问题,连接A1、A2分别交BC、DC于点M、N,利用三角形的内角和定理列式求出∠A1+∠A2,再根据轴对称的性质和角的和差关系即可得∠MAN.【详解】如图,作点A关于BC、CD的对称点A1、A2,连接A1、A2分别交BC、DC于点M、N,连接AM、AN,则此时△AMN的周长最小,∵∠BCD=50°,∠B=∠D=90°,∴∠BAD=360°﹣90°﹣90°﹣50°=130°,∴∠A1+∠A2=180°﹣130°=50°,∵点A关于BC、CD的对称点为A1、A2,∴NA=NA2,MA=MA1,∴∠A2=∠NAD,∠A1=∠MAB,∴∠NAD+∠MAB=∠A1+∠A2=50°,∴∠MAN=∠BAD﹣(∠NAD+∠MAB)=130°﹣50°=80°,故答案为:80.【点睛】本题考查了轴对称的最短路径问题,利用轴对称将三角形周长问题转化为两点间线段最短问题是解决本题的关键.变式2.(2021·江苏九年级一模)如图,Rt△ABC中,∠C=90°,AC=3,BC=4,D,E,F分别是AB,BC,AC边上的动点,则△DEF的周长的最小值是()A.2.5B.3.5C.4.8D.6【答案】C【分析】如图作D关于直线AC的对称点M,作D关于直线BC的对称点N,连接CM,CN,CD,EN,FM,DN,DM.由∠MCA=∠DCA,∠BCN=∠BCD,∠ACD+∠BCD=90°,推出∠MCD+∠NCD=180°,可得M、B、N共线,由DF+DE+EF=FM+EN+EF,FM+EN+EF≥MN,可知当M、F、E、N共线时,且CD⊥AB时,DE+EF+FD的值最小,最小值=2CD,求出CD的值即可解决问题.【详解】解:如图,作D关于直线AC的对称点M,作D关于直线BC的对称点N,连接CM,CN,CD,EN ,FM ,DN ,DM .∴DF =FM ,DE =EN ,CD =CM ,CD =CN ,∴CD =CM =CN ,∵∠MCA =∠DCA ,∠BCN =∠BCD ,∠ACD +∠BCD =90°,∴∠MCD +∠NCD =180°,∴M 、C 、N 共线,∵DF +DE +EF =FM +EN +EF ,∵FM +EN +EF ≥MN ,∴当M 、F 、E 、N 共线时,且CD ⊥AB 时,DE +EF +FD 的值最小,最小值为MN =2CD ,∵CD ⊥AB ,∴12•AB •CD =12•AB•AC ,∴CD =•AB AC AB =125=2.4,∴DE +EF +FD 的最小值为4.8.故选:C .【点睛】本题考查了轴对称-最短问题、两点之间线段最短、垂线段最短等知识,解题的关键是灵活运用轴对称以及垂线段最短解决最短问题,属于中考选择题中的压轴题.变式3.(2021·和平区·天津一中八年级期末)如图,25AOB Ð=°,点M ,N 分别是边OA ,OB 上的定点,点P ,Q 分别是边OB ,OA 上的动点,记MPQ a Ð=,PQN b Ð=,当MP PQ QN ++的值最小时,b a -的大小=__________(度).【答案】50【分析】作M 关于OB 的对称点M ¢,N 关于OA 的对称点N ¢,连接M N ¢¢,交OB 于点P ,交OA 于点Q ,连接MP ,QN ,可知此时MP PQ QN ++最小,此时OPM OPM NPQ OQP AQN AQN ¢¢Ð=Ð=ÐÐ=Ð=Ð,,再根据三角形外角的性质和平角的定义即可得出结论.【详解】作M 关于OB 的对称点M ¢,N 关于OA 的对称点N ¢,连接M N ¢¢,交OB 于点P ,交OA 于点Q ,连接MP ,QN ,如图所示.根据两点之间,线段最短,可知此时MP PQ QN ++最小,即MP PQ QN M N ¢¢++=,∴OPM OPM NPQ OQP AQN AQN ¢¢Ð=Ð=ÐÐ=Ð=Ð,,∵MPQ PQN a b Ð=Ð=,,∴11(180)(180)22QPN OQP a b Ð=°-Ð=°-,,∵QPN AOB OQP Ð=Ð+Ð,25AOB Ð=°,∴11(180)25(180)22a b °-=°+°- ,∴50b a -=° .故答案为:50.【点睛】本题考查轴对称-最短问题、三角形内角和,三角形外角的性质等知识,灵活运用所学知识解决问题是解题的关键,综合性较强.课后训练:1.(2022·重庆八中七年级期末)如图,90A C Ð=Ð=°,且4AB AC ==,D ,E 分别为射线AC 和射线CF 上两动点,且AD CE =,当BD BE +有最小值时,则BDE D 的面积为________.【答案】6【分析】延长AC ,以点C 为圆心,AC 为半径,作圆弧交延长线于点G ,得AC CG =.连接AE 、GE 、BG ,ADB CEA CEG D D D @@,得BD AE GE ==,当点B ,E ,G 三点在一条直线,BD BE GE BE+=+距离最短.过点E ¢作E H AC ¢∥交BA 于点H ,得BHE E CG D D ¢¢@,得BH E C AH ¢==,BE E G ¢¢=,D ¢,过点E ¢作E H AC ¢∥交BA 于点H ∴E H AC ¢∥∴BE Ð又∵AC HE CG ¢==,90BHE E CG ¢¢Ð=Ð=°∴BHE E CG D D ¢¢@∴122CE BH AH AB ¢====2.(2021·山东临沂市·八年级期末)如图,ABC D 中,AB AC =,3BC =,6ABC S D =,AD BC ^于点D ,EF 是AB 的垂直平分线,交AB 于点E ,交AC 于点F ,在EF 上确定一点P ,使PB PD +最小,则这个最小值为( )A .3.5B .4C .4.5D .5【答案】B【分析】根据三角形的面积公式得到AD=4,由EF 垂直平分AB ,得到点A ,B 关于直线EF 对称,于是得到AD=PB+PD 的最小值,即可得到结论.【详解】解:∵AB=AC ,BC=3,S △ABC =6,AD ⊥BC 于点D ,∴AD=4,∵EF 垂直平分AB ,∴点A ,B 关于直线EF 对称,∴EF 与AD 的交点P 即为所求,如图,连接PB ,此时PA=PB ,PB+PD=PA+PD=AD ,AD=PB+PD 的最小值,即PB+PD 的最小值为4,故选:B .【点睛】本题考查了轴对称-最短路线问题,线段的垂直平分线的性质,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.3.(2022·山东八年级期末)如图,在ABC V 中,6AB =,7BC =,4AC =,直线m 是ABC V 中BC 边的垂直平分线,P 是直线m 上的一动点,则APC △的周长的最小值为_________.【答案】10【分析】根据题意知点C 关于直线m 的对称点为点B ,故当点P 与点D 重合时,AP +CP 值的最小,求出AB 长度即可得到结论.【详解】解:∵直线m 垂直平分BC ,∴B 、C 关于直线m 对称,设直线m 交AB 于D ,∴当P 和D 重合时,AP +CP 的值最小,最小值等于AB 的长,∴△APC 周长的最小值是6+4=10.故答案为:10.【点睛】本题考查了勾股定理,轴对称−最短路线问题的应用,解此题的关键是找出P 的位置.4.(2022·陕西安康·八年级期末)如图,ABC V 的面积为24,AB 的长为8,AD 平分BAC Ð,E 、F 分别是AD 和AC 上的动点,则CE EF +的最小值为____________.【点睛】本题考查轴对称—最短路线问题.灵活应用角平分线性质、三角形三边的关系、垂线段最短,将所求最小值转化为求CH 的长是解题的关键.5.(2022·山东临沂·八年级期中)如图,ABC D 中,AB AC =,3BC =,6ABC S D =,AD BC ^于点D ,EF 是AB 的垂直平分线,交AB 于点E ,交AC 于点F ,在EF 上确定一点P ,使PB PD +最小,则这个最小值为( )A .3.5B .4C .4.5D .5【答案】B 【分析】根据三角形的面积公式得到AD=4,由EF 垂直平分AB ,得到点A ,B 关于直线EF 对称,于是得到AD=PB+PD 的最小值,即可得到结论.【详解】解:∵AB=AC ,BC=3,S △ABC =6,AD ⊥BC 于点D ,∴AD=4,∵EF 垂直平分AB ,∴点A ,B 关于直线EF 对称,∴EF 与AD 的交点P 即为所求,如图,连接PB ,此时PA=PB ,PB+PD=PA+PD=AD ,AD=PB+PD 的最小值,即PB+PD 的最小值为4,故选:B .【点睛】本题考查了轴对称-最短路线问题,线段的垂直平分线的性质,凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.6.(2022·河南·安阳市殷都区教科培中心八年级期末)如图,在ABC V 中,AB AC =,边AC 的垂直平分线MN 分别交AB ,AC 于点M ,N ,点D 是边BC 的中点,点P 是MN 上任意一点,连接PD ,PC ,若A a Ð=,CPD b Ð=,PCD V 周长最小时,a ,b 之间的关系是( )A .a b>B .a b <C .a b =D .90a b=°-故选C .【点睛】本题考查线段垂直垂直平分线的性质,等腰三角形的性质,角平分线的定义以及三角形外角性质.根据题意理解当A 、P 、D 在同一直线上时PCD L V 最小是解题关键.7.(2022·全国·八年级期中)如图,在Rt ABC V 中,ACB 90Ð=°,AC 9=,BC 12=,15AB =,AD 是BAC Ð的平分线,若点P 、Q 分别是AD 和AC 上的动点,则PC PQ +的最小值是______.CO=PC+PO=PC+PQ ,此时PC+PQ 有可能取得最小值,∵当CO 垂直于AB 即CO 移到CM 位置时,CO ∴PC+PQ 的最小值即为CM 的长度,8.(2022·清远市八年级期中)如图,点D 是锐角AOB Ð内一点,DE OA ^于点E ,点F 是线段OE 的一个动点,点G 是射线OB 的一个动点,连接DF 、FG 、GD ,当DFG V 的周长最小时,FDG Ð与AOB Ð的数量关系式是________.【答案】2180FDG AOB Ð+Ð=°【分析】作D 关于OA 的对称点D ′,作D 关于OB 的对称得D ″,连接D ′D ″,交OA 、OB 于F 、G ,此时△DFG 的周长最小,最小值为D ′D ″,连OD 、OD ′、OD ″,根据轴对称的性质得出△GOD ≌△GOD ″,△FOD ≌△FOD ′,即可得出∠BOD =∠BOD ′,∠ODG =∠OD ″G ,∠DOA =∠AOD ′,∠ODF =∠ODF ′,由∠D ′OD ″=2∠AOB ,∠GDF =∠ODF ′+∠ODG ″根据三角形内角和定理即可得出2∠AOB +∠GDF =180°.【详解】解:作D 关于OA 的对称点D ′,作D 关于OB 的对称得D ″,连接D ′D ″,交OA 、OB 于F 、G ,此时△DFG 的周长最小,最小值为D ′D ″,连OD 、OD ′、OD ″,由轴对称的性质可知,△GOD ≌△GOD ″,△FOD ≌△FOD ′,∴∠BOD =∠BOD ″,∠ODG =∠OD ″G ,∠DOA =∠AOD ′,∠ODF =∠OD ′F ,∴∠D ′OD ″=2∠AOB ,∠GDF =∠OD ′F +∠OD ″G ,∵∠D ′OD ″+∠OD ′F +∠OD ″G =180°,∴2∠AOB +∠GDF =180°,故答案为2∠AOB +∠GDF =180°.【点睛】本题考查了轴对称-最短路线问题,熟练掌握轴对称的性质是解题的关键.9.(2021·湖北武汉市·八年级期末)如图,点A 在y 轴上,G 、B 两点在x 轴上,且G (﹣3,0),B (﹣2,0),HC 与GB 关于y 轴对称,∠GAH =60°,P 、Q 分别是AG 、AH 上的动点,则BP +PQ +CQ 的最小值是( )A .6B .7C .8D .9【答案】B 【分析】分别作B 、C 关于AG 和AH 对称的点B ¢、C ¢,连接BP 、CQ 、B C ¢、C Q ¢,PQ ,得出BP +PQ +CQ 的最小值为B C ¢¢,再依据等边三角形的性质和判定和轴对称的性质分别求得B P PN ¢+和C Q QN ¢+即可求得.【详解】解:分别作B 、C 关于AG 和AH 对称的点B ¢、C ¢,连接BP 、CQ 、B C ¢、C Q ¢,PQ∵HC 与GB 关于y 轴对称, ∴GO=HO,BO=CO,∵x 轴⊥y 轴,∴AG=AH ,B ¢、C ¢关于y 轴对称,∴当B ¢、C ¢,P 、Q 在同一条直线上时,BP PQ CQ B P PQ C Q B C ¢¢¢¢==++++最小,此时//B C x ¢¢轴,∵∠GAH =60°,∴△AGH 为等边三角形,∴∠AGO=60°,∵//B C x ¢¢轴,B 、B ¢关于AG 对称,∴60BPG B PG PGB ¢Ð=Ð=Ð=°,B P BP ¢=,∴△BPG 为等边三角形,过作PM ⊥GO 交x 轴与M ,∵G (﹣3,0),B (﹣2,0),∴BG=1,BO=2,∴111,22PB PB BG BM BG ¢=====,∴171222B P PN BP MB BO ¢+=++=++=,同理可得72C Q QN ¢+=,即7B C ¢¢=.故选:B .【点睛】本题考查轴对称的性质,等边三角形的性质和判断,坐标与图形变化.能借助轴对称的性质正确变形将折线的长化成一条线段的长是解题关键.10.(2022·河南·九年级专题练习)如图,在ABC D 中,AB AC =,AC 的垂直平分线交AC 于点N ,交AB 于点M ,12AB cm =,BMC D 的周长是20cm ,若点P 在直线MN 上,则PA PB -的最大值为( )A .12cmB .8cmC .6cmD .2cm 【答案】B 【分析】根据已知条件MN 垂直平分AC ,可知MA MC =,即可将BMC D 的周长转换为AB+BC ,即可求出8BC cm =,再通过作辅助线(见详解),可得到PA PB PC PB -=-,则PBC D 中PC PB BC -<,当P B C 、、共线时(PC PB -)有最大值即可得到PA PB -最大值,得到答案.【详解】解:∵MN 垂直平分AC ∴MA MC=又∵20BMC C BM MC BC cmD =++=∴20BM MA BC cm++=12BM MA AB cm +== 8BC cm=在MN 上取点P 1∵MN 垂直平分AC连接1P A 、1PB 、1PC ∴11P A PC = ∴PA PB PC PB-=-在1PBC D 中11PC PB BC -<当1P 运动2P 位置时,即P B C 、、共线时(PC PB -)有最大值,此时8PC PB BC cm -==.即PA PB -最大值是8cm,故答案选B.【点睛】本题考查了垂直平分线的性质,线段垂直平分线上的点到线段两端的距离相等11.(2021·河南商丘·八年级期中)如图,等边△ABC 中,AD 为BC 边上的高,点M 、N 分别在AD 、AC 上,且AM =CN ,连BM 、BN ,当BM +BN 最小时,∠MBN 的度数为( )A .15°B .22.5°C .30°D .47.5°【答案】C 【分析】如图1中,作CH ⊥BC ,使得CH =BC ,连接NH ,BH .证明△ABM ≌△CHN (SAS ),推出BM =HN ,由BN +HN ≥BH ,可知B ,N ,H 共线时,BM +BN =NH +BN 的值最小,求出此时∠MBN 即可解决问题.【详解】解:如图1中,作CH ⊥BC ,使得CH =BC ,连接NH ,BH .∵△ABC是等边三角形,AD⊥BC,CH⊥BC,∴∠DAC=∠DAB=30°,AD∥CH,∴∠HCN=∠CAD=∠BAM=30°,∵AM=CN,AB=BC=CH,∴△ABM≌△CHN(SAS),∴BM=HN,∵BN+HN≥BH,∴B,N,H共线时,BM+BN=NH+BN的值最小,如图2中,当B,N,H共线时,∵△ABM≌△CHN,∴∠ABM=∠CHB=∠CBH=45°,∵∠ABD=60°,∴∠DBM=15°,∴∠MBN=45°﹣15°=30°,∴当BM+BN的值最小时,∠MBN=30°,故选:C.【点睛】本题考查轴对称,等边三角形的性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.12.(2022·湖北青山·八年级期中)如图,在Rt △ABC 中,∠ACB =90°,∠ABC =30°,AC =2,以BC 为边向左作等边△BCE ,点D 为AB 中点,连接CD ,点P 、Q 分别为CE 、CD 上的动点.(1)求证:△ADC 为等边三角形;(2)求PD +PQ +QE 的最小值.【答案】(1)证明见解析;(2)4.【分析】(1)先根据直角三角形的性质可得60,BAC AD CD Ð=°=,再根据等边三角形的判定即可得证;(2)连接,PA QB ,先根据等边三角形的性质可得12ACE ACD Ð=Ð,再根据等腰三角形的三线合一可得CE 垂直平分AD ,然后根据线段垂直平分线的性质可得PA PD =,同样的方法可得QB QE =,从而可得PD PQ QE PA PQ QB ++=++,最后根据两点之间线段最短即可得出答案.【详解】证明:(1)Q 在Rt ABC V 中,90,30,2ACB ABC AC Ð=°Ð=°=,60,24BAC AB AC Ð\=°==,Q 点D 是Rt ABC V 斜边AB 的中点,2AD AC \==,ADC \V 是等边三角形;(2)如图,连接,PA QB ,BCE QV 和ADC V 都是等边三角形,60BCE \Ð=°,60ACD Ð=°,1302ACE ACB BCE ACD \Ð=Ð-Ð=°=Ð,CE \垂直平分AD ,PA PD \=,同理可得:CD 垂直平分BE ,QB QE \=,PD PQ QE PA PQ QB \++=++,由两点之间线段最短可知,当点,,,A P Q B 共线时,PA PQ QB ++取得最小值AB ,故PD PQ QE ++的最小值为4.【点睛】本题考查了等边三角形的判定与性质、含30°角的直角三角形的性质等知识点,熟练掌握等边三角形的性质是解题关键.13.(2022·福建·莆田二中八年级期末)如图,在Rt△ABC中,∠ACB=90°,AC=BC,点C在直线MN上,∠BCN=30°,点P为MN上一动点,连结AP,BP.当AP+BP的值最小时,∠CBP的度数为_____.【答案】15°##15度【分析】作点B关于MN的对称点D,连接AD交MN于P,连接BP,CD,先证明△BCD是等边三角形,从而得到AC=CD,∠ACD=∠ACB +∠BCD=150°,进而求得∠CDP=15°,据轴对称性可得∠CBP的度数.【详解】如图,作点B关于MN的对称点D,连接AD交MN于P,连接BP,CD,∵点B与点D是关于MN的对称点,∠BCN=30°,∴BC=CD,∠BCD=60°,∴△BCD是等边三角形,∵∠ACB=90°,AC=BC,∴AC=CD,∠ACD=∠ACB +∠BCD=150°,∴∠CDP=15°,∵点B与点D是关于MN的对称点,,且△BCD是等边三角形,∴由等边三角形的轴对称性可知:∠CBP=∠CDP=15°,故答案为:15°.【点睛】本题主要考查了等腰直角三角形和等边三角形的性质,轴对称最短线路问题等知识,明确AP+BP的最小值为AD长是解题的关键.14.(2022·湖北·武汉市六中位育中学八年级)如图,//AB DP ,E 为DP 上一动点,AB CB CD ==,过A 作AN EC ^交直线EC 于N ,过D 作DM EC ^交直线EC 于点M ,若114B Ð=°,当AN DM -的值最大时,则ACE Ð= ________ .【答案】123°【分析】当DM 与DP 重合,AN 与AB 重合时,|AN -DM |的值最大,此时|AN -DM |=AB ,画出相应的图形,根据条件,利用三角形的内角和、邻补角的意义,求出结果.【详解】解:当DM 与DP 重合,AN 与AB 重合时,|AN -DM |的值最大,此时|AN -DM |=AB ,∵∠ABC =114°,∴∠CDE =180°-114°=66°,∴∠MCD =90°-66°=24°,又∵AB =BC ,∴∠ACB =(180°-114°)÷2=33°,∴∠ACE =180°-∠ACB -∠DCM =180°-33°-24°=123°,故答案为:123°.【点睛】本题考查了平行线的性质、三角形内角和、直角三角形、等腰三角形的性质等知识,根据题意画出相应图形是解决问题的关键.。
将军一马数学题

将军一马数学题
(原创版)
目录
1.将军一马数学题的背景和起源
2.将军一马数学题的解题思路和方法
3.将军一马数学题的启示和价值
正文
一、将军一马数学题的背景和起源
“将军一马数学题”起源于古代战争中的一个故事。
据说,古时一位将军在战场上遇到了一个棘手的问题:他需要率领部队穿越一片狭窄的峡谷,但敌人在峡谷的另一侧设有重兵把守。
为了尽快通过峡谷,将军需要找到一种方法,使得部队既能够安全通过,又能够最大限度地减少敌人的攻击。
这个问题逐渐演变成了一个著名的数学问题,即“将军一马数学题”。
二、将军一马数学题的解题思路和方法
将军一马数学题的解题思路主要涉及到图论中的最短路径问题。
最短路径问题是指在给定有向图或无向图中,从源节点到目的节点之间寻找一条边权值之和最小的路径问题。
解决这个问题的方法有 Dijkstra 算法、Floyd 算法等。
将军一马数学题的解题过程可以分为以下几个步骤:
1.将将军和马看作两个节点,峡谷看作一条边,构建一个图模型。
2.利用最短路径算法,如 Dijkstra 算法或 Floyd 算法,求解从将军节点到马节点的最短路径。
3.根据算法结果,将军可以通过的最短路径来指导他的行动,以最小化敌人的攻击。
三、将军一马数学题的启示和价值
将军一马数学题不仅具有趣味性,还具有一定的现实意义。
它启示我们在解决实际问题时,可以将问题抽象成数学模型,利用数学方法来求解。
同时,它也体现了数学在战争、工程等领域中的应用价值。
此外,将军一马数学题也反映了图论这一数学分支在实际问题中的广泛应用。
揭秘:粟裕的几次败仗

揭秘:粟裕的几次败仗粟裕素以能征善战、愈战愈奇著称于世。
毛泽东曾说,数粟裕最会打仗。
苏中民谣“毛主席当家家家旺粟司令打仗仗仗胜”,其实粟裕指挥的第三野战军是五大野战军中战绩最大,损失也是最大的一支部队。
在这里仅把所知道一些战役粗略统计了一下,总结了粟裕指挥三野的八大败仗,供大家探讨,有些战例的资料缺乏,仅作参考,欢迎给予补充。
一、泗县战役1946年7月华野山东部队将国民党第7军的172师包围在泗县城里打了两天,华野损失惨重。
此时国民党第7军的171师也突破阻击逼近泗县,对粟裕部队形成内外夹攻之势,华野不得不撤围。
其中华野核心主力之一的鲁南第8师遭受重大损失,伤亡过半。
从此国民党第7军中便流传着“钢军硬,共军不敢碰一碰”的顺口溜。
如果按“8师伤亡过半”的标准,那么泗县战役,仅8师就伤亡5000人左右。
再加上参战的2纵、9纵,此役,解放军伤亡应在7000人左右,国民党军仅损失3000人。
二、淮阴之战1946年9月,张灵甫率国民党整编74师主攻苏皖解放区首府淮阴,整编74师一路突破华野在运河与洪泽湖之间设置三道防线,到达淮阴城下,谭震林下令扒开运河大堤,放水也无法迟滞74师的迅猛攻击。
18日张灵甫亲临一线督战,发起夜战,从解放军各纵队的结合部成功突破,用假口令诈开南门,对华野进行内外夹击,解放军反击未能奏效,全线崩溃,被迫于19日撤出淮阴。
74师继续追击,又于22日攻占淮安,至此,国民党军控制两淮,张灵甫获三等云麾勋章。
解放军在华东只剩下了山东解放区,华中主要工商区两淮的丢失对于华野兵力补充、后勤补给和部队回旋都造成了致命的打击。
三、第二次涟水保卫战1946年12月,张灵甫统一指挥国民党军整编74师和整编第28师第192旅以及新7军一部共5个旅二攻涟水,张灵甫吸取以往教训,以一部从西面攻击涟水,解放军措手不及,华野三大主力之一的第6师奉命回师增援,在涟水城外被74师重创,6师伤亡达5000人以上,完全丧失了战斗力。
江苏省泰兴市黄桥集团2024届中考数学押题试卷含解析

江苏省泰兴市黄桥集团2024届中考数学押题试卷注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(共10小题,每小题3分,共30分)1.如图,∠ACB=90°,D 为AB 的中点,连接DC 并延长到E ,使CE=13CD ,过点B 作BF ∥DE ,与AE 的延长线交于点F ,若AB=6,则BF 的长为( )A .6B .7C .8D .102.全球芯片制造已经进入10纳米到7纳米器件的量产时代. 中国自主研发的第一台7纳米刻蚀机,是芯片制造和微观加工最核心的设备之一,7纳米就是0.000000007米. 数据0.000000007用科学计数法表示为( ) A .9710-⨯ B .10710-⨯ C .11710-⨯ D .12710-⨯3.一球鞋厂,现打折促销卖出330双球鞋,比上个月多卖10%,设上个月卖出x 双,列出方程( ) A .10%x =330B .(1﹣10%)x =330C .(1﹣10%)2x =330D .(1+10%)x =3304.如图,在⊙O 中,弦AB=CD ,AB ⊥CD 于点E ,已知CE•ED=3,BE=1,则⊙O 的直径是( )A .2B 5C .5D .55.下面调查方式中,合适的是( )A .调查你所在班级同学的体重,采用抽样调查方式B .调查乌金塘水库的水质情况,采用抽样调査的方式C.调查《CBA联赛》栏目在我市的收视率,采用普查的方式D.要了解全市初中学生的业余爱好,采用普查的方式6.若分式11x-有意义,则x的取值范围是A.x>1 B.x<1 C.x≠1D.x≠07.如图是由五个相同的小立方块搭成的几何体,则它的俯视图是()A.B.C.D.8.下图是某几何体的三视图,则这个几何体是()A.棱柱B.圆柱C.棱锥D.圆锥9.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于()A.40°B.45°C.50°D.60°10.如图,AD是半圆O的直径,AD=12,B,C是半圆O上两点.若AB BC CD==,则图中阴影部分的面积是()A.6πB.12πC.18πD.24π二、填空题(本大题共6个小题,每小题3分,共18分)11.分解因式:m3–m=_____.12.如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是______.13.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=23,则CE的长为_______14.如果抛物线y=(m﹣1)x2的开口向上,那么m的取值范围是__.15.如图,把一块直角三角板的直角顶点放在直尺的一边上,若∠1=50°,则∠2=_____°.16.布袋中装有2个红球和5个白球,它们除颜色外其它都相同.如果从这个布袋里随机摸出一个球,那么所摸到的球恰好为红球的概率是 ________.三、解答题(共8题,共72分)17.(8分)定义:如果把一条抛物线绕它的顶点旋转180°得到的抛物线我们称为原抛物线的“孪生抛物线”.(1)求抛物线y=x2﹣2x的“孪生抛物线”的表达式;(2)若抛物线y=x2﹣2x+c的顶点为D,与y轴交于点C,其“孪生抛物线”与y轴交于点C′,请判断△DCC’的形状,并说明理由:(3)已知抛物线y=x2﹣2x﹣3与y轴交于点C,与x轴正半轴的交点为A,那么是否在其“孪生抛物线”上存在点P,在y轴上存在点Q,使以点A、C、P、Q为顶点的四边形为平行四边形?若存在,求出P点的坐标;若不存在,说明理由.18.(8分)如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.(1)求证:BD平分∠ABC;(2)连接EC,若∠A=30°,DC=3,求EC的长.19.(8分)如图所示,点B、F、C、E在同一直线上,AB⊥BE,DE⊥BE,连接AC、DF,且AC=DF,BF=CE,求证:AB=DE.20.(8分)如图,要在木里县某林场东西方向的两地之间修一条公路MN,已知C点周围200米范围内为原始森林保护区,在MN上的点A处测得C在A的北偏东45°方向上,从A向东走600米到达B处,测得C在点B的北偏西60°方向上.(1)MN是否穿过原始森林保护区,为什么?(参考数据:3≈1.732)(2)若修路工程顺利进行,要使修路工程比原计划提前5天完成,需将原定的工作效率提高25%,则原计划完成这项工程需要多少天?21.(8分)如图,△ABC中,∠C=90°,AC=BC,∠ABC的平分线BD交AC于点D,DE⊥AB于点E.(1)依题意补全图形;(2)猜想AE与CD的数量关系,并证明.22.(10分)已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB 的延长线于G.求证:△ADE≌△CBF;若四边形BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.23.(12分)﹣(﹣1)2018+4﹣(13)﹣124.为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:2≈1.414,3≈1.732)参考答案一、选择题(共10小题,每小题3分,共30分)1、C【解题分析】∵∠ACB=90°,D为AB的中点,AB=6,∴CD=12AB=1.又CE=13 CD,∴CE=1,∴ED=CE+CD=2.又∵BF∥DE,点D是AB的中点,∴ED是△AFB的中位线,故选C.2、A【解题分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10-n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.【题目详解】数据0.000000007用科学记数法表示为7×10-1.故选A.【题目点拨】本题考查用科学记数法表示较小的数,一般形式为a×10-n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.3、D【解题分析】解:设上个月卖出x双,根据题意得:(1+10%)x=1.故选D.4、C【解题分析】作OH⊥AB于H,OG⊥CD于G,连接OA,根据相交弦定理求出EA,根据题意求出CD,根据垂径定理、勾股定理计算即可.【题目详解】解:作OH⊥AB于H,OG⊥CD于G,连接OA,由相交弦定理得,CE•ED=EA•BE,即EA×1=3,解得,AE=3,∴AB=4,∵OH⊥AB,∴AH=HB=2,∵AB=CD,CE•ED=3,∴CD=4,∵OG⊥CD,∴EG=1,由题意得,四边形HEGO是矩形,由勾股定理得,OA=225AH OH +=,∴⊙O 的直径为25,故选C .【题目点拨】此题考查了相交弦定理、垂径定理、勾股定理、矩形的判定与性质;根据图形作出相应的辅助线是解本题的关键. 5、B【解题分析】由普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似.【题目详解】A 、调查你所在班级同学的体重,采用普查,故A 不符合题意;B 、调查乌金塘水库的水质情况,无法普查,采用抽样调査的方式,故B 符合题意;C 、调查《CBA 联赛》栏目在我市的收视率,调查范围广适合抽样调查,故C 不符合题意;D 、要了解全市初中学生的业余爱好,调查范围广适合抽样调查,故D 不符合题意;故选B .【题目点拨】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.6、C【解题分析】分式分母不为0,所以10x -≠,解得1x ≠.故选:C.7、A【解题分析】试题分析:从上面看易得上面一层有3个正方形,下面中间有一个正方形.故选A .【考点】简单组合体的三视图.8、D【解题分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.【题目详解】由俯视图易得几何体的底面为圆,还有表示锥顶的圆心,符合题意的只有圆锥.故选D .【题目点拨】本题考查由三视图确定几何体的形状,主要考查学生空间想象能力以及对立体图形的认识.9、C【解题分析】分析:根据两直线平行,同位角相等可得1115EGD ∠=∠=︒,再根据三角形内角与外角的性质可得∠C 的度数. 详解:∵AB ∥CD ,∴1115EGD ∠=∠=︒,∵265∠=,∴1156550C ∠=-=,故选C.点睛:考查平行线的性质和三角形外角的性质,三角形的一个外角等于与它不相邻的两个内角的和.10、A【解题分析】根据圆心角与弧的关系得到∠AOB=∠BOC=∠COD=60°,根据扇形面积公式计算即可.【题目详解】∵AB BC CD ==,∴∠AOB=∠BOC=∠COD=60°.∴阴影部分面积=2606=6360⨯ππ. 故答案为:A.【题目点拨】本题考查的知识点是扇形面积的计算,解题关键是利用圆心角与弧的关系得到∠AOB=∠BOC=∠COD=60°.二、填空题(本大题共6个小题,每小题3分,共18分)11、m (m+1)(m-1)【解题分析】根据因式分解的一般步骤:一提(公因式)、二套(平方差公式()()22a b a b a b -=+-,完全平方公式()2222a ab b a b ±+=±)、三检查(彻底分解),可以先提公因式,再利用平方差完成因式分解 【题目详解】解:()()()32111m m m m m m m -=-=+- 故答案为:m (m+1)(m-1).【题目点拨】本题考查因式分解,掌握因式分解的技巧是解题关键.12、①②③④ .【解题分析】由正方形的性质得出∠FAD =90°,AD =AF =EF ,证出∠CAD =∠AFG ,由AAS 证明△FGA ≌△ACD ,得出AC =FG ,①正确;证明四边形CBFG 是矩形,得出S △FAB =12FB •FG =12S 四边形CBFG ,②正确; 由等腰直角三角形的性质和矩形的性质得出∠ABC =∠ABF =45°,③正确;证出△ACD ∽△FEQ ,得出对应边成比例,得出④正确.【题目详解】解:∵四边形ADEF 为正方形,∴∠FAD =90°,AD =AF =EF ,∴∠CAD +∠FAG =90°,∵FG ⊥CA ,∴∠GAF +∠AFG =90°,∴∠CAD =∠AFG ,在△FGA 和△ACD 中,G C AFG CAD AF AD ===∠∠⎧⎪∠∠⎨⎪⎩,∴△FGA ≌△ACD (AAS ),∴AC =FG ,①正确;∵BC =AC ,∴FG =BC ,∵∠ACB =90°,FG ⊥CA ,∴FG ∥BC ,∴四边形CBFG 是矩形,∴∠CBF =90°,S △FAB =12FB •FG =12S 四边形CBFG ,②正确; ∵CA =CB ,∠C =∠CBF =90°,∴∠ABC =∠ABF =45°,③正确;∵∠FQE =∠DQB =∠ADC ,∠E =∠C =90°,∴△ACD ∽△FEQ ,∴AC :AD =FE :FQ ,∴AD •FE =AD 2=FQ •AC ,④正确;故答案为①②③④.【题目点拨】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.13、或【解题分析】分析:由菱形的性质证出△ABD 是等边三角形,得出BD =AB =6,132OB BD ==,由勾股定理得出OC OA ===,即可得出答案. 详解:∵四边形ABCD 是菱形,∴AB =AD =6,AC ⊥BD ,OB =OD ,OA =OC ,∵60BAD ∠=︒,∴△ABD 是等边三角形,∴BD =AB =6, ∴132OB BD ==,∴OC OA ===∴2AC OA ==∵点E 在AC 上,23OE =, ∴当E 在点O 左边时2353CE OC =+=,当点E 在点O 右边时233CE OC =-=,∴53CE =或3;故答案为53或3.点睛:考查菱形的性质,注意分类讨论思想在数学中的应用,不要漏解.14、m >2【解题分析】试题分析:根据二次函数的性质可知,当抛物线开口向上时,二次项系数m ﹣2>2.解:因为抛物线y=(m ﹣2)x 2的开口向上,所以m ﹣2>2,即m >2,故m 的取值范围是m >2.考点:二次函数的性质.15、40【解题分析】如图,∵∠1=50°,∴∠3=∠1=50°,∴∠2=90°﹣50°=40°,故答案为:40.16、【解题分析】试题解析:∵一个布袋里装有2个红球和5个白球,∴摸出一个球摸到红球的概率为:.考点:概率公式.三、解答题(共8题,共72分)17、(1)y=-(x-1)²=-x²+2x-2;(2)等腰Rt △,(3)P1(3,-8),P2(-3,-20).【解题分析】(1)当抛物线绕其顶点旋转180°后,抛物线的顶点坐标不变,只是开口方向相反,则可根据顶点式写出旋转后的抛物线解析式;(2)可分别求出原抛物线和其“孪生抛物线”与y轴的交点坐标C、C′,由点的坐标可知△DCC’是等腰直角三角形;(3)可求出A(3,0),C(0,-3),其“孪生抛物线”为y=-x2+2x-5,当AC为对角线时,由中点坐标可知点P不存在,当AC为边时,分两种情况可求得点P的坐标.【题目详解】(1)抛物线y=x2-2x化为顶点式为y=(x-1)2-1,顶点坐标为(1,-1),由于抛物线y=x2-2x绕其顶点旋转180°后抛物线的顶点坐标不变,只是开口方向相反,则所得抛物线解析式为y=-(x-1)2-1=-x2+2x-2;(2)△DCC'是等腰直角三角形,理由如下:∵抛物线y=x2-2x+c=(x-1)2+c-1,∴抛物线顶点为D的坐标为(1,c-1),与y轴的交点C的坐标为(0,c),∴其“孪生抛物线”的解析式为y=-(x-1)2+c-1,与y轴的交点C’的坐标为(0,c-2),∴CC'=c-(c-2)=2,∵点D的横坐标为1,∴∠CDC'=90°,由对称性质可知DC=DC’,∴△DCC'是等腰直角三角形;(3)∵抛物线y=x2-2x-3与y轴交于点C,与x轴正半轴的交点为A,令x=0,y=-3,令y=0时,y=x2-2x-3,解得x1=-1,x2=3,∴C(0,-3),A(3,0),∵y=x2-2x-3=(x-1)2-4,∴其“孪生抛物线”的解析式为y=-(x-1)2-4=-x2+2x-5,若A、C为平行四边形的对角线,∴其中点坐标为(32,−32),设P(a,-a2+2a-5),∵A、C、P、Q为顶点的四边形为平行四边形,∴Q(0,a-3),∴23252a a a--+-=−32,化简得,a2+3a+5=0,△<0,方程无实数解,∴此时满足条件的点P不存在,若AC为平行四边形的边,点P在y轴右侧,则AP∥CQ且AP=CQ,∵点C和点Q在y轴上,∴点P的横坐标为3,把x=3代入“孪生抛物线”的解析式y=-32+2×3-5=-9+6-5=-8,∴P1(3,-8),若AC为平行四边形的边,点P在y轴左侧,则AQ∥CP且AQ=CP,∴点P的横坐标为-3,把x=-3代入“孪生抛物线”的解析式y=-9-6-5=-20,∴P2(-3,-20)∴原抛物线的“孪生抛物线”上存在点P1(3,-8),P2(-3,-20),在y轴上存在点Q,使以点A、C、P、Q为顶点的四边形为平行四边形.【题目点拨】本题是二次函数综合题型,主此题主要考查了根据二次函数的图象的变换求抛物线的解析式,解题的关键是求出旋转后抛物线的顶点坐标以及确定出点P的位置,注意分情况讨论.18、(1)见解析;(2)EC=【解题分析】(1)直接利用直角三角形的性质得出12DE BE AB==,再利用DE∥BC,得出∠2=∠3,进而得出答案;(2)利用已知得出在Rt△BCD中,∠3=60°,DC=,得出DB的长,进而得出EC的长. 【题目详解】(1)证明:∵AD⊥DB,点E为AB的中点,∴12DE BE AB==.∴∠1=∠2.∵DE∥BC,∴∠2=∠3.∴∠1=∠3.∴BD平分∠ABC.(2)解:∵AD⊥DB,∠A=30°,∴∠1=60°.∴∠3=∠2=60°.∵∠BCD=90°,∴∠4=30°.∴∠CDE=∠2+∠4=90°.在Rt△BCD中,∠3=60°,3DC=,∴DB=2.∵DE=BE,∠1=60°,∴DE=DB=2.∴22437EC DE DC=+=+=.【题目点拨】此题主要考查了直角三角形斜边上的中线与斜边的关系,正确得出DB,DE的长是解题关键.19、证明见解析【解题分析】试题分析:证明三角形△ABC≅△DEF,可得AB=DE.试题解析:证明:∵BF=CE,∴BC=EF,∵AB⊥BE,DE⊥BE,∴∠B=∠E=90°,AC=DF,∴△ABC≅△DEF,∴AB=DE.20、(1)MN不会穿过森林保护区.理由见解析;(2)原计划完成这项工程需要25天.【解题分析】试题分析:(1)要求MN是否穿过原始森林保护区,也就是求C到MN的距离.要构造直角三角形,再解直角三角形;(2)根据题意列方程求解.试题解析:(1)如图,过C作CH⊥AB于H,设CH=x,由已知有∠EAC=45°, ∠FBC=60°则∠CAH=45°, ∠CBA=30°,在RT△ACH中,AH=CH=x,在RT△HBC中,tan∠HBC=CH HB∴HB=tan30CH =33x =3x , ∵AH+HB=AB∴x+3x=600解得x≈220(米)>200(米).∴MN 不会穿过森林保护区.(2)设原计划完成这项工程需要y 天,则实际完成工程需要y-5根据题意得:15y =(1+25%)×1y,解得:y=25知:y=25的根. 答:原计划完成这项工程需要25天.21、 (1)见解析;(2)见解析.【解题分析】(1)根据题意画出图形即可;(2)利用等腰三角形的性质得∠A =45∘.则∠ADE =∠A =45°,所以AE =DE ,再根据角平分线性质得CD =DE ,从而得到AE =CD .【题目详解】解:(1)如图:(2)AE 与 CD 的数量关系为AE =CD .证明:∵∠C =90°,AC =BC ,∴∠A =45°.∵DE ⊥AB ,∴∠ADE =∠A =45°.∴AE =DE ,∵BD 平分∠ABC ,∴CD =DE ,∴AE =CD .【题目点拨】此题考查等腰三角形的性质,角平分线的性质,解题关键在于根据题意作辅助线.22、(1)证明见解析(2)当四边形BEDF 是菱形时,四边形AGBD 是矩形;证明见解析;【解题分析】(1)在证明全等时常根据已知条件,分析还缺什么条件,然后用(SAS ,ASA ,SSS )来证明全等;(2)先由菱形的性质得出AE=BE=DE ,再通过角之间的关系求出∠2+∠3=90°即∠ADB=90°,所以判定四边形AGBD 是矩形.【题目详解】解:()1证明:∵四边形ABCD 是平行四边形,∴4C ∠=∠,AD CB =,AB CD =.∵点E 、F 分别是AB 、CD 的中点, ∴12AE AB =,12CF CD =. ∴AE CF =.在AED 和CBF 中,AD CB DAE C AE CF =⎧⎪∠=∠⎨⎪=⎩,∴()ADE CBF SAS ≅.()2解:当四边形BEDF 是菱形时,四边形AGBD 是矩形.证明:∵四边形ABCD 是平行四边形,∴//AD BC .∵//AG BD ,∴四边形AGBD 是平行四边形.∵四边形BEDF 是菱形,∴DE BE =.∵AE BE =,∴AE BE DE ==.∴12∠=∠,34∠=∠.∵1234180∠+∠+∠+∠=,∴2223180∠+∠=.∴2390∠+∠=.即90ADB ∠=.∴四边形AGBD 是矩形.【题目点拨】本题主要考查了平行四边形的基本性质和矩形的判定及全等三角形的判定.平行四边形基本性质:①平行四边形两组对边分别平行;②平行四边形的两组对边分别相等;③平行四边形的两组对角分别相等;④平行四边形的对角线互相平分.三角形全等的判定条件:SSS ,SAS ,AAS ,ASA .23、-1.【解题分析】直接利用负指数幂的性质以及算术平方根的性质分别化简得出答案.【题目详解】原式=﹣1+1﹣3=﹣1.【题目点拨】本题主要考查了实数运算,正确化简各数是解题的关键.24、凉亭P 到公路l 的距离为273.2m .【解题分析】分析:作PD ⊥AB 于D ,构造出Rt △APD 与Rt △BPD ,根据AB 的长度.利用特殊角的三角函数值求解.【题目详解】详解:作PD ⊥AB 于D .设BD=x,则AD=x+1.∵∠EAP=60°,∴∠PAB=90°﹣60°=30°.在Rt△BPD中,∵∠FBP=45°,∴∠PBD=∠BPD=45°,∴PD=DB=x.在Rt△APD中,∵∠PAB=30°,∴PD=tan30°•AD,即DB=PD=tan30°•AD=x=33(1+x),解得:x≈273.2,∴PD=273.2.答:凉亭P到公路l的距离为273.2m.【题目点拨】此题考查的是直角三角形的性质,解答此题的关键是构造出两个特殊角度的直角三角形,再利用特殊角的三角函数值解答.。
初中数学最值问题01专题-将军饮马模型与最值问题(含答案)

初中数学最值问题专题1 将军饮马模型与最值问题【模型导入】 什么是将军饮马?“白日登山望烽火,黄昏饮马傍交河”,这是唐代诗人李颀《古从军行》里的一句诗。
而由此却引申出一系列非常有趣的数学问题,通常称为“将军饮马”。
【模型描述】如图,将军在图中点A 处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?【模型抽象】如图,在直线上找一点P 使得P A +PB 最小?这个问题的难点在于P A +PB 是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段. 【模型解析】作点A 关于直线的对称点A ’,连接P A ’,则P A ’=P A ,所以P A +PB =P A ’+PB 当A ’、P 、B 三点共线的时候,P A ’+PB =A ’B ,此时为最小值(两点之间线段最短)B 将军军营河P【模型展示】【模型】一、两定一动之点点在OA 、OB 上分别取点M 、N ,使得△PMN 周长最小.此处M 、N 均为折点,分别作点P 关于OA (折点M 所在直线)、OB (折点N 所在直线)的对称点,化折线段PM +MN +NP 为P ’M +MN +NP ’’,当P ’、M 、N 、P ’’共线时,△PMN 周长最小.【例题】如图,点P 是∠AOB 内任意一点,∠AOB =30°,OP =8,点M 和点N 分别是射线OA 和射线OB 上的动点,则△PMN 周长的最小值为___________.BBP OBAMNP''A【模型】二、两定两动之点点在OA 、OB 上分别取点M 、N 使得四边形PMNQ 的周长最小。
考虑PQ 是条定线段,故只需考虑PM +MN +NQ 最小值即可,类似,分别作点P 、Q 关于OA 、OB 对称,化折线段PM +MN +NQ 为P ’M +MN +NQ ’,当P ’、M 、N 、Q ’共线时,四边形PMNQ 的周长最小。
苏版初二上册将军饮马模型浅解讲义

苏版初二上册13将军饮马问题=轴对称问题=最短距离问题(轴对称是工具,最短距离是题 眼)。
所谓轴对称是工具,即这类问题最常用的做法确实是作轴对称。
而最短距离 是题眼,也就意味着归类这类的题目的理由。
比如题目经常会显现线段 a+b 如此 的条件或者问题。
一旦显现能够快速联想到将军饮马问题,然后利用轴对称解题。
将军饮马故事“将军饮马”问题是数学问题中的经典题目,要紧转化成“两点之间线段最短问题” 原题:如图,一位将军,从A 地动身,骑马到河边给马饮水,然后再到B 地,问如何样选择饮水的地点,才能使所走的路程最短?模型一:一条定直线,同侧两定点在直线l 的同侧有两点A,B,在L 上求一点P ,使得PA+PB 值最小。
一样做法:作点 A (B )关于直线的对称点,连接 A ’B ,A ’B 与直线交点即为所求点。
A ’B 即为最短距离 。
理由:A ’为 A 的对称点,因此不管 P 在直线任何位置都能得到 AP =A ’P 。
因此 PA+PB=PA ’+PB 。
如此问题就化成了求 A ’到 B 的最短距离,直截了当相连就能够了。
例一:某供电部门预备在输电主干线L 上连接一个分支线路,分支点为M ,同时向新落成的A 、B 两个居民小区送电。
已知两个居民小区A 、B 分别到主干线的距离AA1=2千米,BB1=1千米,且A1B1=4千米。
(1)假如居民小区A 、B 位于主干线L 的两旁,如图(1)所示,那么分支点M 在什么地点时总路线最短?最短线路的长度是多少千米? (2)假如居民小区A 、B 位于主干线L 的同旁,如图(2)所示,那么分支点M 在什么地点时总路线最短?现在分支点M 与A1的距离是多少千米? 模型二:一条定直线,一定点,一动点•A •B • A • B• B • A • A ’ • B ’ • A ’ • B ’ L L如图,已知直线L和定点A,在直线K上找一点B,在直线L上找一点P,使得AP+PB值最小。
2020中考数学专题8——最值问题之将军饮马 -含答案
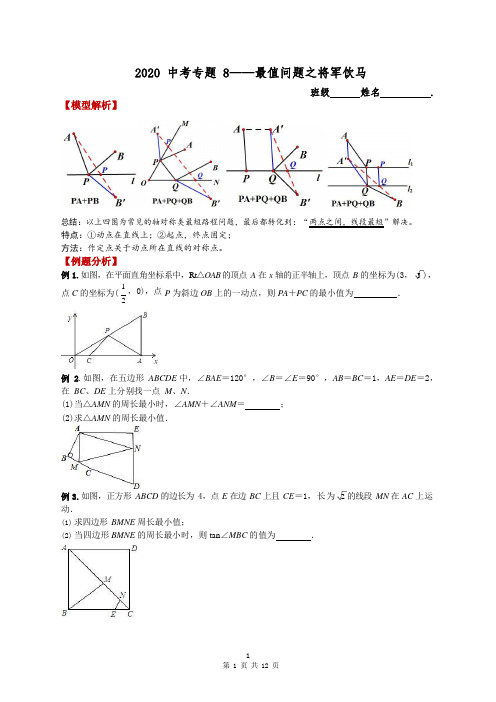
【模型解析】2020 中考专题 8——最值问题之将军饮马班级姓名.总结:以上四图为常见的轴对称类最短路程问题,最后都转化到:“两点之间,线段最短”解决。
特点:①动点在直线上;②起点,终点固定;方法:作定点关于动点所在直线的对称点。
【例题分析】例1.如图,在平面直角坐标系中,Rt△OAB 的顶点A 在x 轴的正半轴上,顶点B 的坐标为(3,3 ),点C 的坐标为(1,0),点2P 为斜边OB 上的一动点,则PA+PC 的最小值为.例 2.如图,在五边形ABCDE 中,∠BAE=120°,∠B=∠E=90°,AB=BC=1,AE=DE=2,在BC、DE 上分别找一点M、N.(1)当△AMN 的周长最小时,∠AMN+∠ANM=;(2)求△AMN 的周长最小值.例3.如图,正方形ABCD 的边长为 4,点E 在边BC 上且CE=1,长为 2 的线段MN 在AC 上运动.(1)求四边形BMNE 周长最小值;(2)当四边形BMNE 的周长最小时,则tan∠MBC 的值为.例4.在平面直角坐标系中,已知点A(一 2,0),点B(0,4),点E 在OB 上,且∠OAE=∠OB A.如图,将△AEO 沿x 轴向右平移得到△AE′O′,连接A'B、BE'.当AB+BE'取得最小值时,求点E'的坐标.例5.如图,已知正比例函数y=kx(k>0)的图像与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P 为y 轴上的一个动点,M、N 为函数y=kx(k>0)的图像上的两个动点,则AM+MP+PN 的最小值为.【巩固训练】1.如图1 所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P,使PD+PE 的和最小,则这个最小值为.图1 图2 图3 图42.如图2,在菱形ABCD 中,对角线AC=6,BD=8,点E、F、P 分别是边AB、BC、AC 上的动点,PE+PF 的最小值是.3.如图3,在边长为2 的等边△ABC 中,D 为BC 的中点,E 是AC 边上一点,则BE+DE 的最小值为.4.如图 4,钝角三角形ABC 的面积为 9,最长边AB=6,BD 平分∠ABC,点M、N 分别是BD、BC 上的动点,则CM+MN 的最小值为.5.如图5,在△ABC 中,AM 平分∠BAC,点D、E 分别为AM、AB 上的动点,=6,则BD+DE的最小值为(1)若AC=4,S△ABC(2)若∠BAC=30°,AB=8,则BD+DE 的最小值为.(3)若AB=17,BC=10,CA=21,则BD+DE 的最小值为.6.如图6,在△ABC中,AB=BC=4,S△ABC=4一点,则PK+QK 的最小值为.,点P、Q、K 分别为线段AB、BC、AC 上任意图6 图7 图8 图97.如图7,AB 是⊙O 的直径,AB=8,点M 在⊙O 上,∠MAB=20°,N 是弧MB 的中点,P 是直径AB 上的一动点,则PM+PN 的最小值为.8.如图 8,在锐角△ABC 中,AB=4,∠BAC=45°,∠BAC 的平分线交BC 于点D,M、N 分别是AD 和AB 上的动点,则BM+MN 的最小值是.9.如图 9,圆柱形玻璃杯高为 12cm、底面周长为 18cm,在杯内离杯底 4cm 的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 4cm 与蜂蜜相对的点A 处,则蚂蚁到达蜂蜜的最短距离为cm.10.如图 10,菱形OABC 中,点A 在x 轴上,顶点C 的坐标为(1,OC、OB 上,则CE+DE+DB 的最小值是.),动点D、E 分别在射线图10 图11 图12 图1311.如图 11,点A(a,1)、B(-1,b)都在双曲线y=-3(x<0)上,点P、Q 分别是x 轴、y 轴上x的动点,当四边形PABQ 的周长取最小值时,PQ 所在直线的解析式是.12.如图12,点P 是∠AOB 内任意一点,OP=5cm,点M 和点N 分别是射线OA 和射线OB 上的动点,△PMN 周长的最小值是5cm,则∠AOB 的度数是.13.如图13,∠AOB=30°,点M、N 分别在边OA、OB 上,且OM=1,ON=3,点P、Q 分别在边OB、OA 上,则MP+PQ+QN 的最小值是.14.如图 14,在Rt△ABC 中,∠ACB=90°,点D 是AB 边的中点,过D 作DE⊥BC 于点E. (1)点P 是边BC 上的一个动点,在线段BC 上找一点P,使得AP+PD 最小,在下图中画出点P; (2)在(1)的条件下,连接CD 交AP 于点Q,求AQ 与PQ 的数量关系;图 143315. 在矩形 ABCD 中,AB =6,BC =8,G 为边 AD 的中点.(1) 如图 1,若 E 为 AB 上的一个动点,当△CGE 的周长最小时,求 AE 的长.(2) 如图 2,若 E 、F 为边 AB 上的两个动点,且 EF =4,当四边形 CGEF 的周长最小时,求 AF的长.16. 如图,抛物线 y = - 1x 2+ 2x + 4 交y 轴于点B ,点A 为x 轴上的一点,OA =2,过点A 作直线MN ⊥ AB2 交抛物线与 M 、N 两点. (1) 求直线 AB 的解析式;(2) 将线段 AB 沿 y 轴负方向平移 t 个单位长度,得到线段 A 1B 1 ,求 MA 1 + MB 1 取最小值时实数 t 的值.33172020 中考专题 8——最值问题之将军饮马参考答案例1.解:作A 关于OB 的对称点D,连接CD 交OB 于P,连接AP,过D 作DN⊥OA 于N,则此时PA+PC 的值最小,∵DP=PA,∴PA+PC=PD+PC=CD,∵B(3,),∴AB=,OA=3,∵tan∠AOB=AB=3,∴∠AOB=30°,∴OB=2AB=2 ,OA 31 1 3 3由三角形面积公式得:×OA×AB=2×OB×AM,∴AM=2,∴AD=2×2=3,2∵∠AMB=90°,∠B=60°,∴∠BAM=30°,∵∠BAO=90°,∴∠OAM=60°,∵DN⊥OA,∴∠NDA=30°,∴AN=1AD=23,由勾股定理得:2DN=33 ,2∵C(1,0),∴CN=3﹣1﹣2 23=1,在Rt△DNC 中,由勾股定理得:DC=,2 2即PA+PC 的最小值是31.2例2.解:作A 关于BC 和ED 的对称点A′,A″,连接A′A″,交BC 于M,交ED 于N,则A′A″即为△AMN 的周长最小值.⑴作EA 延长线的垂线,垂足为H,∠BAE=120°,∴∠AA′A″+∠AA″A′=60°,∠AA′A″=∠A′AM,∠AA″A′=∠EAN,∴∠CAN=120°-∠AA′A″-∠AA″A′=60°,也就是说∠AMN+∠ANM=180°-60°=120°.⑵过点A′作EA 延长线的垂线,垂足为H,∵AB=BC=1,AE=DE=2,∴AA′=2BA=2,AA″=2AE=4,则Rt△A′HA 中,∵∠EAB=120°,∴∠HAA′=60°,∵A′H⊥HA,∴∠AA″H=30°,∴AH=1AA′=1,∴A′H=2,A″H=1+4=5,∴A′A″=2 ,例3.解:作EF∥AC 且EF=于P,,连结DF 交AC 于M,在AC 上截取MN=,延长DF 交BC 作FQ⊥BC 于Q,作出点E 关于AC 的对称点E′,则CE′=CE=1,将MN 平移至E′F′处,3332242 - 22 3 3 则四边形 MNE ′F ′为平行四边形,当 BM +EN =BM +FM =BF ′时,四边形 BMNE 的周长最小, 由∠FEQ =∠ACB =45°,可求得 FQ =EQ =1,∵∠DPC =∠FPQ ,∠DCP =∠FQP ,∴△PFQ ∽△PDC , ∴PQ PQ + QE + EC = PQ ,∴ CD PQ PQ + 2 1 = ,解得:PQ = 4 2 ,∴PC = 8 ,3 3由对称性可求得 tan ∠MBC =tan ∠PDC = 2 .3例 4.【提示】将△AEO 向右平移转化为△AEO 不动,点 B 向左平移,则点 B 移动的轨迹为一平行于 x 轴的直线,所以作点 E 关于该直线的对称点 E 1,连接 AE 1,与该直线交点 F 即为最小时点 B 的位置,求出 BF 长度即可求出点 E 向右平移的距离.例 5.解:如图所示,直线 OC 、y 轴关于直线 y =kx 对称,直线 OD 、直线 y =kx 关于 y 轴对称,点A ′是点 A 关于直线 y =kx 的对称点.作 A ′E ⊥OD 垂足为 E ,交 y 轴于点 P ,交直线 y =kx 于 M ,作 PN ⊥直线 y =kx 垂足为 N , ∵PN =PE ,AM =A ′M ,∴AM +PM +PN =A ′M +PM +PE =A ′E 最小(垂线段最短), 在 RT △A ′EO 中,∵∠A ′EO =90°,OA ′=4,∠A ′OE =3∠AOM =60°, ∴OE =1OA ′=2,A ′E = =2 .2 ∴AM +MP +PN 的最小值为 2 .333337【巩固训练】答案1.解:连接BD,∵点B 与D 关于AC 对称,∴PD=PB,∴PD+PE=PB+PE=BE 最小.∵正方形ABCD 的面积为 12,∴AB=2又∵△ABE 是等边三角形,∴BE=AB=2,,故所求最小值为2 .2.解:∵四边形ABCD 是菱形,对角线AC=6,BD=8,∴AB=5,作E 关于AC 的对称点E′,作E′F⊥BC 于F 交AC 于P,连接PE,则E′F 即为PE+PF 的最小值,∵1⋅AC⋅BD=AD⋅E′F,∴E′F=24,∴PE+PF 的最小值为24.2 5 53.解:作B 关于AC 的对称点B′,连接BB′、B′D,交AC 于E,此时BE+ED=B′E+ED=B′D,根据两点之间线段最短可知B′D 就是BE+ED 的最小值,∵B、B′关于AC 的对称,∴AC、BB′互相垂直平分,∴四边形ABCB′是平行四边形,∵三角形ABC 是边长为2,D 为BC 的中点,∴AD⊥BC,AD=,BD=CD=1,BB′=2AD=2 ,作B′G⊥BC 的延长线于G,∴B′G=AD=,在Rt△B′BG 中,BG=3,∴DG=BG﹣BD=3﹣1=2,在Rt△B′DG 中,B′D=.故BE+ED 的最小值为7 .4.解:过点C 作CE⊥AB 于点E,交BD 于点M,过点M 作MN⊥BC 于N,∵BD 平分∠ABC,ME⊥AB 于点E,MN⊥BC 于N,∴MN=ME,∴CE=CM+ME=CM+MN 是最小值.∵三角形ABC 的面积为 9,AB即CM+MN 的最小值为 3.=6,∴12×6⋅CE=9,∴CE=3.333335.提示:作点E 关于AM 的对称点E′,BH⊥AC 于H,易知BD+DE 的最小值即为BH 的长. 答案:(1)3;(2)4;(3)8.6.解:如图,过A 作AH⊥BC 交CB 的延长线于H,∵AB=CB=4,S△ABC=4,∴AH=2,∴cos∠HAB=AH=2 3=3,∴∠HAB=30°,∴∠ABH=60°,∴∠ABC=120°,AB 4 2∵∠BAC=∠C=30°,作点P 关于直线AC 的对称点P′,过P′作P′Q⊥BC 于Q 交AC 于K,则P′Q 的长度=PK+QK 的最小值,∴∠P′AK=∠BAC=30°,∴∠HAP′=90°,∴∠H=∠HAP′=∠P′QH=90°,∴四边形AP′QH 是矩形,∴P′Q=AH=2 ,即PK+QK 的最小值为2 .7.解:作点N 关于AB 的对称点N′,连接OM、ON、ON′、MN′,则MN′与AB 的交点即为PM+PN 的最小时的点,PM+PN 的最小值=MN′,∵∠MAB=20°,∴∠MOB=2∠MAB=2×20°=40°,∵N 是弧MB 的中点,∴∠BON=12∠MOB=1×40°=20°,2由对称性,∠N′OB=∠BON=20°,∴∠MON′=∠MOB+∠N′OB=40°+20°=60°,∴△MON′是等边三角形,∴MN′=OM=OB=1AB=18 =4,2 2∴PM+PN 的最小值为 4,22338.解:如图,作BH⊥AC,垂足为H,交AD 于M′点,过M′点作M′N′⊥AB,垂足为N′,则BM′+M′N′为所求的最小值.∵AD 是∠BAC 的平分线,∴M′H=M′N′,∴BH 是点 B 到直线AC 的最短距离,∵AB=4,∠BAC=45°,∴BH=AB sin45°=4×2=2 .2∵BM+MN 的最小值是BM′+M′N′=BM′+M′H=BH=2 .9.解:沿过A 的圆柱的高剪开,得出矩形EFGH,过C 作CQ⊥EF 于Q,作A 关于EH 的对称点A′,连接A′C 交EH 于P,连接AP,则AP+PC 就是蚂蚁到达蜂蜜的最短距离,∵AE=A′E,A′P=AP,∴AP+PC=A′P+PC=A′C,∵CQ=1×182cm=9cm,A′Q=12cm﹣4cm+4cm=12cm,在Rt△A′QC 中,由勾股定理得:A′C=15cm,故答案为:15.10.解:连接AC,作B 关于直线OC 的对称点E′,连接AE′,交OC 于D,交OB 于E,此时CE+DE+BD 的值最小,∵四边形OCBA 是菱形,∴AC⊥OB,AO=OC,即A 和C 关于OB 对称,∴CE=AE,∴DE+CE=DE+AE=AD,∵B 和E′关于OC 对称,∴DE′=DB,∴CE+DE+DB=AD+DE′=AE′,过C 作CN⊥OA 于N,∵C(1,),∴ON=1,CN=,由勾股定理得:O C=2,即AB=BC=OA=OC=2,∴∠CON=60°,∴∠CBA=∠COA=60°,∵四边形COAB 是菱形,∴BC∥OA,∴∠DCB=∠COA=60°,∵B 和E′关于OC 对称,∴∠BFC=90°,∴∠E′BC=90°﹣60°=30°,∴∠E′BA=60°+30°=90°,CF=1BC=1,由勾股定理得:BF=2=E′F,在Rt△EBA 中,由勾股定理得:AE′=4,即CE+DE+DB 的最小值是 4.310 ⎩⎩11.解:把点 A (a ,1)、B (﹣1,b )代入 y =﹣ 3(x <0)得 a =﹣3,b =3,则 A (﹣3,1)、B (﹣1,x3),作 A 点关于 x 轴的对称点 C ,B 点关于 y 轴的对称点 D ,所以 C 点为(﹣3,﹣1),D 点为(1, 3),连结 CD 分别交 x 轴、y 轴于 P 点、Q 点,此时四边形 PABQ 的周长最小,设直线 CD 的解析式为 y =kx +b ,则⎧-3k + b = -1 ,解得⎧k = 1,所以直线 CD 的解析式为 y =x +2.⎨k + b = 3 ⎨b = 212.解:分别作点 P 关于 OA 、OB 的对称点 C 、D ,连接 CD ,分别交 OA 、OB 于点 M 、N ,连接 OC 、OD 、PM 、PN 、MN ,如图所示:∵点 P 关于 OA 的对称点为 D ,关于 OB 的对称点为 C ,∴PM =DM ,OP =OD ,∠DOA =∠ POA ;∵点 P 关于 OB 的对称点为 C ,∴PN =CN ,OP =OC ,∠COB =∠POB , ∴OC =OP =OD ,∠AOB =1∠COD ,2∵△PMN 周长的最小值是 5cm ,∴PM +PN +MN =5,∴DM +CN +MN =5,即 CD =5=OP , ∴OC =OD =CD ,即△OCD 是等边三角形,∴∠COD =60°,∴∠AOB =30°;13 解:作 M 关于 OB 的对称点 M ′,作 N 关于 OA 的对称点 N ′,连接 M ′N ′,即为 MP +PQ +QN 的最小值.根据轴对称的定义可知:∠N ′OQ =∠M ′OB =30°,∠ONN ′=60°, ∴△ONN ′为等边三角形,△OMM ′为等边三角形,∴∠N ′OM ′=90°, ∴在 Rt △M′ON′中,M ′N ′= .故答案为 .10314.解:(1)作点 A 关于BC 的对称点 A′,连 DA′交BC 于点P.(2)由(1)可证得PA 垂直平分CD,∴AQ=CQ=3PQ15.解:(1)∵E 为AB 上的一个动点,∴作G 关于AB 的对称点M,连接CM 交AB 于E,那么E 满足使△CGE 的周长最小;∵在矩形ABCD 中,AB=6,BC=8,G 为边AD 的中点,∴AG=AM=4,MD=12,而AE∥CD,∴△AEM∽△DCM,∴AE:CD=MA:MD,∴AE=CD ⨯MA=2;MD(2)∵E 为AB 上的一个动点,∴如图,作G 关于AB 的对称点M,在CD 上截取CH=4,然后连接HM 交AB 于E,接着在EB 上截取EF=4,那么E、F 两点即可满足使四边形CGEF 的周长最小.∵在矩形ABCD 中,AB=6,BC=8,G 为边AD 的中点,∴AG=AM=4,MD=12,而CH=4,∴DH=2,而AE∥CD,∴△AEM∽△DHM,∴AE:HD=MA:MD,∴AE=HD ⨯MAMD=2,3∴AF =4+2=14.3 316.解:(1)依题意,易得B(0,4),A(2,0),则AB解析式:y=-2x+4(2)∵AB⊥MN∴直线MN:y =1x - 12⎧y =-1x2+ 2x + 4⎪与抛物线联立可得:⎨⎪y =⎩21x - 1 2解得:M(-2,-2)将AB向负方向平移t个单位后,A1(2,-t),B1(0,4-t)则A1 关于直线x=-2 的对称点A2 为(-6,-t)当A2、M、B1 三点共线时,MA1 +MB1取最小值∴t =143。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解密:粟裕在黄桥战役中做的三道“数学题”
在1940年的黄桥战役这场以少胜多的著名战役中,作为前线总指挥,粟裕是怎样带领新四军赢得胜利的呢?"打仗就是数学"—一向善于险中求胜的他用这句话诠释了黄桥战役的胜利秘诀。
在这场战役中,粟裕一连做好了三道"数学题"。
战前:7000余人>30000余人
1940年7月,陈毅、粟裕率部进军苏北,开辟敌后抗日根据地,并于8月进驻黄桥(今江苏泰兴东)。
国民党顽固派担忧新四军壮大,妄图趁陈粟部立足未稳之际予以消灭,命在苏北的"反共专家"韩德勤(时任江苏省政府主席兼鲁苏战区副司令)不断制造与新四军的摩擦,并于9月进逼黄桥。
韩德勤将所属精锐倾巢出动,并在动员令中叫嚣"把新四军赶到长江里去喝水!"
9月30日,韩顽军向黄桥出击,行动甚为隐秘。
新四军未及时发现,第二天才获知韩顽进攻的消息。
黄桥的防御工事十分简陋,加紧布置势必造成部队极度疲劳。
更严重的是,新四军兵力不到对方的1/4,处于绝对劣势。
但黄桥之战关系到新四军能否在苏北立足,被逼到墙角,只能打不能退。
陈毅坐镇黄桥西北5公里的严徐庄统揽全局,粟裕在黄桥前线负责战场指挥。
此战成败难料,连陈毅也没有取胜的把握。
据粟裕回忆:陈毅同志有一挑珍贵的书籍文稿,从皖南挑到茅山,又从江南挑到苏北,从来不肯丢开,可这时也从铁皮箱里拿出来埋入地下,显然是做了"破釜沉舟"的打算。
表面上看,韩顽30000余人,新四军7000余人,兵力悬殊。
不过,粟裕看到了常人看不到的另一面,做起了第一道数学题,得出了7000余人>30000余人的结论:韩顽尽管有30000余人之多,但兵分三路进攻,兵力分散,直接投入进攻黄桥的实际只有中路韩顽第89军和独立六旅15000余人。
这样一来,新四军的压力在无形中就减轻了一半。
粟裕还看到,韩顽师出无名,冒破坏抗日统一战线之大不韪,其官兵情绪低落;新四军则是正当防卫,事关生存,群情激昂,战斗精神倍增,再加上群众支持,对韩顽可运用分化瓦解、各个击破的战法。
如此,韩顽兵力优势又被抵消一半,我军胜算就大了。
下定决心后,粟裕立即进行了精心部署。
10月4日凌晨4时,韩顽第89军33师(共4个团)在黄桥东门发起猛烈进攻。
该顽军初战即投入3个团,且来势凶猛,不但突破了新四军前哨部队的防御,其一部还攻入了东门,几乎就要拿下黄桥。
千钧一发之际,第三纵队司令员陶勇和参谋长张震东把上衣一脱,挥动马刀,带领部队硬是将韩顽赶出东门,然后架起机关枪,死死顶住,使其难越雷池一步。
战中:3000余人×1.5米≈四五公里
黄桥激战时,韩顽后续梯队也向黄桥推进,企图增援第33师。
4日16时,粟裕登上黄桥镇北门的土城观望,发现韩顽第6旅成一路纵队正向黄桥开来。
他迅速做起了第二道数学题:"如果两人之间的距离为1.5米,全部3000余人的队形将是长达四五公里的一路长蛇阵。
从黄桥到高桥约7.5公里,其先头部队抵达黄桥以北2.5公里时,后尾必然已过高桥,也就是说敌人已经全部进入了新四军的设伏地区。
"
粟裕见"肉馅"已全部包进"饺子皮",遂令叶飞立即发动进攻,速歼韩顽第6旅。
叶飞遵照粟裕指示,采取"黄鼠狼吃蛇"的战法,将该顽军截成数段,歼其大部,迫使其旅长翁达绝望自杀,打开了局面,扭转了黄桥战役的不利态势。
同日24时,王必成率第二纵队进占分界,断绝了韩顽第33师退路,并与陶勇的第三纵队前后夹攻,迅速全歼该师,还活捉了其师长孙启人。
接着,王必成部与陶勇部兵锋北指,与叶飞部合力围攻韩顽第89军军部。
韩顽见势不妙,渡河逃窜,连军长李守维也在混乱中落水淹死。
至6日晨,进攻黄桥的主力韩顽第89军军部被彻底歼灭。
为痛打落水狗,粟裕下令乘胜追击,进占海安和东台等地。
战后:5天100公里<1天90公里
黄桥一役,新四军以不到1000人的代价,歼韩顽1.1万余人,其第89军中将军长李守维、独立第6旅中将旅长翁达和团长数人毙命,第33师师长孙启人、第99旅旅长苗瑞林、第117师参谋长等师、旅、团级军官10余名及下级军官600名被俘。
国民党军遭到军事和政治上的双重失败,蒋介石哀叹:"诚吾人之奇耻大辱。
"
黄桥决战胜利后,陈毅满心喜悦地赋诗一首:"十年征战几人回,又见同侪并马归。
江淮河汉今谁属?红旗十月满天飞。
"粟裕没有陶醉在胜利的喜悦中,而是清醒地看到了部队在这次战役中暴露的不足。
10月10日,他在战役总结大会上做起了
第三道数学题:"过去一天一夜走90公里还打仗,而我们从黄桥到东台近100公里路追了5天……"也就是说,新四军克服疲劳、连续作战的能力没能充分发挥出来。
战前,沉着冷静,在不利条件下看到有利因素;战中,精确计算,正确指挥部队运动歼敌;战后,保持清醒,在光辉胜利中细察缺点不足。
这就是常胜将军粟裕的非凡之处。
