初二年级数学暑假功课习题精编
2023年暑假新八年级数学预习专题3:全等三角形及其性质(精练教师版)
第 1页(共 22页)
A.AC=AF
B.∠AFC=∠AFE C.EF=BC
D.∠FAB=∠B
5.(2022 秋•袁州区月考)下列图形中被虚线分成的两部分不是全等形的是
()
A.等腰梯形
B.正方形
C.正六边形
D.正五角星
6.(2022 秋•荆州月考)如图,点 B,E,C,F 在同一直线上,△ABC≌△DEF,
△ADC≌△ADC′,△AEB≌△AEB′,且 C′D∥EB′,BE,CD 交于点 F.若
∠BAC=40°,则∠BFC 的度数为
.
27.(2022 春•泰州期末)一个三角形的三条边的长分别是 5,8,10,另一个三
角形的三条边的长分别是 5,4x+2,2y﹣2,若这两个三角形全等,则 x+y 的值是75°,则∠AC源自 的度数为( )A.30°
B.25°
C.20°
D.15°
二、填空题(共 10 小题)
18.(2022 秋•袁州区月考)如图,△ABC≌△DBE,点 A 和点 D 是对应顶点,
且点 C 在边 BD 上.若 AB=9,BE=3,则 CD 的长为
.
19.(2022 秋•新罗区校级月考)如图,若△ADB≌△EDB≌△EDC,则∠C
2023 年暑假新八年级数学预习专题 3 全等三角形及 其性质
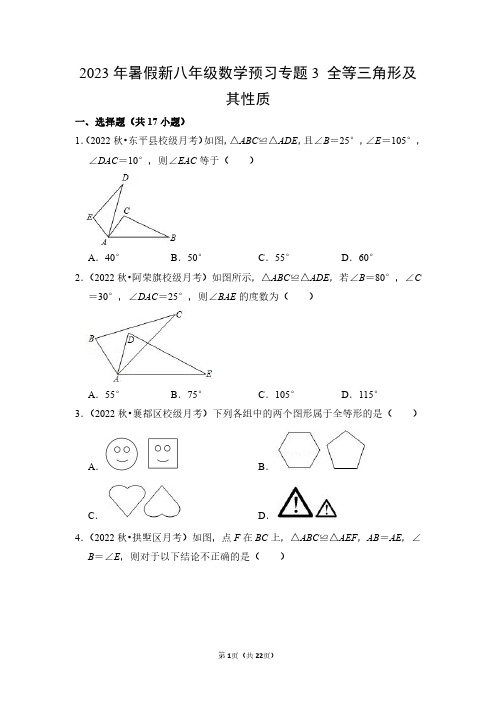
一、选择题(共 17 小题) 1.(2022 秋•东平县校级月考)如图,△ABC≌△ADE,且∠B=25°,∠E=105°,
∠DAC=10°,则∠EAC 等于( )
A.40°
B.50°
C.55°
D.60°
2.(2022 秋•阿荣旗校级月考)如图所示,△ABC≌△ADE,若∠B=80°,∠C
暑假提升专题训练北师大版八年级数学上册第1章勾股定理

专题训练-勾股定理知识点(暑假提升篇)-数学八年级上册(北师版数学)一.选择题(共10小题)1.△ABC是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB =50米,如果要在这块空地上种植草皮,按每平方米草皮a元计算,那么共需要资金()A.50a元B.600a元C.1200a元D.1500a元2.如图,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面.然后将绳子末端拉到距离旗杆8m处,发现此时绳子末端距离地面2m.则旗杆高度为()(滑轮上方的部分忽略不计)A.12m B.13m C.16m D.17m3.如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为()A.45m B.40m C.50m D.56m4.为了测算出学校旗杆的高度,爱动脑筋的小明这样设计出了一个方案如图,将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端5米处,发现此时绳子底端距离打结处约1米,则旗杆的高度是多少米?()A.12B.15C.18D.245.将一根24cm的筷子,置于底面直径为15cm,高8cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度hcm,则h的取值范围是()A.h≤17cm B.h≥8cmC.15cm≤h≤16cm D.7cm≤h≤16cm6.如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC 为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5米,则小巷的宽为()A.2.5米B.2.6米C.2.7米D.2.8米7.如图,一轮船以8海里/时的速度从港口A出发向东北方向航行,另一轮船以6海里/时的速度同时从港口A出发向东南方向航行,离开港口1小时后,则两船相距()A.6海里B.8海里C.10海里D.20海里8.如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是()A.6cm B.7cm C.8cm D.9cm9.如图,小巷左右两侧是竖直的墙壁,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米.若梯子底端位置保持不动,将梯子斜靠在右墙时,顶端距离地面1.5米,则小巷的宽度为()A.2.7米B.2.5米C.2米D.1.8米10.如图,某校攀岩墙的顶部安装了一根安全绳,让它垂到地面时比墙高多出了2米,教练把绳子的下端拉开8米后,发现其下端刚好接触地面(如图),则此攀岩墙的高度是()A.10米B.15米C.16米D.17米二.填空题(共11小题)11.小明把一根70cm长的木棒放到一个长、宽、高分别为40cm、30cm、50cm的木箱中,他能放进去吗?答:(填“能”、或“不能”)12.如图,要在两幢楼房的房顶A、B间拉一根光缆线(按线段计算),则至少米.13.如图,一扇卷闸门用一块宽18cm,长80cm的长方形木板撑住,用这块木板最多可将这扇卷闸门撑起cm高.14.如图:一架云梯AB长13米,底端离墙的距离BC为5米,当梯子下滑到DE时,AD =2米,则BE=米.15.如图,长为8cm的橡皮筋放置在x轴上,固定两端A和B,然后把中点C向上拉升3cm 到D,则橡皮筋被拉长了cm.16.如图,池塘边一棵垂直于水面BM的笔直大树AB在点C处折断,AC部分倒下,点A 与水面上的点E重合,部分沉入水中后,点A与水中的点F重合,CF交水面于点D,DF=2m,∠CEB=30°,∠CDB=45°,求CB部分的高度为m.17.《九章算术》是我国古代最重要的数学著作之一,在“勾股”章中记载了一道“折竹抵地”问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”翻译成数学问题是:如图所示,△ABC中,∠ACB=90°,AC+AB=10,BC=3,求AC的长,如果设AC=x,则可列方程为.18.在一棵树的10米高的B处有两只猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高米.19.如图,一条公路的两边AB∥CD,在AB上有两棵树M,N,在另一边CD上有一棵树P,测得M,N相距50m,∠MPC=30°,∠NPD=75°,则公路的宽度为m.20.有一个水池,水面是一个边长为4米的正方形,在水池正中央有一枝新生的红莲,它高出水面1米.一阵风把这枝红莲垂直吹向岸边,它的顶端恰好到达岸边的水面.则这个水池的水深是米.21.小明和小亮在同一地点出发,小明往东走了20千米,小亮往北走了15千米,这是小明与小亮相距千米.专题训练-勾股定理知识点(暑假提升篇)-数学八年级上册(北师版数学)参考答案与试题解析一.选择题(共10小题)1.B2.D3.B4.A5.D6.C7.C8.B9.A10.B二.填空题(共11小题)11.答案为:能.12.答案为:10.13.答案为:82cm.14.答案为:﹣5.15.答案为:2cm.16.答案为:(2+).17.答案为:x2+32=(10﹣x)2.18.答案为:15m.19.答案为:25.20.答案为:1.5.21.答案为:25.。
2022八年级暑假作业数学答案大全

2022八年级暑假作业数学答案大全在时钟的滴答声中,时间又定格到了一年中的暑假,你们是不是应为做暑假作业而烦恼呢?下面为大家收集整理了2022八年级暑假作业数学答案参考大全,欢迎阅读与借鉴!八年级暑假作业数学答案11-5.daaaa6-10bdcba11.125;12.1.2;13.7;32;14.815.∵是平行四边形,∵∵bad∵adc互补,∵ae平分∵bad,∵adc的平分线平分∵adc∵∵ado与∵dao互余∵∵aod是90度所以do垂直于ae,又∵∵ado与∵cdo相等,∵aod等于doe等于90度且do等于do∵三角形ado与三角形doe全等,∵ao等于oe,因此do垂直平分ae16.∵∵dce+∵ecb=90∵dce:∵ecb=1:3∵dce=22.5,∵ecb=67.5∵bdc+∵dce=90,∵bdc=67.5矩形对角线相等,ac=bd,∵co=do∵acd=∵bdc=67.5∵ace=∵acd-∵dce=4517.∵cd=bd,∵rt∵cde全等于rt∵bde;∵ce=be∵de垂直平分bc,∵ae=eb,:ace为60度等腰∵,因此:ac=ce=ae∵af=ce=ae,∵deb=∵aef=∵bac=60度,∵∵aef为60度等腰∵∵af=ae=ef 因此:ac=af=ef=ce因此四边形ecaf为菱形18.(1)∵e为bc的中点,ae∵bc,即ae是bc的垂直平分线,∵ab=ac,又∵abcd是菱形,∵∵abc是等边三角形,故∵bac=60°,∵ab=ac=4∵菱形abcd的面积=2∵abc的面积=2×(1/2)×4×4=8√2.(2)连接ac,因为e为bc的中点,ae∵bc,所以ae是bc的垂直平分线,所以ac=ab=bc,所以∵abc是等边三角形,所以∵b=∵d=60°,所以∵bad=180°-∵b=120°因为ae∵bc,af∵dc所以∵bae=∵daf=30°,∵eaf=∵bad-∵bae-∵daf=60°,,因为ae‖cg,∵∵ecg=90°所以∵cha=180°-∵eaf=120°19.(1)∵四边形abcd是平行四边形∵∵b=∵cdn,ab=cd,ad=bc.又m.n分别是ad.bc的中点,∵bn=dm=am=cn.∵∵abn全等于∵cdm.(2)解:∵m是ad的中点,∵and=90°,∵mn=md=12ad,∵∵1=∵mnd,∵ad∵bc,∵∵1=∵cnd,∵∵1=∵2,∵∵mnd=∵cnd=∵2,∵pn=pc,∵ce∵mn,∵∵cen=90°,∵∵2=∵pne=30°,∵pe=1,∵pn=2pe=2,∵ce=pc+pe=3,∵cn=cecos30°=2√3,∵∵mnc=60°,cn=mn=md,∵∵cnm是等边三角形,∵∵abn∵∵cdm,∵an=cm=2√3.八年级暑假作业数学答案21.答案:B2.解析:∵α=30°+45°=75°.答案:D3.解析:延长线段CD到M,根据对顶角相等可知∵CDF=∵EDM.又因为AB∵CD,所以根据两直线平行,同位角相等,可知∵EDM=∵EAB=45°,所以∵CDF=45°.答案:B4.解析:∵CD∵AB,∵∵EAB=∵2=80°.∵∵1=∵E+∵EAB=120°,∵∵E=40°,故选A.答案:A5.答案:B6.答案:D7.答案:D8.答案:D9.解析:根据四个选项的描述,画图如下,从而直接由图确定答案. 答案:①②④10.答案:如果两个角是同一个角或相等角的余角,那么这两个角相等11.答案:40°12.答案:112.5°13.解:(1)如果一个四边形是正方形,那么它的四个角都是直角,是真命题;(2)如果两个三角形有两组角对应相等,那么这两个三角形相似,是真命题;(3)如果两条直线不相交,那么这两条直线互相平行,是假命题,如图中长方体的棱a,b所在的直线既不相交,也不平行.14.解:平行.理由如下:∵∵ABC=∵ACB,BD平分∵ABC,CE平分∵ACB,∵∵DBC=∵ECB.∵∵DBF=∵F,∵∵ECB=∵F.∵EC与DF平行.15.证明:∵CE平分∵ACD(已知),∵∵1=∵2(角平分线的定义).∵∵BAC∵1(三角形的一个外角大于任何一个和它不相邻的内角),∵∵BAC∵2(等量代换).∵∵2∵B(三角形的一个外角大于任何一个和它不相邻的内角),∵∵BAC∵B(不等式的性质).16.证明:如图④,设AD与BE交于O点,CE与AD交于P点,则有∵EOP=∵B+∵D,∵OPE=∵A+∵C(三角形的外角等于和它不相邻的两个内角的和).∵∵EOP+∵OPE+∵E=180°(三角形的内角和为180°),∵∵A+∵B+∵C+∵D+∵E=180°.如果点B移动到AC上(如图⑤)或AC的另一侧(如图⑥)时,∵EOP,∵OPE仍然分别是∵BOD,∵APC的外角,所以可与图④类似地证明,结论仍然成立.17.解:(1)∵3=∵1+∵2;证明:证法一:过点P作CP∵l1(点C在点P的左边),如图①,则有∵1=∵MPC.图①∵CP∵l1,l1∵l2,∵CP∵l2,∵∵2=∵NPC.∵∵3=∵MPC+∵NPC=∵1+∵2,即∵3=∵1+∵2.证法二:延长NP交l1于点D,如图②.图②∵l1∵l2,∵∵2=∵MDP.又∵∵3=∵1+∵MDP,∵∵3=∵1+∵2.(2)当点P在直线l1上方时,有∵3=∵2-∵1;当点P在直线l2下方时,有∵3=∵1-∵2.八年级暑假作业数学答案3(一)答案:1-8、DABDDDCA;9、1,2,3;10、a≤b;11、a4且a≠0;12、a-1;13、7; 14、(1)x2,(2)x-3;15、a≤;16、1;17、18厘米;18、2121、18题;22、(1)a=0.6,b=0.4;(2)35%到50%之间(不含35%和50%)。
沪科版八年级数学暑假作业(七)含答案

初中八年级数学(沪科版)多媒体暑假作业(七)一. 相信自己。
1. 如图为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要_7_米.5米3米2. 在直角三角形ABC 中,斜边AB =2,则222AB AC BC ++=_8_.3. 直角三角形的三边长为连续偶数,则其周长为 24 .4. 如图,在△ABC 中,∠C=90°,BC=3,AC=4.以斜边AB 为直径作半圆,则这个半圆的面积是258π.5.如图,某沿海开放城市A 接到台风警报,在该市正南方向100km 的B 处有一台风中心,沿BC 方向以20km/h 的速度向D 移动,已知城市A 到BC 的距离AD=60km ,那么台风中过四/4小时从B 点移到D 点。
如果在距台风中心30km 的圆形区域内都将有受到台风的破坏的危险,正在D 点休闲的游人在接到台风警报后的2.5小时内撤离才可脱离危险。
6. 如图,△ABC 中,∠C =90°,AB 垂直平分线交BC 于D 若BC =8,AD =5,则AC 等于_4_.A BCD7. 如图,四边形ABCD 是正方形,AE 垂直于BE ,且AE =3,BE =4,阴影部分的面积是19. ABDC E8. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边和长为7cm,则正方形A ,B ,C ,D 的面积之和为_49_cm 2.二.择优录用。
1. 直角三角形一直角边长为12,另两条边长均为自然数,则其周长为( D ). (A )30 (B )28 (C )56 (D )不能确定2. 直角三角形的斜边比一直角边长2 cm ,另一直角边长为6 cm ,则它的斜边长(C )(A )4 cm (B )8 cm (C )10 cm (D )12 cm 3. 已知一个Rt △的两边长分别为3和4,则第三边长的平方是(D ) (A )25 (B )14 (C )7 (D )7或254. 等腰三角形的腰长为10,底长为12,则其底边上的高为(B )(A )13 (B )8 (C )25 (D )64ABCD7cm5. 五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中正确的是( C )715242520715202425157252024257202415(A)(B)(C)(D)6. 将直角三角形的三条边长同时扩大同一倍数, 得到的三角形是( C )(A ) 钝角三角形 (B ) 锐角三角形 (C ) 直角三角形 (D ) 等腰三角形. 7. 如图小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( B )(A ) 25 (B ) 12.5 (C ) 9 (D ) 8.5DCBA8. 三角形的三边长为ab c b a 2)(22+=+,则这个三角形是( C )(A ) 等边三角形 (B ) 钝角三角形 (C ) 直角三角形 (D ) 锐角三角形. 9.△ABC 是某市在拆除违章建筑后的一块三角形空地.已知∠C=90°,AC=30米,AB=50米,如果要在这块空地上种植草皮,按每平方米草皮a 元计算,那么共需要资金( B ). (A )50a 元 (B )600a 元 (C )1200a 元 (D )1500a 元10.如图,AB ⊥CD 于B ,△ABD 和△BCE 都是等腰直角三角形,如果CD=17,BE=5,那么AC 的长为( D ).(A )12 (B )7 (C )5 (D )13三.挑战奥数。
初二年级数学下学期暑假作业精选

第 1 页 2021年初二年级数学下册暑假作业精选 很多同学因为假期贪玩而耽误了学习,以致于和别的同学落下了差距,因此,小编为大家准备了这篇2021年初二年级数学下册暑假作业精选,希望可以帮助到您! 1、y与(2x+1)成反比例且当x=0时,y=2,那么当x=-1时,y=________ 2、假如反比例函数 的图象经过点(3,1),那么k=_______。 3、设反比例函数 的图象经过点(-1,y1)和(2,y2)且有y1y2,那么k的取值范围是______ 4、假设点(2,1)是反比例 的图象上一点,当y=6时,那么x=_______ 5、函数 与y=-2x的图象的交点的坐标是____________。 6、假如点(m,-2m)在双曲线 上,那么双曲线在_________象限。 7、一次函数y=ax+b图象在一、二、三象限,那么反比例函数 的函数值随x的增大而__________。 8、 ,那么y与x成_________比例,k=________,其图象在第_______象限。 9、菱形面积为12cm2,且对角线长分别为x cm和y cm,那么y关于x的函数关系式是_________。 10、反比例函数 ,当x0时,y随x的增大而增大,那么m的值是 第 2 页
1、(10分)数 与反比例函数 的图象都过A(m,1)点.求: (1)正比例函数的解析式; (2)正比例函数与反比例函数的另一个交点的坐标 2、一次函数的图象与x轴,y轴分别交于A、B两点,与反比例函数的图象交于C、D两点,假如A点坐标为(2,0),点C、D在第一、三象限,且OA=OB=AC=BD,试求(1)一次函数和反比例函数的解析式。(2)一次函数值大于反比例函数值的自变量的取值范围。 3、(10分)某蓄水池的排水管每时排水8m3,6小时(h)可将满水池全部排空. (1)蓄水池的容积是多少?(2)假如增加排水管,使每时的排水量到达Q(m3),那么将满池水排空所需的时间t(h)将如何变化?
2020年华师大八年级下册数学暑假作业(二)

2020 年光师大版八年级下册数学暑期作业(二)复习的内容:第17章函数及图象1——基础部分【夯实基础】一、选择题1、点( 2m , m 4 )在第四象限,且m 为偶数,则 m 的值为_____。
2、若已知P1(-1, )和P2(,b),且P1P2平行于 x 轴,则b _____。
313、若函数,则当函数值y=8 时,自变量 x 的值是()A.±B. 4C.±或4D.4 或﹣4、某礼拜天下午,小强和同学小明相约在某公共汽车站一同搭车回学校,小强从家出发先步行到车站,等小明到了后两人一同乘公共汽车回到学校.图中折线表示小强走开家的行程 y(公里)和所用的时间x(分)之间的函数关系.以下说法错误的选项是()A.小强从家到公共汽车站步行了 2 公里B.小强在公共汽车站等小明用了10 分钟C.公共汽车的均匀速度是30 公里 / 小时D.小强乘公共汽车用了20 分钟5、如图一次函数y mx n 与正比率函数y mnx ( m, n 为常数,且 mn0 )的图象是()6、(2020?陕西)在平面直角坐标系中,将直线l1: y=﹣ 2x ﹣ 2 平移后,获得直线l2:y=﹣2x+4,则以下平移作法正确的选项是()A.将 l1向右平移 3 个单位长度 B .将 l1向右平移 6 个单位长度C.将 l 1向上平移 2 个单位长度D.将 l 1向上平移 4 个单位长度7、以下表达式中,表示y 是x的反比率函数的是()① xy1② . y 36x③ y2 ④ y30) 3x (m 是常数, mmA. ①②④B. ①③④C.②③D.①③8、已知反比率函数y k 的图象在第二、第四象限内,函数图象上有两点(2 7,xAy 1) 、 B ( 5, y 2) ,则 y 1 与 y 2 的大小关系为( )。
A 、y > y 2B 、 y = y2 C 、 y < y2D 、没法确立1119、函数 y xm 与 ym( m 0) 在同一坐标系内的图象能够是()xyyyyOxOxOxOxA .B .C .D5.10 .如图,反比率函数 y的图象与直线 y kx(k 0) 订交于yxB 两点, AC ∥ y 轴, BC ∥ x 轴,则△ ABC 的面积等于个面积单位 . xA.4B.5C.10D.20二、填空题11、假如函数 y=(m ﹣ 3) x+1﹣m 的图象经过第二、三、四象限,那么常数 m 的取值范围为.12、函数 y (m 1)x m 2 2 是反比率函数,则 m.13、反比率函数 yk的图象如下图,点 M 是该函数图象x上一点,垂直于x 轴,垂足是点,假如 S △MON = 2,则k 的值为.MNN14、点P(3,-4)对于X轴对称点的坐标是,对于 y 轴对称点的坐标是,对于原点对称点的坐标是 ;15、已知点P(2,-3),Q( m ,5),且PQ∥ y 轴,则PQ=,Q点的坐标是;16、函数 y 3x 2 与两坐标轴围成的三角形面积是 _______。
2023年暑假新八年级数学预习专题5:角平分线与垂直平分线(精练教师版)
AD 过点 P 且与 AB 垂直.若 AD=8,BC=10,则△BCP 的面积为( )
第 2页(共 38页)
A.16
B.20
C.40
D.80
8.(2022•鼓楼区校级开学)三条公路围成一个三角形区域,某地区决定在这个
三角形区域内修建一个集贸市场,要使集贸市场到三条公路的距离相等,则
这个集贸市场应建在( )
D.有无数处
16.(2022 春•港北区期末)如图,已知△ABC 的周长是 36cm,∠ABC 和∠ACB
的角平分线交于点 O,OD⊥BC 于点 D,若 OD=3cm,则△ABC 的面积是( )
A.48cm2
B.54cm2
C.60cm2
D.66cm2
17.(2022 春•任城区期末)如图,在△ABC 中,∠ABC 的角平分线和∠ACB 相
的数量关系,下列说法正确的是( )
A.S1=4S2
B.S1=3S2
C.S1=2S2
D.S1=S2
15.(2022 春•兰州期末)某镇要在三条公路围成的一块三角形平地内修建一个
第 4页(共 38页)
砂石场,如图,要使这个砂石场到三条公路的距离相等,则可供选择的地址 ()
A.仅有一处 B.有四处
C.有七处
上修建一个度假村,如图所示,若要使度假村到三条公路的距离相等,则这
个度假村应修建在( )
A.△ABC 三条高线的交点处 B.△ABC 三条中线的交点处 C.△ABC 三条角平分线的交点处 D.△ABC 三边垂直平分线的交点处 3.(2021 秋•西宁期末)如图,在△ABC 中,AD 是高,AE 是角平分线,AF 是 中线.则下列结论错误的是( )
AE 是角平分线,AF 是中线,则下列说法中错误的是( )
初二数学暑假作业及答案
初二数学暑假作业及答案初二数学暑假作业及答案201x年暑假已经到来,家长在在暑假中一定督促孩子认真完成作业和注意假期安全。
初中频道为大家提供了初二数学暑假作业答案,供大家参考。
初二数学暑假作业1一、1D,2C,3D,4A,5B,6B,7B,8A,9C,10D.二、(11)2,(12)10cm或cm,(13)4cm,(14)矩形,(15)5,(16)6,(17)4,(18)x<0.三、19、(1)300人,(2)75、66,(3)66、75.20、(1)m=3,n=1.(5分)(2)x<2.(3分)21(1)解:设AE=x,则ED=4-x,∵四边形EBFD是菱形,∴EB=4-X,由勾股定理建立方程得到x=,(5分)(2)AE=,(3分)22、(1)y=-0.2x+3000.(5分)(2)由题意可得:2x+3(5000-x)≤12000,解得x≥3000,在函数y=-0.2x+3000中,k=-0.2,所以y随x的'增大而减小,所以当x=3000时,最大利润y=-0.2×3000+3000=2400.(4分)23、(1)证明:∵DE⊥BC,∠ACB=90°∴AC∥DE,又∵MN∥AB,∴四边形CADE是平行四边形,∴CE=AD.(5分)(2)四边形BECD是菱形,理由:D是AB边的中点,所以AD=DB,又AD=CE,所以DB=CE,而DB∥CE,四边形DBEC是平行四边形,因为ΔACB是直角三角形,D是斜边AB的中点,所以CD=DB,所以四边形BECD是菱形。
(4分)(3)∠A=45°时,四边形BECD是正方形,理由:∵∠ACB=90°又∠A=45°∴CA=CB,点D是AB的中点,∴CD⊥AB,即∠CDB=90°,而四边形BECD是菱形,∴四边形BECD是正方形。
(3分)初二数学暑假作业2一、填空。
1、中有( )个三角形。
(人教版)八年级数学暑假作业答案
〔人教版〕2022八年级数学暑假作业答案多阅读和积累,可以使学生增长知识,使学生在学习中做到举一反三。
在此查字典数学网初中频道为您提供2022八年级数学暑假作业答案,希望给您学习带来帮助,使您学习更上一层楼!暑假乐园?(一)答案:1-8、DABDDDCA;9、1,2,3;10、a11、a 4且a12、a13、7;14、(1)x2,(2)x15、a16、1;17、18厘米;18、2121、18题;22、(1)a=0.6 ,b=0.4;(2)35%到50%之间(不含35%和50%)。
暑假乐园(2)答案:1:D 2:A 3:A 4::A 5:C 6:C7:-2 8:1,9:x=2,10:x.0且x1,11、略,12、略,13、2-a,14、a-3、1,15、(1)x=4,(2)x=-2/3,16、B,17、C,18、2,19、-1,20、k=1、4、7,21、互为相反数,22、47,23、375,24、略,暑假乐园?三答案1,-1 2,y=2/x 3,B 4,D 5,B 6,C 7,B 8,1/2 9,2 10, B 11,(1)y=4-x (2)略 12,(1)x =1 m=1(2)与x轴交点(-1,0),与y轴交点(0,1) 13,x 0) (2)3000 (3)6000暑假乐园?四答案(四)1、B; 2、B ; 3、B; 4、A; 5、B; 6、B; 7、D; 8、D;9、= 10、t1;11、12、减小;13、a14、3和4;15、19; 16、3或4/3;17、x 18、x19、x3,原式=- ;20、略;21、x=4;22、y=-x+2,6;23、略,BD=6暑假乐园?五答案(五)1.4:3 2.6 3.3858 4.18 5.1:9 6.18 7.①④ 8.D暑假乐园?六答案1-8: CCCBBABC 9:1.6,26;10:8.75;11:A,AFE=B, AEF=C, 12:7;13:6.4;14: 8:5;15: 48;16: 6, 4.8, 8.64; 17: 9:4; 18: 1:3 ;19: 4 20: 13, ;21: 8.3暑假乐园?七答案1、C2、A3、D4、C5、B6、B7、B8、D9、假设在一个三角形中有两个角相等,那么这个三角形是直角三角形。
(八年级数学教案)苏教版八年级数学暑假作业
苏教版八年级数学暑假作业八年级数学教案苏教版八年级数学暑假作业一、选择题:1. 如果代数式有意义,那么x的取值范围是()A.x >0B.x 工1C.x>O D S xx>02. 下列各组数中,以a、b、c为边的三角形不是直角三角形的是()A BC D3•如图,直线上有三个正方形,若的面积分别为5和11,则的面积为()A.4B.6C. 16D.554. 如图,在平行四边形ABCD中,下列结论中错误的是()A. / 仁/ 2B. / BAD二/ BCDC. AB=CDD. ACBD5. 如图,在平行四边形ABCD中,对角线AC,BD相交于点0点E,F分别是边AD,AB的中点,EF交AC于点H,则的值为()A. 1B.C.D.6. 的图象如图所示,当时,的取值范围是()A. B. C. D.7. 体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是进球数0 1 2 345人数1 5 x y 3 2A.y=x+9与y= x+B. y=-x+9与y= x+C. y=-x+9与y=- x+D. y=x+9与y=- x+8. 已知一次函数y二kx+b(k b为常数且k工(的图象经过点A(0,-2)和点B(1,0)则k= ,b=9. 已知:△ AB中,AB=4,AC=3,BC=^U △ ABC勺面积是()A.6B.5C.1.5D.210. 如图,已知一条直线经过点A(0,2)、点B(1,0)将这条直线向左平移与x 轴、y轴分别交与点C、点D.若DB二DC则直线CD的函数解析式为11. 四边形ABCD中,对角线AC BD相交于点0,下列条件不能判定这个四边形是平行四边形的是()A. AB// DC,AD// BCB. AB=DC,AD=BCC. A0=C0,B0=D0 DI. DC,AD=BC12. 有一块直角三角形纸片,如图1所示,两直角边AC=6cm,BC=8cm现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合则CD等于()A.2cmB.3cmC.4cmD.5cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二年级数学暑假功课习题精编?为了帮大家提高学习成绩,查字典数学网在这里为大家整理了初二年级数学暑假作业习题,希望大家可以用心去看,去学习。
【一】选择题1.-3的相反数是A. B.- C.-3 D.32.在以下运算中,计算正确的选项是A. B.C. D.3.数据1,2,3,4,5的平均数是A.1B.2C.3D.44.如图,在△ABC中,D、E分别是AB、AC的中点,假设DE=5,那么BC为A.2.5B.10C.12D.255.用配方法将代数式变形,结果正确的选项是变形A. B. C. D.6.图1是一个底面为正方形的直棱柱金属块,因设计需要将它切去一角,如图2所示,那么切去后金属块的俯视图是7.如图,在梯形ABCD中,AB∥DC,AD=DC=CB,假设∠ABD=25°,那么∠BAD的大小是A.30°B.50°C.45°D.60°8.如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△CMN的面积为y,那么y关于x的函数图象大致形状是【二】填空题9.如果分式的值是零,那么的取值是 .10.2019年3月12日,国家公布全国公共财政收入情况,1-2月累计,全国财政收入20918.28亿元,这个数据用科学记数法表示并保留两个有效数字为亿元.11.如图,⊙O的半径为6,点A、B、C在⊙O上,且∠ACB=45°,那么弦AB的长是 .12. :如图, 互相全等的平行四边形按一定的规律排列.其中,第①个图形中有1个平行四边形,第②个图形中一共有5个平行四边形,第③个图形中一共有11个平行四边形,第④个图形中一共有个平行四边形,……,第n个图形中一共有平行四边形的个数为个.【三】解答题13.计算:14.解分式方程:15.:如图,∠ABC=90°,DC⊥BC,E,F为BC上两点,且, . 求证: ;16.先化简,再求值:,其中 .17.如图,在平面直角坐标系xOy中,一次函数的图象与反比例函数的图象的一个交点为A(-1,n).(1)求反比例函数的【解析】式;(2)假设P是坐标轴上一点(点P不与点O重合),且PA=OA,试写出点的坐标.18.某小型超市购进了两批相同品种的水果,第一批用了200元,第二批用了550元,第二批购进水果的重量是第一批的2.5倍,且进价比第一批每千克多1元.求第一批购进水果多少千克?【四】解答题19.甲、乙两人同时从某地A出发,甲以60米/分钟的速度沿北偏东30°方向行走,乙沿北偏西45°方向行走,10分钟后甲到达B点,乙正好到达甲的正西方向的C点,此时甲、乙两人之间的距离是多少米?20.PMI指数英文全称Purchase Management Index,中文翻译为采购经理指数.PMI是一套月度发布的、综合性的经济监测指标体系,分为制造业PMI、服务业PMI.PMI是通过对采购经理的月度调查汇总出来的指数,反映了经济的变化趋势.以下图来源于2019年3月2日的«都市快报»,反映了2019年2月至2019年2月期间我国制造业PMI指数变化情况,请根据以上信息并结合制造业PMI图,解答以下问题:(1)在以上各月PMI指数,中位数是 ;(2)观察制造业PMI指数图,以下说法正确的有 (请填写序号):①我国制造业PMI指数从2019年11月至2019年2月连续三个月回升,并创下四个月新高;②自2019年2月至2019年2月我国制造业每月PMI指数较前一月下降的次数是10次.21.如图,以△ABC的边AB为直径的⊙O与边BC交于点D,过点D作DE⊥AC,垂足为E,延长AB、ED交于点F,AD平分∠BAC.(1)求证:EF是⊙O的切线;(2)假设⊙O的半径为2,AE=3,求BF的长.22.阅读材料1:把一个或几个图形分割后,不重叠、无缝隙的重新拼成另一个图形的过程叫做〝分割——重拼〞.如图1,一个梯形可以分割——重拼为一个三角形;如图2,任意两个正方形可以分割——重拼为一个正方形.(1)请你在图3中画一条直线将三角形分割成两部分,将这两部分重新拼成两个不同的四边形,并将这两个四边形分别画在图4,图5中;阅读材料2:如何把一个矩形ABCD(如图6)分割——重拼为一个正方形呢?操作如下:①画辅助图:作射线OX,在射线OX上截取OM=AB,MN=BC.以ON为直径作半圆,过点M作MI⊥OX,与半圆交于点I;②如图6,在CD上取点F,使AF=MI ,作BE⊥AF,垂足为E.把△ADF沿射线DC平移到△BCH的位置,把△AEB沿射线AF平移到△FGH的位置,得四边形EBHG.(2)请依据上述操作过程证明得到的四边形EBHG是正方形. 【五】解答题23.在△ABC中,AB=AC,点P为△ABC所在平面内一点,过点P分别作PE∥AC交AB于点E,PF∥AB交BC于点D,交AC于点F.(1)如图1,假设点P在BC边上,此时PD=0,易证PD,PE,PF与AB满足的数量关系是PD+PE+PF=AB;当点P在△ABC内时,先在图2中作出相应的图形,并写出PD,PE,PF与AB 满足的数量关系,然后证明你的结论;(2)如图3,当点P在△ABC外时,先在图3中作出相应的图形,然后写出PD,PE,PF与AB满足的数量关系.(不用说明理由)六、解答题24.二次函数y=ax2+bx+2,它的图像经过点(1,2).(1)如果用含a的代数式表示b,那么b= ;(2)如下图,如果该图像与x轴的一个交点为(-1,0).①求二次函数的【解析】式;②在平面直角坐标系中,如果点P到x轴的距离与点P到y 轴的距离相等,那么称点P为等距点.求出这个二次函数图像上所有等距点的坐标.(3)当a取a1,a2时,二次函数图像与x轴正半轴分别交于点M(m,0),点N(n,0).如果点N在点M的右边,且点M和点N都在点(1,0)的右边.试比较a1和a2的大小,并说明理由.七、解答题25.抛物线y = x2 + bx ,且在x轴的正半轴上截得的线段长为4,对称轴为直线x = c.过点A的直线绕点A (c ,0 ) 旋转,交抛物线于点B ( x ,y ),交y轴负半轴于点C,过点C且平行于x轴的直线与直线x = c交于点D,设△AOB 的面积为S1,△ABD的面积为S2.(1) 求这条抛物线的顶点的坐标;(2) 判断S1与S2的大小关系,并说明理由.参考【答案】:第一卷 (机读卷共32分)【一】选择题(共8道小题,每题4分,共32分)题号 1 2 3 4 5 6 7 8【答案】 D C C B C A B A第二卷 (非机读卷共88分)【二】填空题(共4道小题,每题4分,共16分)题号 9 10 11 12【答案】 x=-1 2.1×104 6 19,n2+n-1【三】解答题(此题共30分,每题5分)13.解:原式= ……………………………………………………4分= …………………………………………………………………………5分14.解:方程的两边同乘,得………………………………………………………………………………2分解得:………………………………………………………3分检验:把代入………………………………4分∴原方程的解为:. (5)分15.证明:(1) ,.…………………………………………………………………………………1分∠ABC=90°,DC⊥BC∴∠ABC=∠DCE=90°………………………………………………………………………3分在和中,.…………………………………………………………………………5分16.解:原式= ………………………………………………2分= ………………………………………………3分= .…………………………………………………………………………4分当时,原式= (5)分17.解:(1)∵ 点A 在一次函数的图象上,∴ 点A的坐标为.…………………………………………………………………1分∵ 点A在反比例函数的图象上,∴反比例函数的【解析】式为. ……………………………………………………3分(2)点的坐标为.………………………………………………………5分18.解:设第一批购进水果千克,那么第二批购进水果2.5 千克,…………………………1分依据题意得:………………………………………………………………………………3分解得x=20,经检验x=20是原方程的解,且符合题意……………………………………………………4分答:第一批购进水果20千克;………………………………………………………………5分【四】解答题(此题共20分,每题5分)19.解:过作交于,那么 ,∴ …………………………………………………………………5分答:甲乙两人之间的距离是米20.解:(1)50.9;…………………………….…………………………………………….2分(2)①……………………………………………………………………………….5分21. 解:(1)连接OD.∵OA=OD∴∠OAD=∠ODA.∵AD平分∠BAC∴∠OAD=∠CAD,∴∠ODA=∠CAD.∴OD∥AC.………………………………………………1分∵DE⊥AC,∴∠DEA=∠FDO=90°∴EF⊥OD.∴EF是⊙O的切线. ……………………………………2分(2)设BF为x.∵OD∥AE,∴△ODF∽△AEF. ……………………………………3分∴ ,即 .解得 x=2∴BF的长为2. ……………………………………5分22.(1)分割正确,且画出的相应图形正确……………………………………………………2分(2)证明:在辅助图中,连接OI、NI.∵ON是所作半圆的直径,∴∠OIN=90°.∵MI⊥ON,∴∠OMI=∠IMN=90°且∠OIM=∠INM.∴△OIM∽△INM.∴OMIM=IMNM .即IM2=OM?NM.…………………………………………………3分∵OM=AB,MN=BC∴IM 2 = AB?BC∵AF=IM∴AF 2=A B?BC=AB?AD.∵四边形ABCD是矩形,BE⊥AF,∴DC∥AB,∠ADF=∠BEA=90°.∴∠DFA=∠EAB.∴△DFA∽△EAB.∴ADBE=AFAB .即AF?BE=AB?AD=AF 2.∴AF=BE.………………………………………………………………………4分∵AF=BH∴BH=BE.由操作方法知BE∥GH,BE=GH.∴四边形EBHG是平行四边形.∵∠GEB=90°,∴四边形EBHG是正方形.……………………………………………………5分【五】解答题(此题总分值7分)23.解:(1)结论:……………………2分证明:过点P作MN BC四边形是平行四边形……………………………………………3分四边形是平行四边形……………………………………………4分又,MN BC…………………………………………5分(2)结论:……………………………7分六、解答题(此题总分值7分)24.解:(1) ……………………………………………1分(2)①∵二次函数经过点(1,2)和(-1,0)解,得即…………………………………………………………………………2分② 该函数图像上等距点的坐标即为此函数与函数和函数的交点坐标,解得P1( ) P2( )P3( ) P4( ) (4)分(3) ∵二次函数与x轴正半轴交于点M(m,0)且当a= 时∴ 即同理故∵ 故∴ ………………………………………………………………………………………7分七、解答题(此题总分值8分)25.解:(1)∵ 抛物线y=x2+bx,在x轴的正半轴上截得的线段的长为4,∴ A(2,0),图象与x轴的另一个交点E的坐标为 (4,0),对称轴为直线x=2.∴ 抛物线为 y = x2 +b x经过点E (4,0) .∴ b= -4,∴ y = x2 -4x .∴ 顶点坐标为(2,-4). ………… 2分(2) S1与S2的大小关系是:S1 = S2 ………… 3分理由如下:设经过点A(2,0)的直线为y=kx+b (k≠0).∴ 0 =2k+b.∴ k = b.∴ y= .∴ 点B 的坐标为(x1 , ),点B 的坐标为(x2 , ).当交点为B1时,.……………………………………… 5分当交点为B2时,∴ S1 = S2.综上所述,S1 =S2. (8)分上文为大家整理的初二年级数学暑假作业习题相关内容大家仔细阅读了吗?希望同学们收获一个快乐健康而又充实的暑假!。
