Coherence and squeezing in superpositions of spin coherent states
物理学名词

1/4波片quarter-wave plateCG矢量耦合系数Clebsch-Gordan vector coupling coefficient; 简称“CG[矢耦]系数”。
X射线摄谱仪X-ray spectrographX射线衍射X-ray diffractionX射线衍射仪X-ray diffractometer[玻耳兹曼]H定理[Boltzmann] H-theorem[玻耳兹曼]H函数[Boltzmann] H-function[彻]体力body force[冲]击波shock wave[冲]击波前shock front[狄拉克]δ函数[Dirac] δ-function[第二类]拉格朗日方程Lagrange equation[电]极化强度[electric] polarization[反射]镜mirror[光]谱线spectral line[光]谱仪spectrometer[光]照度illuminance[光学]测角计[optical] goniometer[核]同质异能素[nuclear] isomer[化学]平衡常量[chemical] equilibrium constant[基]元电荷elementary charge[激光]散斑speckle[吉布斯]相律[Gibbs] phase rule[可]变形体deformable body[克劳修斯-]克拉珀龙方程[Clausius-] Clapeyron equation[量子]态[quantum] state[麦克斯韦-]玻耳兹曼分布[Maxwell-]Boltzmann distribution[麦克斯韦-]玻耳兹曼统计法[Maxwell-]Boltzmann statistics[普适]气体常量[universal] gas constant[气]泡室bubble chamber[热]对流[heat] convection[热力学]过程[thermodynamic] process[热力学]力[thermodynamic] force[热力学]流[thermodynamic] flux[热力学]循环[thermodynamic] cycle[事件]间隔interval of events[微观粒子]全同性原理identity principle [of microparticles][物]态参量state parameter, state property[相]互作用interaction[相]互作用绘景interaction picture[相]互作用能interaction energy[旋光]糖量计saccharimeter[指]北极north pole, N pole[指]南极south pole, S pole[主]光轴[principal] optical axis[转动]瞬心instantaneous centre [of rotation][转动]瞬轴instantaneous axis [of rotation]t 分布student's t distributiont 检验student's t testK俘获K-captureS矩阵S-matrixWKB近似WKB approximationX射线X-rayΓ空间Γ-spaceα粒子α-particleα射线α-rayα衰变α-decayβ射线β-rayβ衰变β-decayγ矩阵γ-matrixγ射线γ-rayγ衰变γ-decayλ相变λ-transitionμ空间μ-spaceχ 分布chi square distributionχ 检验chi square test阿贝不变量Abbe invariant阿贝成象原理Abbe principle of image formation阿贝折射计Abbe refractometer阿贝正弦条件Abbe sine condition阿伏伽德罗常量Avogadro constant阿伏伽德罗定律Avogadro law阿基米德原理Archimedes principle阿特伍德机Atwood machine艾里斑Airy disk爱因斯坦-斯莫卢霍夫斯基理论Einstein-Smoluchowski theory 爱因斯坦场方程Einstein field equation爱因斯坦等效原理Einstein equivalence principle爱因斯坦关系Einstein relation爱因斯坦求和约定Einstein summation convention爱因斯坦同步Einstein synchronization爱因斯坦系数Einstein coefficient安[培]匝数ampere-turns安培[分子电流]假说Ampere hypothesis安培定律Ampere law安培环路定理Ampere circuital theorem安培计ammeter安培力Ampere force安培天平Ampere balance昂萨格倒易关系Onsager reciprocal relation凹面光栅concave grating凹面镜concave mirror凹透镜concave lens奥温电桥Owen bridge巴比涅补偿器Babinet compensator巴耳末系Balmer series白光white light摆pendulum板极plate伴线satellite line半波片halfwave plate半波损失half-wave loss半波天线half-wave antenna半导体semiconductor半导体激光器semiconductor laser半衰期half life period半透[明]膜semi-transparent film半影penumbra半周期带half-period zone傍轴近似paraxial approximation傍轴区paraxial region傍轴条件paraxial condition薄膜干涉film interference薄膜光学film optics薄透镜thin lens保守力conservative force保守系conservative system饱和saturation饱和磁化强度saturation magnetization本底background本体瞬心迹polhode本影umbra本征函数eigenfunction本征频率eigenfrequency本征矢[量] eigenvector本征振荡eigen oscillation本征振动eigenvibration本征值eigenvalue本征值方程eigenvalue equation比长仪comparator比荷specific charge; 又称“荷质比(charge-mass ratio)”。
lecture 7---NOESY
H
H
NO2
H 3C S
NO 2 H 3C S
H
7 .9 8
NO2
H 3C S
6.29
H
NO 2 H 3C S
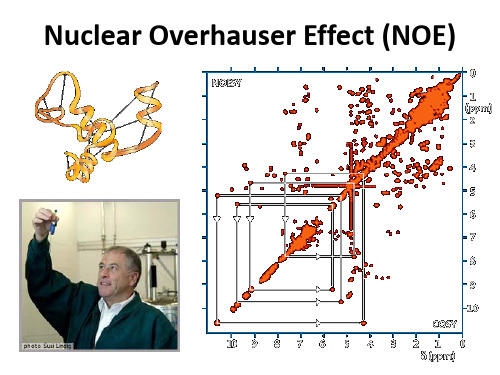
2D NOESY
2D NOESY
8 - 7, 12 7 - 18, 18' 3 - 5, 10 5 - 11, 16, 18'
9 - 10, 17, 17'
10 - 16 11 - 18, 16, 14, 18' 18 - 13, 18' 16 - 14, 17 13 - 14, 17, 17' 13' - 17, 17' 17 - 17'
当两个核AX在空间上很接近时,可以通过偶极--偶 极作用相互影响。选择A的频率照射,会影响X的能级 分布,从而改变其信号强度。
Nuclear Overhauser Effect (NOE)
bb
ba X2 A1 单量子数驰豫W1不产生NOE效应。 A2 ab X1 双量子数驰豫W2和零量子数驰豫W0 W2
2D NOESY
2D NOESY
2D NOESY
TOCSY (solid lines) and NOESY (dotted lines)
AVANCE 900
2.0 mM Lysozyme NOESY
Nuclear Overhauser Effect (NOE)
NOE实验对环境变化非常敏感,为了得到高质量的谱图, 有如下建议
NMR
PBu3 PiBu3 -32.5 ppm -45.3 ppm
PsBu3
PtBu3
7.9 ppm
63 ppm
I=1/2 Natural abundance Reference compound 100% 85% H3PO4 in H2O = 0 ppm 6.67 × 10-3 37.7
Phys. Rev. Lett. 78, 4293–4296 (1997)

We consider the atomic scheme outlined in Fig. 1(b). Three internal long–lived (ground) states levels participate in the transmission. The qubit is stored in |g and |e , whereas |r acts as an auxiliary level. To achieve transmision from atom i to j , one first transfers |e i → |r i via a Raman process, where a photon
FIG. 1. (a) Schematic representation of the protocol for ideal transmission of one qubit from atom 1 in cavity 1 to atom 2 in cavity 2. Atom b is a backup atom and a an auxiliary atom. The steps (i)–(v) in the protocol can be found in the text. (b) Level structure of atoms and couplings induced by laser and cavity fields.
1
+ c1 |1 ) ⊗ |0
2
−→ |0
1
⊗ (c0 |0
2
+ c1 |1 2 ). (1)
to retry sending the qubit until perfect transmission is achieved, thus correcting for transmission errors in the noisy quantum optical channel to all orders. Typical error correction schemes developed in the context of quantum computing [6] perform redundant encoding of a logical qubit in several physical qubits, i.e. add an increasing number of atoms (“permanent qubits”), to correct errors to higher order [7]. In contrast, the physical basis of our scheme, laser manipulation of atoms in CQED [8], makes it comparatively simple to create highly entangled states of atoms with many photons (“transient qubits”). Furthermore, these correction schemes for transmission errors require only a moderate overhead, with (entanglement of) only two atoms on the sending side, and two atoms on the receiving node. Given that small model systems of “ion trap quantum computers” [9] involving a few qubits will be built in the near future, such a scheme opens a realistic perspective of implementing perfect transmission in quantum networks. This will have interesting applications, such as distributing and storing EPR pairs (or N –atom entangled states) in distant nodes for secure public key distribution [1], purification schemes for quantum cryptography [3], and dense coding of quantum information [4].
ls耦合 自旋轨道耦合

ls耦合自旋轨道耦合
LS耦合是指由给定电子组态确定多个价电子原子的能量状态的一种近似方法,是原子中核外电子的能量主要由其电子组态决定的表现。
自旋-轨道LS耦合是指在原子谱项部分,通过将所有电子的轨道角动量耦合,再将自旋角动量耦合,最后将总的轨道角动量和总的自旋角动量耦合为总的角动量的方法。
总量子数J=L+S,其中L为总轨道角动量,S为总自旋角动量。
在LS耦合中,L通常表示角量子数的加和,但在某些情况下,它也可能表示磁量子数的加和。
这主要取决于具体的情况和应用场景。
LS耦合是原子物理和量子力学中的一个重要概念,在研究原子结构和性质方面具有重要作用。
Nonlinear coherent destruction of tunneling

a r X i v :0705.1627v 1 [q u a n t -p h ] 11 M a y 2007Nonlinear Coherent Destruction of TunnelingXiaobing Luo,Qiongtao Xie,and Biao Wu ∗Institute of Physics,Chinese Academy of Sciences,Beijing 100080,ChinaWe study theoretically two coupled periodically-curved optical waveguides with Kerr nonlinearity.We find that the tunneling between the waveguides can be suppressed in a wide range of parameters due to nonlinearity.Such suppression of tunneling is different from the coherent destruction of tun-neling in a linear medium,which occurs only at the isolated degeneracy point of the quasienergies.We call this novel suppression nonlinear coherent destruction of tunneling.This nonlinear phe-nomenon can be observed readily with current experimental capability;it may also be observable in a different physical system,Bose-Einstein condensate.PACS numbers:42.65.Wi,42.82.Et,03.75.Lm,33.80.BePeriodic driving force is an important and effective tool for coherently controlling quantum tunneling.This has been well demonstrated with a paradigmatic model,a free particle in a double-well potential and driven by a periodic external field[1].With appropriately tuned pa-rameters,the periodic driving force is able not only to enhance tunneling[2]-[4]but also to completely suppress it[5]-[8].The latter is rather surprising and was discov-ered first by Grossmann et al [5].It is now known as coherent destruction of tunneling (CDT)[5].When it oc-curs,a localized wave packet prepared in one well re-mains in the same well and does not tunnel to the other well.In a periodically driven system,there are Floquet states and associated quasienergies[9].The CDT is found to occur only at the isolated degeneracy point of the quasienergies[5,6].Recently,this quantum phenomenon of CDT was ob-served experimentally with two coupled periodically-curved waveguides[10](see Fig.1).In this classical optical system,the Maxwellian wave mimics the quantum wave while the periodic driving force is achieved by bending the waveguides periodically.Such a waveguide system is an ideal laboratory system for demonstrating the co-herent control of quantum tunneling by periodic driving force.For example,tunneling enhancement has recently also been reported with two optical waveguides[11].In this Letter we consider a similar coupled waveguide system but with Kerr nonlinearity.With a well-known two-mode approximation,the system can be described by a two-mode nonlinear model with an external peri-odic driving force.This driving is characterized by two parameters,its frequency w (the inverse of the period of the curved waveguide)and its strength S (the curving magnitude of the waveguides)of the driving force.By numerically solving this two-mode nonlinear model,we find that the suppression of tunneling between the two coupled waveguides happens for a wide range of ratio S/w .This is in stark contrast to the CDT in curved lin-ear waveguides that occurs at an isolated point of S/w ,where the quasienergies of the system are degenerate.This extension of tunneling suppression region is caused by nonlinearity.Therefore,we call it nonlinear coherentdestruction of tunneling (NCDT).We find that the range of ratio S/w for NCDT increases steeply with nonlinear strength.The Floquet states and the quasienergies of this nonlinear model are also studied.We discover that there can be more than two Floquet states and quasiener-gies in a certain range of ratio S/w .These additional Floquet states form a triangle in the quasienergy levels.Our study reveals that these additional Floquet states are closely related to the NCDT.The current experimental capability with nonlinear waveguides is examined.We find that the observation of NCDT is well within the current experimental abil-ity.Note that the nonlinear two-mode model that we de-rived for the waveguides can also be used to describe the dynamics of a Bose-Einstein condensate in a double-well potential under a periodic modulation[12].This indicates that NCDT may also be observable with Bose-Einstein condensates.FIG.1:Schematic drawing (not to scale)of two periodically curved optical waveguides placed parallel to each other.In a weakly guiding dielectric structure,the effective two-dimensional wave equation for light propagation in nonlinear directional waveguides reads[13]i λ∂z=−λ2∂x 2+V [x −x 0(z )]ψ−|ψ|2ψ.(1)where λis the free space wavelength of the light,x 0(z )=A cos(2πz/Λ),and V (x )≡[n 2s −n 2(x )]/(2n s )≃n s −n (x ),where n (x )and n s are,respectively,the effective refractive index profile of the waveguides and the sub-strate refractive index.For the coupled waveguides as in2Fig.1,n (x )thus V (x )have a double-well structure.The scalar electric field is related to ψthrough E (x,z,t )=(1/2)(|n 2|n s ǫ0c 0/2)−1/2[ψ(x,z )exp(−iωt +ikn s z )+c.c.],where n 2is the nonlinear refractive index of the medium,k =2π/λ,ω=kc 0,and c 0and ǫ0are the speed of light and the dielectric constant in vacuum,respectively.The field normalization is taken such that |ψ|2/|n 2|gives the light intensity I (in W/m 2).By means of a Kramers-Henneberger transformation[14]x ′=x −x 0(z ),z ′=z ,and φ(x ′,z ′)=ψ(x ′,z ′)exp[−i (2n s π/λ)˙x 0(z ′)x ′−i (n s π/λ) z′0dξ˙x 20(ξ)](the dot indicates the derivativewith respect to z ′),Eq.(1)is then transformed to i λ∂z ′=−λ2∂x ′2+V (x ′)φ−|φ|2φ+x ′F (z ′)φ≡H 0φ−|φ|2φ+x ′F (z ′)φ.(2)where F (z ′)=n s ¨x 0(z ′)=(4π2An s /Λ2)cos(2πz ′/Λ)is the force induced by waveguide bending.It is clear that if we view z (or z ′)as time t ,the above equations can be regarded as describing the system of a nonlinear quan-tum wave in a double-well potential and under a periodic modulation.We assume that the light in each waveguide of the cou-pler is single moded and neglect excitation of radiation modes.With a standard two-mode approximation[15,16,17],we write φ(x ′,z ′)=e −2iπD exp[−(x ′±a/2)2/2b 2],wherea is the distance between the two waveguides,b is the half-width of each waveguide,and D is related to the input power of the system P (0)as D =n 2P (0)/(√2c 2−S 2c 1+S2πn 2P (0)/(λb )is an effective nonlinearcoefficient.When S =0,Eqs.(4),(5)will be reduced to the well-known Jensen equation[17].Note that P (0)has the unit of W/m is because the waveguide is two dimensional in our theoretical model.In experiments,P (0)has the unit of W and the waveguides are three dimensional.As a result,to relate our nonlinear pa-rameter to the real experimental parameters,we chooseFIG.2:The intensity of light in the initially populated waveg-uide for the case of χ=0(dashed lines)and χ/v =0.4(solid lines)with (a)S/w =1.8,(b)S/w =2.2,(c)S/w =2.4.Dis-tance z ′is in units of 1/v .w/v =10.χ=2πn 2P (0)/(λσeff),where σeffis the effective cross-section of the waveguide,according to Ref.[18].To investigate tunneling effect,we solve the two non-linear equations (4)and (5)numerically with the light initially localized in one of the two waveguides.With the numerical solution,we compute the intensity of the lightstaying in the initial well with P ′(z ′)=|c ∗1(0)c 1(z ′)+c ∗2(0)c 2(z ′)|2.Three sets of our results are shown in Fig.2(a,b,c).In the first set for S/w =1.8,we see that P ′(z ′)oscillates between zero and one for both linear case χ=0and nonlinear case χ/v =0.4,demonstrating no suppression of tunneling.In the second set for S/w =2.2,we see a different scenario,the oscillation of P ′(z ′)is lim-ited between ∼0.8and one for the nonlinear case,showing suppression of tunneling,while there is no suppression for the linear case.In the third set for S/w =2.4,sup-pression of tunneling is seen for both linear and nonlinear cases.Such suppression of tunneling for the linear case is known as coherent destruction of tunneling[5].These nu-merical results demonstrate that nonlinearity can extend the parameter range of the suppression of tunneling.We call this new phenomenon nonlinear coherent destruction of tunneling (NCDT).The extension of tunneling suppression regime of ra-tio S/w by nonlinearity is more clearly demonstrated in Fig.3(a).In this figure,we have used localization,which is defined as the minimum value of P ′(z ′),to measure the suppress of tunneling.When there is large suppres-sion of tunneling,localization is close to one;when there is no suppression,localization is zero.As clearly seen in Fig.3(a),the peak of localization (solid line)for χ/v =0.4is much wider than the peak for χ/v =0.0(dashed line).In Fig.3(b),we see the width of localization ∆Γincreases almost linearly with nonlinearity χ(solid line).Note that,analytically,CDT occurs only at isolated points.That it3FIG.3:(a)Localization as a function of S/w .The solid line isfor the nonlinear case χ/v =0.4and the dashed line is for the linear case χ=0.w/v =10.(b)The width ∆Γof the peak in (a)as a function of nonlinearity strength χ/v (solid line).Thedashed line is for the width of the quasienergy triangle in Fig.4.has a narrow range in Fig.3(a)is because the evolution time is finite in numerical simulation.As is well known,the CDT is connected to the degen-eracy point of quasienergies in the system[5].Although our system is nonlinear,one can similarly define its Flo-quet state and quasienergy.That is,Eqs.(4,5)have so-lutions in the form of {c 1,c 2}=e −iεz ′{˜c 1(z ′),˜c 2(z ′)},where both ˜c 1and ˜c 2are periodic with period of Λ.These Floquet states and corresponding quasienergies εcan be found numerically.We first expand the periodic functions ˜c 1,2in terms of Fourier series with a cutoff.After plug-ging them into Eqs.(4,5),we obtain a set of nonlinear equations for the Fourier coefficients.By solving these equations numerically,we obtain the Floquet states and corresponding quasienergies ε.The results are plotted in Fig.4,where we witness a striking difference between the linear and nonlinear cases.As seen in Fig.4(a),for the linear case,there are two Floquet states for a given value of S/w and there is only one isolated degeneracy point.For the nonlinear case,we notice that there are four Flo-quet states and three quasienergies in a certain range of S/w with two of the Floquet states degenerate.The three quasienergies form a triangle in the quasienergy levels as seen in Fig.4(b,c).Our numerical computation shows that the width of the quasienergy triangle increases with nonlinearity χas shown in Fig.3(dashed line).As this increasing trend is similar to the localization width ∆Γ,this offers us the first glimpse of link between NCDT and the quasienergies.Since the right corner of the triangle can be open,we define the width of the quasienergy tri-angle as the horizontal distance between the left corner and the upper corner.A firm link between the NCDT and the triangle struc-ture in the quasienergies can be established by looking into the Floquet states.We focus on the Floquet statesFIG.4:Quasienergies at (a)χ=0;(b)χ/v =0.4;(c)χ/v =0.8.Solid lines are for numerical results obtained with Eqs.(4,5)and circles for the approximation results for high frequencies with Eqs.(7,8).w/v =3.that correspond to the lowest quasienergies in Fig.4.To measure how the Floquet state is localized in one of thetwo waveguides,we define |c 1|2 =( Λ0dz ′|c 1|2)/Λfor a given Floquet state {c 1,c 2}.We have plotted this value for the lowest Floquet states in Fig.5.In this figure,we see clearly that only the Floquet states on the quasienergy triangle are localized.This thus demon-strates a clear link between the quasi-energy triangle and the NCDT.That there are two lines in Fig.5reflects the fact that there is a two-fold degeneracy for the lowest quasienergies on the triangle.FIG.5:Intensity in the first well for every Floquet state in the lowest quasienergy level at χ/v =0.4,w/v =3.The triangular structure in the quasienergy is very similar to the energy loop discovered within the con-text of nonlinear Landau-Zener tunneling[21].In fact,they are mathematically related.For high frequencies,w ≫max {v,χ},which is usually the case for current ex-periments with optical waveguides,we take advantage of the transformationc 1=c ′1exp[iS sin(wz ′)/2w ],c 2=c ′2exp[−iS sin(wz ′)/2w ].(6)4After averaging out the high frequency terms[12],wefind a non-driving nonlinear model,i˙c′1=v2J0(S/w)c′1−χ|c′2|2c′2,(8)where J0is the zeroth-order Bessel function.It is clear from the transformation in Eq.(6)that the eigenstates of the above time-independent nonlinear equations cor-respond to the Floquet states of Eqs.(4,5).We have com-puted the eigenstates of Eqs.(7,8)and the corresponding eigenenergies,which are plotted as circles in Fig.4.The consistency with the previous results is obvious.As is known in Ref.[21],the above nonlinear model admits ad-ditional eigenstates whenχ>J0(S/w)v.Therefore,this can be regarded as the condition for the extra Floquet states to appear for the driving nonlinear model Eqs.(4,5) at high frequencies.So far,we have focused on self-focusing materials.Our approach and results will be very similar if one consid-ers instead self-defocusing materials,for which the sign before the nonlinear term in Eq.(1)should be plus.Non-linear coherent destruction of tunneling still occurs and the triangular structure also appears in the quasienergy levels but its direction is reversed as compared to the self-focusing case.At present the nonlinear waveguides are readily avail-able in labs[18,19,20].We take the experimental parameters in Ref.[19]to estimate our theoretical val-ues in Eqs.(4,5).The wavelength of the laser light is λ=1.55µm,the effective cross-sectional area of the waveguide isσeff=12µm2,the nonlinear index n2= 1.2×10−13cm2/W,and the shortest length for the light transfer from one waveguide to the other waveguide in the weak nonlinearity limit is L c≈2cm.With the power input in the waveguides P(0)∼100W,we haveχπλσeff≈2.(9) This shows that strong nonlinear waveguides are avail-able at optical labs and nonlinear coherent destruction of tunneling can be visualized in an optical experiment similar to the one in Ref.[10].We also want to mention briefly that NCDT may be applied to improve optical switching devices[19,20].The details will be discussed elsewhere.In conclusion,we have studied the light propagation in a nonlinear periodically-curved waveguide directional coupler.We have found a new type of suppression of tunneling in this system,which is induced by nonlinear-ity and has no linear counterpart.We call it nonlinear coherent destruction of tunneling(NCDT)in analogy to a similar but different phenomenon in linear driving sys-tems,coherent destruction of tunneling.The NCDT oc-curs for an extended range of ratio S/w,where S is the strength of the driving and w is its frequency.We have also found that the NCDT is closely related to a trian-gular structure appeared in the quasienergy levels of the nonlinear system.We have also pointed out that obser-vation of the novel nonlinear phenomenon is well within the capacity of current experiments.This work is supported by NSF of China(10504040), the973project of China(2005CB724500,2006CB921400), and the“BaiRen”program of Chinese Academy of Sci-ences.∗Electronic address:bwu@[1]M.Grifoni,and P.H¨a nggi,Phys.Rep.304,229(1998).[2]W.A.Lin and L.E.Ballentine,Phys.Rev.Lett.65,2927(1990).[3]A.Peres,Phys.Rev.Lett.67,158(1991).[4]I.Vorobeichik and N.Moiseyev,Phys.Rev.A,59,2511(1999).[5]F.Grossmann,T.Dittrich,P.Jung,and P.Hanggi,Phys.Rev.Lett.67,516(1991);Z.Phys.B84,315(1991). [6]F.Grossmann and P.Hanggi,Europhys.Lett.18,571(1992).[7]R.Bavli and H.Metiu,Phys.Rev.Lett.69,1986(1992).[8]M.Steinberg and U.Peskin,J.Appl.Phys.85,270(1999).[9]J.H.Shirley,Phys.Rev.138,B979(1965).[10]G.Della Valle,M.Ornigotti, E.Cianci,V.Fogli-etti,porta,and S.Longhi.e-print arXiv:quant-ph/0701121.[11]I.Vorobeichik,E.Narevicius,G.Rosenblum,M.Oren-stein,and N.Moiseyev,Phys.Rev.Lett.90,176806 (2003).[12]Guan-Fang Wang,Li-Bin Fu and Jie Liu,Phys.Rev.A73,013619(2006).[13]R.W.Micallef,Y.S.Kivshar,J.D.Love,D.Burak,andR.Binder,Opt.Quantum Electron.30,751(1998).[14]W.C.Henneberger,Phys.Rev.Lett.21,838(1968).[15]S.Longhi,Phys.Rev.A71,065801(2005).[16]R.Khomeriki,J.Leon,and S.Ruffo,Phys.Rev.Lett.97,143902(2006).[17]S.M.Jensen,IEEE J.Quantum Electron.QE-18,1580(1982).[18]H.S.Eisenberg,Y.Silberberg,R.Morandotti, A.R.Boyd,and J.S.Aitchison,Phys.Rev.Lett.81,3383 (1998).[19]K.Al-hemyari,A.Villeneuve,J.U.Kang,J.S.Aitchison,C.N.Ironside,G.I.Stegeman,Appl.Phys.Lett.63,3562(1993).[20]S.R.Friberg,Y.Silberberg,M.K.Oliver,M.J.Andrejco,M.A.Saifi,P.W.Smith,Appl.Phys.Lett.51,135(1987).[21]B.Wu and Q.Niu,Phys.Rev.A61,023402(2000).。
PhysRevA.87.042115

07_相干态与变换
相位算符的对易关系为:
[ ] ⎧ Nˆ , Sˆ = iCˆ
[ ] ⎪
⎨
Nˆ ,Cˆ = −iSˆ
( ) ⎪⎩[Cˆ, Sˆ] = a+ (Nˆ +1)−1a −1 / 2i
习题7.3 证明上面的对易关系式。
2)相位态
由于C和S不对易,且无零本征值,因此不存在它们的共 同本征态。但可以定义如下的渐近态:
推导3相干态小结除以上介绍的几种以外物理中运用的相干态很多如群相干态费米相干态su3电荷超荷相干态相互作用玻色子相干态ibm相干态双线性费米相干态等等在量子力学量子光学量子场论凝聚态物理核物理粒子物理等离子物理等均有涉及甚至渗透到化学生物等科学领域显示出强大的生命力
第七章 相干态积分与量子变换
§7.1 相干态 §7.2 有序算符积分方法 §7.3 线性量子变换
2)相干态的定义
定义1 相干态(这里指正则相干态,或谐振子相干态)是 湮灭算符的本征态
az =zz
定义2 相干态是平移后的真空态 z = D(z) 0
其中平移算符 D(z) = exp(za+ − z*a)
平移算符对产生与湮灭算符的变换: D(z)aD−1(z) = a − z, D(z)a+ D−1(z) = a+ − z*
使用相干态表象的优点:可将量子理论中力学量期望 值的计算变为普通复数函数的积分计算,算符方程过 渡到复数函数的运动方程。
即:
f
=
1 π
∫∫ d2z
z
z
f
f (z*) =
z
f
e1 z 2 2
∫∫ = 1
d2
zf
(
z*
)e−
1 2
量子光学第二讲,相干态与压缩态
相干态物理性质
于是得到坐标与动量的测不准量为
( ∆pቤተ መጻሕፍቲ ባይዱ)2 = p 2 − p ( ∆q )2 = q 2 − q
2
= ω n+ = ω
(
1 2
)
2
(
n+
1 2
)
测不准关系为
∆p∆q = n +
(
1 2
)
可见最小测不准态是基态 φ0 ( q ) ,最小值为 / 2 。如何通过简单的谐振运动但 保持这个最小测不准波包形状不变?假设在 t = 0 时刻,波函数 ψ (q, 0 ) 具有最 小测不准波包形式,只是在 +q 方向上有一个位移量 q 0 ,于是有
∆q ∆p =
/2
上式说明相干态是最小测不准量子态,因而也是量子理论所容许的最接近 经典极限的量子态。
2004 © Dr. Shutian Liu, Department of Physics, Harbin Institute of Technology 13
相干态物理性质
相干态的能量起伏
利用不等式 A2 + B 2 ≥ 2AB ,我们有
9
相干态物理性质
几率密度随时间的变化为
ω ψ ( q, t ) = π
2
( )
1
2
ω exp ⎡⎢ − ( q − q 0 cos ωt )2 ⎤⎥ ⎣ ⎦
该波包在谐振子势场中来回做简谐振动而形状不变,因此是相干的。该波包 具有最小测不准关系,是最接近经典单模场的量子力学表述形式。相干的最 小测不准波包可以写成
α = exp −
(
1 2 α 2
)
1 2 α exp ( −α*a ) exp ( αa + ) 2 1 = exp − α 2 exp ( αa + ) exp ( −α*a ) 2 ↓ 1 exp ( αa + ) exp ( −α*a ) 0 = exp − α 2 exp ( αa + ) 0 2
斯特恩-盖拉赫量子叠加态-概述说明以及解释
斯特恩-盖拉赫量子叠加态-概述说明以及解释1.引言1.1 概述斯特恩-盖拉赫量子叠加态是量子力学中一个备受关注的概念,其由德国物理学家奥托·斯特恩和沃尔夫冈·保罗·盖拉赫于20世纪初提出。
该概念指的是一种特殊的量子态,可以同时处于多个可能性之间,而非仅限于经典物理学中的单一状态。
通过斯特恩-盖拉赫实验,他们展示了粒子可以同时存在于两个互补状态之间的叠加态,这一发现颠覆了经典物理学中对粒子运动的理解,引发了对量子力学本质的深刻思考。
本文将深入探讨斯特恩-盖拉赫量子叠加态的概念、斯特恩-盖拉赫实验的历史背景以及实验对量子力学的影响,旨在帮助读者更好地理解量子力学中的这一重要概念,并展望未来在该领域的研究方向。
1.2 文章结构文章结构部分的内容应该包括描述整篇文章的章节组成和每个章节的主要内容,以便读者能了解整篇文章的框架和主题内容。
一般情况下,文章结构部分应该包括以下内容:1. 引言部分,介绍文章的主题和目的,引导读者进入文章主题。
2. 正文部分,按照逻辑顺序展开主题,介绍相关概念、实验和影响。
3. 结论部分,总结文章的主要内容,提出未来研究方向和结论。
具体到这篇关于斯特恩-盖拉赫量子叠加态的文章,文章结构部分应该描述包括引言、正文和结论三个主要部分,分别介绍每个部分的主要内容和目的。
引言部分用于引出斯特恩-盖拉赫量子叠加态的概念和重要性,正文部分详细介绍斯特恩-盖拉赫实验的历史背景和对量子力学的影响,结论部分应该总结斯特恩-盖拉赫量子叠加态的重要性,展望未来研究方向,并总结文章的主要结论。
1.3 目的本文的主要目的是探讨斯特恩-盖拉赫量子叠加态在量子力学中的重要性和影响。
通过对斯特恩-盖拉赫实验的历史背景和概念的深入解析,我们希望读者能够更好地理解量子叠加态的概念及其在量子力学中的作用。
同时,我们也将探讨斯特恩-盖拉赫实验对于人类对于量子理论的认识和发展所起到的重要作用。
Er3+,Yb3+BaWO4晶体的光谱特性及上转换发光
2.1 晶体生长
晶体采用提拉法在大气气氛中进行生长,生长设备为DJ-400 型单晶炉。原料为光谱纯 的为BaCO3,WO3, Yb2O3,Er2O3。BaCO3,WO3按 1:1 的摩尔比配料,Er2O3和Yb2O3的掺杂浓度 1mol%。固相反应的方程式为:
*中国科学院物理研究所光物理重点实验室资助。
− 0.02476λ2
(5)Βιβλιοθήκη ne2=3.28033 +
0.03538 λ2 − 0.02810
− 0.01077λ2
(6)
对同一波长BaWO4晶体的no和ne差别不大,计算过程中n值取no和ne的平均值。由吸收光谱求出 Г值,进而求出SedJJ’,代入(3)式中,采用最小二乘法可拟合出Ωt。本实验选取了6个只涉 及到电偶极跃迁的吸收峰对Ωt进行拟合,计算得到的Г及SedJJ’ 值在表2中列出。最终拟合 的结果为:Ω2=0.3926×10-20cm2,Ω4=0.0721×10-20cm2,Ω6=0.0028×10-20cm2。
at room temperature
2S+1LJ
Energy levels/cm-1
∆E/cm-1
α(cm-1)
σabs(×10-21cm2)
4I15/2
0,69,126,159,182,227,243,293
293
---
---
4I13/2
6476,6517*,6564,6609,6641
38.3
表 1. 室温下Er3+,Yb3+:BaWO4晶体中Er3+的能级分裂、吸收系数和吸收截面 Table 1. Value of energy slips, absorption coefficient, absorption cross section of Er3+ in Er3+:Yb3+:BaWO4 crystal
