历年高考数学试题

合集下载

历年全国高考数学考试试卷附详细解析.doc

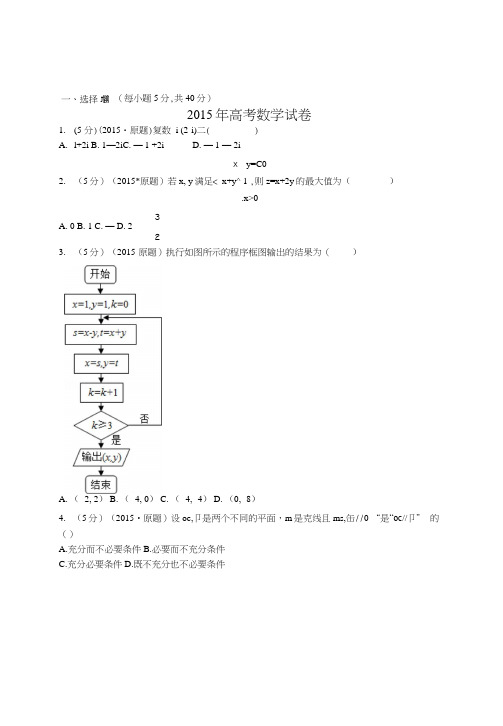
2015年高考数学试卷1. (5 分)(2015・原题)复数 i (2-i)二( )A. l+2iB. 1—2iC. — 1 +2iD. — 1 — 2ix - y=C02. （5分）（2015*原题）若x, y 满足< x+y^ 1 ,则z=x+2y 的最大值为（） .x>03A. 0B. 1C. —D. 2 23. （5分）（2015-原题）执行如图所示的程序框图输出的结果为（）A. （ -2, 2）B. （ -4, 0）C. （ -4, -4）D. （0, -8）4. （5分）（2015•原题）设oc,卩是两个不同的平面，m 是克线且ms,缶//0“是“oc //卩” 的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件一、选择J （每小题5分,共40分）5.（5分）（2015•原题）某三棱锥的三视图如图所示，则该三棱锥的表面积是（）6. （5分）（2015・原题）设{%}是等差数列，下列结论屮正确的是（）八・若 a 1+a 2>0,贝!j a 2+a 3>0 B.若 a 1+a 3<0> 贝lj a]+a 2<07. （5分）（2015•原题）如图，函数f （x ）的图象为折线ACB,则不等式f （x ） >1<）& （x+1）A. {x| -l<x<0}B. {x| -Kx<l}C. {x| - 1<x<1}D. {x| -l<x<2}8. （5分）（2015-原题）汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程，如图描述了甲、乙、丙三辆汽车在不同速度下燃油效率情况，下列叙述中正确的是（）C.若 0<ai <a 2,则 2〉寸8护3D.若 2]V0,贝lj (a 2-a 1) (a 2-a 3) >0 A. 2+V5 B. 4+^5 C. 2+2A /5 D ・ 5A.消耗1升汽油，乙车最多可行驶5千米B.以相同速度行驶相同路程，三辆车屮，甲车消耗汽油最多C.甲车以80千米/小时的速度行驶1小时，消耗10升汽油D. 某城市机动车最高限速80千米/小时，相同条件下，在该市用丙车比用乙车更省油9. （5分）（2015•原题）在（2+x ）'的展开式中，J 的系数为 __________ （用数字作答）10. （5分）（2015-原题）已知双曲线岭-y2=l （a >0）的一条渐近线为V3x+y=0，贝911. （5分）（2015-原题）在极坐标系中，点（2,牛）到直线° （cosO+V3sinO ） =6的距离为 ____________ •12. （5 分）（2015・原题）在AABC 中，a=4, b=5, c=6,则二 ____________________ .sinC在AABC 中，点 M, N 满足 AM=2MC, BN=NC,若MN=xAB+yAC,① 若汗1,则f （x ）的最小值为 _____________ ；② 若f （x ）恰有2个零点，则实数a 的取值范围是 ____________15. （13 分）（2015・原题）已矢U 函数 F （x ） =V2sin —cos — - V2sin ^―.2 2 2（I ）求f （x ）的最小正周期；（H ）求F （x ）在区间［■心0］上的最小值.16. （13分）（2015-原题）A, B 两组各有7位病人，他们服用某种药物后的康复时间（单位: 天）记录如下：A 组:10, 11, 12, 13, 14, 15, 16B 组;12, 13, 15, 16, 17, 14, a假设所有病人的康复时间相互独立，从八，B 两组随机各选1人，八组选出的人记为甲，B 组选出的人记为乙.（I ）求甲的康复时间不少于14天的概率；（U ）如果沪25,求甲的康复时间比乙的康复时间长的概率；（HI ）当a 为何值时，A, B 两组病人康复时间的方差相等？（结论不要求证明）17. （14分）（206原题）如图，在四棱锥A-EFCB 中，AAEF 为等边三角形，平面AEF 丄平面 EFCB, EF//BC, BC=4, EF=2a,上EBC 二上FCB 二60° , O 为 EF 的中点.（I ）求证：AO1BE.二、填空题侮小丿 5分,共30分）13. （5 分）（2015*原题）14. （5分）（2015•原题）设函数f （x ）= 2x-a, 4（x - a ）（x _ 2 a ）,x<l 三、解答］（共6小题 ,共80分）（U）求二面角F-AE-B的余弦值；（HI）若BE丄平面AOC,求a的值.18. (13分)(2015*原题)已知函数f (x)二1门丿注，(I )求曲线尸f (X )在点(0, f (0))处的切线方程; 3(H) 求证,当*€ (0, 1)时，f (x) >2(x+^-)；3(m)设实数k 使得f (x) >k(x+专-)对乂€ (o, 1)恒成立，求k 的最大值.19. (14分)(2015•原题)已知椭圆C:三+笃二1 (a>b>0)的离心率为李，点P (0, 1)/ b ， 2和点A (m, n) (mHO)都在椭圆C±,直线PA 交x 轴于点M.(I) 求椭圆C 的方程，并求点M 的坐标(用n 表示)；(U )设O 为原点，点B 与点A 关于x 轴对称，直线PB 交x 轴于点N,问：y 轴上是否存在点Q,使得ZOQM=ZONQ?若存在，求点Q 的坐标，若不存在，说明理由.2(). (13 分)(2013 •原题)已知数列｛%｝满足： , a t <36，且 a n+1 = (n=l, 2,…)，记集合 M ={a n |n€N +}.(I)若引二6,写出集合M 的所有元素；(n )如集合M 存在一个元素是3的倍数，证明：M 的所有元素都是3的倍数; (111)求集合M 的元索个数的最大值.2%,a n <18 2%-36, %>182015年原题市高考数学试卷（理科）1. （5 分）（2015-原题）复数 i （2-i ）二（）A. l+2iB. 1 -2iC. —l+2iD. - 1 - 2i【分析】利用复数的运算法则解答.【解答】解:原式=2i - i 2=2i - (-1) =l+2i;故选：A.【点评】本题考查了复数的运算；关键是熟记运算法则.注意i 2=-l. &-y<02. （5分）（2015•原题）若x, y 满足《 x+yCl ,则z=x+2y 的最大值为（）、x>03A. 0B. 1C. —D. 2 2【分析】作出题中不等式组表示的平面区域，再将目标函数z 二x+2y 对应的直线进行平移, 即可求出z 取得最大值."x-y<0【解答】解：作出不等式组x+y< 1表示的平面区域，.xi>0当1经过点B 时，目标函数z 达到最大值 z 煨大值二0+2X1 —2・【点评】本题给出二元一次不等式组，求目标函数Z 二x+2y 的最大值，着重考查了二元一次不一、选择题（每小, 5分，共40分）等式组表示的平面区域和简单的线性规划等知识，属于基础题•3.（5分）（2015•原题）执行如图所示的程序框图输出的结果为（）A. (—2, 2)B. (一4, 0) C- (一4, -4) D. (0, -8)【分析】模拟程序框图的运行过程，即可得出程序运行后输出的结果.【解答】解：模拟程序框图的运行过程，如下；x=l, y=l,k=0 时,s=x - y=0, t=x+y=2 ；x=s=0, y=t=2,k二1 时，s=x - y= - 2, t二x+y二2;x二s二一2，y二t二2，k=2 吋,s=x - y= ~ 4, t=x+y=0 ；x=s= -4, y=t=0,k=3时，循环终止，输出(x, y)是(-4, 0).故选：B.【点评】本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，是基础题目•4.(5分)(2015-原题)设冷卩是两个不同的平面，口是直线且muoc, //0 “是、//卩” 的()A.充分而不必耍条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【分析】m // p并得不到a II ,3,根据面面平行的判定定理，只有a内的两相交直线都平行于P，而a//0,并且mua,显然能得到这样即可找出正确选项.【解答】解：mca, 口//(3得不到00”(3,因为oc, 0可能相交，只要m和a,卩的交线平行即可得到m" (3；a // P，mCa, m 和0 没有公共点,.'.m//p,即oc//0 能得到m//0；二“m/邙”是、/人3”的必要不充分条件.故选B.【点评】考查线面平行的定义，线面平行的判定定理，面面平行的定义，面面平行的判定定理，以及充分条件、必要条件，及必要不充分条件的概念.5. （5分）（2015-原题）某三棱锥的三视图如图所示，则该三棱锥的表面积是（）A. 2+^^/5B. 4+A /5C. 2+2A /5D. 5【分析】根据三视图可判断克观图为：（）A 丄面ABC,AC=AB,E 为BC 中点,EA=2,E/\=EB=1, OA二 1,: BC 丄 ffi AEO, AC=V5, OE=V5判断儿何体的各个面的特点，计算边长，求解面积.【解答】解：根据三视图可判断立观图为：（）八丄面ABC, AC 二AB, E 为BC 屮点，EA=2, EC=EB=1, ()A 二 1,•••可彳导/\E 丄BC, BC 丄OA,运用£［线平面的垂立得岀：BC 丄面AEO, AC=V5, OR=V5S/XBCO 二专 X2x V5-V5.故该三棱锥的表面积是2+2丽, 故选：C.【点评】本题考查了空间几何体的三视图的运用，空间想象能力，计算能力，关键是恢复直观图，得出几何体的性质.6. （5分）（2015•原题）设｛%｝是等差数列，下列结论中正确的是（）• • ^AABCX2X2 二 2, S AO/\C =^AOAB-^ XV5>< 1=^^-A.若引+玄2>0,贝lj a2+a3>0B.若卯+%<0,贝lj a1+a2<0C.若0<旬<近，则阴D・若吗<0,贝lj (a2-aj) (a2-a3) >0【分析】对选项分别进行判断，即可得岀结论.【解答】解：若a1+a2>0,则2a]+d>0, a2+a3=2a]+3d>2d, d>0时,结论成立，即A不正确；若吗+%<(),贝lj a1+a2=2a1+d<0, a2+a3=2a1+3d<2d, dV()日寸，结论丿成立，即B 不止确；{%}是詩差数列，0<则<^2，2屯二引+%>2寸3]阴,；•耳>勺a]巧，即C止确；若引V0,贝I」(迈—吗)(a2-a3) =-d2<0,即D不正确.故选：C.【点评】本题考查等差数列的通项，考查学生的计算能力，比较基础.7.(5分)(2015•原题)如图,函数f (x)的图象为折线ACB,则不等式f(x) >lo& (x+1)-l<x<l}C. {x| - l<x<l}D. {x| -l<x<2}【分析】在已知坐标系内作IB y=log2 (x+1)的图象，利用数形结合得到不等式的解集.【解答】解：由已知F(x)的图象，在此坐标系内作出y二1。

历年数学高考真题及答案

历年数学高考真题及答案数学是一门需要反复练习和掌握技巧的学科，对于许多学生来说，通过解析历年数学高考真题是提高解题能力的有效方法。

历年数学高考真题种类繁多，覆盖了各种题型和难度，掌握这些真题并熟悉解题方法，将有助于考生在考试中取得更好的成绩。

以下将介绍一些历年数学高考真题及其答案，供考生参考。

2018年高考数学真题1. （2018年福建卷）在△ABC中，∠B=90°，D和E分别是AC的两个点，使得∠CBD=∠ABE，CB=CA，BD=BE。

（1）求证：△BCD≌△ABE；（2）若BC=2，AC=3，求BC的中线CD与AB的中线BE的交点的坐标。

解析：（1）由题意可知，∠CBD=∠ABE，CB=CA，BD=BE，根据两三角形对应的整角、对边和对角相等可知△BCD≌△ABE。

（2）由题意可知CB=2，AC=3，根据三角形中位线的性质，连接AB的中位线BE，CD交于点P，根据中位线的性质可知CP=0.5BD=BD/2=BE/2=0.5BE，由解（1）可知BE=2，因此BE=2，CD=3.5，点P的坐标为（0.5，1）。

2019年高考数学真题2. （2019年北京卷）已知空间中的四点A、B、C、D满足|AB|=|AC|=4，|AD|=3，|BC|=7，|BD|=5，|CD|=6。

（1）求四面体ABCD的体积；（2）求最大的四面体ABCD的体积。

解析：（1）根据四面体的体积公式V=⅓|det(AB, AC, AD)|，其中|det(AB, AC, AD)|为向量AB、AC、AD的混合积，代入题中数据计算得到V=22.67；（2）根据四面体的体积最大值为三棱锥时的体积可得到最大的四面体ABCD的体积为22.67。

通过解析以上历年高考数学真题，考生可以熟悉各类数学题目的解题方法，并掌握常见题型的解题技巧，提高数学解题能力。

希望考生能够在备考过程中积极练习历年真题，加深对数学知识的理解，取得优异的高考成绩。

历年高考数学试卷附详细解析

高考数学试卷一.选择题〔每题5分，共50分，在每题给出四个选项中，只有一个是正确〕1．〔5分〕〔2021 •原题〕设i 是虚数单位，那么复数在复平面内对应点位于〔〕 A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．〔5分〕〔2021 •原题〕以下函数中，既是偶函数又存在零点是〔〕A ． y =cosxB ． y =sinxC ． y =lnxD ． y =x 2+13．〔5分〕〔2021 •原题〕设p ：1＜x ＜2，q ：2x ＞1，那么p 是q 成立〔〕 A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件4．〔5分〕〔2021 •原题〕以下双曲线中，焦点在y 轴上且渐近线方程为y=±2x是〔〕 A ． x 2﹣=1 B ． ﹣y 2=1 C ． ﹣x 2=1 D ． y 2﹣=15．〔5分〕〔2021 •原题〕m ，n 是两条不同直线，α，β是两个不同平面，那么以下命题正确是〔〕 A ．假设α，β垂直于同一平面，那么α与β平行 B ．假设m ，n 平行于同一平面，那么m 与n 平行 C ．假设α，β不平行，那么在α内不存在与β平行直线 D ．假设m ，n 不平行，那么m 与n 不可能垂直于同一平面6．〔5分〕〔2021 •原题〕假设样本数据x 1，x 2，…，x 10标准差为8，那么数据2x 1﹣1，2x 2﹣1，…，2x 10﹣1标准差为〔〕 A ． 8 B ． 15 C ． 16 D ． 327．〔5分〕〔2021 •原题〕一个四面体三视图如下图，那么该四面体外表积是〔〕 A ． 1+ B ． 2+ C ． 1+2 D ． 28．〔5分〕〔2021 •原题〕△ABC 是边长为2等边三角形，向量，满足=2，=2+，那么以下结论正确是〔〕 A ． ||=1 B ． ⊥ C ． •=1 D ．〔4+〕⊥9．〔5分〕〔2021 •原题〕函数f 〔x 〕=图象如下图，那么以下结论成立是〔〕 A ． a ＞0，b ＞0，c ＜0 B ． a ＜0，b ＞0，c ＞0 C ． a ＜0，b ＞0，c ＜0 D ． a ＜0，b ＜0，c＜010．〔5分〕〔2021 •原题〕函数f 〔x 〕=Asin 〔ωx+φ〕〔A ，ω，φ均为正常数〕最小正周期为π，当x=时，函数f 〔x 〕取得最小值，那么以下结论正确是〔〕 A ． f 〔2〕＜f 〔﹣2〕＜f 〔0〕 B ． f 〔0〕＜f 〔2〕＜f 〔﹣2〕 C ． f 〔﹣2〕＜f 〔0〕＜f 〔2〕 D ． f 〔2〕＜f 〔0〕＜f 〔﹣2〕二.填空题〔每题5分，共25分〕11．〔5分〕〔2021 •原题〕〔x3+〕7展开式中x5系数是〔用数字填写答案〕12．〔5分〕〔2021 •原题〕在极坐标系中，圆ρ=8sinθ上点到直线θ=〔ρ∈R〕距离最大值是．13．〔5分〕〔2021 •原题〕执行如下图程序框图〔算法流程图〕，输出n为14．〔5分〕〔2021 •原题〕数列{a n}是递增等比数列，a1+a4=9，a2a3=8，那么数列{a n}前n项与等于．15．〔5分〕〔2021 •原题〕设x3+ax+b=0，其中a，b均为实数，以下条件中，使得该三次方程仅有一个实根是〔写出所有正确条件编号〕①a=﹣3，b=﹣3．②a=﹣3，b=2．③a=﹣3，b＞2．④a=0，b=2．⑤a=1，b=2．三.解答题〔共6小题，75分〕16．〔12分〕〔2021 •原题〕在△ABC中，∠A=，AB=6，AC=3，点D在BC边上，AD=BD，求AD长．17．〔12分〕〔2021 •原题〕2件次品与3件正品混放在一起，现需要通过检测将其区分，每次随机一件产品，检测后不放回，直到检测出2件次品或者检测出3件正品时检测完毕．〔Ⅰ〕求第一次检测出是次品且第二次检测出是正品概率；〔Ⅱ〕每检测一件产品需要费用100元，设X表示直到检测出2件次品或者检测出3件正品时所需要检测费用〔单位：元〕，求X分布列与均值〔数学期望〕18．〔12分〕〔2021 •原题〕设n∈N*，x n是曲线y=x2n+2+1在点〔1，2〕处切线与x轴交点横坐标〔Ⅰ〕求数列{x n}通项公式；〔Ⅱ〕记T n=x12x32…x2n﹣12，证明：T n≥．19．〔13分〕〔2021 •原题〕如下图，在多面体A1B1D1DCBA中，四边形AA1B1B，ADD1A1，ABCD均为正方形，E为B1D1中点，过A1，D，E平面交CD1于F．〔Ⅰ〕证明：EF∥B1C；〔Ⅱ〕求二面角E﹣AD﹣B1余弦值．20．〔13分〕〔2021 •原题〕设椭圆E方程为+=1〔a＞b＞0〕，点O为坐标原点，点A坐标为〔a，0〕，点B坐标为〔0，b〕，点M在线段AB上，满足|BM|=2|MA|，直线OM斜率为〔Ⅰ〕求E离心率e；〔Ⅱ〕设点C坐标为〔0，﹣b〕，N为线段AC中点，点N关于直线AB对称点纵坐标为，求E方程．21．〔13分〕〔2021 •原题〕设函数f〔x〕=x2﹣ax+b．〔Ⅰ〕讨论函数f〔sinx 〕在〔﹣，〕内单调性并判断有无极值，有极值时求出最值；〔Ⅱ〕记f n〔x〕=x2﹣a0x+b0，求函数|f〔sinx〕﹣f0〔sinx〕|在[﹣，]上最大值D2〔Ⅲ〕在〔Ⅱ〕中，取a n=b n=0，求s=b ﹣满足条件D≤1时最大值．高考数学试卷〔理科〕一.选择题〔每题5分，共50分，在每题给出四个选项中，只有一个是正确〕1．〔5分〕〔2021 •原题〕设i 是虚数单位，那么复数在复平面内对应点位于〔〕A．第一象限B．第二象限C．第三象限D．第四象限考点：复数代数表示法及其几何意义．专题：计算题；数系扩大与复数．分析：先化简复数，再得出点坐标，即可得出结论．解答：解：=i〔1+i〕=﹣1+i，对应复平面上点为〔﹣1，1〕，在第二象限，应选：B．点评：此题考察复数运算，考察复数几何意义，考察学生计算能力，比拟根底．2．〔5分〕〔2021 •原题〕以下函数中，既是偶函数又存在零点是〔〕A．y=cosx B．y=sinx C．y=lnx D．y=x2+1考点：函数零点；函数奇偶性判断．专题：函数性质及应用．分析：利用函数奇偶性判断方法以及零点判断方法对选项分别分析选择．解答：解：对于A，定义域为R，并且cos〔﹣x〕=cosx，是偶函数并且有无数个零点；对于B，sin〔﹣x〕=﹣sinx，是奇函数，由无数个零点；对于C，定义域为〔0，+∞〕，所以是非奇非偶函数，有一个零点；对于D，定义域为R，为偶函数，都是没有零点；应选A．点评：此题考察了函数奇偶性与零点判断．①求函数定义域；②如果定义域关于原点不对称，函数是非奇非偶函数；如果关于原点对称，再判断f〔﹣x〕与f〔x〕关系；相等是偶函数，相反是奇函数；函数零点与函数图象与x轴交点以及与对应方程解个数是一致．3．〔5分〕〔2021 •原题〕设p：1＜x＜2，q：2x＞1，那么p是q成立〔〕A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件判断．专题：简易逻辑．分析：运用指数函数单调性，结合充分必要条件定义，即可判断．解答：解：由1＜x＜2可得2＜2x＜4，那么由p推得q成立，假设2x＞1可得x＞0，推不出1＜x＜2．由充分必要条件定义可得p是q成立充分不必要条件．应选A．点评：此题考察充分必要条件判断，同时考察指数函数单调性运用，属于根底题．4．〔5分〕〔2021 •原题〕以下双曲线中，焦点在y轴上且渐近线方程为y=±2x 是〔〕A．x2﹣=1B．﹣y2=1C．﹣x2=1D．y2﹣=1考点：双曲线简单性质．专题：圆锥曲线定义、性质与方程．分析：对选项首先判定焦点位置，再求渐近线方程，即可得到答案．解答：解：由A可得焦点在x轴上，不符合条件；由B可得焦点在x轴上，不符合条件；由C可得焦点在y轴上，渐近线方程为y=±2x，符合条件；由D可得焦点在y轴上，渐近线方程为y=x，不符合条件．应选C．点评：此题考察双曲线方程与性质，主要考察双曲线焦点与渐近线方程求法，属于根底题．5．〔5分〕〔2021 •原题〕m，n是两条不同直线，α，β是两个不同平面，那么以下命题正确是〔〕A．假设α，β垂直于同一平面，那么α与β平行B．假设m，n平行于同一平面，那么m与n平行C．假设α，β不平行，那么在α内不存在与β平行直线D．假设m，n不平行，那么m与n不可能垂直于同一平面考点：空间中直线与平面之间位置关系；空间中直线与直线之间位置关系；平面与平面之间位置关系．专题：空间位置关系与距离．分析：利用面面垂直、线面平行性质定理与判定定理对选项分别分析解答．解答：解：对于A，假设α，β垂直于同一平面，那么α与β不一定平行，如果墙角三个平面；故A错误；对于B，假设m，n平行于同一平面，那么m与n平行．相交或者异面；故B错误；对于C，假设α，β不平行，那么在α内存在无数条与β平行直线；故C错误；对于D，假设m，n不平行，那么m与n不可能垂直于同一平面；假设两条直线同时垂直同一个平面，那么这两条在平行；故D正确；应选D．点评：此题考察了空间线面关系判断；用到了面面垂直、线面平行性质定理与判定定理．6．〔5分〕〔2021 •原题〕假设样本数据x1，x2，…，x10标准差为8，那么数据2x1﹣1，2x2﹣1，…，2x10﹣1标准差为〔〕A．8B．15C．16D．32考点：极差、方差与标准差．专题：概率与统计．分析：根据标准差与方差之间关系先求出对应方差，然后结合变量之间方差关系进展求解即可．解答：解：∵样本数据x1，x2，…，x10标准差为8，∴=8，即DX=64，数据2x1﹣1，2x2﹣1，…，2x10﹣1方差为D〔2X﹣1〕=4DX=4×64，那么对应标准差为==16，应选：C．点评：此题主要考察方差与标准差计算，根据条件先求出对应方差是解决此题关键．7．〔5分〕〔2021 •原题〕一个四面体三视图如下图，那么该四面体外表积是〔〕A．1+B．2+C．1+2D．2考点：由三视图求面积、体积．专题：计算题；空间位置关系与距离．分析：根据几何体三视图，得出该几何体是底面为等腰直角三角形三棱锥，结合题意画出图形，利用图中数据求出它外表积．解答：解：根据几何体三视图，得；该几何体是底面为等腰直角三角形三棱锥，如下图；∴该几何体外表积为S外表积=S△PAC+2S△PAB+S△ABC=×2×1+2××+×2×1=2+．应选：B．点评：此题考察了空间几何体三视图应用问题，解题关键是由三视图得出几何体构造特征，是根底题目．8．〔5分〕〔2021 •原题〕△ABC是边长为2等边三角形，向量，满足=2，=2+，那么以下结论正确是〔〕A．||=1B．⊥C．•=1D．〔4+〕⊥。

高考数学历年真题及答案详解

高考数学历年真题及答案详解一、选择题1. 题目描述：在平面直角坐标系中，点A(-3, 4)关于y轴的对称点是（）。

A. (3, -4)B. (-3, -4)C. (-3, 4)D. (3, 4)答案解析：点关于y轴对称即x取相反数，所以答案为A.(3, -4)。

2. 题目描述：已知函数 f(x) = 2^(2x-3)，则当 x = 1 时，f(x) 的值是（）。

A. 1B. 2C. 4D. 8答案解析：将x=1代入函数中，即f(1) = 2^(2*1-3)，化简得f(1)= 2^(-1) = 1/2，所以答案为A. 1。

二、填空题1. 题目描述：已知三角形ABC中，∠B = 90°，AC = 5 cm，BC =12 cm，求AB的长度。

答案解析：根据勾股定理，AB^2 + BC^2 = AC^2，代入已知数据得AB^2 + 12^2 = 5^2，化简得AB^2 = 25 - 144 = -119，由于长度不能为负数，所以不存在满足要求的三角形ABC。

2. 题目描述：若a1, a2, a3为等差数列的前三项，且满足a1 + a3 = 18，a2 - a3 = 4，求a1, a2和a3的值。

答案解析：由等差数列的性质可知，a2 = (a1 + a3) / 2，代入已知数据得a2 = 9.5，将a2带入a2 - a3 = 4解得a3 = 5.5，再将a3带入a1 +a3 = 18解得a1 = 12.5，所以a1 = 12.5，a2 = 9.5，a3 = 5.5。

三、解答题1. 题目描述：设函数f(x) = cos(x + 1) - sin(x - 1)，求f(x)的单调递增区间。

答案解析：对f(x)求导得f'(x) = -sin(x + 1) - cos(x - 1)，令f'(x) = 0，解方程得x = 1/4 (4πn + 3π/2) - 1，其中n为整数。

通过二阶导数的符号判断可知，当x < -1或x > -3/4 + 4πn，f(x)单调递增；当-3/4 + 4πn < x< -1，f(x)单调递减。

历年高考数学真题答案

历年高考数学真题答案【篇一：新课标数学历年高考试题汇总及详细答案解析】/p> 第Ⅰ卷一.选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合m=｛0,1,2｝，n=?x|x2?3x?2≤0?，则m?n=() a. ｛1｝【答案】db. ｛2｝c. ｛0，1｝d. ｛1，2｝把m=｛0,1,2}中的数,代入不等式x2-3x+2≤0,经检验x=1,2满足。

所以选d.2.设复数z1，z2在复平面内的对应点关于虚轴对称，z1?2?i，则z1z2?（） a. - 5 【答案】bb.5c. - 4+ id. - 4 - iz1=2+i,z1与z2关于虚轴对称，∴z2=-2+i,∴z1z2=-1-4=-5,故选b.3.设向量a,b满足|a+b|a-ba?b = () a. 1 【答案】ab. 222c. 322d. 5|a+b|=,|a-b|=6,，∴a+b+2ab=10，a+b-2ab=6,联立方程解得=1,故选a.4.钝角三角形abc的面积是，ab=1，，则ac=()2a. 5【答案】bb.c. 2d. 11112∴b=，使用余弦定理，b2=a2+c2-2accosb,解得b=.故选b.5.某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是（）a. 0.8b. 0.75c. 0.6d. 0.45【答案】a设某天空气质量优良，则随后一个空气质量也优良的概率为p,则据题有0.6=0.75?p,解得p=0.8,故选a.6.如图，网格纸上正方形小格的边长为1（表示1cm）,图中粗线画出的是某零件的三视图，该零件由一个底面半径为3cm，高为6cm 的圆柱体毛坯切削得到，则切削掉部分的体积与原来毛坯体积的比值为（）a. b. c. d.279273【答案】c7.执行右图程序框图，如果输入的x,t均为2，则输出的s= （） a.4 b. 5c. 6 d. 7【答案】cx=2,t=2,变量变化情况如下： m s k 13 125 2 27 3 故选c.8.设曲线y=ax-ln(x+1)在点(0,0)处的切线方程为y=2x，则a= a. 0b. 1c. 2d. 3【答案】df(x)=ax-ln(x+1),∴f′(x)=a-1.x+1∴f(0)=0,且f′(0)=2.联立解得a=3.故选d.?x?y?7≤0?9.设x,y满足约束条件?x?3y?1≤0，则z?2x?y的最大值为（）?3x?y?5≥0?a. 10b. 8c. 3d. 2【答案】b画出区域，可知区域为三角形，经比较斜率，可知目标函数z=2x-y 在两条直线x-3y+1=0与x+y-7=0的交点(5,2)处,取得最大值z=8.故选b.a.c. d.b.324 【答案】d设点a、b分别在第一和第四象限，af=2m,bf=2n，则由抛物线的定义和直角三角形知识可得，33332m=2?+m,2n=2?-3n，解得m=(2+),n=(2-3),∴m+n=6.4422139244c.d.【答案】c0-1+4=.故选c.106f?x0m2，则m的12.设函数f?x??.若存在f?x?的极值点x0满足x02m2取值范围是（）a.,?66,??b.,?44,??c.,?22,??d.,?14,?? 【答案】cf(x)=sin22mm2∴x0+[f(x0)]2+3，∴+3m2,解得|m|2.故选c.44第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题，每个试题考生必须做答.第22题~第24题为选考题，考生根据要求做答. 二.填空题13.?x?a?的展开式中，x7的系数为15，则a=________.(用数字填写答案)101【答案】21137333c10xa=15x7∴c10a=15,a=.故a=.2214.函数f?x??sin?x?22sin?cos?x的最大值为_________. 【答案】115.已知偶函数f?x?在?0,单调递减，f?2??0.若f?x?1??0，则x的取值范围是__________.，-1）∪（3，+∞）【答案】(-∞偶函数y=f(x)在[0,+∞)上单增，且f(2)=0∴f(x)0的解集为|x|2.故解集为|x-1|2，解得x∈(-∞，-1）∪（3，+∞）.∴f(x-1)0的解集为|x-1|2，解得x∈(-∞，-1）∪（3，+∞）.在坐标系中画出圆o和直线y=1,其中m(x0,1)在直线上.由圆的切线相等及三角形外角知识，可得x0∈[-1,1].故x0∈[-1,1].已知数列?an?满足a1=1，an?1?3an?1.（Ⅰ）证明an?是等比数列，并求?an?的通项公式；（Ⅱ）证明：??…+?.12n【答案】(1) 无（1）（2）无a1=1,an+1=3an+1.n∈n*.111=3an+1+=3(an+). 222113∴{an+是首项为a1+=,公比为3的等比数列。

历年成人高考数学试题及答案word

历年成人高考数学试题及答案word一、选择题（每题3分，共30分）1. 函数f(x) = 2x^2 - 3x + 1的零点个数是（）。

A. 0B. 1C. 2D. 32. 如果一个等差数列的首项为a1，公差为d，那么它的第n项an可以表示为（）。

A. an = a1 + (n-1)dB. an = a1 + ndC. an = a1 + (n-1)(2d)D. an = a1 + (n-1)(-d)3. 已知集合A={1,2,3}，B={2,3,4}，则A∩B=（）。

A. {1}B. {2,3}C. {3,4}D. {1,2,3,4}4. 若直线y=kx+b与x轴交于点(2,0)，则b的值为（）。

A. 2B. -2C. 0D. 45. 函数y=x^3-3x^2+2的导数是（）。

A. y' = 3x^2-6xB. y' = x^2-3xC. y' = 3x^2-6x+2D. y' = x^3-3x^26. 已知抛物线方程为y=x^2-4x+3，其顶点坐标为（）。

A. (2,-1)B. (2,1)C. (-2,1)D. (-2,-1)7. 函数y=sin(x)的周期是（）。

A. πB. 2πC. π/2D. 4π8. 已知向量a=(3,-2)，b=(1,2)，则向量a·b的值为（）。

A. 1B. -1C. 5D. -59. 函数y=e^x的反函数是（）。

A. y=ln(x)B. y=e^(-x)C. y=ln(-x)D. y=e^(x-1)10. 已知双曲线方程为x^2/a^2 - y^2/b^2 = 1，其中a>0，b>0，则该双曲线的焦点位于（）。

A. x轴上B. y轴上C. 原点D. 第一象限二、填空题（每题2分，共20分）11. 圆的方程为(x-3)^2 + (y+2)^2 = 9，该圆的半径是______。

12. 函数y=cos(x)在区间[0, π]上的最大值是______。

历年高考数学试题

历年高考数学试题向量一、选择题，在每小题给出的四个选择题只有一项是符合题目要求的。

1.已知向量a = （1,2）,b （一2,-4）,1 c 1= Y '5,若（a + b ）• c =则a 与c 的夹角为（） A. 30°B. 60°C. 120°D. 150°2.已知向量凡b ，且分=a + 2b,BC = -5^ + 6b , CD = 7a-2B,则一定共线的三点是（）4 .若l 〃l=l,lBl=2,c = + + b ，且。

la ，则向量a 与b 的夹角为（） (A )30°(B )60°(C )120°(D )150°5 .已知向量a W e ,|e |=1满足：对任意t £七恒有|@—土3|三|@—3|.则( ) A. a ±eB. a ±(a —e )C. e ±(a —e )D. (a +e )±(a —e )6 .已知向量a = (1,2),b (-2,-4),l c 1=、5若(a + b )• c =-,则a 与C 的夹角为( )2A.30°B.60°C.120°D.150°7 .设向量a 二( — 1, 2), b= (2,—1),则(a ・b) (a +b)等于( ) A. (1, 1)B. (—4, —4)C. -4D. (—2, —2)8 .若l 〃l=l,lBl=2,c = + + b ，且。

La ，则向量a 与b 的夹角为() (A )30°(B )60°(C )120°(D )150°9 .已知向量0= (—2, 2), b= (5, k).若|a +b|不超过5,则k 的取值范围是( )A.[—4,6]B.[—6,4]C.[—6,2]D.[—2,6]th1.L..10 .点。

历年高考数学真题(全国卷整理版)

参考公式：如果事件A 、B 互斥，那么球的表面积公式()()()P A B P A P B 24S R如果事件A 、B 相互独立，那么其中R 表示球的半径()()()P A B P A P B 球的体积公式如果事件A 在一次试验中发生的概率是p ，那么334VRn 次独立重复试验中事件A 恰好发生k 次的概率其中R 表示球的半径()(1)(0,1,2,)k kn kn nP k C p p k n …普通高等学校招生全国统一考试一、选择题1、复数131i i=A 2+IB 2-IC 1+2iD 1- 2i2、已知集合A ＝{1.3. m }，B ＝{1，m} ,AB ＝A, 则m=A0或3B 0或3C 1或3D 1或33 椭圆的中心在原点，焦距为4 一条准线为x=-4 ，则该椭圆的方程为A216x+212y=1 B212x+28y=1C28x+24y=1 D212x+24y=14 已知正四棱柱ABCD- A 1B 1C 1D 1中，AB=2，CC 1=22E 为CC 1的中点，则直线AC 1与平面BED 的距离为A 2B3C2D 1（5）已知等差数列{a n }的前n 项和为S n ，a 5=5，S 5=15，则数列的前100项和为(A)100101(B)99101(C)99100(D)101100（6）△ABC 中，AB 边的高为CD ，若a ·b=0，|a|=1，|b|=2，则(A)（B ）(C)(D)（7）已知α为第二象限角，sinα＋sinβ=33，则cos2α=(A)5-3（B）5-9(C)59(D)53（8）已知F1、F2为双曲线C：x2-y2=2的左、右焦点，点P在C上，|PF1|=|2PF2|，则cos ∠F1PF2=(A)14（B）35(C)34(D)45（9）已知x=lnπ，y=log52，12z=e，则(A)x＜y＜z （B）z＜x＜y (C)z＜y＜x (D)y＜z＜x(10) 已知函数y＝x2-3x+c的图像与x恰有两个公共点，则c＝（A）-2或2 （B）-9或3 （C）-1或1 （D）-3或1（11）将字母a,a,b,b,c,c,排成三行两列，要求每行的字母互不相同，梅列的字母也互不相同，则不同的排列方法共有（A）12种（B）18种（C）24种（D）36种（12）正方形ABCD的边长为1，点E在边AB上，点F在边BC上，AE＝BF＝73。

历年(2019-2024)全国高考数学真题分类(数列)汇编(附答案)

历年(2019-2024)全国高考数学真题分类(数列)汇编考点01 数列的增减性1．（2022∙全国乙卷∙高考真题）嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造行星，为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列{}n b ：1111b α=+，212111b αα=++，31231111b ααα=+++，…，依此类推，其中(1,2,)k k α*∈=N ．则（） A ．15b b < B ．38b b <C ．62b b <D ．47b b <2．（2022∙北京∙高考真题）已知数列{}n a 各项均为正数，其前n 项和n S 满足9(1,2,)n n a S n ⋅== ．给出下列四个结论：①{}n a 的第2项小于3； ②{}n a 为等比数列； ③{}n a 为递减数列； ④{}n a 中存在小于1100的项．其中所有正确结论的序号是．3．（2021∙全国甲卷∙高考真题）等比数列{}n a 的公比为q ，前n 项和为n S ，设甲：0q >，乙：{}n S 是递增数列，则（）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件4．（2020∙北京∙高考真题）在等差数列{}n a 中，19a =-，51a =-．记12(1,2,)n n T a a a n ==……，则数列{}n T （）． A ．有最大项，有最小项 B ．有最大项，无最小项 C ．无最大项，有最小项D ．无最大项，无最小项考点02 递推数列及数列的通项公式1．（2023∙北京∙高考真题）已知数列{}n a 满足()31166(1,2,3,)4n n a a n +=-+= ，则（） A ．当13a =时，{}n a 为递减数列，且存在常数0M ≤，使得n a M >恒成立 B ．当15a =时，{}n a 为递增数列，且存在常数6M ≤，使得n a M <恒成立 C ．当17a =时，{}n a 为递减数列，且存在常数6M >，使得n a M >恒成立 D ．当19a =时，{}n a 为递增数列，且存在常数0M >，使得n a M <恒成立2．（2022∙北京∙高考真题）已知数列{}n a 各项均为正数，其前n 项和n S 满足9(1,2,)n n a S n ⋅== ．给出下列四个结论：①{}n a 的第2项小于3； ②{}n a 为等比数列； ③{}n a 为递减数列； ④{}n a 中存在小于1100的项．其中所有正确结论的序号是．3．（2022∙浙江∙高考真题）已知数列{}n a 满足()21111,3n n n a a a a n *+==-∈N ，则（）A ．100521002a <<B ．100510032a << C ．100731002a <<D ．100710042a << 4．（2021∙浙江∙高考真题）已知数列{}n a满足)111,N n a a n *+==∈.记数列{}n a 的前n 项和为n S ，则（）A ．100332S << B ．10034S << C ．100942S <<D ．100952S << 5．（2020∙浙江∙高考真题）我国古代数学家杨辉，朱世杰等研究过高阶等差数列的求和问题，如数列(1)2n n +⎧⎫⎨⎬⎩⎭就是二阶等差数列，数列(1)2n n +⎧⎫⎨⎬⎩⎭(N )n *∈ 的前3项和是．6．（2020∙全国∙高考真题）数列{}n a 满足2(1)31nn n a a n ++-=-，前16项和为540，则1a = .7．（2019∙浙江∙高考真题）设,a b R ∈，数列{}n a 中，211,n n a a a a b +==+，N n *∈ ,则A ．当101,102b a =>B ．当101,104b a =>C ．当102,10b a =->D ．当104,10b a =->考点03 等差数列及其前n 项和一、单选题 1．（2024∙全国甲卷∙高考真题）记n S 为等差数列{}n a 的前n 项和，已知510S S =，51a =，则1a =（） A ．72B ．73 C ．13-D ．711-2．（2024∙全国甲卷∙高考真题）已知等差数列{}n a 的前n 项和为n S ，若91S =，则37a a +=（） A ．2-B ．73C ．1D ．293．（2023∙全国甲卷∙高考真题）记n S 为等差数列{}n a 的前n 项和．若264810,45a a a a +==，则5S =（） A ．25B ．22C ．20D ．154．（2023∙全国乙卷∙高考真题）已知等差数列{}n a 的公差为23π，集合{}*cos N n S a n =∈，若{},S a b =，则ab =（）A ．－1B ．12-C ．0D ．125．（2023∙全国新Ⅰ卷∙高考真题）记n S 为数列{}n a 的前n 项和，设甲：{}n a 为等差数列；乙：{}nS n为等差数列，则（）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件6．（2022∙北京∙高考真题）设{}n a 是公差不为0的无穷等差数列，则“{}n a 为递增数列”是“存在正整数0N ，当0n N >时，0n a >”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件7．（2020∙浙江∙高考真题）已知等差数列{an }的前n 项和Sn ，公差d ≠0，11a d≤．记b 1=S 2，bn+1=S2n+2–S 2n ，n N *∈，下列等式不可能．．．成立的是（） A ．2a 4=a 2+a 6B ．2b 4=b 2+b 6C ．2428a a a = D ．2428b b b =8．（2019∙全国∙高考真题）记n S 为等差数列{}n a 的前n 项和．已知4505S a ==，，则 A ．25n a n =-B ． 310n a n =-C ．228n S n n =-D ．2122n S n n =-二、填空题 15．（2024∙全国新Ⅱ卷∙高考真题）记n S 为等差数列{}n a 的前n 项和，若347a a +=，2535a a +=，则10S = .16．（2022∙全国乙卷∙高考真题）记n S 为等差数列{}n a 的前n 项和．若32236S S =+，则公差d = ． 17．（2020∙山东∙高考真题）将数列{2n –1}与{3n –2}的公共项从小到大排列得到数列{an }，则{an }的前n 项和为．18．（2020∙全国∙高考真题）记n S 为等差数列{}n a 的前n 项和．若1262,2a a a =-+=，则10S = ．19．（2019∙江苏∙高考真题）已知数列*{}()n a n ∈N 是等差数列，n S 是其前n 项和.若25890,27a a a S +==，则8S 的值是 .20．（2019∙北京∙高考真题）设等差数列{an }的前n 项和为Sn ，若a 2=−3，S 5=−10，则a 5= ，Sn 的最小值为．21．（2019∙全国∙高考真题）记n S 为等差数列{}n a 的前n 项和，若375,13a a ==，则10S = . 22．（2019∙全国∙高考真题）记Sn 为等差数列{an }的前n 项和，12103a a a =≠，，则105S S = .考点04 等比数列及其前n 项和一、单选题 1．（2023∙全国甲卷∙高考真题）设等比数列{}n a 的各项均为正数，前n 项和n S ，若11a =，5354S S =-，则4S =（） A ．158B ．658C ．15D ．402．（2023∙天津∙高考真题）已知数列{}n a 的前n 项和为n S ，若()112,22N n n a a S n *+==+∈，则4a =（）A ．16B ．32C ．54D ．1623．（2023∙全国新Ⅱ卷∙高考真题）记n S 为等比数列{}n a 的前n 项和，若45S =-，6221S S =，则8S =（）． A ．120B ．85C ．85-D ．120-4．（2022∙全国乙卷∙高考真题）已知等比数列{}n a 的前3项和为168，2542a a -=，则6a =（） A ．14B ．12C ．6D ．35．（2021∙全国甲卷∙高考真题）记n S 为等比数列{}n a 的前n 项和.若24S =，46S =，则6S =（） A ．7B ．8C ．9D ．106．（2020∙全国∙高考真题）设{}n a 是等比数列，且1231a a a ++=，234+2a a a +=，则678a a a ++=（） A ．12B ．24C ．30D ．327．（2020∙全国∙高考真题）记Sn 为等比数列{an }的前n 项和．若a 5–a 3=12，a 6–a 4=24，则n nS a =（）A ．2n –1B ．2–21–nC ．2–2n –1D ．21–n –18．（2020∙全国∙高考真题）数列{}n a 中，12a =，对任意 ,,m n m n m n N a a a ++∈=，若155121022k k k a a a ++++++=- ，则 k =（） A ．2B ．3C ．4D ．5二、填空题 11．（2023∙全国甲卷∙高考真题）记n S 为等比数列{}n a 的前n 项和．若6387S S =，则{}n a 的公比为． 12．（2023∙全国乙卷∙高考真题）已知{}n a 为等比数列，24536a a a a a =，9108a a =-，则7a = . 13．（2019∙全国∙高考真题）记Sn 为等比数列{an }的前n 项和.若13314a S ==，，则S 4= ． 14．（2019∙全国∙高考真题）记Sn 为等比数列{an }的前n 项和．若214613a a a ==，，则S 5= ．考点05 数列中的数学文化1．（2023∙北京∙高考真题）我国度量衡的发展有着悠久的历史，战国时期就已经出现了类似于砝码的、用来测量物体质量的“环权”．已知9枚环权的质量（单位：铢）从小到大构成项数为9的数列{}n a ，该数列的前3项成等差数列，后7项成等比数列，且1591,12,192a a a ===，则7a = ；数列{}n a 所有项的和为．2．（2022∙全国新Ⅱ卷∙高考真题）图1是中国古代建筑中的举架结构，,,,AA BB CC DD ''''是桁，相邻桁的水平距离称为步，垂直距离称为举，图2是某古代建筑屋顶截面的示意图．其中1111,,,DD CC BB AA 是举，1111,,,OD DC CB BA 是相等的步，相邻桁的举步之比分别为11111231111,0.5,,DD CC BB AAk k k OD DC CB BA ====．已知123,,k k k 成公差为0.1的等差数列，且直线OA 的斜率为0.725，则3k =（）A ．0.75B ．0.8C ．0.85D ．0.93．（2021∙全国新Ⅰ卷∙高考真题）某校学生在研究民间剪纸艺术时，发现剪纸时经常会沿纸的某条对称轴把纸对折，规格为20dm 12dm ⨯的长方形纸，对折1次共可以得到10dm 12dm ⨯，20dm 6dm ⨯两种规格的图形，它们的面积之和21240dm S =，对折2次共可以得到5dm 12dm ⨯，10dm 6dm ⨯，20dm 3dm ⨯三种规格的图形，它们的面积之和22180dm S =，以此类推，则对折4次共可以得到不同规格图形的种数为；如果对折n次，那么1nk k S ==∑ 2dm .4．（2020∙浙江∙高考真题）我国古代数学家杨辉，朱世杰等研究过高阶等差数列的求和问题，如数列(1)2n n +⎧⎫⎨⎬⎩⎭就是二阶等差数列，数列(1)2n n +⎧⎫⎨⎬⎩⎭(N )n *∈ 的前3项和是．5．（2020∙全国∙高考真题）0‐1周期序列在通信技术中有着重要应用.若序列12n a a a 满足{0,1}(1,2,)i a i ∈= ，且存在正整数m ，使得(1,2,)i m i a a i +== 成立，则称其为0‐1周期序列，并称满足(1,2,)i m i a a i +== 的最小正整数m 为这个序列的周期.对于周期为m 的0‐1序列12n a a a ，11()(1,2,,1)mi i k i C k a a k m m +===-∑ 是描述其性质的重要指标，下列周期为5的0‐1序列中，满足1()(1,2,3,4)5C k k ≤=的序列是（） A ．11010B ．11011C ．10001D ．110016．（2020∙全国∙高考真题）北京天坛的圜丘坛为古代祭天的场所，分上、中、下三层，上层中心有一块圆形石板(称为天心石)，环绕天心石砌9块扇面形石板构成第一环，向外每环依次增加9块，下一层的第一环比上一层的最后一环多9块，向外每环依次也增加9块，已知每层环数相同，且下层比中层多729块，则三层共有扇面形石板(不含天心石)（）A ．3699块B ．3474块C ．3402块D ．3339块考点06 数列求和1．（2021∙浙江∙高考真题）已知数列{}n a满足)111,N n a a n *+==∈.记数列{}n a 的前n 项和为n S ，则（）A ．100332S << B ．10034S << C ．100942S <<D ．100952S << 2．（2021∙全国新Ⅱ卷∙高考真题）（多选）设正整数010112222k kk k n a a a a --=⋅+⋅++⋅+⋅ ，其中{}0,1i a ∈，记()01k n a a a ω=+++ ．则（） A ．()()2n n ωω= B ．()()231n n ωω+=+C ．()()8543n n ωω+=+D ．()21nn ω-=3．（2020∙江苏∙高考真题）设{an }是公差为d 的等差数列，{bn }是公比为q 的等比数列．已知数列{an +bn }的前n 项和221()n n S n n n +=-+-∈N ，则d +q 的值是．参考答案考点01 数列的增减性1．（2022∙全国乙卷∙高考真题）嫦娥二号卫星在完成探月任务后，继续进行深空探测，成为我国第一颗环绕太阳飞行的人造行星，为研究嫦娥二号绕日周期与地球绕日周期的比值，用到数列{}n b ：1111b α=+，212111b αα=++，31231111b ααα=+++，…，依此类推，其中(1,2,)k k α*∈=N ．则（） A ．15b b +，得到12b b >，同理11223111ααααα+>++，可得23b b <，13b b >又因为223411,11αααα>++112233411111ααααααα++<+++，故24b b <，34b b >；以此类推，可得1357b b b b >>>>…，78b b >，故A 错误； 178b b b >>，故B 错误；26231111αααα>++…，得26b b <，故C 错误；11237264111111αααααααα>++++++…，得47b b <，故D 正确.[方法二]：特值法不妨设1,n a =则1234567835813213455b 2,b b ,b b ,b b ,b 2358132134========，，，47b b <故D 正确.2．（2022∙北京∙高考真题）已知数列{}n a 各项均为正数，其前n 项和n S 满足9(1,2,)n n a S n ⋅== ．给出下列四个结论：①{}n a 的第2项小于3； ②{}n a 为等比数列； ③{}n a 为递减数列； ④{}n a 中存在小于1100的项．其中所有正确结论的序号是．【答案】①③④ 【详细分析】推导出199n n n a a a -=-，求出1a 、2a 的值，可判断①；利用反证法可判断②④；利用数列单调性的定义可判断③.【答案详解】由题意可知，N n *∀∈，0n a >，当1n =时，219a =，可得13a =；当2n ≥时，由9n nS a =可得119n n S a --=，两式作差可得199n n n a a a -=-，所以，199n n n a a a -=-，则2293a a -=，整理可得222390a a +-=，因为20a >，解得2332a =<，①对；假设数列{}n a 为等比数列，设其公比为q ，则2213a a a =，即2213981S S S ⎛⎫= ⎪⎝⎭，所以，2213S S S =，可得()()22221111a q a q q +=++，解得0q =，不合乎题意，故数列{}n a 不是等比数列，②错；当2n ≥时，()1119990n n n n n n n a a a a a a a ----=-=>，可得1n n a a -<，所以，数列{}n a 为递减数列，③对；假设对任意的N n *∈，1100n a ≥，则10000011000001000100S ≥⨯=，所以，1000001000009911000100a S =≤<，与假设矛盾，假设不成立，④对. 故答案为：①③④.【名师点评】关键点名师点评：本题在推断②④的正误时，利用正面推理较为复杂时，可采用反证法来进行推导.3．（2021∙全国甲卷∙高考真题）等比数列{}n a 的公比为q ，前n 项和为n S ，设甲：0q >，乙：{}n S 是递增数列，则（）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件【答案】B【详细分析】当0q >时，通过举反例说明甲不是乙的充分条件；当{}n S 是递增数列时，必有0n a >成立即可说明0q >成立，则甲是乙的必要条件，即可选出答案．【答案详解】由题，当数列为2,4,8,--- 时，满足0q >，但是{}n S 不是递增数列，所以甲不是乙的充分条件．若{}n S 是递增数列，则必有0n a >成立，若0q >不成立，则会出现一正一负的情况，是矛盾的，则0q >成立，所以甲是乙的必要条件．故选：B ．【名师点评】在不成立的情况下，我们可以通过举反例说明，但是在成立的情况下，我们必须要给予其证明过程．4．（2020∙北京∙高考真题）在等差数列{}n a 中，19a =-，51a =-．记12(1,2,)n n T a a a n ==……，则数列{}n T （）．A ．有最大项，有最小项B ．有最大项，无最小项C ．无最大项，有最小项D ．无最大项，无最小项【答案】B【详细分析】首先求得数列的通项公式，然后结合数列中各个项数的符号和大小即可确定数列中是否存在最大项和最小项.【答案详解】由题意可知，等差数列的公差511925151a a d --+===--，则其通项公式为：()()11912211n a a n d n n =+-=-+-⨯=-，注意到123456701a a a a a a a <<<<<<=<< ，且由50T <可知()06,i T i i N <≥∈，由()117,ii i T a i i N T -=>≥∈可知数列{}n T 不存在最小项，由于1234569,7,5,3,1,1a a a a a a =-=-=-=-=-=，故数列{}n T 中的正项只有有限项：263T =，46315945T =⨯=. 故数列{}n T 中存在最大项，且最大项为4T . 故选：B.【名师点评】本题主要考查等差数列的通项公式，等差数列中项的符号问题，分类讨论的数学思想等知识，属于中等题.考点02 递推数列及数列的通项公式1．（2023∙北京∙高考真题）已知数列{}n a 满足()31166(1,2,3,)4n n a a n +=-+= ，则（） A ．当13a =时，{}n a 为递减数列，且存在常数0M ≤，使得n a M >恒成立 B ．当15a =时，{}n a 为递增数列，且存在常数6M ≤，使得n a M <恒成立 C ．当17a =时，{}n a 为递减数列，且存在常数6M >，使得n a M >恒成立 D ．当19a =时，{}n a 为递增数列，且存在常数0M >，使得n a M <恒成立【答案】B【详细分析】法1：利用数列归纳法可判断ACD 正误，利用递推可判断数列的性质，故可判断B 的正误. 法2：构造()()31664x f x x =-+-，利用导数求得()f x 的正负情况，再利用数学归纳法判断得各选项n a 所在区间，从而判断{}n a 的单调性；对于A ，构造()()32192647342h x x x x x =-+-≤，判断得11n n a a +<-，进而取[]4m M =-+推得n a M >不恒成立；对于B ，证明n a 所在区间同时证得后续结论；对于C ，记()0143log 2log 61m M ⎡⎤⎢⎥⎣=+⎦-，取[]01m m =+推得n a M >不恒成立；对于D ，构造()()32192649942g x x x x x =-+-≥，判断得11n n a a +>+，进而取[]1m M =+推得n a M <不恒成立. 【答案详解】法1：因为()311664n n a a +=-+，故()311646n n a a +=--，对于A ，若13a =，可用数学归纳法证明：63n a -≤-即3n a ≤，证明：当1n =时，1363a -=≤--，此时不等关系3n a ≤成立；设当n k =时，63k a -≤-成立，则()3162514764,4k k a a +⎛⎫-∈--- ⎝=⎪⎭，故136k a +≤--成立，由数学归纳法可得3n a ≤成立. 而()()()()231116666441n n n n n n a a a a a a +⎡⎤=---=---⎢⎣-⎥⎦， ()20144651149n a --=-≥>，60n a -<，故10n n a a +-<，故1n n a a +<，故{}n a 为减数列，注意1063k a +-≤-< 故()()()()23111666649644n n n n n a a a a a +-=≤-=-⨯--，结合160n a +-<，所以()16694n n a a +--≥，故19634n n a +⎛⎫-≥ ⎪⎝⎭，故19634nn a +⎛⎫≤- ⎪⎝⎭，若存在常数0M ≤，使得n a M >恒成立，则9634nM ⎛⎫-> ⎪⎝⎭，故6934nM -⎛⎫> ⎪⎝⎭，故946log 3M n -<，故n a M >恒成立仅对部分n 成立，故A 不成立.对于B ，若15,a =可用数学归纳法证明：106n a --≤<即56n a ≤<，证明：当1n =时，10611a ---≤≤=，此时不等关系56n a ≤<成立；设当n k =时，56k a ≤<成立，则()31164416,0k k a a +⎛⎫-∈-⎪⎝=⎭-，故1106k a +--≤<成立即由数学归纳法可得156k a +≤<成立. 而()()()()231116666441n n n n n n a a a a a a +⎡⎤=---=---⎢⎣-⎥⎦， ()201416n a --<，60n a -<，故10n n a a +->，故1n n a a +>，故{}n a 为增数列，若6M =，则6n a <恒成立，故B 正确.对于C ，当17a =时，可用数学归纳法证明：061n a <-≤即67n a <≤，证明：当1n =时，1061a <-≤，此时不等关系成立；设当n k =时，67k a <≤成立，则()31160,4164k k a a +⎛⎤-∈ ⎥⎝=⎦-，故1061k a +<-≤成立即167k a +<≤ 由数学归纳法可得67n a <≤成立.而()()21166014n n n n a a a a +⎡⎤=--<⎢⎥⎣⎦--，故1n n a a +<，故{}n a 为减数列，又()()()2111666644n n n n a a a a +-=-⨯-≤-，结合160n a +->可得：()111664n n a a +⎛⎫-≤- ⎪⎝⎭，所以1164nn a +⎛⎫≤+ ⎪⎝⎭，若1164nn a +⎛⎫≤+ ⎪⎝⎭，若存在常数6M >，使得n a M >恒成立，则164nM ⎛⎫-≤ ⎪⎝⎭恒成立，故()14log 6n M ≤-，n 的个数有限，矛盾，故C 错误.对于D ，当19a =时，可用数学归纳法证明：63n a -≥即9n a ≥，证明：当1n =时，1633a -=≥，此时不等关系成立；设当n k =时，9k a ≥成立，则()3162764143k k a a +-≥=>-，故19k a +≥成立由数学归纳法可得9n a ≥成立.而()()21166014n n n n a a a a +⎡⎤=-->⎢⎥⎣⎦--，故1n n a a +>，故{}n a 为增数列，又()()()2119666446n n n n a a a a +->=-⨯--，结合60n a ->可得：()11116396449n n n a a --+⎭-⎛⎫⎛⎫-= ⎪⎪⎝⎝⎭> ，所以114963n n a -+⎛⎫⎪⎭≥+⎝，若存在常数0M >，使得n a M <恒成立，则19643n M -⎛⎫⎪⎝>+⎭，故19643n M -⎛⎫⎪⎝>+⎭，故946log 13M n -⎛⎫<+ ⎪⎝⎭，这与n 的个数有限矛盾，故D 错误.故选：B.法2：因为()3321119662648442n n n n n n n a a a a a a a +-=-+-=-+-，令()3219264842f x x x x =-+-，则()239264f x x x =-+'，令()0f x ¢>，得06x <<6x >+；令()0f x '<，得66x << 所以()f x在,6⎛-∞ ⎝⎭和63⎛⎫++∞ ⎪ ⎪⎝⎭上单调递增，在633⎛⎫-+ ⎪ ⎪⎝⎭上单调递减，令()0f x =，则32192648042x x x -+-=，即()()()146804x x x ---=，解得4x =或6x =或8x =，注意到465<<，768<<，所以结合()f x 的单调性可知在(),4-∞和()6,8上()0f x <，在()4,6和()8,+∞上()0f x >，对于A ，因为()311664n n a a +=-+，则()311646n n a a +=--，当1n =时，13a =，()32116643a a =--<-，则23a <，假设当n k =时，3k a <，当1n k =+时，()()331311646364k k a a +<---<-=，则13k a +<，综上：3n a ≤，即(),4n a ∈-∞，因为在(),4-∞上()0f x <，所以1n n a a +<，则{}n a 为递减数列，因为()332111916612647442n n n n n n n a a a a a a a +-+=-+-+=-+-，令()()32192647342h x x x x x =-+-≤，则()239264h x x x '=-+，因为()h x '开口向上，对称轴为96324x -=-=⨯，所以()h x '在(],3-∞上单调递减，故()()2333932604h x h ''≥=⨯-⨯+>，所以()h x 在(],3-∞上单调递增，故()()321933326347042h x h ≤=⨯-⨯+⨯-<，故110n n a a +-+<，即11n n a a +<-，假设存在常数0M ≤，使得n a M >恒成立，取[]14m M =-+，其中[]1M M M -<≤，且[]Z M ∈，因为11n n a a +<-，所以[][]2132431,1,,1M M a a a a a a -+-+<-<-<- ，上式相加得，[][]()14333M a a M M M -+<--+≤+-=，则[]14m M a a M +=<，与n a M >恒成立矛盾，故A 错误；对于B ，因为15a =，当1n =时，156a =<，()()33211166566644a a =-+=⨯-+<，假设当n k =时，6k a <，当1n k =+时，因为6k a <，所以60k a -<，则()360k a -<，所以()3116664k k a a +=-+<，又当1n =时，()()332111615610445a a =-+=⨯+-->，即25a >，假设当n k =时，5k a ≥，当1n k =+时，因为5k a ≥，所以61k a -≥-，则()361k a -≥-，所以()3116654k k a a +=-+≥，综上：56n a ≤<，因为在()4,6上()0f x >，所以1n n a a +>，所以{}n a 为递增数列，此时，取6M =，满足题意，故B 正确；对于C ，因为()311664n n a a +=-+，则()311646n n a a +=--，注意到当17a =时，()3216617644a =-+=+，3341166441664a ⎪⎛⎫⎫+=+ ⎪⎝+-⎭⎭⎛= ⎝，143346166144416a ⎢⎛⎫+=⎡⎤⎛⎫=+-⎢⎥ ⎪⎝+ ⎪⎭⎭⎥⎦⎝⎣猜想当2n ≥时，)1312164k k a -⎛⎫+ ⎪=⎝⎭，当2n =与3n =时，2164a =+与43164a ⎛⎫=+ ⎪⎝⎭满足()1312164nn a -⎛⎫+ ⎪=⎝⎭，假设当n k =时，)1312164k k a -⎛⎫+ ⎪=⎝⎭，当1n k =+时，所以()())13113131122311666116664444k k k k a a +-+-⎡⎤⎛⎫⎛⎫⎢⎥=+-+ ⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦-+=+=，综上：()()13121624n n a n - =⎛⎫+≥⎪⎝⎭，易知310n->，则)13121014n -⎛⎫<< ⎪⎝⎭，故()()()1312166,724n n a n -⎛⎪=⎫+∈≥ ⎝⎭，所以(],67n a ∈，因为在()6,8上()0f x <，所以1n n a a +<，则{}n a 为递减数列，假设存在常数6M >，使得n a M >恒成立，记()0143log 2log 61m M ⎡⎤⎢⎥⎣=+⎦-，取[]01m m =+，其中[]*00001,N m m m m -<≤∈，则()0142log 6133m mM ->=+，故()()14log 61312m M ->-，所以()1312614m M -⎛⎫ ⎪<⎝-⎭，即)1312164m M -⎛⎫+ ⎪⎭<⎝，所以m a M <，故n a M >不恒成立，故C 错误；对于D ，因为19a =，当1n =时，()32116427634a a ==->-，则29a >，假设当n k =时，3k a ≥，当1n k =+时，()()331116936644k k a a +≥=-->-，则19k a +>，综上：9n a ≥，因为在()8,+∞上()0f x >，所以1n n a a +>，所以{}n a 为递增数列，因为()332111916612649442n n n n n n n a a a a a a a +--=-+--=-+-，令()()32192649942g x x x x x =-+-≥，则()239264g x x x '=-+，因为()g x '开口向上，对称轴为96324x -=-=⨯，所以()g x '在[)9,+∞上单调递增，故()()2399992604g x g ≥=⨯-⨯+'>'，所以()()321999926949042g x g ≥=⨯-⨯+⨯->，故110n n a a +-->，即11n n a a +>+，假设存在常数0M >，使得n a M <恒成立，取[]21m M =+，其中[]1M M M -<≤，且[]Z M ∈，因为11n n a a +>+，所以[][]213211,1,,1M M a a a a a a +>+>+>+ ，上式相加得，[][]1191M a a M M M +>+>+->，则[]21m M a a M +=>，与n a M <恒成立矛盾，故D 错误. 故选：B.【名师点评】关键名师点评：本题解决的关键是根据首项给出与通项性质相关的相应的命题，再根据所得命题结合放缩法得到通项所满足的不等式关系，从而可判断数列的上界或下界是否成立.2．（2022∙北京∙高考真题）已知数列{}n a 各项均为正数，其前n 项和n S 满足9(1,2,)n n a S n ⋅== ．给出下列四个结论：①{}n a 的第2项小于3； ②{}n a 为等比数列； ③{}n a 为递减数列； ④{}n a 中存在小于1100的项．其中所有正确结论的序号是．【答案】①③④ 【详细分析】推导出199n n n a a a -=-，求出1a 、2a 的值，可判断①；利用反证法可判断②④；利用数列单调性的定义可判断③.【答案详解】由题意可知，N n *∀∈，0n a >，当1n =时，219a =，可得13a =；当2n ≥时，由9n n S a =可得119n n S a --=，两式作差可得199n n n a a a -=-，所以，199n n n a a a -=-，则2293a a -=，整理可得222390a a +-=，因为20a >，解得2332a =<，①对；假设数列{}n a 为等比数列，设其公比为q ，则2213a a a =，即2213981S S S ⎛⎫= ⎪⎝⎭，所以，2213S S S =，可得()()22221111a q a q q +=++，解得0q =，不合乎题意，故数列{}n a 不是等比数列，②错；当2n ≥时，()1119990n n n n n n n a a a a a a a ----=-=>，可得1n n a a -<，所以，数列{}n a 为递减数列，③对；假设对任意的N n *∈，1100n a ≥，则10000011000001000100S ≥⨯=，所以，1000001000009911000100a S =≤<，与假设矛盾，假设不成立，④对. 故答案为：①③④.【名师点评】关键点名师点评：本题在推断②④的正误时，利用正面推理较为复杂时，可采用反证法来进行推导.3．（2022∙浙江∙高考真题）已知数列{}n a 满足()21111,3n n n a a a a n *+==-∈N ，则（）A ．100521002a <-，累加可求出11(2)3n n a >+，得出1001003a <，再利用11111111333132n n n a a a n n +⎛⎫-=<=+ ⎪-+⎝⎭-+，累加可求出()111111113323nn a n ⎛⎫-<-++++ ⎪⎝⎭ ，再次放缩可得出10051002a >．【答案详解】∵11a =，易得()220,13a =∈，依次类推可得()0,1n a ∈ 由题意，1113n n n a a a +⎛⎫=- ⎪⎝⎭，即()1131133n n n n na a a a a +==+--，∴1111133n n n a a a +-=>-，即211113a a ->，321113a a ->，431113a a ->，…，1111,(2)3n n n a a -->≥，累加可得()11113n n a ->-，即11(2),(2)3n n n a >+≥， ∴()3,22n a n n <≥+，即100134a <，100100100334a <<, 又11111111,(2)333132n n n n a a a n n +⎛⎫-=<=+≥ ⎪-+⎝⎭-+， ∴211111132a a ⎛⎫-=+ ⎪⎝⎭，321111133a a ⎛⎫-<+ ⎪⎝⎭，431111134a a ⎛⎫-<+ ⎪⎝⎭，…，111111,(3)3n n n a a n -⎛⎫-<+≥ ⎪⎝⎭，累加可得()11111111,(3)3323n n n a n ⎛⎫-<-++++≥ ⎪⎝⎭ ，∴100111111111333349639323100326a ⎛⎫⎛⎫-<++++<+⨯+⨯< ⎪ ⎪⎝⎭⎝⎭ ，即100140a <，∴100140a >，即10051002a >；综上：100510032a <<．故选：B ．【名师点评】关键点名师点评：解决本题的关键是利用递推关系进行合理变形放缩. 4．（2021∙浙江∙高考真题）已知数列{}n a满足)111,N n a a n *+==∈.记数列{}n a 的前n 项和为n S ，则（）A ．100332S <，利用倒数法得到21111124n n a a +⎛⎫==+-⎪⎪⎭，再放缩可得12<，由累加法可得24(1)n a n ≥+，进而由1n a +=113n n a n a n ++≤+，然后利用累乘法求得6(1)(2)n a n n ≤++，最后根据裂项相消法即可得到1003S <，从而得解．【答案详解】因为)111,N n a a n *+==∈，所以0n a >，10032S >．由211111124n n n a a a ++⎛⎫=⇒=+=+-⎪⎪⎭2111122n a +⎛⎫∴<⇒<⎪⎪⎭12<()111,222n n n -+<+=≥，当1n =112+=，12n +≤，当且仅当1n =时等号成立，12412(1)311n n n n a n a a a n n n ++∴≥∴=≤=++++ 113n n a n a n ++∴≤+，由累乘法可得()6,2(1)(2)n a n n n ≤≥++，且16(11)(12)a =++，则6(1)(2)n a n n ≤++，当且仅当1n =时取等号，由裂项求和法得：所以10011111111116632334451011022102S ⎛⎫⎛⎫≤-+-+-++-=-< ⎪ ⎪⎝⎭⎝⎭，即100332S <<．故选：A ．【名师点评】的不等关系，再由累加法可求得24(1)n a n ≥+，由题目条件可知要证100S 小于某数，从而通过局部放缩得到1,n n a a +的不等关系，改变不等式的方向得到6(1)(2)n a n n ≤++，最后由裂项相消法求得1003S <．5．（2020∙浙江∙高考真题）我国古代数学家杨辉，朱世杰等研究过高阶等差数列的求和问题，如数列(1)2n n +⎧⎫⎨⎬⎩⎭就是二阶等差数列，数列(1)2n n +⎧⎫⎨⎬⎩⎭(N )n *∈ 的前3项和是．【答案】10【详细分析】根据通项公式可求出数列{}n a 的前三项，即可求出．【答案详解】因为()12n n n a +=，所以1231,3,6a a a ===．即312313610S a a a =++=++=．故答案为：10.【名师点评】本题主要考查利用数列的通项公式写出数列中的项并求和，属于容易题．6．（2020∙全国∙高考真题）数列{}n a 满足2(1)31nn n a a n ++-=-，前16项和为540，则1a = .【答案】7【详细分析】对n 为奇偶数分类讨论，分别得出奇数项、偶数项的递推关系，由奇数项递推公式将奇数项用1a 表示，由偶数项递推公式得出偶数项的和，建立1a 方程，求解即可得出结论.【答案详解】2(1)31nn n a a n ++-=-，当n 为奇数时，231n n a a n +=+-；当n 为偶数时，231n n a a n ++=-. 设数列{}n a 的前n 项和为n S ，16123416S a a a a a =+++++135********()()a a a a a a a a =+++++++111111(2)(10)(24)(44)(70)a a a a a a =++++++++++ 11(102)(140)(5172941)a a ++++++++ 118392928484540a a =++=+=，17a ∴=.故答案为：7.【名师点评】本题考查数列的递推公式的应用，以及数列的并项求和，考查分类讨论思想和数学计算能力，属于较难题.7．（2019∙浙江∙高考真题）设,a b R ∈，数列{}n a 中，211,n n a a a a b +==+，N n *∈ ,则A ．当101,102b a =>B ．当101,104b a =>C ．当102,10b a =->D ．当104,10b a =->【答案】A【解析】若数列{}n a 为常数列，101a a a ==，则只需使10a ≤，选项的结论就会不成立.将每个选项的b 的取值代入方程20x x b -+=，看其是否有小于等于10的解.选项B 、C 、D 均有小于10的解，故选项B 、C 、D 错误.而选项A 对应的方程没有解，又根据不等式性质，以及基本不等式，可证得A 选项正确.【答案详解】若数列{}n a 为常数列，则1n a a a ==，由21n n a a b +=+，可设方程20x x b -+= 选项A ：12b =时，2112n n a a +=+，2102x x -+=， 1210∆=-=-<，故此时{}n a 不为常数列，222112n n n n a a a +=+=+≥ ，且2211122a a =+≥，792a a ∴≥≥21091610a a >≥>，故选项A 正确；选项B ：14b =时，2114n n a a +=+，2104x x -+=，则该方程的解为12x =，即当12a =时，数列{}n a 为常数列，12n a =，则101102a =<，故选项B 错误；选项C ：2b =-时，212n n a a +=-，220x x --=该方程的解为=1x -或2，即当1a =-或2时，数列{}n a 为常数列，1n a =-或2，同样不满足1010a >，则选项C 也错误；选项D ：4b =-时，214n n a a +=-，240x x --=该方程的解为12x =，同理可知，此时的常数列{}n a 也不能使1010a >，则选项D 错误. 故选：A.【名师点评】遇到此类问题，不少考生会一筹莫展.利用函数方程思想，通过研究函数的不动点，进一步讨论a 的可能取值，利用“排除法”求解.考点03 等差数列及其前n 项和一、单选题 1．（2024∙全国甲卷∙高考真题）记n S 为等差数列{}n a 的前n 项和，已知510S S =，51a =，则1a =（） A ．72B ．73 C ．13-D ．711-【答案】B【详细分析】由510S S =结合等差中项的性质可得80a =，即可计算出公差，即可得1a 的值. 【答案详解】由105678910850S S a a a a a a -=++++==，则80a =，则等差数列{}n a 的公差85133a a d -==-，故151741433a a d ⎛⎫=-=-⨯-= ⎪⎝⎭.故选：B.2．（2024∙全国甲卷∙高考真题）已知等差数列{}n a 的前n 项和为n S ，若91S =，则37a a +=（） A ．2-B ．73C ．1D ．29【答案】D【详细分析】可以根据等差数列的基本量，即将题目条件全转化成1a 和d 来处理，亦可用等差数列的性质进行处理，或者特殊值法处理.【答案详解】方法一：利用等差数列的基本量由91S =，根据等差数列的求和公式，911989193612S a d a d ⨯=+=⇔+=，又371111222628(936)99a a a d a d a d a d +=+++=+=+=. 故选：D方法二：利用等差数列的性质根据等差数列的性质，1937a a a a +=+，由91S =，根据等差数列的求和公式， 193799()9()122a a a a S ++===，故3729a a +=.故选：D方法三：特殊值法不妨取等差数列公差0d =，则9111199S a a ==⇒=，则371229a a a +==. 故选：D3．（2023∙全国甲卷∙高考真题）记n S 为等差数列{}n a 的前n 项和．若264810,45a a a a +==，则5S =（） A ．25B ．22C ．20D ．15【答案】C【详细分析】方法一：根据题意直接求出等差数列{}n a 的公差和首项，再根据前n 项和公式即可解出；方法二：根据等差数列的性质求出等差数列{}n a 的公差，再根据前n 项和公式的性质即可解出．【答案详解】方法一：设等差数列{}n a 的公差为d ，首项为1a ，依题意可得，2611510a a a d a d +=+++=，即135a d +=,又()()48113745a a a d a d =++=，解得：11,2d a ==，所以515455210202S a d ⨯=+⨯=⨯+=．故选：C.方法二：264210a a a +==，4845a a =，所以45a =，89a =，从而84184a a d -==-，于是34514a a d =-=-=，所以53520S a ==．故选：C.4．（2023∙全国乙卷∙高考真题）已知等差数列{}n a 的公差为23π，集合{}*cos N n S a n =∈，若{},S a b =，则ab =（） A ．－1B ．12-C ．0D ．12【答案】B【详细分析】根据给定的等差数列，写出通项公式，再结合余弦型函数的周期及集合只有两个元素详细分析、推理作答.【答案详解】依题意，等差数列{}n a 中，112π2π2π(1)()333n a a n n a =+-⋅=+-，显然函数12π2πcos[()]33y n a =+-的周期为3，而N n *∈，即cos n a 最多3个不同取值，又{cos |N }{,}n a n a b *∈=，则在123cos ,cos ,cos a a a 中，123cos cos cos a a a =≠或123cos cos cos a a a ≠=，于是有2πcos cos()3θθ=+，即有2π()2π,Z 3k k θθ++=∈，解得ππ,Z 3k k θ=-∈，所以Z k ∈，2ππ4πππ1cos(π)cos[(π)]cos(π)cos πcos πcos 333332ab k k k k k =--+=--=-=-.故选：B5．（2023∙全国新Ⅰ卷∙高考真题）记n S 为数列{}n a 的前n 项和，设甲：{}n a 为等差数列；乙：{}nS n为等差数列，则（）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件【答案】C【详细分析】利用充分条件、必要条件的定义及等差数列的定义，再结合数列前n 项和与第n 项的关系推理判断作答.，【答案详解】方法1，甲：{}n a 为等差数列，设其首项为1a ，公差为d ，则1111(1)1,,222212n n n n S S S n n n d d dS na d a d n a nn n +--=+=+=+--=+，因此{}nS n为等差数列，则甲是乙的充分条件；反之，乙：{}nS n为等差数列，即111(1)1(1)(1)n n n n n n S S nS n S na S n n n n n n +++-+--==+++为常数，设为t ，即1(1)n nna S t n n +-=+，则1(1)n n S na t n n +=-⋅+，有1(1)(1),2n n S n a t n n n -=--⋅-≥，两式相减得：1(1)2n n n a na n a tn +=---，即12n n a a t +-=，对1n =也成立，因此{}n a 为等差数列，则甲是乙的必要条件，所以甲是乙的充要条件，C 正确.方法2，甲：{}n a 为等差数列，设数列{}n a 的首项1a ，公差为d ，即1(1)2n n n S na d -=+，则11(1)222n S n d d a d n a n-=+=+-，因此{}n S n 为等差数列，即甲是乙的充分条件；反之，乙：{}nS n 为等差数列，即11,(1)1n n n S S S D S n D n n n+-==+-+，即1(1)n S nS n n D =+-，11(1)(1)(2)n S n S n n D -=-+--，当2n ≥时，上两式相减得：112(1)n n S S S n D --=+-，当1n =时，上式成立，于是12(1)n a a n D =+-，又111[22(1)]2n n a a a nD a n D D +-=+-+-=为常数，因此{}n a 为等差数列，则甲是乙的必要条件，所以甲是乙的充要条件. 故选：C6．（2022∙北京∙高考真题）设{}n a 是公差不为0的无穷等差数列，则“{}n a 为递增数列”是“存在正整数0N ，当0n N >时，0n a >”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件【答案】C【详细分析】设等差数列{}n a 的公差为d ，则0d ≠，利用等差数列的通项公式结合充分条件、必要条件的定义判断可得出结论.【答案详解】设等差数列{}n a 的公差为d ，则0d ≠，记[]x 为不超过x 的最大整数. 若{}n a 为单调递增数列，则0d >，若10a ≥，则当2n ≥时，10n a a >≥；若10a <，则()11n a a n d +-=，由()110n a a n d =+->可得11a n d >-，取1011a N d ⎡⎤=-+⎢⎥⎣⎦，则当0n N >时，0n a >，所以，“{}n a 是递增数列”⇒“存在正整数0N ，当0n N >时，0n a >”；若存在正整数0N ，当0n N >时，0n a >，取N k *∈且0k N >，0k a >，假设0d <，令()0n k a a n k d =+-<可得k a n k d >-，且k ak k d->，当1k a n k d ⎡⎤>-+⎢⎥⎣⎦时，0n a <，与题设矛盾，假设不成立，则0d >，即数列{}n a 是递增数列.所以，“{}n a 是递增数列”⇐“存在正整数0N ，当0n N >时，0n a >”.所以，“{}n a 是递增数列”是“存在正整数0N ，当0n N >时，0n a >”的充分必要条件. 故选：C.7．（2020∙浙江∙高考真题）已知等差数列{an }的前n 项和Sn ，公差d ≠0，11a d≤．记b 1=S 2，bn+1=S2n+2–S 2n ，n N *∈，下列等式不可能．．．成立的是（） A ．2a 4=a 2+a 6B ．2b 4=b 2+b 6C ．2428a a a = D ．2428b b b =【答案】D【详细分析】根据题意可得，21212222n n n n n b S a a S ++++=+=-，而1212b S a a ==+，即可表示出题中2468,,,b b b b ，再结合等差数列的性质即可判断各等式是否成立．【答案详解】对于A ，因为数列{}n a 为等差数列，所以根据等差数列的下标和性质，由4426+=+可得，4262a a a =+，A 正确；对于B ，由题意可知，21212222n n n n n b S a a S ++++=+=-，1212b S a a ==+，∴234b a a =+，478b a a =+，61112b a a =+，81516b a a =+． ∴()47822b a a =+，26341112b b a a a a +=+++．根据等差数列的下标和性质，由31177,41288+=++=+可得()26341112784=2=2b b a a a a a a b +=++++，B 正确；对于C ，()()()()2224281111137222a a a a d a d a d d a d d d a -=+-++=-=-，当1a d =时，2428a a a =，C 正确；对于D ，()()22222478111213452169b a a a d a a d d =+=+=++，()()()()2228341516111125229468145b b a a a a a d a d a a d d =++=++=++， ()22428112416832b b b d a d d d a -=-=-．当0d >时，1a d ≤，∴()113220d a d d a -=+->即24280b b b ->；当0d <时，1a d ≥，∴()113220d a d d a -=+-<即24280b b b ->，所以24280b b b ->，D 不正确．故选：D.【名师点评】本题主要考查等差数列的性质应用，属于基础题．8．（2019∙全国∙高考真题）记n S 为等差数列{}n a 的前n 项和．已知4505S a ==，，则。

历年(2020-2024)全国高考数学真题分类(等式与不等式综合)汇编(附答案)

历年(2020-2024)全国高考数学真题分类(等式与不等式综合)汇编解不等式1．（2024∙全国新Ⅰ卷∙高考真题）已知集合{}355,{3,1,0,2,3}A xx B =-<<=--∣，则A B = （） A ．{1,0}- B ．{2,3} C ．{3,1,0}-- D ．{1,0,2}-2．（2024∙上海∙高考真题）已知,x ∈R 则不等式2230x x --<的解集为．3．（2023∙全国新Ⅰ卷∙高考真题）已知集合{}2,1,0,1,2M =--，{}260N x x x =--≥，则M N ⋂=（）A ．{}2,1,0,1--B ．{}0,1,2C ．{}2-D ．{}24．（2020∙全国∙高考真题）已知集合2{|340},{4,1,3,5}A x x x B =--<=-，则A B = （） A ．{4,1}- B ．{1,5} C ．{3,5}D ．{1,3}基本不等式1．（2024∙北京∙高考真题）已知()11,x y ，()22,x y 是函数2x y =的图象上两个不同的点，则（） A ．12122log 22y y x x ++ C ．12212log 2y y x x +<+ D ．12212log 2y y x x +>+ 2．（2021∙全国乙卷∙高考真题）下列函数中最小值为4的是（） A ．224y x x =++ B ．4sin sin y x x=+ C ．2y 22x x -=+D ．4ln ln y x x=+3．（2021∙全国新Ⅰ卷∙高考真题）已知1F ，2F 是椭圆C ：22194x y +=的两个焦点，点M 在C 上，则12MF MF ⋅的最大值为（） A ．13B ．12C ．9D ．64．（2020∙全国∙高考真题）设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b ab-=>>的两条渐近线分别交于,D E 两点，若ODE 的面积为8，则C 的焦距的最小值为（） A ．4B ．8C ．16D ．32参考答案解不等式1．（2024∙全国新Ⅰ卷∙高考真题）已知集合{}355,{3,1,0,2,3}A xx B =-<<=--∣，则A B = （） A ．{1,0}- B ．{2,3}C ．{3,1,0}--D ．{1,0,2}-【答案】A【详细分析】化简集合A ，由交集的概念即可得解.【答案详解】因为{{}|,3,1,0,2,3A x x B =<<=--，且注意到12<<，从而A B = {}1,0-. 故选：A.2．（2024∙上海∙高考真题）已知,x ∈R 则不等式2230x x --<的解集为．【答案】{}|13x x -<<【详细分析】求出方程2230x x --=的解后可求不等式的解集. 【答案详解】方程2230x x --=的解为=1x -或3x =，故不等式2230x x --<的解集为{}|13x x -<<，故答案为：{}|13x x -<<.3．（2023∙全国新Ⅰ卷∙高考真题）已知集合{}2,1,0,1,2M =--，{}260N x x x =--≥，则M N ⋂=（）A ．{}2,1,0,1--B ．{}0,1,2C ．{}2-D ．{}2【答案】C【详细分析】方法一：由一元二次不等式的解法求出集合N ，即可根据交集的运算解出．方法二：将集合M 中的元素逐个代入不等式验证，即可解出．【答案详解】方法一：因为{}(][)260,23,N x x x ∞∞=--≥=--⋃+，而{}2,1,0,1,2M =--，所以M N ⋂={}2-．故选：C ．方法二：因为{}2,1,0,1,2M =--，将2,1,0,1,2--代入不等式260x x --≥，只有2-使不等式成立，所以M N ⋂={}2-．故选：C ．4．（2020∙全国∙高考真题）已知集合2{|340},{4,1,3,5}A x x x B =--<=-，则A B = （） A ．{4,1}- B ．{1,5} C ．{3,5} D ．{1,3}【答案】D【详细分析】首先解一元二次不等式求得集合A ，之后利用交集中元素的特征求得A B ⋂，得到结果. 【答案详解】由2340x x --<解得14x -<<，所以{}|14A x x =-<<，又因为{}4,1,3,5B =-，所以{}1,3A B = ，故选：D.【名师点评】本题考查的是有关集合的问题，涉及到的知识点有利用一元二次不等式的解法求集合，集合的交运算，属于基础题目.基本不等式1．（2024∙北京∙高考真题）已知()11,x y ，()22,x y 是函数2x y =的图象上两个不同的点，则（） A ．12122log 22y y x x ++ C ．12212log 2y y x x +<+ D ．12212log 2y y x x +>+ 【答案】B【详细分析】根据指数函数和对数函数的单调性结合基本不等式详细分析判断AB ；举例判断CD 即可. 【答案详解】由题意不妨设12x x <，因为函数2x y =是增函数，所以12022x x <<，即120y y <<，对于选项AB ：可得121222222x xx x ++>=，即12122202x x y y ++>>，根据函数2log y x =是增函数，所以121212222log log 222x x y y x x+++>=，故B 正确，A 错误；对于选项D ：例如120,1x x ==，则121,2y y ==，可得()12223log log 0,122y y +=∈，即12212log 12y y x x +<=+，故D 错误；对于选项C ：例如121,2x x =-=-，则1211,24y y ==，可得()122223log log log 332,128y y +==-∈--，即12212log 32y y x x +>-=+，故C 错误，故选：B.2．（2021∙全国乙卷∙高考真题）下列函数中最小值为4的是（） A ．224y x x =++ B ．4sin sin y x x=+ C ．2y 22x x -=+ D ．4ln ln y x x=+【答案】C【详细分析】根据二次函数的性质可判断A 选项不符合题意，再根据基本不等式“一正二定三相等”，即可得出,B D 不符合题意，C 符合题意．【答案详解】对于A ，()2224133y x x x =++=++≥，当且仅当=1x -时取等号，所以其最小值为3，A 不符合题意；对于B ，因为0sin 1x <≤，4sin 4sin y x x=+≥=，当且仅当sin 2x =时取等号，等号取不到，所以其最小值不为4，B 不符合题意；对于C ，因为函数定义域为R ，而20x >，2422242x x xx y -=+=+≥=，当且仅当22x =，即1x =时取等号，所以其最小值为4，C 符合题意；对于D ，4ln ln y x x=+，函数定义域为()()0,11,+∞ ，而ln x R ∈且ln 0x ≠，如当ln 1x =-，5y =-，D 不符合题意．故选：C ．【名师点评】本题解题关键是理解基本不等式的使用条件，明确“一正二定三相等”的意义，再结合有关函数的性质即可解出．3．（2021∙全国新Ⅰ卷∙高考真题）已知1F ，2F 是椭圆C ：22194x y +=的两个焦点，点M 在C 上，则12MF MF ⋅的最大值为（） A ．13 B ．12C ．9D ．6【答案】C【详细分析】本题通过利用椭圆定义得到1226MF MF a +==，借助基本不等式212122MF MF MF MF ⎛+⎫⋅≤ ⎪⎝⎭即可得到答案．【答案详解】由题，229,4a b ==，则1226MF MF a +==，所以2121292MF MF MF MF ⎛+⎫⋅≤= ⎪⎝⎭（当且仅当123MF MF ==时，等号成立）．故选：C ．【名师点评】4．（2020∙全国∙高考真题）设O 为坐标原点，直线x a =与双曲线2222:1(0,0)x y C a b ab-=>>的两条渐近线分别交于,D E 两点，若ODE 的面积为8，则C 的焦距的最小值为（） A ．4 B ．8 C ．16 D ．32【答案】B【详细分析】因为2222:1(0,0)x y C a b a b -=>>，可得双曲线的渐近线方程是b y x a=±，与直线x a =联立方程求得D ，E 两点坐标，即可求得||ED ，根据ODE 的面积为8，可得ab值，根据2c =等式，即可求得答案. 【答案详解】 2222:1(0,0)x y C a b a b -=>> ∴双曲线的渐近线方程是b y x a=±直线x a =与双曲线2222:1(0,0)x y C a b a b -=>>的两条渐近线分别交于D ，E 两点不妨设D 为在第一象限，E 在第四象限联立x ab y x a =⎧⎪⎨=⎪⎩，解得x a y b =⎧⎨=⎩ 故(,)D a b联立x ab y x a =⎧⎪⎨=-⎪⎩，解得x a y b =⎧⎨=-⎩ 故(,)E a b -∴||2ED b =∴ODE 面积为：1282ODE S a b ab =⨯==△双曲线2222:1(0,0)x y C a b a b-=>>∴其焦距为28c =≥==当且仅当a b ==∴C 的焦距的最小值：8故选：B.【名师点评】本题主要考查了求双曲线焦距的最值问题，解题关键是掌握双曲线渐近线的定义和均值不等式求最值方法，在使用均值不等式求最值时，要检验等号是否成立，考查了详细分析能力和计算能力，属于中档题.。

各省高考真题数学及答案

各省高考真题数学及答案高考数学试题是每年高考的重要部分，很多考生对于数学部分的考试难度颇为担忧。

为了帮助考生更好地应对高考数学试题，以下将列举各省历年高考数学试题及答案，供考生参考。

北京高考数学试题及答案：1. (2019年北京高考数学试题)题目：已知函数$f(x)=\frac{x}{2}+3$，则$f(4)=$?A. 5B. 6C. 7D. 8答案：B. 6上海高考数学试题及答案：1. (2018年上海高考数学试题)题目：在等边三角形ABC中，点M是边AC上的动点，若BM=2CM，则三角形MBC的面积是三角形ABC的几分之一？A. 1/2B. 1/3C. 1/4D. 1/6答案：C. 1/4广东高考数学试题及答案：1. (2017年广东高考数学试题)题目：已知函数$f(x)=\frac{3x-1}{2}$，则对任意实数x，不等式$f(x)<4$的解集为？A. x<5B. x>5/3C. x>5D. x<5/3答案：A. x<5江苏高考数学试题及答案：1. (2016年江苏高考数学试题)题目：已知AB=AC，AD⊥BC，BD=CD，角BAD=40°，求角ACD的度数。

A. 70°B. 60°C. 50°D. 40°答案：B. 60°浙江高考数学试题及答案：1. (2015年浙江高考数学试题)题目：已知直角三角形ABC中，AB=3，BC=4，∠ABC=90°，若D为BC边上一点且∠ACD=∠BAD，求BD的长度。

A. 2B. 3C. 4D. 5答案：C. 4各省高考数学试题虽然难度不尽相同，但通过细心复习及多做练习，相信考生们定能应对。

祝愿所有参加高考的考生都能取得优异的成绩，实现自己的高考梦想！。

(完整版)历年高考数学真题(全国卷整理版)

2013年普通高等学校夏季招生全国统一考试数学理工农医类(大纲全国卷)一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．(2013大纲全国，理1)设集合A ＝{1,2,3}，B ＝{4,5}，M ＝{x |x ＝a ＋b ，a ∈A ，b ∈B }，则M 中元素的个数为( )．A ．3B ．4C ．5D ．62．(2013大纲全国，理2)3＝( )．A ．－8B ．8C ．－8iD ．8i3．(2013大纲全国，理3)已知向量m ＝(λ＋1,1)，n ＝(λ＋2,2)，若(m ＋n )⊥(m －n )，则λ＝( )．A ．－4B ．－3C ．－2D ．－14．(2013大纲全国，理4)已知函数f (x )的定义域为(－1,0)，则函数f (2x ＋1)的定义域为( )．A ．(－1,1)B ．11,2⎛⎫-- ⎪⎝⎭ C ．(－1,0) D ．1,12⎛⎫ ⎪⎝⎭ 5．(2013大纲全国，理5)函数f (x )＝21log 1x ⎛⎫+⎪⎝⎭(x ＞0)的反函数f －1(x )＝( )． A ．121x -(x ＞0) B ．121x-(x≠0) C ．2x －1(x ∈R) D ．2x －1(x ＞0)6．(2013大纲全国，理6)已知数列{a n }满足3a n ＋1＋a n ＝0，a 2＝43-，则{a n }的前10项和等于( )． A ．－6(1－3－10) B ．19(1－310) C ．3(1－3－10) D ．3(1＋3－10)7．(2013大纲全国，理7)(1＋x )8(1＋y )4的展开式中x 2y 2的系数是( )．A ．56B ．84C ．112D ．1688．(2013大纲全国，理8)椭圆C ：22=143x y +的左、右顶点分别为A 1，A 2，点P 在C 上且直线PA 2斜率的取值范围是[－2，－1]，那么直线PA 1斜率的取值范围是( )．A ．13,24⎡⎤⎢⎥⎣⎦ B ．33,84⎡⎤⎢⎥⎣⎦ C ．1,12⎡⎤⎢⎥⎣⎦ D ．3,14⎡⎤⎢⎥⎣⎦ 9．(2013大纲全国，理9)若函数f (x )＝x 2＋ax ＋1x 在1,2⎛⎫+∞ ⎪⎝⎭是增函数，则a 的取值范围是( )． A ．[－1,0] B ．[－1，＋∞) C ．[0,3] D ．[3，＋∞)10．(2013大纲全国，理10)已知正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2AB ，则CD 与平面BDC 1所成角的正弦值等于( )．A ．23 B．3 C．3 D ．1311．(2013大纲全国，理11)已知抛物线C ：y 2＝8x 与点M (－2,2)，过C 的焦点且斜率为k 的直线与C 交于A ，B 两点．若0MA MB ⋅=，则k ＝( )．A ．12 B．2 CD ．212．(2013大纲全国，理12)已知函数f (x )＝cos x sin 2x ，下列结论中错误的是( )．A ．y ＝f(x)的图像关于点(π，0)中心对称B ．y ＝f(x)的图像关于直线π=2x 对称C ．f(x)的最大值为2 D ．f(x)既是奇函数，又是周期函数二、填空题：本大题共4小题，每小题5分．13．(2013大纲全国，理13)已知α是第三象限角，sin α＝13-，则cot α＝__________. 14．(2013大纲全国，理14)6个人排成一行，其中甲、乙两人不相邻的不同排法共有__________种．(用数字作答)15．(2013大纲全国，理15)记不等式组0,34,34x x y x y ≥⎧⎪+≥⎨⎪+≤⎩所表示的平面区域为D .若直线y ＝a (x ＋1)与D 有公共点，则a 的取值范围是__________．16．(2013大纲全国，理16)已知圆O 和圆K 是球O 的大圆和小圆，其公共弦长等于球O 的半径，OK ＝32，且圆O 与圆K 所在的平面所成的一个二面角为60°，则球O 的表面积等于__________．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．(2013大纲全国，理17)(本小题满分10分)等差数列{a n }的前n 项和为S n .已知S 3＝22a ，且S 1，S 2，S 4成等比数列，求{a n }的通项公式．18．(2013大纲全国，理18)(本小题满分12分)设△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，(a ＋b ＋c )(a －b ＋c )＝ac . (1)求B ； (2)若sin A sin C＝14，求C .19．(2013大纲全国，理19)(本小题满分12分)如图，四棱锥P－ABCD中，∠ABC＝∠BAD＝90°，BC＝2AD，△PAB和△PAD都是等边三角形．(1)证明：PB⊥CD；(2)求二面角A－PD－C的大小．20．(2013大纲全国，理20)(本小题满分12分)甲、乙、丙三人进行羽毛球练习赛，其中两人比赛，另一人当裁判，每局比赛结束时，负的一方在下一局当裁判．设各局中双方获胜的概率均为12，各局比赛的结果相互独立，第1局甲当裁判．(1)求第4局甲当裁判的概率；(2)X表示前4局中乙当裁判的次数，求X的数学期望．21．(2013大纲全国，理21)(本小题满分12分)已知双曲线C：2222=1x ya b(a＞0，b＞0)的左、右焦点分别为F1，F2，离心率为3，直线y＝2与C.(1)求a，b；(2)设过F2的直线l与C的左、右两支分别交于A，B两点，且|AF1|＝|BF1|，证明：|AF2|，|AB|，|BF2|成等比数列．22．(2013大纲全国，理22)(本小题满分12分)已知函数f(x)＝1ln(1+)1x xxxλ(+)-+.(1)若x≥0时，f(x)≤0，求λ的最小值；(2)设数列{a n}的通项111=1+23nan+++，证明：a2n－a n＋14n＞ln 2.2013年普通高等学校夏季招生全国统一考试数学理工农医类(大纲全国卷)一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．答案：B解析：由题意知x ＝a ＋b ，a ∈A ，b ∈B ，则x 的可能取值为5,6,7,8.因此集合M 共有4个元素．故选B. 2．答案：A解析：323=13=8-.故选A.3．答案：B解析：由(m ＋n )⊥(m －n )⇒|m |2－|n |2＝0⇒(λ＋1)2＋1－[(λ＋2)2＋4]＝0⇒λ＝－3.故选B. 4．答案：B解析：由题意知－1＜2x ＋1＜0，则－1＜x ＜12-.故选B. 5．答案：A解析：由题意知11+x＝2y⇒x ＝121y -(y ＞0)，因此f －1(x )＝121x -(x ＞0)．故选A. 6．答案：C解析：∵3a n ＋1＋a n ＝0，∴a n ＋1＝13n a -.∴数列{a n }是以13-为公比的等比数列．∵a 2＝43-，∴a 1＝4. ∴S 10＝101413113⎡⎤⎛⎫--⎢⎥⎪⎝⎭⎢⎥⎣⎦+＝3(1－3－10)．故选C.7．答案：D解析：因为(1＋x )8的展开式中x 2的系数为28C ，(1＋y )4的展开式中y 2的系数为24C ，所以x 2y 2的系数为2284C C 168=.故选D. 8．答案：B解析：设P 点坐标为(x 0，y 0)，则2200=143x y +， 2002PA y k x =-，1002PA y k x =+，于是12220222003334244PA PA x y k k x x -⋅===---.故12314PA PA k k ＝－. ∵2PA k ∈[－2，－1]， ∴133,84PA k ⎡⎤∈⎢⎥⎣⎦.故选B.9．答案：D解析：由条件知f ′(x )＝2x ＋a －21x ≥0在1,2⎛⎫+∞ ⎪⎝⎭上恒成立，即212a x x ≥-在1,2⎛⎫+∞ ⎪⎝⎭上恒成立．∵函数212y x x =-在1,2⎛⎫+∞ ⎪⎝⎭上为减函数，∴max 211<23212y -⨯=⎛⎫⎪⎝⎭.∴a ≥3.故选D. 10．答案：A解析：如下图，连结AC 交BD 于点O ，连结C 1O ，过C 作CH ⊥C 1O 于点H .∵11BD ACBD AA AC AA A ⊥⎫⎪⊥⎬⎪=⎭1111BD ACC A CH ACC A ⊥⎫⎬⊂⎭平面平面11=CH BDCH C O BD C O O ⊥⎫⎪⊥⎬⎪⎭CH ⊥平面C 1BD ，∴∠HDC 为CD 与平面BDC 1所成的角．设AA 1＝2AB ＝2，则=2AC OC，1C O =由等面积法，得C 1O ·CH ＝OC ·CC 12CH ， ∴2=3CH . ∴sin ∠HDC ＝223==13HC DC .故选A.11．答案：D解析：由题意知抛物线C 的焦点坐标为(2,0)，则直线AB 的方程为y ＝k (x －2)，将其代入y 2＝8x ，得k 2x 2－4(k2＋2)x ＋4k 2＝0.设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2242k k (+)，x 1x 2＝4.①由112222y k x y k x =(-)⎧⎨=(-)⎩∵0MA MB ⋅=，∴(x 1＋2，y 1－2)·(x 2＋2，y 2－2)＝0. ∴(x 1＋2)(x 2＋2)＋(y 1－2)(y 2－2)＝0，即x 1x 2＋2(x 1＋x 2)＋4＋y 1y 2－2(y 1＋y 2)＋4＝0.④ 由①②③④解得k ＝2.故选D. 12．答案：C解析：由题意知f (x )＝2cos 2x ·sin x ＝2(1－sin 2x )sin x . 令t ＝sin x ，t ∈[－1,1]，则g (t )＝2(1－t 2)t ＝2t －2t 3. 令g ′(t )＝2－6t 2＝0，得=t ±. 当t ＝±1时，函数值为0；当t =；当t =.∴g (t )max ，即f (x )的最大值为9.故选C. 二、填空题：本大题共4小题，每小题5分．13．答案：解析：由题意知cos α＝3==-.故cot α＝cos sin αα14．答案：480解析：先排除甲、乙外的4人，方法有44A 种，再将甲、乙插入这4人形成的5个间隔中，有25A 种排法，因此甲、乙不相邻的不同排法有4245A A 480⋅=(种)．15．答案：1,42⎡⎤⎢⎥⎣⎦解析：作出题中不等式组表示的可行域如图中阴影部分所示． ∵直线y ＝a (x ＋1)过定点C (－1,0)，由图并结合题意可知12BC k =，k AC ＝4，∴要使直线y ＝a (x ＋1)与平面区域D 有公共点，则12≤a ≤4. 16．答案：16π解析：如下图，设MN 为两圆的公共弦，E 为MN 的中点，则OE ⊥MN ，KE ⊥MN ，结合题意可知∠OEK ＝60°.又MN ＝R ，∴△OMN 为正三角形．∴OE ＝2R .又OK ⊥EK ，∴32＝OE ·sin 60°＝22R ⋅∴R ＝2.∴S ＝4πR 2＝16π.三、解答题：解答应写出文字说明，证明过程或演算步骤．17．解：设{a n }的公差为d .由S 3＝22a 得3a 2＝22a ，故a 2＝0或a 2＝3. 由S 1，S 2，S 4成等比数列得22S ＝S 1S 4. 又S 1＝a 2－d ，S 2＝2a 2－d ，S 4＝4a 2＋2d ，故(2a 2－d )2＝(a 2－d )(4a 2＋2d )．若a 2＝0，则d 2＝－2d 2，所以d ＝0，此时S n ＝0，不合题意；若a 2＝3，则(6－d )2＝(3－d )(12＋2d )，解得d ＝0或d ＝2. 因此{a n }的通项公式为a n ＝3或a n ＝2n －1. 18．解：(1)因为(a ＋b ＋c )(a －b ＋c )＝ac ，所以a 2＋c 2－b 2＝－ac .由余弦定理得cos B ＝222122a cb ac +-=-，因此B ＝120°.(2)由(1)知A ＋C ＝60°，所以cos(A －C )＝cos A cos C ＋sin A sin C ＝cos A cos C －sin A sin C ＋2sin A sin C ＝cos(A ＋C )＋2sin A sin C＝11+2242⨯=，故A －C ＝30°或A －C ＝－30°，因此C ＝15°或C ＝45°. 19．(1)证明：取BC 的中点E ，连结DE ，则ABED 为正方形．过P 作PO ⊥平面ABCD ，垂足为O .连结OA ，OB ，OD ，OE .由△PAB 和△PAD 都是等边三角形知PA ＝PB ＝PD ，所以OA ＝OB ＝OD ，即点O 为正方形ABED 对角线的交点，故OE ⊥BD ，从而PB ⊥OE .因为O 是BD 的中点，E 是BC 的中点，所以OE ∥CD .因此PB ⊥CD .(2)解法一：由(1)知CD ⊥PB ，CD ⊥PO ，PB ∩PO ＝P ，故CD ⊥平面PBD .又PD ⊂平面PBD ，所以CD ⊥PD .取PD 的中点F ，PC 的中点G ，连结FG ，则FG ∥CD ，FG ⊥PD .连结AF ，由△APD 为等边三角形可得AF ⊥PD .所以∠AFG 为二面角A －PD －C 的平面角．连结AG ，EG ，则EG ∥PB .又PB ⊥AE ，所以EG ⊥AE .设AB ＝2，则AE ＝，EG ＝12PB ＝1，故AG 3.在△AFG 中，FG ＝12CD =，AF =AG ＝3，所以cos ∠AFG ＝22223FG AF AG FG AF +-=-⨯⨯因此二面角A －PD －C 的大小为π-解法二：由(1)知，OE ，OB ，OP 两两垂直．以O 为坐标原点，OE 的方向为x 轴的正方向建立如图所示的空间直角坐标系O －xyz .设|AB |＝2，则A (，0,0)，D (0，，0)，C (，0)，P (0,0)．PC ＝(，)，PD ＝(0，，)．AP ＝，0)，AD ＝，，0)．设平面PCD 的法向量为n 1＝(x ，y ，z )，则n 1·PC ＝(x ，y ，z )·(，)＝0，n 1·PD ＝(x ，y ，z )·(0，，)＝0，可得2x －y －z ＝0，y ＋z ＝0.取y ＝－1，得x ＝0，z ＝1，故n 1＝(0，－1,1)．设平面PAD 的法向量为n 2＝(m ，p ，q )，则n 2·AP ＝(m ，p ，q ，0)＝0，n 2·AD ＝(m ，p ，q ，，0)＝0，可得m＋q＝0，m－p＝0.取m＝1，得p＝1，q＝－1，故n2＝(1,1，－1)．于是cos〈n1，n2〉＝1212||||3=-·n nn n.由于〈n1，n2〉等于二面角A－PD－C的平面角，所以二面角A－PD－C的大小为π-20．解：(1)记A1表示事件“第2局结果为甲胜”，A2表示事件“第3局甲参加比赛时，结果为甲负”，A表示事件“第4局甲当裁判”．则A＝A1·A2.P(A)＝P(A1·A2)＝P(A1)P(A2)＝14.(2)X的可能取值为0,1,2.记A3表示事件“第3局乙和丙比赛时，结果为乙胜丙”，B1表示事件“第1局结果为乙胜丙”，B2表示事件“第2局乙和甲比赛时，结果为乙胜甲”，B3表示事件“第3局乙参加比赛时，结果为乙负”．则P(X＝0)＝P(B1·B2·A3)＝P(B1)P(B2)·P(A3)＝18，P(X＝2)＝P(1B·B3)＝P(1B)P(B3)＝14，P(X＝1)＝1－P(X＝0)－P(X＝2)＝1151848--=，EX＝0·P(X＝0)＋1·P(X＝1)＋2·P(X＝2)＝98.21．(1)解：由题设知ca＝3，即222a ba+＝9，故b2＝8a2.所以C的方程为8x2－y2＝8a2.将y＝2代入上式，求得x=由题设知，=a2＝1.所以a＝1，b＝(2)证明：由(1)知，F1(－3,0)，F2(3,0)，C的方程为8x2－y2＝8.①由题意可设l的方程为y＝k(x－3)，k(k2－8)x2－6k2x＋9k2＋8＝0.设A(x1，y1)，B(x2，y2)，则x1≤－1，x2≥1，x1＋x2＝2268kk-，x1·x2＝22988kk+-.于是|AF1|＝－(3x1＋1)，|BF1|3x2＋1.由|AF1|＝|BF1|得－(3x1＋1)＝3x2＋1，即x1＋x2＝23 -.故226283kk=--，解得k2＝45，从而x1·x2＝199-.由于|AF2|＝1－3x1，|BF2|3x2－1，故|AB|＝|AF2|－|BF2|＝2－3(x1＋x2)＝4，|AF2|·|BF2|＝3(x1＋x2)－9x1x2－1＝16. 因而|AF2|·|BF2|＝|AB|2，所以|AF2|，|AB|，|BF2|成等比数列．22．(1)解：由已知f(0)＝0，f′(x)＝22121x xxλλ(-)-(+)，f′(0)＝0.若12λ<，则当0＜x＜2(1－2λ)时，f′(x)＞0，所以f(x)＞0.若12λ≥，则当x＞0时，f′(x)＜0，所以当x＞0时，f(x)＜0.综上，λ的最小值是12.(2)证明：令12λ=.由(1)知，当x＞0时，f(x)＜0，即2ln(1) 22x xxx(+)>++．取1xk=，则211>ln21k kk k k++(+).于是212111 422(1)n n n k n a a n k k -=⎡⎤-+=+⎢⎥+⎣⎦∑ ＝2121211ln 21n n k n k n k k k k k --==++>(+)∑∑ ＝ln 2n －ln n ＝ln 2.所以21ln 24n n a a n-+>. 2013年普通高等学校夏季招生全国统一考试数学理工农医类(全国新课标卷I)第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2013课标全国Ⅰ，理1)已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |－5＜x ＜5}，则( )．A ．A ∩B ＝ B ．A ∪B ＝RC ．B ⊆AD ．A ⊆B2．(2013课标全国Ⅰ，理2)若复数z 满足(3－4i)z ＝|4＋3i|，则z 的虚部为( )．A ．－4B ．45-C ．4 D ．45 3．(2013课标全国Ⅰ，理3)为了解某地区的中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大．在下面的抽样方法中，最合理的抽样方法是( )．A ．简单随机抽样B ．按性别分层抽样C ．按学段分层抽样D ．系统抽样4．(2013课标全国Ⅰ，理4)已知双曲线C ：2222=1x y a b-(a ＞0，b ＞0)的离心率为52，则C 的渐近线方程为( )．A ．y ＝14x ±B ．y ＝13x ±C ．y ＝12x± D ．y ＝±x 5．(2013课标全国Ⅰ，理5)执行下面的程序框图，如果输入的t ∈[－1,3]，则输出的s 属于( )．A ．[－3,4]B ．[－5,2]C ．[－4,3]D ．[－2,5]6．(2013课标全国Ⅰ，理6)如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6 cm ，如果不计容器的厚度，则球的体积为( )．A ．500π3cm3B ．866π3cm3C ．1372π3cm3D ．2048π3cm37．(2013课标全国Ⅰ，理7)设等差数列{a n }的前n 项和为S n ，若S m －1＝－2，S m ＝0，S m ＋1＝3，则m ＝( )．A ．3B ．4C ．5D ．68．(2013课标全国Ⅰ，理8)某几何体的三视图如图所示，则该几何体的体积为( )．A ．16＋8πB ．8＋8πC ．16＋16πD ．8＋16π9．(2013课标全国Ⅰ，理9)设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m ＋1展开式的二项式系数的最大值为b .若13a ＝7b ，则m ＝( )．A ．5B ．6C ．7D ．8 10．(2013课标全国Ⅰ，理10)已知椭圆E ：2222=1x y a b+(a ＞b ＞0)的右焦点为F (3,0)，过点F 的直线交E 于A ，B 两点．若AB 的中点坐标为(1，－1)，则E 的方程为( )．A ．22=14536x y +B ．22=13627x y +C ．22=12718x y +D ．22=1189x y +11．(2013课标全国Ⅰ，理11)已知函数f (x )＝220ln(1)0.x x x x x ⎧-+≤⎨+>⎩，，，若|f (x )|≥ax ，则a 的取值范围是( )．A ．(－∞，0]B ．(－∞，1]C ．[－2,1]D ．[－2,0]12．(2013课标全国Ⅰ，理12)设△A n B n C n 的三边长分别为a n ，b n ，c n ，△A n B n C n 的面积为S n ，n ＝1,2,3，….若b 1＞c 1，b 1＋c 1＝2a 1，a n ＋1＝a n ，b n ＋1＝2n n c a +，c n ＋1＝2n n b a +，则( )． A ．{Sn}为递减数列 B ．{Sn}为递增数列C ．{S2n －1}为递增数列，{S2n}为递减数列D ．{S2n －1}为递减数列，{S2n}为递增数列第Ⅱ卷本卷包括必考题和选考题两部分．第(13)题～第(21)题为必考题，每个试题考生都必须做答．第(22)题～第(24)题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13．(2013课标全国Ⅰ，理13)已知两个单位向量a，b的夹角为60°，c＝ta＋(1－t)b.若b·c＝0，则t ＝__________.14．(2013课标全国Ⅰ，理14)若数列{an}的前n项和2133n nS a=+，则{an}的通项公式是an＝_______.15．(2013课标全国Ⅰ，理15)设当x＝θ时，函数f(x)＝sin x－2cos x取得最大值，则cos θ＝__________.16．(2013课标全国Ⅰ，理16)若函数f(x)＝(1－x2)(x2＋ax＋b)的图像关于直线x＝－2对称，则f(x)的最大值为__________．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．(2013课标全国Ⅰ，理17)(本小题满分12分)如图，在△ABC中，∠ABC＝90°，AB，BC＝1，P为△ABC内一点，∠BPC＝90°.(1)若PB＝12，求PA；(2)若∠APB＝150°，求tan∠PBA.18．(2013课标全国Ⅰ，理18)(本小题满分12分)如图，三棱柱ABC－A1B1C1中，CA＝CB，AB＝AA1，∠BAA1＝60°.(1)证明：AB⊥A1C；(2)若平面ABC⊥平面AA1B1B，AB＝CB，求直线A1C与平面BB1C1C所成角的正弦值．19．(2013课标全国Ⅰ，理19)(本小题满分12分)一批产品需要进行质量检验，检验方案是：先从这批产品中任取4件作检验，这4件产品中优质品的件数记为n.如果n＝3，再从这批产品中任取4件作检验，若都为优质品，则这批产品通过检验；如果n＝4，再从这批产品中任取1件作检验，若为优质品，则这批产品通过检验；其他情况下，这批产品都不能通过检验．假设这批产品的优质品率为50%，即取出的每件产品是优质品的概率都为12，且各件产品是否为优质品相互独立．(1)求这批产品通过检验的概率；(2)已知每件产品的检验费用为100元，且抽取的每件产品都需要检验，对这批产品作质量检验所需的费用记为X(单位：元)，求X的分布列及数学期望．20．(2013课标全国Ⅰ，理20)(本小题满分12分)已知圆M：(x＋1)2＋y2＝1，圆N：(x－1)2＋y2＝9，动圆P与圆M外切并且与圆N内切，圆心P的轨迹为曲线C.(1)求C的方程；(2)l是与圆P，圆M都相切的一条直线，l与曲线C交于A，B两点，当圆P的半径最长时，求|AB|.21．(2013课标全国Ⅰ，理21)(本小题满分12分)设函数f(x)＝x2＋ax＋b，g(x)＝e x(cx＋d)．若曲线y＝f(x)和曲线y＝g(x)都过点P(0,2)，且在点P处有相同的切线y＝4x＋2.(1)求a，b，c，d的值；(2)若x≥－2时，f(x)≤kg(x)，求k的取值范围．请考生在第(22)、(23)、(24)三题中任选一题做答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分，做答时请用2B铅笔在答题卡上将所选题号后的方框涂黑．22．(2013课标全国Ⅰ，理22)(本小题满分10分)选修4—1：几何证明选讲如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D.(1)证明：DB＝DC；(2)设圆的半径为1，BC CE交AB于点F，求△BCF外接圆的半径．23．(2013课标全国Ⅰ，理23)(本小题满分10分)选修4—4：坐标系与参数方程已知曲线C1的参数方程为45cos,55sinx ty t=+⎧⎨=+⎩(t为参数)，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ＝2sin θ.(1)把C1的参数方程化为极坐标方程；(2)求C1与C2交点的极坐标(ρ≥0,0≤θ＜2π)．24．(2013课标全国Ⅰ，理24)(本小题满分10分)选修4—5：不等式选讲：已知函数f(x)＝|2x－1|＋|2x＋a|，g(x)＝x＋3.(1)当a＝－2时，求不等式f(x)＜g(x)的解集；(2)设a＞－1，且当x∈1,22a⎡⎫-⎪⎢⎣⎭时，f(x)≤g(x)，求a的取值范围．2013年普通高等学校夏季招生全国统一考试数学理工农医类(全国卷I 新课标)第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．答案：B解析：∵x (x －2)＞0，∴x ＜0或x ＞2.∴集合A 与B 可用图象表示为：由图象可以看出A ∪B ＝R ，故选B.2．答案：D解析：∵(3－4i)z ＝|4＋3i|， ∴55(34i)34i 34i (34i)(34i)55z +===+--+. 故z 的虚部为45，选D. 3．答案：C 解析：因为学段层次差异较大，所以在不同学段中抽取宜用分层抽样．4．答案：C解析：∵c e a ==，∴22222254c a b e a a +===. ∴a 2＝4b 2，1=2b a ±. ∴渐近线方程为12b y x x a =±±. 5．答案：A解析：若t ∈[－1,1)，则执行s ＝3t ，故s ∈[－3,3)．若t ∈[1,3]，则执行s ＝4t －t 2，其对称轴为t ＝2.故当t ＝2时，s 取得最大值4.当t ＝1或3时，s 取得最小值3，则s ∈[3,4]．综上可知，输出的s ∈[－3,4]．故选A.6．答案：A解析：设球半径为R ，由题可知R ，R －2，正方体棱长一半可构成直角三角形，即△OBA 为直角三角形，如图．BC ＝2，BA ＝4，OB ＝R －2，OA ＝R ，由R 2＝(R －2)2＋42，得R ＝5，所以球的体积为34500π5π33=(cm 3)，故选A. 7．答案：C解析：∵S m －1＝－2，S m ＝0，S m ＋1＝3，∴a m ＝S m －S m －1＝0－(－2)＝2，a m ＋1＝S m ＋1－S m ＝3－0＝3.∴d ＝a m ＋1－a m ＝3－2＝1.∵S m ＝ma 1＋12m m (-)×1＝0，∴112m a -=-. 又∵a m ＋1＝a 1＋m ×1＝3，∴132m m --+=. ∴m ＝5.故选C.8．答案：A 解析：由三视图可知该几何体为半圆柱上放一个长方体，由图中数据可知圆柱底面半径r ＝2，长为4，在长方体中，长为4，宽为2，高为2，所以几何体的体积为πr 2×4×12＋4×2×2＝8π＋16.故选A. 9．答案：B解析：由题意可知，a ＝2C m m ，b ＝21C m m +，又∵13a ＝7b ，∴2!21!13=7!!!1!m m m m m m ()(+)⋅⋅(+)，即132171m m +=+.解得m ＝6.故选B. 10．答案：D解析：设A (x 1，y 1)，B (x 2，y 2)，∵A ，B 在椭圆上， ∴2211222222221,1,x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩①② ①－②，得1212121222=0x x x x y y y y a b(+)(-)(+)(-)+，即2121221212=y y y y b a x x x x (+)(-)-(+)(-)， ∵AB 的中点为(1，－1)，∴y 1＋y 2＝－2，x 1＋x 2＝2，而1212y y x x --＝k AB ＝011=312-(-)-，∴221=2b a . 又∵a 2－b 2＝9，∴a 2＝18，b 2＝9. ∴椭圆E 的方程为22=1189x y +.故选D. 11．答案：D解析：由y ＝|f (x )|的图象知：①当x ＞0时，y ＝ax 只有a ≤0时，才能满足|f (x )|≥ax ，可排除B ，C.②当x ≤0时，y ＝|f (x )|＝|－x 2＋2x |＝x 2－2x .故由|f (x )|≥ax 得x 2－2x ≥ax .当x ＝0时，不等式为0≥0成立．当x ＜0时，不等式等价于x －2≤a .∵x －2＜－2，∴a ≥－2.综上可知：a ∈[－2,0]．12．答案：B第Ⅱ卷本卷包括必考题和选考题两部分．第(13)题～第(21)题为必考题，每个试题考生都必须做答．第(22)题～第(24)题为选考题，考生根据要求做答．二、填空题：本大题共4小题，每小题5分．13．答案：2解析：∵c ＝t a ＋(1－t )b ，∴b ·c ＝t a ·b ＋(1－t )|b |2.又∵|a |＝|b |＝1，且a 与b 夹角为60°，b ⊥c ，∴0＝t |a ||b |cos 60°＋(1－t )，0＝12t ＋1－t . ∴t ＝2.14．答案：(－2)n －1 解析：∵2133n n S a =+，① ∴当n ≥2时，112133n n S a --=+.② ①－②，得12233n n n a a a -=-，即1n n a a -＝－2. ∵a 1＝S 1＝12133a +， ∴a 1＝1. ∴{a n }是以1为首项，－2为公比的等比数列，a n ＝(－2)n －1. 15．答案：5- 解析：f (x )＝sin x －2cos xx x ⎫⎪⎭，令cos αsin α＝则f (x )α＋x )，当x ＝2k π＋π2－α(k ∈Z )时，sin(α＋x )有最大值1，f (x ) 即θ＝2k π＋π2－α(k ∈Z )，所以cos θ＝πcos 2π+2k α⎛⎫- ⎪⎝⎭＝πcos 2α⎛⎫- ⎪⎝⎭＝sin α＝5=-. 16．答案：16解析：∵函数f (x )的图像关于直线x ＝－2对称，∴f (x )满足f (0)＝f (－4)，f (－1)＝f (－3)，即15164,0893,b a b a b =-(-+)⎧⎨=-(-+)⎩解得8,15.a b =⎧⎨=⎩∴f (x )＝－x 4－8x 3－14x 2＋8x ＋15.由f ′(x )＝－4x 3－24x 2－28x ＋8＝0，得x 1＝－2x 2＝－2，x 3＝－2易知，f (x )在(－∞，－2上为增函数，在(－2，－2)上为减函数，在(－2，－2)上为增函数，在(－2∴f (－2＝[1－(－22][(－2)2＋8(－2＋15]＝(－8－－＝80－64＝16.f (－2)＝[1－(－2)2][(－2)2＋8×(－2)＋15]＝－3(4－16＋15)＝－9.f (－2＝[1－(－22][(－22＋8(－2)＋15]＝(－8＋＋＝80－64＝16.故f (x )的最大值为16.三、解答题：解答应写出文字说明，证明过程或演算步骤．17．解：(1)由已知得∠PBC ＝60°，所以∠PBA ＝30°.在△PBA 中，由余弦定理得PA 2＝11732cos 30424+-︒=. 故PA＝2. (2)设∠PBA ＝α，由已知得PB ＝sin α.在△PBA中，由正弦定理得sin sin150sin(30)αα=︒︒-，cos α＝4sin α.所以tan α＝4，即tan ∠PBA＝4. 18． (1)证明：取AB 的中点O ，连结OC ，OA 1，A 1B .因为CA ＝CB ，所以OC ⊥AB .由于AB ＝AA 1，∠BAA 1＝60°，故△AA 1B 为等边三角形，所以OA 1⊥AB .因为OC ∩OA 1＝O ，所以AB ⊥平面OA 1C .又A 1C ⊂平面OA 1C ，故AB ⊥A 1C .(2)解：由(1)知OC ⊥AB ，OA 1⊥AB .又平面ABC ⊥平面AA 1B 1B ，交线为AB ，所以OC ⊥平面AA 1B 1B ，故OA ，OA 1，OC 两两相互垂直．以O 为坐标原点，OA 的方向为x 轴的正方向，|OA |为单位长，建立如图所示的空间直角坐标系O －xyz . 由题设知A (1,0,0)，A 1(0，0)，C (0,0，B (－1,0,0)．则BC ＝(1,0，1BB ＝1AA ＝(－10)，1AC ＝(0，．设n ＝(x ，y ，z )是平面BB 1C 1C 的法向量，则10,0,BC BB ⎧⋅=⎪⎨⋅=⎪⎩n n即0,0.x x ⎧+=⎪⎨-+=⎪⎩可取n ＝，1，－1)．故cos 〈n ，1AC 〉＝11A CA C⋅n n ＝. 所以A 1C 与平面BB 1C 1C 19．解：(1)设第一次取出的4件产品中恰有3件优质品为事件A 1，第一次取出的4件产品全是优质品为事件A 2，第二次取出的4件产品都是优质品为事件B 1，第二次取出的1件产品是优质品为事件B 2，这批产品通过检验为事件A ，依题意有A ＝(A 1B 1)∪(A 2B 2)，且A 1B 1与A 2B 2互斥，所以P (A )＝P (A 1B 1)＋P (A 2B 2)＝P (A 1)P (B 1|A 1)＋P (A 2)P (B 2|A 2)＝41113161616264⨯+⨯=. (2)X 可能的取值为400,500,800，并且 P (X ＝400)＝41111161616--=，P (X ＝500)＝116，P (X ＝800)＝14. 所以X 的分布列为EX ＝1111400+500+80016164⨯⨯⨯＝506.25. 20．解：由已知得圆M 的圆心为M (－1,0)，半径r 1＝1；圆N 的圆心为N (1,0)，半径r 2＝3.设圆P 的圆心为P (x ，y )，半径为R .(1)因为圆P 与圆M 外切并且与圆N 内切，所以|PM |＋|PN |＝(R ＋r 1)＋(r 2－R )＝r 1＋r 2＝4.由椭圆的定义可知，曲线C 是以M ，N 为左、右焦点，长半轴长为2的椭圆(左顶点除外)，其方程为22=143x y +(x ≠－2)． (2)对于曲线C 上任意一点P (x ，y )，由于|PM |－|PN |＝2R －2≤2，所以R ≤2，当且仅当圆P 的圆心为(2,0)时，R ＝2.所以当圆P 的半径最长时，其方程为(x －2)2＋y 2＝4.若l 的倾斜角为90°，则l 与y 轴重合，可得|AB |＝若l 的倾斜角不为90°，由r 1≠R 知l 不平行于x 轴，设l 与x 轴的交点为Q ，则1||||QP R QM r =，可求得Q (－4,0)，所以可设l ：y ＝k (x ＋4)．由l 与圆M，解得k＝4±. 当k＝4时，将4y x =代入22=143x y +，并整理得7x 2＋8x －8＝0，解得x 1,2＝47-±. 所以|AB |2118|7x x -=.当k =时，由图形的对称性可知|AB |＝187. 综上，|AB |＝|AB |＝187. 21．解：(1)由已知得f (0)＝2，g (0)＝2，f ′(0)＝4，g ′(0)＝4.而f ′(x )＝2x ＋a ，g ′(x )＝e x (cx ＋d ＋c )，故b ＝2，d ＝2，a ＝4，d ＋c ＝4.从而a ＝4，b ＝2，c ＝2，d ＝2.(2)由(1)知，f (x )＝x 2＋4x ＋2，g (x )＝2e x (x ＋1)．设函数F (x )＝kg (x )－f (x )＝2k e x (x ＋1)－x 2－4x －2，则F ′(x )＝2k e x (x ＋2)－2x －4＝2(x ＋2)(k e x－1)．由题设可得F (0)≥0，即k ≥1.令F ′(x )＝0得x 1＝－ln k ，x 2＝－2.①若1≤k ＜e 2，则－2＜x 1≤0.从而当x ∈(－2，x 1)时，F ′(x )＜0；当x ∈(x 1，＋∞)时，F ′(x )＞0.即F (x )在(－2，x 1)单调递减，在(x 1，＋∞)单调递增．故F (x )在[－2，＋∞)的最小值为F (x 1)．而F (x 1)＝2x 1＋2－21x －4x 1－2＝－x 1(x 1＋2)≥0.故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．②若k＝e2，则F′(x)＝2e2(x＋2)(e x－e－2)．从而当x＞－2时，F′(x)＞0，即F(x)在(－2，＋∞)单调递增．而F(－2)＝0，故当x≥－2时，F(x)≥0，即f(x)≤kg(x)恒成立．③若k＞e2，则F(－2)＝－2k e－2＋2＝－2e－2(k－e2)＜0.从而当x≥－2时，f(x)≤kg(x)不可能恒成立．综上，k的取值范围是[1，e2]．请考生在第(22)、(23)、(24)三题中任选一题做答．注意：只能做所选定的题目．如果多做，则按所做的第一个题目计分，做答时请用2B铅笔在答题卡上将所选题号后的方框涂黑．22．(1)证明：连结DE，交BC于点G.由弦切角定理得，∠ABE＝∠BCE.而∠ABE＝∠CBE，故∠CBE＝∠BCE，BE＝CE.又因为DB⊥BE，所以DE为直径，∠DCE＝90°，由勾股定理可得DB＝DC.(2)解：由(1)知，∠CDE＝∠BDE，DB＝DC，故DG是BC的中垂线，所以BG＝2.设DE的中点为O，连结BO，则∠BOG＝60°.从而∠ABE＝∠BCE＝∠CBE＝30°，所以CF⊥BF，故Rt△BCF外接圆的半径等于2.23．解：(1)将45cos,55sinx ty t=+⎧⎨=+⎩消去参数t，化为普通方程(x－4)2＋(y－5)2＝25，即C1：x2＋y2－8x－10y＋16＝0.将cos,sinxyρθρθ=⎧⎨=⎩代入x2＋y2－8x－10y＋16＝0得ρ2－8ρcos θ－10ρsin θ＋16＝0. 所以C1的极坐标方程为ρ2－8ρcos θ－10ρsin θ＋16＝0.(2)C 2的普通方程为x 2＋y 2－2y ＝0. 由2222810160,20x y x y x y y ⎧+--+=⎨+-=⎩ 解得1,1x y =⎧⎨=⎩或0,2.x y =⎧⎨=⎩所以C 1与C 2交点的极坐标分别为π4⎫⎪⎭，π2,2⎛⎫ ⎪⎝⎭. 24．解：(1)当a ＝－2时，不等式f (x )＜g (x )化为|2x －1|＋|2x －2|－x －3＜0. 设函数y ＝|2x －1|＋|2x －2|－x －3，则y ＝15,,212,1,236, 1.x x x x x x ⎧-<⎪⎪⎪--≤≤⎨⎪->⎪⎪⎩其图像如图所示．从图像可知，当且仅当x ∈(0,2)时，y ＜0.所以原不等式的解集是{x |0＜x ＜2}．(2)当x ∈1,22a ⎡⎫-⎪⎢⎣⎭时，f (x )＝1＋a . 不等式f (x )≤g (x )化为1＋a ≤x ＋3.所以x ≥a －2对x ∈1,22a ⎡⎫-⎪⎢⎣⎭都成立．故2a -≥a －2，即43a ≤. 从而a 的取值范围是41,3⎛⎤- ⎥⎝⎦. 2013年普通高等学校夏季招生全国统一考试数学理工农医类(全国新课标卷II)第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．(2013课标全国Ⅱ，理1)已知集合M ＝{x |(x －1)2＜4，x ∈R }，N ＝{－1,0,1,2,3}，则M ∩N ＝( )．A ．{0,1,2}B ．{－1,0,1,2}C ．{－1,0,2,3}D ．{0,1,2,3} 2．(2013课标全国Ⅱ，理2)设复数z 满足(1－i)z ＝2i ，则z ＝( )．A ．－1＋iB ．－1－IC ．1＋iD ．1－i3．(2013课标全国Ⅱ，理3)等比数列{a n }的前n 项和为S n .已知S 3＝a 2＋10a 1，a 5＝9，则a 1＝( )．A ．13B ．13-C ．19D ．19-4．(2013课标全国Ⅱ，理4)已知m ，n 为异面直线，m ⊥平面α，n ⊥平面β.直线l 满足l ⊥m ，l ⊥n ，lα，l β，则( )．A ．α∥β且l ∥αB ．α⊥β且l ⊥βC ．α与β相交，且交线垂直于lD ．α与β相交，且交线平行于l5．(2013课标全国Ⅱ，理5)已知(1＋ax )(1＋x )5的展开式中x 2的系数为5，则a ＝( )．A ．－4B ．－3C ．－2D ．－16．(2013课标全国Ⅱ，理6)执行下面的程序框图，如果输入的N ＝10，那么输出的S ＝( )．A ．1111+2310+++B ．1111+2!3!10!+++C ．1111+2311+++D ．1111+2!3!11!+++7．(2013课标全国Ⅱ，理7)一个四面体的顶点在空间直角坐标系O －xyz 中的坐标分别是(1,0,1)，(1,1,0)，(0,1,1)，(0,0,0)，画该四面体三视图中的正视图时，以zOx 平面为投影面，则得到的正视图可以为( )． 8．(2013课标全国Ⅱ，理8)设a ＝log 36，b ＝log 510，c ＝log 714，则( )．A ．c ＞b ＞aB ．b ＞c ＞aC ．a ＞c ＞bD ．a ＞b ＞c9．(2013课标全国Ⅱ，理9)已知a ＞0，x ，y 满足约束条件1,3,3.x x y y a x ≥⎧⎪+≤⎨⎪≥(-)⎩若z ＝2x ＋y 的最小值为1，则a ＝( )．A．14 B．12 C．1 D．210．(2013课标全国Ⅱ，理10)已知函数f(x)＝x3＋ax2＋bx＋c，下列结论中错误的是( )．A．∃x0∈R，f(x0)＝0B．函数y＝f(x)的图像是中心对称图形C．若x0是f(x)的极小值点，则f(x)在区间(－∞，x0)单调递减D．若x0是f(x)的极值点，则f′(x0)＝011．(2013课标全国Ⅱ，理11)设抛物线C：y2＝2px(p＞0)的焦点为F，点M在C上，|MF|＝5，若以MF为直径的圆过点(0,2)，则C的方程为( )．A．y2＝4x或y2＝8x B．y2＝2x或y2＝8xC．y2＝4x或y2＝16x D．y2＝2x或y2＝16x12．(2013课标全国Ⅱ，理12)已知点A(－1,0)，B(1,0)，C(0,1)，直线y＝ax＋b(a＞0)将△ABC分割为面积相等的两部分，则b的取值范围是( )．A．(0,1) B．1122⎛⎫-⎪⎪⎝⎭ C．1123⎛⎤-⎥⎝⎦ D．11,32⎡⎫⎪⎢⎣⎭第Ⅱ卷本卷包括必考题和选考题两部分，第13题～第21题为必考题，每个试题考生都必须做答。

历年高考数学真题(全国卷整理版)完整版完整版

参考公式：如果事件 A、B互斥，那么球的表面积公式P( A B) P( A) P(B)S 4R2如果事件 A、B相互独立，那么其中 R表示球的半径P(A B) P( A) P(B)球的体积公式如果事件 A 在一次试验中发生的概率是p ，那么V3R3n 次独立重复试验中事件 A 恰好发生k次的概率4其中 R 表示球的半径P n (k ) C n k p k (1 p)n k (k 0,1,2, n)普通高等学校招生全国统一考试一、选择题13i 1、复数i =1A 2+I B2-I C 1+2i D 1- 2i2、已知集合 A ＝{1.3.m }，B＝{1，m} ,A B ＝ A, 则 m=A0或3 B 0或3C1或3 D 1或33椭圆的中心在原点，焦距为 4 一条准线为 x=-4 ，则该椭圆的方程为A x2y2=1Bx2y2=1 16++12128C x2y2=1Dx2y28+12+=1 444已知正四棱柱ABCD- A 1B 1C1D1中，AB=2 ，CC1= 2 2 E 为 CC1的中点，则直线 AC 1与平面 BED 的距离为A2B3C2D1（5）已知等差数列{a n} 的前 n 项和为 S n， a5=5， S5=15，则数列的前100项和为10099(C)99101(A)(B)(D)100101101100（6）△ ABC 中， AB 边的高为 CD ，若a· b=0， |a|=1， |b|=2，则(A)（B）(C)(D)3（7）已知α为第二象限角，sinα＋ sinβ =3，则 cos2α = 5555--(C) 9(D)3(A)3（B）9（8）已知 F1、 F2 为双曲线 C： x2-y2=2的左、右焦点，点P 在 C 上， |PF1|=|2PF2|，则 cos ∠F1PF2=1334(A) 4（B）5(C)4(D)51（9）已知 x=ln π， y=log52 ，z=e2，则(A)x ＜ y＜ z（B）z＜x＜y(C)z ＜ y＜ x(D)y ＜ z＜ x(10) 已知函数y＝ x2-3x+c 的图像与 x 恰有两个公共点，则c＝（A ）-2 或 2 （B）-9 或 3 （C）-1 或 1 （D）-3 或 1（11）将字母 a,a,b,b,c,c,排成三行两列，要求每行的字母互不相同，梅列的字母也互不相同，则不同的排列方法共有（A）12 种（ B）18 种（ C）24 种（ D）36 种7（12）正方形 ABCD 的边长为1，点 E 在边 AB 上，点 F 在边 BC 上， AE ＝ BF ＝3。

(word完整版)历年高考数学真题(全国卷整理版)43964.doc

实用文档参考公式：如果事件 A、B互斥，那么P( A B) P( A)P( B)如果事件 A、B相互独立，那么P(AgB)P( A)gP( B)如果事件 A 在一次试验中发生的概率是p ，那么n 次独立重复试验中事件 A 恰好发生 k 次的概率P n (k ) C n k p k (1 p)n k (k 0,1,2,⋯n) 球的表面积公式S 4R2其中 R 表示球的半径球的体积公式V 3 R34其中 R表示球的半径普通高等学校招生全国统一考试一、选择题1、复数 1 3i =1 iA 2+IB 2-IC 1+2iD 1- 2i2、已知集合 A＝ {1.3. m }，B＝{1，m} ,A U B＝A, 则 m=A 0 或3B 0 或 3C 1或3D 1 或 33 椭圆的中心在原点，焦距为4 一条准线为 x=-4 ，则该椭圆的方程为A x2 + y2 =1B x2 + y2 =116 12 12 8C x2 + y2 =1D x2 + y2 =18 4 12 44 已知正四棱柱ABCD- A1B1C1D1中， AB=2， CC= 2 2 E 为 CC的中点，则直线AC与平面1 1 1 BED的距离为A 2B 3C 2D 1（5）已知等差数列{a n} 的前 n 项和为 S n，a5=5， S5=15，则数列的前100项和为(A) 100(B)99(C)99(D)101 101101100100（6）△ ABC中， AB边的高为 CD，若a· b=0， |a|=1 ， |b|=2 ，则(A)（ B）(C)(D)3（7）已知α为第二象限角， sin α＋ sin β =3，则 cos2α =555 5--9(D) 3(A) 3 （B ） 9 (C)（8）已知 F1、 F2 为双曲线 C ： x2 -y 2 =2 的左、右焦点，点 P 在 C 上， |PF1|=|2PF2| ，则 cos ∠ F1PF2=1 334(A) 4（ B ） 5(C)4(D)51（ 9）已知 x=ln π， y=log52 ， z=e 2，则 (A)x ＜ y ＜ z （ B ） z ＜ x ＜y (C)z ＜ y ＜ x (D)y＜ z ＜ x(10) 已知函数 y ＝ x2 -3x+c 的图像与 x 恰有两个公共点，则 c ＝（A ） -2 或 2 （ B ） -9 或 3 （C ） -1 或 1 （ D ）-3 或 1（ 11）将字母 a,a,b,b,c,c, 排成三行两列，要求每行的字母互不相同，梅列的字母也互不相同，则不同的排列方法共有（ A ） 12 种（ B ） 18 种（ C ） 24 种（ D ） 36 种7（12）正方形 ABCD 的边长为 1，点 E 在边 AB 上，点 F 在边 BC 上， AE ＝ BF ＝ 3。

历年高考数学试题及答案word

历年高考数学试题及答案word 以下是历年高考数学试题及答案的格式示例：
一、选择题（每题4分，共40分）
1. 若函数f(x)=x^2+2x+1，则f(-1)的值为（）
A. 0
B. 1
C. 2
D. 3
答案：B
2. 已知数列{an}满足a1=1，an+1=2an+1，求a3的值为（）
A. 5
B. 7
C. 9
D. 11
答案：A
二、填空题（每题4分，共20分）
3. 函数y=x^3-3x在区间（-1，1）上的单调性为（）。

答案：单调递减
4. 已知向量a=(1,2)，b=(2,-1)，则|a+b|的值为（）。

答案：√5
三、解答题（共40分）
5. 已知函数f(x)=x^2-4x+3，求函数的零点。

答案：函数的零点为x=1和x=3。

6. 已知直线l的方程为y=2x+1，求直线l与x轴的交点坐标。

答案：直线l与x轴的交点坐标为(-1/2, 0)。

结束语：以上为历年高考数学试题及答案的示例，希望对同学们的复
习有所帮助。

在实际考试中，题目的难度和类型可能会有所不同，但
解题的基本方法和思路是相通的。

建议同学们在复习过程中多做练习，掌握各种题型的解题技巧，提高解题速度和准确率。

同时，也要注意
培养良好的考试心态，保持冷静和自信，相信自己能够取得理想的成绩。

北京历年高考试卷真题数学

北京历年高考试卷真题数学【试卷说明】本试卷包含选择题、填空题和解答题，旨在全面考察学生对高中数学知识的掌握和运用能力。

考生需在规定时间内完成所有题目。

【第一部分：选择题】1. 若函数$ f(x) = 3x^2 - 2x + 1 $，求$ f(-1) $的值。

A. 0B. 4C. 6D. 82. 已知集合A={1, 2, 3}，B={2, 3, 4}，求A∩B。

A. {1}B. {2, 3}C. {3, 4}D. {1, 2}3. 根据题目所给的三角函数关系，求$ \sin(60^\circ) $的值。

A. $ \frac{1}{2} $B. $ \frac{\sqrt{2}}{2} $C. $ \frac{\sqrt{3}}{2} $D. 14. 若$ a $，$ b $，$ c $为实数，且$ a^2 + b^2 = c^2 $，则下列哪个选项是正确的？A. $ a $，$ b $，$ c $成等差数列B. $ a $，$ b $，$ c $成等比数列C. $ a $，$ b $，$ c $可以构成直角三角形的边长D. 以上都不是【第二部分：填空题】5. 若$ \cos(\alpha) = \frac{3}{5} $，$ \alpha $在第一象限，求$ \sin(\alpha) $的值。

6. 已知数列$ \{a_n\} $满足$ a_1 = 1 $，$ a_{n+1} = a_n + 2n $，求$ a_3 $的值。

7. 若直线$ y = 2x + 3 $与$ x $轴相交，求交点坐标。

8. 已知圆的方程为$ (x - 2)^2 + (y - 3)^2 = 9 $，求圆心坐标。

【第三部分：解答题】9. 证明：若$ n $为正整数，$ 1^n + 2^n + 3^n + ... + n^n $是$ n $的倍数。

历年(2019-2024)全国高考数学真题分类(数列、函数与集合新定义)汇编(附答案)

历年(2019-2024)全国高考数学真题分类(数列、函数与集合新定义)汇编考点01 数列新定义一、小题1．（2021∙全国新Ⅱ卷∙高考真题）（多选）设正整数010112222k kk k n a a a a --=⋅+⋅++⋅+⋅ ，其中{}0,1i a ∈，记()01k n a a a ω=+++ ．则（） A ．()()2n n ωω= B ．()()231n n ωω+=+C ．()()8543n n ωω+=+D ．()21nn ω-=2．（2020∙全国新Ⅱ卷∙高考真题）0‐1周期序列在通信技术中有着重要应用.若序列12n a a a 满足{0,1}(1,2,)i a i ∈= ，且存在正整数m ，使得(1,2,)i m i a a i +== 成立，则称其为0‐1周期序列，并称满足(1,2,)i m i a a i +== 的最小正整数m 为这个序列的周期.对于周期为m 的0‐1序列12n a a a ，11()(1,2,,1)m i i k i C k a a k m m +===-∑ 是描述其性质的重要指标，下列周期为5的0‐1序列中，满足1()(1,2,3,4)5C k k ≤=的序列是（） A ．11010 B ．11011C ．10001D ．11001二、大题1．（2024∙全国新Ⅰ卷∙高考真题）设m 为正整数，数列1242,,...,m a a a +是公差不为0的等差数列，若从中删去两项i a 和()j a i j <后剩余的4m 项可被平均分为m 组，且每组的4个数都能构成等差数列，则称数列1242,,...,m a a a +是(),i j -可分数列．(1)写出所有的(),i j ，16i j ≤<≤，使数列126,,...,a a a 是(),i j -可分数列； (2)当3m ≥时，证明：数列1242,,...,m a a a +是()2,13-可分数列；(3)从1,2,...,42m +中一次任取两个数i 和()j i j <，记数列1242,,...,m a a a +是(),i j -可分数列的概率为m P ，证明：18m P >． 2．（2024∙北京∙高考真题）已知集合(){}{}{}{}{},,,1,2,3,4,5,6,7,8,M i j k w i j k w i j k w =∈∈∈∈+++且为偶数．给定数列128:,,,A a a a ，和序列12:,,s T T T Ω ，其中()(),,,1,2,,t t t t t T i j k w M t s =∈= ，对数列A 进行如下变换：将A 的第1111,,,i j k w 项均加1，其余项不变，得到的数列记作()1T A ；将()1T A 的第2222,,,i j k w 项均加1，其余项不变，得到数列记作()21T T A ；……；以此类推，得到()21s T T T A ，简记为()A Ω．(1)给定数列:1,3,2,4,6,3,1,9A 和序列()()():1,3,5,7,2,4,6,8,1,3,5,7Ω，写出()A Ω；(2)是否存在序列Ω，使得()A Ω为123456782,6,4,2,8,2,4,4a a a a a a a a ++++++++，若存在，写出一个符合条件的Ω；若不存在，请说明理由；(3)若数列A 的各项均为正整数，且1357a a a a +++为偶数，求证：“存在序列Ω，使得()A Ω的各项都相等”的充要条件为“12345678a a a a a a a a +=+=+=+”．3．（2023∙北京∙高考真题）已知数列{}{},n n a b 的项数均为m (2)m >，且,{1,2,,},n n a b m ∈ {}{},n n a b 的前n项和分别为,n n A B ，并规定000A B ==．对于{}0,1,2,,k m ∈ ，定义{}max ,{0,1,2,,}k i k r iB A i m =≤∈∣ ，其中，max M 表示数集M 中最大的数.(1)若1231232,1,3,1,3,3a a a b b b ======，求0123,,,r r r r 的值； (2)若11a b ≥，且112,1,2,,1,j j j r r r j m +-≤+=- ，求n r ；(3)证明：存在{},,,0,1,2,,p q s t m ∈ ，满足,,p q s t >> 使得t p s q A B A B +=+．4．（2022∙北京∙高考真题）已知12:,,,k Q a a a 为有穷整数数列．给定正整数m ，若对任意的{1,2,,}n m ∈ ，在Q 中存在12,,,,(0)i i i i j a a a a j +++≥ ，使得12i i i i j a a a a n +++++++= ，则称Q 为m -连续可表数列． (1)判断:2,1,4Q 是否为5-连续可表数列？是否为6-连续可表数列？说明理由； (2)若12:,,,k Q a a a 为8-连续可表数列，求证：k 的最小值为4；(3)若12:,,,k Q a a a 为20-连续可表数列，且1220k a a a +++< ，求证：7k ≥．5．（2021∙北京∙高考真题）设p 为实数.若无穷数列{}n a 满足如下三个性质，则称{}n a 为p ℜ数列：①10a p +≥，且20a p +=； ②414,1,2,n n a a n -<=⋅⋅⋅()；③{},1m n m n m n a a a p a a p +∈+++++，(),1,2,m n =⋅⋅⋅．（1）如果数列{}n a 的前4项为2，‐2，‐2，‐1，那么{}n a 是否可能为2ℜ数列？说明理由；（2）若数列{}n a 是0ℜ数列，求5a ；（3）设数列{}n a 的前n 项和为n S .是否存在p ℜ数列{}n a ，使得10n S S ≥恒成立？如果存在，求出所有的p ；如果不存在，说明理由．6．（2020∙北京∙高考真题）已知{}n a 是无穷数列．给出两个性质：①对于{}n a 中任意两项,()i j a a i j >，在{}n a 中都存在一项m a ，使2i m ja a a =；②对于{}n a 中任意项(3)n a n …，在{}n a 中都存在两项,()k l a a k l >．使得2k n l a a a =． ()Ⅰ若(1,2,)n a n n == ，判断数列{}n a 是否满足性质①，说明理由；()Ⅱ若12(1,2,)n n a n -== ，判断数列{}n a 是否同时满足性质①和性质②，说明理由；()Ⅲ若{}n a 是递增数列，且同时满足性质①和性质②，证明：{}n a 为等比数列.7．（2020∙江苏∙高考真题）已知数列{}*()∈n a n N 的首项a 1=1，前n 项和为Sn ．设λ与k 是常数，若对一切正整数n ，均有11111k k k n n n S S a λ++-=成立，则称此数列为“λ~k ”数列．（1）若等差数列{}n a 是“λ~1”数列，求λ的值；（2）若数列{}n a 是2”数列，且an ＞0，求数列{}n a 的通项公式；（3）对于给定的λ，是否存在三个不同的数列{}n a 为“λ~3”数列，且an ≥0?若存在，求λ的取值范围；若不存在，说明理由，8．（2019∙江苏∙高考真题）定义首项为1且公比为正数的等比数列为“M －数列”. （1）已知等比数列{a n }满足：245132,440a a a a a a =-+=，求证:数列{a n }为“M －数列”；（2）已知数列{b n }满足:111221,n n n b S b b +==-，其中S n 为数列{b n }的前n 项和． ①求数列{b n }的通项公式；②设m 为正整数，若存在“M －数列”{c n }，对任意正整数k ，当k ≤m 时，都有1k k k c b c +≤≤成立，求m 的最大值．考点02 函数新定义一、大题1．（2024∙上海∙高考真题）对于一个函数()f x 和一个点(),M a b ，令()()22()()s x x a f x b =-+-，若()()00,P x f x 是()s x 取到最小值的点，则称P 是M 在()f x 的“最近点”．(1)对于1()(0)f x x x=>，求证：对于点()0,0M ，存在点P ，使得点P 是M 在()f x 的“最近点”； (2)对于()()e ,1,0xf x M =，请判断是否存在一个点P ，它是M 在()f x 的“最近点”，且直线MP 与()y f x =在点P 处的切线垂直；(3)已知()y f x =在定义域R 上存在导函数()f x '，且函数 ()g x 在定义域R 上恒正，设点()()()11,M t f t g t --，()()()21,M t f t g t ++．若对任意的t ∈R ，存在点P 同时是12,M M 在()f x 的“最近点”，试判断()f x 的单调性．2．（2020∙江苏∙高考真题）已知关于x 的函数(),()y f x y g x ==与()(,)h x kx b k b =+∈R 在区间D 上恒有()()()f x h x g x ≥≥．（1）若()()2222()f x x x g x x x D =+=-+=-∞+∞，，，，求h (x )的表达式；（2）若2()1()ln (),(0)f x x x g x k x h x kx k D =-+==-=+∞，，，，求k 的取值范围；（3）若()()()()422342248432(0f x x x g x x h x t t x t t t =-=-=--+<≤，，，[],D m n ⎡=⊆⎣，求证：n m -≤．考点03 集合新定义一、小题1．（2020∙浙江∙高考真题）设集合S，T，S⊆N*，T⊆N*，S，T中至少有两个元素，且S，T满足： ①对于任意x，y∈S，若x≠y，都有xy∈T②对于任意x，y∈T，若x<y，则yx∈S；下列命题正确的是（）A．若S有4个元素，则S∪T有7个元素B．若S有4个元素，则S∪T有6个元素C．若S有3个元素，则S∪T有5个元素D．若S有3个元素，则S∪T有4个元素考点04 其他新定义1．（2020∙北京∙高考真题）2020年3月14日是全球首个国际圆周率日（π Day）．历史上，求圆周率π的方法有多种，与中国传统数学中的“割圆术”相似．数学家阿尔∙卡西的方法是：当正整数n充分大时，计算单位圆的内接正6n边形的周长和外切正6n边形（各边均与圆相切的正6n边形）的周长，将它们的算术平均数作为2π的近似值．按照阿尔∙卡西的方法，π的近似值的表达式是（）．A．30303sin tannn n︒︒⎛⎫+⎪⎝⎭B．30306sin tannn n︒︒⎛⎫+⎪⎝⎭C．60603sin tannn n︒︒⎛⎫+⎪⎝⎭D．60606sin tannn n︒︒⎛⎫+⎪⎝⎭参考答案考点01 数列新定义一、小题1．（2021∙全国新Ⅱ卷∙高考真题）（多选）设正整数010112222k kk k n a a a a --=⋅+⋅++⋅+⋅ ，其中{}0,1i a ∈，记()01k n a a a ω=+++ ．则（） A ．()()2n n ωω= B ．()()231n n ωω+=+C ．()()8543n n ωω+=+D ．()21nn ω-=【答案】ACD【详细分析】利用()n ω的定义可判断ACD 选项的正误，利用特殊值法可判断B 选项的正误.【答案详解】对于A 选项，()01k n a a a ω=+++ ，12101122222k k k k n a a a a +-=⋅+⋅++⋅+⋅ ，所以，()()012k n a a a n ωω=+++= ，A 选项正确；对于B 选项，取2n =，012237121212n +==⋅+⋅+⋅，()73ω∴=，而0120212=⋅+⋅，则()21ω=，即()()721ωω≠+，B 选项错误；对于C 选项，3430234301018522251212222k k k k n a a a a a a +++=⋅+⋅++⋅+=⋅+⋅+⋅+⋅++⋅ ，所以，()01852k n a a a ω+=++++ ，2320123201014322231212222k k k k n a a a a a a +++=⋅+⋅++⋅+=⋅+⋅+⋅+⋅++⋅ ，所以，()01432k n a a a ω+=++++ ，因此，()()8543n n ωω+=+，C 选项正确；对于D 选项，01121222n n --=+++ ，故()21nn ω-=，D 选项正确.故选：ACD.2．（2020∙全国新Ⅱ卷∙高考真题）0‐1周期序列在通信技术中有着重要应用.若序列12n a a a 满足{0,1}(1,2,)i a i ∈= ，且存在正整数m ，使得(1,2,)i m i a a i +== 成立，则称其为0‐1周期序列，并称满足(1,2,)i m i a a i +== 的最小正整数m 为这个序列的周期.对于周期为m 的0‐1序列12n a a a ，11()(1,2,,1)m i i k i C k a a k m m +===-∑ 是描述其性质的重要指标，下列周期为5的0‐1序列中，满足1()(1,2,3,4)5C k k ≤=的序列是（） A ．11010 B ．11011C ．10001D ．11001【答案】C【详细分析】根据新定义，逐一检验即可【答案详解】由i m i a a +=知，序列i a 的周期为m ，由已知，5m =，511(),1,2,3,45i i k i C k a a k +===∑对于选项A ，511223344556111111(1)()(10000)55555i i i C a a a a a a a a a a a a +===++++=++++=≤∑52132435465711112(2)()(01010)5555i i i C a a a a a a a a a a a a +===++++=++++=∑，不满足；对于选项B ，51122334455611113(1)()(10011)5555i i i C a a a a a a a a a a a a +===++++=++++=∑，不满足；对于选项D ，51122334455611112(1)()(10001)5555i i i C a a a a a a a a a a a a +===++++=++++=∑，不满足；故选：C【点晴】本题考查数列的新定义问题，涉及到周期数列，考查学生对新定义的理解能力以及数学运算能力，是一道中档题.二、大题1．（2024∙全国新Ⅰ卷∙高考真题）设m 为正整数，数列1242,,...,m a a a +是公差不为0的等差数列，若从中删去两项i a 和()j a i j <后剩余的4m 项可被平均分为m 组，且每组的4个数都能构成等差数列，则称数列1242,,...,m a a a +是(),i j -可分数列．(1)写出所有的(),i j ，16i j ≤<≤，使数列126,,...,a a a 是(),i j -可分数列； (2)当3m ≥时，证明：数列1242,,...,m a a a +是()2,13-可分数列；(3)从1,2,...,42m +中一次任取两个数i 和()j i j <，记数列1242,,...,m a a a +是(),i j -可分数列的概率为m P ，证明：18m P >．【答案】(1)()()()1,2,1,6,5,6 (2)证明见解析 (3)证明见解析【详细分析】（1）直接根据(),i j -可分数列的定义即可；（2）根据(),i j -可分数列的定义即可验证结论；（3）证明使得原数列是(),i j -可分数列的(),i j 至少有()21m m +-个，再使用概率的定义.【答案详解】（1）首先，我们设数列1242,,...,m a a a +的公差为d ，则0d ≠.由于一个数列同时加上一个数或者乘以一个非零数后是等差数列，当且仅当该数列是等差数列，故我们可以对该数列进行适当的变形()111,2,...,42k ka a a k m d-=+=+'，得到新数列()1,2, (42)a k k m ==+'，然后对1242,,...,m a a a +'''进行相应的讨论即可. 换言之，我们可以不妨设()1,2,...,42k a k k m ==+，此后的讨论均建立在该假设下进行.回到原题，第1小问相当于从1,2,3,4,5,6中取出两个数i 和()j i j <，使得剩下四个数是等差数列. 那么剩下四个数只可能是1,2,3,4，或2,3,4,5，或3,4,5,6. 所以所有可能的(),i j 就是()()()1,2,1,6,5,6.（2）由于从数列1,2,...,42m +中取出2和13后，剩余的4m 个数可以分为以下两个部分，共m 组，使得每组成等差数列：①{}{}{}1,4,7,10,3,6,9,12,5,8,11,14，共3组；②{}{}{}15,16,17,18,19,20,21,22,...,41,4,41,42m m m m -++，共3m -组. （如果30m -=，则忽略②）故数列1,2,...,42m +是()2,13-可分数列.（3）定义集合{}{}410,1,2,...,1,5,9,13,...,41A k k m m =+==+，{}{}420,1,2,...,2,6,10,14,...,42B k k m m =+==+.下面证明，对142i j m ≤<≤+，如果下面两个命题同时成立，则数列1,2,...,42m +一定是(),i j -可分数列：命题1：,i A j B ∈∈或,i B j A ∈∈；命题2：3j i -≠.我们分两种情况证明这个结论.第一种情况：如果,i A j B ∈∈，且3j i -≠. 此时设141i k =+，242j k =+，{}12,0,1,2,...,k k m ∈.则由i j <可知124142k k +<+，即2114k k ->-，故21k k ≥.此时，由于从数列1,2,...,42m +中取出141i k =+和242j k =+后，剩余的4m 个数可以分为以下三个部分，共m 组，使得每组成等差数列： ①{}{}{}11111,2,3,4,5,6,7,8,...,43,42,41,4k k k k ---，共1k 组；②{}{}{}11111111222242,43,44,45,46,47,48,49,...,42,41,4,41k k k k k k k k k k k k ++++++++--+，共21k k -组； ③{}{}{}2222222243,44,45,46,47,48,49,410,...,41,4,41,42k k k k k k k k m m m m ++++++++-++，共2m k -组. （如果某一部分的组数为0，则忽略之）故此时数列1,2,...,42m +是(),i j -可分数列.第二种情况：如果,i B j A ∈∈，且3j i -≠. 此时设142i k =+，241j k =+，{}12,0,1,2,...,k k m ∈. 则由i j <可知124241k k +<+，即2114k k ->，故21k k >. 由于3j i -≠，故()()2141423k k +-+≠，从而211k k -≠，这就意味着212k k -≥.此时，由于从数列1,2,...,42m +中取出142i k =+和241j k =+后，剩余的4m 个数可以分为以下四个部分，共m 组，使得每组成等差数列：①{}{}{}11111,2,3,4,5,6,7,8,...,43,42,41,4k k k k ---，共1k 组；②{}112121241,31,221,31k k k k k k k +++++++，{}121212232,222,32,42k k k k k k k +++++++，共2组； ③全体{}11212124,3,22,3k p k k p k k p k k p +++++++，其中213,4,...,p k k =-，共212k k --组；④{}{}{}2222222243,44,45,46,47,48,49,410,...,41,4,41,42k k k k k k k k m m m m ++++++++-++，共2m k -组. （如果某一部分的组数为0，则忽略之）这里对②和③进行一下解释：将③中的每一组作为一个横排，排成一个包含212k k --个行，4个列的数表以后，4个列分别是下面这些数：{}111243,44,...,3k k k k +++，{}12121233,34,...,22k k k k k k +++++，{}121212223,223,...,3k k k k k k +++++，{}1212233,34,...,4k k k k k ++++.可以看出每列都是连续的若干个整数，它们再取并以后，将取遍{}11241,42,...,42k k k +++中除开五个集合{}1141,42k k ++，{}121231,32k k k k ++++，{}1212221,222k k k k ++++，{}121231,32k k k k ++++，{}2241,42k k ++中的十个元素以外的所有数.而这十个数中，除开已经去掉的142k +和241k +以外，剩余的八个数恰好就是②中出现的八个数. 这就说明我们给出的分组方式满足要求，故此时数列1,2,...,42m +是(),i j -可分数列.至此，我们证明了：对142i j m ≤<≤+，如果前述命题1和命题2同时成立，则数列1,2,...,42m +一定是(),i j -可分数列.然后我们来考虑这样的(),i j 的个数.首先，由于A B ⋂=∅，A 和B 各有1m +个元素，故满足命题1的(),i j 总共有()21m +个；而如果3j i -=，假设,i A j B ∈∈，则可设141i k =+，242j k =+，代入得()()2142413k k +-+=. 但这导致2112k k -=，矛盾，所以,i B j A ∈∈. 设142i k =+，241j k =+，{}12,0,1,2,...,k k m ∈，则()()2141423k k +-+=，即211k k -=.所以可能的()12,k k 恰好就是()()()0,1,1,2,...,1,m m -，对应的(),i j 分别是()()()2,5,6,9,...,42,41m m -+，总共m 个.所以这()21m +个满足命题1的(),i j 中，不满足命题2的恰好有m 个.这就得到同时满足命题1和命题2的(),i j 的个数为()21m m +-.当我们从1,2,...,42m +中一次任取两个数i 和()j i j <时，总的选取方式的个数等于()()()()424121412m m m m ++=++.而根据之前的结论，使得数列1242,,...,m a a a +是(),i j -可分数列的(),i j 至少有()21m m +-个. 所以数列1242,,...,m a a a +是(),i j -可分数列的概率m P 一定满足()()()()()()()()()22221111124214121412142221218m m m m m m m m P m m m m m m m m ⎛⎫+++ ⎪+-++⎝⎭≥=>==++++++++. 这就证明了结论.【点评】关键点点评：本题的关键在于对新定义数列的理解，只有理解了定义，方可使用定义验证或探究结论.2．（2024∙北京∙高考真题）已知集合(){}{}{}{}{},,,1,2,3,4,5,6,7,8,M i j k w i j k w i j k w =∈∈∈∈+++且为偶数．给定数列128:,,,A a a a ，和序列12:,,s T T T Ω ，其中()(),,,1,2,,t t t t t T i j k w M t s =∈= ，对数列A 进行如下变换：将A 的第1111,,,i j k w 项均加1，其余项不变，得到的数列记作()1T A ；将()1T A 的第2222,,,i j k w 项均加1，其余项不变，得到数列记作()21T T A ；……；以此类推，得到()21s T T T A ，简记为()A Ω．(1)给定数列:1,3,2,4,6,3,1,9A 和序列()()():1,3,5,7,2,4,6,8,1,3,5,7Ω，写出()A Ω；(2)是否存在序列Ω，使得()A Ω为123456782,6,4,2,8,2,4,4a a a a a a a a ++++++++，若存在，写出一个符合条件的Ω；若不存在，请说明理由；(3)若数列A 的各项均为正整数，且1357a a a a +++为偶数，求证：“存在序列Ω，使得()A Ω的各项都相等”的充要条件为“12345678a a a a a a a a +=+=+=+”．【答案】(1)():3,4,4,5,8,4,3,10A Ω (2)不存在符合条件的Ω，理由见解析 (3)证明见解析【详细分析】（1）直接按照()ΩA 的定义写出()ΩA 即可；（2）解法一：利用反证法，假设存在符合条件的Ω，由此列出方程组，进一步说明方程组无解即可；解法二：对于任意序列，所得数列之和比原数列之和多4，可知序列Ω共有8项，可知：()()2122128,1,2,3,4n n n n b b a a n --+-+==，检验即可；（3）解法一：分充分性和必要性两方面论证；解法二：若12345678a a a a a a a a +=+=+=+，分类讨论1357,,,a a a a 相等得个数，结合题意证明即可；若存在序列Ω，使得()ΩA 为常数列，结合定义详细分析证明即可.【答案详解】（1）因为数列:1,3,2,4,6,3,1,9A ，由序列()11,3,5,7T 可得()1:2,3,3,4,7,3,2,9T A ；由序列()22,4,6,8T 可得()21:2,4,3,5,7,4,2,10T T A ；由序列()31,3,5,7T 可得()321:3,4,4,5,8,4,3,10T T T A ；所以()Ω:3,4,4,5,8,4,3,10A .（2）解法一：假设存在符合条件的Ω，可知()ΩA 的第1,2项之和为12a a s ++，第3,4项之和为34a a s ++，则()()()()121234342642a a a a sa a a a s⎧+++=++⎪⎨+++=++⎪⎩，而该方程组无解，故假设不成立，故不存在符合条件的Ω；解法二：由题意可知：对于任意序列，所得数列之和比原数列之和多4，假设存在符合条件的Ω，且()128Ω:,,,A b b b ⋅⋅⋅，因为2642824484+++++++=，即序列Ω共有8项，由题意可知：()()2122128,1,2,3,4n n n n b b a a n --+-+==，检验可知：当2,3n =时，上式不成立，即假设不成立，所以不存在符合条件的Ω.（3）解法一：我们设序列()21...s T T T A 为{}(),18s n a n ≤≤，特别规定()0,18n n a a n =≤≤. 必要性：若存在序列12:,,s T T T Ω ，使得()ΩA 的各项都相等.则,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a =======，所以,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+. 根据()21...s T T T A 的定义，显然有,21,21,211,21s j s j s j s j a a a a ----+=++，这里1,2,3,4j =，1,2,...s =. 所以不断使用该式就得到12345678,1,2s s a a a a a a a a a a s +=+=+=+=+-，必要性得证. 充分性：若12345678a a a a a a a a +=+=+=+.由已知，1357a a a a +++为偶数，而12345678a a a a a a a a +=+=+=+，所以()()24681213574a a a a a a a a a a +++=+-+++也是偶数.我们设()21...s T T T A 是通过合法的序列Ω的变换能得到的所有可能的数列()ΩA 中，使得,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-最小的一个.上面已经说明,21,21,211,21s j s j s j s j a a a a ----+=++，这里1,2,3,4j =，1,2,...s =.从而由12345678a a a a a a a a +=+=+=+可得,1,2,3,4,5,6,7,812s s s s s s s s a a a a a a a a a a s +=+=+=+=++. 同时，由于t t t t i j k w +++总是偶数，所以,1,3,5,7t t t t a a a a +++和,2,4,6,8t t t t a a a a +++的奇偶性保持不变，从而,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数. 下面证明不存在1,2,3,4j =使得,21,22s j s j a a --≥.假设存在，根据对称性，不妨设1j =，,21,22s j s j a a --≥，即,1,22s s a a -≥.情况1：若,3,4,5,6,7,80s s s s s s a a a a a a -+-+-=，则由,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数，知,1,24s s a a -≥.对该数列连续作四次变换()()()()2,3,5,8,2,4,6,8,2,3,6,7,2,4,5,7后，新的4,14,24,34,44,54,64,74,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-减少4，这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾；情况2：若,3,4,5,6,7,80s s s s s s a a a a a a -+-+->，不妨设,3,40s s a a ->.情况2‐1：如果,3,41s s a a -≥，则对该数列连续作两次变换()()2,4,5,7,2,4,6,8后，新的2,12,22,32,42,52,62,72,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-至少减少2，这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾；情况2‐2：如果,4,31s s a a -≥，则对该数列连续作两次变换()()2,3,5,8,2,3,6,7后，新的2,12,22,32,42,52,62,72,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-相比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-至少减少2，这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾.这就说明无论如何都会导致矛盾，所以对任意的1,2,3,4j =都有,21,21s j s j a a --≤. 假设存在1,2,3,4j =使得,21,21s j s j a a --=，则,21,2s j s j a a -+是奇数，所以,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+都是奇数，设为21N +.则此时对任意1,2,3,4j =，由,21,21s j s j a a --≤可知必有{}{},21,2,,1s j s j a a N N -=+.而,1,3,5,7s s s s a a a a +++和,2,4,6,8s s s s a a a a +++都是偶数，故集合{},s m m a N =中的四个元素,,,i j k w 之和为偶数，对该数列进行一次变换(),,,i j k w ，则该数列成为常数列，新的1,11,21,31,41,51,61,71,8s s s s s s s s a a a a a a a a ++++++++-+-+-+-等于零，比原来的,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-更小，这与,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a -+-+-+-的最小性矛盾.综上，只可能(),21,201,2,3,4s j s j a a j --==，而,1,2,3,4,5,6,7,8s s s s s s s s a a a a a a a a +=+=+=+，故{}(),Ωs n a A =是常数列，充分性得证.解法二：由题意可知：Ω中序列的顺序不影响()ΩA 的结果，且()()()()12345678,,,,,,,a a a a a a a a 相对于序列也是无序的，（ⅰ）若12345678a a a a a a a a +=+=+=+，不妨设1357a a a a ≤≤≤，则2468a a a a ≥≥≥， ①当1357a a a a ===，则8642a a a a ===，分别执行1a 个序列()2,4,6,8、2a 个序列()1,3,5,7，可得1212121212121212,,,,,,,a a a a a a a a a a a a a a a a ++++++++，为常数列，符合题意； ②当1357,,,a a a a 中有且仅有三个数相等，不妨设135a a a ==，则246a a a ==，即12121278,,,,,,,a a a a a a a a ，分别执行2a 个序列()1,3,5,7、7a 个序列()2,4,6,8可得1227122712272778,,,,,,,a a a a a a a a a a a a a a a a ++++++++，即1227122712272712,,,,,,,a a a a a a a a a a a a a a a a ++++++++，因为1357a a a a +++为偶数，即173a a +为偶数，可知17,a a 的奇偶性相同，则*712a a -∈N ，分别执行712a a -个序列()1,3,5,7，()1,3,6,8，()2,3,5,8，()1,4,5,8，可得7217217217217217217217213232323232323232,,,,,,,22222222a a a a a a a a a a a a a a a a a a a a a a a a +-+-+-+-+-+-+-+-，为常数列，符合题意；③若1357a a a a =<=，则2468a a a a =>=，即12125656,,,,,,,a a a a a a a a ，分别执行5a 个()1,3,6,8、1a 个()2,4,5,7，可得1512151215561556,,,,,,,a a a a a a a a a a a a a a a a ++++++++，因为1256a a a a +=+，可得1512151215121512,,,,,,,a a a a a a a a a a a a a a a a ++++++++，即转为①，可知符合题意；④当1357,,,a a a a 中有且仅有两个数相等，不妨设13a a =，则24a a =，即12125678,,,,,,,a a a a a a a a ，分别执行1a 个()2,4,5,7、5a 个()1,3,6,8，可得1512151215561758,,,,,,,a a a a a a a a a a a a a a a a ++++++++，且1256a a a a +=+，可得1512151215121758,,,,,,,a a a a a a a a a a a a a a a a ++++++++，即转为②，可知符合题意；⑤若1357a a a a <<<，则2468a a a a >>>，即12345678,,,,,,,a a a a a a a a ，分别执行1a 个()2,3,5,8、3a 个()1,4,6,7，可得1312133415363718,,,,,,,a a a a a a a a a a a a a a a a ++++++++，且1234a a a a +=+，可得1312131215363718,,,,,,,a a a a a a a a a a a a a a a a ++++++++，即转为③，可知符合题意；综上所述：若12345678a a a a a a a a +=+=+=+，则存在序列Ω，使得()ΩA 为常数列；（ⅱ）若存在序列Ω，使得()ΩA 为常数列，因为对任意()128Ω:,,,A b b b ⋅⋅⋅，均有()()()()12123434b b a a b b a a +-+=+-+()()()()56567878b b a a b b a a =+-+=+-+成立，若()ΩA 为常数列，则12345678b b b b b b b b +=+=+=+，所以12345678a a a a a a a a +=+=+=+；综上所述：“存在序列Ω，使得()ΩA 为常数列”的充要条件为“12345678a a a a a a a a +=+=+=+”. 【点评】关键点点评：本题第三问的关键在于对新定义的理解，以及对其本质的详细分析.3．（2023∙北京∙高考真题）已知数列{}{},n n a b 的项数均为m (2)m >，且,{1,2,,},n n a b m ∈ {}{},n n a b 的前n项和分别为,n n A B ，并规定000A B ==．对于{}0,1,2,,k m ∈ ，定义{}max ,{0,1,2,,}k i k r iB A i m =≤∈∣ ，其中，max M 表示数集M 中最大的数.(1)若1231232,1,3,1,3,3a a a b b b ======，求0123,,,r r r r 的值； (2)若11a b ≥，且112,1,2,,1,j j j r r r j m +-≤+=- ，求n r ；(3)证明：存在{},,,0,1,2,,p q s t m ∈ ，满足,,p q s t >> 使得t p s q A B A B +=+．【答案】(1)00r =，11r =，21r =，32r = (2),n r n n =∈N (3)证明见答案详解【详细分析】（1）先求01230123,,,,,,,A A A A B B B B ，根据题意详细分析求解；（2）根据题意题意详细分析可得11i ir r +-≥，利用反证可得11i i r r +-=，在结合等差数列运算求解；（3）讨论,m m A B 的大小，根据题意结合反证法详细分析证明.【答案详解】（1）由题意可知：012301230,2,3,6,0,1,4,7A A A A B B B B ========，当0k =时，则0000,,1,2,3i B A B A i ==>=，故00r =；当1k =时，则01111,,,2,3i B A B A B A i <<>=，故11r =；当2k =时，则22232,0,1,,,i B A i B A B A ≤=>>故21r =；当3k =时，则333,0,1,2,i B A i B A ≤=>，故32r =；综上所述：00r =，11r =，21r =，32r =. （2）由题意可知：nr m≤，且nr ∈N，因为1,1n n a b ≥≥，且11a b ≥，则10n A B B ≥>对任意*n ∈N 恒成立，所以010,1r r =≥，又因为112ii i r r r -+≤+，则11i i i i r r r r +--≥-，即112101m m m m r r r r r r ----≥-≥⋅⋅⋅≥-≥，可得11i ir r +-≥，反证：假设满足11n n r r +->的最小正整数为01j m ≤≤-，当i j ≥时，则12i i r r +-≥；当1i j ≤-时，则11i ir r +-=，则()()()112100m m m m m r r r r r r r r ---=-+-+⋅⋅⋅+-+()22m j j m j ≥-+=-，又因为01j m ≤≤-，则()2211m r m j m m m m ≥-≥--=+>，假设不成立，故11n n r r +-=，即数列{}n r 是以首项为1，公差为1的等差数列，所以01,n r n n n =+⨯=∈N . （3）因为,n n a b 均为正整数，则{}{},n n A B 均为递增数列，（ⅰ）若m m A B =，则可取0t q ==，满足,,p q s t >> 使得t p s q A B A B +=+；（ⅱ）若m m A B <，则k r m <，构建,1n n r n S B A n m =-≤≤，由题意可得：0n S ≤，且n S 为整数，反证，假设存在正整数K ，使得K S m ≤-，则1,0K K r K r K B A m B A +-≤-->，可得()()111K K K K K r r r r K r K b B B B A B A m +++=-=--->，这与{}11,2,,K r b m +∈⋅⋅⋅相矛盾，故对任意1,n m n ≤≤∈N ，均有1n S m≥-.①若存在正整数N ，使得0N N r N S B A =-=，即N N r A B =，可取0,,N t q p N s r ====，满足,p q s t >>，使得t p s q A B A B +=+； ②若不存在正整数N ，使得0NS =，因为(){}1,2,,1n S m ∈--⋅⋅⋅--，且1n m ≤≤，所以必存在1X Y m ≤<≤，使得X Y S S =，即X Y r X r Y B A B A -=-，可得X Y Y r X r A B A B +=+，可取,,,Y X p Y s r q X t r ====，满足,p q s t >>，使得t p s q A B A B +=+；（ⅲ）若m m A B >，定义{}max ,{0,1,2,,}k i k R i A B i m =≤∈L ∣，则k R m <，构建,1n n R n S A B n m =-≤≤，由题意可得：0n S ≤，且n S 为整数，反证，假设存在正整数,1K K m ≤≤，使得K S m ≤-，则1,0K K R K R K A B m A B +-≤-->，可得()()111K K K K K R R R R K R K a A A A B A B m +++=-=--->，这与{}11,2,,K R a m +∈⋅⋅⋅相矛盾，故对任意11,n m n ≤≤-∈N ，均有1n S m≥-.①若存在正整数N ，使得0N N R N S A B =-=，即N R N A B =，可取0,,N q t s N p R ====，即满足,p q s t >>，使得t p s q A B A B +=+； ②若不存在正整数N ，使得0NS =，因为(){}1,2,,1n S m ∈--⋅⋅⋅--，且1n m ≤≤，所以必存在1X Y m ≤<≤，使得X Y S S =，即X Y R X R Y A B A B -=-，可得Y X R X R Y A B A B +=+，可取,,,Y X p R t X q R s Y ====，满足,p q s t >>，使得t p s q A B A B +=+.综上所述：存在0,0q p m t s m ≤<≤≤<≤使得t p s q A B A B +=+．4．（2022∙北京∙高考真题）已知12:,,,k Q a a a 为有穷整数数列．给定正整数m ，若对任意的{1,2,,}n m ∈ ，在Q 中存在12,,,,(0)i i i i j a a a a j +++≥ ，使得12i i i i j a a a a n +++++++= ，则称Q 为m -连续可表数列． (1)判断:2,1,4Q 是否为5-连续可表数列？是否为6-连续可表数列？说明理由； (2)若12:,,,k Q a a a 为8-连续可表数列，求证：k 的最小值为4；(3)若12:,,,k Q a a a 为20-连续可表数列，且1220k a a a +++< ，求证：7k ≥．【答案】(1)是5-连续可表数列；不是6-连续可表数列． (2)证明见解析． (3)证明见解析．【详细分析】（1）直接利用定义验证即可；（2）先考虑3k ≤不符合，再列举一个4k =合题即可；（3）5k ≤时，根据和的个数易得显然不行，再讨论6k =时，由12620a a a +++< 可知里面必然有负数，再确定负数只能是1-，然后分类讨论验证不行即可．【答案详解】（1）21a =，12a =，123a a +=，34a =，235a a +=，所以Q 是5-连续可表数列；易知，不存在,i j 使得16i i i j a a a +++++= ，所以Q 不是6-连续可表数列．（2）若3k ≤,设为:Q ,,a b c ,则至多,,,,,a b b c a b c a b c ++++，6个数字，没有8个，矛盾；当4k =时,数列:1,4,1,2Q ，满足11a =，42a =，343a a +=，24a =，125a a +=，1236a a a ++=，2347a a a ++=，12348a a a a +++=， min 4k ∴=．（3）12:,,,k Q a a a ，若i j =最多有k 种，若i j ≠，最多有2C k 种，所以最多有()21C 2k k k k ++=种，若5k ≤，则12,,,k a a a …至多可表()551152+=个数，矛盾, 从而若7k <,则6k =，,,,,,a b c d e f 至多可表6(61)212+=个数，而20a b c d e f +++++<，所以其中有负的，从而,,,,,a b c d e f 可表1~20及那个负数（恰 21个），这表明~a f 中仅一个负的，没有0，且这个负的在~a f 中绝对值最小，同时~a f 中没有两数相同,设那个负数为(1)m m -≥ ，则所有数之和125415m m m m m ≥++++++-=+ ，415191m m +≤⇒=，{,,,,,}{1,2,3,4,5,6}a b c d e f ∴=-，再考虑排序，排序中不能有和相同，否则不足20个，112=-+ （仅一种方式），1∴-与2相邻，若1-不在两端,则",1,2,__,__,__"x -形式，若6x =，则56(1)=+-（有2种结果相同，方式矛盾），6x ∴≠，同理5,4,3x ≠ ，故1-在一端，不妨为"1,2,,,"A B C D -形式，若3A =,则523=+ （有2种结果相同，矛盾），4A =同理不行，5A =，则6125=-++ （有2种结果相同，矛盾），从而6A =，由于7126=-++,由表法唯一知3,4不相邻,、故只能1,2,6,3,5,4-，①或1,2,6,4,5,3-，② 这2种情形，对①：96354=+=+，矛盾，对②：82653=+=+，也矛盾，综上6k ≠，当7k =时，数列1,2,4,5,8,2,1--满足题意，7k ∴≥．【点评】关键点评，先理解题意，是否为m -可表数列核心就是是否存在连续的几项（可以是一项）之和能表示从1到m 中间的任意一个值．本题第二问3k ≤时，通过和值可能个数否定3k ≤；第三问先通过和值的可能个数否定5k ≤，再验证6k =时，数列中的几项如果符合必然是{1,2,3,4,5,6}-的一个排序，可验证这组数不合题．5．（2021∙北京∙高考真题）设p 为实数.若无穷数列{}n a 满足如下三个性质，则称{}n a 为p ℜ数列：①10a p +≥，且20a p +=； ②414,1,2,n n a a n -<=⋅⋅⋅()；③{},1m n m n m n a a a p a a p +∈+++++，(),1,2,m n =⋅⋅⋅．（1）如果数列{}n a 的前4项为2，‐2，‐2，‐1，那么{}n a 是否可能为2ℜ数列？说明理由；（2）若数列{}n a 是0ℜ数列，求5a ；（3）设数列{}n a 的前n 项和为n S .是否存在p ℜ数列{}n a ，使得10n S S ≥恒成立？如果存在，求出所有的p ；如果不存在，说明理由．【答案】（1）不可以是2R 数列；理由见解析；（2）51a =；（3）存在；2p =．【详细分析】(1)由题意考查3a 的值即可说明数列不是2ℜ数列； (2)由题意首先确定数列的前4项，然后讨论计算即可确定5a 的值；(3)构造数列n n b a p =+，易知数列{}n b 是0ℜ的，结合(2)中的结论求解不等式即可确定满足题意的实数p 的值.【答案详解】(1)因为 122,2,2,p a a ===- 所以12122,13a a p a a p ++=+++=，因为32,a =-所以{}312122,21a a a a a ∈+++++ 所以数列{}n a ，不可能是2ℜ数列. (2)性质①120,0a a ≥=，由性质③{}2,1m m m a a a +∈+，因此31a a =或311a a =+，40a =或41a =，若40a =，由性质②可知34a a <，即10a <或110a +<，矛盾；若4311,1a a a ==+，由34a a <有111a +<，矛盾. 因此只能是4311,a a a ==.又因为413a a a =+或4131a a a =++，所以112a =或10a =. 若112a =，则{}{}{}2111111110,012,211,2a a a a a a a a +=∈+++++=+=，不满足20a =，舍去.当10a =，则{}n a 前四项为:0，0，0，1，下面用数学归纳法证明()444(1,2,3),1n i n a n i a n n N ++===+∈：当0n =时，经验证命题成立，假设当(0)n k k ≤≥时命题成立，当1n k =+时：若1i =，则()()4541145k k j k j a a a +++++-==，利用性质③：{}*45,144{,1}jk j aa j N j k k k +-+∈≤≤+=+∣，此时可得：451k a k +=+；否则，若45k a k +=，取0k =可得：50a =，而由性质②可得：{}5141,2a a a =+∈，与50a =矛盾. 同理可得：{}*46,145{,1}jk j a a j N j k k k +-+∈≤≤+=+∣，有461k a k +=+； {}*48,246{1,2}jk j a a j N j k k k +-+∈≤≤+=++∣，有482k a k +=+；{}*47,146{1}jk j aa j N j k k +-+∈≤≤+=+∣，又因为4748k k a a ++<，有47 1.k a k +=+ 即当1n k =+时命题成立，证毕. 综上可得：10a =，54111a a ⨯+==. (3)令n nb a p =+，由性质③可知：*,,m n m n m n N b a p ++∀∈=+∈{},1m n m n a p a p a p a p +++++++{},1m n m n b b b b =+++，由于11224141440,0,n n n n b a p b a p b a p a p b --=+≥=+==+<+=，因此数列{}n b 为0ℜ数列. 由（2）可知:若444,(1,2,3),1n i n n N a n p i a n p ++∀∈=-==+-；11111402320a S S a p ⨯+-==-≥=，91010422(2)0S S a a p ⨯+-=-=-=--≥，因此2p =，此时1210,,,0a a a ⋯≤，()011j a j ≥≥，满足题意.【点评】本题属于数列中的“新定义问题”，“新定义”主要是指即时定义新概念、新公式、新定理、新法则、新运算五种，然后根据此新定义去解决问题，有时还需要用类比的方法去理解新的定义，这样有助于对新定义的透彻理解.但是，透过现象看本质，它们考查的还是基础数学知识，所以说“新题”不一定是“难题”，掌握好三基，以不变应万变才是制胜法宝.6．（2020∙北京∙高考真题）已知{}n a 是无穷数列．给出两个性质：①对于{}n a 中任意两项,()i j a a i j >，在{}n a 中都存在一项m a ，使2i m ja a a =；②对于{}n a 中任意项(3)n a n …，在{}n a 中都存在两项,()k l a a k l >．使得2k n la a a =． ()Ⅰ若(1,2,)n a n n == ，判断数列{}n a 是否满足性质①，说明理由；()Ⅱ若12(1,2,)n n a n -== ，判断数列{}n a 是否同时满足性质①和性质②，说明理由；()Ⅲ若{}n a 是递增数列，且同时满足性质①和性质②，证明：{}n a 为等比数列.【答案】()Ⅰ详见解析；()Ⅱ答案详解解析；()Ⅲ证明详见解析. 【详细分析】()Ⅰ根据定义验证，即可判断；()Ⅱ根据定义逐一验证，即可判断；()Ⅲ解法一：首先，证明数列中的项数同号，然后证明2231a a a =，最后，用数学归纳法证明数列为等比数列即可.解法二：首先假设数列中的项数均为正数，然后证得123,,a a a 成等比数列，之后证得1234,,,a a a a 成等比数列，同理即可证得数列为等比数列，从而命题得证.【答案详解】()Ⅰ{}2323292,3,2n a a a a Z a ===∉∴Q 不具有性质①； ()Ⅱ{}22*(2)1*2,,,2,2i j i i i j n j ja a i j N i j i j N a a a a ---∀∈>=-∈∴=∴Q 具有性质①； {}2*(2)11,3,1,2,22,k l n k n n la n N n k n l a n a a ---∀∈≥∃=-=-===∴Q 具有性质②；()Ⅲ解法一首先，证明数列中的项数同号，不妨设恒为正数：显然()0*n a n N ≠∉，假设数列中存在负项，设{}0max |0n N n a =<，第一种情况：若01N =，即01230a a a a <<<<< ，由①可知：存在1m ，满足12210m a a a =<，存在2m ，满足22310m a a a =<，由01N =可知223211a a a a =，从而23a a =，与数列的单调性矛盾，假设不成立.第二种情况：若02N ≥，由①知存在实数m ，满足0210Nm a a a =<，由0N 的定义可知：0m N ≤，另一方面，000221NNm N N a a a a a a =>=，由数列的单调性可知：0m N >，这与0N 的定义矛盾，假设不成立. 同理可证得数列中的项数恒为负数. 综上可得，数列中的项数同号.其次，证明2231a a a =：利用性质②：取3n =，此时()23kla a k l a =>，由数列的单调性可知0k l a a >>，而3kk k la a a a a =⋅>，故3k <，此时必有2,1k l ==，即2231a a a =，最后，用数学归纳法证明数列为等比数列：假设数列{}n a 的前()3k k ≥项成等比数列，不妨设()111s s a a q s k -=≤≤，其中10,1a q >>，（10,01a q <<<的情况类似）由①可得：存在整数m ，满足211k k m k k a a a q a a -==>，且11k m k a a q a +=≥ （*）由②得：存在s t >，满足：21s s k s s t t a aa a a a a +==⋅>，由数列的单调性可知：1t s k <≤+，由()111s s a a qs k -=≤≤可得：2211111s t k s k k ta a a q a a q a ---+==>= （**）由（**）和（*）式可得：211111k s t k a q a qa q ---≥>，结合数列的单调性有：211k s t k ≥-->-，注意到,,s t k 均为整数，故21k s t =--，代入（**）式，从而11kk a a q +=.总上可得，数列{}n a 的通项公式为：11n n a a q -=.即数列{}n a 为等比数列. 解法二：假设数列中的项数均为正数：首先利用性质②：取3n =，此时23()kla a k l a =>，由数列的单调性可知0k l a a >>，而3kk k la a a a a =⋅>，故3k <，此时必有2,1k l ==，即2231a a a =，即123,,a a a 成等比数列，不妨设22131,(1)a a q a a q q ==>，然后利用性质①：取3,2i j ==，则224331121m a a q a a q a a q===，即数列中必然存在一项的值为31a q ，下面我们来证明341a a q =，否则，由数列的单调性可知341a a q <，在性质②中，取4n =，则24k k k k l la aa a a a a ==>，从而4k <，与前面类似的可知则存在{,}{1,2,3}()k l k l ⊆>，满足24kl a a a =，若3,2k l ==，则：2341kla a a q a ==，与假设矛盾；若3,1k l ==，则：243411k la a a q a q a ==>，与假设矛盾；若2,1k l ==，则：22413k la a a q a a ===，与数列的单调性矛盾；即不存在满足题意的正整数,k l ，可见341a a q <不成立，从而341a a q =，然后利用性质①：取4,3i j ==，则数列中存在一项2264411231m a a q a a q a a q===，下面我们用反证法来证明451a a q =，否则，由数列的单调性可知34151a q a a q <<，在性质②中，取5n =，则25k k k k l la aa a a a a ==>，从而5k <，与前面类似的可知则存在{}{}(),1,2,3,4k l k l ⊆>，满足25k la a a =，即由②可知：22222115111k k l k l l a a q a a q a a q----===，若214k l --=，则451a a q =，与假设矛盾；若214k l -->，则451a a q >，与假设矛盾；若214k l --<，由于,k l 为正整数，故213k l --≤，则351a a q ≤，与315a q a <矛盾；综上可知，假设不成立，则451a a q =.同理可得：566171,,a a q a a q == ，从而数列{}n a 为等比数列，同理，当数列中的项数均为负数时亦可证得数列为等比数列.由推理过程易知数列中的项要么恒正要么恒负，不会同时出现正数和负数. 从而题中的结论得证，数列{}n a 为等比数列.【点评】本题主要考查数列的综合运用，等比数列的证明，数列性质的应用，数学归纳法与推理方法、不等式的性质的综合运用等知识，意在考查学生的转化能力和推理能力.7．（2020∙江苏∙高考真题）已知数列{}*()∈n a n N 的首项a 1=1，前n 项和为Sn ．设λ与k 是常数，若对一切正整数n ，均有11111k k k n n n S S a λ++-=成立，则称此数列为“λ~k ”数列．（1）若等差数列{}n a 是“λ~1”数列，求λ的值；。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

历年高考数学试题向量一、选择题，在每小题给出的四个选择题只有一项是符合题目要求的。

1．已知向量的夹角为与则若c a c b a c b a ,25)(,5||),4,2(),2,1(=⋅+=--=（） A ．30°B ．60°C ．120°D ．150°2．已知向量,a b ，且2,56AB a b BC a b =+=-+，72CD a b =-，则一定共线的三点是（）（A ）A 、B 、D （B ）A 、B 、C （C ）B 、C 、D （D ）A 、C 、D3．已知A （3，1），B （6，1），C （4，3），D 为线段BC 的中点，则向量AC 与DA 的夹角为（） A ．54arccos 2-πB ．54arccosC ．)54arccos(-D ．－)54arccos(-4．若||1,||2,a b c a b ===+，且c a ⊥，则向量a 与b 的夹角为（）（A ）30° （B ）60° （C ）120° （D ）150°5．已知向量a ≠e ，|e |=1满足：对任意∈t R ，恒有|a －t e |≥|a －e |. 则（） A ．a ⊥eB ．a ⊥（a －e ）C ．e ⊥（a －e ）D ．（a +e ）⊥（a －e ）6．已知向量的夹角为与则若c a c b a c b a ,25)(,5||),4,2(),2,1(=⋅+=--=（） A ．30°B ．60°C ．120°D ．150°7．设向量a =（－1，2），b =（2，－1），则（a ·b ）（a +b ）等于（） A ．（1，1）B ．（－4，－4）C ．－4D ．（－2，－2）8．若||1,||2,a b c a b ===+，且c a ⊥，则向量a 与b 的夹角为（）（A ）30° （B ）60° （C ）120° （D ）150°9．已知向量a =（－2，2），b =（5，k ）.若|a +b |不超过5，则k 的取值范围是（） A ．[－4，6]B ．[－6，4]C ．[－6，2]D ．[－2，6]10．点O 是三角形ABC 所在平面内的一点，满足OA OC OC OB OB OA ⋅=⋅=⋅，则点O 是ABC ∆的（）（A ）三个内角的角平分线的交点（B ）三条边的垂直平分线的交点（C ）三条中线的交点（D ）三条高的交点11．设平面向量1a 、2a 、3a 的和1230a a a ++=。

如果向量1b 、2b 、3b ，满足2i i b a =，且i a 顺时针旋转30o后与i b 同向，其中1,2,3i =，则（）A ．1230b b b -++=B ．1230b b b -+=C ．1230b b b +-=D ．1230b b b ++= 12．已知向量a 、b 满足|a |=1，|b |=4，且ab =2，则a 与b 的夹角为（A ）6π （B ）4π （C ）3π （D ）2π13．已知,0||2||≠=b a 且关于x 的方程0||2=⋅++b a x a x 有实根, 则a 与b 的夹角的取值范围是 A ．]6,0[πB ．],3[ππC ．]32,3[ππD ．],6[ππ14．已知等差数列｛a n ｝的前n 项和为S n ，若1O a B ＝200OA a OC ＋，且A 、B 、C 三点共线（该直线不过原点O ），则S 200＝（）A ．100 B. 101 C.20015．ABC ∆的三内角,,A B C 所对边长分别为,,a b c ，设向量()(),,,p a c b q b a c a =+=--，若p ∥q ，则角C 的大小为A.6π B 3π C 2πD 23π16．设()()()0,0,1,0,0,1O A B ，点P 是线段AB 上的一个动点，.AP AB λ=若,OP AB PA PB •≥•则实数λ的取值范围是A112λ≤≤B 112λ-≤≤C 1122λ≤≤+D 1122λ-≤≤+ 17．设向量a=(1, －2),b=(－2,4),c =(－1,－2)，若表示向量4a ,4b －2c ,2(a －c ),d 的有向线段首尾相接能构成四边形，则向量d 为(A)(2,6) (B)(－2,6) (C)(2,－6) (D)(－2,－6) 18．如图，在平行四边形ABCD 中，下列结论中错误的是（）（A ）→--AB ＝→--DC ；（B ）→--AD ＋→--AB ＝→--AC ；（C ）→--AB －→--AD ＝→--BD ；（D ）→--AD ＋→--CB ＝→0．19．若a 与b c -都是非零向量，则“a b a c ⋅=⋅”是“()a b c ⊥-”的（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件ABCD20．已知1,3,.0,OA OB OAOB ===点C 在AOC ∠30o =，设(,)OC mOA nOB m n R =+∈，则mn等于（A ）13（B ）3 （C ）33 （D 321．已知向量()1,3=a ，b 是不平行于x 轴的单位向量，且3=⋅b a ，则b =A.⎪⎪⎭⎫ ⎝⎛21,23 B. ⎪⎪⎭⎫ ⎝⎛23,21 C. ⎪⎪⎭⎫⎝⎛433,41 D. ()0,1 22．设过点()y x P ,的直线分别与x 轴的正半轴和y 轴的正半轴交于A 、B 两点，点Q 与点P 关于y 轴对称，O 为坐标原点，若PA BP 2=，且1=⋅AB OQ ，则P 点的轨迹方程是A. ()0,0123322>>=+y x y x B. ()0,0123322>>=-y x y x C. ()0,0132322>>=-y x y x D. ()0,0132322>>=+y x y x23．已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC →| =12 , 则△ABC 为( )A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形24．如图，已知正六边形123456PP P P P P ，下列向量的数量积中最大的是（A ）1213PP PP ⋅ （B ）1214PP PP ⋅ （C ）1215PP PP ⋅ （D ）1216PP PP ⋅ 25．与向量a =-⎪⎭⎫⎝⎛b ,21,27⎪⎭⎫ ⎝⎛27,21的夹解相等，且模为1的向量是(A) ⎪⎭⎫-⎝⎛53,54 (B) ⎪⎭⎫- ⎝⎛53,54或⎪⎭⎫ ⎝⎛-53,54 （C ）⎪⎭⎫- ⎝⎛31,322 （D ）⎪⎭⎫- ⎝⎛31,322或⎪⎭⎫ ⎝⎛-31,322 26．已知两点M （－2，0）、N （2，0），点P 为坐标平面内的动点，满足MP MN MP MN ⋅+⋅|||| ＝0，则动点P （x ，y ）的轨迹方程为（）（A ）x y 82= （B ）x y 82-= （C ）x y 42= （D ）x y 42-= 27．如图1所示，D 是ABC ∆的边AB 上的中点，则向量CD =（）A.12BC BA -+B. 12BC BA -- C. 12BC BA - D. 12BC BA +AD CB 图128．已知非零向量a 、b ，若a ＋2b 与a －2b 互相垂直，则=ba （）A.41 B. 4 C. 21D. 2 29．设过点P （x ，y ）的直线分别与x 轴的正半轴和y 轴的正半轴交于A 、B 两点，若1,2＝且AB OQ PA BP ⋅=，则点P 的轨迹方程是（） A. )0,0(123322>>=+y x y x B. )0,0(123322>>=-y x y x 30．ABC △的三内角A B C ，，所对边的长分别为a b c ，，．设向量p ()=+，a c b ，q ()=--，b a c a ．若p q ∥，则角C 的大小为（）Ａ．π6Ｂ．π3Ｃ．π2Ｄ．2π331．已知向量a b 、满足1,4,a b ==，且2a b =，则a 与b 的夹角为 A ．6π B ．4π C ．3π D ．2π 32．设向量a=(1,－3),b=(－2,4),若表示向量4a 、3b －2a,c 的有向线段首尾相接能构成三角形，则向量c 为 (A)（1，－1） (B)（－1， 1） (C) （－4，6） (D) （4，－6）33．设向量a 与b 的夹角为θ，(33)a =，，2(11)b a -=-，，则cos θ= ． 34．设向量,,a b c 满足0a b c ++=,,||1,||2a b a b ⊥==,则2||c =(A)1 (B)2 (C)4 (D)535．已知三点(2,3),(1,1),(6,)A B C k --，其中k 为常数。

若AB AC =，则AB 与AC 的夹角为（A ）24arccos()25-（B ）2π或24arccos 25 （C ）24arccos 25 （D ）2π或24arccos 25π-36．已知向量a 与b 的夹角为120o，3,13,a a b =+=则b 等于（A ）5 （B ）4 （C ）3 （D ）137．已知向量),2,1(),,2(==b t a 若1t t =时，a ∥b；2t t =时，b a ⊥，则A ．1,421-=-=t t B. 1,421=-=t t C. 1,421-==t t D. 1,421==t t38．如图1：OM ∥AB ，点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区A域内（不含边界）.且OB y OA x OP +=，则实数对（x ,y ）可以是A ．)43,41( B. )32,32(-C. )43,41(-D. )57,51(-39．已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC →| =12 , 则△ABC 为( )A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形40．设向量 a ，b ，c 满足 a+b+c=0，且 a ⊥b ，|a|=1，|b|=2，则|c| 2 = （A ）1 （B ）2 （C ）4 （D ）541．对于向量，a 、b 、c 和实数，下列命题中真命题是 A 若，则a ＝0或b ＝0 B 若，则λ＝0或a ＝0C 若＝，则a ＝b 或a ＝－bD 若，则b ＝c42．已知平面向量(11)(11)==-，，，a b ，则向量1322-=a b （）Ａ．(21)--，Ｂ．(21)-，Ｃ．(10)-，Ｄ．(12)-，43．在直角ABC ∆中，CD 是斜边AB 上的高，则下列等式不成立的是（A ）2AC AC AB =⋅ （B ） 2BC BA BC =⋅ （C ）2AB AC CD =⋅ （D ） 22()()AC AB BA BC CD AB⋅⨯⋅=44．若向量a 与b 不共线，0≠a b ，且⎛⎫⎪⎝⎭a a c =a -b a b ，则向量a 与c 的夹角为（） A ．0B ．π6C ．π3D ．π245．已知O 是ABC △所在平面内一点，D 为BC 边中点，且2OA OB OC ++=0，那么（）Ａ．AO OD = Ｂ．2AO OD = Ｃ．3AO OD = Ｄ．2AO OD =46．连掷两次骰子得到的点数分别为m 和n ，记向量()m n ，a =与向量(11)=-，b 的夹角为θ，则0θπ⎛⎤∈ ⎥2⎝⎦，的概率是（）A ．512B ．12C ．712D ．5647．已知向量(56)=-，a ，(65)=，b ，则a 与b （） A ．垂直B ．不垂直也不平行C ．平行且同向D ．平行且反向48．设F 为抛物线24y x =的焦点，A B C ，，为该抛物线上三点，若FA FB FC ++=0，则FA FB FC ++=（） A ．9B ．6C ．4D ．349．设A ｛a ,1｝，B ｛2，b ｝，C ｛4,5｝，为坐标平面上三点，O 为坐标原点，若方向在与→→→OC OB OA 上的投影相同，则a 与b 满足的关系式为 (A)354=-b a(B)345=-b a (C)1454=+b a(D)1445=+b a50．设两个向量22(2cos )λλα=+-，a 和sin 2m m α⎛⎫=+ ⎪⎝⎭，b ，其中mλα，，为实数．若2=a b ，则mλ的取值范围是（）Ａ．Ｂ．[48]，Ｃ．Ｄ．51．若非零向量a 、b 满足|a +b |=|b |，则（）（A ）|2a |>|2a +b | （B ）|2a |<|2a +b | （C ）|2b |>|a +2b | （D ）|2b |<|a +2b | 52．如右图，在四边形ABCD 中，4||||||=++DC BD AB ，4||||||||=⋅+⋅DC BD BD AB ，0=⋅=⋅DC BD BD AB ，则AC DC AB ⋅+)(的值为（）A 、2B 、22C 、4D 、2453．已知平面向量(11)(11)==-，，，a b ，则向量1322-=a b （）Ａ．(21)--，Ｂ．(21)-，Ｃ．(10)-，Ｄ．(12)，54．若非零向量a 、b 满足｜a 一b ｜＝｜b ｜，则（） (A) ｜2b ｜＞｜a 一2b ｜ (B) ｜2b ｜＜｜a 一2b ｜ (C) ｜2a ｜＞｜2a 一b ｜ (D) ｜2a ｜＜｜2a 一b ｜55．若向量a 、b 满足|a |=|b |=1，a 与b 的夹角为60︒，则a a +a b =（）A ．12 B ．32C. 12+ D ．256．若O 、E 、F 是不共线的任意三点，则以下各式中成立的是（） A ．EF OF OE =+ B. EF OF OE =- C. EF OF OE =-+ D. EF OF OE =-- 57．若向量a 与b 不共线，0≠a b ，且⎛⎫- ⎪⎝⎭a a c =ab a b ，则向量a 与c 的夹角为（） A ．0B ．π6C ．π3D ．π258．已知向量OA =（4，6），OB =（3，5），且OC ⊥OA ，AC ∥OB ，则向量OC =（）（A ）⎪⎭⎫⎝⎛-72,73（B ）⎪⎭⎫ ⎝⎛-214,72 （C ）⎪⎭⎫ ⎝⎛-72,73（D ）⎪⎭⎫ ⎝⎛-214,7259．已知a ，b 是平面内两个互相垂直的单位向量，若向量c 满足0)()(=-⋅-c b c a ,则c 的最大值是（）（A ）1 （B ）2 （C ）2 （D ）22 60．在平行四边形ABCD 中，AC 与BD 交于点O E ，是线段OD 的中点，AE 的延长线与CD 交于点F ．若AC =a ，BD =b ，则AF =（）A ． 1142+a b B ．2133+a b C ．1124+a bD ．1233+a b 61．设a =(1,－2),b =(－3,4),c =(3,2),则(a +2b )·c =（） A.(－15,12) B.0 C.－3 D.－1162．设D 、E 、F 分别是△ABC 的三边BC 、CA 、AB 上的点，且2,DC BD = 2,CE EA = 2,AF FB = 则AD BE CF ++与BC （） A.反向平行B.同向平行C.互相垂直D.既不平行也不垂直63．已知O ，A ，B 是平面上的三个点，直线AB 上有一点C ，满足20AC CB +=，则OC =（） A ．2OA OB -B ．2OA OB -+C ．2133OA OB - D ．1233OA OB -+64．平面向量a ，b 共线的充要条件是（） A. a ，b 方向相同B. a ，b 两向量中至少有一个为零向量C. R λ∃∈，b a λ=D. 存在不全为零的实数1λ，2λ，120a b λλ+=65．在ABC △中，AB =c ，AC =b ．若点D 满足2BD DC =，则AD =（）A ．2133+b cB ．5233-c b C ．2133-b cD ．1233+b c 66．已知两个单位向量a 与b 的夹角为135︒，则||1a b λ+>的充要条件是（）（A ）λ∈ （B ）(λ∈（C ）(,0)(2,)λ∈-∞+∞ （D ）(,(2,)λ∈-∞+∞67．已知平面向量，(2,)b m =-，且a b 23a b +(5,10)--(4,8)--(3,6)--(2,4)--(15,12)- B.0 C.－3 D.－1169．在ABC ∆中，AB=3，AC=2，BC=10，则AB AC ⋅= ( ) A ．23-B ．32- C ．32 D ．2370．已知平面向量a =（1，－3），b =（4，－2），a b λ+与a 垂直，则λ是（） A. －1 B. 1C. －2D. 271．已知a,b,c 为△ABC 的三个内角A,B,C 的对边，向量m = (1-),n =(cosA,sinA),若m ⊥n ,且a cos B +b cos A =c sin C ,则角A,B 的大小分别为（）(A),63ππ(B)2,36ππ(C),36ππ (D),33ππ 72．已知两个单位向量a 与b 的夹角为3π，则a b λ+与a b λ-互相垂直的充要条件是（）A ．2λ=-或2λ= B ．12λ=-或12λ= C ．1λ=-或1λ= D ．λ为任意实数 73．已知向量a 、b 不共线，c k =a +b (k ∈R ),d =a -b ,如果c //d ，那么（） A ．1k =且c 与d 同向 B ．1k =且c 与d 反向 C ．1k =-且c 与d 同向 D ．1k =-且c 与d 反向74．设a ，b ，c 为同一平面内具有相同起点的任意三个非零向量，且满足a 与b 不共线，a ⊥c ，∣a ∣=∣c ∣,则∣b •c ∣的值一定等于（）A ．以a ，b 为两边的三角形面积B 以b ，c 为两边的三角形面积C ．以a ，b 为邻边的平行四边形的面积D 以b ，c 为邻边的平行四边形的面积 75．对于非零向量“”是“”的【 A 】A ．充分不必要条件 B. 必要不充分条件C ．充分必要条件 D. 既不充分也不必要条件76．平面向量a 与b 的夹角为060，(2,0)a =，1b = 则2a b +=（）（A 77．设a 、b 、c 是单位向量，且a ·b ＝0，则()()a c b c -•-的最小值为 ( D )（A ）2- （B 2 （C ）1- (D)178．已知向量()2,1,10,||a a b a b =⋅=+=||b =（）C.5D. 2579．设向量a ，b 满足：||3=a ，||4=b ，0⋅=a b ．以a ，b ，-a b 的模为边长构成三角形，则它的边与半径为1的圆的公共点个数最多为 ( )A ．3 B ．4 C ．5 D ．680．已知1,6,()2==-=a b a b a ，则向量a 与向量b 的夹角是（） A ．6π B ．4π C ．3π D ．2π 81．已知向量(1,0),(0,1),(),a b c ka b k R d a b ===+∈=-，如果//c d ，那么（） A ．1k =且c 与d 同向 B ．1k =且c 与d 反向 C ．1k =-且c 与d 同向 D ．1k =-且c 与d 反向82．设→a ，→b ，→c 为同一平面内具有相同起点的任意三个非零向量，且满足→a 与→b 不共线，→a ⊥→c ，∣→a ∣=∣→c ∣,则∣→b •→c ∣的值一定等于（） A ．以→a ，→b 为邻边的平行四边形的面积 B. 以→b ，→c 为两边的三角形面积 C ．→a ，→b 为两边的三角形面积 D. 以→b ，→c 为邻边的平行四边形的面积83．如图1 D ，E ，F 分别是∆ABC 的边AB ，BC ，CA 的中点，则【 A 】 A ．AD + BE + CF =0 B ．BD CE DF -+=0 C ．AD CE CF +-=0D ．BD BE FC --=0 图1 84．平面向量a 与b 的夹角为060，a=(2,0),|b|=1，则|a+2b|=（）（A （B ）（C ）4 （D ）1285．设非零向量a 、b 、c 满足c b a c b a =+==|,|||||，则>=<b a ,（）（A ）150° （B ）120° （C ）60° （D ）30°86．已知向量a =(2,1)，a ·b = 10，︱a +b ︱=b ︱=（）（A （B （C ）5 （D ）2587．已知向量(1,2)=a ，(2,3)=-b ．若向量c 满足()//+c a b ，()⊥+c a b ，则c =（）A ．77(,)93 B ．77(,)39-- C ．77(,)39 D ．77(,)93--88．已知向量(1,1),(2,),x ==a b 若a +b 与-4b 2a 平行，则实数x 的值是（） A ．-2B ．0C ．1D ．289．a ，b 为平面向量，已知a=（4，3），2a+b=（3，18），则a ，b 夹角的余弦值等于（）（A ）865 （B ）865- （C ）1665 （D ）1665- 90．设向量)21,21(),0,1(==b a ，则下列结论中正确的是（）（A ）||||b a =（B ）22=⋅b a （C ）b b a 与-垂直（D ）b a // 91．已知ABC ∆和点M 满足0MA MB MC --→--→--→+=+.若存在实数m 使得AB AC AM m --→--→--→+=成立，则m=（） A ．2 B ．3 C ．4 D ．592．在Rt ABC ∆中，90C ∠=，4AC =，则AB AC 等于（） A ．16-B ．8-C ．8D ．1693．平面上O,A,B 三点不共线，设,OA=a OB b =，则△OAB 的面积等于（） 2)a b (B) 2)a b 2)a b (D) 2)a b 94．ABC 中，点D 在AB 上，CD 平方ACB ∠．若CB a =，CA b =，1a =，2b =，则CD = （A ）1233a b +（B ）2133a b + （C ）3455a b + （D ）4355a b + 95．设点M 是线段BC 的中点，点A 在直线BC 外，216,BC AB AC AB AC =∣+∣=∣-∣,则AM ∣∣=（）（A ）8（B ）4（C ） 2 （D ）196．已知向量b a ,满足2||,1||,0===⋅b a b a ，则=-|2|b a （）A 、0B 、22C 、4D 、897．设向量(1,0)a =,11(,)22b =,则下列结论中正确的是（） (A)a b = (B)22a b = (C)//a b (D)a b -与b 垂直98．已知ABC ∆和点M 满足0MA MB MC ++=.若存在实m 使得AM AC mAM +=成立，则m =（）B.399．若非零向量a 、b 满足||||b a =，02=⋅+b b a )(，则a 与b 的夹角为( )A ．300 B. 600 C. 1200 D. 1500100．设点M 是线段BC 的中点，点A 在直线BC 外，216,BC AB AC AB AC =+=-,则AM =( )(A) 8 (B) 4 (C) 2 (D) 1101．a ，b 为平面向量，已知a=（4，3），2a+b=（3，18），则a ，b 夹角的余弦值等于（）（A ）865 （B ）865- （C ）1665 （D ）1665- 102．若向量，，，则实数的值为（）（A ）（B ）（C ）2 （D ）6103．设1234...A A A A 是平面直角坐标系中两两不同的四点，若1312A A A A λ=()R λ∈,14A A ,12A A μ(),R μ∈且11λμ+=2，则称14.A A 调和分割13.A A ，一直平面上的点.C D 调和分割点.A B ，则下面说法正确的是（）（A ）C 可能是线段.A B 的中点 (B)(C) .C D 可能同时在线段.A B 上 (D) .C D 不可能同时在线段.A B 的延长线上104．若向量ａ，ｂ，ｃ满足ａ∥ｂ且ａ⊥ｂ，则(2)c a b •+=（）Ａ．4 Ｂ．3 Ｃ．2 Ｄ．0105．若a ，b ，c 均为单位向量，且0=⋅b a ，0)()(≤-⋅-c b c a ，则||c b a -+的最大值为（）A ．12-B ．1C ．2D ．2106．设向量,,a b c 满足1||||1,,,602a b a b a c b c ==⋅=-<-->=，则||c 的最大值等于（）(D)1107．设是向量，命题“若，则∣∣=∣∣”的逆命题是（）（A ）若，则∣∣∣∣ （B ）若，则∣∣∣∣（C ）若∣∣∣∣，则∣∣∣∣ （D ）若∣∣=∣∣，则= -108．设是空间中给定的5个不同的点，则使成立的点的个数为（）A 0B 1C 5D 10109．已知a 与b 均为单位向量，其夹角为θ，有下列四个命题12:10,3P a b πθ⎡⎫+>⇔∈⎪⎢⎣⎭ 22:1,3P a b πθπ⎛⎤+>⇔∈ ⎥⎝⎦ 3:10,3P a b πθ⎡⎫->⇔∈⎪⎢⎣⎭ 4:1,3P a b πθπ⎛⎤->⇔∈ ⎥⎝⎦其中的真命题是（A ）14,P P （B ）13,P P （C ）23,P P （D ）24,P P110．已知向量a=（1,2），b=（1,0），c=（3,4）。