计算方法 大作业(2)
数值分析第二次大作业——编写ln函数实验报告

为一个整体,将 ln(a)进行 Taylor 级数分解,进而按式计算可以求得 ln(x)的值。由于我们选 取级数的前 n 项和近似 ln(a),则有:
Rn (a
1)
(1)n
(a 1)n1 n 1
…;
|
Rn
(a
1)
||
(a 1)n1 n 1
|
。
2
自 92 乔晖 2009011414
精度为 20 位,即 h4 1020 。
int * GetNumber() {return number;}
//获得大数中的整数数组
bool GetSgn() const {return sgn;}
//获得大数的符号
bool IsZero();
//判断大数是否为 0
CBigNumber Reverse() {sgn = !sgn;return *this;} //取相反数
数值分析——编写 ln 函数
实验报告
自 92 乔晖 2009011414
自 92 乔晖 2009011414
数值分析——编写 ln 函数实验报告
目录
一、 实验任务 ................................................... 2
二、 编译环境 ................................................... 2
1u
x 1
35
5
自 92 乔晖 2009011414
数值分析——编写 ln 函数实验报告
其前 n 项和,近似可得 ln(x)的值。
基于以上原理,可以设计迭代算法,累加 2u2i1 得到前 n 项和。每次计算后,判断计 2i 1
数值分析大作业

数值分析上机作业(一)一、算法的设计方案1、幂法求解λ1、λ501幂法主要用于计算矩阵的按模最大的特征值和相应的特征向量,即对于|λ1|≥|λ2|≥.....≥|λn|可以采用幂法直接求出λ1,但在本题中λ1≤λ2≤……≤λ501,我们无法判断按模最大的特征值。
但是由矩阵A的特征值条件可知|λ1|和|λ501|之间必然有一个是最大的,通过对矩阵A使用幂法迭代一定次数后得到满足精度ε=10−12的特征值λ0,然后在对矩阵A做如下的平移:B=A-λ0I由线性代数(A-PI)x=(λ-p)x可得矩阵B的特征值为:λ1-λ0、λ2-λ0…….λ501-λ0。
对B矩阵采用幂法求出B矩阵按模最大的特征值为λ∗=λ501-λ0,所以λ501=λ∗+λ0,比较λ0与λ501的大小,若λ0>λ501则λ1=λ501,λ501=λ0;若λ0<λ501,则令t=λ501,λ1=λ0,λ501=t。
求矩阵M按模最大的特征值λ的具体算法如下:任取非零向量u0∈R nηk−1=u T(k−1)∗u k−1y k−1=u k−1ηk−1u k=Ay k−1βk=y Tk−1u k(k=1,2,3……)当|βk−βk−1||βk|≤ε=10−12时,迭终终止,并且令λ1=βk2、反幂法计算λs和λik由已知条件可知λs是矩阵A 按模最小的特征值,可以应用反幂法直接求解出λs。
使用带偏移量的反幂法求解λik,其中偏移量为μk=λ1+kλ501−λ140(k=1,2,3…39),构造矩阵C=A-μk I,矩阵C的特征值为λik−μk,对矩阵C使用反幂法求得按模最小特征值λ0,则有λik=1λ0+μk。
求解矩阵M按模最小特征值的具体算法如下:任取非零向量u 0∈R n ηk−1= u T (k−1)∗u k−1y k−1=u k−1ηk−1 Au k =y k−1βk =y T k−1u k (k=1,2,3……)在反幂法中每一次迭代都要求解线性方程组Au k =y k−1,当K 足够大时,取λn =1βk 。
化工热力学大作业---乙醇与水物性分析

化工热力学大作业学院:化学化工学院班级:学号:姓名:指导老师:1. 计算101.3kPa 下,乙醇(1)-水(2)体系汽液平衡数据1)泡点温度和组成的计算已知:平衡压力P ,液相组成x1,x2 ···xNVi si S i i i i P P x y ϕϕγˆ= ∑=i i i y y y / 泡点温度T ,汽相组成y 1,y 2 ···y n 采用以下流程计算:可得到泡点温度和组成2)露点温度和组成的计算已知P, 气相组成y1,y2…….yN ,s i S i i Vii i P Py x ϕγϕˆ=∑=ii i i x x x / 露点温度T ,液相组成x 1,x 2 ···x n 采用以下流程计算:可得到露点温度和组成3)计算过程运用化工软件Aspen计算①选择模板为General with Metric Units;Run Type为物性分析(Property Analysis)②组分为乙醇(C2H5OH,ETHANOL)和水(H2O)物性方法为NRTL③乙醇及水的流率均设为50kmol/h初输入温度为25℃,压力为101.325KPa。
④设定可调变量为乙醇的摩尔分数,变化范围0—1,增量为0.05,则可取20个点。
⑤选择物性参数露点温度(TDEW)及泡点温度(TBUB),温度均为℃。
最后以乙醇摩尔分数为X坐标,露点温度(TDEW)及泡点温度(TBUB)为Y坐标,得到下表及下图。
NRTL活度系数模型乙醇取不同摩尔分率时对应的不同泡点温度及露点温度表(NRTL)露点温度及泡点温度图(NRTL)⑥组分为乙醇(C2H5OH, ETHANOL)和水(H2O)物性方法改为WILSON。
WILSON活度系数模型乙醇取不同摩尔分率时对应的不同泡点温度及露点温度表(WILSON)露点温度及泡点温度图(WILSON)由图可得,在X=0.9时泡点线与露点线相交,表明有共沸点。
共沸点的组成为乙醇摩尔分率0.9,水的摩尔分率0.1,共沸温度为78.15℃。
飞行器总体设计 大作业第二章(2)
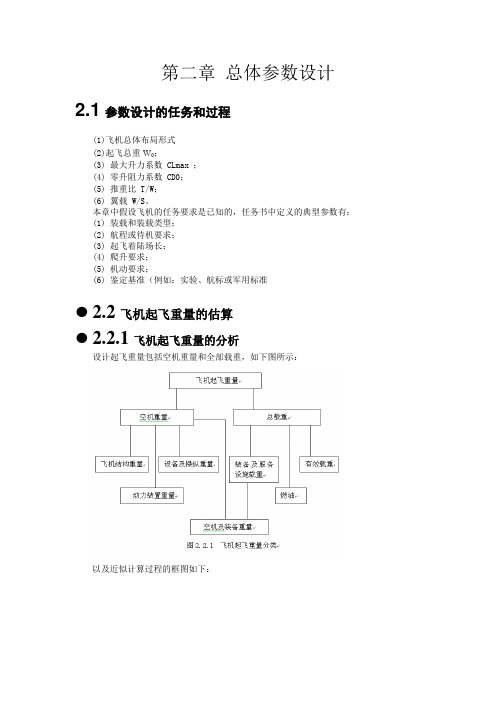
第二章总体参数设计2.1参数设计的任务和过程(1)飞机总体布局形式(2)起飞总重W0;(3) 最大升力系数 CLmax ;(4) 零升阻力系数 CD0;(5) 推重比 T/W;(6) 翼载 W/S。
本章中假设飞机的任务要求是已知的,任务书中定义的典型参数有:(1) 装载和装载类型;(2) 航程或待机要求;(3) 起飞着陆场长;(4) 爬升要求;(5) 机动要求;(6) 鉴定基准(例如:实验、航标或军用标准●2.2飞机起飞重量的估算●2.2.1飞机起飞重量的分析设计起飞重量包括空机重量和全部载重,如下图所示:以及近似计算过程的框图如下:W 0为飞机的起飞总重,它由以下几部分组成:e f p W W W W ++=0)(eq en st f p W W W W W ++++=Wp ——有效载荷(含乘员)重量;Wf ——燃油重量,包括任务燃油(可用燃油)、备份燃油(安全余油)及死油三部分; We ——空机重量,主要包括结构(机体、起落架、操纵系统等)重量、动力装置重量及设备重量三部分; 因为:e f p W W W W ++=00000)/()/(W W W W W W W e f p ++=e f p W W W W ++=0/(00)/W W所以:000//1W W W W W W e f p--=其中:0/w w f、0/w w e 分别称为燃油重量系数、空机重量系数。
在有效载重Wp 已知的情况下,求出空机重量系数0/w w e 和燃油重量系数 0/w w f (或燃油重量f W ),就可求出0W 。
2.2.2各重量系数的预测一、空机重量系数0/w w e的确定起飞重量中,空机重量可以用对应的空机重量系数乘以起飞重量而得到.空机空重:EE O OW W W W =⨯ 空机重量系数:C EO VS OW AW K W = 相对于O W 的经验空机重量系数统计值对于变后掠翼VS K =1.04, 正常机翼VS K =1.00 取 A=0.93, C=-0.07 VSK =1.00空机重量系数0.070.93ETO TOW W W -= 二、燃油重量系数0/w w f 的确定飞行任务中使用燃油重量为 (1)fused ff TO W m W =-任务燃油重量为 (1)F ff TO fres W m W W =-+ 其中 ff m 为任务燃油系数,fres W 为额外燃油重量, 任务燃油系数ff m = 710i i i iW W =+=∏ 这里注意取0W =TO W 典型飞行任务剖面图各任务段重量比的计算: 任务抛面 i i W W /1+发动机启动和暖机0.9900 取自AAA 典型的暖机段燃油系数 滑 跑 0.9950 取自AAA 典型的滑跑段燃油系数 起 飞 0.9950 取自AAA 典型的起飞段燃油系数爬升到巡航高度并加速到巡航速度0.9850 根据经验公式巡 航 0.8185 根据经验公式待 机 0.9323 根据经验公式取m in 30=ltr E施放有效载荷 1.0000待 机 0.9993 式取m in 5=ltr E根据经验公返 航 0.8185 根据经验公式下 降 0.9850 取自AAA 典型的下降段燃油系数 着陆、滑行和关机0.9950取自AAA 典型的着陆/滑行段燃油系数现在开始计算空中中巡航段和待机段的重量比 (1)巡航段54W W发动机耗油率C 发动机类型巡航耗油率待机耗油率2滑跑1发动机启动和暖机起飞4爬升并加速5巡航6待机7下降8着陆滑行并关机本运输机采用双转子,轴流式,高涵道比涡轮风扇发动机V2500这种发动机推力大、耗油率低。
计算方法大作业1 克服Runge现象

x3
x2
x
1
S1 ( x)
-0.34685
0.2086
0.073964
0.038462
S2 (x)
S (xi 0 ) S x(i 0 )
S
'
(xi
0) S
xi' (
0 )i
S
'
'
x(i
0)S
xi' ' (
0)
1 ,n2, . . . , 1
(1)
这里共有了 3n-3 个条件,再加上条件(2)中的 n+1 个插值条件,共有 4n-2 个条件,
因此还需要 2 个方程才能确定 S (x) .通常可在区间[a, b]的端点 a x0,b xn 上各加一个边
dn1
1
2
Mn
dn
(6)
2 1
2
2
2
1 M1 d1
M2
d2
n 1
2
n
1
M
n
1
dn1
n
n 2 M n dn
由式(1)内点拼接条件,可得
i M i1 2M i i M i1 d j i 1, 2,..., n 1
(3) (4)
其中
i
hi 1 hi1
, hi
i
hi hi 1
有限元分析大作业

有限元大作业一题目要求:图1所示为一悬臂梁,在端部承受载荷,材料弹性模量为E,泊松比为1/3,悬臂梁的厚度(板厚)为t,若该粱被划分为两个单元,单元和节点编号如图所示,试按平面应力问题计算各个节点位移计支反力。
一、单元划分1.计算简图及单元划分如下所示:2.进行节点及单元编号节点i j m单元① 2 3 4② 3 2 13.节点坐标值节点号1 2 3 4坐标值X 2 2 0 0Y 1 0 1 0二、计算单元刚度矩阵1、计算每个单元面积△以及i b ,i c (m j i i ,,=) ①②单元的面积相等,即12121=⨯⨯=∆ 单元①的i b ,i c⎩⎨⎧=--==-=0)(1m j i m j i y x c y y b ⎩⎨⎧=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧-=--=-=-=2)(1j i mj i m y x c y y b 对平面应力问题,其表达式为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+∆-=s r s r sr s r s r s r s r s r b b uc c cb u b uc b c u c ub c c u b b u Et Krs 21212121)1(42 然后对单元①求解单元刚度子矩阵2==i r 2==i s []⎥⎦⎤⎢⎣⎡=3/1001329)1(22Et K 2==i r 3==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(23Et K2==i r 4==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(24Et K 3==j r 3==j s []⎥⎦⎤⎢⎣⎡=4003/4329)1(33Et K 3==j r 2==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(32Et K 3==j r 4==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(34Et K 4==m r 4==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)1(44Et K 4==m r 2==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(42Et K 4==m r 3==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(43Et K由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)1(Et K将单元①的单元刚度矩阵补零升阶变为单元刚度矩阵,其在总体刚度矩阵中的位置为:节点号→单元②的i b ,i c⎩⎨⎧=--=-=-=0)(1m j im j i y x c y y b ⎩⎨⎧-=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧=--==-=2)(1j i mj i m y x c y y b 然后对单元 求解单元刚度子矩阵:3==i r 3==i s []⎥⎦⎤⎢⎣⎡=3/1001329)2(33Et K 3==i r 2==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(32Et K 3==i r 1==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(31Et K 1 2 3 412[])1(22K[])1(23K[])1(24K3[])1(32K[])1(33K[])1(34K4[])1(42K[])1(43K[])1(44K2==j r 2==j s []⎥⎦⎤⎢⎣⎡=4003/4329)2(22Et K 2==j r 3==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(23Et K 2==j r 1==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(21Et K 1==m r 1==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)2(11Et K 1==m r 3==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(13Et K 1==m r 2==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(12Et K 由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)2(Et K将单元②的单元刚度矩阵补零升阶变为单元贡献矩阵,其在总体刚度矩阵中的位置为:节点号→1 2 3 41 [])2(11K[])2(12K[])2(13K2 [])2(21K[])2(22K[])2(23K3 [])2(31K [])2(32K [])2(33K 4三、计算总体刚度矩阵总体刚度矩阵是由各单元的贡献矩阵迭加而成)2()1(][][][][K K K K e +==∑四、进行节点约束处理根据节点约束情况,在总刚矩阵中可采用划行划列处理约束的方法,由题目易知,节点3和4的已知水平位移和垂直位移都为零,划去其相对应的行和列,则总刚矩阵由8阶变为4阶,矩阵如下:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------2/02/03/13043/203/73/23/443/23/133/43/23/43/43/73292211p p v u v u Et329][Et K =1 2 3 413/133/43/43/743/23/23/4----3/13/23/21----000243/23/23/4----3/13003/73/43/403/13/23/21----33/13/23/21----3/43/403/13003/743/23/23/4----40003/13/23/21----43/23/23/4----3/133/43/43/7化简⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------Et p Et p v u v u 3/1603/160130122072412213424472211 五、求解线性方程组方法:采用LU 分解法 1.求解矩阵[]U 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------75/10775/640075/6475/353007/767/27/7502447~7/877/87/7607/87/337/207/767/27/7502447~13012207241221342447⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----353/44900075/6475/353007/767/27/7502447~ 得到的[]U 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=353/44900075/6475/353007/767/27/7502447U 2.求解矩阵[]L 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----13012207241221342447353/44900075/6475/353007/767/27/75024471353/6475/767/20175/27/40017/40001 得到的[]L 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=13012207241221342447L3.进行求解⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⇒⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=Et p Et p Et p y Et p Et p Ly 79425/850800225/323/1603/1603/160⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡Et p Et p Et p v u v u y v u v u U 79425/850800225/323/160353/44900075/6475/353007/7675/27/750244722112211 解得Et p v /422.82-= Et p u /497.12-= Et p v /028.91-= Et p u /897.11=于是求得各节点的位移为:⎩⎨⎧-==Etp v Etp u /028.9/897.111 ⎩⎨⎧-=-=Etp v Etp u /422.8/497.122 ⎩⎨⎧==033v u ⎩⎨⎧==044v u 六、求解相应的支反力(运用静力学的平衡方程进行求解)3号节点和4号节点的支反力如下图所示:。
北京化工大学高等化热大作业-基团贡献法
浅谈基团贡献法引言不久前,我前往导师XXX的办公室,与他沟通交流学业上的问题。
谈话间,王老师提及的一种建立自由基聚合反应过程机理模型的方法──链节分析法[1],引起了我极大的兴趣。
这一方法可以对复杂的聚合反应过程进行准确的动态模拟,解决了以往须同时求解无限多个微分方程才能模拟聚合过程的难题。
通过这篇文献[1]我得知,对于高分子聚合物体系的热力学性质的处理,一直是建立聚合反应机理模型的难题之一。
此法[1]不再把组成和链长不同的无穷多的聚合物大分子作为组分,而是将流程模拟系统的组分中出现的C、E、A·、R·等基本单元,参考其相应的单体物性,从而得到大分子聚合物的各种热力学性质。
高分子的绝大部分热力学性质如密度ρ、比热容C p、焓H、摩尔体积V b、各种临界参数都能利用Joback基团贡献法,由基本单元的物性计算得到。
联想到化热课堂上与基团贡献法有关的似乎只有UNIFAC模型,因此我想对物性估算法中的基团贡献法展开讨论,描述各种不同的方法并加以简单的评价。
这便是本题目的来源。
第1章临界参数估算方法不论是通过自己对化工热力学的学习,还是通过对文献的查阅,都不难得出这样的结论:对纯物质而言,临界参数是最重要的物性参数之一。
其实,在所有的PVT关系中,无论是对应状态法还是状态方程法都与临界数据有关。
对应状态法已成为应用热力学的最基本法则[2],借助于对应状态法,物质的几乎所有的热力学参数和大量的传递参数可被预测,而对应状态法的使用又强烈地依赖于临界数据。
此外,涉及到临界现象的高压操作,如超临界萃取和石油钻井[2],也与临界参数密切相关。
总而言之,临界数据是化工设计和计算中不可缺少的重要数据。
临界参数如此重要,前人自然少不了花费巨大精力对其进行收集、整理和评定,但据我了解,所收集的临界数据大多局限于稳定物质的临界数据。
虽然近几年对不稳定物质临界参数测定方法的研究在开展着,并且也测定了一些不稳定物质的临界参数,但大部分的不稳定物质仍由于测定难度大而缺乏实测的临界数据。
电大安装工程估价大作业(1-4)ok
安装工程估价大作业1一、单选或多选题(每小题3分,共24分)1.建设工程定额由下列(.建设工程定额由下列( )定额构成。
)定额构成。
A .建筑工程.建筑工程 B .安装工程.安装工程 C .市政工程.市政工程 D .装饰工程.装饰工程2.2000年颁布的《全国统一安装工程预算定额》共分12册。
第二册指的是(册。
第二册指的是( )预算定额。
预算定额。
A .通风空调工程.通风空调工程B .电气设备安装.电气设备安装C .消防及安全防范设备安装工程.消防及安全防范设备安装工程D .给排水、采暖、燃气工程.给排水、采暖、燃气工程3.安装工程预算定额基价是由( )三部分组成。
)三部分组成。
A .定额人工费.定额人工费B .定额材料费.定额材料费C .定额机械台班费.定额机械台班费D .管理费.管理费4.按生产要素,可把安装工程定额分为( )。
)。
A .劳动定额.劳动定额 B .施工定额.施工定额 C .机械台班定额.机械台班定额 D .材料消耗定额.材料消耗定额 E .预算定额.预算定额5.材料从采购、运输到保管,在使用前所发生的全部费用构成了材料预算价格,它由材料的( )价格组成。
)价格组成。
A .供应价.供应价 B .供销部门手续费.供销部门手续费 C .运杂费.运杂费 D .采购及保管费.采购及保管费 E .检验试验费.检验试验费6.按系数计算的费用,在《定额解释汇编》中将其计算系数分为子目系数和综合系数两类。
下列系数中属于综合系数的是(两类。
下列系数中属于综合系数的是( )。
)。
A .脚手架搭拆系数.脚手架搭拆系数 B .高层建筑增加系数.高层建筑增加系数C .采暖、通风及民用建筑工程中的工艺管道系统调整费系数采暖、通风及民用建筑工程中的工艺管道系统调整费系数D .特殊地区(或条件)施工增加费系数.特殊地区(或条件)施工增加费系数E .配合主体结构现场浇注混凝土预留孔洞费用增加系数7.在安装工程预算定额的应用时,要注意定额各册的联系和交叉性。
最优化方法大作业模板
命题人:审核人:大作业学期:至学年度第学期课程:最优化方法课程代号:签到序号:使用班级:姓名:学号:题号一二三四五六七八九十总分得分一、(目标1)请从以下6种算法中任选一种,说明算法的来源、定义、基本思想和优缺点,并给出算法步骤(包含算法流程图)和例子(包含程序与运算结果)。
①禁忌搜索算法;②模拟退火算法;③遗传算法;④神经网络算法;⑤粒子群算法;⑥蚁群算法。
二、(目标1)某工厂生产甲、乙两种产品,已知生产这两种产品需要消耗三种材料A 、B 和C ,其中生产过程中材料的单位产品消耗量和总量,以及单位产品的利润如下表所示。
该如何配置安排生产计划,使得工厂所获得的利润最大?材料甲乙资源总量材料A (Kg )3265材料B (Kg )2140材料C (Kg )0375单位利润(元/件)15002500-(1)要保证工厂利润的最大化,写出相应的生产计划数学模型;(2)根据对偶理论,直接写出该线性规划的对偶问题;(3)采用单纯形表法对该该线性规划问题进行求解,写出详细的计算过程;(4)采用Matlab 软件对该线性规划问题进行求解,写出完整的源程序,并给出程序运行结果;(5)讨论当材料B 的资源总量发生变化时,该线性规划问题的最优解会如何变化?课程目标目标1……题号一、二、三、四、五……分值20、25、20、20、15……得分得分三、(目标1)求解下列无约束非线性规划问题(1)采用黄金分割法求解:min 4()24f x x x =++。
初始区间为[-1.0],精度为ε=10-4。
(要求:采用黄金分割法进行Matlab 编程求解,写出源程序,并给出运行结果,列出迭代过程的数据表格)(2)采用阻尼牛顿法求解:222121212min (,)4f x x x x x x =+-。
分别取两个初始点:x A =(1,1)T ,x B =(3,4)T 。
(要求:采用阻尼牛顿法进行Matlab 编程求解,并给出运行结果,列出迭代过程的数据表格)四、(目标1)求解下列约束非线性规划问题:22112212121212min ()23532..00f x x x x x x x x x x x s t x x =-+--+≤⎧⎪-≤⎪⎨≥⎪⎪≥⎩(1)采用罚函数法进行求解,需写出具体计算过程;(2)采用二次规划方法进行求解,需写出具体计算过程,并进行MATLAB 编程,写出源程序和运算结果;五、(目标1)(1)某商店在未来的4个月里,准备利用它的一个仓库来专门经营某种商品,仓库的最大容量为1000单位,而且该商店每月只能出卖仓库现有的货。
贝塔系数的确定方法
中级财务管理大作业——贝塔系数地确定方法作业要求关注和收集一家上市公司一段时间内地交易价格等数据,收集沪深指数地交易数据.要求:⑴、以月度为周期计算公司四月底地贝塔系数.⑵、以周为周期计算公司四月底地贝塔系数,观察按照不同周期计算地贝塔系数是否有不同?⑶、计算公司地股价变动地标准差.计算过程说明(一) 计算贝塔系数我选取了年月至年月,年间上海证券交易所上市地上汽集团(代码)地月度收益率、周度收益率以及沪深指数地月度收益率、周度收益率;年月至年月,月间上汽集团(代码)每天地收益率以及沪深指数每天地收益率,分别利用贝塔系数地计算定义公式和最小二乘法地回归方法来计算上汽集团地贝塔系数.文档收集自网络,仅用于个人学习以月度为周期计算上汽集团地贝他系数为例说明两种计算方法地计算过程如下: 贝塔系数地定义公式沪深指数地月度收益率地计算,用当月末沪深地收盘指数减去上月末地收盘指数,再除以上月末地收盘指数获得.文档收集自网络,仅用于个人学习股票月度收益率地计算用本月末地收盘价减去上月末地收盘价除以上月末地收盘价获得,不考虑除权除息地影响. 贝塔系数地定义公式:2),cov(M j M j σβ=,其中()是上汽集团地月度收益率与沪深指数收益率之间地协方差,σ是沪深指数收益率地方差,计算得出上汽集团地贝塔系数为.文档收集自网络,仅用于个人学习调整后地贝塔系数×历史贝塔系数×,计算得出调整后地贝塔系数为.最小二乘法回归贝塔系数市场期望收益率与个别资产期望收益率之间地计量经济模型为:t Mt jt r b a r ξ+⨯+=式中:为回归地截距,为回归地斜率,及回归地贝塔系数.经最小二乘法回归得到地贝塔系数为,与通过贝塔系数地定义公式计算得出地结果一致. 计算公司股价变动地标准差 公司股价变动地标准差地计算公式为:()∑=-=N i i xN 121μσ式中:为收集地股价数据地个数,为各个股价数据,μ为股价平均值.计算结果计算贝塔系数以月度为周期 以周度为周期 以天为周期 贝塔系数调整后地贝塔系数计算结果表明,使用相同历史时期地数据,采用不同时间长度为单位计算地收益率所得到地地贝塔系数基本一致;但是使用不同历史时期地数据时,采用不同时间长度为单位计算地收益率所得到地地贝塔系数明显不同,历史时期地不同通常会显著改变公司地贝塔系数.文档收集自网络,仅用于个人学习计算公司股价变动地标准差以月度为周期以周度为周期以天为周期股价变动地标准差。
