机器人应用系统三维建模2-3圆弧命令
圆弧运动指令

圆弧运动指令什么是圆弧运动指令?圆弧运动指令是指在机器人控制系统中,通过指令实现机器人末端执行器(例如机器人手臂)在平面或空间中描述一个圆弧轨迹运动的操作。
圆弧运动指令具有精确性和灵活性,可用于各种应用领域,如工业自动化、物流和装配线、医疗和服务机器人等。
圆弧运动指令的应用圆弧运动指令广泛应用于许多领域,以下是其中的一些示例:1.工业自动化:在汽车制造、电子产品装配等工业生产线上,通过使用圆弧运动指令可以实现机器人手臂的高速、高精度的路径规划和运动控制,从而提高生产效率和产品质量。
2.物流和装配线:在物流仓储和装配线中,机器人通常需要将物体从一个位置移动到另一个位置。
通过使用圆弧运动指令,机器人可以更准确地沿着曲线轨迹进行运动,从而避免碰撞并提高物体的处理效率。
3.医疗和服务机器人:在医疗行业和服务领域中,机器人有时需要在空间中进行精细操作,例如手术和康复训练。
圆弧运动指令可以帮助机器人在患者身体周围绘制圆弧运动,以实现更准确和安全的操作。
4.艺术和娱乐:圆弧运动指令也可以应用于艺术装置和娱乐设备中。
例如,在表演舞台上,机器人可以通过圆弧运动指令展示精巧的舞蹈动作,给观众带来视觉上的享受。
圆弧运动指令的实现方式实现圆弧运动指令的方法取决于具体的机器人控制系统和硬件。
以下是一些常见的实现方式:1.关节插补:在具备多个关节的机器人中,可以通过控制每个关节的角度和速度来实现圆弧运动。
控制系统根据指定的圆弧轨迹,计算每个关节应该移动的位置和速度,从而实现整个机器人末端执行器的圆弧运动。
2.笛卡尔插补:在一些特殊的机器人系统中,可以通过控制机器人末端执行器的位置和姿态来实现圆弧运动。
控制系统根据指定的圆弧轨迹,计算机器人末端执行器应该移动的位置和方向,从而实现圆弧运动。
3.传递函数:在一些高级的机器人控制系统中,可以使用传递函数来实现圆弧运动。
传递函数是一种数学方法,可以将指定的输入参数映射到机器人的输出运动参数,从而实现圆弧路径的控制。
第三节 圆弧指令的格式及应用

(1)指令格式 G02(03)X Z R ; G02表示顺时针圆弧插补; G03表示逆时针圆弧插补。
X Z 为圆弧的终点坐标值 R 为圆弧半径。
(AB)1 (AB)2
G03 X40.0 Z2.68 R20.0; G02 X40.0 Z2.68 R20.0;
(1)倒角指令格式
指令格式 G01 X(U)_C_ F ; G01 Z(W) C F ;
X(U) 为倒角前轮廓尖角处(图中A、C点)在 X向的绝对坐标或增量坐标;
Z(W) 为倒角前轮廓尖角处(图中A、C点)在 Z向的绝对坐标或增量坐标;
C 为倒角的直角 X(U) R F ; G01 Z(W) R F ;
2)FANUC系统中的倒角与倒圆指令仅适用于两直
角边间的倒角与倒圆。
3)倒角与倒圆指令格式可用于凸、凹形尖角轮廓。
O0302; …… G01 X30.0 C-5.0 F100;
W-20.0 R5.0; X50.0 C-2.0; ……
X(U) 为倒圆前轮廓尖角处(图中B点) 在X向的绝对坐标或增量坐标;
Z(W) 为倒圆前轮廓尖角处(图中B点) 在Z向的绝对坐标或增量坐标;
R 为倒圆半径。
(3)使用倒角与倒圆指令时的注意事项
1)倒角与倒圆指令中的R值与C值有正负之分。当
倒角与倒圆的方向指向另一坐标轴的正方向时,其
R值与C值为正,反之则为负。(实际机床情况)
4、G2-G3命令的应用

2、G02 G03指令的格式:
1用R指定圆心位置,其格式如下: G02(G03)X(U) Z(W) R F ;
2用I、K指定圆心位置,其格式如下: G02(G03)X(U) Z(W) I K F ;
注意事项:
1、以上格式中 G02 为顺圆插补 G03为逆圆插补; 2 、X Z 为绝对编程坐标,U W 为相对编程坐标; 3、 I K 为圆心相对起点的坐标(I以半径量表达); 4、 用R指定圆心位置时从圆弧起点到终点有两个圆弧可能编 程时,小于等于180°弧为正,圆心角大于180°R为负值。此 时最好以I K指定圆心); 5、 I、K、R同时指定时 R有效,I、K无效。 6 、G02、G03 用R指定圆心时不能描述整圆;
G0 Z0.2; G0 X20.0;
G0 X100.0 Z100.0;
G03 X40.5 Z-10.0 R20.0 F0.15; 、、、、、、
专题练习:综合倒角
素材:
综合倒角程序:(不记刀尖角)
O0005;
素材:
M18;
N1 G0 T101;
G97 X13.5 M1 2)
3、绝对值用R表圆心位置
G0 X20.0 Z2.0;
G99 G01 Z-30.0 F0.08
G02 X40.0Z-40.0 R10.0 F0.06
4、增量值R表圆心位置
G0 X100.0 Z100.0; G0 U-80.0 W-98.0; G99 G01 W-32.0 F0.08; G02 U20.0 W-10.0 R10.0F0.06;
2、车圆法:利用不同圆弧车削,最终达 到加工要求
R1=OA=OB BD=AE= R12 R 2 BC=AC=R- R12 R 2 R1=OA=OB BD=AE= R12 R 2 BC=AC=R- R12 R 2
机器人空间三点圆弧的圆心算法及MATLAB实现

信 息 技 术DOI:10.16661/ki.1672-3791.2104-5042-9113机器人空间三点圆弧的圆心算法及MATLAB实现张辉 李应岐 方晓峰(火箭军工程大学基础部 陕西西安 710025)摘 要:基于机器人终端TCP经历的空间三个不共线的点,利用两种算法得到了通过此三点的空间圆弧圆心坐标的解析表达式,完善了已有文献的方法和结论;同时对于给定空间三点的坐标值,利用新提出的算法得到了圆心坐标的值;最后给定三组三点坐标值进行MATLAB运行平均时间比较,新提出的算法运行效率最高,优于已有文献提出的算法可作为首选算法,为机器人利用示教过程进行现场应用提供了有效支撑。
关键词:机器人 圆弧 圆心 MATLAB 向量积中图分类号:TP242 文献标识码:A文章编号:1672-3791(2021)05(c)-0021-04Center Algorithm of Three-Points Arc in Robot Space and ItsRealization with MATLABZHANG Hui LI Yingqi FANG Xiaofeng(Department of Basic Courses, Rocket Force University of Engineering, Xi'an, Shaanxi Province,710025 China )Abstract : Based on the three non-collinear points in the space experienced by the robot terminal TCP, using two algorithms, the analytic expression of the space arc center coordinates through the three points is obtained, which improves the methods and conclusions of the existing literature; at the same time, for a given coordinate value of the three points in the space, the value of the center coordinates is obtained by using the new algorithm; f inally, for the given three groups of three-point coordinate values, the average running time of MATLAB is compared. The new algorithm has the highest running eff iciency, which is better than the algorithm proposed in the existing literature. It can be used as the preferred algorithm, and provides effective support for the robot to use the teaching process for f ield application.Key Words : Robot; Arc; Center of circle; MATLAB; Vector product基金项目:陕西高等教育教学改革研究重点攻关项目(项目编号:19BG038)。
G2G3 圆弧插补指令
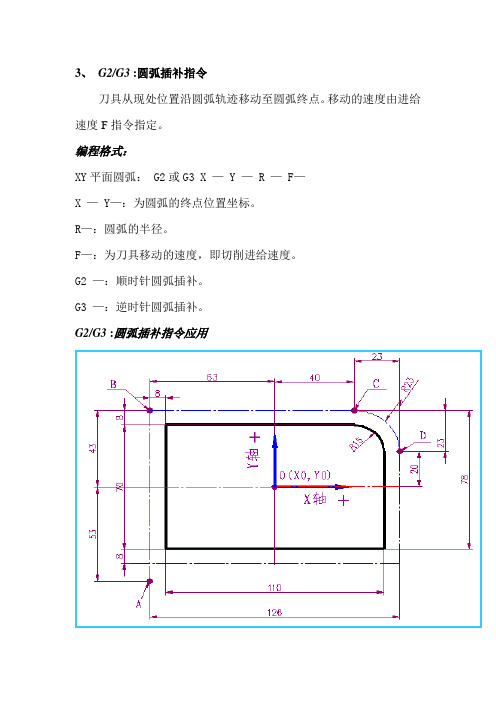
3、G2/G3 :圆弧插补指令刀具从现处位置沿圆弧轨迹移动至圆弧终点。
移动的速度由进给速度F指令指定。
编程格式:XY平面圆弧: G2或G3 X — Y — R — F—X — Y—:为圆弧的终点位置坐标。
R—:圆弧的半径。
F—:为刀具移动的速度,即切削进给速度。
G2 —:顺时针圆弧插补。
G3 —:逆时针圆弧插补。
G2/G3 :圆弧插补指令应用将执行动作:刀具从现处位置C点沿CD之间的圆弧轨迹移移动至圆弧终点D。
CD段圆弧是一段顺时针圆弧轨迹,所以用G2指令。
加工程序:绝对坐标编程:N80 G90 G2 X63.0 Y20.0 R23.0相对坐标编程:N80 G91 G2 X23.0 Y-23.0 R23.0 F100平面的选择:数控系统一般可以加工XY、XZ、YZ平面的圆弧。
G17:该指令表示选择XY平面,在此平面中进行圆弧插补和刀具补偿。
此代码为系统初始代码。
电源一接通G17 就作为平面选择的起始代码而自动生效。
G18:该指令表示选择XZ平面,在此平面中进行圆弧插补和刀具补偿。
G19:该指令表示选择YZ平面,在此平面中进行圆弧插补和刀具补偿。
G17、G18、G19平面顺逆圆弧判断示意图:G17、G18、G19平面顺逆圆弧判断用IJK代替R编程I:表示圆心点相对起点在X轴上的增量坐标。
J:表示圆心点相对起点在Y轴上的增量坐标。
K:表示圆心点相对起点在Z轴上的增量坐标。
用IJK代替R编程应用加工程序:。
N50 G1 G90 X15 Y0N60 G2 I-15 。
(完整word版)圆弧插补指令G02G03教案

圆弧插补指令G02、G03备课:刘明教学目标:1.正确分析给定的零件图,制订合理的加工工艺和编写正确的精加工程序。
2.针对不同的加工对象会选择合理的进刀、退刀路线。
3.熟练掌握G02和G03指令的使用,顺圆弧和逆圆弧的判断方法。
4.培养学生应用所学知识解决实际生产中的问题,学会举一反三和与他人进行合作和交流,培养学生的团队意识。
教学重点:1.G02G03指令的格式应用判断方法。
2.工艺分析和加工工艺路线的制订。
教学过程:学生在课下或自习课上对本节所要学习的内容进行全面的预习,在此基础上由老师先来讲解本节课的内容。
首先来学习G2、G3指令一、圆弧插补(G02或G2,G03或G3)1)指令格式:G02 X(U)_Z(W)_I_K_F_ ;G02 X(U) Z(W) R F ;G03 X(U)_Z(W)_I_K_F_ ;G03 X(U) Z(W) R F ;2)指令功能:3)指令说明:①G02为顺时针圆弧插补指令,G03为逆时针圆弧插补指令。
圆弧的顺、逆方向判断见图1左图,朝着与圆弧所在平面相垂直的坐标轴的负方向看,顺时针为G02,逆时针为G03,图1右图分别表示了车床前置刀架和后置刀架对圆弧顺与逆方向的判断;图1 圆弧的顺、逆方向②如图2,采用绝对坐标编程,X、Z为圆弧终点坐标值;采用增量坐标编程,U、W为圆弧终点相对圆弧起点的坐标增量,R是圆弧半径,当圆弧所对圆心角为0°~180°时,R取正值;当圆心角为180°~360°时,R取负值。
I、K为圆心在X、Z轴方向上相对圆弧起点的坐标增量(用半径值表示),I、K为零时可以省略。
图2 圆弧绝对坐标,相对坐标图3 圆弧插补G02 X50.0 Z30.0 I25.0 F0.3; G03 X87.98 Z50.0 I-30.0 K-40.0 F0.3;G02 U20.0 W-20.0 I25.0 F0.3; /绝对坐标,直径编程G02 X50.Z30.0 R25.0 F0.3; G03 U37.98 W-30.0 I-30.0 K-40.0 F0.3;G02 U20.0 W-20.0 R25.0 F0.3; /相对坐标,直径编程教学环节:一、复习G00、G01指令引入新课请用G0、G1指令编出图4的精加工程序。
G02、G03圆弧插补指令应用比赛说课课件
圆弧顺、逆 圆弧终点坐标
绝对值 X、Z 增量值 U、W
F—
确定圆心位置 进给速度
α≤180° 用+R 360°>α>180° 用-R
说 教 学 过 程——讲授新课
格式二(多媒体课件和公式计算法)
(启发提问和实体展示法)
以车间现有实体零件为例进 行展示,设问、导入新课。
说 教 学 过 程——讲授新课
(多媒体演示法)
圆弧插补指令——命令刀具在指定平面内按给 定的进给速度F作圆弧运动,切削出圆弧轮廓。
一、定义
圆弧插 补指令 顺时针圆弧插补指令G02 逆时针圆弧插补指令G03
说 教 学 过 程——讲授新课
(小组讨论法)
任务一:编制国际象棋——象的圆弧部分程序
编程格式 格式一
格式二
程序段
绝对值 增量值 绝对值 增量值
结论:使用格式一较方便。因为通常情况下数控 车床的车削的圆弧角度大多小于180°。
任务二
完成国际象棋——象的精加工程序编制
建议:分析; %0001; G90 G00 M03 S1000 T0101 F0.2; X0 Z2; G01 Z0; X6; G03 X10 Z-2 R2; G01 Z-4; G02 X14 Z-6 R2; G01 Z-11; X10 Z-16; Z-31; G02 X18 Z-35 R4; G01 X20 Z-36; Z-38.5 X17.5 Z-40.5; X20 Z-42.5; Z-45; X24; G00 X50 Z50 M05; M30;
说 教 学 过 程——讲授新课
三、圆弧顺逆的判断(角色扮演法)
电子教案-工业机器人应用系统三维建模(SolidWorks)+文清平+教学资源教学课件2-3圆弧命令
一、绘制圆弧
在进行草图绘制时,草图中的曲线除了直线之外,圆弧也是常见的曲线之一。 所以,也必须掌握圆弧的绘制,从而能快速高效地进行solidworks草图绘制。
二、圆弧绘制分类及绘制11、 Nhomakorabea弧绘制方法
3
一般分种两种:圆心/起/终点圆弧、切线圆 弧和3点圆弧。
其圆弧工具的调用方法有如下三种: 2
单击【草图】工具栏上的【圆心/起/ 终点圆弧】按钮
移动鼠标至绘图区域,变成“笔”状 单击图形区确定圆弧中心。
移动指针并单击设定圆弧的半径及圆 弧起点,然后松开鼠标。在圆弧上单 击确定其终点位置。
2 1
第1点 圆弧圆心
第2点 圆弧起点
可修改 圆心坐标 圆半径
第3点 圆弧终点点
二、圆绘制分类及绘制 3、绘制切线圆弧绘制方法 单击【草图】工具栏上的【切线圆弧】 按钮
• 菜单
菜单方法
单击【工具】下的【草图绘制实体】来选取圆弧 工具。
• 草图选项卡。
单击【草图】工具栏,从圆弧弹出工具
选取相应工具。 • 圆 PropertyManager。
草图选项卡方法 属性管理器方法
从【 圆弧属性管理器】 更改到不同的圆弧工具。
二、圆弧绘制分类及绘制 2、圆心/起/终点圆弧绘制方法
拖动到圆弧结束的位置松开鼠标。拖 动圆弧以设置圆弧的半径。
2
第1点 圆弧起点
第2点 圆弧终点
可修改圆心坐标、圆半径
拖动到圆弧结束 的位置松开鼠标
二、总结
圆弧的类型主要有分为三种,主要是利用圆弧工具在草图中绘制,在绘 图过程中我们绘图的已知条件,确定绘制圆弧的方式,在绘制过程中一定要 注意圆弧参数的确定,才能达到圆的绘制要求。
电子教案-工业机器人应用系统三维建模(SolidWorks)+文清平+教学资源教学课件2-2圆命令
可修改 圆心坐标 圆半径
3 第三点
三、总结
圆的类型主要有圆和周边圆两种,主要是利用圆工具在草图中绘制,在 绘图过程中我们绘图的已知条件,确定绘制圆的方式,在绘制过程中一定要 注意圆心、周边圆点适 当处再次单击鼠标左键,便可完成 圆的绘制。
2
1 圆心
2 可修改
第二点
圆心坐标
圆半径
二、圆绘制分类及绘制
2、周边圆绘制方法
1
单击工具栏中【圆】按钮旁边的下拉 菜单
移动光标图形区,光标变成“笔状 , 通过单击鼠标, 确定圆上的第1、2和3点, 从而绘制出所需要的圆。
2
1 第一点 2 第二点
单击【草图】工具栏,从圆 工具选取圆工具。
弹出 1
3
菜单方法
2
1 2
• 圆 PropertyManager。
从【 圆属性管理器】 更改到不同的 圆工具。
草图选项卡方法
属性管理器方法
三、圆绘制分类及绘制
1、圆绘制方法
1
单击工具栏中【圆】按钮
光标变成“笔”状 ,移动光标至 圆心位置处,单击鼠标左键并移动 光标,这时在绘图区域中会显示出 将要绘制的圆预览
草图绘制 ——圆命令
一、绘制圆
在进行草图绘制时,草图中的曲线除了直线之外,圆也是常见的曲线之 一。所以,也必须掌握圆的绘制,从而能快速高效地进行solidwoorks草图 绘制。
1
二、圆命令的调用方法
其圆工具的调用方法有如下三种:
• 菜单
2
单击【草图】、 【草图绘制实体】来
选取圆工具。
• 草图选项卡。
机器人空间三点圆弧功能的实现
机器人空间三点圆弧功能的实现第35卷2007拄第8期8月华中科技大学(自然科学版)J.HuazhongUniv.ofSci.8LTech.(NatureScienceEdition)V o1.35No.8Aug.2007机器人空间三点圆弧功能的实现叶伯生(华中科技大学国家数控系统工程技术研究中心,湖北武汉430074)摘要:基于机器人终端执行器经历的空间任意三点,求出空间圆弧的圆心和半径,继而推导出机器人控制系统中任意空间圆弧的实现方法.该算法不仅理论上可使所有插补点均落在圆弧上,而且由于采用了矢量算法,并以三点的次序作为圆弧的方向,从而避免了插补方向和过象限的判断,可以使用统一的实时插补递推公式.研究成果已在实际机器人中得到应用该成果同样适用于需要空间圆弧功能的机床数控系统.关键词:机器人;空间圆弧;插补;矢量;误差中图分类号:TP242文献标识码:A文章编号:167卜4512(2007)08—0005—04 ImplementationofarcinterpolationinarobotbyusingthreearbitrarypointsYeBosheng(NationalNCSystemEngineeringResearchCenter,HuazhongUniversity ofScienceandTechnology,Wuhan430074,China)Abstract:Amethodisproposedtocalculatethecenterandradiusofanarcinaspacethroughthr eear—bitrarypoints.Thecorrespondinginterpolationalgorithmforanarbitraryspecialarcinarobot controlsystemwasdeduced.Allinterpolatedpointscouldfallonthecurvethroughthealgorithmtheo retical一1y.Aunifiedrecurrenceformulacouldbeusedwithoutthedirectionjudgment,becausevecto ralgo—rithmwasusedandthesequenceofthreepointswastakenastheinterpolationdirection.Theres ulthasbeenappliedtoapracticalrobot.ThisachievecanbealsousedinCNCsystemsinmachinet ools.Keywords:robot;areinspace;interpolation;vector;error机器人一般应用于比较恶劣或人难于企及的环境以替代劳动者完成必要的任务,因而机器人的编程,很多情况下是采用示教完成的口].示教过程包括把机器人移动到几个所要求的目标点并把这些点的位置记录在存储器中,然后定义经过这些点的曲线轨迹及速度.当曲线轨迹为圆弧时,除了示教圆弧起点(当前点)和终点外,至少还应知道圆心或圆弧上一中间点.显然,示教圆心是很困难的,因而机器人终端执行器的轨迹圆弧通常由示教的圆弧起点,中间点及圆弧终点决定,而这三点所决定的平面通常不一定平行于某一坐标平面,因而需要研究空间任意三点圆弧的插补算法.本研究以上述需求为出发点,基于机器人终端执行器(根据使用场合的不同,可以是爪,焊枪,电磁铁和其他装置)经历的空间任意三点,推导出了机器人控制系统中任意空间圆弧的实现方法,并分析了该算法的性能及特点.1由空间任意三点求圆弧的圆心和半径已知空间任意三点分别为圆弧起点P.(X.,y.,Z.),中间点P(X,Y,Z)和圆弧终点P(X,Y,Z),如图1所示.设圆心为C(Xc,y,Zc),半径为R,则有lc--P.l===lc--Pl—lc--Pl—R;(1)c--P.×一(丽×).(2)收稿日期:2006—07—12.作者简介:叶伯生(1966一),男,副教授;武汉,华中科技大学国家数控系统工程技术研究中心(430074).E-mail:yebosh@?6?华中科技大学(自然科学版)第35卷图1空间三点决定的圆弧由式(1)得(X一Xc)+(y—yc)+(Z—Zc)一R(一0,1,2).(3)设坐标系0XyZ上各坐标轴的单位坐标矢量分别为i,-,,k,则有.:(x.一xc,y0一yc,z.一Zc),P0一(X1一X0,Y1一y0,Z1一Zo),P1P一(X2一X1,Y2~Yl,Z2一Z1).于是.x—PoP1一liJ『klJX.一Xcy0一ycZo—ZcJ,Ixl—x.y1一y0z1~z.I—-----——●—-——?——+P0P1×PlP;:}i-,kIlX1一X.y1一y0Z1一Z.I.1x2一x1y2一ylz2一z1J由式(2)得[(y0一yc)(Z一Z.)一(一Zc)(y一Yo~3/E(Y一Yo)(Z2一Z)一(z一Z.)(y2~Y1)]一E(z.一Zc)(Xl—Xo)~(X.一Xc)(Z1一Zo)-1/Uz一Z.)(X2一X)一(X1一X.)(Z2一Z1)]一.(4)式(3)和式(4)化简后可得aExcZc]一B,(5)R一[(X.一Xc)+(—yc)+(Z0一Zc)]1/(6)式(5)中,A为3×3矩阵,a..一2(x.一X1),ao.一2(y0一Y1),a02=2(Zo—Z1),alo一2(Xl—X2).a11:2(Y1一Y2),al2—2(Z1一Z2),一口02(口o2a11一a01al2)/8,a2I==:ao2(a0oai2一aL)2lf)/ 8,a22一[a00(a02口11一a0la12)+abl(a)l!一a.2a1.)]/8;B为3×1矩阵,b.一(++Z)一(X}+y}+Z}),b=(X}++Z})一(x;+y;+Z;),b2一口20X0+a21Y0+a22Z0.由式(5)求得,yc,Zc,由式(6)求得R.在求解过程中应注意平行于某一坐标平面的圆弧的处理.此时X,,Zi(i一0,1,2)中,有一个坐标值是不变的,容易出现detA一0(矩阵A的秩rantc4—2)的情况.在这种情况下,应去掉矩阵A和矩阵B的第3行以及矩阵A等于0的1列和EX.,Yc,Z.=rr的相应1行(若X一0,则去掉A的第1列和[X.,y.,Z.]r的第1行X.;若Y=0,则去掉A的第2列和Exc,Yc,Z]的第2行Yc;若Z:0,则去掉A的第3列和[X.,y.,Z.]的第3行Z),形成一个二元一次方程组,求解未知的两个圆心坐标.2插补算法2.1插补原理任意空间圆弧插补,就是求出在一个插补周期T内,机器人终端执行器从当前位置(X,Y,Zi)和方位(,∞,)沿圆弧割线上截取弦长厂一FT(F为编程速度)后,所到达的下一个插补点的位置(X…,Yi+1,Z川)和方位(+1,a,届+1)~.方位的插补一般采取线性方式,即把终端执行器在圆弧终点和起点的方位差均匀地分配到插补的每一步,算法简单,本文不作讨论.2.2插补递推公式在数控机床中,平行于坐标平面的圆弧编程一般只给出起点,终点和圆心,因而需要用G02和G03区分为顺时针圆弧和逆时针圆弧.而给定了起点,终点和一个中间点的空间三点圆弧的走向是确定的,因此无需用顺时针和逆时针区分.事实上,用丽×丽表示空间三点圆弧所在平面的法矢量,l,则从,l的正方向看,从P到P到P的圆弧始终是逆时针圆弧.所以,可用统一格式ARCX.一y.一ZfX1一y1一Zl—X2一y2一Z2一描述空间三点圆弧-6_.机器人的控制系统读入此段程序后,首先求出圆心和半径,然后再计算插补点的坐标.设,l一丽×一++,则"一(yl—Yo)(Z2一Z1)一(Z.一Z0)(y2一Y1);一(z,一)(x2一x1)一(7)(X1一Xo)(Z2一Z1);叫一(X1一Xo)(y2一Y1)一(y,一Yo)(X2一X1).空间三点圆弧上任一点P(X,Y,Z)处沿前进方向的切矢量第8期叶伯生:机器人空间三点圆弧功能的实现?7?i+J『+llk=,l×一I"Xt—Xc.,y一yc硼Z—Zc则rf一(Z一Zc)一硼(Y—Yc);f=硼(X—Xc)~"(Zf—Zc);(8)lz一"(Y—Yc)一(X—Xc).设经过一个插补周期后,机器人的终端执行器从P(X,Y,Z)沿圆弧切向移动FT后(其中:F为编程速度;T为插补周期),到达P:+(x:+,t+,z:+),女Ⅱ图2所示,贝UrX斗1一X+△X一X+Em;1一Y+△—Y+En;(9)lZ1一Z+△=Z+E/,式中E—FY/(++l).可以证明++z一("硼)?[(X—Xc)+(y—yc).+(Z一Zc)]+ [(X—Xc)"+(y一Yc)+(Z一Zc)∞]一(硼)R,.从而,E—FT/ER("++硼)].(10)从图2可以看出,点P:+并不在圆弧上,为使所有插补点都落在圆弧上,需对式(9)进行修正.连接cPi+交圆弧于P点,以P…代替+作为插补点,则插补点始终在圆弧上.图2空间圆弧插补原理在直角ACPP:+中,I+Iz—IIz+I+I,即(R+△R)一Rz+FTz,有rx斗1一xc+R(x1一xc)/(R+FT)1/2;JY斗1一Yc+R(1一yc)/(R+FT)/;Iz斗一zc+R(ZI+1一zc)//(R+FT)/.(11)令G—R/(R+)1/2一l/[1+(/R)],(12)并把式(9)代人式(11),得插补递推公式rX1一Xc+G(X+Em一Xc);Y一Yc+G(Y+Enf—yc);(13)IZ斗1一Zc+G(Z+E/~Zc).2.3终点判别圆弧插补的终点判别只需算出圆心角和步距角,以两者的商作为插补次数,参考图2,有一arcsin(FT/R)≈FT/R.(14)圆心角的计算则要考虑如图3所示的≤丌(圆弧P.PP)和>丌(圆弧P.PP)两种情况. 当≤丌时,0—2arcsin{[(X2一Xo)+(y2一y.)+(Z2一Z.)]/(2R)};(15)当>丌时,0—2丌一2arcsin{[(X2一Xo)+(y2一)+(Z一)]/(2R)).(16)从图3可以看出,当≤丌时,矢量.×P.P.PPo图3圆心角的计算与圆弧所在平面的法矢量,l(一×)方向相同;当>丌时,矢量.×与,l方向相反.因而可用公式H一训1+删1+伽1(17)的正负来判断的范围,当H≥0时,≤丌;当H<O时,>丌.式中",1,硼1为矢量Cp.×P.在各坐标轴方向上的分量,"1一(yo—Yc)(Z2一Zn)一(一Zc)(y2一Y.);1一(一Zc)(x2一Xo)一(18)(X.一Xc)(Z2一);硼1一(Xo—Xc)(y2一Y0)一(yo—Yc)(X2一Xo).算出和后,插补次数(不包括点)N—Eo/a~+1.(19)2.4误差分析由插补递推过程知,插补点总在圆弧上,算法没有累积误差.?8?华中科技大学(自然科学版)第35卷从图2和式(14)可知,每次插补走过的步距角是不变的,因而每个插补周期走过的弦长是不变的,即进给速度是恒定的.只是弦长lPP…l稍稍小于切线段长度lPP:+l(=FT),相对误差为很小,可以忽略其高次项)(1PPl—IPPI)/lPPl=(L~2Rsin(8/2)/(F丁)=1—2sin(8/2)/8—1—218/2一(8/2)./(31)+(8/2)/(51)~…3/8≈/(241).插补的弓高误差约为F/(8R).2.5插补算法步骤及实时性分析根据以上分析,可以构造出如下空间三点圆弧的插补算法步骤(注意:为避免混淆插补动点与圆弧起点,中间点和终点,此处用XE1]描述x,用y[]描述y,用zEi]描述Z).a.获取已知条件:圆弧起点P.(X.,Y.,Zo),中间点P(X,y,Z1)和圆弧终点Pz(Xz,y2,Z2),编程速度F及插补周期T.b.由式(5)求圆弧的圆心C(X.,Y.,),由式(6)求圆弧半径尺.c.由式(7)求圆弧所在平面的法矢量n的分量u,,,由式(18)求"1,1,1,由式(12)求G,由式(14)求.d.由步骤c求得的结果,根据式(10)算出E,根据式(17)算出H.e.根据H的正负由式(15)和式(16)算出,并由式(19)算出插补次数N.f.置一0,插补起点为P.(X.,Y.,Zo),即x[o3:X.,y[O]一Yo,zro3一Z0.g.=+1,由式(8)求m,,z.h.由式(13)确定下一插补点.i.若<N,则转g.j.xEN3=X2,y[N]一Y2,Z[』\r]一Z2,结束.步骤a~e在插补预处理中完成.因而实时插补过程由式(8)和式(13)构成,共有9次乘法运算,计算量不大,在主频166MHz的工控机上验证,平均每次的插补运行时间约为0.1ms.大部分机器人是关节机器人,系统控制的是关节坐标轴.因此,用上述方法算得插补动点后, 还得通过坐标变换把动点的位置和方位转换为关节坐标,然后控制相应的关节转动一定的角度,到达所要求的位置和方位.不同结构的机器人,其变换矩阵会不同,但对于任一给定的机器人,其位置和方位与关节的关系是一定的.因而只要插补点的位置在机器人的运动范围内,总可以找到相应关节坐标系下的解83.误差分析和实时性分析表明,本文研究的算法能满足机器人控制的精度及实时性要求,本研究成果已成功应用于华中I型教学机器人.事实上,在机械加工中,如果机床数控系统具有空间任意圆弧插补功能,可达到简化编程,提高加工效率和精度的目的.因此,本研究成果也可应用于高性能机床数控系统.参考文献[1]熊有伦.机器人技术基础[M].武汉:华中理工大学出版社,1996.[2]叶伯生.计算机数控系统原理,编程与操作[M].武汉:华中理工大学出版社,1999.[3]秦开怀,金建新,宾鸿赞.CNC系统中任意三维椭圆弧的高速插补新方法[J].华中理工大学,1992,20(6):7-11.[4]金建新.机床CNG系统中任意空间曲线的可控步长插补方法[J].机械工程,2002(4):95—97.[5]别卫春,朱志红,叶伯生.HNC—IR机器人语言解释系统的研究与实践[J].机电一体化,2000(3):27—3O. [6]叶伯生,朱志红,刘恩沧.基于PC的教学机器人控制系统[J].机械与电子,2000(6):43—45.[7]张毅,叶伯生,朱志红.HNc——IR机器人运动学方程的研究及求逆的新方法[J].机械设计与制造. 2000(3):40—42.[8]王奇志,徐新和,尹朝万.PUMA机械手逆运动方程新的推导方法及求解[J].机器人,1998(3:81—87.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、圆绘制分类及绘制
单击【草图】工具栏上的
2
3、绘制切线圆弧绘制方法
第1点 圆弧起点
1ห้องสมุดไป่ตู้
【切线圆弧】按钮
移动鼠标至绘图区域,变
成“笔”状在直线、圆弧、
椭圆或样条曲线的端点单
第2点 圆弧终点
击。
拖动圆弧以绘制所需的形
可修改圆心坐标、圆半径
二、圆绘制分类及绘制
单击【草图】工具栏上的 【3点圆弧】按钮 移动鼠标至绘图区域,变 成“笔”状单击图形区域 确定圆弧的起点位置。 拖动到圆弧结束的位置松 开鼠标。拖动圆弧以设置
属性管理器方法
二、圆弧绘制分类及绘制
1 2、圆心/起/终点圆弧绘制方法
2
单击【草图】工具栏上的
【圆心/起/终点圆弧】按钮
第 1点 圆弧圆心 第 2点 圆弧起点
移动鼠标至绘图区域,变成
“笔”状单击图形区确定圆
弧中心。
移动指针并单击设定圆弧的
可修改 圆心坐标 圆半径
第 3点 圆弧终点点
半径及圆弧起点,然后松开
草图绘制
——圆弧命令
一、绘制圆弧
在进行草图绘制时,草图中的曲线除了直线之外,圆弧 也是常见的曲线之一。所以,也必须掌握圆弧的绘制,从而 能快速高效地进行solidworks草图绘制。
二、圆弧绘制分类及绘制 1、圆弧绘制方法
一般分种两种:圆心/起/终点圆 弧、切线圆弧和3点圆弧。 2 其圆弧工具的调用方法有如下 菜单方法 三种: • 菜单 单击【工具】下的【草图绘制实体】 来选取圆弧工具。 • 草图选项卡。 草图选项卡方法 单击【草图】工具栏,从圆弧弹出 工具 1 3
可修改圆心坐标、圆半径
拖动到圆弧结束 的位置松开鼠标
4、绘制3点圆弧绘制方法
第1点 圆弧起点
1
2
第2点 圆弧终点
二、总结
