高中数学人教版选修1-2课时提升作业十二 4.1 流程图 精讲优练课型 Word版含答案
苏教版高中数学选修1-2同步课堂精练:4.1流程图 Word版含答案
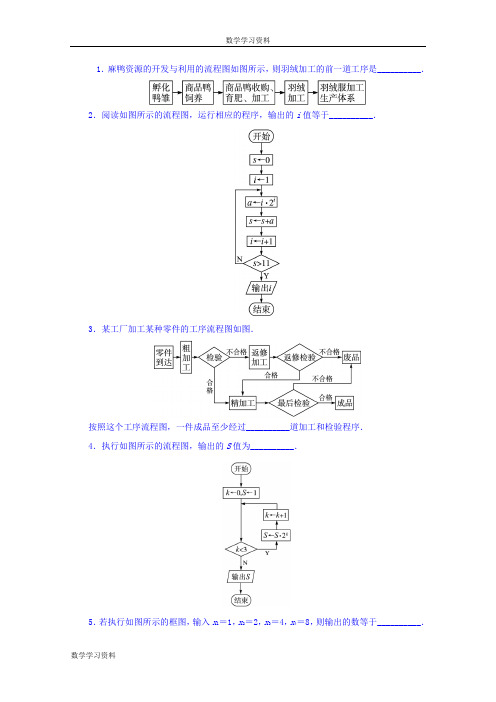
1.麻鸭资源的开发与利用的流程图如图所示,则羽绒加工的前一道工序是__________.2.阅读如图所示的流程图,运行相应的程序,输出的i值等于__________.3.某工厂加工某种零件的工序流程图如图.按照这个工序流程图,一件成品至少经过__________道加工和检验程序.4.执行如图所示的流程图,输出的S值为__________.5.若执行如图所示的框图,输入x1=1,x2=2,x3=4,x4=8,则输出的数等于__________.6.小明每天早晨起床后要做如下事情:洗漱5分钟,收拾床铺4分钟,听广播15分钟,吃早饭8分钟,要完成这些事情,小明至少要花费的时间为__________分钟.7.某工程的工序流程图如图所示(工时单位:天),现已知工程总工时数为10天,则工序c所需工时为________天.8.在选举过程中常用差额选举(候选人数多于当选人数).某班选举班长,具体方法是:筹备选举,由班主任提名候选人,同学投票(同意,不同意,弃权),验票统计,若得票多者,则选为班长;若票数相同则由班主任决定谁当选.请用流程图表示该选举的过程.9.写出求过两点P1(x1,y1),P2(x2,y2)的直线的斜率的算法步骤,并画出流程图.10.机床的大修有如下的工作项目:拆卸清洗,部件检查,零件加工,零件修理,床身和工作台研合,部件组装(不含电器),变速器组装,试车.试画出工序流程图.参考答案1答案:商品鸭收购、育肥、加工2答案:4 解析:初始值:s =0,i =1;第一步:a =1×21=2,s =2,i =2;第二步:a =2×22=8,s =2+8=10,i =3;第三步:a =3×23=24,s =10+24=34,i =4,故输出4.3答案:四 解析:由流程图可知加工零件有三道工序:粗加工、返修加工和精加工,每道工序完成都要对产品进行检验,粗加工的合格品进入精加工,不合格品进入返修加工,返修加工的合格品进入精加工,不合格品作为废品处理;精加工的合格品为成品,不合格品为废品.由上可知一件成品至少要经过粗加工、检验、精加工、检验四道程序.4答案:8 解析:初始:k =0,S =1,第一次循环:由0<3,得S =1×20=1,k =1; 第二次循环:由1<3得,S =1×21=2,k =2;第三次循环:由2<3得,S =2×22=8,k =3.经判断此时要跳出循环.因此输出的S 值为8.5答案:3.75 解析:这个程序的作用是求x 1,x 2,x 3,x 4四个数的平均数,1+2+4+8 3.754. 6答案:17 解析:小明可以在听广播的时间里同时进行洗漱、收拾床铺、吃早饭,这样花费的时间最少,是15+{8-}=17(分钟).7答案:4 解析:设工序c 所需工时为x 天.由题意知:按①→③→④→⑥→⑦→⑧所需工时为0+2+3+1=9(天),按①→②→④→⑥→⑦→⑧所需工时为1+0+3+3+1=8(天),故按①→②→⑤→⑦→⑧所需工时应为10天.∴1+x +4+1=10.∴x =4.8答案:解:流程图如下:9答案:解:第一步:输入x 1,y 1,x 2,y 2; 第二步:如果x 1=x 2,输出“斜率不存在”,否则2121y y k x x -=-; 第三步:输出k .相应的流程图如下:10答案:解:机床大修的工序流程图如下:。
人教A版高中数学选修1-1课时提升作业 十二 2.2.1 双曲线及其标准方程 精讲优练课型 Word版含答案

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业十二双曲线及其标准方程一、选择题(每小题5分,共25分)1.设θ∈,则关于x,y的方程-=1所表示的曲线是( )A.焦点在y轴上的双曲线B.焦点在x轴上的双曲线C.焦点在y轴上的椭圆D.焦点在x轴上的椭圆【解析】选 C.方程即+=1,因为θ∈,所以sinθ>0,cosθ<0,且-cos θ>sinθ,故方程表示焦点在y轴上的椭圆.【补偿训练】在方程mx2-my2=n中,若mn<0,则方程的曲线是( )A.焦点在x轴上的椭圆B.焦点在x轴上的双曲线C.焦点在y轴上的椭圆D.焦点在y轴上的双曲线【解析】选D.方程mx2-my2=n可化为:-=1,因为mn<0,所以->0,所以方程的曲线是焦点在y轴上的双曲线.2.(2016·枣庄高二检测)双曲线-=1上的点到一个焦点的距离为12,则到另一个焦点的距离为( )A.22或2B.7C.22D.2【解析】选A.因为a2=25,所以a=5.由双曲线定义可得||PF1|-|PF2||=10,由题意知|PF1|=12,所以|PF1|-|PF2|=±10,所以|PF2|=22或2.3.设动点P到A(-5,0)的距离与它到B(5,0)距离的差等于6,则P点的轨迹方程是( )A.-=1B.-=1C.-=1(x≤-3)D.-=1(x≥3)【解析】选D.由题意知,动点P的轨迹应为以A(-5,0),点B(5,0)为焦点的双曲线的右支. 由c=5,a=3,知b2=16,所以P点的轨迹方程为-=1(x≥3).【误区警示】容易忽视x的取值范围而导致错选A.4.(2016·泉州高二检测)已知定点A,B且|AB|=4,动点P满足|PA|-|PB|=3,则|PA|的最小值是( )A. B. C. D.5【解析】选C.由题意知,动点P的轨迹是以定点A,B为焦点的双曲线的一支(如图),从图上不难发现,|PA|的最小值是图中AP′的长度,即a+c=.5.(2016·潍坊高二检测)双曲线-y2=1(n>1)的两焦点为F1,F2,P在双曲线上,且满足|PF1|+|PF2|=2,则△PF1F2的面积为( )A. B.1 C.2 D.4【解析】选B.不妨设F1,F2是双曲线的左、右焦点,P为右支上一点,|PF1|-|PF2|=2,①|PF1|+|PF2|=2,②由①②解得:|PF1|=+,|PF2|=-,得:|PF1|2+|PF2|2=4n+4=|F1F2|2,所以PF1⊥PF2,又由①②分别平方后作差得:|PF1||PF2|=2,所以=|PF1|·|PF2|=1.二、填空题(每小题5分,共15分)6.(2016·唐山高二检测)已知P是双曲线-=1上一点,F1,F2是双曲线的两个焦点,若|PF1|=17,则|PF2|的值为.【解析】由条件知a2=64,即a=8,c2=b2+a2=100,c=10,所以双曲线右支上的点到左焦点F1的最短距离a+c=18>17,故点P在双曲线左支上.所以|PF2|-|PF1|=2a=16,即|PF2|=16+|PF1|=33.答案:33【误区警示】本题易直接利用定义求解,忽视右支上的点到左焦点的最短距离为a+c,而出现错误结论|PF2|=1或|PF2|=33.【补偿训练】在平面直角坐标系xOy中,已知△ABC的顶点A(-6,0)和C(6,0),若顶点B在双曲线-=1的左支上,则= .【解题指南】由正弦定理可将转化为边的比,而△ABC的顶点A,C已知,故边AC 长可求,B在双曲线上,由定义可求|BC|-|BA|.【解析】由条件可知|BC|-|BA|=10,且|AC|=12,又在△ABC中,有===2R,从而==.答案:7.(2016·烟台高二检测)已知双曲线中心在坐标原点且一个焦点为F1(-,0),点P位于该双曲线上,线段PF1的中点坐标为(0,2),则该双曲线的方程是.【解析】设双曲线方程为-=1,因为c=,c2=a2+b2,所以b2=5-a2,所以-=1.由于线段PF1的中点坐标为(0,2),则P点的坐标为(,4).代入双曲线方程得-=1,解得a2=1或a2=25(舍去),所以双曲线方程为x2-=1.答案:x2-=18.已知双曲线-=1上一点M 的横坐标为5,则点M 到左焦点的距离是 .【解题指南】利用双曲线的定义求解. 【解析】由于双曲线-=1的右焦点为F(5,0),将x M =5代入双曲线方程可得|y M |=,即为点M 到右焦点的距离,由双曲线的定义知M 到左焦点的距离为+2×3=.答案:三、解答题(每小题10分,共20分) 9.已知双曲线与椭圆+=1有相同的焦点,且与椭圆的一个交点的纵坐标为4,求双曲线的方程.【解析】椭圆的焦点为F 1(0,-3),F 2(0,3),故可设双曲线方程为-=1(a>0,b>0),且c=3,a 2+b 2=9.由条件知,双曲线与椭圆有一个交点的纵坐标为4,可得两交点的坐标为A(,4),B(-,4), 由点A 在双曲线上知,-=1.解方程组得所以所求双曲线的方程为-=1.10.如图,在△ABC 中,已知|AB|=4,且三内角A,B,C 满足2sinA+sinC=2sinB,建立适当的坐标系,求顶点C 的轨迹方程.【解析】以AB 边所在的直线为x 轴,AB 的垂直平分线为y 轴,建立平面直角坐标系如图所示,则A(-2,0),B(2,0).由正弦定理,得sinA=,sinB=,sinC=(R为△ABC的外接圆半径).因为2sinA+sinC=2sinB,所以2a+c=2b,即b-a=,从而有|CA|-|CB|=|AB|=2<|AB|.由双曲线的定义知,点C的轨迹为双曲线的右支(除去与x轴的交点),因为a=,c=2,所以b2=c2-a2=6,即所求轨迹方程为-=1(x>)一、选择题(每小题5分,共10分)1.(2016·合肥高二检测)已知双曲线-=1的焦点为F1,F2,点M在双曲线上,且MF1⊥x轴,则F1到直线F2M的距离为( )A. B. C. D.【解析】选C.设F1到直线F2M的距离为d,不妨设点F1(-3,0),容易计算得出|MF1|=,|MF2|-|MF1|=2.解得|MF2|=.而|F1F2|=6,在直角三角形MF1F2中,由|MF1|·|F1F2|=|MF2|·d,求得F1到直线F2M的距离d为.2.(2016·沈阳高二检测)已知点P在曲线C1:-=1上,点Q在曲线C2:(x-5)2+y2=1上,点R 在曲线C3:(x+5)2+y2=1上,则|PQ|-|PR|的最大值是( )A.6B.8C.10D.12【解析】选C.由双曲线的知识可知:C1:-=1的两个焦点分别是F1(-5,0)与F2(5,0),且|PF1|-|PF2|=8,而这两点正好是两圆(x+5)2+y2=1和(x-5)2+y2=1的圆心,两圆(x+5)2+y2=1和(x-5)2+y2=1的半径分别是r1=1,r2=1,所以|PQ|max=|PF1|+1,|PR|min=|PF2|-1,所以|PQ|-|PR|的最大值为:(|PF1|+1)-(|PF2|-1)=|PF1|-|PF2|+2=8+2=10.【补偿训练】(2016·太原高二检测)设F1,F2分别是双曲线x2-=1的左、右焦点.若点P在双曲线上,有·=0,则|+|= ( )A. B.2 C. D.2【解析】选B.因为·=0,所以PF1⊥PF2,即△PF1F2为直角三角形,所以|PF1|2+|PF2|2=|F1F2|2=(2)2=40,|+|====2.二、填空题(每小题5分,共10分)3.(2016·黄冈高二检测)已知F是双曲线-=1的左焦点,A(1,4),点P是双曲线右支上的动点,则|PF|+|PA|的最小值是.【解析】由双曲线-=1,得c=4,所以左焦点F(-4,0),右焦点F′(4,0),由双曲线的定义得:|PF|-|PF′|=2a=4,所以|PF|+|PA|=4+|PF′|+|PA|≥4+|AF′|=4+=9,此时P为AF′与双曲线的交点,即|PF|+|PA|的最小值为9.答案:94.(2016·杭州高二检测)已知双曲线的两个焦点为F1(-,0),F2(,0),M是此双曲线上一点,若·=0,||·||=2,则该双曲线的方程是.【解析】设双曲线的方程为-=1(a>0,b>0),由题意得||MF1|-|MF2||=2a,|MF1|2+|MF2|2=(2)2=20,又因为||·||=2,所以|MF1|2+|MF2|2-2|MF1||MF2|=4a2,即20-2×2=4a2,所以a2=4,b2=c2-a2=5-4=1,所以双曲线的方程为-y2=1.答案:-y2=1三、解答题(每小题10分,共20分)5.当0°≤α≤180°时,方程x2cosα+y2sinα=1表示的曲线怎样变化?【解析】(1)当α=0°时,方程为x2=1,它表示两条平行直线x=1和x=-1.(2)当0°<α<90°时,方程为+=1.①当0°<α<45°时,0<<,它表示焦点在y轴上的椭圆.②当α=45°时,它表示圆x2+y2=.③当45°<α<90°时,>>0,它表示焦点在x轴上的椭圆.(3)当α=90°时,方程为y2=1,它表示两条平行直线y=1和y=-1.(4)当90°<α<180°时,方程为-=1,它表示焦点在y轴上的双曲线.(5)当α=180°时,方程为x2=-1,它不表示任何曲线.【误区警示】解答本题时容易忽略α=90°的情况.6.(2016·济南高二检测)已知F1,F2为双曲线C:x2-y2=1的左、右焦点,点P在C上,∠F1PF2=60°,求P到x轴的距离.【解析】因为||PF1|-|PF2||=2,所以|PF1|2-2|PF1|·|PF2|+|PF2|2=4,所以|PF1|2+|PF2|2=4+2|PF1|·|PF2|,由余弦定理知|PF1|2+|PF2|2-|F1F2|2=2|PF1|·|PF2|cos60°,得|PF1|2+|PF2|2=|F1F2|2+|PF1|·|PF2|,又a=1,b=1,所以c==,所以|F1F2|=2c=2,所以4+2|PF1||PF2|=|PF1|·|PF2|+8,所以|PF1|·|PF2|=4.设P到x轴的距离为|y0|,=|PF1||PF2|sin60°=|F1F2|·|y0|,所以×4×=×2|y0|,所以|y0|==.即P点到x轴的距离为.关闭Word文档返回原板块。
人教A版高中数学选修1-1课时提升作业 四 1.2.1 充分条件与必要条件 精讲优练课型 Word版含答案

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业四充分条件与必要条件一、选择题(每小题5分,共25分)1.“φ=”是“cosφ=0”的( )A.充分条件B.必要条件C.既是充分条件,又是必要条件D.既不是充分条件,也不是必要条件【解析】选A.当φ=时,有cosφ=0,但当cosφ=0时,φ=kπ+,k∈Z.2.(2016·嘉兴高二检测)设集合A={x∈R|x-2>0},B={x∈R|x<0},C={x∈R|x(x-2)>0},则“x∈A∪B”是“x ∈C”的( )A.充分条件B.必要条件C.既是充分条件又是必要条件D.既不是充分条件也不是必要条件【解析】选C.A∪B={x∈R|x<0,或x>2},C={x∈R|x<0,或x>2},因为A∪B=C,所以x∈A∪B⇒x∈C,且x∈C⇒x∈A∪B,所以x∈A∪B是x∈C的充分条件,同时也是必要条件.3.下列各小题中,p是q的充分条件的是( )①p:m<-2,q:y=x2+mx+m+3有两个不同的零点;②p:=1,q:y=f(x)是偶函数;③p:cosα=cosβ,q:tanα=tanβ.A.①B.③C.②③D.①②【解析】选D.①y=x2+mx+m+3有两个不同的零点,则Δ=m2-4(m+3)>0,得m>6或m<-2,所以p是q的充分条件;②因为=1,所以f(-x)=f(x),所以f(x)为偶函数,所以p是q的充分条件;③当α=β=kπ+时,tanα,tanβ无意义,所以p是q的必要条件.4.已知q是等比数列{a n}的公比,则“q<1”是“数列{a n}是递减数列”的( )A.充分条件B.必要条件C.既是充分条件,又是必要条件D.既不是充分条件也不是必要条件【解析】选D.等比数列的单调性与首项和公比都有关系.【误区警示】本题中的等比数列易与等差数列混淆,忽略首项的作用.5.(2015·成都高二检测)已知α,β是两个不同的平面,则“平面α∥平面β”成立的一个充分条件是( )A.存在一条直线l,l⊂α,l∥βB.存在一个平面γ,γ⊥α,γ⊥βC.存在一条直线l,l⊥α,l⊥βD.存在一个平面γ,γ∥α,γ⊥β【解析】选C.A.存在一条直线l,l⊂α,l∥β,此时α,β可能相交.B.若存在一个平面γ,γ⊥α,γ⊥β,则α与β可能平行,可能相交.C.若存在一条直线l,l⊥α,l⊥β,则α∥β成立,反之不一定成立,满足条件.D.若存在一个平面γ,γ∥α,γ⊥β,则α⊥β,所以不满足题意.【补偿训练】(2015·佛山高二检测)已知p:x2-x<0,那么命题p的一个充分条件是( )A.1<x<3B.-1<x<1C.<x<D.<x<5【解析】选C. x2-x<0⇒0<x<1,运用集合的知识,易知只有C中由<x<可以推出0<x<1,其余均不可. 二、填空题(每小题5分,共15分)6.设A,B是非空集合,则A∩B=A是A=B的条件(填“充分”“必要”).【解析】当A∩B=A时,只能得出A⊆B,得不出A=B,但当A=B时,一定有A∩B=A,即由A=B可以推出A∩B=A. 答案:必要7.设x,y∈R,那么“x>y>0”是“>1”的条件(填“充分”“必要”).【解析】由>1⇒>0⇒x>y>0或x<y<0.因此“x>y>0”能推断“>1”.答案:充分8.(2015·济南高二检测)条件p:1-x<0,条件q:x>a,若p是q的充分条件,则a的取值范围是.【解析】p:x>1,若p是q的充分条件,则p⇒q,即p对应集合是q对应集合的子集,故a≤1.答案:(-∞,1]三、解答题(每小题10分,共20分)9.判断“x=1”“x=2”“x=1或x=2”是方程x2-3x+2=0的充分条件还是必要条件.【解析】当x=1时,方程成立,所以“x=1”是方程的充分条件,同理“x=2”、“x=1或x=2”都是方程的充分条件;当方程成立时,x=1或x=2,所以“x=1”“x=2”是方程的充分条件,但不是必要条件,“x=1或x=2”既是方程的充分条件,也是方程的必要条件10.(2015·昆明高二检测)已知命题p:对数log a(-2t2+7t-5)(a>0,且a≠1)有意义,q:关于实数t的不等式t2-(a+3)t+(a+2)<0.(1)若命题p为真,求实数t的取值范围.(2)若命题p是q的充分条件,求实数a的取值范围.【解析】(1)因为命题p为真,则对数的真数-2t2+7t-5>0,解得1<t<.所以实数t的取值范围是.(2)因为命题p是q的充分条件,所以{t|1<t<是不等式t2-(a+3)t+(a+2)<0的解集的子集.方法一:因为方程t2-(a+3)t+(a+2)=0的两根为1和a+2,所以只需a+2≥,解得a≥.即实数a的取值范围为.方法二:令f(t)=t2-(a+3)t+(a+2),因为f(1)=0,所以只需f≤0,解得a≥.即实数a的取值范围为.一、选择题(每小题5分,共10分)1.(2016·新乡高二检测)“sinx=1”是“cosx=0”的( )A.充分条件B.必要条件C.既是充分条件,又是必要条件D.既不是充分条件也不是必要条件【解析】选A.当sinx=1时,由sin2x+cos2x=1得cos2x=0即cosx=0;所以“sinx=1”是“cosx=0”的充分条件,当cosx=0时,由sin2x+cos2x=1,得sin2x=1,即sinx=±1,因此由cosx=0不能推出sinx=1,因此“sinx=1”不是“cosx=0”的必要条件.2.(2015·福州高二检测)集合A=,B={x|-a<x-b<a}.若“a=1”是“A∩B≠∅”的充分条件,则实数b的取值范围是( )A. C.(-2,2) D.【解析】选 C.A=={x|-1<x<1},B={x|-a<x-b<a}={x|b-a<x<b+a},因为“a=1”是“A∩B ≠∅”的充分条件,所以-1≤b-1<1或-1<b+1≤1,即-2<b<2.二、填空题(每小题5分,共10分)3.下列不等式:①x<1;②0<x<1;③-1<x<0;④-1<x<1.其中,可以为x2<1的一个充分条件的所有序号为. 【解析】由于x2<1即-1<x<1,①显然不能使-1<x<1一定成立,②③④满足题意.答案:②③④4.已知m,n为不同的直线,α,β为不同的平面,若①m∥n,n∥α;②m⊥n,n⊥α;③m⊄α,m∥β,α∥β;④m⊥β,α⊥β.则其中能使m∥α成立的充分条件有.【解析】①m∥n,n∥α,不能推得m∥α,m可能在平面α内;②m⊥n, n⊥α,不能推得m∥α,m可能在平面α内;③m⊄α,m∥β,α∥β,能推得m∥α;④m⊥β,α⊥β,不能推得m∥α,m可能在平面α内.答案:③三、解答题(每小题10分,共20分)5.(2015·青岛高二检测)已知p:x2-2x-3<0,若-a<x-1<a是p的一个必要条件,求使a>b恒成立的实数b的取值范围.【解析】由于p:x2-2x-3<0⇔-1<x<3,-a<x-1<a⇔1-a<x<1+a(a>0).依题意,得{x|-1<x<3}⊆{x|1-a<x<1+a}(a>0),所以解得a≥2,则使a>b恒成立的实数b的取值范围是b<2,即(-∞,2).6.(2015·宝鸡高二检测)已知集合A={y|y=x2-x+1,x∈,B={x||x-m|≥1},命题p:t∈A,命题q:t∈B,并且命题p是命题q的充分条件,求实数m的取值范围.【解题指南】本题先根据已知条件表示出集合A,B,然后根据条件求出实数m的取值范围.【解析】先化简集合A,由y=x2-x+1,配方,得y=+.因为x∈,所以y∈.所以A=.由|x-m|≥1,解得x≥m+1或x≤m-1.所以B={x|x≥m+1或x≤m-1}.因为命题p是命题q的充分条件,所以A⊆B.所以m+1≤或m-1≥2,解得m≤-或m≥3.故实数m的取值范围是∪[3,+∞).关闭Word文档返回原板块。
高中数学人教版选修1-2课时自测 当堂达标:2.1.2 演绎推理 精讲优练课型 Word版含答案

温馨提示:此套题为Word 版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word 文档返回原板块。
课时自测·当堂达标1.“π是无限不循环小数,所以π是无理数”,以上推理的大前提是 ( )A.实数分为有理数和无理数B.π不是有理数C.无限不循环小数都是无理数D.有理数都是有限循环小数【解析】选C.演绎推理的结论蕴含于前提之中,本题由小前提和结论知,C 是大前提.2.对于推理:若a>b,则a 2>b 2,因为1>-2,所以12>(-2)2,以下说法中正确的是 ( )A.大前提错误B.小前提错误C.推理形式错误D.不是演绎推理【解析】选A.本题中大前提是“若a>b,则a 2>b 2”,小前提是“1>-2”.结论是“12>(-2)2”,显然大前提是错误的.3.在推理“因为y=sinx 在上是增函数,所以sin >sin ”中,大前提是______;[0,π2]3π72π5小前提是______;结论是______.【解析】大前提是“y=sinx 在上是增函数”.[0,π2]小前提是“,∈且>”.结论为“sin >sin ”.3π72π5[0,π2]3π72π53π72π5答案:y=sinx 在上是增函数 ,∈且> sin >sin [0,π2]3π72π5[0,π2]3π72π53π72π54.已知数列{a n }满足a 1=1,a 2=3,a n+2=3a n+1-2a n (n∈N *).(1)证明:数列{a n+1-a n }是等比数列.(2)求数列{a n }的通项公式.【解题指南】(1)利用等比数列的定义证明.(2)利用累加法求数列的通项公式.【解析】(1)因为a n+2=3a n+1-2a n ,所以a n+2-a n+1=2a n+1-2a n =2(a n+1-a n ),所以=2(n∈N *)而a 2-a 1=2.a n +2‒a n +1a n +1‒a n 所以数列{a n+1-a n }是以2为首项,2为公比的等比数列.(2)由(1)得a n+1-a n =2n (n∈N *).所以a n =(a n -a n-1)+(a n-1-a n-2)+…+(a 2-a 1)+a 1=2n-1+2n-2+…+2+1=2n -1(n∈N *).关闭Word 文档返回原板块。
高中数学人教版选修1-2课时提升作业四 2.1.2 演绎推理 精讲优练课型 Word版含答案

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业四演绎推理一、选择题(每小题5分,共25分)1.(2016·滨州高二检测)“三段论”①只有船准时起航,才能准时到达目的港,②这艘船是准时到达目的港的,③这艘船是准时起航的,其中的大前提是( )A.①B.②C.①②D.③【解析】选A.由演绎推理可知,①是大前提.2.(2016·福州高二检测)“所有金属都能导电,铁是金属,所有铁能导电”这种推理方法属于( )A.演绎推理B.类比推理C.合情推理D.归纳推理【解析】选A.由题意知,这种推理包含有大前提、小前提、结论,是演绎推理.3.(2016·聊城高二检测)“所有9的倍数都是3的倍数,某奇数是9的倍数,故该奇数是3的倍数.”上述推理( )A.小前提错误B.结论错误C.正确D.大前提错误【解析】选C.因为9是3的倍数,所以某奇数是9的倍数,它一定是3的倍数.4.(2016·大同高二检测)函数y=xcosx-sinx在下列哪个区间内是增函数( ) A. B.C. D.(2π,3π)【解析】选B.y′=cosx+x(-sinx)-cosx=-xsinx>0,由选项知x>0,所以sinx<0,故π<x<2π.5.(2016·三明高二检测)观察(x2)′=2x,(x4)′=4x3,(cosx)′=-sinx,由归纳推理可得:若定义在R上的函数f(x)满足f(-x)=f(x),记g(x)为f(x)的导函数,则g(-x)= ( )A.f(x)B.-f(x)C.g(x)D.-g(x)【解析】选D.由给出的例子可以归纳推理得出:若函数f(x)是偶函数,则它的导函数是奇函数,因为定义在R上的函数f(x)满足f(-x)=f(x),即函数f(x)是偶函数,所以它的导函数是奇函数,即有g(-x)=-g(x).二、填空题(每小题5分,共15分)6.(2016·大连高二检测)若不等式ax2+2ax+2<0的解集为∅,则实数a的取值范围为________.【解析】①a=0时,不等式变为2<0,显然此不等式解集为∅.②a≠0时,需有即解得0<a≤2.综合上述,a的取值范围为.答案:7.有一段演绎推理:大前提:整数是自然数;小前提:-3是整数;结论:-3是自然数.这个推理显然错误,则错误的原因是________错误.(从“大前提”“小前提”“结论”中择一填写).【解析】自然数是非负整数,因此整数不一定是自然数,即大前提是错误的.答案:大前提8.已知f(x)=a-为奇函数,则a=________.【解析】因f(x)是奇函数,且在x=0处有定义,即f(0)=0.即a-=0,得a=.答案:三、解答题(每小题10分,共20分)9.把下列演绎推理写成三段论的形式.(1)一切奇数都不能被2整除,(22015+1)是奇数,所以(22015+1)不能被2整除.(2)三角函数都是周期函数,y=tanα是三角函数,因此y=tanα是周期函数;(3)因为△ABC三边的长依次为3,4,5,所以△ABC是直角三角形.【解析】(1)一切奇数都不能被2整除,……………………………………大前提22015+1是奇数,…………………………………………………………………小前提22015+1不能被2整除.…………………………………………………………结论(2)三角函数都是周期函数,…………………………………………………大前提y=tanα是三角函数.…………………………………………………………小前提y=tanα是周期函数.…………………………………………………………结论(3)一条边的平方等于其他两条边平方和的三角形是直角三角形,…大前提△ABC三边的长依次为3,4,5,且32+42=52, …………………………………………………………………小前提△ABC是直角三角形. ………………………………………………………结论10.(2016·南京高二检测)设m为实数,利用三段论证明方程x2-2mx+m-1=0有两个相异实根. 【证明】因为如果一元二次方程ax2+bx+c=0(a≠0)的判别式Δ=b2-4ac>0,那么方程有两个相异实根. …………………………………………………大前提Δ=(-2m)2-4(m-1)=4m2-4m+4=(2m-1)2+3>0, ………………………………小前提所以方程x2-2mx+m-1=0有两个相异实根. ……………………………………………………………………………………结论一、选择题(每小题5分,共10分)1.(2016·鞍山高二检测)有一段演绎推理是这样的:“若一直线平行于平面,则该直线平行于平面内所有直线;已知直线b⊄平面α,直线a⊂平面α,直线b∥平面α,则直线b∥直线a”的结论显然是错误的,这是因为( )A.大前提错误B.小前提错误C.推理形式错误D.非以上错误【解析】选A.因“直线与平面平行”,不能推出“直线平行于平面内的所有直线”,即大前提是错误的.2.(2016·海港高二检测)若平面四边形ABCD满足+=0,(-)·=0,则四边形ABCD一定是( )A.直角梯形B.矩形C.正方形D.菱形【解析】选D.由+=0可得AB∥CD且AB=CD.由(-)·=0即·=0可知BD⊥AC.故四边形ABCD是菱形.二、填空题(每小题5分,共10分)3.(2016·重庆高二检测)已知函数f(x)=,则f+f+…+f+f=________.【解析】因为f(x)===2+.f(1-x)=2+=2-,所以f(x) +f(1-x)=4,所以f+f=4,…,f+f=4,所以f+f+…+f+f=4×1007=4028.答案:40284.如图,四棱锥P-ABCD的底面是平行四边形,E,F分别为AB,CD的中点,则AF与平面PEC的位置关系是________.(填“相交”或“平行”)【解析】因为四棱锥P-ABCD的底面是平行四边形.所以AB∥CD且AB=CD.又点E,F分别是AB,CD的中点.所以CF∥AE且CF=AE.所以四边形AECF为平行四边形.所以AF∥CE,又AF⊄平面PEC,CE⊂平面PEC.所以AF∥平面PEC.答案:平行三、解答题(每小题10分,共20分)5.(2016·临沂高二检测)如图A,B,C,D为空间四点,在△ABC中,AB=2,AC=BC=.等边三角形ADB以AB为轴旋转.(1)当平面ADB⊥平面ABC时,求CD.(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.【解析】(1)取AB的中点E,连接CE,DE.因为AC=BC=,AB=2,所以△ABC为等腰直角三角形,所以CE⊥AB.因为△ADB是等边三角形,所以DE⊥AB.又平面ADB⊥平面ABC且平面ADB∩平面ABC=AB,所以DE⊥平面ABC.所以DE⊥CE,由已知得DE=AB=,CE=1.所以在Rt△CDE中,CD==2.(2)当△ADB以AB为轴转动时,总有AB⊥CD.证明如下:当D在平面ABC内时因为BC=AC,AD=BD,所以C,D都在AB的垂直平分线上.所以AB⊥CD.当D不在平面ABC内时,由(1)知AB⊥DE,AB⊥CE,又DE∩CE=E,所以AB⊥平面CDE,又CD⊂平面CDE.所以AB⊥CD.综合上述,当△ADB转动时,总有AB⊥CD.6.已知a,b,c是实数,函数f(x)=ax2+bx+c,g(x)=ax+b.当-1≤x≤1时,|f(x)|≤1.(1)求证:|c|≤1.(2)当-1≤x≤1时,求证:-2≤g(x)≤2.【解题指南】(1)利用f(0)=c结合-1≤x≤1时|f(x)|≤1来证明.(2)先分a>0和a<0两种情况取g(1),g(-1)结合单调性证明再讨论a=0的情况.【证明】(1)因为x=0满足-1≤x≤1的条件,所以|f(0)|≤1.而f(0)=c,所以|c|≤1.(2)当a>0时,g(x)在上是增函数,所以g(-1)≤g(x)≤g(1).又g(1)=a+b=f(1)-c,g(-1)=-a+b=-f(-1)+c,所以-f(-1)+c≤g(x)≤f(1)-c,又-1≤f(-1)≤1,-1≤f(1)≤1,-1≤c≤1,所以-f(-1)+c≥-2,f(1)-c≤2,所以-2≤g(x)≤2.当a<0时,可用类似的方法,证得-2≤g(x)≤2.当a=0时,g(x)=b,f(x)=bx+c,g(x)=f(1)-c,所以-2≤g(x)≤2.综上所述,-2≤g(x)≤2.关闭Word文档返回原板块。
高中数学人教版选修1-2课时提升作业一 1.1 回归分析的基本思想及其初步应用 精讲优练课型 Word版含答案

温馨提示:此套题为版,请按住,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭文档返回原板块。
课时提升作业一回归分析的基本思想及其初步应用一、选择题(每小题分,共分).下列四个命题中正确的是( )①在线性回归模型中,是预报真实值的随机误差,它是一个观测的量;②残差平方和越小的模型,拟合的效果越好;③用来刻画回归方程,越小,拟合的效果越好;④在残差图中,残差点比较均匀地落在水平的带状区域中,说明选用的模型比较合适,带状区域宽度越窄,说明拟合精度越高,回归方程的预报精度越高..①③.②④.①④.②③【解析】选是预报变量的随机误差,故①不正确;越接近,拟合的效果越好,故③不正确. .甲、乙、丙、丁位同学各自对,两个变量进行回归分析,分别得到散点图与残差平方和()如表:哪位同学的试验结果体现拟合,两变量关系的模型拟合精度高?( ).甲.乙.丙.丁【解析】选.根据线性相关的知识,散点图中各样本点带状分布越均匀,同时保持残差平方和越小,回归分析建立的线性回归模型的拟合效果越好.由试验结果知,丁拟合效果较好些. .关于残差的叙述正确的是( ).残差就是随机误差.残差就是方差.残差都是正数.残差可以用来判断模型拟合的效果【解析】选.根据残差的意义及作用知,正确..(·大连高二检测)在一次试验中,测得(,)的组值分别为(,),(,),(,),(,),则与之间的回归直线方程为( )【解析】选.由已知条件可知,,而回归直线必经过样本点的中心,故选项符合题意..(·济南高二检测)设某大学的女生体重(单位:)与身高(单位:)具有线性相关关系,根据一组样本数据(,)(,,…,),用最小二乘法建立的回归方程为,则下列结论中不正确的是( )与具有正的线性相关关系.回归直线过样本点的中心(,).若该大学某女生身高增加,则其体重约增加.若该大学某女生身高为,则可断定其体重必为【解题指南】根据线性相关、回归直线、样本点的中心等相关概念判断.【解析】选.由回归直线方程的计算公式,由一次函数的单调性知,每增加,体重平均增加,是估计变量。
高中数学人教版选修1-2课时提升作业(一) 1.1 回归分析的基本思想及其初步应用 探究导学课型 Word版含答案

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(一)回归分析的基本思想及其初步应用(25分钟60分)一、选择题(每小题5分,共25分)1.下列三个说法:(1)残差平方和越小的模型,拟合的效果越好;(2)用R2来刻画回归的效果时,R2的值越小,说明模型拟合的效果越好;(3)直线y=b x+a和各点(x 1,y1),(x2,y2),…,(x n,y n)的偏差[y i-(b x i+a)]2是该坐标平面上所有直线中与这些点的偏差最小的直线.其中正确的个数为( )A.1个B.2个C.3个D.4个【解析】选B.由R2的定义可知:R2越接近于1,表明两个随机变量线性相关性越强,所以(2)不正确,其余说法正确.2.某单位为了了解用电量y(度)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:由表中数据得回归直线方程y=b x+a中b≈-2,预测当气温为-4℃时,用电量的度数约为( )A.68℃B.67℃C.66℃D.65℃【解析】选A.由表格得(,)为(10,40),又(,)在回归方程y=b x+a上且b≈-2,所以40=10×(-2)+ a,解得: a=60,所以y=-2x+60.当x=-4时, y=-2×(-4)+60=68.3.(2014·重庆高考)已知变量x与y正相关,且由观测数据算得样本平均数=3,=3.5,则由该观测数据测算的线性回归方程可能是( )A.y=0.4x+2.3B.y=2x-2.4C.y=-2x+9.5D.y=-0.3x+4.4【解题指南】根据正相关可知斜率为正,再根据线性回归方程经过点(,)可求出结果.【解析】选A.由正相关可知斜率为正,故可排除C,D两项,又因为y=0.4x+2.3经过点(3,3.5),故A项正确.【补偿训练】(2015·临沂高二检测)某饮料店的日销售收入y(单位:百元)与当天平均气温x(单位:度)之间有下列数据关系:甲、乙、丙三位同学对上述数据进行了研究,分别得到了x与y之间的三个线性回归方程:①y=-x+2.8,②y=-x+3,③y=-1.2x+2.6;其中正确的是 ( )A.①B.②C.③D.①③【解析】选A.回归方程y =b x+a 表示的直线必过点(,),即必过点(0,2.8),而给出的三个线性回归方程中,只有①表示的直线过点(0,2.8),故正确的是①.4.(2015·泰安高二检测)在回归分析中,R 2的值越大,说明残差平方和 ( )A.越大B.越小C.可能大也可能小D.以上均错【解析】选B.因为R 2=n2ii i 1n2ii 1(y y )1(yy)==---∑∑,所以当R 2越大时,(y i -i y )2越小,即残差平方和越小.5.(2015·福建高考)为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:根据上表可得回归直线方程y =b x+a ,其中b =0.76, a =-b .据此估计,该社区一户年收入为15万元家庭的年支出为 ( ) A.11.4万元 B.11.8万元 C.12.0万元 D.12.2万元【解题指南】样本中心点(,)一定在回归直线上.【解析】选B.由题意得==10,==8,所以a=8-0.76×10=0.4,所以y=0.76x+0.4,把x=15代入得到y=11.8.二、填空题(每小题5分,共15分)6.在研究身高和体重的关系时,求得相关指数R2≈,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”,所以身高对体重的效应比随机误差的效应大得多.【解析】结合R2的计算公式R2=n2i ii1n2ii1(y y)1(y y)==---∑∑可知,当R2=0.64时,身高解释了64%的体重变化.答案:0.647.若根据10名儿童的年龄x(岁)和体重y(kg)数据用最小二乘法得到用年龄预报体重的回归方程是y=2x+7,已知这10名儿童的年龄分别是2,3,3,5,2,6,7,3,4,5,则这10名儿童的平均体重是. 【解析】由题意可得=2+7,又=4,所以=15.答案:15kg8.(2015·扬州高二检测)某校高二(8)班学生每周用于数学学习的时间x(单位:小时)与数学成绩y(单位:分)构成如下数据(15,79),(23,97),(16,64),(24,92),(12,58),求得的回归直线方程为y=2.5x+a,则某同学每周学习20小时,估计数学成绩约为 分. 【解析】=×(15+23+16+24+12)=18, =×(79+97+64+92+58)=78, 把(,)代入y =2.5x+a ,可求得a =33,把x=20代入y =2.5x+33得y =2.5×20+33=83. 答案:83三、解答题(每小题10分,共20分) 9.关于x 与y 有如下数据关系:为了对x,y 两个变量进行统计分析,现有以下两种线性模型:甲模型y =6.5x+17.5,乙模型y =7x+17,试比较哪一个模型拟合的效果更好.【解析】=52ii i 152ii 1(yy )1(yy)==---∑∑=1-=0.845,=52ii i 152ii 1(yy )1(yy)==---∑∑=1-=0.82,84.5%>82%,所以甲模型拟合效果更好.【拓展延伸】R 2=1-n2ii 1n2ii 1(y y)1(yy)==---∑∑的意义R 2越大,残差平方和越小,从而回归模型的拟合效果越好.在线性回归模型中,R2表示解释变量对于预报变量变化的贡献率,R2越接近1,表示回归的效果越好(因为R2越接近1,表示解释变量和预报变量的线性相关性越强).10.(2015·深圳高二检测)PM2.5是指大气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:(1)根据上表数据,请在下列坐标系中画出散点图.(2)根据上表数据,用最小二乘法求出y关于x的线性回归方程y=b x+a.(3)若周六同一时间段车流量是25万辆,试根据(2)求出的线性回归方程预测,此时PM2.5的浓度为多少(保留整数).【解析】(1)散点图如图所示.(2)因为==54,==74,(x i -)(y i -)=4×5+3×4+3×4+4×5=64, (x i -)2=(-4)2+(-3)2+32+42=50,b =5ii i 152ii 1(xx)y y (xx)==---∑∑()==1.28,a =-b =74-1.28×54=4.88,故y 关于x 的线性回归方程是y =1.28x+4.88. (3)当x=25时,y =1.28×25+4.88=36.88≈37,所以可以预测此时PM2.5的浓度约为37微克/立方米.(20分钟 40分)一、选择题(每小题5分,共10分)1.(2015·眉山高二检测)已知样本点散落在某一条曲线y=a bx e +附近,作变换z=lny,利用线性回归模型来求其中的参数a,b,则拟合其变换后的样本点的直线方程为( )=+ =+ =+ =+A.z bx aB.z bx eaC.z bx lnaD.z bxln a【解析】选A.对方程y=a bxe+两边取以e为底的对数即得.2.已知一系列样本点(x i,y i)(i=1,2,3,…,n)的回归直线方程为y=2x+a,若样本点(r,1)与(1,s)的残差相同,则有( )A. r=sB.s=2rC.s=3-2rD.s=2r+1【解析】选C.由残差的定义可得,1-(2r+a)=s-(2+a),化简得s=3-2r.【延伸探究】若将题中的“y=2x+a”改为“y=bx+a”,同时将“样本点(r,1)与(1,s)”改为“样本点(1,1)与(2,4)”,则b= . 【解析】由残差的定义可得1-(b+a)=4-(2b+a),化简得b=3.答案:3二、填空题(每小题5分,共10分)3.已知回归方程为y=2x+1,而实验得到的一组数据为(2,4.9),(3,7.1),(4,9.1),则残差平方和为.【解析】(y i-y i)2=(4.9-5)2+(7.1-7)2+(9.1-9)2=0.03.答案:0.034.(2015·石家庄高二检测)已知一组具有线性相关关系的数据(x1,y1),(x2,y2),…,(x n,y n),其样本点的中心为(2,3),若其回归直线的斜率估计值为-1.2,则该回归直线方程为.【解析】由题意可设回归直线为y=-1.2x+a,由于回归直线过样本点的中心(2,3),故有3=-1.2×2+a,解得a=5.4,故回归直线方程为y=-1.2x+5.4.答案:y=-1.2x+5.4【补偿训练】(2014·渭南高二检测)已知x与y之间的几组数据如下表:则y与x的线性回归方程y=b x+a过点( )A.(0,1)B.(1,4)C.(2,5)D.(5,9)【解析】选C.因为==2,==5,所以根据线性回归方程必过样本中心点,可得y=b x+a必过(2,5).三、解答题(每小题10分,共20分)5.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:(1)求回归直线方程y=b x+a,其中b=-20,a=-b.(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)【解题指南】(1)利用线性回归系数公式求出a,b的值,从而可确定回归直线方程.(2)利用二次函数求最值.【解析】(1)由于=×(8+8.2+8.4+8.6+8.8+9)=8.5,=×(90+84+83+80+75+68)=80,又b=-20,所以a=-b=80+20×8.5=250,从而回归直线方程为y=-20x+250.(2)设工厂获得的利润为L元,依题意得L=x(-20x+250)-4(-20x+250)=-20x2+330x-1000=-20(x-8.25)2+361.25.当且仅当x=8.25时,L取得最大值.故当单价定为8.25元时,工厂可获得最大利润.【拓展延伸】建立回归模型的基本步骤(1)确定解释变量和预报变量.(2)画散点图,观察是否存在线性相关关系.(3)确定回归方程的类型,如y=b x+a.(4)按最小二乘法估计回归方程中的参数.(5)得结果后分析残差图是否异常,若存在异常,则检查数据是否有误,或模型是否合适.6.(2015·重庆高考)随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:(1)求y 关于t 的回归方程=t+.(2)用所求回归方程预测该地区2015年(t=6)的人民币储蓄存款.附:回归方程=t+中,ni ii 1n22ii 1t yntyb a y bt.tnt ,==-==--∑∑【解题指南】(1)直接利用回归系数公式求解即可.(2)利用回归方程代入直接进行计算即可. 【解析】(1)列表计算如下:n n i i i 1i 1nn222tt ity i i i 1i 1ty tt115136n 5,t t 3,y y 7.2.n 5n 5t nt 555310,t y nty 120537.212,121.2,10a y t 7.21.23 3.6,============-=-⨯==-=-⨯⨯======⨯=∑∑∑∑这里又从而b -b -l l l l故所求回归方程为=1.2t+3.6.(2)将t=6代入回归方程可预测该地区2015年的人民币储蓄存款为=1.2×6+3.6=10.8(千亿元).【补偿训练】(2015·西安高二检测)下表是某年美国旧轿车价格的调查资料,以x(年)表示轿车的使用年数,y(美元)表示相应的年均价格,求y 关于x 的非线性回归方程.【解题指南】画出散点图或进行相关性检验,确定两变量x,y 是否线性相关.由散点图得x,y 之间的回归模型.然后转化为线性回归模型进行拟合,预报回归模型,求回归方程. 【解析】画散点图如图1所示,看出y 与x 呈指数关系,于是令z=lny.变换后得数据:画散点图如图2所示,由图可知各点基本处于一条直线, 由于==5.5,==6.5274,10i i i 11022ii 1x z10xz b 0.298,a z bx 6.527 40.298 5.58.166,x10x==-==-=-=+⨯≈-∑∑所以由表中数据可得线性回归方程为z =8.166-0.298x,因此旧轿车的平均价格对使用年数的非线性回归方程为y =e 8.166-0.298x .关闭Word 文档返回原板块。
高中数学人教版选修1-2课时自测 当堂达标:2.2.1.1 综合法 精讲优练课型 Word版含答案

温馨提示:此套题为Word 版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word 文档返回原板块。
课时自测·当堂达标1.设a=lg2+lg5,b=e x (x<0),则a 与b 的大小关系为 ( )A.a>bB.a=bC.a<bD.无法确定【解析】选A.因为a=lg2+lg5=lg(2×5)=lg10=1,所以b=e x <e 0=1=a.2.设0<x<1,则a=,b=x+1,c=中最大的是 ( )2x 11‒x A.c B.bC.aD.随x 取值不同而不同【解析】选A.因为x>0,所以(1+x)2=1+2x+x 2>2x.所以1+x>.即b>a.2x 又c-b=-(1+x)===>0,所以c>b 即11‒x 1‒(1‒x)(1+x)1‒x 1‒(1‒x 2)1‒x x21‒x c>b>a.3.已知a>0,b>0且a+b=2,则 ( )A.a≤B.ab≥1212C.a 2+b 2≥2D.a 2+b 2≤3【解析】选C.因为a>0,b>0,所以a+b≥2,所以ab≤1,a b a 2+b 2≥(a+b)2=2.124.在平面内有四边形ABCD 和点O,满足+=+,则四边形的形状为____.→O A →O C →O B →O D 【解析】由已知+=+得-=-,→O A →O C →O B →O D →O A →O B →O D →O C 即=,所以四边形ABCD 为平行四边形.→B A →C D 答案:平行四边形5.设数列{a n }的前n 项和为S n ,满足(3-m)S n +2ma n =m+3(n∈N *).其中m 为常数,且m≠-3,m≠0.(1)求证:数列{a n }是等比数列.(2)若数列{a n }的公比q=f(m),数列{b n }满足b 1=a 1,b n =f(b n-1)(n∈N *,n≥2),求证:数列32为等差数列.{1b n }【解析】(1)由(3-m)S n +2ma n =m+3,得(3-m)S n+1+2ma n+1=m+3,两式相减得(3+m)a n+1=2ma n ,因为m≠0且m≠-3,所以=,a n +1a n 2mm +3所以数列{a n }是等比数列.(2)因为b 1=a 1=1,q=f(m)=,2mm +3所以n∈N *且n≥2时,b n =f(b n-1)=·,32322b n ‒1b n ‒1+3b n b n-1+3b n=3b n-1,-=,1b n 1b n ‒113所以数列是以1为首项,为公差的等差数列.{1b n }13关闭Word 文档返回原板块。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
温馨提示:
此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业十二
流程图
一、选择题(每小题5分,共25分)
1.下列判断不正确的是( )
A.画工序流程图类似于算法的流程图,要先把每一个工序逐步细化,按自上向下或自左到右的顺序
B.在工序流程图中可以出现循环回路,这一点不同于算法流程图
C.工序流程图中的流程线表示相邻两工序之间的衔接关系
D.工序流程图中的流程线都是有方向的指向线
【解析】选B.工序流程图不可以出现循环回路,故B错.
2.某麻鸭资源的开发与利用的流程图如图所示,则羽绒加工的前一道工序是
( )
A.孵化鸭雏
B.商品鸭饲养
C.商品鸭收购、育肥、加工
D.羽绒服加工生产体系
【解题指南】按照箭头所指方向读图.
【解析】选C.由工序流程图可知,羽绒加工的前一道工序是商品鸭收购、育肥、加工.
3.(2016·广州高二检测)执行如图所示的程序框图,若输入n的值为3,则输出s的值是( )
A.1
B.2
C.4
D.7
【解析】选C.根据程序框图得s=1+0+1+2=4.
4.(2016·太原高二检测)某流程图如图所示,现输入如下四个函数,则可以输出的函数是
( )
A.f (x)=
B.f(x)=ln(-x)
C.f(x)=
D.f(x)=
【解析】选B.由框图知,f(x)为有零点的奇函数,A,C中函数f(x)无零点;D中函数f(x)
为偶函数,B中函数f(x)=ln(-x)满足f(0)=0且f(-x)=ln(+x)=ln=-ln(-x)=-f(x).
5.(2016·广州高二检测)如图所示流程图中,判断正整数x是奇数还是偶数,判断框内的条
件是( )
A.余数是1?
B.余数是0?
C.余数是3?
D.余数不为0?
【解析】选B.依据判断框的出口进行选择,出口为“是”时x为偶数.故判断框内应该填余数是0?.
【补偿训练】写出如图流程图的功能是什么.
【解析】由该流程图中的条件结构可得其功能为求函数y=的函数
值.
二、填空题(每小题5分,共15分)
6.(2016·重庆高二检测)某算法的程序框图如图所示,若输出,则输入的实数x的值为________.
【解析】由程序框图知:该算法是求分段函数
y=的函数值,所以由y=,得x=.
答案:
7.某工程的工序流程图如图(工时单位:天),现已知工程总时数为10天,则工序c所需工时数为________天.
【解析】设工序c所需工时数为x天,
由题设知关键路线是a→c→e→g,
需工时1+x+4+1=10,
所以x=4,
即工序c所需工时数为4天.
答案:4
8.(2016·福州高二检测)某地区规划道路建设,考虑道路铺设方案.方案设计图中,点表示城市,两点之间连线表示两城市间可铺设道路,连线上数据表示两城市间铺设道路的费用,要求从任一城市都能到达其余各城市,并且铺设道路的总费用最小.例如:在三个城市道路设计中,若城市间可铺设道路的线路图如图(1),则最优设计方案如图(2),此时铺设道路的最小总费用为10.现给出该地区可铺设道路的线路图如图(3),则铺设道路的最小总费用为________.
【解析】根据题目中图(3)给出的信息及题意,要求的是铺设道路的最小总费用,且从任一城市都能到达其余各城市,可将图(3)调整为如图所示的结构(线段下方的数字为两城市之间
铺设道路的费用).
此时铺设道路的总费用为2+3+1+2+3+5=16.
答案:16
三、解答题(每小题10分,共20分)
9.计算1+++…+的值,写出算法,画出程序框图.
【解析】用i表示循环次数,用sum表示总和,算法如下:
第一步输入i,sum,i的初始值为1,sum的初始值为0;
第二步从1开始循环到1000,sum=sum+1/i;
第三步循环结束后,输出sum.
程序框图如图所示.
10.有关专家建议,在未来几年内,中国的通货膨胀率保持在3%左右,这将对我国经济的稳定有利无害.所谓通货膨胀率为3%,指的是每年消费品的价格增长率为3%.在这种情况下,某种品牌的钢琴2014年的价格是10000元,试分析其算法并用流程图描述这种钢琴今后四年的价格变化情况,并输出四年后的价格.
【解析】用P表示钢琴的价格,算法步骤如下:
2015年P=10000×(1+3%)=10300,
2016年P=10300×(1+3%)=10609,
2017年P=10609×(1+3%)=10927.27,
2018年P=10927.27×(1+3%)=11255.0881.
因此,价格的变化情况表为:
流程图为:
【补偿训练】有一个农夫带一条狼、一只羊和一筐白菜过河.如果没有农夫看管,则狼要吃羊,羊要吃白菜,但是船很小,只够农夫带一样东西过河,问农夫该如何解决此难题?画出相应的流程图.
【解析】流程图如图所示.
一、选择题(每小题5分,共10分)
1.(2015·陕西高考)根据下边框图,当输入x为6时,输出的y=( )
A.1
B.2
C.5
D.10
【解析】选D.模拟执行程序框图,可得
x=6
x=3
满足条件x≥0,x=0
满足条件x≥0,x=-3
不满足条件x≥0,y=10
输出y的值为10.
2.如图,小圆圈表示网络的结点,结点之间的连线表示它们有网线相连,连线标注的数字表示该段网线单位时间内可以通过的最大信息量.现从结点A向结点B传递信息,信息可以分开沿不同的路线同时传递,则单位时间内传递的最大信息量为( )
A.26
B.24
C.20
D.19
【解析】选D.路线A→D→C→B的最大信息量是3;
路线A→D→E→B的最大信息量为4;
路线A→G→F→B的最大信息量为6;
路线A→G→H→B的最大信息量为6.
故从A到B的最大信息量为3+4+6+6=19.
二、填空题(每小题5分,共10分)
3.(2016·南京高二检测)如图是一个程序框图,则输出的k的值是__________.
【解析】根据循环结构的流程图,当k=1时,此时k2-5k+4=0,不满足条件,继续执行循环体;当k=2时,k2-5k+4=-2,不满足条件,继续执行循环;当k=3时,k2-5k+4=-2,不满足条件,继续执行循环体;当k=4时,k2-5k+4=0,不满足条件,继续执行循环体;当k=5时,k2-5k+4=4,满足条件跳出循环,输出k的值为5.
答案:5
4.执行如图所示的程序框图,输出的S的值为________.
【解析】S=sin+sin+sin+sin+sin+sin+…+sin
答案:0
三、解答题(每小题10分,共20分)
5.高考成绩公布后,考生如果认为公布的高考成绩与本人估算的成绩有误,可以在规定的时间内申请查分.
(1)本人填写《查分登记表》,交县(区)招办申请查分,县(区)招办呈交市招办,再报省招办.
(2)省招办复查,无误,则查分工作结束后通知;有误,则再具体认定,并改正,也在查分工作结束后通知.
(3)市招办接通知,再由县(区)招办通知考生.
试画出该事件的流程图.
【解析】流程图如图所示
6.(2016·成都高二检测)景泰蓝是深受人们喜爱的手工艺品,它的制作流程叙述如下:第一步是制胎;第二步是掐丝;第三步是点蓝;第四步是烧蓝;第五步是打磨;第六步是镀金.其中第二步完成后需经检验,检验合格进入下一步;不合格返回第一步重新制胎,第四步完成后需经检验,检验合格进入下一步;不合格为废品.请你用工序流程图画出上述流程. 【解析】工序流程图如图所示:
【补偿训练】某市环境保护局信访工作流程如下:(1)信访办受理来访,一般信访填单转办;
重大信访报局长批示后转办.
(2)及时转送有关部门办理、督办,如特殊情况未能按期办理完毕,批准后可延办,办理完毕后反馈.
(3)信访办理情况反馈后,归档备查,定期通报.
据上画出该局信访工作流程图.
【解析】流程图如图所示.
关闭Word文档返回原板块高中数学学习技巧:
在学习的过程中逐步做到:提出问题,实验探究,展开讨论,形成新知,应用反思。
重视基础题和领悟数学思想方法,多做综合题目。
高中数学学习技巧:
在学习的过程中逐步做到:提出问题,实验探究,展开讨论,形成新知,应用反思。
重视基础题和领悟数学思想方法,多做综合题目。
