高中数学顺序结构和选择结构检测试题(附答案)

合集下载

高中数学第二章算法初步2.2.1顺序结构与选择结构课时作业(含解析)北师大版必修3

第二章算法初步(本栏目内容，在学生用书中以独立形式分册装订！)一、选择题(每小题5分，共20分)1．下列是流程图中的一部分，表示恰当的是( )解析： B 选项应该用处理框而非输入、输出框，C 选项应该用输入、输出框而不是处理框，D 选项应该在出口处标明“是”和“否”．故选A.答案： A2．下列算法中可以用选择结构表示的是( )A ．求点到直线的距离B ．已知梯形的两底及高求面积C ．解一元二次方程D ．求两个数的积解析： C 选项中需要判断判别式与零的大小关系，所以用到选择结构．答案： C3．已知函数y ＝⎩⎪⎨⎪⎧ x －1，x ＜0，0，0≤x ≤6，3x ，x ＞6，输入自变量x 的值，求对应的函数值，设计算法框图时所含有的基本逻辑结构是( )A ．顺序结构B ．选择结构C ．顺序结构、选择结构D ．以上都不是解析：任何算法框图中都有顺序结构，由于自变量在不同的范围内有不同的对应法则，因此要用选择结构．答案： C4．如图是计算函数y ＝⎩⎪⎨⎪⎧ ln (－x )，x ≤－2，3x ，－2<x ≤3，2x ，x >3的函数值的算法框图，在①②③处应分别填入的是()A．y＝ln(－x)，y＝3x，y＝2xB．y＝ln(－x)，y＝2x，y＝3xC．y＝3x，y＝2x，y＝ln(－x)D．y＝3x，y＝ln(－x)，y＝2x解析：依题意得，当x≤－2时，y＝ln(－x)，因此①处应填y＝ln(－x)；当－2<x≤3时，y＝3x，因此③处应填y＝3x；当x<3时，y＝2x，因此②处应填y＝2x.答案： B二、填空题(每小题5分，共15分)5．下列关于算法框图的说法正确的是________．①算法框图只有一个入口，也只有一个出口；②算法框图中的每一部分都应有一条从入口到出口的路径通过它；③算法框图虽可以描述算法，但不如用自然语言描述算法直观．解析：由算法框图的要求知①②正确；由算法框图的优点知③不正确．答案：①②6．已知函数y＝|x－3|，以下程序框图表示的是给定x值，求其相应函数值的算法．请将该程序框图补充完整．其中①处应填________，②处应填________．解析：由f (x )＝|x －3|＝⎩⎪⎨⎪⎧x －3，x ≥3，3－x ，x ＜3及程序框图知，①处应填x ＜3，②处应填y ＝x －3.答案： x ＜3 y ＝x －37．执行如图所示的程序框图，如果输入a ＝1，b ＝2，则输出的a 的值为________．解析：利用程序框图表示的算法逐步求解．当a ＝1，b ＝2时，a >8不成立，执行a ＝a ＋b 后a 的值为3，当a ＝3，b ＝2时，a >8不成立，执行a ＝a ＋b 后a 的值为5，当a ＝5，b ＝2时，a >8不成立，执行a ＝a ＋b 后a 的值为7，当a ＝7，b ＝2时，a >8不成立，执行a ＝a ＋b 后a 的值为9，由于9>8成立，故输出a 的值为9.答案： 9三、解答题(每小题10分，共20分)8．已知两个单元分别存放了变量x 和y ，试变换两个变量的值，并输出x 和y ，请写出算法并画出程序框图．解析：算法如下．第一步，输入x ，y .第二步，把x 的值赋给p .第三步，把y的值赋给x.第四步，把p的值赋给y.第五步，输出x，y.程序框图如右．9．如图，是判断“美数”的程序框图，在[30,40]内的所有整数中“美数”的个数是多少？解析：由程序框图知美数是满足：能被3整除不能被6整除或能被12整除的数，在[30,40]内的所有整数中，所有的能被3整除的数有30,33,36,39，共有4个数，在这四个数中能被12整除的有36，在这四个数中不能被6整除的有33,39，所以在[30,40]内的所有整数中“美数”的个数是3个.。

2017-2018学年高二数学必修三学业分层测评：第2章 2.1 顺序结构与选择结构 2.2 变量与赋值

学业分层测评(建议用时：45分钟)[学业达标]一、选择题1．如图224所示的算法框图中含有的基本结构是( )图224A．顺序结构B．选择结构C．模块结构D．顺序结构和选择结构【解析】　顺序结构是任何算法都离不开的一种算法结构，并且此算法流程中含有判断框，因此此算法框图中既含有顺序结构又含有选择结构．【答案】　D2．在如下所示的算法语句中输入x＝1 000，y＝4，则输出的结果M是( )输入　x，yM＝2*x+4*y输出MA．2 014　B．2 015C．2 016D．2 017【解析】　M＝2×1 000＋4×4＝2 016.【答案】　C3．下列算法语句执行后的结果是( )i＝2；j＝5；i＝i＋j；j＝i＋j；输出i，j.A．i＝12，j＝7B．i＝12，j＝4C．i＝7，j＝7D．i＝7，j＝12【解析】　i＝2＋5＝7，j＝7＋5＝12.【答案】　D4．如图225所示的算法框图，能判断任意输入的数x的奇偶性，其中判断框内的条件是( )图225A．m＝0B．x＝0C．x＝1D．m＝1【解析】　判断框中填写的应该是余数与0的关系，偶数即整数除以2的余数为0，而余数在这个算法框图中用字母m表示，所以判断框中应填写“m＝0”．【答案】　A5．运行如图226所示的算法框图，若要使输入的x的值与输出的y的值相等，则这样的x的值有( )图226A ．1个B ．2个C ．3个D ．4个【解析】　当x ≤2时，由x 2＝x 得x ＝0或x ＝1，可以．当2<x ≤5时，由2x －3＝x 得x ＝3，可以．当x >5时，由＝x 得x ＝±1，舍去．1x 【答案】　C 二、填空题6．如图227是一个算法的框图，当输入的值为3时，输出的结果是________．图227【解析】　因为3<5，所以y ＝32－1＝8.【答案】　87．如图228②所示的框图是计算①(其中大正方形的边长为a )中空白部分面积的算法，则①中应填________．① ②图228【答案】　S ＝a 2－a 2π28．给出如图229所示的算法框图．图229若输入的实数x 的值为0，则输出的y 值为________．【解析】　由算法框图可得到一个分段函数．y ＝Error!将x ＝0代入可得y 的值为1.【答案】　1三、解答题9．已知直线l ：Ax ＋By ＋C ＝0(ABC ≠0)，求直线l 与两坐标轴围成的三角形的面积S .试画出解决这一问题的算法的程序框图．【解】　程序框图如图：10．下面是某同学写的求一元二次方程x 2－3x ＋2＝0的根的算法，请帮他填写完整并画出算法框图．1．a ＝1，b ＝－3，c ＝2；2．________；3．________；4．x 1＝p ＋q ，x 2＝p －q ；5．输出x 1，x 2.【解】　根据求根公式可知p ＝－，q ＝.算法框图如下：b2a b 2－4ac 2a[能力提升]1．任给x的值，计算函数y＝Error!中y值的程序框图如图2210所示，其中①②③分别是( )A．x＞1，x＜1，y＝3B．x＝1，x＞1，y＝3C．x＜1，x＝1，y＝3图2210D．x＜1，x＞1，y＝3【解析】　当“是”时y＝1，故①处应为x＜1.当②处“否”时y＝2，故②处应为x＞1.则③处只能y＝3.【答案】　D2．为确保信息安全，信息需加密传输，发送方由明文→密文(加密)，接收方由密文→明文(解密)，已知加密规则如图2211所示，例如，明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时，则解密得到的明文为( )图2211A．4,6,1,7B．7,6,1,4C．6,4,1,7D．1,6,4,7【解析】　由题意得Error!解得Error!故选C.【答案】　C3．(2016·北京高一检测)如图2212所示的算法框图的功能是________；若执行该算法框图，输出结果为3，则输入的x值的个数为________．图2212【解析】　求函数y＝Error!的函数值．当y＝3时，若x>2，则log2x＝3，所以x＝8，若x≤2，则x2－1＝3，所以x＝±2.【答案】　求函数y＝Error!的函数值　34．f(x)＝x2－2x－3.求f(3)、f(－5)、f(5)，并计算f(3)＋f(－5)＋f(5)的值．设计出解决该问题的一个算法并画出算法框图．【解】　算法如下：1．令x＝3；2．把x＝3代入y1＝x2－2x－3；3．令x＝－5；4．把x＝－5代入y2＝x2－2x－3；5．令x＝5；6．把x＝5代入y3＝x2－2x－3；7．把y1，y2，y3的值代入y＝y1＋y2＋y3；8．输出y1，y2，y3，y的值．该算法对应的算法框图如下图所示：。

高中数学北师大版必修三顺序结构与选择结构课时提升作业Word版含答案

课时提升作业十二顺序结构与选择结构一、选择题(每小题5分，共15分)1.已知函数y=输入x的值，求对应的函数值，设计框图时所含有的基本逻辑结构是( )A.顺序结构B.选择结构C.顺序结构、选择结构D.顺序结构、选择结构、模块结构【解析】选C.由于函数解析式取决于自变量的取值范围，所以必须有选择结构，又任何框图中都要用到顺序结构，故选C.2.如图所示的算法框图，若能判断任意输入的数x的奇偶性，其中判断框内的条件是( )A.m=0B.x=0C.x=1D.m=1【解析】选A.判断框中填写的应该是余数与0的关系，偶数即整数除以2的余数为0，而余数在这个算法框图中用字母m表示，所以判断框中应填写“m=0”.3.(2016·烟台高一检测)对任意非零实数a，b，若a☉b的运算原理如算法框图所示，则(3☉2)☉4的值是( )A.2B.3C.D.【解题指南】根据a☉b的运算原理知a=3，b=2，通过算法框图知须执行，故把值代入求解，类似地即可求得(3☉2)☉4的值.【解析】选C.由题意知，a=3，b=2，再由算法框图得，3≤2不成立，故执行，得到3⊗2==2.同样，2☉4=.二、填空题(每小题5分，共15分)4.(2016·榆林高一检测)如图是一个算法的框图，当输入的值为3时，输出的结果是________.【解析】因为3<5，所以y=32-1=8.答案：8【延伸探究】本题条件不变，若输出的值为48，则输入的值是什么？【解析】当2x2-2=48时，x=5，当x2-1=48时，x=7>5，所以输入的值为5.5.阅读如图的算法框图，若输入的a，b，c分别是sin30°，sin45°，sin60°，则输出的max=________.【解析】由算法框图知，第一个判断框中条件若成立，则将a赋给max，否则将b赋给max，第二个判断框原理也是取出最大值，此算法框图的功能是找出三数中的最大值，又sin60°=>sin45°=>sin30°=，所以最大值为sin60°. 答案：sin60°6.已知函数f(x)=补充完成其求值的算法框图，则①处应填________.【解析】由该算法框图的功能知①处应填x≤1.答案：x≤1【延伸探究】若本题算法框图中“是”与“否”的位置互换，则①处应填________.【解析】由该算法框图的功能知①处应填x>1.答案：x>1三、解答题(每小题10分，共20分)7.已知f(x)=x2-1，求f(2)，f(-3)，f(3)，并计算f(2)+f(-3)+f(3)的值，设计出解决该问题的一个算法，并画出算法框图.【解析】算法如下：1.x=2.2.y1=x2-1.3.x=-3.4.y2=x2-1.5.x=3.6.y3=x2-1.7.y=y1+y2+y3.8.输出y1，y2，y3，y.算法框图如下：【补偿训练】如图所示的算法框图是为解决某个问题而绘制的，仔细分析各框图内的内容及框图之间的关系，回答下面的问题：(1)该算法框图解决的是怎样的一个问题？(2)若最终输出的结果y1=3，y2=-2，当x取5时输出的结果5a+b的值应该是多大？(3)在(2)的前提下，输入x的值越大，输出ax+b的值是不是越大？为什么？(4)在(2)的前提下，当输入x的值为多大时，输出ax+b的值等于0？【解析】(1)该算法框图解决的是当x=2，-3时，求函数f(x)=ax+b的函数值的问题.其中输入的是自变量x的值，输出的是x对应的函数值.(2)y1=3，即2a+b=3. ①y2=-2，即-3a+b=-2. ②由①②得a=1，b=1，所以f(x)=x+1.所以当x取5时，f(5)=5a+b=5×1+1=6.(3)输入x的值越大，输出ax+b的值越大.因为f(x)=x+1是R上的增函数.(4)令f(x)=0，即x+1=0，解得x=-1，因此当输入x的值为-1时，输出ax+b的值等于0.8.如图是判断“美数”的算法框图，在[30，40]内的所有整数中“美数”的个数是多少？【解析】由算法框图知美数是满足：能被3整除不能被6整除或能被12整除的数，在[30，40]内的所有整数中，所有的能被3整除的数有30，33，36，39，共有4个数，在这四个数中能被12整除的有36，在这四个数中不能被6整除的有33，39，所以在[30，40]内的所有整数中“美数”的个数是3个.一、选择题(每小题5分，共10分)1.如图所示的算法框图，当x1=6，x2=9，p=8.5时，x3等于( )A.7B.8C.10D.11【解题指南】注意题设中满足的条件，以便判断判断框执行哪一个出口.【解析】选B.本题只看输出的p即可.因为==7.5≠8.5，所以p=8.5=.所以x3=2×8.5-x2=17-9=8.2.(2015·全国卷Ⅱ)如图算法框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该算法框图，若输入的a，b分别为14，18，则输出的a为( )。

高中数学 2.2.1 顺序结构与选择结构课时提升作业北师大版必修3

顺序结构与选择结构一、选择题(每小题4分,共16分)1.下列关于算法框图的说法中,正确的个数是( )①用算法框图表示算法直观、形象,容易理解;②算法框图能够清楚地展现算法的逻辑结构,也就是通常所说的“一图胜万言”;③在算法框图中,起止框是任何流程不可少的;④输入和输出框可用在算法中任何需要输入、输出的位置.A.1B.2C.3D.4【解析】选D.由算法框图的意义与作用易知.2.如图所示算法框图中,不含有的框图是( )A.起止框B.输入、输出框C.判断框D.处理框【解析】选C.由算法框图知,不含有判断框.3.运行如图所示的算法框图,若要使输入的x的值与输出的y的值相等,则这样的x的值有( )A.1个B.2个C.3个D.4个【解析】选C.当x≤2时,由x2=x得x=0或x=1,可以.当2<x≤5时,由2x-3=x得x=3,可以.当x>5时,由=x得x=±1,舍去.【举一反三】若输出的值为9,则输入的x的值为________.【解析】当x≤2时,由x2=9,所以x=-3.当2<x≤5时,由2x-3=9,得x=6,舍去.当x>5时,由=9,得x=,舍去.答案:-34.如图所示的算法框图,能判断任意输入的数x的奇偶性,其中判断框内的条件是( )A.m=0B.x=0C.x=1D.m=1【解析】选A.判断框中填写的应该是余数与0的关系,偶数即整数除以2的余数为0,而余数在这个算法框图中用字母m表示,所以判断框中应填写“m=0”.二、填空题(每小题5分,共10分)5.对任意非零实数a,b,若a⊗b的运算原理如图所示,则e2ln 2⊗=________(e为自然对数的底数).【解题指南】先分别求出e2ln2与的值,然后比较大小,选择下一步执行的语句,代入计算即可.【解析】e2ln2=4,=8.因为4<8,执行输出b-1,e2ln2⊗=7.答案:76.已知函数f(x)=补充完成其求值的算法框图,则①处应填________.【解析】由该算法框图的功能知①处应填x≤1.答案:x≤1【举一反三】若本题算法框图中“是”与“否”的位置互换,则①处应填________.【解析】由该算法框图的功能知①处应填x>1.答案:x>1三、解答题(每小题12分,共24分)7.已知f(x)=x2-1,求f(2),f(-3),f(3),并计算f(2)+f(-3)+f(3)的值,设计出解决该问题的一个算法,并画出算法框图.【解题指南】先求f(2),f(-3),f(3),写出算法,然后计算f(2)+f(-3)+f(3)的值利用赋值语句进行表示,最后根据算法画出相应的算法框图即可.【解析】算法如下:1.x=2.2.y1=x2-1.3.x=-3.4.y2=x2-1.5.x=3.6.y3=x2-1.7.y=y1+y2+y3.8.输出y1,y2,y3,y.算法框图:8.“特快专递”是目前人们经常使用的异地寄信或托运物品的一种快捷方式,某快递公司规定甲、乙两地之间物品的托运费用根据下列方法运算:y=其中y(单位:元)为托运费,x(单位:千克)为托运物品的质量,试画出计算托运费用y的算法框图.【解析】算法框图如图所示:一、选择题(每小题4分,共12分)1.下列关于选择结构的说法正确的是( )A.无论选择结构中的条件满足与否,都只能执行两条路途之一B.选择结构的两条路途可以同时执行C.对于一个选择结构而言,判断框中的条件是唯一的D.以上说法均不对【解析】选A.选择结构虽然有2个出口,但每次只能走一个出口.2.某算法框图如图所示,现输入如下四个函数,则可以输出的函数是( )A.f(x)=x2B.f(x)=C.f(x)=lnx+2x-6D.f(x)=x3+x【解析】选 D.由框图可知,当输入的函数f(x)为奇函数且存在零点时,才可输出f(x),由选项可知,仅f(x)=x3+x同时满足这两个条件,故选D.【举一反三】若把判断框内条件“f(x)+f(-x)=0”改为“f(x)-f(-x)=0”,则结果如何?【解析】选A.因为f(x)-f(-x)=0,所以f(x)是偶函数.因为f(x)=x2是偶函数且存在零点.3.(2013·新课标全国卷Ⅰ)执行如图所示的算法框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]【解题指南】观察算法框图,知t<1对应的函数为s=3t,t≥1对应的函数为s=4t-t2,再结合函数的性质求出s的取值范围.【解析】选A.由算法框图可知,s与t的关系可用分段函数表示为s=则s∈[-3,4].二、填空题(每小题4分,共8分)4.阅读如图的算法框图,若输入的a,b,c分别是sin30°,sin45°,sin60°,则输出的max=________.【解析】由算法框图知,判断框中条件若成立,则将a赋给max,否则b较大,将b赋给max,第二个判断框原理也是取出最大值,此程序的功能是找出三数中的最大值,又sin60°=>sin45°=>sin30°=,所以最大值为sin60°.答案:sin60°5.某算法的算法框图如图所示,若输出结果为,则输入的实数x的值是________.【解析】当x>1时,log2x=,所以x=可以,当x≤1时,x-1=,x=舍去.答案:【变式训练】阅读如图所示的算法框图,若输出y的值为0,则输入x的值为________.【解析】当x>1时,x2-4x+4=0得x=2.当x<1时,x=0可以.当x=1时,y=1舍去.答案:0或2三、解答题(每小题10分,共20分)6.如图是判断“美数”的算法框图,在[30,40]内的所有整数中“美数”的个数是多少?【解析】由算法框图知美数是满足:能被3整除不能被6整除或能被12整除的数,在[30,40]内的所有整数中,所有的能被3整除的数有30,33,36,39,共有4个数,在这四个数中能被12整除的有36,在这四个数中不能被6整除的有33,39,所以在[30,40]内的所有整数中“美数”的个数是3个.7.某商场购物实行优惠措施,若购物金额x在800元以上的打8折,若购物金额x在600元以上且不超过800元时打9折,否则不打折,请设计出该商场打折优惠措施的算法框图.【解析】根据题意,实际交款额y与购物金额x的函数关系式为:y=由函数的关系式可以知道,购物金额优惠措施可分为三种情况,故需用到条件结构设计算法.算法框图如图所示:【拓展提升】用条件结构解题的注意事项(1)应用条件结构画算法框图应注意两点:一是需要判断的条件是什么,二是判断后的条件分别对应着什么样的结果.(2)凡必须先根据条件作出判断,然后再决定进行哪一步骤的问题,在画算法框图时,必须引入判断框.。

苏教版高中数学必修三练习：1.2.1顺序结构含答案

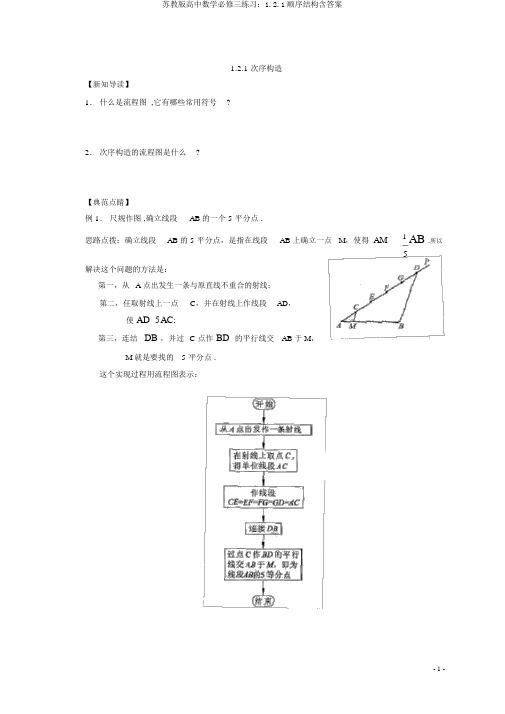
1.2.1 次序构造【新知导读】1．什么是流程图 ,它有哪些常用符号?2．次序构造的流程图是什么?【典范点睛】例 1．尺规作图 ,确立线段AB 的一个 5 平分点 .思路点拨：确立线段AB 的 5 平分点，是指在线段AB 上确立一点M，使得AM 1 AB .所以5解决这个问题的方法是：第一，从 A 点出发生一条与原直线不重合的射线；第二，任取射线上一点C，并在射线上作线段AD，使 AD 5AC;第三，连结DB ，并过C点作 BD 的平行线交AB 于 M，M 就是要找的 5 平分点 .这个实现过程用流程图表示：易错辨析：有些同学想直接从已知线段AB 下手取 5 平分点，实质上用尺规是作不出来的。

方法评论：这个算法拥有一般性，对于随意自然数n ，都能够依据这个算法的思想，设计出确立线段 n 平分点的步骤，获得解决这个一般问题的算法．【课外链接】1．经过市场检查剖析得悉，2006 年第一季度内，某地域对某件商品的需求量为12000 件 .为保证商品不畅销，商家在月初时将商品按同样数目投放市场.已知年初商品的库存量为50000件，用S 表示商品的库存量，请设计一个算法，求出第一季度结束时商品的库存量，并画出流程图 .思路点拨：由于第一季度商品的需求量为12000 件，并且每个月以同样数目投放市场，所以每个月向市场投放4000 件商品 .能够用下表表示库存量跟着月份的变化状况【随堂操练】1．算法的三种基本构造是()A. 次序构造、模块构造、条件构造B. 次序构造、循环构造、模块构造C. 次序构造、条件构造、循环构造D. 模块构造、条件构造、循环构造2.以下图形符号中，表示输入输出框的是（）3.以下对于流程图（符号）的几种说法：①任何一个流程图都一定有起止框；②输入框只好放在开始框后，输出框只好放在结束框前；③判断框是独一拥有超出一个退出点的符号.此中正确说法的个数是（）A．1个B．2 个C．3 个D．0 个4．流程图中的判断框，有m 个进口和n 个出口，则m,n 的值分别为（）A． 1，1 B. 1，2C ．2， 1D ．2，25．将两个数 a=8,b=17 互换 ,使 a=17,b=8,下边语句正确一组是 ()a=b c=b a=cb=ab=ab=a c=ba=ba=cAB C D6．对次序构造，以下说法：（ 1）是最基本、最简单的算法构造；（ 2）框与框之间是挨次进行办理；（ 3）除输入框、输出框以外，中间过程都为办理框；（ 4）能够从一个框跳到另一个框图进行履行，此中正确的有（）A.1 个B.2 个C.3 个D.4 个7．用赋值语句写出以下算法，并画出流程图：摄氏温度 C 为 23.5℃，将它变换成华氏温度 F ，并输出.已知 F5C 3298．相关专家建议，在将来几年，中国的通货膨胀率保持在3％左右将对中国经济的稳固有益无害 .所谓通货膨胀为 3％，指的是每年花费品的价钱增加率为3％ .在这类状况下，某种品牌的钢琴 2006年的价钱为 10000 元，请用流程图描绘这类钢琴此后4 年的价钱变化状况，并输出4 年后钢琴的价钱 .。

高考数学复习顺序结构与选择结构专项练习(附解析)

高考数学复习顺序结构与选择结构专项练习（附解析）顺序结构的程序设计是最简单的，只要按照解决问题的顺序写出相应的语句就行，它的执行顺序是自上而下，依次执行。

以下是顺序结构与选择结构专题练习，请考生及时进行练习。

一、选择题1.在算法框图中，表示判定框的图形符号是()[答案] C[解析] 依照各框图符号及其表示的意义能够确信是C.2.在算法框图中，算法中要运算和处理的数据，能够分别写在不同的()A.处理框内B.判定框内C.输入输出框内D.起止框内[答案] A[解析] 处理框的功能是赋值和运算.3.给出以下四个问题：输入一个数x，输出它的相反数.求面积为6的正方形的周长.求三个数a，b，c中的最大数.求函数f(x)=的函数值.其中不需要用选择结构来描述其算法有的()A.1个B.2个C.3个D.4个[答案] A[解析] 只有不需要用选择结构来描述其算法，只用顺序结构就行.4.已知函数y=，输入x的值，求对应的函数值，设计框图时所含有的差不多逻辑结构是()A.顺序结构B.选择结构C.顺序结构、选择结构D.顺序结构、选择结构、模块结构[答案] C[解析] 由于函数解析式取决于自变量的取值范畴，因此必须有选择结构，又任何框图中都要用到顺序结构，故选C.5.如下图所示，流程图的输出结果是()A.0.5B.1.5C.2.5D.3[答案] C[解析] a=2，b=4，S=+=+=2.5.6.已知函数f(x)=求f(a)(0) y=2x-5[解析] 当2x-50，即x时，y=2x-5，当2x-50时，x时，y=5-2x.故处填x(填x也能够);处填y=2x-5.8.如下图所示的框图，若输入-4，则输出结果为________.[答案] 是负数[解析] 利用选择结构解题.由于-40，故应选择否那一支，因此输出是负数.三、解答题9.函数y=，写出求该函数值的算法，并画出流程图.[解析] 算法如下：1 输入x;2 假如x0，那么使y=-x2;假如x=0，那么使y=0;假如x0，那么使y=x 2;3 输出函数值y.流程图如下图所示一、选择题1.如下框图，当x1=6，x2=9，p=8.5时，x3等于()A.7B.8C.10D.11[答案] B[解析] 本题考查了算法程序框图.只看输出的p即可.因为==7.58.5，因此p=8.5=.x3=28.5-x2=17-9=8.2.在佛山市禅城区和南海区打的士收费方法如下：不超过2千米收7元，超过2千米的每千米收2.6元，另每车次超过2千米收燃油附加费1元(其他因素不考虑).相应收费系统的算法流程图如图所示，则处应为()A.y=7+2.6xB.y=8+2.6xC.y=7+2.6(x-2)D.y=8+2.6(x-2)[答案] D[解析] 设的士行驶的里程为x千米，收费为y元，y=f(x)为关于x的函数，当x2时，由于超过2千米的里程每千米收2.6元，另每车次超过2千米收燃油附加费1元，故函数的解析式为y=7+1+2.6(x-2)=8+2.6(x-2).二、填空题3.对任意非零实数a，b，若ab的运算原理如图所示，则lg1000-2=___ _____.[答案] 1死记硬背是一种传统的教学方式,在我国有悠久的历史。

高中数学 1.2.2 选择结构检测试题苏教版必修3

选择结构基础巩固1．执行如下图所示的程序框图，输出的S值为( )A．2 B．4 C．8 D．16答案：C2．根据如图所示的框图，当输入的x为6时，输出的y＝(D)A ．1B ．2C ．5D ．10解析：当x ＝6时，x ＝6－3＝3，此时x ＝3≥0；当x ＝3时，x ＝3－3＝0，此时x ＝0≥0；当x ＝0时，x ＝0－3＝－3，此时x ＝－3＜0，则y ＝(－3)2＋1＝10.3．为函数y ＝⎩⎪⎨⎪⎧－1，x ＞0，0，x ＝0，1，x ＜0设计流程图．答案：4．根据如下图所示的流程图回答下列问题．(1)若输入12，18，7，5，则最终输出结果是多少？(2)该流程图的算法功能是什么？(3)根据流程图写出它的算法．解析：(1)若输入12，18，7，5，则最终输出的结果是5.(2)该流程图的算法功能是求四个数a，b，c，d中的最小数．(3)算法：S1 输入a，b，c，d；S2 如果a＜b，a＜c，a＜d，则输出a，否则执行S3；S3 如果b＜c，b＜d，则输出b，否则执行S4；S4 如果c＜d，则输出c，否则执行S5；S5 输出d.5．到银行办理个人异地汇款(不超过100万元)，银行收取一定的手续费．汇款额不超过100元，收取1元；汇款额超过100元，但不超过5 000元，按汇款额的1%收取；超过5 000元一律收取50元手续费．设计汇款额为x元时，银行收取的手续费y元的过程的流程图．解析：流程图如下图所示：6．已知A(x 1，y 1)，B(x 2，y 2)，求AB 的斜率，试设计算法并画出流程图．解析：算法如下： S1 输入x 1，y 1，x 2，y 2. S2 判断x 1＝x 2是否成立，若成立，则输出“斜率不存在”，并结束；若不成立，则计算k ←y 2－y 1x 2－x 1. S3 输出斜率k . 流程图如下图所示：能力升级7．已知函数f(x)＝⎩⎪⎨⎪⎧4x ，0＜x≤5，20，5＜x≤9，56－4x ，9＜x≤14，求f(a)(0＜a≤14)的算法中，需要用到选择结构，其中判断框的形式是________(填序号)．答案：④ 8．下面的程序框图所表示的算法的功能是________________________________________________________________________．答案：求a ，b ，c 三个数中的最大数9．某商场为迎接店庆举办促销活动，活动规定：购物额为100元以内不予优惠；在100～300元之间优惠货款的5%；超过300元，超过部分优惠8%，原优惠条件仍然有效．画出顾客的购物额与应付金额之间的一个算法流程图．解析：依题意，实际交款额y 与购物金额x 的函数关系式为y ＝⎩⎪⎨⎪⎧x （x ≤100），0.95x （100＜x ≤300），285＋（x －300）×0.92（x ＞300）.流程图如下图所示：10．给出一百分制成绩，要求输出成绩等级“A ”，“B ”，“C ”，“D ”，“E ”，90分以上为“A”，80～89分为“B”，70～79分为“C”，60～69分为“D”，60分以下为“E”，请设计流程图．解析：可设计如下图所示的流程图：11．写出求方程a x 2＋bx ＋c ＝0(a ，b ，c 为常数)的解的算法，并画出流程图．解析：算法设计如下： S1 输入a ，b ，c .S2 如果a ≠0，转S3；如果a ＝0，转S7.S3 Δ←b 2－4ac .S4 如果Δ＜0，输出“方程无实数根”；如果Δ≥0，则转S5. S5 x 1←－b ＋Δ2a ，x 2←－b －Δ2a .S6 输出x 1，x 2.S7 如果b ≠0，转S8；如果b ＝0，则转S10. S8 x ←－c b. S9 输出x .S10 如果c ≠0，输出“方程无实数根”；如果c ＝0，输出“方程的解是全体实数”．流程图如下图所示：12．为了加强居民的节水意识，某市制定了以下生活用水收费标准：每户每月用水未超过7立方米时，每立方米收费1.0元，并加收0.2元的城市污水处理费；超过7立方米的部分，每立方米的收费1.5元，并加收0.4元的城市污水处理费．设某户每月用水量为x 立方米，应缴纳水费y 元，请你设计一个输入用水量、输出应缴水费的算法，并画出流程图．解析：算法设计如下：S1 输入每月用水量x(x≥0)；S2 判断输入的x是否超过7，若x>7，则应缴纳水费y←1.9x－4.9；否则应缴纳水费y←1.2x；S3 输出应缴纳水费y.流程图如图所示．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中数学顺序结构和选择结构检测试题（附答案）
高中数学顺序结构和选择结构检测试题（附答
案）
顺序结构与选择结构同步练习思路导引
1.设计求|x|的算法，并画出流程图.
解：具体算法如下：
（1）若x0，则|x|等于－x；（2）若x0，则|x|等于x.
算法流程图如图2－2－11.
图2－2－11
2.画出由梯形两底a、b和高h，求梯形面积的算法流程图. 解：算法流程图如图2－2－12.
图2－2－12
3.画出从a，b，c三个数中找出最大值的算法流程图.
解：算法流程图如图2－2－13.
图2－2－13
4.已知点P（x0，y0）和直线l：Ax+By+C=0，写出求点P到直线l的距离d的算法流程图.
解：算法流程图如图2－2－14.
图2－2－14
5.设汽车托运重量为P kg的货物时，托运每千米的费用标准为
画出行李托运费用的算法流程图.
5.解：算法流程图如图2－2－15.（x为托运路程）
图2－2－15 根据绝对值的意义.
两两之间进行大小比较.
d= .
分段函数函数值的算法一般用选择结构.。