多项式的加减
整式加减运算法则

整式加减运算法则在代数学中,整式加减运算是一种基本的运算法则,它是解决代数表达式加减运算的重要方法。
整式加减运算法则包括了多项式的加减法规则和运算步骤,下面我们将详细介绍整式加减运算的相关知识。
一、多项式的加减法规则1. 同类项的加减法则:对于多项式来说,只有同类项才能进行加减运算。
同类项是指具有相同字母部分的项,它们的指数可以不同,但字母部分必须相同。
例如,3x^2和5x^2就是同类项,可以进行加减运算;而3x^2和5y^2就不是同类项,不能进行加减运算。
2. 加减法的运算步骤:对于多项式的加减法,首先要将同类项合并在一起,然后按照同类项的加减法则进行运算。
具体步骤如下:a) 将同类项合并:将多项式中的同类项合并在一起,例如将3x^2+5x^2合并为8x^2。
b) 按照同类项的加减法则进行运算:对合并后的同类项按照加减法则进行运算,得到最终的结果。
二、整式加减运算的例题现在我们通过一些例题来演示整式加减运算的具体步骤。
例题1:计算多项式2x^2-3x+5和3x^2+4x-7的和。
解:首先将同类项合并,得到5x^2+x-2,然后按照同类项的加减法则进行运算,最终结果为5x^2+x-2。
例题2:计算多项式4x^3-2x^2+3x-1和2x^3+5x^2-2x+4的差。
解:首先将同类项合并,得到6x^3+3x^2+x-5,然后按照同类项的加减法则进行运算,最终结果为6x^3+3x^2+x-5。
三、整式加减运算的性质整式加减运算具有以下性质:1. 交换律:多项式加法满足交换律,即a+b=b+a;多项式减法不满足交换律。
2. 结合律:多项式加法和减法都满足结合律,即(a+b)+c=a+(b+c);(a-b)-c=a-(b+c)。
3. 对于任意的多项式a,都存在一个多项式-b,使得a+(-b)=0,这个多项式-b被称为a的相反数。
四、整式加减运算的应用整式加减运算在代数表达式的化简和求解中有着广泛的应用。
小学六年级上册认识多项式和单项式的加减法

小学六年级上册认识多项式和单项式的加减法在小学六年级上册的数学学习中,我们开始接触了多项式和单项式的加减法。
这是一个较为重要的内容,因此我们需要认真理解并掌握其中的规律和方法。
本文将详细介绍多项式和单项式的概念,并以具体例子来说明加减法的运算步骤和技巧。
一、多项式和单项式的概念在学习多项式和单项式之前,我们首先要了解它们的定义。
1. 多项式:由常数项、一次项、二次项等有限个单项式通过加法或减法运算得到的式子称为多项式。
例如,2x^2 + 3x + 1就是一个多项式,其中的2x^2、3x和1都是单项式。
2. 单项式:只含有一个字母及其系数的项称为单项式。
例如,2x^2、3xy和7z都属于单项式。
总结起来,多项式是由多个单项式通过加法或减法运算得到的式子。
二、多项式和单项式的加法运算接下来,我们将详细介绍多项式和单项式的加法运算规则。
1. 多项式的加法:将多个多项式相加时,只需对应同类项进行系数相加。
同类项是指具有相同字母幂次及字母的相同的项。
例如,将4x^2 + 3x + 1和2x^2 + 5x + 2进行相加,我们首先将同类项分组,即将x^2、x和常数分别相加,得到6x^2 + 8x + 3。
2. 单项式的加法:将多个单项式相加时,直接对应字母幂次相同的项进行系数相加。
例如,将3x^2和2x^2相加,我们得到5x^2。
同理,将4xy和2xy 相加,我们得到6xy。
需要注意的是,若没有对应的同类项,则保持原样。
三、多项式和单项式的减法运算除了加法,我们还需要了解多项式和单项式的减法运算规则。
1. 多项式的减法:将多个多项式相减时,同样对应同类项进行系数相减。
例如,将3x^2 + 4x - 2和2x^2 - 3x + 5进行相减,我们首先将同类项分组,即将x^2、x和常数分别相减,得到x^2 + 7x - 7。
2. 单项式的减法:将多个单项式相减时,同样对应字母幂次相同的项进行系数相减。
例如,将5x^2和3x^2相减,我们得到2x^2。
多项式的加减乘除四则运算
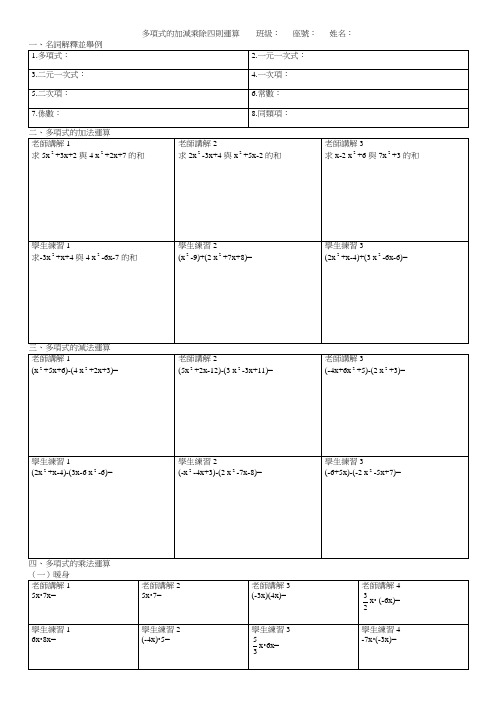
多項式的加減乘除四則運算班級:座號:姓名:
五、多項式的除法運算
四、十字交乘法(三項式) 班級:座號:姓名:
2
2. x2項的係數「不是1」的十字交乘法
二、完全平方數:背1~20的平方
三、平方根的定義
四、利用方格紙畫圖,作出面積是2 平方單位、5 平方單位、18平方單位的正方形-----介紹無理數
五、非完全平方數的平方根:根號引入的必須
六、利用方格紙畫圖,作出1、2、3、4、5、……. 、n
七、正數、零、負數的平方根
(一)正數:
(二)零:
(三)負數:
八、利用標準分解式計算平方根
九、十分逼近法:求無理數的近似值
十、電算器求平方根
一元二次方程式班級:座號:姓名:
5. a x2+bx+c=0,a和b 和c是常數(、十字交乘法)
6. 綜合題
7. 應用問題。
多项式的加减过关训练100道

1、3(a+5b)-2(b-a)2、3a-(2b-a)+b3、2(2a2+9b)+3(-5a2-4b)4、(x3-2y3-3x2y)-(3x3-3y3-7x2y)5、3x2-[7x-(4x-3)-2x2]6、(2xy-y)-(-y+yx)7、5(a2b-3ab2)-2(a2b-7ab)8、(-2ab+3a)-2(2a-b)+2ab9、(7m2n-5mn)-(4m2n-5mn)10、(5a2+2a-1)-4(3-8a+2a2).11、-3x2y+3xy2+2x2y-2xy2;12、2(a-1)-(2a-3)+3.13、-2(ab-3a2)-[2b2-(5ab+a2)+2ab]14、(x2-xy+y)-3(x2+xy-2y)15、3x2-[7x-(4x-3)-2x2]16、a2b-[2(a2b-2a2c)-(2bc+a2c)];17、-2y3+(3xy2-x2y)-2(xy2-y3).18、2(2x-3y)-(3x+2y+1)19、-(3a2-4ab)+[a2-2(2a+2ab)].20、5m-7n-8p+5n-9m-p;21、(5x2y-7xy2)-(xy2-3x2y);22、3(-3a2-2a)-[a2-2(5a-4a2+1)-3a].23、3a2-9a+5-(-7a2+10a-5);24、-3a2b-(2ab2-a2b)-(2a2b+4ab2).25、(5a-3a2+1)-(4a3-3a2);26、-2(ab-3a2)-[2b2-(5ab+a2)+2ab]27、(8xy-x2+y2)+(-y2+x2-8xy);28、(2x2-21+3x)-4(x-x2+21);29、3x2-[7x-(4x-3)-2x2].30、5a+(4b-3a)-(-3a+b);31、(3a2-3ab+2b2)+(a2+2ab-2b2);32、2a2b+2ab2-[2(a2b-1)+2ab2+2].33、(2a2-1+2a)-3(a-1+a2);34、2(x2-xy)-3(2x2-3xy)-2[x2-(2x2-xy+y2)].35、-32ab+43a2b+ab+(-43a2b)-136、(8xy-x2+y2)+(-y2+x2-8xy);37、2x-(3x-2y+3)-(5y-2);38、-(3a+2b)+(4a-3b+1)-(2a-b-3)39、4x3-(-6x3)+(-9x3)40、3-2xy+2yx2+6xy-4x2y 41、1-3(2ab+a)十[1-2(2a-3ab)].42、3x-[5x+(3x-2)];43、(3a2b-ab2)-(ab2+3a2b)44、()[]{}yxxyx--+--3233245、(-x2+5+4x3)+(-x3+5x-4)46、(5a2-2a+3)-(1-2a+a2)+3(-1+3a-a2).47、5(3a2b-ab2)-4(-ab2+3a2b).48、4a2+2(3ab-2a2)-(7ab-1).49、21xy+(-41xy)-2xy2-(-3y2x)50、5a2-[a2-(5a2-2a)-2(a2-3a)]51、5m-7n-8p+5n-9m+8p52、(5x2y-7xy2)-(xy2-3x2y)5556、(a2+4ab-4b2)-3(a2+b2)-7(b2-ab).57、a2+2a3+(-2a3)+(-3a3)+3a2;58、5ab+(-4a2b2)+8ab2-(-3ab)+(-a2b)+4a2b2;59、(7y-3z)-(8y-5z);60、-3(2x2-xy)+4(x2+xy-6).61、(x3+3x2y-5xy2+9y3)+(-2y3+2xy2+x2y-2x3)-(4x2y-x3-3xy2+7y3)62、-3x2y+2x2y+3xy2-2xy2;63、3(a2-2ab)-2(-3ab+b2);64、5abc-{2a2b-[3abc-(4a2b-ab2]}.65、5m2-[m2+(5m2-2m)-2(m2-3m)].66、-[2m-3(m-n+1)-2]-1.67、31a-(21a-4b-6c)+3(-2c+2b)68. -5a n-a n-(-7a n)+(-3a n)69、x 2y-3xy 2+2yx 2-y 2x70、41a 2b-0.4ab 2-21a 2b+52ab 2;71、3a-{2c-[6a-(c-b )+c+(a+8b-6)]}72、-3(xy-2x 2)-[y 2-(5xy-4x 2)+2xy];73、化简、求值21x 2-2212- (x + y )2⎡⎤⎢⎥⎣⎦-23(-32x 2+31y 2),其中x =-2, y =-3474、化简、求值21x -2(x -31y 2)+(-23x +31y 2),其中x =-2,y =-32.75、x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛---其中x =-121;76、 化简,求值(4m+n )-[1-(m-4n )],m=52 n=-13177、化简、求值2(a2b+2b3-ab3)+3a3-(2ba2-3ab2+3a3)-4b3,其中a=-3,b=278、化简,求值:(2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3.79、化简,求值:5x2-[3x-2(2x-3)+7x2],其中x=-2.80、若两个多项式的和是2x2+xy+3y2,一个加式是x2-xy,求另一个加式.81、若2a2-4ab+b2与一个多项式的差是-3a2+2ab-5b2,试求这个多项式.82、求5x2y-2x2y与-2xy2+4x2y的和.83、求3x2+x-5与4-x+7x2的差.84、计算5y+3x+5z2与12y+7x-3z2的和85、计算8xy2+3x2y-2与-2x2y+5xy2-3的差86、 多项式-x 2+3xy-21y 与多项式M 的差是-21x 2-xy+y ,求多项式M87、当x=- 21,y=-3时,求代数式3(x 2-2xy )-[3x 2-2y+2(xy+y )]的值.88、化简再求值5abc-{2a2b-[3abc-(4ab 2-a 2b )]-2ab 2},其中a=-2,b=3,c=-4189、已知A=a 2-2ab+b 2,B=a 2+2ab+b 2(1)求A+B ;(2)求41(B-A);90、小明同学做一道题,已知两个多项式A ,B ,计算A+B ,他误将A+B 看作A-B ,求得9x 2-2x+7,若B=x 2+3x-2,你能否帮助小明同学求得正确答案?91、已知:M=3x 2+2x-1,N=-x 2-2+3x ,求M-2N .92、已知222244,5A x xy y B x xy y =-+=+-,求3A -B93、已知A =x 2+xy +y 2,B =-3xy -x 2,求2A -3B . 94、已知2 a +(b +1)2=0,求5ab 2-[2a 2b-(4ab 2-2a 2b )]的值. 95、化简求值:5abc-2a 2b+[3abc-2(4ab 2-a 2b )],其中a 、b 、c 满足|a-1|+|b-2|+c 2=0. 96、已知a ,b ,z 满足: (1)已知|x-2|+(y+3)2=0, (2)z 是最大的负整数,化简求值: 2(x 2y+xyz )-3(x 2y-xyz )-4x 2y .97、已知a+b=7,ab=10,求代数式(5ab+4a+7b )+(6a-3ab )-(4ab-3b )的值.98、已知m 2+3mn=5,求5m 2-[+5m 2-(2m 2-mn )-7mn-5]的值99、设A=2x 2-3xy+y 2+2x+2y ,B=4x 2-6xy+2y 2-3x-y ,若|x-2a|+(y-3)2=0,且B-2A=a ,求a 的值.100、有两个多项式:A =2a 2-4a +1,B=2(a 2-2a )+3,当a 取任意有理数时,请比较A 与B 的大小.。
多项式与其加减运算

x (A). 1322+-x 。
(B). 53+x 。
(C). 12-x 。
(D). 0。
(E).23-+x 。
(F). 12--x 。
(G). 02=+x 。
2 下列何者为二次多项式?_______(A). 32)(-=x x f 。
(B). 1231)(3-+-=x x x f 。
(C). 3)(=x f 。
(D). 0)(=x f 。
(E). 25)(x x f -=。
3 5231)(3+--=x x x f 为几次多项式?又各项系数为何?国(三)1-74 多项式532425-+-x x x 为______次多项式,共有______项,2x 项系数为______,3x 项系数为______,又常数项为______。
5 多项式)5()3()2(2+-++-c x b x a 为x 的零多项式,求c b a ,,?6 设5722)(2323-+++-=x ax x x ax x f 为二次多项式,则2x 项系数为何?7 合并同类项,化简64332-+-+-x x x x 。
8 化简=+++--)73()321(22x x x x ?9 化简=+--++)765()432(22x x x x ?10 化简=---+-+-+)12()724()843(222x x x x x x ?(结果以升幂排列)11 化简=+--+----)532()624(2)832(232x x x x x x ?(结果以降序排列)国(三)1-812 设)(x f 为一多项式,)(x f 减去多项式18932-+-x x 的差为1211102++x x ,则=)(x f ?13 下图是用面积为2x 、x 、1的纸板拼成的长方形,请用x 的多项式表示此长方形的面积。
2~1 习作1 _______若多项式c bx ax ++2为一次多项式,则可断言(A)0≠a (B)0=b (C)0=a ,0=b(D)0=a ,0≠b 。
初中数学知识归纳多项式的基本概念与运算

初中数学知识归纳多项式的基本概念与运算多项式是初中数学中的一个重要概念,它是由多个单项式通过加减运算得到的。
在初中数学学习中,我们需要学会多项式的基本概念,并掌握其运算规则。
本文将介绍多项式的定义与表示方式、多项式的次数、常数项、系数、同类项、多项式的加减法运算、多项式的乘法运算以及多项式的因式分解等知识点。
一、多项式的定义与表示方式多项式是由多个单项式(即只包含一个字母和系数的式子)通过加减运算得到的。
一般形式为:\[P(x) = a_nx^n + a_{n-1}x^{n-1} + \ldots + a_1x^1 + a_0\]其中,\(a_n, a_{n-1}, \ldots, a_1, a_0\)为实数,\(x\)为变量,\(n\)为多项式的次数。
二、多项式的次数多项式的次数等于最高次项的次数。
次数可通过观察最高次项的指数得出。
例如,多项式 \(2x^3 + 4x^2 + 3x + 1\) 的次数为3。
三、常数项与系数常数项是次数为0的项,也就是没有\(x\)的项。
在多项式 \(3x^2 - 2x + 5\) 中,常数项为5。
系数是单项式中字母的前面的数字,如多项式 \(3x^2 - 2x + 5\) 中,系数为3、-2和5。
四、同类项同类项是具有相同字母和相同次数的项。
在多项式运算中,我们通常需要合并同类项,以简化表达式。
例如,多项式 \(2x^3 + 4x^2 + 3x + 1\) 中,\(2x^3\) 和 \(4x^2\) 是同类项。
五、多项式的加减法运算多项式的加减法运算就是将同类项相加或相减。
具体步骤如下:1. 对于同类项,合并系数,保留字母和次数。
2. 对于非同类项,直接写出来即可。
例如,给定两个多项式\(P(x) = 2x^3 + 4x^2 + 3x + 1\)\(Q(x) = x^2 + 2x - 1\)进行加法运算,按照上述步骤,我们有:\(P(x) + Q(x) = 2x^3 + (4+1)x^2 + (3+2)x + (1-1)\)经过合并同类项和化简,可得\(P(x) + Q(x) = 2x^3 + 5x^2 + 5x\)六、多项式的乘法运算多项式的乘法运算可以用分配率进行展开。
一元多项式.加减

荆楚理工学院课程设计成果学院:_计算机工程学院_ 班级: 09级计算机科学与技术(一)班学生姓名: …学号: 2009404010…设计地点(单位)_观涧3栋104宿舍___设计题目:_ 一元多项式的计算_________完成日期:2011年01月03日指导教师评语:______________ _________________________ ___________________________________________________________ ___________________________________________________________ ___________________________________________________________ _______________________ __________ _成绩(五级记分制):_____ _ __________教师签名:__________ _______________数据结构课程设计目录第一节课程设计的问题描述第二节本次设计的基本要求第三节存储结构及基本算法第四节源程序第五节测试数据及结果第六节算法的时间复杂度及改进第七节参考资料第一节课程设计的问题描述能够按照指数降序排列建立并输出多项式;能够完成两个多项式的相加、相减,并将结果输入;第二节本次设计的基本要求在上交资料中请写明:存储结构、多项式相加的基本过程的算法(可以使用程序流程图)、源程序、测试数据和结果、算法的时间复杂度、另外可以提出算法的改进方法;第三节存储结构及基本算法存储结构:一元多项式的表示在计算机内可以用链表来表示,为了节省存储空间,只存储多项式中系数非零的项。
链表中的每一个结点存放多项式的一个系数非零项,它包含三个域,分别存放该项的系数、指数以及指向下一个多项式项结点的指针。
创建一元多项式链表,对一元多项式的运算中会出现的各种可能情况进行分析,实现一元多项式的相加、相减操作。
数学-多项式的加减与乘除

数学-多项式的加减与乘除一、多项式的定义与性质1.多项式的概念:若干个单项式的和称为多项式。
2.单项式的概念:数与字母的乘积称为单项式,单独的一个数或一个字母也是单项式。
3.多项式的项:组成多项式的各个单项式称为多项式的项。
4.多项式的系数:多项式中,数与字母相乘前面的数称为系数。
5.多项式的度:多项式中,最高次单项式的次数称为多项式的度。
6.多项式的系数与度:一个多项式的系数有有限个,次数也有界限。
二、多项式的加减法1.同类项的概念:字母相同且相同字母的指数也相同的项称为同类项。
2.多项式加减法的原则:同类项相加(减)时,只把系数相加(减),字母与字母的指数不变。
3.多项式加减法的步骤:a.找出同类项b.合并同类项c.化简结果三、多项式的乘法1.多项式乘以单项式:将单项式的系数与多项式的每一项相乘,字母与字母的指数相加。
2.多项式乘以多项式:a.先用一个多项式的每一项乘以另一个多项式的每一项b.合并同类项c.化简结果四、多项式的除法1.多项式除以单项式:将多项式的每一项除以单项式的系数,字母与字母的指数不变。
2.多项式除以多项式:a.用多项式的每一项除以另一个多项式的每一项b.求商和余数c.化简结果五、多项式的应用1.解一元二次方程:利用因式分解法将方程化为两个一元一次方程,求解得到方程的解。
2.解二元一次方程组:利用加减消元法、代入消元法或矩阵法求解方程组的解。
3.函数的图像:利用多项式函数的表达式,绘制函数的图像,分析函数的性质。
六、多项式的恒等变形1.合并同类项:将多项式中的同类项合并,化简结果。
2.因式分解:将多项式分解为几个单项式的乘积,提取公因式,化简结果。
3.展开与简化:将多项式展开,化简结果,使其更简洁。
七、多项式的实际应用1.物理问题:利用多项式表示物体运动的速度、加速度等物理量,解决物理问题。
2.化学问题:利用多项式表示化学反应的平衡常数、反应速率等,解决化学问题。
3.经济问题:利用多项式表示成本、利润等经济指标,解决经济问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多项式的加减
引言
多项式是数学中常见的一种表达式形式,由常数项和各项的系数和指数的算术运算组成。
在数学中,我们经常需要对多项式进行加减运算,以便简化表达式或者解决问题。
本文将介绍多项式加减的基本原理和方法。
加法运算
多项式的加法运算是将两个或多个多项式相加得到一个新的多项式。
加法的基本原理是将相同指数项的系数相加,而对于不同指数项,则保持原样。
例如,给定两个多项式:
多项式A:2x^2 + 4x + 1
多项式B:3x^2 - 2x + 2
我们可以将相同指数项的系数相加得到新的多项式:
A +
B = (2x^2 + 3x^2) + (4x - 2x) + (1 + 2)
化简合并同类项后,得到最终结果:
A +
B = 5x^2 + 2x + 3
减法运算
多项式的减法运算是将一个多项式减去另一个多项式得到一个
新的多项式。
减法的基本原理是将被减多项式的各项系数取相反数,然后进行加法运算。
例如,给定两个多项式:
多项式A:2x^2 + 4x + 1
多项式B:3x^2 - 2x + 2
我们可以将被减多项式B的各项系数取相反数,然后进行加法运算:
A -
B = (2x^2 - 3x^2) + (4x + 2x) + (1 - 2)
化简合并同类项后,得到最终结果:
A -
B = -x^2 + 6x - 1
结论
多项式的加减运算是基于各项指数和系数的算术运算。
通过将相同指数项的系数相加或相减,我们可以简化多项式的表达式,使其更易于处理和理解。
在实际应用中,多项式的加减运算常常用于解决数学问题或者简化数学模型。
以上是关于多项式的加减运算的简要介绍。
希望本文可以帮助您理解多项式的基本运算规则,进一步提升数学的解题能力和应用能力。
参考文献:。
