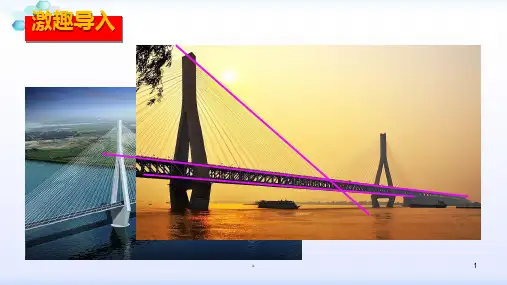
《相交线》冀教版七年级数学下册PPT教材课件(2篇)
合集下载
七年级数学下册5.1-相交线--5.1.1:相交线(共38张)PPT课件
∴ ∠1=∠3(同角的补角相等),
同理 ∠2=∠4 .
-
26
知识点二:对顶角的性质
归纳总结
邻补角性质:
A
邻补角互补(两个角的和是180°)
几何语言:
C
∵∠1与∠ 2互为邻补角(已知) ∴ ∠1+∠ 2 =1800
D 1 42
O
3
B
-
27
知识点二:对顶角的性质
归纳总结
对顶角的性质:
几何语言:
对顶角相等。
如果两条直 线有一个公共点, 就说这两条直线 相交,公共点叫 做这两条直线的 交点。
A O
直线AB、CD相
C
交于点O
-
D B
7
复习备用
方法
1、用三个大写 字母表示
2、用一个大写 字母表示 3、用一个数字 来表示
4、用一个希腊 字母来表示
图标
A
O
B
O
A 1B
O
2C
αβAB
O
C
记法 ∠AOB 或∠BOA
对顶角的定义:∠1和∠3有一个公共顶
点O,并且∠1的两边分别是∠3的两边
的反向延长线,具有这种位置关系的两
个角,互为对顶角.
C
图中还有哪些对顶角?
A
对顶角是成对出现的
-
23
1 4O
B
D
21
知识点一:邻补角和对顶角
学以致用
1、(1)下列各图中,∠1和∠2是邻补角吗?为什么?
12 (1)
ቤተ መጻሕፍቲ ባይዱ
12 (2)
12 (3)
达标测试
一、判断题
1、有公共顶点且相等的两个角是对顶角。( × )
同理 ∠2=∠4 .
-
26
知识点二:对顶角的性质
归纳总结
邻补角性质:
A
邻补角互补(两个角的和是180°)
几何语言:
C
∵∠1与∠ 2互为邻补角(已知) ∴ ∠1+∠ 2 =1800
D 1 42
O
3
B
-
27
知识点二:对顶角的性质
归纳总结
对顶角的性质:
几何语言:
对顶角相等。
如果两条直 线有一个公共点, 就说这两条直线 相交,公共点叫 做这两条直线的 交点。
A O
直线AB、CD相
C
交于点O
-
D B
7
复习备用
方法
1、用三个大写 字母表示
2、用一个大写 字母表示 3、用一个数字 来表示
4、用一个希腊 字母来表示
图标
A
O
B
O
A 1B
O
2C
αβAB
O
C
记法 ∠AOB 或∠BOA
对顶角的定义:∠1和∠3有一个公共顶
点O,并且∠1的两边分别是∠3的两边
的反向延长线,具有这种位置关系的两
个角,互为对顶角.
C
图中还有哪些对顶角?
A
对顶角是成对出现的
-
23
1 4O
B
D
21
知识点一:邻补角和对顶角
学以致用
1、(1)下列各图中,∠1和∠2是邻补角吗?为什么?
12 (1)
ቤተ መጻሕፍቲ ባይዱ
12 (2)
12 (3)
达标测试
一、判断题
1、有公共顶点且相等的两个角是对顶角。( × )
《相交线》优质ppt课件
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
Байду номын сангаас
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
《相交线》优质实用课件(PPT优秀课 件) 《相交线》优质实用课件(PPT优秀课 件)
2023-2024学年七年级数学下册第七章相交线与平行线7.3平行线上课课件新版冀教版

8.如图,AC⊥AE,BD⊥BF,∠1=35°,∠2=35°, (1)AC与BD平行吗?请说明理由. (2)AE与BF平行吗?请说明理由.
答案
8.解:(1)AC与BD平行.理由如下: 因为∠1=35°,∠2=35°,(已知) 所以∠1=∠2. 所以AC∥BD(同位角相等,两直线平行). (2)AE与BF平行.理由如下: 因为AC⊥AE,BD⊥BF,(已知) 所以∠EAC=90°,∠FBD=90°,(垂直的定义) 所以∠EAB=∠EAC+∠1=125°, ∠FBG=∠FBD+∠2=125°, 所以∠EAB=∠FBG,(等量代换) 所以AE∥BF(同位角相等,两直线平行).
知识点5 同位角相等,两直线平行
8.[2020湖南娄底期末]如图, 两直线a,b被第三条直线c所截,若∠1=50°,∠2=130°,则直线
a,b的位置关系是
.
答案
8.平行 因为∠2+∠3=180°,∠2=130°,所以∠3=50°,所以∠1=∠3=50°,所以a∥b.
知识点5 同位角相等,两直线平行
答案
6.D 当点在直线上时,不存在;当点在直线外时,有且只有一条直线与已知直线平行.
知识点4 平行线的基本事实
7.如图,如果CD∥AB,CE∥AB,那么C,D,E三点是否在同一条直线上?请说明理由.
答案
7.解:C,D,E三点在同一条直线上. 理由如下: ∵CD∥AB,CE∥AB,过点C有且只有一条直线与AB平行, ∴C,D,E在同一条直线上.
答案
3.C
知识点2 平行线间的距离
4.如图,直线AB∥CD,P是AB上的动点,当点P的位置变化时,三角形PCD的面积将( ) A.变大 B.变小 C.不变 D.变大或变小要看点P向左还是向右移动
冀教版七年级下册数学课件 第七章 相交线与平行线 第2课时 平行线的判定与性质的综合运用 (2)

当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540°
当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720°
若有n个拐点,你能找到规律吗?
A
B
E1
E2 …
En
C
D
当有n个拐点时: ∠A+∠ E1 + ∠ E2 +…+∠ En +∠C = 180°(n+1)
变式3:如图,若AB∥CD, 则:
A
BA
E
F
BA
E
F1
C
DC
DC
当左边有两个角,右边有一个角时: ∠A+∠C= ∠E
B E1
E2 D
当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D
当左边有三个角,右边有两个角时:∠A+∠ F1 +∠C = ∠ E1 +∠ E2
若左边有n个角,右边有m个角;你能找到规律吗?
A
F1 F2 Fn
C
D
方法归纳
与平行线相关的问题一般都是平行线的判定与 性质的综合应用,主要体现在以下两个方面: 1. 由角定角
已知角的关系 判定 两直线平行
2. 由线定线
性质
已知两直线平行
角的关系
性质 判定
确定其它 角的关系
确定其它两 直线平行
二 判定平行线的其他方法
互动探究
画一画:先画直线l1,再画直线l2,l3分别l1与平行.
16 54
a
C. ①③ D. ④
27
b
83
3. 如图,AB//CD,∠A=100°, ∠C=110°,求∠AEC
