管理运筹学(第3版)案例题解
运输管理 第3版习题答案机工版

第一章习题答案基本训练1、单选(1)C (2)C (3) A (4)B2.判断(1)错(2)错(3)对(4)对(5)错(6)对3.多选(1)ABCDE (2)ABCD (3)CD (4)ABCD4.问答(1)如何理解运输的储存功能?答案要点:即将运输车辆临时作为储存设施。
在仓库空间有限的情况下,利用运输车辆储存是一种可行性的选择。
但本质上,利用车辆进行储存只是一种临时的、动态的储存设施。
它的使用还要结合装卸成本、储存能力、延长前置时间进行综合考虑。
因此,对物资的临时储存是一项比较特别的运输功能。
(2)运输价格与运输需求之间的关系是什么?答案要点:运输价格是运输企业对特定货物或旅客所提供的运输劳务的价钱。
它是运输业借以计算和取得运输收入的根本依据。
运输价格在一定程度内能有效地调节各种运输方式的运输需求,即在总体运输能力基本不变的情况下,运输需求会因运输价格的变动而改变。
(3)发展绿色运输有何意义?答案要点:传统运输有很多弊端。
诸如:破坏了环境,大量占用土地资源,频发交通事故和产生大量不合理运输等。
绿色运输是绿色物流的一项重要内容,它是指以节约能源,减少废气排放为特征的运输。
发展绿色运输是改善环境的关键;是经济可持续发展的必然选择;是改善环境的关键;有利于企业获取新的竞争优势;代表着21世纪物流管理发展的新趋势。
第二章练习答案■案例分析P55答案答:(要点)(1)运输方式不协调可产生如下不利结果:①运输衔接过程中的信息传递与处理能力较差,使得运输的及时性、迅速性受到制约。
②由于铁路、公路没能实现场站的有效衔接,必然会增加中转过程中的装卸、搬运量和次数,使得:A.装卸、搬运成本大增;B.装卸、搬运效率低,时间长;C.运输商品货损货差率大,影响安全性和准确性。
③对于托运人而言,不得不自己办理相关中转业务,由于不是专业人员,因此,在迅速、及时、经济、安全等方面效果较差。
(2)对运输方式的协调产生了什么作用?①在国家政策、法规方面提出促进联合运输的相关政策或要求,这让运输业整体运作更有法可依。
规划数学(运筹学)第三版课后习题答案 习 题 2
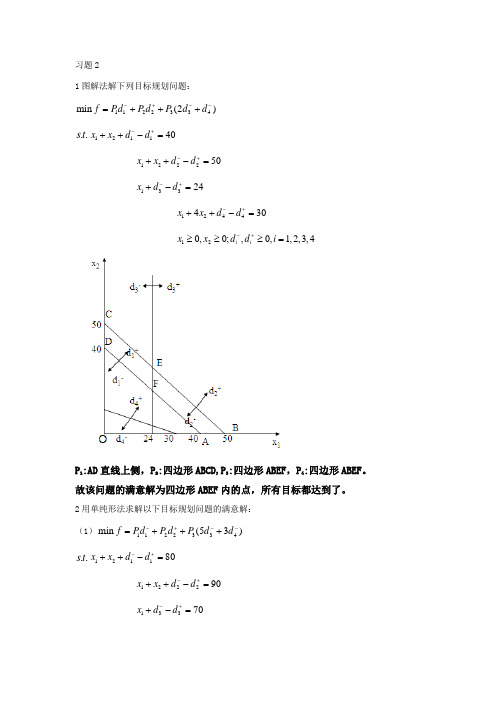
习题21图解法解下列目标规划问题:1122334min (2)f Pd P d P d d -+--=+++..s t 121140x x d d -+++-=122250x x d d -+++-=13324x d d -++-=1244430x x d d -+++-=120,0;,0,1,2,3,4i i x x d d i -+≥≥≥=P 1:AD 直线上侧,P 2:四边形ABCD,P 3:四边形ABEF ,P 4:四边形ABEF 。
故该问题的满意解为四边形ABEF 内的点,所有目标都达到了。
2用单纯形法求解以下目标规划问题的满意解:(1)1122334min (53)f Pd P d P d d -+--=+++..s t 121180x x d d -+++-=122290x x d d -+++-=13370x d d -++-=24445x d d -++-=120,0;,0,1,2,3,4i i x x d d i -+≥≥≥=(2)1122234min ()f P d d P d P d -+--=+++..s t 12114580x x d d -+++-=12224248x x d d -+++-=123381080x x d d -+++-=1445x d d -++-=120,0;,0,1,2,3,4i i x x d d i -+≥≥≥=5案例练习(1)某厂生产甲、乙两种产品,每件利润分别为20、30元。
这两种产品都要在A 、B 、C 、D 四种设备上加工,每件甲产品需,而这4种设备正常生产能力依次为每天12、8、16、12机时。
此外,A 、B 两种设备每天还可加班运行。
试拟订一个满足下列目标的生产计划: 1P :两种产品每天总利润不低于120元;2P :两种产品的产量尽可能均衡;3P :A 、B 设备都应不超负荷,其中A 设备能力还应充分利用(A 比B 重要3倍)。
管理运筹学试题及解题思路

习题答案或解题思路习题1x 1 、x 2吨,则问题是数学模型为: 1.2设一般时间、黄金时间、广播、报纸广告单元数分别为x 1、x 2、x 3、x 4,则线性规划模型为:1.3 设x 1为每周动物饲料量,x 2为每周谷物饮料量。
其数学模型为:1.4 设x 1、x 2、x 3分别为按各种下料所得的钢筋根数,y 1、y 2分别为满足90、60根后多余的根数,Z1.5用图解法得最优解为 X* =(10, 30)T ,Z*= 6800 1.6最优解为:X *= (15/4 , 3/4 , 0 , 0 )T ,Z * = 33/41.7最优解为:X* = (0,10)T ,Z* = 20当 -20 ≤ △b 1 ≤ 60时,原最优解基不变,最优解为:X* = (0,10+1/2△b 1,0,25+1/2△b 1,30-1/2△b 1,60+3/2△b 1)T ,Z* = 20 +△b 1 1.8 (1) 最优解X * = (2.5,25,0,0,0)T ,MaxZ = 57.5(2)最优解X * = (5.5,19,3,0,0)T 1.9 甲395,乙45,丙01.10 A 1生产40万瓶,A 2生产100万瓶,最大利润62万元。
1.11 原问题的最优解如表1所示:1.12 设x j (j=1,…,8)分别表示八种产品的产量,则问题的数学模型如下:1.13 设 x j为第 j 种生产过程的日产量,j=1,2,3;y 为第 j 种生产过程是否可用,y j =0、1。
1.14 设购买远、中、短程客机分别为1.15(1)设定变量名称(各系列机床所安排的产销量)设i 为产品系列种类,i = 1~6;设j 为指标种类,j = 1~3;设x i 为第i 种产品系列的计划产销量,设A ij 为第i 种产品所实现的第j 种指标数值。
(2)编制目标函数(利润最大化)Max Z = (A 11-A 13) x 1 + (A 21-A 23) x 2+ (A 31-A 33) x 3+ (A 41-A 43) x 4 + (A 51-A 53) x 5+ (A 61-A 63) x 6(3)编制约束条件:CA系列生产9124台,小CAK系列生产1720台,普及型生产156台,则满足所有约束,并可得最大利润为6617.6万元。
管理运筹学答案.docx
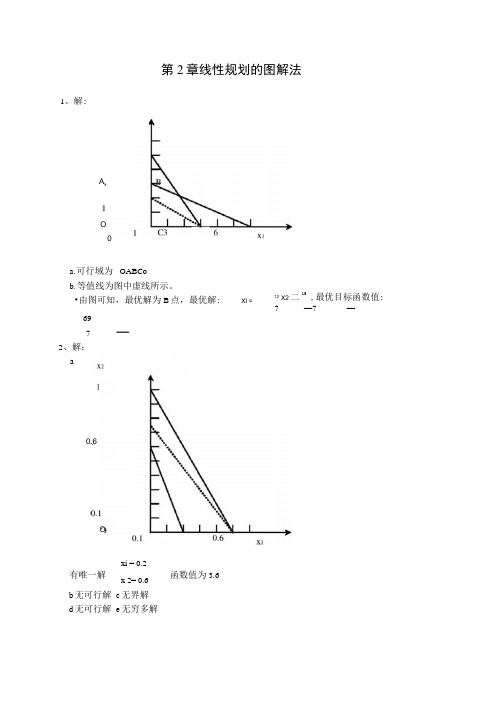
第2章线性规划的图解法1、解:12X2二15,最优目标函数值:7 —7—b 无可行解c 无界解d 无可行解e 无穷多解AO 0a. 可行域为b. 等值线为图中虚线所示。
OABCo69 0.6O72、解:axi = 0.2有唯一解x 2= 0.6函数值为3.6•由图可知,最优解为B 点,最优解:Xl =3、解:a 标准形式: max f = 3xi + 2 x 2 + Osi + 0 s 2 + Os 39 xi + 2 x 2 + si = 30 3xi + 2 x 2+ s 2= 13 2 xi+ 2x2 +S3 =9 X1 , X 2, Si , S 2, S3> 0max f = - xr+ 2 X2- 2 X2- Osi 一 0s2—3xi + 5 x 2— 5 x 2•+ si = 70 2 xr- 5 x‘2+ 5 x'2'= 50 3xr+ 2 x 2— 2 x T — S 2= 30 xr, X*2, X 21, Si , S 2> 03xi + 4 x 2 + si = 9 5 xi + 2 x 2+ s 2= 8 xi, x 2, si, s 2> 0f 有唯一解X2 =3函数值为—834、解:标准形式: max z = 10X 】 + 5X 2+0SI + 0S 2SI = 2, S2 = 0b 标准形式:max f = -4 xi - 6 X3- Osi - 0s23xi - x 2 - si = 6 XI + 2 X 2+ S 2= 10 7 xi - 6 x 2= 4 X1 , X 2, Si , S 2> 0c 标准形式:min f = 1 lxi + 8 x 2 + Osi + Os 2+ Os310 xi + 2 x 2- si = 20 3xi + 3x 2— s 2= 18 4XI + 9X 2-S3=36Xl,X2,Sl,S2,S3>0Si = 0, S2= 0, S3= 13 6、解:b 1 < ci< 3c 2 < C2 < 6xi = 6X2= 4e xi 丘[4,8] x 2= 16 - 2 xif 变化。
《管理运筹学》案例分析报告

秋季流行服饰与衣料的准备(五人)目从办公室的十层大楼里,凯瑟琳·拉里俯视着下面忙忙碌碌的人流,在充塞着黄色出租车的街道以及乱放着一些买热狗的摊位的人行道上,成群的纽约人来来往往,好不热闹。
在这闷热的暑天里,她注视着各类女性的穿衣时尚,心里想的却是这些人在秋季将会选择怎样的款式。
这并非是她的一时的灵感,而是她工作的重要的一部分因为她拥有并经营着一家妇女精品时装公司――时尚隧道(TrendLines)公司。
今天对她来说是很重要的,因为她将与生产部经理泰德·罗森碰面,一起商讨下一个月秋季生产线的生产计划,特别是在一定的生产能力的基础上确定要各种服装的生产量。
制定下个月的周密的生产计划对于秋季的销售是至关重要的,因为这些产品在9 月份将会上市,而妇女们通常在服装一上市时就会购买大部分的秋天的服饰。
凯瑟琳回转身,走到宽大的玻璃台旁去看铺上面的大量的资料及设计图。
她扫视着6个月以前就设计出来的服装图样,各种样式所需要的材料,以及在时装展上通过消费者调研取得的各种样式的需求预测。
现在,她还记得当时是如何设汁图样并将样品在纽约,米兰和巴黎的服装展上展出,那些天可真是既兴奋而又痛苦。
最后,她付给六个设计者的总酬金为$860,000。
除此外,每次时装展的费用为$2,700,000,包括雇用职业模特、发型师、化妆师,以及衣服的裁制与缝纫、展台背景的设计、模特的走步与排练、会场的租用。
她研究着衣服的样式和所需的材料。
秋季的服装包括职业装和休闲装,而每种服装的价格是由衣服的质量、材料的成本、人工成本、机器成本,以及对该产品的需求与品牌的知名度等因素来确定的。
她知道已经为下个月采购了下面的这些材料:羊毛45,000码、开司米28,000码、丝绸18,000码、人造纤维30,000码、天鹅绒20,000码、棉布30,000码。
各种材料的价格如下图所示:多余的材料(不包括下脚料)可以运回给衣料供应商,并得到全额的偿还。
广工管理运筹学第三章运输问题

闭合回路法的优点是能够找到全局最 优解,适用于大型复杂运输问题。但 该方法的计算复杂度较高,需要较长 的计算时间。
商位法
01
商位法是一种基于商位划分的优化算法,用于解决运输问题。该方法通过将供 应点和需求点划分为不同的商位,并最小化总运输成本。
02
商位法的计算步骤包括:根据地理位置和货物需求量,将供应点和需求点划分 为不同的商位;根据商位的地理位置和货物需求量,计算总运输成本;通过比 较不同商位的总运输成本,确定最优的配送路线。
80%
线性规划法
通过建立线性规划模型,利用数 学软件求解最优解,得到最小化 总成本的运输方案。
100%
启发式算法
采用启发式规则逐步逼近最优解 ,常用的算法包括节约算法、扫 描算法等。
80%
遗传算法
基于生物进化原理的优化算法, 通过模拟自然选择和遗传机制来 寻找最优解。
02
运输问题的数学模型
变量与参数
约束条件
供需平衡
每个供应点的供应量等于对应 需求点的需求量,这是运输问 题的基本约束条件。
非负约束
运输量不能为负数,即每个供 应点对每个需求点的运输量都 应大于等于零。
其他约束条件
根据实际情况,可能还有其他 约束条件,如运输能力的限制 、运输路线的限制等。
03
运输问题的求解算法
表上作业法
总结词
直到达到最优解。这两种方法都可以通过构建线性规划模型来求解最优解。
04
运输问题的优化策略
节约法
节约法是一种基于节约里程的优化算法,用于解决 运输问题。该方法通过比较不同配送路线的距离和 货物需求量,以最小化总运输距离为目标,确定最 优的配送路线。
节约法的计算步骤包括:计算各供应点到需求点的 距离,找出最短路径;根据最短路径和货物需求量 ,计算节约里程;按照节约里程排序,确定最优配 送路线。
管理运筹学案例

案例3-1产品混合问题TJ公司生产3中坚果什锦产品,分销给遍布东南地区的食品连锁店。
产品有3个品种,分别是普通型、高级型和假日型,不同品种的区别就是各种坚果的比例不同。
普通型的产品含有15%的杏仁,25%的巴西果,25%的榛子,10%的核桃,25%的胡桃。
高级型的产品各种坚果均含20%。
假日型的产品含25%的杏仁,15%的巴西果,15%的榛子,25%的核桃,20%的胡桃。
TJ公司的会计对包装材料费用、售价等数值进行分析后预测,每磅普通型产品的利润是1.65美元,每磅高级型产品的利润是2.00美元,每磅假日型产品的利润是2.25美元。
这些数值没有包括坚果的价格,因为它们的价格变化非常大。
客户的订单如下:因为对产品的需求在不断增加,预计TJ公司将会获得大于其生产能力的订单。
TJ公司的目的在于合理安排坚果产品的类型,使公司的利润最大;公司不用的坚果都捐献给当地的慈善机构。
还有,无论盈利与否,公司都将满足已经签署的订单。
管理报告分析TJ公司的问题,并准备一个报告向TJ公司总经理简要介绍一下你的观点。
报告的内容必须包括以下几个方面:(1)普通型、高级型和假日型坚果产品的成本。
(2)最优生产组合和总利润。
(3)如果还可以购买一些坚果,分析如何才能使产品的利润增加。
(4)思考公司是否应该从一个供应商那里再以1000美元的价格购入1000磅的杏仁。
(5)如果TJ不必满足全部的已签订单,公司会增加的利润量。
案例3-2投资战略J.D.威廉姆斯公司是一个投资咨询公司,为大量的客户管理高达1.2亿美元的资金。
公司运用一个很有价值的模型,为每个客户安排投资量,分贝在股票增长基金、收入基金和货币市场基金。
为了保证客户投资的多元化,公司对这3种投资的数额加以限制。
一般来说,投资在股票方面的资金应该占总投资的20%-40%,投资在收入基金上的资金应该确保在20%-50%之间,货币市场方面的投资至少应该占30%。
此外,公司还尝试着投入了风险承受能力指数,以迎合不同投资者的需求。
运筹学第三版存贮论习题答案 ppt课件

C0=
2C3 T0
=
2c1c3 R =2236元/月
(2)允许缺货, c2=100元/件年=100/12(元/件月)
T0=
2c3 c1 R
c1 c2 =0.4796月=14.4天 c2
Q0=T0R=1918件
C0=
2C3 T0
=2085元/月
运筹学第三版存贮论习题答案
[解]R=150件/月, c3=400元/次,c1=0.96元/件月,
(1)
T0=
2c3 = 2 400 =2.357月 c1R 0.96150
练习6
Q0=T0R=
2c3R =353.55件
c1
C0=
2C3 =
T0
2c1c3 R=339.41元/月
(2)该厂为少占用流动资金,希望进一步降低存贮量。因此,
决定使每月订购和存贮总费用可以超过原最低费用的10%,求
这时的最优存贮策略。
1 2 c1Rt
+
c3 t
1
0.96150t
+
400
2
t
72t2-373t +400 =0
b
t=
b2 4ac = 373
3732 4 72 400
2a
2 72
t1 =3.6646月, t2 =1.516月
此时最优策略:取T=1.516月,Q=RT=227件
运筹学第三版存贮论习题答案
7、 [解]R=15000个/年, c3=80元/次,c1=1元/个年,
习题3
T0=
2c3 c1 c2 p = 215000 10 20 1000 =4.5月
c1R c2 p R
10333 20 1000 333
