2012高一精品数学上册课后强化训练题2
【优化方案】2012高中数学 第2章2.2.2第二课时知能优化训练 新人教A版选修2-1

1.已知点(2,3)在椭圆x 2m 2+y 2n 2=1上,则下列说法正确的是( )A .点(-2,3)在椭圆外B .点(3,2)在椭圆上C .点(-2,-3)在椭圆内D .点(2,-3)在椭圆上答案:D 2.直线y =x +2与椭圆x 2m +y 23=1有两个公共点,则m 的取值X 围是( ) A .m >1 B .m >1且m ≠3C .m >3D .m >0且m ≠3答案:B3.直线y =a 与椭圆x 23+y 22=1恒有两个不同的交点,则a 的取值X 围是________. 答案:(-2,2)4.如图,已知斜率为1的直线l 过椭圆y 28+x 24=1的下焦点,交椭圆于A 、B 两点,求弦AB 之长.解:令A 、B 坐标分别为A (x 1,y 1)、B (x 2,y 2).由椭圆方程知a 2=8,b 2=4,∴c =a 2-b 2=2,∴椭圆的下焦点F 的坐标为F (0,-2),∴直线l 的方程为y =x -2.将其代入y 28+x 24=1, 化简整理得3x 2-4x -4=0,∴x 1+x 2=43,x 1·x 2=-43, ∴|AB |=x 2-x 12+y 2-y 12 =2x 2-x 12=2x 1+x 22-4x 1x 2=2⎝ ⎛⎭⎪⎫432-4×-43 =823.一、选择题1.点A (a,1)在椭圆x 24+y 22=1的内部,则a 的取值X 围是( ) A .-2<a <2B .a <-2或a > 2C .-2<a <2D .-1<a <1答案:A2.椭圆x 24+y 23=1的右焦点到直线y =3x 的距离是( )A.12B.32 C .1 D. 3 解析:选B.椭圆的右焦点为F (1,0), ∴d =33+1=32. 3.过椭圆x 225+y 29=1的右焦点且倾斜角为45°的弦AB 的长为( ) A .5 B .6C.9017D .7 解析:选C.椭圆的右焦点为(4,0),直线的斜率为k =1,∴直线AB 的方程为y =x -4, 由⎩⎪⎨⎪⎧ y =x -4x 225+y 29=1得9x 2+25(x -4)2=225, 由弦长公式易求|AB |=9017. 4.直线y =x +m 与椭圆x 2144+y 225=1有两个公共点,则m 的取值X 围是( ) A .(-5,5) B .(-12,12)C .(-13,13)D .(-15,15)解析:选C.联立直线与椭圆方程,由判别式Δ>0,可得-13<m <13. 5.已知椭圆x 2a 2+y 2b2=1(a >b >0)的左焦点为F ,右顶点为A ,点B 在椭圆上,且BF ⊥x 轴,直线AB 交y 轴于点P .若AP →=2PB →,则椭圆的离心率是( )A.32B.22C.13D.12解析:选D.如图,由于BF ⊥x 轴,故x B =-c ,y B =b 2a.设P (0,t ), ∵AP →=2PB →,∴(-a ,t )=2⎝ ⎛⎭⎪⎫-c ,b 2a -t . ∴a =2c ,∴c a =12. 6.经过椭圆x 22+y 2=1的一个焦点作倾斜角为45°的直线l ,交椭圆于A 、B 两点.设O 为坐标原点,则OA →·OB →等于( )A .-3B .-13C .-13或-3D .±13解析:选B.不妨设l 过椭圆的右焦点(1,0),则直线l 的方程为y =x -1.由⎩⎪⎨⎪⎧ y =x -1,x 22+y 2=1,消去y ,得3x 2-4x =0. 设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=43,x 1x 2=0, ∴OA →·OB →=x 1x 2+y 1y 2=x 1x 2+(x 1-1)(x 2-1)=2x 1x 2-(x 1+x 2)+1=-43+1=-13. 二、填空题7.已知以F 1(-2,0),F 2(2,0)为焦点的椭圆与直线x +3y +4=0有且仅有一个公共点,则椭圆的长轴长为________.解析:由题意可设椭圆方程x 2a 2+y 2a 2-4=1,联立直线与椭圆方程,由Δ=0得a =7. 答案:278.已知椭圆x 249+y 224=1上一点P 与椭圆两焦点F 1、F 2连线的夹角为直角,则|PF 1|·|PF 2|=________.解析:两焦点的坐标分别为F 1(-5,0)、F 2(5,0),由PF 1⊥PF 2,得|PF 1|2+|PF 2|2=|F 1F 2|2=100.而|PF 1|+|PF 2|=14,∴(|PF 1|+|PF 2|)2=196.∴100+2|PF 1|·|PF 2|=196.∴|PF 1|·|PF 2|=48.答案:489.过椭圆x 25+y 24=1的右焦点作一条斜率为2的直线与椭圆交于A ,B 两点,O 为坐标原点,则△OAB 的面积为________.解析:椭圆的右焦点为F (1,0),∴l AB :y =2x -2.设A (x 1,y 1),B (x 2,y 2), 由⎩⎪⎨⎪⎧ y =2x -2,x 25+y 24=1,得3x 2-5x =0, ∴x =0或x =53, ∴A (0,-2),B (53,43), ∴S △AOB =12|OF |(|y B |+|y A |) =12×1×(2+43)=53. 答案:53三、解答题10.焦点分别为(0,52)和(0,-52)的椭圆截直线y =3x -2所得椭圆的弦的中点的横坐标为12,求此椭圆方程.解:设此椭圆的标准方程为x 2b 2+y 2a 2=1(a >b >0), 且a 2-b 2=(52)2=50 ①由⎩⎪⎨⎪⎧ x 2b 2+y 2a2=1y =3x -2, 得(a 2+9b 2)x 2-12b 2x +4b 2-a 2b 2=0.∵x 1+x 22=12,∴6b 2a 2+9b 2=12, ∴a 2=3b 2②,此时Δ>0,由①②得a 2=75,b 2=25,∴x 225+y 275=1. 11.如图,点A 是椭圆C :x 2a 2+y 2b2=1(a >b >0)的短轴位于y 轴下方的端点,过点A 且斜率为1的直线交椭圆于点B ,若P 在y 轴上,且BP ∥x 轴,AB →·AP →=9.点P 的坐标为(0,1),求椭圆C 的方程.解:∵直线AB 的斜率为1,∴∠BAP =45°,即△BAP 是等腰直角三角形,|AB |=2|AP |. ∵AB →·AP →=9,∴|AB ||AP |cos 45°=2|AP |2cos 45°=9,∴|AP |=3.∵P (0,1),∴|OP |=1,|OA |=2,即b =2,且B (3,1).∵B 在椭圆上,∴9a 2+14=1,得a 2=12, ∴椭圆C 的方程为x 212+y 24=1. 12.(2010年高考某某卷)已知中心在坐标原点O 的椭圆C 经过点A (2,3),且点F (2,0)为其右焦点.(1)求椭圆C 的方程;(2)是否存在平行于OA 的直线l ,使得直线l 与椭圆C 有公共点,且直线OA 与l 的距离等于4?若存在,求出直线l 的方程;若不存在,说明理由.解:(1)依题意, 可设椭圆C 的方程为x 2a 2+y 2b2=1(a >b >0), 且可知其左焦点为F ′(-2,0).从而有⎩⎪⎨⎪⎧ c =2,2a =|AF |+|AF ′|=3+5=8,解得⎩⎪⎨⎪⎧ c =2,a =4. 又a 2=b 2+c 2,所以b 2=12,故椭圆C 的方程为x 216+y 212=1. (2)假设存在符合题意的直线l ,设其方程为y =32x +t . 由⎩⎪⎨⎪⎧ y =32x +t ,x 216+y 212=1,得3x 2+3tx +t 2-12=0. 因为直线l 与椭圆C 有公共点,所以Δ=(3t )2-4×3×(t 2-12)≥0,解得-43≤t≤4 3.另一方面,由直线OA与l的距离d=4,得|t|94+1=4,解得t=±213.由于±213∉[-43,43],所以符合题意的直线l不存在.。
高一精品数学上册课后强化训练题9.pdf

《13.2 重力和摩擦力》导学案 学习目标: 1、知道重力是由于地球的吸引而产生的 2、理解重力与质量的正比关系; 3、能用G=mg计算有关的问题。
学习过程: 任务一:知道什么叫重力 学习要求:1、观察图7-12,认识重力作用下物体的运动。
2、知道重力的方向及应用。
思考题: 质量均匀的球挂在墙上,如果质量为2千克,用力的图示画出它受到的重力 任务二、重力与质量的关系 学习要求:阅读教材并实验探究重力与质量的关系 思考题: 关于G=mg,下列说法正确的是( ) A它表示m与G成正比 B它表示G与g成正比 C它表示g与m成反比 D它表示G与m成正比 ? : 1、重为3N的贡柑,从树上落下的过程中,受到重力的作用. 对于贡柑所受重力的大小和方向,以下说法中正确的是…………………………( ?) A.大于3N,方向竖直向下? ?B.小于3N,方向竖直向下 C.等于3N,方向竖直向上? D.等于3N,方向竖直向下 2、有一苹果它的重力是2.45N,则它的质量是? 克. 3、甲乙两物体的质量之比是1:3,则它们受到的重力之比为( ),若甲物体的物重为196N,则乙物体的质量为( )。
4、一盒小铁丸的重量为25N,假如一粒铁丸的质量是0.025kg,那么一盒小铁丸有多少粒?(g=10N/kg) 步骤5: 第三节 摩擦力(第二课时)----摩擦与我们 学习目标1.知道日常中常见的摩擦现象.2.知道增大或减小摩擦的方法. 【知识回顾】1.滑动摩擦力的大小与___________________和__________________有关. 2.接触面受到的压力越大,物体受到的摩擦力越______,接触面越粗糙,摩擦力越_____. 课前预习 阅读课本16—17页的内容和插图,了解日常生活中常见的摩擦现象,以及常见的增大和减小摩擦的方法.回答下列问题: 在生活中人们根据实际需要,有时需要增大摩擦(有益),有时又需要减小摩擦(有害),所以就想出了各种各样的办法来增大或减小摩擦.在各种车辆上安装轮子以及在机器的轴上安装滚动轴承,可以大大减小摩擦,这是通过_______________________的方法来减小摩擦.在机器部件之间加润滑油使两个表面之间形成油膜,这是通过____________________的方法减小摩擦. 我们知道摩擦力与接触面受到的压力和接触面的粗糙程度有关,试判断一下下面几个示例中是通过改变什么因素来增大还是减小摩擦力的: 乒乓球拍上的胶粒:______________________________ 足球鞋上的鞋钉:________________________________. 水泥路上的刻痕:________________________________. 用力刹车,使车快速停住:_________________________. 雪橇的底部要做得光滑一些 :________________________. 根据以上事例总结出改变摩擦的方法: 增大摩擦的方法减小摩擦的方法 典型例题 例1.摩擦无处不在,在生活中或生产中有时需要增大有益摩擦,有时需要减小有害摩擦,下列叙述中,属于增大有益摩擦的是( )A 螺丝刀的手柄上刻有一些凹槽B 旱冰场冰场的地面做得很光滑 C自行车的转动部位要经常加一些润滑油 D 行礼包的包底上装有四个小轮 思路引导:旱冰场的冰场的地面做得很光滑,这是减小接触面的__________,从而______摩擦,这样可以滑得更顺畅.自行车的转动部分加润滑油是使部件之间形成一层油膜,使它们互不接触,从而______摩擦;行礼包的底部装上四个小轮,是变滑动为滚动,从而_______摩擦.螺丝刀的手柄上刻有一些凹槽,是为了增大接触面的___________,从而______摩擦. 课堂达标1.下列事例中为了增大摩擦的是( )A 足球守门员的手套B 塑胶跑道表层的胶粒C 鞋底的花纹D 轮胎的花纹E 在石碑的底部垫上圆木拉动石碑F 拔河时用力握住绳子G 气垫船底部的气垫使船与水面分开H 雪后路面上撒一些煤渣 2.下列各种摩擦力中:①走路时鞋与地面之间的摩擦力②骑车时车轮与轴之间的摩擦粒 ③皮带传动中,皮带与轮之间的摩擦力④汽车行驶时,空气与汽车之间的摩擦力;其中属于有益摩擦的是( )A ①④B ②④C ①③D ②③ 课后作业1.在奥运会上,体操运动员在上单杠之前,总是要在手上抹一些镁粉,而在杠上做回环运动时,手握杠又不能太紧,他这样做的目的是( )A 前者是增大摩擦,后者是减小摩擦B 前者是减小摩擦,后者是增大摩擦C 两者都是增大摩擦D 两者都是减小摩擦 2.在家里的浴室中,为了防止地面沾水使人打滑跌倒,下列采取的措施中错误的是( )A 浴室地面应铺上带有花纹的地板砖B 人沐浴时穿的拖鞋底带有凹凸花纹C 脚底下放一条毛巾D 穿上平底的塑料拖鞋 3.磁悬浮列车靠强大的磁性将列车悬浮在轨道上方,从而可高速行驶,那么列车能高速行驶的原因是( )A 依靠列车的惯性B 减小了列车的重力C 减小了列车与轨道间的摩擦 D 减小了列车所受的空气阻力 4.下列现象中可以减小摩擦的是( )A 拔河时用力握住绳子B 旅行箱的下面安装小轮子 C 钢笔拧得太紧不易打开,往往在手与钢笔之间垫一块毛巾 D 为了把桌面上得污渍擦干净,常常用大一点力压抹布 5.下列事例中,增大摩擦的措施是( ) A 为了容易推动很重的木箱,在木箱下面垫上几根圆木 B 在汽车轮胎上做成有凹凸的花纹C 在机器的传动部分安装滚动轴承D 自衣服的拉链上涂些蜡 6.下列事例中,增大有益摩擦的是( )A 推动笨重物体时,常垫滚木B 旅游鞋底刻有凹凸不平的花纹C 雪橇的底部非常光滑D 给机器的轴承加润滑油 7.自行车是我们熟悉的交通工具,从自行车的结构和使用看,它涉及不少有关摩擦的知识,例如:A 轮胎上刻有花纹 B 车轮做成圆形 C 塑料套紧套在车把手上 D 刹车时用力捏闸E 在转动部分添加润滑油 F 脚踏板凹凸不平 G 车轴处装有滚珠 H 车的把手上有凹槽 上述各项内容中属于通过改变接触粗糙程度而增大摩擦的是:___________;通过增大压力而增大摩擦的是:__________;通过变滑动为滚动而减小摩擦的是:______________;通过使接触面彼此分开而减小摩擦的是:______________.用力踩动脚踏板使自行车前进时,后轮与地面间的摩擦力的方向朝_______(填“前”或“后”) 8.拔河比赛中,运动员要穿比较新的球鞋,而且不希望地面上有沙子,这是因为比较新的球鞋能增大接触面的粗糙程度从而_____________,而地面上的沙子能_________而减小摩擦 9.马路上一旦泼洒了机油,容易造成交通事故,特别是骑摩托车、自行车时很容易摔倒,这是由于__________________的缘故. 10.旱冰鞋上的轮子的作用是通过_____________的方法,使_______大大减少,而演奏二胡前往往要在琴弦上抹一些松香,这是通过_____________的方法增大摩擦. 11.全班同学正在上课,突然摩擦力消失,对可能出现的现象描述错误的是( ) A 同学们稍微活动就会从椅子上纷纷滑到地面上 B 固定吊灯的螺丝从天花板上滑出,使吊灯落到地上 C 写字时铅笔从手中滑出飘在空中 D 由于太滑,稍一用力桌椅就会在地面上不停地滑着、碰撞着 初中学习网,资料共分享!我们负责传递知识!。
2012高中数学2.1.2课时同步练习新人教A版选修2-1

第 2 章一、选择题 ( 每题 5 分,共 20 分)1.与点 A ( -1,0) 和点 B (1,0) 连线的斜率之和为- 1 的动点 P 的轨迹方程是 ()A .x 2+ y 2= 3B . x 2+ 2xy = 1( x ≠± 1)C .y = 1- x 2D . x 2+ y 2=9( x ≠0)分析: 设 P ( x , y ) ,∵ k + k =- 1,PAPBy - 0y - 02∴x --+ x - 1=- 1,整理得 x + 2xy = 1( x ≠± 1) .答案: B2.已知两点 M ( - 2,0) 、N (2,0) ,点 P →→ → → 为坐标平面内的动点, 知足 | M N |·|MP |+MN ·NP= 0,则动点( ,y ) 的轨迹方程为 ()P xA .y 2=- 8xB . y 2= 8xC .y 2= 4xD . y 2=- 4x分析:由| → | · |→| + → · → ,得M NM P MN NP 4× [ x --2+ y - 2+(4,0) ·(x - 2, y - 0) = 0,∴ y 2=- 8x .答案:A3.已知两定点 A ( -2,0) , B (1,0) ,假如动点 P 知足 | PA | = 2| PB | ,则点 P 的轨迹所包围的图形的面积等于 ()A .πB . 4πC .8πD . 9π分析:设 P ( x , y ) ,由 | PA | =2| PB | 得x +2+ y 2= 2x -2+ y 2,整理得 x 2- 4x +y 2= 0即( x - 2) 2+ y 2=4.因此点 P 的轨迹是以 (2,0) 为圆心,以2 为半径的圆,故 = 4π .S答案: B4.已知 A ( -1,0) , B (1,0) → →,且 MA · M B = 0,则动点 M 的轨迹方程是 ()A .x 2+ y 2= 1B . x 2+ y 2=2C .x 2+ y 2= 1( x ≠± 1)D . x 2+ y 2=2( x ≠± 2)分析:→设动点 M( x,y),则 MA=(-1- x,- y),→M B=(1- x,- y).→→,得(-1- x)(12= 0,由MA· M B=0-x)+(-y)即 x2+y2=1.应选A.答案:A二、填空题 ( 每题 5 分,共 10 分 )5.已知点A(0,-1),当点 B 在曲线 y=2x2+1上运动时,线段AB的中点 M的轨迹方程是 ________.分析:2设点 B( x0, y0),则 y0=2x0+1.①x0y0-1设线段 AB中点为 M( x, y),则 x=2, y=2,即 x0=2x, y0=2y+1,代入①式,得22y+ 1=2·(2 x) + 1.即 y=4x2为线段 AB中点的轨迹方程.答案: y=4x26.已知动圆P 与定圆C:( x+2)2+ y2=1相外切,又与定直线l :x=1相切,那么动圆的圆心P 的轨迹方程是________.分析:设 P( x, y),动圆P 在直线x=1的左边,其半径等于1-x,则 | PC| = 1-x+ 1,即 x+2+ y2=2-x,整理得y2=-8x.答案:y 2=- 8x三、解答题 ( 每题 10 分,共 20 分 )7.设过点P( x,y) 的直线分别与x 轴的正半轴和y 轴的正半轴交于A,B 两点,点 Q与点→→→→求 P 点的轨迹方程.P 对于 y 轴对称, O为坐标原点,若 B P=2PA,且OQ·AB=1.→→3, 0分析:由 B P =2PA, P( x,y)可得 B(0,3y), A 2x,→3.∴A B =- x,3y2∵Q与 P 对于 y 轴对称,→∴Q(- x, y),且 OQ=(- x, y).→→322由 OQ· AB =1得2x +3y =1( x>0,y>0).8.过点P1(1,5)作一条直线交x 轴于点A,过点P2(2,7)作直线P1A 的垂线,交 y 轴于点B,点 M在线段 AB上,且 BM∶MA=1∶2,求动点 M的轨迹方程.分析:如下图,1设过 P2的直线方程为y-7= k( x-2)( k≠0),则过 P1的直线方程为y-5=-k( x-1),因此 A(5 k+1,0), B(0,-2k+7).①设 M( x, y),则由 BM∶ MA=1∶2,x=5k+ 1,3得②-4k+ 14y=,3消去 k,整理得12x+15y- 74=0.故点的轨迹方程为 12x + 15 -74=0. ③M y尖子生题库☆☆☆9.(10 分 ) 已知圆C:x2+ ( y- 3) 2= 9,过原点作圆C的弦 OP,求 OP中点 Q的轨迹方程.(分别用直接法、定义法、代入法求解)分析:方法一(直接法):如图,由于Q是 OP的中点,因此∠ OQC=90°.设 Q( x, y),由题意,得| OQ|2+| QC|2=| OC|2,即 x2+y2+[ x2+( y-3)2]=9,因此 x2+ y-32=9(去掉原点).24方法二 (定义法 ):如下图,由于Q 是 的中点,OP2- 3 2 9因此∠ OQC =90°,则 Q 在以 OC 为直径的圆上,故 Q 点的轨迹方程为 x + y2 =4(去掉原点).方法三 ( 代入法 ) :设 P ( x 1, y 1) , Q ( x , y ) ,x = x 12x 1= 2x由题意,得,即1= 2,1y yy = y22 + ( y -3) 2又由于 x= 9,1 1232因此 4x + 4 y -2 = 9,即 x 2+ y - 3 2=9( 去掉原点 ) . 2 4。
基本不等式(2知识点+4题型+强化训练)(教师版) 2024-2025学年高一数学上学期必修第一册

2.1.2 基本不等式知识点01 基本不等式若a >0 , b >0,则a +b ≥(当且仅当a =b 时,等号成立).①a+b2叫做正数a , ba ,b 的几何平均数.② 基本不等式的几何证明(当点D、O重合,即a =b 时,取到等号)③运用基本不等式求解最值时,牢记:一正,二定,三等.一正指的是a >0 , b >0;二定指的是ab 是个定值,三等指的是不等式中取到等号.【即学即练1】 求函数y =x +4x (x >0)的最值.解 x +4x ≥4,当x =2是取到等号,故最小值是4.知识点02 基本不等式的变形21a +1b ≤a +b 2当且仅当a =b 时等号成立)(调和均值≤几何均值≤算术均值≤平方均值)以上不等式把常见的二元关系(倒数和,乘积,和,平方和)联系起来,我们要清楚它们在求最值中的作用.① a +b ≥② ab ≤,和定求积:③ a 2+b 2≥(a+b )22(联系了a +b 与平方和a 2+b 2)④ ab ≤a 2+b 22(联系了ab 与平方和a 2+b 2)【即学即练2】若a >0,b >0,a +b =1,则( )A .1a +1b ≤1B .4ab ≤1C .a 2+b 2≥1D +1【题型一:基本不等式的内容及辨析】例1.下列命题中正确的是( )A .当x >1时,x +1x 的最小值为2B .当x <0时,x +1x ≤―2C .当0<x <1+2D .当x >1变式1-1.下列说法正确的是( )A .x +1x 最小值为2B .x +1x 最大值为2C +2D +2故选:C.变式1-2.下列不等式中等号可以取到的是()A≥2B.x2+2+1x2+2≥2C.x2+1x2≥2D.|x|+3+1|x|+3≥2【方法技巧与总结】在利用基本不等式求最值时,要注意“一正二等三定”六字.【题型二:基本不等式求和的最小值】方法1 直接法例2.若x>0,y>0,3x+2y=1,则8x+4y的最小值为()A B.C.D.变式2-1.x 2+7x 2 )A .B .C .D .变式2-2.下列命题中正确的是( )A .若a ,b ∈R ,则ba +ab ≥2B .若x >0,则x +1x >2C .若x <0,则x +4x ≥―=―4D .若x ∈R ,则2x +2―x ≥2方法2 凑项法例3.已知x >1,则2x +2x―1的最小值是( )A .3B .4C .6D .7变式3-1.已知x >―1,则x +2x+1的最小值为( )A .B .2C .1D .变式3-2.已知a>0,b>0且a+b=1,则14a +4a2a+b的最小值为()A.32B.74C.2D.94方法3 巧1法例4.已知正实数x,y满足2x+y=2,则8y +1x的最小值为()A.7B.8C.9D.10变式4-1.已知a,b为正实数,且满足a+2b=1,则2a +1b的最小值为()A.B.4+C.8D.6【答案】C变式4-2.已知a>0,b>0,且a+3b=2,则1a+1+13b的最小值为()A.23B.1C.43D.2方法4 换元法例5.设f(x)=x2―2x+22x―2,x∈(―1,1),则()A.f(x)min=1B.f(x)max=1 C.f(x)min=―1D.f(x)max=―1变式5-1.函数f(x)=x2―5x+3x+1(x⩾0)的最小值是()A.-1B.3C.6D.12变式5-2.已知a,b∈R,a+b=4,则1a2+1+1b2+1的最大值为()A B C D【方法技巧与总结】1 利用基本不等式求最值的方法有很多,常见的是直接法、凑项法、巧1法、换元法、消元法等,要理解各种方法的“基本套路”和思考“什么情况下会想到这个方法”;2 一般一道题目的方法可有很多种,解题时要多尝试多思考.【题型三:条件等式求最值】例6.已知2a+b=ab(a>0,b>0),下列说法正确的是()A.ab的最大值为8B.1a―1+2b―2的最小值为2C.a+b有最小值3+D.a2―2a+b2―4b有最大值4变式6-1.已知x>0,y>0,且3x +1y=1,则2x+y+xy的最小值为()A.9B.10C.12D.13变式6-2.(多选)已知正数a,b 满足4a +b +ab =5,则下列结论正确的是( )A .ab 的最大值为1B .4a +b 的最小值为4C .16a 2+b 2的最小值为9D .1a+1+1b 的最小值为109变式6-3.已知正实数x,y 满足4x 2+25y 2=1,则5x +2y 的最小值为( )A .20B .40C .D .【方法技巧与总结】理解基本不等式的各种变形,以及变形公式中把什么联系在一起了,多熟悉下!21a +1b ≤a +b 2当且仅当a =b 时等号成立)(调和均值≤几何均值≤算术均值≤平方均值)以上不等式把常见的二元关系(倒数和,乘积,和,平方和)联系起来,我们要清楚它们在求最值中的作用.① a +b ≥② ab ≤,和定求积:③ a 2+b 2≥(a+b )22(联系了a +b 与平方和a 2+b 2)④ ab ≤a 2+b 22(联系了ab 与平方和a 2+b 2)【题型四:基本不等式的恒成立问题】例7.若正实数x 、y 满足(x ―1)(y ―4)=4,且x +y4≥a 2―3a 恒成立,则实数a 的取值范围是( )A .{a|―1<a <4}B .{a|―1≤a ≤4}C .{a|―4≤a ≤1}D .{a|―4<a <1}变式7-1.当x >0,y >0,且满足2x +y ―2xy =0时,有2x +y >k 2+k ―8恒成立,则k 的取值范围为( )A .(―4,3)B .[―4,3]C .(―3,4)D .[―3,4]【答案】A【分析】把恒成立问题转化成求最值问题,利用基本不等式求出2x +y 的最小值,然后解二次不等式即可.变式7-2.“a =9”是“不等式 (x +y ≥8(a >0)对于任意正实数x ,y 恒成立”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件变式7-3.若不等式a 2+b 22+3≥x (a +b )对任意正数a ,b 恒成立,则实数x 的最大值为( )A B .2C D .1【方法技巧与总结】恒成立问题,常见的分离参数法,把问题转化为某式子或函数的最值问题,若式子中含有两个变量常常会想到基本不等式求最值.一、单选题1.已知a ,b 为实数,且a ⋅b ≠0,则下列命题错误的是( )A .若a >0,b >0,则a+b 2≥B .若a+b 2a >0,b >0C .若a ≠b ,则a+b 2>D .若a+b 2a ≠bA .当x <2时,x +1x―2≥4B .当x ≥2时,x +2x 的最小值是C .当x >04D .当x >0时,x +1x+1的最小值为13.若x >1,则函数f(x)=9x +x―1的最小值为( )A .6B .9C .12D .15A .函数y =x +1x 的最小值为2.B .函数y 22.C .函数y =2―3x ―4x (x >0)的最小值为2―D .函数y =2―3x ―4x (x >0)的最大值为2―5. 若0<x<1,则x +1―x的最小值是()A.1B.4C.2+D.3+A.ab有最大值14B.1a+1b有最小值4C.a2+b2D+A.(―∞,6]B.(―∞,16] C.(―∞,8]D.(―∞,9]A B C D9.设a>0,b>0,已知M=a2+b2,N)abA.M有最小值B.M有最大值C.N D.N10.若对于任意x>0,x2+3x+1≤a恒成立,则实数a的取值可以是()A.15B.110C.12D.13A.已知a,b为正实数,a+b=3,则1a+1+1b+2的最小值为23B.y=2C.已知正数x,y满足x+y=2,则xy的最大值是1D.若对任意x>0,x3+5x2+4x≥ax2恒成立,则实数a的取值范围是(―∞,9]12.已知a,b均为实数且a>0,b>0,a+b=3,则1a+1+1b的最小值为.13.已知a>―1,则a―a+1的最小值是.14.若正数x,y满足y =4,则y的最大值为.四、解答题15.(1)若x>0,y>0,且2x +8y=1,求:(i)xy的最小值;(ii)x+y的最小值.(2)求f(x)=4x+9x―5(x>5)的最小值.为1m的小路,中间A,B,C三个矩形区域将种植牡丹、郁金香、月季(其中B,C区域的形状、大小完全相同).设矩形花园的一条边长为x m,鲜花种植的总面积为S m2.(1)用含有x的代数式表示a,并写出x的取值范围;(2)当x的值为多少时,才能使鲜花种植的总面积最大?12n 12n 12n 12n 中的最大数.(1)设a ,b 都是正实数,且a +b =1,求max (2)解不等式:min x +1,x 2+3,|x ―1|>2x ―3;(3)设a ,b 都是正实数,求max a +1b ,2a+b 的最小值.(1)求证:m2=4n+4;(2)若m≤―4,求x21x2―4x1+x2+x22x1的最小值.它在数学的众多分支中有精彩应用,柯西不等式的一般形式为:设a1,a2,a3,⋅⋅⋅,a n,b1,b2,b3,⋅⋅⋅,b n∈R,则a21+a22+⋅⋅⋅+a2n b21+b22+⋅⋅⋅+b2n≥(a1b1+a2b2+⋅⋅⋅+a n b n)2当且仅当b i=0(i=1,2,⋅⋅⋅,n)或存在一个数k,使得a i=kb i(i=1,2,⋅⋅⋅,n)时,等号成立.(1)请你写出柯西不等式的二元形式;(2)设P ABCD内的任意一点,点P到四个面的距离分别为d1、d2、d3、d4,求d21+ d22+d23+d24的最小值;(3)已知无穷正数数列{a n}满足:①存在m∈R,使得a i≤m(i=1,2,⋅⋅⋅);②对任意正整数i、j(i≠j),均有.求证:对任意n≥4,n∈N∗,恒有m≥1.|a i―a j|≥1i+j。
#高一数学必修3(人教版)课后强化训练(含详解):1.1.2.3
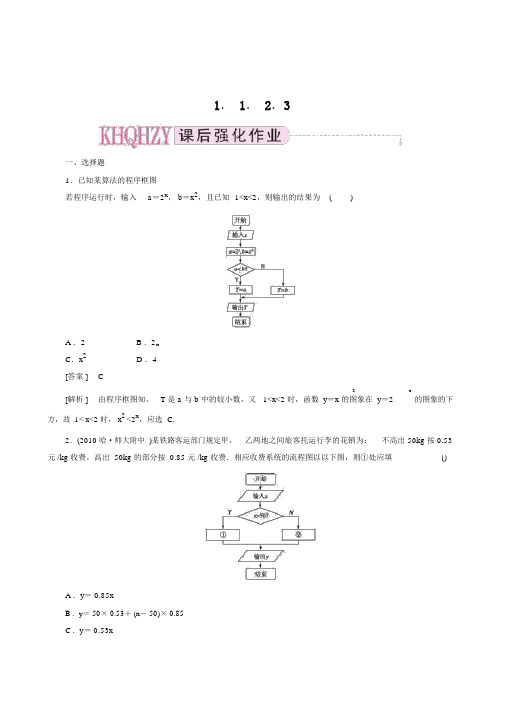
1. 1. 2.3一、选择题1.已知某算法的程序框图若程序运行时,输入a=2x, b=x2,且已知1<x<2,则输出的结果为()A .2B .2xC.x2 D .4[答案 ]C[解析 ]由程序框图知,2x的图象的下T 是 a 与 b 中的较小数,又 1<x<2 时,函数 y=x 的图象在 y=2方,故 1< x<2 时, x2<2x,应选 C.2.(2010 哈·师大附中 )某铁路客运部门规定甲、乙两地之间旅客托运行李的花销为:不高出 50kg 按 0.53元 /kg 收费,高出 50kg 的部分按 0.85 元 /kg 收费.相应收费系统的流程图以以下图,则①处应填()A.y= 0.85xB.y= 50× 0.53+ (x- 50)× 0.85C.y= 0.53xD.y= 50× 0.53+0.85x [答案] B3.以以下图的程序框图运行后,输出的结果是()A.-10 B .0C.10 D .20[答案 ]C[解析 ]由程序框图中的 (- 1)n知, S中的项一负一正,最大项为(-1)20× 20= 20,∴S=- 1+ 2- 3+- 19+ 20= 10.4. (2010 ·宁锦州辽 )下面的程序框图,输出的结果为()A .1B.2C.4 D .16[答案] D[解析 ]运行过程为:a=1≤ 3→ b=21=2,a=1+1=2,a=2≤ 3成立→ b=22=4,a=2+1=3,a=3≤ 3 成立→ b= 24= 16,a= 3+ 1= 4,此时 a≤ 3 不成立,输出b= 16.5.在如图的程序框图中,若输入m= 77, n= 33,则输出的n 的值是 ()A .3B .7C.11 D .33[答案 ]C[解析 ]这个程序框图执行的过程是:第一次循环:m= 77,n= 33,r =11;第二次循环:m= 33,n= 11, r = 0.因为r=0,则结束循环,输出n= 11.6. (2010·建莆田市质检福)阅读以以下图的程序框图,运行相应的程序,则输出 A 的值为()3115A. 16B.16157C. 8D.4[答案 ]C113[解析 ]运行过程为 A=2× 0+ 1= 1;i =0≥ 3不成立→ i= 0+ 1= 1,A=2×1+ 1=2;i =1≥ 3不成立→ i =1+ 1= 2,A=13717152×2+ 1=4; i = 2≥ 3不成立→ i= 2+ 1= 3, A=2×4+1=8; i= 3≥ 3成立,输出 A15的值8.7. (2010 ·徽合肥安 )若是执行如图的程序框图,那么输出的值是()A .2010B.- 11C.2 D .2[答案 ]D[解析 ]程序运行过程依次为:k= 0<2010→ S=1=- 1,k= 1<2010→ S=1=1,k= 2<2010→ S=1= 2,k= 3,故 S 的值1- 21- (-1)21-121依次循环取值- 1,2, 2,因为 2010 = 670× 3,故最后输出结果为 S= 2.[议论 ]遇到这种数值较大,循环次数很多的状况,可将数值变小,∵2010 能被 3 整除,故可取 k<6,k<3 来检验输出结果.你能指出条件改为k<32010 时输出的结果吗?8. (2010 东·北师大隶属中学 )若是执行如图的程序框图,那么输出的C= ()A .3B.5C.8 D .13[答案]B[解析 ] K 初值 2,不满足K≥ 5→C= 1+1= 2, A= 1, B= 2, K= 3.K =3≥ 5 不成立,执行第二次循环,→C= 1+2= 3, A= 2, B= 3, K= 4. K =4≥ 5 不成立,执行第三次循环,→C= 2+3= 5, A= 3, B= 5, K= 5. K =5≥ 5 成立,结束循环输出 C 的值5,应选 B.二、填空题9.(2010·南湘潭市湖)以以下图,这是计算1+ 1+ 1++2 461 的值的一个程序框图,其中判断框内应填20入的条件是 ________.[答案 ]n≤ 20[解析 ]n 初值为2,每循环一次,S 的值增加1n,即1S= S+n;n 的值增加2,即n=n+ 2,S 加上最后一个数120后,结束循环,故条件为n≤ 20.10. (2010 ·京东城区北 )以下图是某个函数求值的程序框图,则满足该程序的函数解析式为________.2x- 3 x<0[答案 ] f(x)=5- 4x x≥ 0三、解答题11.设计一个算法,找出区间[1,1000] 内的能被7 整除的整数,画出程序框图.[解析 ] S1取k=1.S2判断 k≤ 1000可否成立,若不成立,则执行S5.若 k 除以 7 的余数为 0,则输出 k.3SS4将 k 的值增加1,返回执行 S2.S5结束.程序框图如图.2x- 1(x<0)12.画出求函数 f(x)=0 ( x=0)的函数值的程序框图.log2x(x>0)[解析 ]程序框图以以下图.13.求使 1+ 2+ 3+ 4+ 5++ n<100 成立的最大自然数n 的值,画出程序框图.[解析 ][议论 ]用S表示加上自然数n 后所得的和,设满足题意的最大自然数为k,则 1+ 2++ k<100,1 + 2+ 3++ k+ (k+1)>100 ,因此控制条件S≥ 100 满足时的n 值比本质 n 的值大了2(n= n+ 1 在 S= S+ n 后时 )或大了 1(n= n+ 1 在语句 S= S+ n 前面时 )备选题1.以以下图是某程序的框图,运行该程序,输出的T= ________.[答案 ] 20[解析 ] T=0, S= 0,T>S 不成立;执行第一次循环后,S= 4,n= 2, T= 2; 2>4 仍不成立,执行第二次循环后,S= 8,n= 4, T= 6; 6>8 仍不成立,执行第三次循环后,S= 12, n= 6, T= 12; 12>12 仍不成立,执行第四次循环后,S=16, n= 8, T= 20; 20>16 成立,输出 T 的值 20.2.在如图的程序框图中,输入n= 2010 ,则程序运行后输出的结果是________.[答案 ]620101005-3 [解析 ]输入 n= 2010,第一次循环后,n=2= 1005, i =1;第二次循环后,n=2= 501,i= 2;第三次循环后, n=501- 3249- 3= 249, i = 3;第四次循环后, n== 123, i = 4;第五次循环后, n 22123- 360=2= 60, i= 5;第六次循环后, n=2= 30, i= 6,此时满足 n≤ 30,输出 i 的值 6.3.以以下图的算法流程图运行后,输出的结果T 为________.[答案 ] 10[解析 ]算法完成两次循环,依次是x= 3, T= 3;x= 7, T= 10,即可输出.T的输出值为10.[ 议论 ]算法是高中数学一个崭新的知识点,以其凑近考生的思想,简单融化其他知识块成为高考及各种过关测试的新宠,主要察看的是程序框图,同时兼顾对考生推理能力的察看.。
高一精品数学上册课后强化训练题6.pdf

《12.5 牛顿第一定律》导学案(无答案) 学习目标1.知道力和运动的关系的发展过程.2.理解牛顿第一定律的内容和含义.3.知道理想实验是科学探究的一种重要方法.4.再次运用控制变量法设计实验的过程. 课前预习力可以使运动的物体______,可以使静止的物体_______,也可以使物体速度的______、_______发生改变.力还可以使物体发生_______.所以力的作用效果可以总结为___________________和_______________________. 自学指导 1.阅读课本19页的第一段以及插图,想一想运动的物体为什么会停下来.通过所学的知识分析出运动的物体停下来的原因是____________________. 2.阅读19页第二段,了解一下亚里士多德、伽利略和牛顿的观点分别是什么. 牛顿第一定律的发展过程: 上述观点哪一个是正确的,需要通过实验来证明,课本上的实验叫“伽利略斜面小车实验” 在这个实验中,再次用到了控制变量法,实验中让每次让小车从斜面的同一高度滑下,目的是让小车在进入水平表面时具有相同的速度,这样才能比较小车在不同表面运动的情况.如下图所示,是小车从斜面上滑下后,在平面上最终停下的位置. 在下表中的空格填写完整.(填“大”、“较大”或“小”) 表面状况阻力的大小小车运动的距离毛巾木板玻璃分析上表得出结论:平面越光滑,小车运动的距离越_____,这说明小车受到的阻力越_____,速度减小的越______.如果小车不受阻力,小车将_________________________. 推理:如果物体不受力,它将_______________________________________. 上述实验证明__________的观点是正确的.后来,_____国物理学家________总结了前人的研究成果,概括出一条重要的物理规律:___________________________________________ _______________________________________________这就是著名的牛顿第一定律. 说明:1.该定律说明力并不是维持物体运动的条件,而是改变物体运动状态的原因.车之所以会停下来,是因为物体在运动过程中受到阻力,所以才会慢慢停下来,当给车施加的牵引力并不是维持车的运动,而是去克服受到的阻力,这样才能使车不停地运动,如果牵引力变大,大于阻力,那么车就会加速运动,从而改变车的运动状态,进一步说明了这个力是改变物体运动状态的原因. 2.任何物体,在不受外力作用时,总保持静止状态或匀速直线运动状态,直到有其它物体对它施加作用了迫使它改变这种状态为止. 3.牛顿第一定律是在大量经验事实的基础上,运用科学的推理的方法而概括出来的规律,是一个非常重要的规律,是整个力学的基础和出发点.所以它不能用实验验证,因为任何物体都受到其它物体的作用,但是它能经受住实践的检验. 典型例题例.正在路上行驶的汽车,突然受到的所有的力消失,那么它会( )A 突然停止B 慢慢停下来C 做匀速直线运动D 加速运动 方法总结:根据牛顿第一定律,原来静止的物体不受外力,将继续保持静止状态,原来运动的物体,突然不受外力,将以力撤销的那一瞬间的速度大小和方向做匀速直线运动. 原来静止的物体 不受力 永远保持静止状态 原来运动的物体 不受力 永远做匀速直线运动 课堂达标 1.下列关于“牛顿第一定律”的建立的说法中正确的是( )A 它是通过日常生活推导出来的B 它是通过理论推导出来的C 它是通过实验直接证明的D 它是以实验事实为基础,通过推理而概括出来的 2.在下图所示的实验中,每次必须让小车从斜面的同一高度滑下,这是为了使小车在三种平面上开始滑行时有_________,在越光滑的平面上,小车受到的__________越小,它运动的距离越_______,它的速度________得越慢,进一步推理可得出这样得结论:如果物体不受任何外力的作用,物体将_______________________________. 3.在水平桌面上铺上粗糙程度不同的物体,让小车自斜面顶端同一高度、从静止开始滑下,小车在不同表面运动的距离见下表,通过探究,我们可以反驳下列说法中的哪一个( ) 表面情况毛巾棉布木板小车运动的距离/m0.270.420.79A 摩擦力越小,小车的速度减小得越慢 B 小车受到力就运动,不受力就不运动 C 若平面非常光滑,小车的速度将保持不变,永远运动下去 D 运动物体不受力,将保持匀速直线运动 4.正在做匀速直线运动的物体,若所受的各力突然消失,则物体( )A 仍做匀速直线运动B 继续向前运动,且速度越来越快C 慢慢停下来D 立即停下来 5.足球比赛中,运动员用头顶球,球在向上飞,若此时受到的力都消失,则球将会( ) A静止 B 做匀速直线运动 C 下落 D 无法判断 6.用绳子拴住一个小球在光滑的水平面上做圆周运动,若绳子突然断裂,小球将( )A 保持原来的圆周运动状态B 保持绳断时的速度做匀速直线运动C 小球运动速率减小,但保持直线运动状态D 以上三种都有可能 第五节 惯性学案(第二课时) 学习目标1.知道惯性的定义,知道一切物体都有惯性.2.会用惯性知识解释生活中的惯性现象.3.知道惯性和惯性规律的区别. 课前预习1.一切物体在没有受到力的作用时,总保持__________或_____________,这就是牛顿第一定律. 2.原来静止的物体,如果不受任何力,则保持______________. 3.原来运动的物体,如果突然不受任何力,则保持_____________________. 自学指导1.阅读课本21页第一段,找出惯性的概念,并填写下空. 物体__________________________的特性叫做惯性,_____________________也叫惯性定律.___________都有惯性. 2.阅读课本上的“想想做做”部分,猜想一下发生的现象是:_______________________. 然后自己找一块橡皮,放在一张纸条上,快速把纸条抽出,看一下有什么现象? 3.阅读课本21页最后几段,了解一下日常中常见的惯性现象,学会解释现象的方法,然后合上课本,自己试着用惯性的知识解释一下,最后再考虑一下下面的问题: (1)当汽车开动时,站在车上的人为什么向后仰? (2)解释一下课本图6.5-5中锤头为什么能紧套在锤柄上? 4.阅读课本21页的“想想议议” 部分,想一想跳起后你会落在哪里,为什么? 典型例题 1.惯性现象的识别 例1.飞机投弹时,不是飞到目标的正上方投弹,而是要提前投掷才能命中目标,这是因为( )A 炸弹有向前的冲力B 炸弹受到向前惯力的作用C 炸弹具有惯性D 炸弹受到重力的作用 2.惯性现象的解释 例2.人走路时,被石头绊会向前倒,这是为什么? 思路引导:人走路时,脚被石头绊住,由于________,上身仍要保持原来的________状态,而向前倾倒. 【课外补充】物体的惯性越小,运动状态越容易改变,物体的惯性越大,运动状态越不容易改变.例如:为了能够灵活地改变速度,调整方向,歼击机不仅做得轻巧,作战中有时还需要甩掉副油箱;让足球和铅球都静止在地面上,足球轻轻一踢就能运动起来,但要使铅球运动起来却不那么容易;小轿车转弯灵活,起步很快,而火车起步却很慢;这些现象充分说明改变物体运动状态的容易程度与物体的_______有关,即物体的惯性与物体的_______有关,且物体的______越大,惯性越大. 课堂达标 1.骑自行车高速行驶时(尤其是下坡),往往要刹后闸,这是因为当刹前轮时,前轮被刹住而停止运动,由于_____,后轮仍要保持原来的________状态,而容易向前翻车. 2.在一个水杯的口上放上一张硬纸片,上面放一个鸡蛋,用力在水平方向上弹纸片,将会观察到的现象是:__________________________________________________________. 3.运动员百米冲刺后,并不能立即停下来,这是因为运动员( )A 失去了惯性B 具有惯性C 不受力的作用D 惯性大于阻力 4.下列现象,不能用惯性知识解释的是( )A 人走路时脚被绊了一下,会向前倒下B 投出去的篮球会继续向前飞行C 关闭了发动机的汽车会向前滑行D 熟透了的桃子会从树上掉下来 5.下列现象或做法与惯性有关的是( )A 骑车驾驶员必须系好安全带B 水从高处流向低处C 多数人习惯用右手写字D 电动机通电时转动 6.下列现象不能用惯性知识解释的是( )A 运动员跳远时往往要助跑B 子弹离开枪口后仍能继续高速向前飞行C 空中篮球正在落向地面D 古代打仗时,使用绊马索将敌方飞奔的战马绊倒 7.摩托车做飞跃障碍物的表演时为了减少向前翻车的危险( )A 应该前轮先着地B 应该后轮先着地C 应该前后轮同时着地D 哪个车轮先着地与翻车的危险没有关系 8.惯性在日常生活和生产中有利有弊,下面现象有弊的是( ) A 锤头松了,把锤柄在地上撞击几下,锤头就紧紧的套在锤柄上 B 拍打衣服可以去掉衣服上的尘土 C 往锅炉内添煤时,不用把铲子送进炉灶内,煤就随着铲子运动的方向进入灶内 D 汽车刹车时,站在车内的人向前倾倒 9.许多高档轿车中安装了安全气囊,特定情况下它会“蹦”出来,以免身体直接撞到车身上而受伤,安全气囊最有可能“蹦”出来的情况是轿车在( )A 高速公路上急速行驶时B 盘山公路上缓慢行驶时C 刚开始突然启动时D 与前方物体发生猛烈碰撞时 10.下列有关物体惯性的说法中正确的是( )A 静止时,它没有惯性B 不运动的物体没有惯性 C 船在水中匀速行驶时,一人在船尾处竖直向上抛出一物体,物体落下时将掉入水中 D 子弹离开枪口后,仍能继续高度向前飞行,是由于子弹具有惯性 11.阅读下面一则新闻报道,找出一处科学性错误,在错误字句的下面画上横线. 遇险情急刹车 乘客受伤 本报讯 今天清晨6:30,本市21路公共汽车在行驶途中遇险情,司机紧急刹车,有三名坐在后排的乘客由于突然失去惯性向前急冲而受伤. 初中学习网,资料共分享!我们负责传递知识! 伽利略的观点:。
高一精品数学上册课后强化训练题4.pdf
《12.3 长度、时间及其测量》导学案 学习目标1.知道国际单位制的来源. 2.知道长度的基本单位及其换算单位. 3.初学会用刻度尺测量一般的长度. 4.知道时间的单位,并会用钟表测量时间. 5.知道什么是误差以及减小误差的方法. 6 .长度的基本单位及其单位之间的换算. 7.用刻度尺测量长度以及刻度尺的读数. 8.误差及其产生原因,误差和错误的区别. 典型例题 一、长度单位之间的换算. 例1.某同学的身高是1.6m,则他的身高应为_______cm. 例2.某原子的半径为20nm,则相当于__________m. 方法总结 :_______________________________________________________________ 课堂达标1.下列单位换算关系式中,正确的是( )A 3.75m=3.75m×100=375cmB 3.75m=3.75m×100cm=375cmC 3.75m=3.75×cm=0.375cm D3.75m=3.75×100cm=375cm 2.单位换算:4×105μm=_______m; 7.84×106m=______km 25nm=________m 15km=__________cm 3.6m=__________nm 3×105km=______mm 3.我国的长江全长6300km,如果换算成以米为单位,当相当于__________m 二、刻度尺的读数. 例2.如图所示,刻度尺的分度值为________,木块的长度为_________. 方法总结: 2.下图所示是用最小刻度为毫米的直尺测量一物体的长度,甲同学的读数为41毫米,乙同学的读数为41.0毫米,丙同学的读数为16毫米,丁的读数为16.0毫米.上述四位同学中读数正确的是_______. 三、误差和平均值法测量物体的长度. 例3.一个同学用同一把刻度尺先后四次测量同一物体的长度:L1=2.45cm;L2=2.46cm; L3=2.47cm;L4=2.48cm,那么物体的长度大约是__________cm 方法总结: 课堂达标31.某同学测量物体的长度,四次测量结果分别是5.51cm,5.51cm,5.53cm,5.55cm,则这个物体的长度应记作( )A 5.51cmB 5.52cmC 5.525cmD 5.53cm 2.某同学用一刻度尺先后5次测量某物体的长度,分别为:8.46cm、8.45cm、8.56cm、8.44cm、8.47cm,那么错误的是________,该物体的长度是______. 课后巩固 1.一位同学测量了一些物体的长度,忘记了写单位,你帮他填上合适的单位: 小明的身高为1.64_____;课桌宽46____;物理课本的长为250______,一枚硬币的厚度为2_____.小红的鞋长为24_______,金星到南麻的距离为40_____.刘翔在奥运会上跑的距离为110_____. 2.无线电波在1s内通过的距离为3×105km=__________cm=__________mm. A.对一个物体的长度进行多次测量取平均值,可以避免误差。
高一数学上册期末强化试题答案
高一数学上册期末强化试题答案一、选择题1.设集合{}012345U =,,,,,,{}035M =,,,{}145N =,,,则()UM N =( )A .{}5B .{}03,C .{}0235,,,D .{}01345,,,, 2.函数()2xf x x =-的定义域是( ) A .{}|2x x < B .{}|2x x > C .{}2|x x ≤ D .{}|2x x ≥3.已知cos sin 1θθ->,则角θ的终边在( )A .第二象限B .第三象限C .第二象限或第四象限D .第四象限4.在平面直角坐标系中,角θ的顶点与原点重合,始边与x 轴的非负半轴重合,终边经过点()3,4P -,那么sin 2cos θθ+=( )A .15B .15-C .25-D .255.方程24x x +=的根所在的区间为( )A .()0,1B .()1,2C .()2,3D .()3,46.《几何原本》中的几何代数法是以几何方法研究代数问题,这种方法是后西方数学家处理问题的重要依据,通过这一原理,很多的代数公理或定理都能够通过图形实现证明,也称之为无字证明.下图是我国古代数学家赵爽创作的弦图,弦图由四个全等的直角三角形与一个小正方形拼成的一个大正方形.若直角三角形的直角边长分别为a 和b ,则该图形可以完成的无字证明为( ).A .)0,02a bab a b +≥>> B .()22200a b ab a b +≥>>,C ()20,011ab a b a b>>+ D ()220022a b a b a b ++≥>>,7.已知函数f (x )是偶函数,且f (x )在[0,)+∞上是增函数,若1()02f =,则不等式()4log 0f x >的解集为( ) A .{x |x >2}B .1{|0}2x x <<C .{1|02x x <<或x >2} D .{1|12x x <<或x >2} 8.已知函数()f x 是定义在R 上的增函数,()0,1A -,()3,1B 是其图象上的两点,那么|(2sin 1)|1f x +≤ 的解集为( )A .,33xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ B .722,66xk x k k ππππ⎧⎫+≤≤+∈⎨⎬⎩⎭Z ∣ C .,63xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ D .722,66xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣ 二、填空题9.狄利克雷是德国著名数学家,是最早倡导严格化方法的数学家之一,狄利克雷函数()1,0,x Qf x x Q ∈⎧=⎨∉⎩(Q 是有理数集)的出现表示数学家对数学的理解开始了深刻的变化,从研究“算”到研究更抽象的“概念、性质、结构”.关于()f x 的性质,下列说法正确的是( )A .函数()f x 是偶函数B .函数()f x 是周期函数C .对任意的1x R ∈,2x ∈Q ,都有()()121f x x f x +=D .对任意的1x R ∈,2x ∈Q ,都有()()121f x x f x ⋅=10.已知定义在R 上的函数()f x 的图象连续不断,若存在常数λ(R λ∈),使得()()0f x f x λλ++=对任意的实数x 恒成立,则称()f x 是回旋函数.给出下列四个命题中,正确的命题是( ).A .函数()f x a =(其中a 0≠)为回旋函数的充要条件是1λ=-.B .若函数()x f x a =(1a >)为回旋函数,则1λ>.C .函数()cos f x x π=不是回旋函数.D .若()f x 是2λ=的回旋函数,则()f x 在[0,2020]上至少有1010个零点. 11.下列四个命题中,正确的有( )A .命题p :“1x ∃≤,2320x x -+≥”,则p ⌝为“1x ∀>,2320x x -+<”B .函数1()1x f x a -=+(0a >,且1a ≠)的图象恒过定点1,2C .若a b >,0c d >>,则a bd c> D .若函数2()24f x x x =-+在区间[]0,m 上的最大值为4,最小值为3,则实数m的取值范围是[]1,212.双曲函数是一类与常见的三角函数类似的函数.最基本的双曲函数是双曲正弦函数2x x e e shx --=和双曲余弦函数2x xe e chx -+=,其中e 是自然对数的底数.则下列结论正确的是( )A .222ch x ch x sh x =+B .222sh x ch x sh x =-C .()sh x y shxchy chxshy +=+D .()ch x y chxchy shxshy +=+三、多选题13.已知集合{}0,1,A a =,()0,2B =,若{}1A B ⋂=,则实数a 的取值范围是________. 14.计算102554(1)2100.25log log π-++++=_____. 15.已知0a >,且1a ≠.若函数223()xx f x a -+=有最大值,则关于x 的不等式()2log 570a x x -+>的解集为_________.16.设函数2()f x ax bx c =++且()()10f a λλ=≠,对于0a ∀>,,b c R ∈,()f x 在区间()0,2内至少有一个零点,则符合条件的实数λ的一个..值是________. 四、解答题17.已知a R ∈,集合{}2230A x x x =--≤,{}220B x x ax =--=.(1)若a =1,求A B ,R C A ; (2)若A B A ⋃=,求实数a 的取值范围.18.已知函数()2cos 2cos f x x x x =⋅+. (1)求函数()f x 的最小正周期; (2)求该函数的单调递增区间;(3)求函数()f x 在区间π5π,612⎡⎤-⎢⎥⎣⎦上的最小值和最大值.19.已知函数22()log (1)log (1)f x x x =-++. (1)判断该函数的奇偶性,并说明理由;(2)判断并证明该函数的单调性,写出该函数在区间2⎫⎪⎢⎪⎣⎭上的值域.20.如图,现有一块半径为2m ,圆心角为3π的扇形木板,按如下方式切割一平行四边形:在弧AB 上任取一点P (异于A 、B ),过点P 分别作PC 、PD 平行于OB 、OA ,交OA 、OB 分别于C 、D 两点,记AOP α∠=.(1)当点P 位于何处时,使得平行四边形OCPD 的周长最大?求出最大值;(2)试问平行四边形OCPD 的面积是否存在最大值?若存在,求出最大值以及相应的α的值;若不存在,请说明理由.21.如图,一个水轮的半径为4米,水轮圆心O 距离水面2米,已知水轮每分钟逆时针转动1圈,当水轮上点P 从水中浮现时(图中点0P )开始计算时间.(1)将点P 距离水面的距离z (单位:米,在水面以下,则z 为负数)表示为时间t (单位:秒)的函数;(2)在水轮转动1圈内,有多长时间点P 位于水面上方?22.已知函数()13x mf x -⎛⎫= ⎪⎝⎭,其中m R ∈.(1)当函数()f x 为偶函数时,求m 的值; (2)若0m =,函数()()31xg x f x k=+-,[]2,0x ∈-,是否存在实数k ,使得()g x 的最小值为0?若存在,求出k 的值,若不存在,说明理由; (3)设函数()2327mx h x x =+,()()(),39,3h x x g x f x x ⎧≥⎪=⎨<⎪⎩,若对每一个不小于3的实数1x,都有小于3的实数2x ,使得()()12g x g x =成立,求实数m 的取值范围.【参考答案】一、选择题 1.B 【分析】利用集合的补集和交集运算求解. 【详解】因为集合{}012345U =,,,,,,{}145N =,,, 所以{}0,2,3UN =又{}035M =,,, 所以()UM N ={}03,故选:B 2.B 【分析】由分式中的分母不为零,二次根式中的被开方数大于等于零可得选项. 【详解】 因为函数()f x =,所以2>0x -,解得>2x ,所以函数()f x ={}|2x x >,故选:B . 【点睛】方法点睛:常见的具体函数求定义域:(1)偶次根号下的被开方数大于等于0;(2)分式中的分母不为0;(3)对数函数中真数大于0. 3.D 【分析】可采取同时平方的方式,判断θ在第二象限或第四象限,再结合cos sin 1θθ->,结合符号法则进行判断即可 【详解】由cos sin 112sin cos 1θθθθ->⇒-⋅>,sin cos 0θθ⋅<,故θ在第二象限或第四象限,当θ在第二象限时,cos 0,sin 0θθ<>,cos sin 0θθ-<,不符合题意,舍去; 当θ在第四象限时,cos 0,sin 0θθ><,cos sin 0θθ->,符合题意; 综上所述,角θ的终边在第四象限 故答案为:D 【点睛】本题考查由三角函数的正负值判断具体角所在象限,属于基础题 4.C 【分析】由三角函数的定义得43sin ,cos 55αα==-,进而得sin 2cos θθ+=25-【详解】解:由三角函数的定义得5r ==,所以43sin ,cos 55αα==-,所以sin 2cos θθ+=25-.故选:C. 5.B 【分析】构造函数()24xf x x =+-,利用零点存在定理可得出结论.【详解】构造函数()24xf x x =+-,则函数()f x 为R 上的增函数,()110f =-<,()220f =>,则()()120f f ⋅<,因此,方程24x x +=24x x +=的根所在的区间为()1,2. 故选:B. 6.B 【分析】由图可知大正方形的面积大于等于4个直角三角形的面积和,从而可得结论 【详解】解:因为直角三角形的直角边长分别为a 和b ,所以大正方形的面积为22a b + 由图可知大正方形的面积大于等于4个直角三角形的面积和, 所以221422a b ab ab +≥⨯=(0,0a b >>)故选:B7.C 【分析】利用函数()f x 的奇偶性和单调性将不等式等价为41log 2x >,进而可求得结果. 【详解】依题意,不等式()()441log 0log 2f x f x f ⎛⎫>⇔> ⎪⎝⎭,又()f x 在[)0,+∞上是增函数,所以41log 2x >, 即41log 2x <-或41log 2x >,解得102x <<或2x >.故选:C. 8.D 【分析】由题意可得()01f =-,()31f =,所要解的不等式等价于()()0(2sin 1)3f f x f ≤+≤,再利用单调性脱掉f ,可得02sin 13x ≤+≤,再结合正弦函数的图象即可求解. 【详解】由|(2sin 1)|1f x +≤可得1(2sin 1)1f x -≤+≤, 因为()0,1A -,()3,1B 是函数()f x 图象上的两点, 所以()01f =-,()31f =,所以()()0(2sin 1)3f f x f ≤+≤, 因为()f x 是定义在R 上的增函数,可得02sin 13x ≤+≤,解得:1sin 12x -≤≤,由正弦函数的性质可得722,66k x k k Z ππππ-+≤≤+∈, 所以原不等式的解集为722,66xk x k k ππππ⎧⎫-≤≤+∈⎨⎬⎩⎭Z ∣, 故选:D 【点睛】关键点点睛:本题解题的关键点是将要解得不等式转化为()()0(2sin 1)3f f x f ≤+≤利用单调性可得02sin 13x ≤+≤.二、填空题9.ABC 【分析】利用函数奇偶性的定义可判断A 选项的正误;验证()()1f x f x +=,可判断B 选项的正误;分1x Q ∈、1x Q ∉两种情况讨论,结合函数()f x 的定义可判断C 选项的正误;取20x =,1x Q ∉可判断D 选项的正误.【详解】对于A 选项,任取x Q ∈,则x Q -∈,()()1f x f x ==-; 任取x Q ∉,则x Q -∉,()()0f x f x ==-.所以,对任意的x ∈R ,()()f x f x -=,即函数()f x 为偶函数,A 选项正确; 对于B 选项,任取x Q ∈,则1x Q +∈,则()()11f x f x +==; 任取x Q ∉,则1x Q +∉,则()()10f x f x +==.所以,对任意的x ∈R ,()()1f x f x +=,即函数()f x 为周期函数,B 选项正确; 对于C 选项,对任意1x Q ∈,2x ∈Q ,则12x Q x +∈,()()1211f x x f x +==; 对任意的1x Q ∉,2x ∈Q ,则12x x Q +∉,()()1210f x x f x +==. 综上,对任意的1x R ∈,2x ∈Q ,都有()()121f x x f x +=,C 选项正确; 对于D 选项,取20x =,若1x Q ∉,则()()()12101f x x f f x ⋅==≠,D 选项错误. 故选:ABC. 【点睛】关键点点睛:本题解题的关键在于根据已知函数的定义依次讨论各选项,分自变量为无理数和有理数两种情况讨论,对于D 选项,可取1x Q ∉,20x =验证. 10.AD 【分析】对于选项A,B,C 利用回旋函数的定义判断其是否正确;对于选项D ,由回旋函数的定义可得:(2)2()f x f x +=-,由零点存在性定理知在区间[x ,2]x +上至少有一个零点,可令0x =,2,4,6,⋯,10102⨯,即可得到正确选项.【详解】因为函数()f x a =(其中a 0≠)为回旋函数()()(1)01f x a f x a a λλλλλ⇔+==-=-⇔+=⇔=-,所以选项A 正确;若(1)x y a a =>为回旋函数,则0x x a a λλ++=,即0a λλ+=,0λ∴<,结论不成立,故选项B 错误;假设函数()cos f x x π=是回旋函数,所以cos ()cos 0x x πλλπ++=对任意实数x 都成立, 令12x =,则1cos ()0,sin 0,sin 02πλλπλπ+=∴-=∴=;令1x =得cos()0,cos 0,cos =ππλλπλλπλλ+-=∴--=∴-,所以21,1λλ=∴=±,经检验当1λ=±时,cos ()cos 0x x πλλπ++=对任意实数x 都成立,所以函数()cos f x x π=是回旋函数,所以选项C 错误;若()f x 是2λ=的回旋函数,则(2)2()0f x f x ++=,即(2)2()f x f x +=-恒成立,()(2)0f x f x +,∴由零点存在性定理得:函数()f x 在区间[x ,2]x +上至少有一零点,可令0x =,2,4,6,⋯,10102⨯,∴函数()f x 在[0,2020]上至少有1010个零点,故选项D 正确. 故选:AD 【点睛】方法点睛:类似本题的定义题,解答时,首先必须要理解掌握这个新的定义,再利用这个定义来解题.所以要解答本题,首先必须理解回旋函数的定义. 11.BD 【分析】对于A ,直接将特称命题否定为全称命题即可;对于B ,由指数函数的性质判断;对于C,举反例可判断,对于D ,由二次函数的性质求解 【详解】解:对于A ,特称命题否定为全称命题时,改量词否结论即可,命题p :“1x ∃≤,2320x x -+≥”,则p ⌝为“1x ∀≤,2320x x -+<”,所以A 错误;对于B ,由10x -=得1x =,此时0(1)12f a =+=,所以函数1()1x f x a -=+(0a >,且1a ≠)的图象恒过定点1,2,所以B 正确; 对于C ,若1,2,2,1a b c d =-=-==,则1,1a b d c =-=-,此时a bd c=,所以C 错误; 对于D ,函数2()24f x x x =-+的对称轴为1x =,此时取得函数最小值(1)3f =,又(0)(2)4f f ==,所以实数m 的取值范围是[]1,2,所以D 正确,故选:BD 12.ACD 【分析】利用指数的运算以及双曲正弦、余弦函数的定义可判断各选项的正误. 【详解】 对于A 选项,()()2222222222224x x x x x x x x e e e e e e e e ch x sh x ----++++-⎛⎫⎛⎫+-+=+=⎪ ⎪⎝⎭⎝⎭2222x x e e ch x -+==,A 选项正确; 对于B 选项,()()222222222212224x x x xx x x x e e e e e e e e ch x sh x sh x ----++-+-⎛⎫⎛⎫+--=-==≠ ⎪ ⎪⎝⎭⎝⎭,B 选项错误;对于C 选项,()()()()4xx y y x x y y ee e e e e e e shxchy chxshy -----+++-+=()()()42x yx y y x x y x y x y y x x y x y x y e e e e e e e e e e sh x y +----+----+--+--+-+--===+,C 选项正确; 对于D 选项,()()()()4xx y y x x y y e e e e e e e e chxchy shxshy ----+++--+=()()()42x yx yy xx yx yx yy x x y x y x y eeeeeee e e e ch x y +----+----+--++++--++===+,D 选项正确.故选:ACD.三、多选题 13.()[),02,-∞+∞【分析】由题意可得出实数a 所满足的不等式,由此可求得实数a 的取值范围. 【详解】已知集合{}0,1,A a =,()0,2B =,且{}1A B ⋂=,所以0a <或2a ≥. 因此,实数a 的取值范围是()[),02,-∞+∞. 故答案为:()[),02,-∞+∞. 【点睛】本题考查利用交集运算求参数的取值范围,考查计算能力,属于基础题.14.72【分析】根据指数、对数的运算法则和性质求解. 【详解】 102554(1)2100.25π-++++log log ,551211000.1254=+++log log ,511252=++log 171222=++=. 故答案为:72【点睛】本题主要考查了对数,指数的运算,还考查了运算求解的能力,属于基础题.15.()2,3【分析】由复合函数单调性可确定223u x x =-+在(),1-∞上单调递减,在()1,+∞上单调递增;由函数有最大值可知()uf u a =单调递减,得到01a <<;根据对数函数单调性可将不等式化为20571x x <-+<,解不等式求得结果.【详解】223()xx f x a -+=,()f x ∴定义域为R223u x x =-+在(),1-∞上单调递减,在()1,+∞上单调递增()f x 有最大值,()u f u a ∴=需在R 上单调递减,01a ∴<<由()2log 570a x x -+>,得20571x x <-+<,解得:23x <<∴不等式的解集为()2,3故答案为:()2,3 【点睛】关键点点睛:本题考查根据函数单调性求解函数不等式,涉及到复合函数单调性的求解、根据函数有最值求解参数范围等知识,解题的关键是通过复合函数的单调性确定函数有最值时,对数的底数所处的范围,再利用对数函数的单调性解不等,考查学生的转化能力与运算求解能力,属于中档题. 16.()1,0-内的任何一个数均可 【分析】根据题意,求得(1)b c a λ+=-,其中0a >,根据二次函数的性质,分0c 、0c >和0c <三种情况讨论,结合零点的存在定理,即可求解. 【详解】由题意,函数2()f x ax bx c =++且()()10f a λλ=≠, 可得a b c a λ++=,即(1)b c a λ+=-,其中0a >, 又由()(0),(1),242f c f a b c a f a b c λ==++==++若0c ,可得()00,(2)4242(1)0f f a b c a a λ==++=+->,解得1λ>-; 若0c >,可得(0)0f c =>,则(1)0f a b c a λ=++=<,则0λ<,符合题意; 若0c <,可得(0)0f c =<,()242(22)0f a b c a c λ=++=+->, 所以220λ+>,解得1λ>-, 综上可得,实数λ的取值范围是(1,0)-. 故答案为:()1,0-内的任何一个数均可.有关函数零点的判定方法及策略:(1)直接法:令()0f x =,有几个解,函数就有几个零点;(2)零点的存在定理法:要求函数()f x 在区间[],a b 上连续不断的曲线,且()()0f a f b <,再结合函数的图象与性质确定零点的个数;(3)图象法:利用图象交点的个数,作出两函数的图象,观察其交点的个数,得出函数()f x 的零点个数.四、解答题17.(1){}12A B =-,,()()13R C A =-∞-+∞,,;(2)713⎡⎤⎢⎥⎣⎦,. 【分析】(1)当1a =,先求出集合B ,再利用集合的交集和补集计算即可;(2)先利用已知条件得到B A ⊆,由一元二次方程的根的分布建立不等式组,即可得出结果. 【详解】(1)由题意知:{}[]223013A x x x =--≤=-,,当a =1时,{}{}22012B x x x =--==-,, 所以{}12A B =-,,()()13R C A =-∞-+∞,,; (2)A B A B A ⋃=∴⊆,,因为()2+8>0a =-∆恒成立,所以B ≠∅,所以要使B A ⊆,则需()()2213211203320a a a ⎧-<<⎪⎪⎪--⨯--≥⎨⎪--≥⎪⎪⎩,解得713a ≤≤,所以实数a 的取值范围为:713⎡⎤⎢⎥⎣⎦,.18.(1)πT =;(2)πππ,π36k k ⎡⎤-++⎢⎥⎣⎦()k ∈Z ;(3)最大值为3,最小值为0.【分析】(1)利用二倍角公式以及辅助角公式化简()f x ,再由正弦函数的周期公式即可求解; (2)解不等式πππ2π22π262k x k -+≤+≤+,()k ∈Z 即可求解;(3)根据π5π,612x ⎡⎤∈-⎢⎥⎣⎦求出π26x +的范围,根据正弦函数的性质即可求解.(1)()2cos 2cos 2cos21f x x x x x x =⋅+=++π2sin 216x ⎛⎫=++ ⎪⎝⎭,所以函数()f x 的最小正周期为2ππ2T ==, (2)令πππ2π22π262k x k -+≤+≤+,解得:ππππ36k x k -+≤≤+,()k ∈Z所以该函数的单调递增区间为πππ,π36k k ⎡⎤-++⎢⎥⎣⎦()k ∈Z ;(3)因为π5π,612x ⎡⎤∈-⎢⎥⎣⎦,所以ππ2,π66x ⎡⎤+∈-⎢⎥⎣⎦,所以当ππ266x +=-即π6x =-时,πsin 26⎛⎫+ ⎪⎝⎭x 最小为12-,当ππ262x +=即π6x =时,πsin 26⎛⎫+ ⎪⎝⎭x 最大为1,所以1πsin 2126x ⎛⎫-≤+≤ ⎪⎝⎭,π12sin 226x ⎛⎫-≤+≤ ⎪⎝⎭, ()[]π2sin 210,36f x x ⎛⎫=++∈ ⎪⎝⎭,所以函数()f x 在区间π5π,612⎡⎤-⎢⎥⎣⎦上的最小值为0,最大值为3.19.(1)偶函数,理由见解析(2)函数在(1,0)-上为增函数,在[0,1)上为减函数,证明见解析,值域为(,1]-∞-. 【分析】(1)令1010x x +>⎧⎨->⎩求得函数的定义域关于原点对称,再根据()()f x f x -=,可得函数()f x 为偶函数;(2)利用函数单调性的定义证明,根据单调性求值域即可. 【详解】(1)由1010x x +>⎧⎨->⎩解得11x -<<,所以函数定义域为()1,1-,关于原点对称, 又22()log (1)log (1)()f x x x f x -=++-=, 所以函数()f x 为偶函数.(2)函数在(1,0)-上为增函数,在[0,1)上为减函数.设12,[0,1)x x ∀∈且12x x <, 则210x x x ∆=->,2222()log (1)log (1)log (1)f x x x x =-++=-,22212211()()()log 1()x f x f x x -∴-=-,而222112121()[1()]()()0x x x x x x ---=-+<,所以22211()011()x x -<<-, 故22212211()()()log 01()x f x f x x --=<-, 所以函数在[0,1)上为减函数, 因为函数为偶函数, 所以函数在(1,0)-上为增函数,当x ⎫∈⎪⎪⎣⎭时,()f x 为减函数,所以21()log 12f x f ≤==-, 即函数值域为(,1]-∞- 【点睛】关键点点睛:根据奇偶函数的定义判断函数奇偶性注意分析函数定义域;利用函数单调性的定义证明,要注意做差后变形求证,属于中档题.20.(1)点P 位于弧AB 的中点时,使得平行四边形OCPD;(2【分析】过P 点作OC 的垂线,垂足为H ,从而可得PH =2sin α,OH =2cos α,PC =CH =,得出2cos OC OH CH α=-= (1)平行四边形OCPD 的周长为f (α) 3πα⎛⎫+ ⎪⎝⎭,利用三角函数的性质即可求解. (2)()26S OC PH παα⎛⎫=⋅=+ ⎪⎝⎭. 【详解】过P 点作OC 的垂线,垂足为H ,因为OP =2,∠AOP =α,则PH =2sin α,OH =2cos α,2sin 43sin sin3PC ααπ=,123sin 2CH PC α== 所以23sin 2cos OC OH CH αα=-= (1)设平行四边形OCPD 的周长为f (α), 则43sin 83sin 43sin ()2()4cos 4cos f OC PC αααααα=+=833πα⎛⎫+ ⎪⎝⎭, 因为点P 异于A 、B 两点,所以03πα<<,所以当6πα=,即点P 位于弧AB 的中点时,使得平行四边形OCPD 83. (2)设平行四边形OCPD 的面积为S (α),则23sin ()2cos 2sin S OC PH αααα⎛=⋅=⋅ ⎝⎭243sin 4sin cos ααα=23(1cos 2)2sin 2αα-=432326πα⎛⎫+ ⎪⎝⎭, 由(1)得,03πα<<,所以52666πππα<+<, 所以当262ππα+=,即6πα=,也就是点P 位于弧AB 的中点时,使得平行四边形OCPD 2321.(1)()4sin 20306t z t ππ⎛⎫=-+≥ ⎪⎝⎭;(2)40秒.(1)以圆心为原点建立平面直角坐标系,根据O 距离水面的高度计算出0P 坐标,再利用三角函数表示出P 点坐标,将P 的纵坐标加2即可得到z 关于t 的函数;(2)根据条件可知0z >,解对应的不等式求解出t 的范围,由此确定出有多长时间点P 位于水面上方. 【详解】(1)建立如图所示平面直角坐标系,由题意可知:()023,2P -,则3tan ϕ=6π=ϕ,因为水轮每分钟逆时针转动1圈,所以t 秒可转动的角度为26030tt ππ=, 所以P 的坐标为4cos ,4sin 306306t t ππππ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,且P 的纵坐标加上2即为P 到水面的距离,所以()4sin 20306t z t ππ⎛⎫=-+≥ ⎪⎝⎭;(2)因为[]110,60,,30666t t ππππ⎛⎫⎡⎤∈-∈- ⎪⎢⎥⎝⎭⎣⎦,令4sin 20306t ππ⎛⎫-+> ⎪⎝⎭, 所以1sin 3062t ππ⎛⎫->- ⎪⎝⎭,所以763066t ππππ-<-<,所以040t <<,所以在水轮转动1圈内,有40秒时间点P 位于水面上方 【点睛】关键点点睛:解答本题的关键是通过建立合适平面直角坐标系结合三角函数定义求解出z 关于t 的函数,其中着重去分析P 点的纵坐标值得注意.22.(1)0m =;(2)83k =;(3)06m <<(1)由()()f x f x =-可得m 的值; (2)当[]2,0x ∈-时,()()21x xg x k =+⋅-,令1,13x t ⎡⎤=∈⎢⎥⎣⎦,则()2221124k kg t t kt t ⎛⎫=+-=+-- ⎪⎝⎭,分类讨论求出()g t 的最小值,列方程即可求解;(3)将题目的条件转化为:对于任意一条直线y k =,如果y k =与()g x 图象中满足3x ≥的部分图象有交点,则y k =必然与()g x 的图象中满足3x <的部分图象也有交点,分四种情况讨论即可得实数m 的取值范围. 【详解】(1)当函数()f x 为偶函数时,()()f x f x =-, 所以x m x m -=--,解得:0m =, 经检验,0m =符合,故0m =; (2)当[]2,0x ∈-时,()()21113xxx xg x k k ⎛⎫=+⋅-=+⋅- ⎪⎝⎭,令1,13xt ⎡⎤=∈⎢⎥⎣⎦,则()2221124k k g t t kt t ⎛⎫=+-=+-- ⎪⎝⎭, 当123k -<即23k >-时,()g t 在1,13⎡⎤⎢⎥⎣⎦上单调递增, 所以2111033k ⎛⎫+-= ⎪⎝⎭,解得:83k =,符合;当1132k ≤-≤即223k -≤≤-时,2104k --=无解; 当12k ->即2k <-时,()g t 在1,13⎡⎤⎢⎥⎣⎦上单调递减, 所以110k +-=,解得:0k =,应舍去;综上,83k =;(3)()193m h x x x=⋅+,将题目的条件转化为:对于任意一条直线y k =,如果y k =与()g x 图象中满足3x ≥的部分图象有交点,则y k =必然与()g x 的图象中满足3x <的部分图象也有交点. 当3x ≥时,9y x x=+是单调递增的,所以当0m ≠时,()h x 是单调函数, 分四种情况讨论:①当0m <时,()g x 在[)3,+∞上符号是负,而在(),3-∞上符号是正的,所以不满足题目的条件;②当0m =时,当3x ≥时,()0g x =,而当3x <时,()1303xg x ⎛⎫=⋅> ⎪⎝⎭,所以也不符合条件;③当03m <<时,要满足条件只需()()93f m h >即162m <,所以03m <<;④当3m ≥时,要满足条件只需()()933f h >即732m m ->,即3log 702mm +-<, 令()3log 72mt m m =+-, 因为()t m 在[)3,+∞上单调递增,且()60t =,所以解()()06t m t <=得6m <, 所以36m ≤<,综上,实数m 的取值范围为06m <<. 【点睛】关键点睛:本题的关键是能够将题目的条件转化为:对于任意一条直线y k =,如果y k =与()g x 图象中满足3x ≥的部分图象有交点,则y k =必然与()g x 的图象中满足3x <的部分图象也有交点,结合图象就能求解出实数m 的取值范围;当然再分析当3m ≥情况时,需要构造函数()3log 72mt m m =+-,利用单调性求解不等式.。
2012高考线性规划——强化训练
线性规划中档题——强化训练1.(2010年北京理7)设不等式组 110330530x y x y x y 9+-≥⎧⎪-+≥⎨⎪-+≤⎩表示的平面区域为D ,若指数函数y=x a 的图像上存在区域D 上的点,则a 的取值范围是(A )(1,3] (B )[2,3] (C ) (1,2] (D )[ 3, +∞]2.( 2010年福建理8)设不等式组x 1x-2y+30y x ≥⎧⎪≥⎨⎪≥⎩所表示的平面区域是1Ω,平面区域是2Ω与1Ω关于直线3490x y --=对称,对于1Ω中的任意一点A 与2Ω中的任意一点B, ||AB 的最小值等于( ) A.285 B.4 C. 125D.2 3.(2010年浙江理7)若实数x ,y 满足不等式组330,230,10,x y x y x my +-≥⎧⎪--≤⎨⎪-+≥⎩且x y +的最大值为9,则实数m =(A )2- (B )1- (C )1 (D )24.(2009年陕西理11)若x ,y 满足约束条件1122x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩,目标函数2z ax y =+仅在点(1,0)处取得最小值,则a 的取值范围是(A) (1-,2 ) (B) (4-,2 ) (C) (4,0]- (D) (2,4)-5.(2009年山东理12) 设x ,y 满足约束条件⎪⎩⎪⎨⎧≥≥≥+-≤--0,002063y x y x y x ,若目标函数z=ax+by (a>0,b>0)的值是最大值为12,则23a b+的最小值为( ).A.625B.38C. 311 D. 4 6.(2011年高考浙江卷理科5)设实数,x y 满足不等式组250270,0x y x y x +->⎧⎪+->⎨⎪≥≥⎩,y 0,若,x y 为整数,则34x y +的最小值是(A )14 (B )16 (C )17 (D )197.(2011年高考安徽卷理科4)设变量,x y 满足1,x y +≤则2x y +的最大值和最小值分别为 (A)1,-1 (B)2,-2 (C)1,-2 (D)2,-18. (2011年高考湖南卷理科7)设,1>m 在约束条件⎪⎩⎪⎨⎧≤+≤≥1y x mx y x y 下,目标函数my x z +=的最大值小于2,则m 的取值范围为A.()21,1+B. ()+∞+,21 C. ()3,1 D. ()+∞,39. (2011年高考广东卷理科5)已知平面直角坐标系xOy 上的区域D由不等式组02x y x ⎧≤≤⎪≤⎨⎪≤⎩给定.若M(x ,y)为D 上动点,点A 的坐标为,1).则z OM OA =的最大值为( )A.B. C.4 D.310.(2011年高考湖北卷理科8)已知向量(,3),(2,)a x z b y z =+=-,且a b ⊥,若,x y 满足不等式1x y +≤,则z 的取值范围为A.[—2,2]B. [—2,3]C. [—3,2]D. [—3,3]11.(2011年高考福建卷理科8)已知O 是坐标原点,点A (-1,1)若点M (x,y )为平面区域21y 2x y x +≥⎧⎪≤⎨⎪≤⎩,上的一个动点,则OA ·OM的取值范围是A .[-1.0]B .[0.1]C .[0.2]D .[-1.2]12. (2011全国新课标13)若变量,x y 满足约束条件329,69,x y x y ≤+≤⎧⎨≤-≤⎩则2z x y =+的最小值为 。
高一数学必修4(新人教)课后强化训练(含详解):第一、二章综合能力检测题.docx
第一、二章综合能力检测题本试卷分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.点C 在线段AB 上,且AC →=25AB →,若AC →=λBC →,则λ等于( ) A.23 B.32 C .-23D .-32[答案] C[解析] 由AC →=25AB →知,|AC →||BC →|=23,且方向相反,∴AC →=-23BC →,∴λ=-23.2.要想得到函数y =sin ⎝ ⎛⎭⎪⎫x -π3的图象,只须将y =cos x 的图象( )A .向右平移π3个单位B .向左平移π3个单位C .向右平移5π6个单位D .向左平移5π6个单位[答案] C[解析] ∵y =sin ⎝ ⎛⎭⎪⎫x -π3=cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫x -π3 =cos ⎝⎛⎭⎪⎫5π6-x =cos ⎝ ⎛⎭⎪⎫x -5π6,∴将y =cos x 的图象向右移5π6个单位可得到y =sin ⎝⎛⎭⎪⎫x -π3的图象.3.设e 1与e 2是不共线向量,a =k e 1+e 2,b =e 1+k e 2,若a ∥b 且a ≠b ,则实数k 的值为( ) A .1 B .-1 C .0 D .±1 [答案] B[解析] ∵a ∥b ,∴存在实数λ,使a =λb (b ≠0), ∴k e 1+e 2=λ(e 1+k e 2),∴(k -λ)e 1=(λk -1)e 2,∵e 1与e 2不共线,∴⎩⎪⎨⎪⎧k -λ=0λk -1=0,∴λ=k =±1,∵a ≠b ,∴k ≠1.[点评] e 1与e 2不共线,又a ∥b ,∴可知1k =k1,∴k =±1,∵a ≠b ,∴k =-1.一般地,若e 1与e 2不共线,a =m e 1+n e 2,b =λe 1+μe 2,若a ∥b ,则有m λ=n μ. 4.若sin θ=m ,|m |<1,-180°<θ<-90°,则tan θ等于( ) A.m1-m2B .-m1-m2C .±m1-m2D .-1-m2m[答案] B[解析] ∵-180°<θ<-90°, ∴sin θ=m <0,tan θ>0, 故可知tan θ=-m 1-m2.5.△ABC 中,AB →·BC →<0,BC →·AC →<0,则该三角形为( ) A .锐角三角形B .直角三角形C .钝角三角形D .不能确定 [答案] C[解析] 由AB →·BC →<0知,∠ABC 为锐角;由BC →·AC →<0知∠ACB 为钝角,故选C. 6.设α是第二象限的角,且⎪⎪⎪⎪⎪⎪cos α2=-cos α2,则α2所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 [答案] C[解析] ∵α为第二象限角,∴α2为第一或三象限角,∵⎪⎪⎪⎪⎪⎪cos α2=-cos α2,∴cos α2≤0,∴选C.7.已知点A (2,-1),B (4,2),点P 在x 轴上,当PA →·PB →取最小值时,P 点的坐标是( ) A .(2,0) B .(4,0) C.⎝⎛⎭⎪⎫103,0D .(3,0) [答案] D[解析] 设P (x,0),则PA →=(2-x ,-1),PB →=(4-x,2),PA →·PB →=(2-x )(4-x )-2=x 2-6x +6=(x -3)2-3,当x =3时,取最小值-3,∴P (3,0).8.O 是△ABC 所在平面内一点,且满足|OB →-OC →|=|OB →+OC →-2OA →|,则△ABC 为( ) A .等腰三角形 B .直角三角形 C .等边三角形 D .等腰直角三角形 [答案] B[解析] ∵|OB →-OC →|=|OC →+OB →-2OA →|,∴|CB →|=|AB →+AC →|,由向量加法的平行四边形法则知,以AB 、AC 为邻边的平行四边形两对角线长度相等,∴AB →⊥AC →.9.如图是函数f (x )=A sin ωx (A >0,ω>0)一个周期的图象,则f (1)+f (2)+f (3)+f (4)+f (5)+f (6)的值等于( )A. 2B.22C .2+ 2D .2 2 [答案] A[解析] 由图知:T =8=2πω,∴ω=π4,又A =2,∴f (x )=2sin π4x ,∴f (1)+f (2)+f (3)+f (4)+(5)+f (6)=2sin π4+sin 2π4+sin 3π4+sin 4π4+sin 5π4+sin 6π4=2sin 3π4= 2.[点评] 观察图象可知f (x )的图象关于点(4,0)中心对称,故f (3)+f (5)=0,f (2)+f (6)=0,又f (4)=0,故原式=f (1)= 2.10.已知y =A sin(ωx +φ)在同一周期内,x =π9时有最大值12,x =4π9时有最小值-12,则函数的解析式为( )A .y =2sin ⎝ ⎛⎭⎪⎫x 3-π6B .y =12sin ⎝ ⎛⎭⎪⎫3x +π6C .y =2sin ⎝ ⎛⎭⎪⎫3x -π6D .y =12sin ⎝ ⎛⎭⎪⎫3x -π6[答案] B[解析] 由条件x =π9时有最大值12,x =4π9时有最小值-12可知,A =12,T 2=4π9-π9,∴T =2π3,∴ω=3,∴y =12sin(3x +φ),将⎝ ⎛⎭⎪⎫π9,12代入得,12=12sin ⎝ ⎛⎭⎪⎫π3+φ, ∴π3+φ=2k π+π2(k ∈Z ),∴φ=2k π+π6, 取k =0知选B.11.设点O 是面积为4的△ABC 内部一点,且有OA →+OB →+2OC →=0,则△AOC 的面积为( ) A .2 B .1 C.12 D.13 [答案] B[解析] 如图,以OA 、OB 为邻边作▱OADB ,则OD →=OA →+OB →,结合条件OA →+OB →+2OC →=0知,OD →=-2OC →,设OD 交AB 于M ,则OD →=2OM →,∴OM →=-OC →, 故O 为CM 的中点,∴S △AOC =12S △CAM =14S △ABC =14×4=1.12.已知sin α+cos α=713 (0<α<π),则tan α=( )A .-512B .-125C.512D .-125或-512[答案] B[解析] 解法一:∵sin α+cos α=713,0<713<1,0<α<π,∴π2<α<π,∴sin α>0,cos α<0,且|sin α|>|cos α|, ∴tan α<0且|tan α|>1,故选B.解法二:两边平方得sin αcos α=-60169,∴tan αtan 2α+1=-60169,∴60tan 2α+169tan α+60=0, ∴(12tan α+5)(5tan α+12)=0, ∴tan α=-125或-512,∵0<α<π,sin α+cos α=713>0,∴tan α=-125. 第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上) 13.已知扇形的圆心角为72°,半径为20cm ,则扇形的面积为________. [答案] 8πcm 2[解析] ∵72°=π180×72=2π5,∴l =2π5×20=8π,S =12l ·r =12×8π×20=80π(cm 2).14.已知a =(3,4),b =(2,m )且a 与b 夹角为锐角,则m 的取值范围是________. [答案] m >-32且m ≠83[解析] a ·b =6+4m >0,∴m >-32,又当a 与b 同向时,23=m 4,∴m =83,故m >-32且m ≠83.15.集合A ={x |k π-π4<x <k π+π4,k ∈Z },B ={x |sin x >12},则A ∩B =________.[答案] {x |π6+2k π<x <π4+2k π,k ∈Z }∪{x |3π4+2k π<x <5π6+2k π,k ∈Z }[解析] B ={x |π6+2k π<x <5π6+2k π,k ∈Z }.如图可求A ∩B .16.已知θ为第三象限角,1-sin θcos θ-3cos 2θ=0,则5sin 2θ+3sin θcos θ=________. [答案]265[解析] ∵1-sin θcos θ-3cos 2θ=0, ∴sin 2θ-sin θcos θ-2cos 2θ=0, ∴(sin θ-2cos θ)(sin θ+cos θ)=0, ∵θ为第三象限角,∴sin θ+cos θ<0, ∴sin θ=2cos θ,∴tan θ=2,∴5sin 2θ+3sin θcos θ=5tan 2θ+3tan θtan 2θ+1=265. 三、解答题(本大题共6个小题,共74分,解答应写出文字说明,证明过程或演算步骤) 17.(本题满分12分)已知cos ⎝⎛⎭⎪⎫θ+π2=-12,求cos(θ+π)sin ⎝ ⎛⎭⎪⎫π2-θ[]cos(3π-θ)-1+cos(θ-2π)cos(-θ)·cos(π-θ)+sin ⎝ ⎛⎭⎪⎫θ+5π2的值.[解析] ∵cos ⎝⎛⎭⎪⎫θ+π2=-12,∴sin θ=12,原式=-cos θcos θ(-cos θ-1)+cos θcos θ·(-cos θ)+cos θ=11+cos θ+11-cos θ=2sin 2θ=8. 18.(本题满分12分)已知A (-1,2),B (2,8). (1)若AC →=13AB →,DA →=-23AB →,求CD →的坐标;(2)设G (0,5),若AE →⊥BG →,BE →∥BG →,求E 点坐标. [解析] (1)∵AB →=(3,6),AC →=13AB →=(1,2),DA →=-23AB →=(-2,-4),∴C (0,4),D (1,6),∴CD →=(1,2).(2)设E (x ,y ),则AE →=(x +1,y -2),BE →=(x -2,y -8),∵BG →=(-2,-3),AE →⊥BG →,BE →∥BG →,∴⎩⎪⎨⎪⎧-2(x +1)-3(y -2)=0-3(x -2)+2(y -8)=0,∴⎩⎪⎨⎪⎧x =-2213y =3213.∴E 点坐标为⎝ ⎛⎭⎪⎫-2213,3213.19.(本题满分12分)在▱ABCD 中,点M 在AB 上,且AM =3MB ,点N 在BD 上,且BN →=λBD →,C 、M 、N 三点共线,求λ的值.[证明] 设AB →=e 1,AD →=e 2,则BD →=e 2-e 1, BN →=λBD →=λ(e 2-e 1),MB →=14AB →=14e 1,BC →=AD →=e 2,∴MC →=MB →+BC → =14e 1+e 2, MN →=MB →+BN →=14e 1+λ(e 2-e 1)=λe 2+⎝ ⎛⎭⎪⎫14-λe 1,∵M 、N 、C 共线,∴MN →与MC →共线,∵e 1与e 2不共线,∴14-λ14=λ1,∴λ=15.20.(本题满分12分)是否存在实数a ,使得函数y =sin 2x +a cos x -1+58a 在闭区间⎣⎢⎡⎦⎥⎤0,π2上最大值为1?若存在,求出对应的a 值,若不存在,说明理由.[解析] y =-cos 2x +a cos x +5a 8=-(cos x -a2)2+a 24+5a8,∵0≤x ≤π2,∴0≤cos x ≤1,∵最大值为1,∴(Ⅰ)⎩⎪⎨⎪⎧0≤a 2≤1a 24+5a8=1或(Ⅱ)⎩⎪⎨⎪⎧a2<05a8=1或(Ⅲ)⎩⎪⎨⎪⎧a2>1-1+a +5a8=1,由(Ⅰ)解得a =89-54,(Ⅱ)(Ⅲ)无解, ∴a =89-54. [点评] 此类问题一般把cos x (或sin x )看成未知数整理为二次函数,然后由x 的范围,得出cos x (或sin x )的取值范围A 后,分为①A 在对称轴左侧(或右侧),用单调性讨论;②对称轴在A 内,在顶点处取得最值.试一试解答下题:是否存在实数λ,使函数f (x )=-2sin 2x -4λcos x +1⎝ ⎛⎭⎪⎫0≤x ≤π2的最小值是-32?若存在,求出对应的λ值,若不存在,试说明理由.答案为λ=58或12.21.(本题满分12分)(1)角α的终边经过点P (sin150°,cos150°),求tan α. (2)角α的终边在直线y =-3x 上,求sin α、cos α.[解析] (1)∵P ⎝ ⎛⎭⎪⎫12,-32,∴tan α=-3212=- 3.(2)在角α终边上任取一点P (x ,y ),则y =-3x ,P 点到原点距离r =x 2+y 2=10|x |,当x >0时,r =10x ,∴sin α=y r=-3x10x=-31010,cos α=xr=x10x=1010, 当x <0时,r =-10x ,∴sin α=y r =31010,cos α=xr =-1010. 22.(本题满分14分)函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的一段图象如图所示.(1)求f (x )的解析式;(2)求f (x )的单调减区间,并指出f (x )的最大值及取到最大值时x 的集合;(3)把f (x )的图象向左至少平移多少个单位,才能使得到的图象对应的函数为偶函数? [解析] (1)由图知A =3,34T =4π-π4=15π4,∴T =5π,∴ω=25,∴f (x )=3sin ⎝ ⎛⎭⎪⎫25x +φ,∵过(4π,-3),∴-3=3sin ⎝ ⎛⎭⎪⎫8π5+φ,∴8π5+φ=2k π-π2,∴φ=2k π-21π10, ∵|φ|<π2,∴φ=-π10,∴f (x )=3sin ⎝ ⎛⎭⎪⎫25x -π10.& 鑫达捷致力于精品文档 精心制作仅供参考 &鑫达捷 (2)由2k π+π2≤25x -π10≤2k π+3π2得, 5k π+3π2≤x ≤5k π+4π (k ∈Z ), ∴函数f (x )的单调减区间为⎣⎢⎡⎦⎥⎤5k π+3π2,5k π+4π (k ∈Z ). 函数f (x )的最大值为3,取到最大值时x 的集合为{x |x =5k π+3π2,k ∈Z }. (3)解法一:f (x )=3sin ⎝ ⎛⎭⎪⎫2x 5-π10 =3cos ⎣⎢⎡⎦⎥⎤π2-⎝ ⎛⎭⎪⎫2x 5-π10=3cos ⎝ ⎛⎭⎪⎫2x 5-3π5 =3cos ⎣⎢⎡⎦⎥⎤25⎝⎛⎭⎪⎫x -3π2, 故至少须左移3π2个单位才能使所对应函数为偶函数. 解法二:f (x )=3sin ⎝ ⎛⎭⎪⎫2x 5-π10的图象的对称轴方程为25x -π10=k π+π2,∴x =5k π2+3π2,当k =0时,x =3π2,k =-1时,x =-π,故至少左移3π2个单位. 解法三:函数f (x )在原点右边第一个最大值点为2x 5-π10=π2,∴x =3π2,把该点左移到y 轴上,需平移3π2个单位. 解法四:观察图象可知,欲使函数图象左移后为偶函数,由其周期为5π可知,须把⎝ ⎛⎭⎪⎫π4,0点变为⎝ ⎛⎭⎪⎫-5π4,0或把点(4π,-3)变为⎝ ⎛⎭⎪⎫5π2,-3等,可知应左移3π2个单位.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
版权所有:中华资源库 www.ziyuanku.com 3.1.2 一、选择题 1.已知cos(α+β)=45,cos(α-β)=-45,则cosαcosβ的值为( ) A.0 B.45 C.0或45 D.0或±45 [答案] A [解析] 由条件得,cosαcosβ-sinαsinβ=45,
cosαcosβ+sinαsinβ=-45, 左右两边分别相加可得cosα·cosβ=0. 2.设a=sin14°+cos14°,b=sin16°+cos16°,c=62,则a、b、c的大小关系是( ) A.aB.aC.bD.b[答案] B [解析] a=2sin(14°+45°)=2sin59°,
b=2sin(16°+45°)=2sin61°,c=2·32=2sin60°, 由y=sinx在(0°,90°)上单调增知:a3.2sinπ4-x+6sinπ4+x的化简结果是( )
A.22sin5π12+x B.22sinx-5π12 C.22sin7π12+x 版权所有:中华资源库 www.ziyuanku.com
D.22sinx-7π12 [答案] A [解析] 2sinπ4-x+6sinπ4+x
=2sinπ2-π4+x+6sinπ4+x =2cosπ4+x+6sinπ4+x =2212cosπ4+x+32sinπ4+x =22sinπ6cosπ4+x+cosπ6sinπ4+x =22sinπ6+π4+x=22sin5π12+x. 4.若α、β均为锐角,sinα=255,sin(α+β)=35,则cosβ等于( ) A.255 B.2525 C.255或2525 D.-2525 [答案] B [解析] ∵α与β均为锐角,且sinα=255>sin(α+β)=35,∴α+β为钝角, 又由sin(α+β)=35得,cos(α+β)=-45, 由sinα=255得,cosα=55, ∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-45×55+35×255=2525,故选B. 5.若α、β为两个锐角,则( ) A.cos(α+β)>cosα+cosβ B.cos(α+β)C.cos(α+β)>sinα+sinβ D.cos(α+β)版权所有:中华资源库 www.ziyuanku.com
[答案] B [解析] cos(α+β)-(cosα+cosβ)=cosαcosβ-sinαsinβ-cosα-cosβ=cosα(cosβ-1)-sinαsinβ-cosβ ∵α、β是锐角,∴cosβ-1<0,cosβ>0,cosα>0,sinβ>0,sinα>0 ∴cos(α+β)-(cosα+cosβ)<0, ∴cos(α+β)[点评] ∵α、β均为锐角,∴cosβ>0,0∴cosα>cos(α+β),∴cosα+cosβ>cos(α+β).故A错,B对;当α、β很接近于0时,sinα
+sinβ接近于0,cos(α+β)接近于1,故D错,当α=β=π4时,C错. 6.若sin(α-β)cosα-cos(α-β)sinα=m,且β为第三象限角,则cosβ的值为( ) A.1-m2 B.-1-m2 C.m2-1 D.-m2-1 [答案] B [解析] 由条件得,sin[(α-β)-α]=sin(-β) =-sinβ=m,∴sinβ=-m. 又∵β为第三象限角, ∴cosβ=-1-sin2β=-1-m2.
7.若sinα-sinβ=1-32,cosα-cosβ=-12,则cos(α-β)的值是( ) A.12 B.32 C.34 D.1 [答案] B
[解析] ∵sinα-sinβ=1-32,cosα-cosβ=-12,
∴(sinα-sinβ)2+(cosα-cosβ)2=(1-32)2+(-12)2 ∴2-2(cosαcosβ+sinαsinβ)=2-3 版权所有:中华资源库 www.ziyuanku.com
∴cosαcosβ+sinαsinβ=32, 即cos(α-β)=32. 8.若cosαcosβ=1,则sin(α+β)等于( ) A.-1 B.0 C.1 D.±1 [答案] B [解析] ∵cosαcosβ=1, ∴cosα=1,cosβ=1或cosα=-1,cosβ=-1, ∴sinα=0,sinβ=0, ∴sin(α+β)=sinαcosβ+cosαsinβ=0.
9.函数y=2sinπ3-x-cosπ6+x(x∈R)的最小值等于( ) A.-3 B.-2 C.-1 D.-5 [答案] C
[解析] y=2sinπ3-x-cosπ6+x =2cosπ6+x-cosπ6+x =cosx+π6(x∈R). ∵x∈R,∴x+π6∈R,∴ymin=-1. 10.在锐角△ABC中,设x=sinA·sinB,y=cosA·cosB,则x,y的大小关系是( ) A.x≤y B.x<y C.x≥y D.x>y [答案] D
[解析] ∵π>A+B>π2,∴cos(A+B)<0, 版权所有:中华资源库 www.ziyuanku.com
即cosAcosB-sinAsinB<0,∴x>y,故应选D. 二、填空题
11.若cos(α+β)cosα+sin(α+β)sinα=-45,且450°
[答案] -3+4310 [解析] 由已知得cos[(α+β)-α]=cosβ=-45, ∵450°∴sin(60°-β)=32·-45-12×35=-3+4310. 12.已知α、β为锐角,且tanα=23,tanβ=34,则sin(α+β)=________. [答案] 171365 [解析] ∵α为锐角,tanα=23, ∴sinα=213,cosα=313, 同理可由tanβ=34得,sinβ=35,cosβ=45. ∴sin(α+β)=sinαcosβ+cosαsinβ =213×45+313×35=171365. 13.化简(tan10°-3)·cos10°sin50°=________. [答案] -2 [解析] (tan10°-3)·cos10°sin50°
=(tan10°-tan60°)·cos10°sin50° =sin10°cos10°-sin60°cos60°·cos10°sin50° =sin10°·cos60°-cos10°·sin60°cos10°·cos60°·cos10°sin50° =sin(-50°)cos60°·1sin50°=-sin50°12·1sin50°=-2.
14.函数y=cosx+cosx+π3的最大值是________. 版权所有:中华资源库 www.ziyuanku.com
[答案] 3 [解析] 法一:y=cosx+π3-π3+cosx+π3 =cosx+π3·cosπ3+sinx+π3sinπ3+cosx+π3 =32cosx+π3+32sinx+π3 =332cosx+π3+12sinx+π3 =3cosπ6-x-π3=3cosx+π6≤3. 法二:y=cosx+cosxcosπ3-sinxsinπ3 =32cosx-32sinx=332cosx-12sinx =3cosx+π6, 当cosx+π6=1时,ymax=3. 三、解答题 15.已知π2
[解析] ∵π2∴π∴sin(α-β)=1-cos2(α-β)=1-12132=513. ∴cos(α+β)=-1-sin2(α+β) =-1--352=-45. 则sin2α=sin[(α+β)+(α-β)] =sin(α+β)cos(α-β)+cos(α+β)sin(α-β)
=-35×1213+-45×513=-5665.
16.求证:sin(2α+β)sinα-2cos(α+β)=sinβsinα. [解析] sin(2α+β)-2cos(α+β)sinα =sin[(α+β)+α]-2cos(α+β)sinα =sin(α+β)cosα+cos(α+β)sinα-2cos(α+β)sinα
