第11章典型例题精解
第11章 网络计划与图解评审法习题详解习题.doc

第11章 网络计划与图解评审法习题详解(习题)
11. 1根据表11-1的给定条件,绘制PERT 网络图 表 11-1
(a)
作业代号
紧前作业
无
偽
a 3 a 2
* 无
X
C
1
a x ,
b 、
C2
q, a?, b? C
3
C2, Q3,
方3 a x
(b)
作业代号 紧前作业 A 无 B 无 c
无
D A,B
E B
F B
G F, C
H B
I E, H
J E, H
K C, D, F, J
L K M
L, I, G
(c)
作业代号 紧前作业 A 无 B 无
c B D c E A, D F D G A, D H E I G, H J I K G L I.K M
L
11. 2试根据表11-2给定的条件,绘制PERT 网络图
表 11-2
F D, E P J,L
G A Q I
H E,G R P,Q
I E, H s 0, R
J F
11. 3分别计算下列PERT网络图(见图11-1 (a)、(b))中各作业的①最开始与最早结束时间;②最迟开始与最迟结束时间;③总时差与自由时差;④找出关健路线。
图11-1
11.4已知下列资料
要求:(1)绘制网络图;
(2)用图上计算法计算各项时间参数(r除卜);
(3)确定关健路线。
11.5已知下列资料
要求:绘制图络图;
(2)计算各项时间参数;
(3 )确定关健路线。
第十一章课后题及答案(邱俊)

十一章习题及答案11-1. 举出日常生活中和机械工程中应用飞轮调速的例子,并说明其原理。
飞轮调速原理:是利用飞轮具有的储存与释放动能的功能。
飞轮具有较大的转动惯量,在机械系统获得盈功时,吸收储存多余的能量,而在出现亏功时释放其能量,以弥补能量的不足,从而使机械系统的角速度变化幅度得以缓减,即达到调节作用。
11-2. 设起重机的电动机特性曲线可近似用抛物线代替,若其等效驱动力矩为21450.34040.01ed M ωω=--,等效阻力矩和等效转动惯量为常数,分别为223er M N m =, 2e kgm1J = ,若电动机在t 0=10sec 的角速度为0100/rad s ω=。
试分析电机主轴从t 0开始的角速度ω与角加速度ε随时间t 的变化关系。
解:由于()()ed er ed M M J dtωωω-=,将式中变量分离后,得/[()()]e ed er dt J d M M ωωω=-积分得 0()()e e d e rd t t J M Mωωωωω=+-⎰2100101450.34040.01223d t ωωωω=+---⎰()10010 1.154arctan 0.0120.196t ωω=-+162.390.9t a n (/t ω=-21450.34040.01223780.3404(162.390.9tan(/1.154))0.01(162.390.9tan(/1.154))d dtt t ωεωω==---=----31.85tan(0.867)21.1t ε=+11-3. 牛头刨床主运动机构中含一导杆机构,如图11.18所示。
已知2100l m m =,当AB AC⊥时,430ϕ=︒,导杆4对轴C 的转动惯量20.08C J kg m =⋅,其他构件的质量和转动惯量忽略不计;作用在导杆4的阻力矩为410M N m =⋅。
若取曲柄2为等效构件,求该机构的等效阻力矩er M 和等效转动惯量e J 。
第11章(高斯定理及安培环路定理)习题答案

ò ×
S
ò
S
= 0. ”这个推理正确吗? [ B 不一定要等于零 ] 答:不正确, B d S 各自有不同的方向,B 不一定要等于零 116 如图,在一圆形电流 I 所在的平面内,选取一个同心圆形闭合回路 L,则由安培 环路定理可知 (A) (B) I L O 思考题 116 图
q 1 1 ( - ) ] 4 pe 0 r R
解;
U 1 =
q 4 peo r
+
Q 4 peo R
U 2 =
q + Q 4 peo R
U1-U2 =
q 1 1 ( - ) 4 pe 0 r R
117 [
已 知 某 静 电 场 的 电 势 分 布 为 U = 8x + 12x2 y - 20y2 (SI) , 求 场 强 分 布 E .
B r r U C = U C - U B = ò E × d l = C
ò 4 pe r
o
2
115 两块面积均为 S 的金属平板 A 和 B 彼此平行放置,板间距离为 d(d 远小于板的 线度) , 设 A 板带有电荷 q1, B 板带有电荷 q2, 求 AB 两板间的电势差 UAB. [
(1)dq =
q dl 2 L
U = ò dU = ò
dq q q x + L = ò dl = ln 4pe o ( x - l ) 4pe o 2 L ( x - l ) 8pL e o x - L
(2)E= -
¶u q 1 1 1 q r = ( ) = i 2 ¶x 8p L e o x - L x + L 4 pe 0 x 2 - L
最新第11章练习题+答案
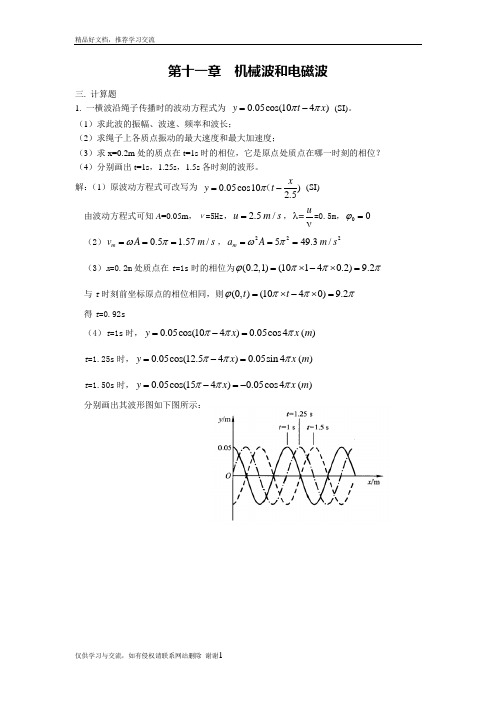
第十一章 机械波和电磁波三. 计算题1. 一横波沿绳子传播时的波动方程式为 0.05cos(104)y t x ππ=- (SI)。
(1)求此波的振幅、波速、频率和波长;(2)求绳子上各质点振动的最大速度和最大加速度;(3)求x=0.2m 处的质点在t=1s 时的相位,它是原点处质点在哪一时刻的相位? (4)分别画出t=1s ,1.25s ,1.5s 各时刻的波形。
解:(1)原波动方程式可改写为 0.05cos10)2.5xy t =-π( (SI) 由波动方程式可知A =0.05m ,ν=5Hz , 2.5/u m s =,u=λν=0.5m ,00ϕ=(2)0.5 1.57/m v A m s ωπ===,222549.3/m a A m s ωπ===(3)x =0.2m 处质点在t =1s 时的相位为(0.2,1)(10140.2)9.2ϕπππ=⨯-⨯= 与t 时刻前坐标原点的相位相同,则(0,)(1040)9.2t t ϕπππ=⨯-⨯= 得t =0.92s(4)t =1s 时,0.05cos(104)0.05cos 4()y x x m πππ=-=t =1.25s 时,0.05cos(12.54)0.05sin 4()y x x m πππ=-= t =1.50s 时,0.05cos(154)0.05cos 4()y x x m πππ=-=-分别画出其波形图如下图所示:图42. 设有一平面简谐波 0.02cos 2()0.010.3t xy π=- (SI)。
(1)求其振幅、波长、频率和波速。
(2)求x=0.1m 处质点振动的初相位。
解:(1)由波动方程有A =0.02m ,λ=0.3m ,ν=100Hz ,00ϕ=,且30/u m s λν==(2)00.100.122()0.010.33x πϕπ==-=-3. 已知一沿x 轴正向传播的平面余弦波在t=1/3s 时的波形如图4所示,且周期T=2s 。
微生物学习题及答案 第十一章

136第ll章微生物的生态四、习题填空题1.从__________,__________,__________,__________生境中可以分离到嗜热微生物;从__________,__________生境中可以分离到嗜冷微生物;从__________,__________生境中可分离到嗜酸微生物,__________,__________,生境中可分离到嗜碱微生物;从__________,__________和__________生境中可分离到嗜盐微生物。
2.磷的生物地球化学循环包括3种基本过程:__________,__________,__________。
3.微生物种群相互作用的基本类型包括:__________,__________,__________,__________,__________,__________,__________和__________。
4.嗜热细菌耐高温的__________使DNA体外扩增技术得到突破,为__________技术的广泛应用提供基础。
5.微生物推动的氮循环实际上是氮化合物的氧化还原反应,其循环过程包括__________,__________,__________和__________。
6.按耐热能力的不同,嗜热微生物可被分成5个不同类群__________,__________,__________,__________ 和__________。
7.有机污染物生物降解过程中经历的主要反应包括__________,__________,__________,和__________。
8.评价有机化合物生物降解性的基本试验方法是__________和__________。
9.污水处理按程度可分为__________,__________和__________。
lO.汞的微生物转化主要包括3个方面__________,__________和__________。
11章12章-例题讲解

11章12章-例题讲解D解答过程:依据GB 50057-1994(2000版)《建筑物防雷设计规范》,表6.4.4。
2、无电涌出现时为高阻抗,随着电涌电流和电压的增加,阻抗跟着连续变小,通常采用压敏电阻、抑制二级管做这类SPD的组件,这种SPD应属于下列哪些类型?A.电压开关型SPD;B.限压型SPD;C.组合型SPD;D.短路开关型SPD。
答案【 B 】解答过程:依据同上,附表8.1倒数第2行。
3、防雷规范中为防雷击电磁脉冲,将需要保护的空间划分为不同的防雷区(LPZ)。
如一栋有防雷装置的高层公共建筑物的外窗,应将其划在下述的哪个区是正确的?A.LPZ0A区;B.LPZ0B区;C.LPZ1区;D.LPZ2区。
答案【 A 】解答过程:依据同上,第6.2.1条一款。
高层建筑的外窗高度超过滚球半径时,可能遭到直接雷击。
(按:本题已知条件不够明确。
应给出建筑物的防雷分类和高度。
)【案例三05】某企业变电所,进线电压35kV,经降压变压器后,以10kV向厂区高压电气设备及用户供电,再经10/0.4kV配电变压器向附近低压用户供电。
1、现已知10kV系统全部以电缆馈电,其中截面95mm2的电缆总长15km,截面120mm2的长10km,试计算10kV系统单相接地电容电流最接近下列那些数值:A. 21AB. 27AC. 30AD. 35A答案【 C 】解答过程:依据《工业与民用配电设计手册》,P152表4-20及表4-20:95mm2电缆的接地电容电流为1.0 A/km×15=15A;120mm2电缆的接地电容电流为1.1 A/km×10=11A;变电所增加的接地电容电流值10kV为16%;共计:(15+11)1.16=30A。
(按:也可用简化公式4-41估算。
10kV 系统单相接地电容电流为()251015101.01.0=+⨯⨯=l U n A ;计入变电所增加16%,总接地电容电流29)16.1(25=⨯A 。
第11章 利润最大化
第11章 利润最大化1.约翰割草服务公司是一个小厂商,是一个价格接受者(即)。
修剪草坪的现MR P =行市场价格为每亩20美元,约翰公司的成本为:20.11050C q q =++其中,是约翰公司选择的每天修剪的亩数。
q a .为达到利润最大化,约翰公司将选择修剪多少亩草坪?b .计算约翰公司每日的最大利润额。
c .用图形显示这些结果并画出约翰公司的供给曲线。
解:a .约翰公司的利润函数为:()22200.110500.11050Pq C q q q q q π=-=-++=-+-利润最大化的一阶条件为:,解得。
且,故为d 0.2100d q q π=-+=*50q =22d 0.20d qπ=-<实现利润最大化,约翰公司每天将选择修剪50亩草坪。
b .约翰公司每天的最大利润额为:(美元)220.110500.150105050200q q π=-+-=-⨯+⨯-=c .由于约翰公司是价格接受者,则有,此为约翰公司的供给曲0.210P MR MC q ===+线。
约翰公司的供给曲线如图11-1所示。
图11-1 约翰公司的供给曲线2.环球小器械公司在它设在内华达州的工厂生产高质量的小器械,销往世界各地。
小器械的总成本函数为。
20.25C q =小器械的需求地只有澳大利亚(其需求曲线为)与拉普兰(其需求曲线为A P q 2100-=)。
如果该公司能够控制它在每一个市场上的供给量,为了使总的利润最大化,L P q 4100-=它应该在每个地方各出售多少产品?在每个地方以什么价格出售?解:假设该公司在澳大利亚销量为,在拉普兰的销量为。
A q L q 该公司的总成本为:,,,因此()220.250.25A L C q q q ==+500.5A A P q =-250.25L L P q =-可得该公司的总利润函数为:()22,0.75500.50.525A L A A L L A A A L L L q q P q P q C q q q q q q π=+-=-+--+利润最大化的一阶条件为:1.5500.50A L Aq q q π∂=-+-=∂250.50L A Lq q q π∂=-+-=∂解得:,。
第十一章习题
表示三面焊接,单面角焊缝,焊角尺寸为5, 有4条相同的角焊接。
表示点焊缝,焊点直径5,焊点的间距15,焊 点至板边的间距40 。
第十一章 焊接图
焊接图
3.根据左图中的焊缝形式和尺寸,在右图上 标注出相应的焊接符号。
答案
第64页
第十一章 焊接图
焊接图
1.解释下列焊接符号的含义
答案
表示用手工电弧焊,V形坡口,坡口角度为60°, 根部间隙为3,有10段焊缝,焊缝长度为15。
表示在现场装配时进行角焊接,且焊角尺寸 为8 ,有2条相同的角焊接。
表示双面角焊接,焊角尺寸为10,有6段断续 双面角焊缝,焊缝长度30,断续焊缝的间距10。
高考一轮复习 基础知识与典型例题 第十一章 函数极限与导数
知识网数学归纳法、数列的极限与运算1.数学归纳法:(1)由特殊事例得出一般结论的归纳推理方法,通常叫做归纳法.归纳法包含不完全归纳法和完全归纳法.①不完全归纳法:根据事物的部分(而不是全部)特殊事例得出一般结论的推理方法.②完全归纳法: 根据事物的所有特殊事例得出一般结论的推理方法数学归纳法常与不完全归纳法结合起来使用,用不完全归纳法发现规律, 用数学归纳法证明结论.(2)数学归纳法步骤:①验证当n取第一个n时结论()P n成立;②由假设当n k=(,k N k n+∈≥)时,结论()P k成立,证明当1n k=+时,结论(1)P k+成立;根据①②对一切自然数n n≥时,()P n都成立.2.数列的极限(1)数列的极限定义:如果当项数n无限增大时,无穷数列{}n a的项n a无限地趋近于某个常数a(即na a-无限地接近于),那么就说数列{}na以a为极限,或者说a是数列{}na的极限.记为lim nna a→∞=或当n→∞时,na a→.(2)数列极限的运算法则: 如果{}n a、{}n b的极限存在,且lim,limn nn na ab b→∞→∞==,那么lim()n nna b a b→∞±=±;lim();n nna b a b→∞⋅=⋅lim(0)nnna abb b→∞=≠特别地,如果C是常数,那么lim()lim limn nn n nC a C a Ca→∞→∞→∞⋅=⋅=.⑶几个常用极限: ①limnC C→∞=(C为常数)②lim0nan→∞=k(,a k均为常数且N*∈k)③(1)1lim0(1)(1或1)不存在nnqq qq q④首项为1a,公比为q(1q<)的无穷等比数列的各项和为lim1nnaSq→∞=-.注:⑴并不是每一个无穷数列都有极限.⑵四则运算法则可推广到任意有限个极限的情况,但不能推广到无限个情况.数学归纳法、数列的极限与运算例 1. 某个命题与正整数有关,若当)(*Nkkn∈=时该命题成立,那么可推得当=n1+k时该命题也成立,现已知当5=n时该命题不成立,那么可推得()(A)当6=n时,该命题不成立 (B)当6=n时,该命题成立(C)当4=n时,该命题成立 (D)当4=n时,该命题不成立例2. 用数学归纳法证明:“)1(111212≠--=++++++aaaaaann”在验证1=n时,左端计算所得的项为 ( ) (A)1 (B)a+1 (C)21aa++ (D)321aaa+++例3.2221lim2nnn→∞-+等于( ) (A)2 (B)-2 (C)-21(D)21例4. 等差数列中,若nnSLim∞→存在,则这样的数列( )(A)有且仅有一个 (B)有无数多个(C)有一个或无穷多个 (D)不存在例5. lim(1)nn n n→∞+-等于( ) (A)13(B)0 (C)12(D)不存在例6. 若2012(2)n nnx a a x a x a x+=++++,12n nA a a a=+++,则2lim83nnnAA→∞-=+( )(A)31- (B)111 (C)41 (D)81-例7. 在二项式(13)nx+和(25)nx+的展开式中,各项系数之和记为,,n na b n是正整数,则2lim34n nnn na ba b→∞--= .例8. 已知无穷等比数列{}n a的首项Na∈1,公比为q,且nnaaaSNq+++=∈21,1,且3lim=∞→nnS,则=+21aa _____ .例9. 已知数列{na}前n项和11(1)n n nS bab=-+-+, 其中b是与n无关的常数,且0<b<1,若limnnS→∞=存在,则limnnS→∞=________.例10. 若数列{na}的通项21na n=-,设数列{nb}的通项11nnba=+,又记nT是数列{nb}的前n项的积.(Ⅰ)求1T,2T,3T的值;(Ⅱ)试比较nT与1+na的大小,并证明你的结论.例 1.D 2.C 例 3.A 例 4.A例 5.C将分子局部有理化,原式=11limlim21111n n nn n n→∞→∞==++++例6.A 例7.12 例8. 38例9.1 例10(见后面) 函数的极限及函数的连续性1.函数的极限(1) 函数的六种极限定义:①lim ()x f x a →+∞=的意义是当自变量x 取正值并且无限增大时,()f x 无限趋进于一个常数a ;②lim ()x f x a →-∞=的意义是当自变量x 取负值并且绝对值无限增大时,()f x 无限趋进于一个常数a ;③lim ()lim (),lim ()x x x f x a f x f x →∞→+∞→-∞=⇔都存在,且等于a ;④0lim ()x x f x a +→=的意义是当自变量x 从0x x =右侧(即0x x >)无限趋近于常数0x (但不等于0x )时,如果函数()f x 无限趋近于一个常数a ;⑤0lim ()x x f x a -→=的意义是当自变量x 从0x x =右侧(即0x x <)无限趋近于常数0x (但不等于0x )时,如果函数()f x 无限趋近于一个常数a ;⑥0lim ()x x f x a +→=的意义是当自变量x 无限趋近于常数0x (但不等于0x )时,如果函数()f x 无限趋近于一个常数a ; 注: 0lim ()x x f x a →=⇔0lim ()x x f x -→,0lim ()x xf x +→都存在,且等于a ;(2)函数极限的运算法则: 如果0lim ()x xf x →,0lim ()x xg x →存在,且0lim ()x x f x a →=,0lim ()x x g x b →=那么[]0lim ()()x x f x g x a b →±=±,[]0lim ()()x x f x g x ab →=,0()lim (0)()x x f x a b g x b→=≠.这些法则对于其他情况仍然成立.⑶几个常用极限:①1lim 0n x→∞=;②lim 0x x a →+∞=(0<a <1);lim 0x x a →-∞=(a >1)③0sin lim 1x x x→=0lim 1sin x x x→⇒=2.函数的连续性:(1)定义:如果函数()y f x =在点0x x =处及其附近有定义,而且00lim ()()x xf x f x →=,就说函数()f x 在点0x 处连续.(2)函数()y f x =在点0x x =处连续的充要条件是00lim ()()x x f x f x →=.注:等式0lim ()()x x f x f x →=的含义有三点:①()f x 在点0x x =处及其附近有定义; ②0lim ()x x f x →存在;③()f x 在点0x 处的极限值等于这一点的函数值0()f x .(3) “ 函数()y f x =在点0x 处不连续”就说()y f x =的图象在点0x x =处间断. (4) 函数()y f x =在区间上连续:①若函数()y f x =在开区间(,)a b 内每一点处连续,就说函数()y f x =在开区间(,)a b 内连续; ②若函数()y f x =在开区间(,)a b 内每一点处连续,并且lim ()()x a f x f a +→=,lim ()()x bf x f b -→=就说函数()y f x =在闭区间[],a b 上连续. (5)初等函数在其定义域内每一点处都连续.(6) 连续函数的性质:闭区间[],a b 上的连续函数()f x 的图象是坐标平面上的一条有始点(,())a f a 和终点(,())b f b 的连续曲线.它有如下性质:①(最大值和最小值定理)若()f x 是闭区间[],a b 上的连续函数,则()f x 在闭区间[],a b 上有最大、最小值.②零点定理:若()f x 是闭区间[],a b 上的连续函数,且()()0f a f b ⋅<,则方程()0f x =在区间(,)a b 上至少有一个实数解.③介值定理:设函数()f x 在闭区间[,]a b 上连续,且在这区间的端点取不同函数值,(),()f a A f b B ==,那么对于,A B 之间任意的一个数C ,在开区间(,)a b 内至少有一点ξ,使得()f C ξ=(a <ξ<b ).函数的极限及函数的连续性例11.2112lim 11x x x →⎛⎫- ⎪--⎝⎭的值等于()11()()0()()22A B C D -不存在 例12. 011limx x x →+-= ( ) (A )21(B )1 (C )2 (D)0例13. 已知211lim31x ax bx x →++=-,则b 的值为 ( ) (A )4 (B )-5 (C )-4 (D)5 例14. 极限0lim ()x x f x →存在是函数()f x 在点0x x =处连续的( )(A)充分而不必要的条件 (B)必要而不充分的条件 (C)充要条件 (D)既不充分也不必要的条件例15. 如果 0() 0x e x f x x a x ⎧<=⎨+⎩≥是连续函数,则a 等于( )(A)-1(B)0(C)1 (D)2例16. 设函数)(x f 在1=x 处连续,且21)(lim 1=-→x x f x ,则)1(f 等于( )(A)1- (B)0 (C)1 (D)2例17.函数1(1)()0(1)(1)x x f x x x x ⎧>⎪⎪==⎨⎪<⎪⎩在x =1处不连续是因为( )(A)f (x )在x =1处无定义 (B)1lim →n f (x )不存在(C)1lim →n f (x )≠f (1)(D)+→1lim n f (x )≠1lim n -→f (x )例18. 为使函数f x xx()=+-112在x =-1处连续,则定义f ()-=1__________. 例19. 设*,n N ∈若函数1()lim n nn x f x x →∞+=,则()f x 的定义域为 .例20. 已知sin ,0()0,0cos 1,0a x b x f x x x x +>⎧⎪==⎨⎪+<⎩,当a ,b 取值何值时,0lim ()x f x →存在,其值为多少.例11. 211212111111.lim ..111111112x x C x x x x x x x x →-⎛⎫⎛⎫-=-=⋅=--=- ⎪ ⎪---+-+++⎝⎭⎝⎭而选 例12.A 例13.B 例14B.例15.C 例16.B 例17.C 例18.12例19. (,1)[1,)-∞-+∞例20(见后面)导数1.曲线的切线和切线的斜率:曲线在点00(,)P x y 处的切线,是指曲线上点P 的邻近点00(,)x x y y +∆+∆Q 沿曲线逐渐向点P 接近时,割线P Q 的极限位置所在的直线.根据切线的定义,切线的斜率应通过极限过程求得,即0tan limx y xα∆→∆=∆k =.2.瞬时速度: 非匀速直线运动物体在时刻t 的临近时间间隔t ∆内的平均速度v (v =st ∆∆),当0t ∆→时, v 的极限值v 叫做物体在时刻t 的速度,也叫瞬时速度.即0lim t s v t∆→∆=∆ 3.导数的定义:设0x 是函数()y f x =定义域的一点,如果自变量x 在0x 处有增量x ∆,则函数值y 也引起相应的增量00()()y f x x f x ∆=+∆-;比值0()()f x x f x y xx+∆-∆=∆∆称为函数()y f x =在点0x 到0x x +∆之间的平均变化率;如果极限000()()lim limx x f x x f x y xx∆→∆→+∆-∆=∆∆存在,则称函数()y f x =在点0x 处可导,并把这个极限叫做()y f x =在0x 处的导数,记作0()f x '或0|x x y =',即0()f x '=000()()lim lim x x f x x f x y xx∆→∆→+∆-∆=∆∆.由定义可知函数()y f x =在点0x 处的导数的几何意义是曲线()y f x =在点00(,)P x y 处的切线的斜率. 也就是说,曲线()y f x =在点P 0(,())x f x 处的切线的斜率是0()f x ',切线方程为00()().y y f x x x '-=-注:⑴x ∆是增量,我们也称为“改变量”,因为x ∆可正,可负,但不为零. ⑵函数()y f x =在点0x 处连续与点0x 处可导的关系:①函数()y f x =在点0x 处连续是()y f x =在点0x 处可导的必要不充分条件. 可以证明,如果()y f x =在点0x 处可导,那么()y f x =点0x 处连续. 事实上,令0x x x =+∆,则0x x →相当于0x ∆→.于是000000lim ()lim ()lim[()()()]x x x x f x f x x f x x f x f x →∆→∆→=+∆=+-+0000()()lim[()]x f x x f x x f x x ∆→+∆-=⋅∆+∆000000000()()lim lim lim ()()0()()x x x f x x f x f x f x f x f x x∆→∆→∆→+∆-'=⋅+=⋅+=∆.③如果()y f x =点0x 处连续,那么()y f x =在点0x 处可导,是不成立的. 例:()||f x x =在点00x =处连续,但在点00x =处不可导,因为||y x x x∆∆=∆∆, 当x ∆>0时,1y x ∆=∆;当x ∆<0时,1y x ∆=-∆,故0limx yx∆→∆∆不存在. 4.导函数:函数()y f x =在开区间(,)a b 内每一点处的导数都存在,就说()f x 在(,)a b 内可导,其导数也是(,)a b 内的函数,这一新函数叫做()f x 在开区间(,)a b 内的导函数,记作()f x '或y '(需指明自变量时记作x y ')函数()f x 的导函数()f x '在0x x =时的函数值0()f x '就是()y f x =在点0x 处的导数.注:①可导的奇函数,其导函数为偶函数. ②可导的偶函数,其导函数为奇函数.导数5.几种常见函数的导数:①0;C '= ②()1;nn xnx-'= ③(sin )cos x x '=; ④(cos )sin x x '=-;⑤();xxe e '=⑥()ln xxa a a '=; ⑦()1ln x x '=; ⑧()1l g log a a o x e x'=. 6.可导法则: ①()u v u v '''±=± 推广:1212()()...()()()...()n n y f x f x f x y f x f x f x ''''=+++⇒=+++; ②()uv vu v u '''=+;③2(0)u vu v u v v v '''-⎛⎫=≠ ⎪⎝⎭④()Cu C μ''=(C 为常数);⑤复合函数求导x x y y μμ'''=⋅ 注:① ,u v 必须是可导函数. ②若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导.例如:设2()2sin f x x x =+,2()cos g x x x=-,则(),()f x g x 在0x =处均不可导,但它们和()()f x g x +=sin cos x x +在0x =处均可导.7.导数的运用:⑴判断函数()f x 在某个区间内的单调性的方法:一般地,设函数()y f x =在某个区间内可导,如果()0f x '>,则()f x 为增函数; 如果()0f x '<则()f x 为减函数;如果()0f x =׳,则()f x 为常数函数.注:① ()0f x >是f (x )递增的充分条件,但不是必要条件,如32y x =在(,)-∞+∞上并不是都有()0f x '>,有一个点例外即x =0时()0f x '=,同样()0f x '<也是f (x )递减的充分非必要条件.②一般地,如果()f x '在某区间内有限个点处为零,在其余各点均为正(或负),那么f (x )在该区间上仍旧是单调增加(或单调减少)的. ⑵函数的极值:一般地,设函数()y f x =在点0x 附近有定义,如果对0x 附近的所有的点,都有0()()f x f x <,则0()f x 是()f x 的一个极大值;如果对0x 附近的所有的点,都有0()()f x f x >,则0()f x 是()f x 的一个极小值.注:①求可导函数的极值点可用导数来找,极值点一定是导数为0的点.若点0x 是可导函数()f x 的极值点,则()f x '=0. 但反过来不一定成立. 对于可导函数,其一点0x 是极值点的必要条件是若函数在该点可导,则导数值为零.例如:函数3()y f x x ==,0x =使()f x '=0,但0x =不是极值点.又例如:函数()||y f x x ==,在点0x =处不可导,但点0x =是函数的极小值点. ②当函数()f x 在点0x 处连续时,(Ⅰ)如果在0x 附近的左侧()f x '>0,右侧()f x '<0,那么0()f x 是极大值; (Ⅱ)如果在0x 附近的左侧()f x '<0,右侧()f x '>0,那么0()f x 是极小值. 也就是说0x 是极值点的充分条件是0x 点两侧导数异号,而不是()f x '=0. 此外,函数不可导的点也可能是函数的极值点.当然,极值是一个局部概念,极值点的大小关系是不确定的,即有可能极大值比极小值小(因为函数在某一点附近的点不同).③0()f x '=0不能得到当x =x 0时,函数有极值判断极值,还需结合函数的单调性说明;但是,当x =x 0时,函数有极值⇒ 0()f x '=0⑶函数的最值: 函数()y f x =在区间上如果存在0x ,若使得对区间内任意x 都有0()()f x f x ≥,则0()f x 叫最小值; 若使得对区间内任意x 都有0()()f x f x ≤,则0()f x 叫最大值;注: ①一般地, 闭区间[],a b 上的连续函数()y f x =在[],a b 上必有最大值与最小值.②极值与最值不是同一个概念. 极值是在局部对函数值进行比较,最值是在整体区间上对函数值进行比较.开区间内的最值点一定是极值点,反过来不成立.③函数f (x )在区间[a ,b ]上的最大值为极大值和f (a ) 、f (b )中最大的一个;最小值为极小值和f (a ) 、f (b )中最小的一个。
第十一章 选讲部分(课件+随堂训练及解析+课时跟踪演练及解析+综合测试)10份课时跟踪训练58
课时跟踪训练(五十八) 一、选择题 1.在极坐标系中,圆ρ=-2sin θ的圆心的极坐标是( )
A.1,π2 B.1,-π2 C.(1,0) D.(1,π) 解析:ρ2=-2ρsin θ,∴x2+y2=-2y 即x2+(y+1)2=1,圆心为(0,-1) ∴圆心的极坐标为
1,-
π
2.
答案:B 2.在极坐标系中,直线l过点A(2,0),且极轴按逆时针方向旋转到直
线l所形成的角的大小为π6,则直线l的极坐标方程为( )
A.ρsinπ6-θ=1 B.ρsinθ-π6=1 C.ρsin θ=1 D.ρsinπ6=1 解析:在极坐标系中,设直线l上任意一点P(ρ,θ),则在△AOP中,由正弦定理得ρsinπ-π6=2sinπ6-θ,化简得ρsinπ6-θ=1,所以,直线l的极坐
标方程为 ρsinπ6-θ=1.
答案:A 3.(2014·江西卷)若以直角坐标系的原点为极点,x轴的非负半轴为极轴建立极坐标系,则线段y=1-x(0≤x≤1)的极坐标方程为( ) A.ρ=1cos θ+sin θ,0≤θ≤π2 B.ρ=1cos θ+sin θ,0≤θ≤π4 C.ρ=cos θ+sin θ,0≤θ≤π2 D.ρ=cos θ+sin θ,0≤θ≤π4 解析:由x=ρcos θ,y=ρsin θ,y=1-x可得ρsin θ=1-ρcos θ,即ρ=1cos θ+sin θ,
再结合线段y=1-x(0≤x≤1)在极坐标系中的情形,可知θ∈
0,
π
2.
因此线段y=1-x(0≤x≤1)的极坐标方程为ρ=1cos θ+sin θ,0≤θ≤π2.
故选A. 答案:A 4.(2014·安徽卷)以平面直角坐标系的原点为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的长度单位,已知直线l的参数方
程是 x=t+1,y=t-3(t为参数),圆C的极坐标方程是ρ=4cos θ,则直线l被圆C截得的弦长为( ) A.14 B.214 C.2 D.22 解析:由题意得直线l的方程为x-y-4=0,圆C的方程为(x-2)2+
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例11.1 如图11.1(a )所示的蜗杆传动和圆锥齿轮传动的组合,已知输出轴上圆锥齿轮4z 的转向4n 。
(1) 为使中间轴上的轴向力能抵消一部分,试确定蜗杆传动的螺旋线方向和蜗杆的转向。
(2) 在图上标出各轴轴向力的方向。
解 (1) 在3z 和4z 组成的圆锥齿轮传动中,各轮所受轴向力的方向都是从小端指向大端,因此,3a F 和4a F 的方向如图11.1(b )所示。
为了使中间轴上的轴向力能抵消一部分,2a F 的方向应与3a F 的方向相反。
根据的转向可知的转向如图11.1(b )所示,进而可知2t F 的方向应为有里到外,即1a F 的方向应为有外向里。
由于1t F 与2a F 方向相反,故蜗杆的转向1n 应为顺时针方向。
由于蜗杆的转向和轴向力的关系符合右手定则,因此蜗杆为右旋蜗杆,其螺旋线旋向标在蜗轮上。
(2) 将上述对轴向力的分析结果标在图上,如图11.1(b )所示。
(a) (b) 图11.1 例11.2 如图11.2(a )所示,蜗杆主动,蜗杆的输入扭矩为120T N m =⋅,模数4m mm =,蜗杆头数12z =,蜗杆分度圆直径150d mm =,蜗轮齿数250z =,传动的效率0.75η=。
(1) 试确定蜗轮的转向;
(2) 试确定蜗杆和蜗轮上作用力的大小和方向。
解 (1)由图11.2(a )可知蜗杆为左旋蜗杆,根据左手定则判定出1a F 的方向,如图11.2(b )所示。
由于2t F 的方向与1a F 相反,因此2n 为顺时针转向。
(2) 蜗杆和蜗轮上作用力的方向如图11.2(b )所示。
各力的大小为:
1121222000080050
t a T F F N d ×==== K U S T
21212222220000250.753750504
t a T T i F F N d z m η×××=====× 122tan 3750tan 201364.9r r t F F F N α===×°=
(a) (b)
图11.2
例11.3 已知一蜗杆传动,蜗杆主动,转速11440min n r =,蜗杆头数12z =,模数4m mm =,蜗杆直径系数10q =,蜗杆材料为钢,齿面硬度大于450HRC ,磨削,蜗轮材料为铸锡青铜,求该传动的啮合效率。
解 由教材表11—2查得140d mm =,111836γ′′′=°,则滑动速度为 11401440 3.08601000cos 601000cos 111836s d n v m s ππγ××===′′′×××° 由教材表11—18查得,则啮合效率为136v ϕ′=°
()()1tan tan1118360.87tan tan 111836136v γηγϕ′′′°=
==′′′′+°+° K U S T。
