集合讲义及真题

合集下载

高中必修1第一章集合复习(讲义+例题+练习)

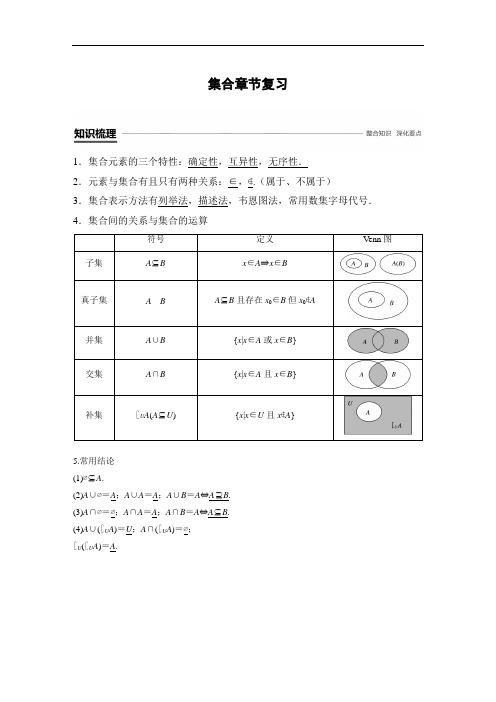
集合章节复习1．集合元素的三个特性：确定性，互异性，无序性．2．元素与集合有且只有两种关系：∈，∉.（属于、不属于）3．集合表示方法有列举法，描述法，韦恩图法，常用数集字母代号．4．集合间的关系与集合的运算符号定义Venn图子集A⊆B x∈A⇒x∈B真子集A B A⊆B且存在x0∈B但x0∉A并集A∪B {x|x∈A或x∈B}交集A∩B {x|x∈A且x∈B}补集∁U A(A⊆U) {x|x∈U且x∉A}5.常用结论(1)∅⊆A.(2)A∪∅＝A；A∪A＝A；A∪B＝A⇔A⊇B.(3)A∩∅＝∅；A∩A＝A；A∩B＝A⇔A⊆B.(4)A∪(∁U A)＝U；A∩(∁U A)＝∅；∁U(∁U A)＝A.1．若A ＝{}x ，|x |，则x <0.( √ ) 2．任何集合至少有两个子集．( × )3．若{}x |ax 2＋x ＋1＝0有且只有一个元素，则必有Δ＝12－4a ＝0.( × ) 4．设A ，B 为全集的子集，则A ∩B ＝A ⇔A ∪B ＝B ⇔∁U A ⊇∁U B .( √ )类型一集合的概念及表示法例1 下列表示同一集合的是( ) A ．M ＝{(2,1)，(3,2)}，N ＝{(1,2)} B ．M ＝{2,1}，N ＝{1,2}C ．M ＝{y |y ＝x 2＋1，x ∈R }，N ＝{y |y ＝x 2＋1，x ∈N }D ．M ＝{(x ，y )|y ＝x 2－1，x ∈R }，N ＝{y |y ＝x 2－1，x ∈R } 答案 B解析 A 选项中M ，N 两集合的元素个数不同，故不可能相同；B 选项中M ，N 均为含有1,2两个元素的集合，由集合中元素的无序性可得M ＝N ；C 选项中M ，N 均为数集，显然有NM ；D 选项中M 为点集，即抛物线y ＝x 2－1上所有点的集合，而N 为数集，即抛物线y ＝x 2－1的值域，故选B.反思与感悟要解决集合的概念问题，必须先弄清集合中元素的性质，明确是数集，还是点集等．跟踪训练1 设集合A ＝{(x ，y )|x －y ＝0}，B ＝{(x ，y )|2x －3y ＋4＝0}，则A ∩B ＝________. 答案 {(4,4)}解析由⎩⎪⎨⎪⎧ x －y ＝0，2x －3y ＋4＝0，得⎩⎪⎨⎪⎧x ＝4，y ＝4.∴A ∩B ＝{(4,4)}．类型二集合间的基本关系例2 若集合P ＝{x |x 2＋x －6＝0}，S ＝{x |ax ＋1＝0}，且S ⊆P ，求由a 的可能取值组成的集合．解由题意得，P ＝{－3,2}．当a ＝0时，S ＝∅，满足S ⊆P ；当a ≠0时，方程ax ＋1＝0的解为x ＝－1a ，为满足S ⊆P ，可使－1a ＝－3或－1a ＝2，即a ＝13或a ＝－12.故所求集合为⎩⎨⎧⎭⎬⎫0，13，－12.反思与感悟 (1)在分类时要遵循“不重不漏”的原则，然后对于每一类情况都要给出问题的解答．(2)对于两集合A ，B ，当A ⊆B 时，不要忽略A ＝∅的情况．跟踪训练2 下列说法中不正确的是________．(填序号) ①若集合A ＝∅，则∅⊆A ；②若集合A ＝{x |x 2－1＝0}，B ＝{－1,1}，则A ＝B ； ③已知集合A ＝{x |1<x <2}，B ＝{x |x <a }，若A ⊆B ，则a >2. 答案 ③解析 ∅是任何集合的子集，故①正确； ∵x 2－1＝0，∴x ＝±1，∴A ＝{－1,1}， ∴A ＝B ，故②正确；若A ⊆B ，则a ≥2，故③错误．类型三集合的交、并、补运算命题角度1用符号语言表示的集合运算例3设全集为R，A＝{x|3≤x<7}，B＝{x|2<x<10}，求∁R(A∪B)及(∁R A)∩B.解把全集R和集合A，B在数轴上表示如下：由图知，A∪B＝{x|2<x<10}，∴∁R(A∪B)＝{x|x≤2或x≥10}，∵∁R A＝{x|x<3或x≥7}．∴(∁R A)∩B＝{x|2<x<3或7≤x<10}．反思与感悟求解用不等式表示的数集间的集合运算时，一般要借助于数轴求解，此法的特点是简单直观，同时要注意各个端点的画法及取到与否．跟踪训练3已知集合U＝{x|0≤x≤6，x∈Z}，A＝{1,3，6}，B＝{1,4,5}，则A∩(∁U B)等于() A．{1} B．{3,6}C．{4,5} D．{1,3,4,5,6}答案 B解析∵U＝{0,1,2,3,4,5,6}，B＝{1,4,5}，∴∁U B＝{0,2,3,6}，又∵A＝{1,3,6}，∴A∩(∁U B)＝{3,6}，故选B.命题角度2用图形语言表示的集合运算例4设全集U＝R，A＝{x|0<x<2}，B＝{x|x<1}．则图中阴影部分表示的集合为____________．答案{x|1≤x<2}解析图中阴影部分表示的集合为A∩(∁U B)，因为∁U B＝{x|x≥1}，画出数轴，如图所示，所以A∩(∁U B)＝{x|1≤x＜2}．反思与感悟解决这一类问题一般用数形结合思想，借助于Venn图和数轴，把抽象的数学语言与直观的图形结合起来．跟踪训练4学校举办了排球赛，某班45名同学中有12名同学参赛，后来又举办了田径赛，这个班有20名同学参赛，已知两项都参赛的有6名同学，两项比赛中，这个班共有多少名同学没有参加过比赛？解设A＝{x|x为参加排球赛的同学}，B＝{x|x为参加田径赛的同学}，则A∩B＝{x|x为参加两项比赛的同学}．画出V enn图(如图)，则没有参加过比赛的同学有：45－(12＋20－6)＝19(名)．答这个班共有19名同学没有参加过比赛．类型四关于集合的新定义题例5设A为非空实数集，若对任意的x，y∈A，都有x＋y∈A，x－y∈A，且xy∈A，则称A 为封闭集．①集合A＝{－2，－1,0,1,2}为封闭集；②集合A＝{n|n＝2k，k∈Z}为封闭集；③若集合A1，A2为封闭集，则A1∪A2为封闭集；④若A为封闭集，则一定有0∈A.其中正确结论的序号是________．答案②④解析①集合A＝{－2，－1,0,1,2}中，－2－2＝－4不在集合A中，所以不是封闭集；②设x，y∈A，则x＝2k1，y＝2k2，k1，k2∈Z，故x＋y＝2(k1＋k2)∈A，x－y＝2(k1－k2)∈A，xy＝4k1k2∈A，故②正确；③反例是：集合A1＝{x|x＝2k，k∈Z}，A2＝{x|x＝3k，k∈Z}为封闭集，但A1∪A2不是封闭集，故③不正确；④若A为封闭集，则取x＝y，得x－y＝0∈A.故填②④. 反思与感悟新定义题是近几年高考中集合题的热点题型，解答这类问题的关键在于阅读理解，也就是要在准确把握新信息的基础上，利用已有的知识来解决问题．跟踪训练5 设数集M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ m ≤x ≤m ＋34，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪n －13≤x ≤n ，且M ，N 都是集合{x |0≤x ≤1}的子集，如果b －a 叫做集合{x |a ≤x ≤b }(b >a )的“长度”，那么集合M ∩N 的“长度”的最小值是( ) A.13 B.23 C.112 D.512 答案 C解析方法一由已知可得⎩⎪⎨⎪⎧m ≥0，m ＋34≤1，⎩⎪⎨⎪⎧n －13≥0，n ≤1，解得0≤m ≤14，13≤n ≤1.取字母m 的最小值0，字母n 的最大值1，可得M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪0≤x ≤34，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪23≤x ≤1，所以M ∩N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ 0≤x ≤34∩⎩⎨⎧⎭⎬⎫x ⎪⎪ 23≤x ≤1＝⎩⎨⎧⎭⎬⎫x ⎪⎪ 23≤x ≤34，此时得集合M ∩N 的“长度”为34－23＝112.方法二集合M 的“长度”为34，集合N 的“长度”为13.由于M ，N 都是集合{x |0≤x ≤1}的子集，而{x |0≤x ≤1}的“长度”为1，由此可得集合M ∩N 的“长度”的最小值是⎝⎛⎭⎫34＋13－1＝112.1．已知集合M ＝{0,1,2,3,4}，N ＝{1,3,5}，P ＝M ∩N ，则P 的子集共有( ) A ．2个 B ．4个 C ．6个 D ．8个答案 B2．下列关系中正确的个数为( ) ①22∈R ；②0∈N ＋；③{－5}⊆Z . A ．0 B ．1 C ．2 D ．3答案 C解析 ①③正确．3．已知集合A ＝{x |－1＜x ＜2}，B ＝{x |0＜x ＜3}，则A ∪B 等于( ) A ．{x |－1<x <3} B ．{x |－1<x <0} C ．{x |0<x <2} D ．{x |2<x <3}答案 A解析由A ＝{x |－1＜x ＜2}，B ＝{x |0＜x ＜3}，得A ∪B ＝{x |－1＜x ＜3}．故选A.4．设全集I ＝{a ，b ，c ，d ，e }，集合M ＝{a ，b ，c }，N ＝{b ，d ，e }，那么(∁I M )∩(∁I N )等于( ) A ．∅ B ．{d } C ．{b ，e } D ．{a ，c } 答案 A5．已知集合U ＝R ，集合A ＝{}x |x <－2或x >4，B ＝{}x |－3≤x ≤3，则(∁U A )∩B ＝________. 考点交并补集的综合问题题点无限集合的交并补运算答案{}x |－2≤x ≤3.解析由图知(∁U A )∩B ＝{}x |－2≤x ≤3.1．要注意区分两大关系：一是元素与集合的从属关系，二是集合与集合的包含关系． 2．在利用集合中元素相等列方程求未知数的值时，要注意利用集合中元素的互异性这一性质进行检验，忽视集合中元素的性质是导致错误的常见原因之一．课时对点练一、选择题1．若集合M＝{x|(x＋4)(x＋1)＝0}，N＝{x|(x－4)·(x－1)＝0}，则M∩N等于() A．{1,4} B．{－1，－4}C．{0} D．∅答案 D解析因为M＝{x|(x＋4)(x＋1)＝0}＝{－4，－1}，N＝{x|(x－4)(x－1)＝0}＝{1,4}，所以M∩N ＝∅，故选D.2．已知集合A＝{x|x＋3>0}，B＝{x|x≥2}，则下列结论正确的是()A．A＝B B．A∩B＝∅C．A⊆B D．B⊆A考点集合的包含关系题点集合包含关系的判定答案 D解析A＝{x|x>－3}，B＝{x|x≥2}，结合数轴可得：B⊆A.3．已知集合A，B均为集合U＝{1,3,5,7,9}的子集，若A∩B＝{1,3}，(∁U A)∩B＝{5}，则集合B等于()A．{1,3} B．{3,5}C．{1,5} D．{1,3,5}答案 D解析画出满足题意的Venn图，由图可知B＝{1,3,5}．4．设集合M＝{－1,0,1}，N＝{a，a2}，若M∩N＝N，则a的值是()A．－1 B．0 C．1 D．1或－1答案 A解析由M∩N＝N得N⊆M.当a＝0时，与集合中元素的互异性矛盾；当a＝1时，也与集合中元素的互异性矛盾；当a＝－1时，N＝{－1,1}，符合题意．5．设全集U＝R，已知集合A＝{x|x＜3或x≥7}，B＝{x|x＜a}．若(∁U A)∩B≠∅，则a的取值范围为()A．a＞3 B．a≥3C．a≥7 D．a＞7答案 A解析因为A＝{x|x＜3或x≥7}，所以∁U A＝{x|3≤x＜7}，又(∁U A)∩B≠∅，则a＞3.6．定义差集A－B＝{x|x∈A，且x∉B}，现有三个集合A，B，C分别用圆表示，则集合C－(A－B)可表示下列图中阴影部分的为()答案 A解析如图所示，A－B表示图中阴影部分，故C－(A－B)所含元素属于C，但不属于图中阴影部分，故选A.二、填空题7．设全集U＝R，若集合A＝{1,2,3,4}，B＝{x|2≤x≤3}，则A∩(∁U B)＝________.答案{1,4}解析∵∁U B＝{x|x<2或x>3}，∴A∩(∁U B)＝{1,4}．8．设集合A＝{1，－1，a}，B＝{1，a}，A∩B＝B，则a＝______.答案0解析∵A ∩B ＝B ，即B ⊆A ，∴a ∈A . 要使a 有意义，a ≥0. ∴a ＝a ，∴a ＝0或a ＝1，由元素互异，舍去a ＝1.∴a ＝0.9．已知集合M ＝{(x ，y )|x ＋y ＝2}，N ＝{(x ，y )|x －y ＝4}，那么集合M ∩N ＝________. 答案 {(3，－1)}解析 M ，N 中的元素是平面上的点，M ∩N 是集合，并且其中的元素也是点，解方程组⎩⎪⎨⎪⎧ x ＋y ＝2，x －y ＝4，得⎩⎪⎨⎪⎧x ＝3，y ＝－1.∴M ∩N ＝{(3，－1)}．10．已知集合A ＝{x |2a ≤x ≤a ＋3}，B ＝{x |x <－1或x >5}，若A ∩B ＝∅，则a 的取值范围是________．答案 ⎩⎨⎧⎭⎬⎫a ⎪⎪－12≤a ≤2或a >3 解析 ①若A ＝∅，则A ∩B ＝∅，此时2a >a ＋3，即a >3.②若A ≠∅，如图，由A ∩B ＝∅，可得⎩⎪⎨⎪⎧2a ≥－1，a ＋3≤5，2a ≤a ＋3，解得－12≤a ≤2.综上所述，a 的取值范围是⎩⎨⎧⎭⎬⎫a ⎪⎪－12≤a ≤2或a >3. 三、解答题11．如图，用适当的方法表示阴影部分的点(含边界上的点)组成的集合M .解结合图形可得M＝⎩⎨⎧⎭⎬⎫(x，y)⎪⎪xy≥0，－2≤x≤52，－1≤y≤32.12．已知集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}．(1)若A∪B＝A，求实数m的取值范围；(2)当A＝{x∈Z|－2≤x≤5|}时，求A的非空真子集的个数；(3)若A∩B＝∅，求实数m的取值范围．考点集合各类问题的综合题点集合各类问题的综合解(1)因为A∪B＝A，所以B⊆A，当B＝∅时，由m＋1>2m－1，得m<2，符合；当B≠∅时，根据题意，可得⎩⎪⎨⎪⎧2m－1≥m＋1，m＋1≥－2，2m－1≤5，解得2≤m≤3.综上可得，实数m的取值范围是{m|m≤3}．(2)当x∈Z时，A＝{x∈Z|－2≤x≤5}＝{－2，－1,0,1,2,3,4,5}，共有8个元素，所以A的非空真子集的个数为28－2＝254.(3)当B＝∅时，由(1)知m<2；当B≠∅时，根据题意作出如图所示的数轴，可得⎩⎪⎨⎪⎧2m－1≥m＋1，2m－1<－2或⎩⎪⎨⎪⎧2m－1≥m＋1，m＋1>5，解得m>4.综上可得，实数m 的取值范围是{m |m <2或m >4}．13．设集合A ＝{0，－4}，B ＝{x |x 2＋2(a ＋1)x ＋a 2－1＝0，x ∈R }．若B ⊆A ，求实数a 的取值范围．解因为A ＝{0，－4}，所以B ⊆A 分以下三种情况：①当B ＝A 时，B ＝{0，－4}，由此知0和－4是方程x 2＋2(a ＋1)x ＋a 2－1＝0的两个根，则⎩⎪⎨⎪⎧ Δ＝4(a ＋1)2－4(a 2－1)>0，－2(a ＋1)＝－4，a 2－1＝0，解得a ＝1；②当B ≠∅且B A 时，B ＝{0}或B ＝{－4}，并且Δ＝4(a ＋1)2－4(a 2－1)＝0，解得a ＝－1，此时B ＝{0}满足题意；③当B ＝∅时，Δ＝4(a ＋1)2－4(a 2－1)<0，解得a <－1.综上所述，所求实数a 的取值范围是a ≤－1或a ＝1.四、探究与拓展14．已知全集U ＝{2,4，a 2－a ＋1}，A ＝{a ＋4,4}，∁U A ＝{7}，则a ＝________.答案－2解析由题意，得a 2－a ＋1＝7，即a 2－a －6＝0，解得a ＝－2或a ＝3.当a ＝3时，A ＝{7,4}，不合题意，舍去，故a ＝－2.15．对于集合A ，B ，我们把集合{}(a ，b )|a ∈A ，b ∈B 记作A ×B .例如，A ＝{}1，2，B ＝{}3，4，则有：A ×B ＝{}(1，3)，(1，4)，(2，3)，(2，4)，B ×A ＝{}(3，1)，(3，2)，(4，1)，(4，2)，A ×A ＝{}(1，1)，(1，2)，(2，1)，(2，2)，B ×B ＝{}(3，3)，(3，4)，(4，3)，(4，4). 据此，试回答下列问题：(1)已知C ＝{}a ，D ＝{}1，2，3，求C ×D ；(2)已知A ×B ＝{}(1，2)，(2，2)，求集合A ，B ；(3)若集合A 中有3个元素，集合B 中有4个元素，试确定A ×B 中有多少个元素．考点集合各类问题的综合题点集合各类问题的综合解析 (1)C ×D ＝{}(a ，1)，(a ，2)，(a ，3).(1，2)，(2，2)，(2)因为A×B＝{}所以A＝{}1，2，B＝{}2.(3)由题意可知A×B中元素的个数与集合A和B中的元素个数有关，即集合A中的任何一个元素与B中的任何一个元素对应后，得到A×B中的一个新元素．若A中有m个元素，B中有n个元素，则A×B中应有m×n个元素．于是，若集合A中有3个元素，集合B中有4个元素，则A×B中有12个元素．。

高中数学集合的表示讲义

第2讲：集合的表示【知识梳理】一、集合的表示【考点解读】考点一：用列举法表示集合例1．用列举法表示下列给定的集合：(1)不大于12的非负偶数组成的集合A ；(2)小于9的质数组成的集合B ；(3)方程2230x x --=的实数根组成的集合C ； (4)方程组42x y x y +=⎧⎨-=⎩的解集D .变式训练1：用列举法表示下列集合：(1)方程22x x =的所有实数解组成的集合；(2)直线21y x =+与y 轴的交点所组成的集合；(3)由所有正整数构成的集合．考点二：用描述法表示集合文字描述；式子描述例2．用描述法表示下列集合：(1)不等式231x -<的解组成的集合A ；(2)被3除余1的正整数的集合B ；(3){2,4,6,8,10}C =；(4)平面直角坐标系中第一象限内的点组成的集合D .变式训练1：用描述法表示下列集合：(1)比1大又比11小的实数组成的集合；(2)不等式342x x +≥的所有解；(3)到两坐标轴距离相等的点的集合．考点三：集合的表示综合例3．下列命题中正确的（）①0与{0}表示同一个集合；②由1,2,3组成的集合可表示为{1,2,3}或{3,2,1}；③方程2(1)(2)0x x --=的所有解的集合可表示为{1,1,2}；④集合{|45}x x <<可以用列举法表示．A ．只有①和④B ．只有②和③C ．只有②D ．以上语句都不对变式训练1：方程组149x y x y +=⎧⎨-=⎩的解集是（）A ．()2,1-B ．()1,2-C ．(){}1,2-D ．(){}2,1-变式训练2：下列集合恰有2个元素的集合是（）A ．2{0}x x -=B ．2{|}x y x x =-C ．2{|0}y y y -=D ．2{|}y y x x =-变式训练3：已知集合{}21,1,3A a a a =+--，若1A ∈，则实数a 的值为__________.考点四：元素个数相同元素根据互异性，只能计算一次（主要考查互异性）例4．设集合{123}{45}}{|A C x B y x A y B ===+∈∈，，，，，，，则C 中元素的个数为（）A ．3B ．4C ．5D ．6变式训练1：已知集合{}1,2A =，{}2,4B =，则集合{},,M z z x y x A y B ==⋅∈∈中元素的个数为（）A ．1个B ．2个C ．3个D ．4个变式训练2：设集合(){},1,,A x y x y x Z y Z =+≤∈∈，则A 中元素的个数为（）A ．3B ．4C ．5D ．6变式训练3：集合{}2*70,A xx x x =-<∈N ∣，则*8{,}B y y A y =∈∈N ∣中元素的个数为（）A ．1个B ．2个C ．3个D ．4个考点五：元素个数（求参）相同元素根据互异性，只能计算一个（主要考查互异性）例5．已知集合{}2|210,A x ax x a =++=∈R 只有一个元素，则a 的取值集合为（）A ．{1}B ．{0}C ．{0,1,1}-D ．{0,1}变式训练1：已知集合{}2310A x ax x =-+=中有且只有一个元素，则实数a 的取值集合是（）A ．9{0,}4B ．1{0,}3C ．{0}D ．9{}4变式训练2：式子22a b a a b a++________.变式训练3：已知集合{}2320,,A x ax x x R a R =-+=∈∈.（1）若A 是空集，求a 的取值范围；（2）若A 中只有一个元素，求a 的值，并求集合A ；（3）若A 中至多有一个元素，求a 的取值范围考点六：集合新定义例6．给定集合A ，若对于任意a 、b A ∈，有a b A +∈，且a b A -∈，则称集合A 为闭集合，给出如下三个结论：①集合{}4,2,0,2,4A =--为闭集合； ②集合{}3,A n n k k Z ==∈为闭集合；③若集合1A 、2A 为闭集合，则12A A 为闭集合．其中正确结论的个数是（）A ．0B ．1C ．2D ．3变式训练1：已知集合A 中的元素均为整数，对于k A ∈，如果1k A -∉且1k A +∉，那么称k 是A 的一个“孤立元”．给定集合{1,2,3,4,5,6,7,8}S =，由S 中的3个元素构成的所有集合中，不含“孤立元”的集合共有________个．变式训练2：已知集合{|31,},{|32,},{|63,}A x x n n B x x n n M x x n n ==+∈==+∈==+∈Z Z Z ．(1)若m M ∈，则是否存在,a A b B ∈∈，使m a b =+成立？(2)对于任意,a A b B ∈∈，是否一定存在m M ∈，使a b m +=？证明你的结论．【课堂检测】1、若用列举法表示集合27{(,)|}2y x A x y x y -=⎧=⎨+=⎩，则下列表示正确的是（）A ．{1,3}x y =-=B ．{(-1,3)}C ．{3,-1}D ．{-1,3}2、已知集合{}1,2,3,4,5A =，(){},|,,B x y x A y A x y A =∈∈+∈，则集合B 中所含元素的个数为（）A ．4B ．6C ．8D ．103、已知集合{}2,2A =-，{}|,,B m m x y x A y A ==+∈∈，则集合B 等于（）A ．{}4,4-B ．{}4,0,4-C ．{}4,0-D ．{}04、已知{}232,2a a ∈++，则实数a 的值为（）A ．1或1-B ．1C ．1-D ．1-或05、下列四个命题：①{0}是空集；②若a ∈N ，则a -∉N ；③集合2{|210}x x x ∈-+=R 含有两个元素；④集合6{|}x Q N x ∈∈是有限集．其中正确命题的个数是（）A ．1B ．2C ．3D ．06、若集合{}210x ax x -+=中只有一个元素，则实数a 的值为（）A ．14B ．0C ．4D ．0或147、设P 是一个数集，且至少含有两个元素．若对任意的,a b P ∈，都有,,,a ab a b ab P b +-∈(除数0b ≠)，则称P 是一个数域，例如有理数集Q 是一个数域，有下列说法正确的是（）A ．数域必含有0,1两个数；B ．整数集是数域；C ．若有理数集Q M ⊆，则数集M 必为数域；D ．数域必为无限集．8、设P 是一个数集，且至少含有两个数，若对任意a b P ∈、，都有+a b 、-a b 、ab 、a P b ∈（除数0b ≠）则称数集P 是一个数域．例如有理数集Q 是数域；数集{,}F a a b Q =+∈也是数域．下列命题是真命题的是（）A ．整数集是数域B ．若有理数集Q M ⊆，则数集M 必为数域C ．数域必为无限集D ．存在无穷多个数域9、用适当的方法表示下列集合：（1）大于2且小于5的有理数组成的集合．（2）30的正因数组成的集合．（3）由0,1,2这三个数字抽出一部分或全部数字(没有重复)所组成的自然数组成的集合．10、已知集合{}2210,A x ax x a R =++=∈．（1）若A 中只有一个元素，求a 的值；（2）若A 中至少有一个元素，求a 的取值范围；（3）若A 中至多有一个元素，求a 的取值范围.11、已知集合{}2|210A x R ax x =∈++=，其中a R ∈.（1）1是A 中的一个元素，用列举法表示A ；（2）若A 中至多有一个元素，试求a 的取值范围.。

集合讲义及例题解析1

专题01 集合4题型分类1．集合与元素（1）集合中元素的三个特性：确定性、互异性、无序性．（2）元素与集合的关系是属于或不属于，用符号∈或∉表示．（3）集合的表示法：列举法、描述法、图示法．（4）常见数集的记法．2．集合间的基本关系（1）子集：一般地，对于两个集合A，B，如果集合A中任意一个元素都是集合B中的元素，就称集合A为集合B的子集，记作A⊆B(或B⊇A．（2）真子集：如果集合A⊆B，但存在元素x∈B，且x∉A，就称集合A是集合B 的真子集，记作A⊂B(或B⊃A)．（3）相等：若A⊆B，且B⊆A，则A＝B．（4）空集：不含任何元素的集合叫做空集，记为∅.空集是任何集合的子集，是任何非空集合的真子集．3．集合的基本运算（一）集合的含义与表示1．元素与集合关系的判断（1）元素与集合的关系：①一般地，我们把研究对象称为元素，把一些元素组成的总体称为集合，简称集．①元素一般用小写字母a，b，c表示，集合一般用大写字母A，B，C表示，两者之间的关系是属于与不属于关系，符号表示如：a①A或a①A．（2）集合中元素的特征：确定性、互异性、无序性2．解决集合含义问题的关键有三点．（1）确定构成集合的元素．（2）确定元素的限制条件．（3）根据元素的特征(满足的条件)构造关系式解决相应问题．3M -∈当21-m 当3m -=所以m =（二）集合间的基本关系1．集合的相等（1）若集合A 与集合B 的元素相同，则称集合A 等于集合B ．（2）对集合A 和集合B ，如果集合A 的任何一个元素都是集合B 的元素，同时集合B 的任N【分析】分别分析两个集合中的元素所代表的意思即可判断选项若M N ⊆，则0a ≤. 故答案为：0a ≤2-3．（2024高一下·重庆万州·开学考试）已知集合{}1,3,21A m =-，集合{}23,B m =．若B A ⊆，则实数m = ．【答案】1-【分析】利用B A ⊆列方程求出m ，注意到集合中元素的互异性，得到正确答案.【详解】集合{}1,3,21A m =-，集合{}23,B m =B A ⊆．①若21m =，解得：1m =或1m =-.当1m =时，{}1,3,1A =与元素的互异性相矛盾，舍去. 当1m =-时，{}1,3,3A =-符合题意. ②若221m m =-，解得：1m =.舍去. 故1m =-. 故答案为：-1.2-4．（2023-2024学年山东省济宁市兖州区高一上学期期中考试数学试卷（带解析））已知集合2|1},{|}{1A x x B x ax ====，若B A ⊆，则实数a 的值为．【答案】0，±1 【详解】试题分析：当时，集合B φ=，满足B A ⊆；当时，，又，所以若B A ⊆，则有，综上实数a 的值为0，±1．考点：利用子集关系求参数．2-5．（2024高一上·江苏宿迁·阶段练习）已知集合{}25A x x =-≤≤，{}121B x m x m =+≤≤-，若B A ⊆，则实数m 的取值范围为 . 【答案】(,3]-∞【分析】根据B A ⊆，分B =∅和B ≠∅，两种情况讨论求解.【详解】因为集合{}25A x x =-≤≤，{}121B x m x m =+≤≤-，且B A ⊆，当B =∅时，则121m m +>-，解得2m <，。

复习集合及其运算讲义

__教学目标1、初步了解学生高一的知识点的掌握情况2、复习集合及其运算重点难点1、了解学生高二目前的学习情况2、复习集合及其运算的知识一、基本概念：1、集合及元素集合：集合是某些指定对象的全体，只能作描述性说明元素：集合中每个对象叫做这个集合的元素.集合通常用大写的拉丁字母表示，如A、B、C、……元素通常用小写的拉丁字母表示，如a、b、c、……空集：不含任何元素的集合叫做空集集合的分类：有限集和无限集；含有有限个元素的集合叫做有限集，含有无限个元素的集合叫做无限集。

例1．下列研究的对象能否构成集合（1）世界上最高的山峰（2）高一数学课本中的难题（3）中国国旗的颜色（4）充分小的负数的全体（5）book中的字母（6）立方等于本身的实数（7）不等式2x-8<13的正整数解2、元素与集合的关系（1）属于：如果a是集合A的元素，就说a属于A，记作a∈A（2）不属于：如果a不是集合A的元素，就说a不属于A，记作Aa∉注意：“∈”的方向，不能把a∈A颠倒过来写.例2：集合A中的元素由x=a+b2(a∈Z,b∈Z)组成，判断下列元素与集合A的关系？（1）0 （2）121-（3）132-3、常用数集及其表示方法（1）非负整数集（自然数集）：全体非负整数的集合.记作N （2）正整数集：非负整数集内排除0的集.记作N*或N+（3）整数集：全体整数的集合.记作Z第一部分：集合及其运算11、点的集合M ＝｛(x,y)｜xy≥0｝是指（）A 、第一象限内的点集B 、第三象限内的点集C 、第一、第三象限内的点集D 、不在第二、第四象限内的点集12、方程组 11x y x y +=-=- 的解集是 ( )A 、{x=0,y=1}B 、{0,1}C 、{(0,1)}D 、{(x,y)|x=0或y=1}13、如果集合A={x |ax 2＋2x ＋1=0}中只有一个元素，则a 的值是（）A 、0B 、0 或1C 、1D 、不能确定二简答题：1 已知集合A={a-2,2a 2+5a,10},且-3∈A,求实数a2 集合{a,ab ,1}也可以表示成{a 2,a+b,0},求a 2006+b 2006的值3 已知集合A={x|ax 2-3x+3=0,x ∈R }至多有一个元素，求a 的取值范围4 已知，，，求5 已知，若集合P 中恰有3个元素，求6 已知A ＝{x ｜x ＜－2或x ＞3}，B ＝{x ｜4x ＋m ＜0}，当A ⊇B 时，求实数m 的取值范围.课后作业：1、已知集合{}21,1,3A x x =--,求实数x 应满足的条件.2、不等式组⎩⎨⎧>+>03,42a x x 的解集是{x |x ＞2}，求实数a 的取值范围。

第一章集合课程讲义

1.1 集合的含义及其表示一、知识梳理1．集合的定义2．元素与集合的关系3．集合中元素的特性：确定性、互异性、无序性4．常用数集及其记法：5．集合的表示方法：二、例题讲解例1：集合M中的元素为1，x，x2-x，求x的范围？例2：三个元素的集合1，a，ba，也可表示为0，a2，a+b，求a2005+ b2006的值．例3：集合A中的元素由(a∈Z,b∈Z)组成，判断下列元素与集合A的关系？（1）0 （2（3例4．用描述法表示下列集合：（1）所有被3整除的整数的集合；（2）使yx=有意义的x的集合；（3）方程x2+x+1=0所有实数解的集合；（4）抛物线y=-x2+3x-6上所有点的集合；例5．已知A={a|6,3N a Za∈∈-}，试用列举法表示集合A．例6．已知集合P={-1,a,b}，Q={-1,a2,b2}，且Q=P，求1+a2+b2的值．三、巩固练习1、用∈或∉填空________N________R0_______N* π________R 227_______Q cos300_______Z2、由实数-x，|x|x，组成的集合最多含有元素的个数是_________________个.3、用列举法表示下列集合：(1) {x|x为不大于10的正偶数}(2){(x,y)|0≤x ≤2，0≤y<2，x ，y ∈Z}4、用描述法表示下列集合：(1)不等式2x-3>5的解集；(2)直角坐标平面内属于第四象限的点的集合；5、集合A={x|y=x 2+1}，B={t|p=t 2+1}，，这三个集合的关系？ 6、已知A={x|12,6N x N x∈∈-}，试用列举法表示集合A ．1.2 子集、全集、补集一、知识梳理1．子集的概念及记法：2．子集的性质：① A ⊆ A② A ∅⊆3．真子集的概念及记法：4．真子集的性质：①∅是任何非空集合的真子集5．全集的概念：6．补集的概念：二、例题讲解例1：以下各组是什么关系，用适当的符号表示出来．（1）a 与{a} 0 与 ∅（2）∅与{20，35，∅} （3）S={-2，-1，1，2}，A={-1，1}，B={-2，2}；（4）S=R ，A={x|x ≤0，x ∈R}，B={x|x>0 ，x ∈R }；例2：设集合A={x|x 2+4x=0，x ∈R}，B={x|x 2+2(a+1)x+a 2-1=0，x ∈R}，若B ⊆A ，求实数a 的取值范围．例3：①方程组210360x x +>⎧⎨-≤⎩的解集为A ，U=R ，试求A 及u C A ． ②设全集U=R ，A={x|x>1}，B={x|x+a<0}，B 是R C A 的真子集，求实数a 的取值范围．三、巩固练习1．指出下列各组中集合A 与B 之间的关系．(1) A={-1，1}，B=Z ；(2)A={1，3，5，15}，B={x|x 是15的正约数}；(3) A = N*，B=N(4) A ={x|x=1+a 2,a ∈N*}，B={x|x=a 2-4a+5,a ∈N*}2．（1）已知{1，2 }⊆M ⊆{1，2，3，4，5}，则这样的集合M 有多少个？（2）已知M={1，2，3，4，5，6， 7,8，9}，集合P 满足：P ⊆M ，且若P α∈，则10-α∈P ，则这样的集合P 有多少个？3.若U=Z ，A={x|x=2k ，k ∈Z}，B={x|x=2k+1， k ∈Z}，则U C A ___________ U C B ___________：4．设全集是数集U={2，3，a 2+2a-3}，已知A={b ，2}，U C A ={5}，求实数a ，b 的值．5．已知集合A={x|x 2-1=0 }，B={x|x 2-2ax+b=0},B ⊆ A ，求a ，b 的取值范围．1.3 交集、并集一、知识梳理1．交集的定义：注意：当集合A 与B 没有公共元素时，不能说A 与B 没有交集，而是A ∩B=∅.2．交集的常用性质：（1）(A ∩B)∩C =A ∩(B ∩C)；（2） A ∩B ⊆A ， A ∩B ⊆B3．区间的表示法：4．并集的定义：注意：并集（A ∪B ）实质上是A 与B 的所有元素所组成的集合，但是公共元素在同一个集合中要注意元素的互异性.5．并集的常用性质：（1）(A ∪B)∪C =A ∪(B ∪C)；（2） A ⊆A ∪B ， B ⊆A ∪B二、例题讲解例1．（1）设A={-1，0，1}，B={0，1，2，3}，求A ∩B ；（2）设A={x|x>0}，B={x|x≤1}，求A∩B；（3）设A={x|x=3k，k∈Z}，B={y|y=3k+1 k∈Z }，C={z|z=3k+2，k∈Z}，D={x|x=6k+1，k∈Z}，求A∩B；A∩C；C∩B；D∩B；例2：已知数集 A={a2，a+1，-3}，数集B={a-3,a-2，a2+1}，若A∩B={-3}，求a的值．例3：（1）设集合A={y|y=x2-2x+3，x∈R}，B={y|y=-x2+2x+10，x∈R}，求A∩B；（2）设集合A={(x,y)|y=x+1，x∈R}，B={(x,y)|y=-x2+2x+34，x∈R}，求A∪B；例4：已知集合A={x|x2-1=0 }，B={x|x2-2ax+b=0}，A∪B=A，求a，b的值或a,b所满足的例5：若A={x|x2-ax+a2-19=0}，B={x|x2-5x+6=0}，C={x|x2+2x-8=0}，（1）若A∪B=A∩B，求a的值；（2）∅ A∩B，A∩C=∅，求a的值．例6：已知集合A={2，5}，B={x|x2+px+q=0，x∈R}（1）若B={5}，求p，q的值．（2）若A∩B= B ，求实数p，q满足的条件．例10、已知集合A={x|－2<x<－1，或x>0}，B={x|a≤x≤b}，满足A∩B={x|0<x≤2}，A∪B={x|x>－2}，求a、b的值。

高考数学一轮专项复习讲义(通用版)-集合(含解析)

集合复习要点1.了解集合的含义，体会元素与集合的属于关系；能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.理解集合之间包含与相等的含义，能识别给定集合的子集；在具体情境中了解全集与空集的含义.3.理解两个集合的并集与交集的含义，会求两个简单集合的并集与交集.4.理解在给定集合中一个子集的补集的含义，会求给定子集的补集.5.能使用Venn 图表达集合间的基本关系及集合的基本运算，体会图形对理解抽象概念的作用．一集合与元素1．集合中元素的三个特性：确定性、互异性、无序性．2．元素与集合的关系是属于或不属于，用符号∈或∉表示．3．集合的表示法：列举法、描述法、图示法．4．常见数集的记法集合非负整数集(或自然数集)正整数集整数集有理数集实数集符号NN *(或N ＋)Z QR二集合间的基本关系表示关系文字语言符号语言相等集合A 与集合B 中的所有元素相同A ⊆B 且B ⊆A ⇔A ＝B 子集集合A 中任意一个元素均为集合B 中的元素A ⊆B 或B ⊇A真子集集合A 中任意一个元素均为集合B中的元素，且B 中至少有一个元素不是A 中的元素A B 或B A空集空集是任何集合的子集，是任何非空集合的真子集∅⊆A ，∅B (B ≠∅)三集合的基本运算集合的并集集合的交集集合的补集符号A ∪BA ∩B若全集为U ，则集合表示A 的补集为U A图形表示意义{x |x ∈A 或x ∈B }{x |x ∈A 且x ∈B }{x |x ∈U 且x ∉A }常/用/结/论1．若集合A 有n (n ≥1)个元素，则集合A 有2n 个子集，(2n －1)个真子集．非空子集有(2n －1)个，非空真子集有(2n －2)个．2．A ⊆B ⇔A ∩B ＝A ⇔A ∪B ＝B ⇔U A ⊇U B .3.U (A ∩B )＝(U A )∪(U B )，U (A ∪B )＝(U A )∩(U B )．这一结论称为德·摩根定律，又叫反演律，可利用Venn 图解释．4．集合中元素的个数：card(A ∪B )＝card(A )＋card(B )－card(A ∩B )．1．判断下列结论是否正确．(1)集合{x ∈N |x 3＝2x }，用列举法表示为{－2，0，2}．()(2){x |y ＝x 2＋1}＝{y |y ＝x 2＋1}＝{(x ，y )|y ＝x 2＋1}．()(3)若1∈{x 2，x }，则x ＝－1或x ＝1.()(4)对任意集合A ，B ，都有(A ∩B )⊆(A ∪B )．(√)2．设A ，B ，U 均为非空集合，且满足A ⊆B ⊆U ，则下列各式中错误的是()A ．(U A )∪B ＝U B ．(U A )∩(U B )＝U BC ．A ∩(U B )＝∅D ．(U A )∪(U B )＝U解析：A ⊆B ⊆U ，则U B ⊆U A ，(U A )∪B ＝U ，选项A 正确；(U A )∩(U B )＝U B ，选项B 正确；A ∩(U B )＝∅，选项C 正确；(U A )∪(U B )＝U A ≠U ，所以选项D 错误．故选D ．答案：D3．(2023·全国甲卷，文)设全集U ＝{1,2,3,4,5}，集合M ＝{1,4}，N ＝{2,5}，则N ∪U M ＝()A ．{2,3,5}B ．{1,3,4}C ．{1,2,4,5}D ．{2,3,4,5}解析：因为全集U ＝{1,2,3,4,5}，集合M ＝{1,4}，所以U M ＝{2,3,5}，又N ＝{2,5}，所以N ∪U M＝{2,3,5}．故选A ．答案：A4．已知集合A ＝{(x ，y )|x 2＋y 2＝1}，B ＝{(x ，y )|x ，y ∈R ，且y ＝x }，则A ∩B 中元素的个数为________．解析：集合A 表示圆心在原点的单位圆上所有点的集合，集合B 表示直线y ＝x 上所有点的集合，易知直线y ＝x 和圆x 2＋y 2＝1相交，即有2个交点，故A ∩B 中有2个元素．答案：2题型集合基本概念的理解典例1(1)已知集合A ＝{x |x ＝k ＋12，k ∈Z}，B ＝{x |x ＝k2，k ∈Z}，则A 与B 之间的关系是()A ．A ＝B B ．ABC ．B AD ．无法比较(2)设集合A ＝{x |(x －a )2＜1}，且2∈A,3∉A ，则实数a 的取值范围为________．解析：(1)方法一(列举法)：A，－12，12，32，52，72，列举法形象、直观.B，－12，0，12，1，32，2，52，3，72，显然A B .方法二(描述法)：集合A|x ＝k ＋12，k ∈Z|x ＝2k ＋12，k ∈Z B|x ＝k2，k ∈Z2k ＋1可以表示任意奇数，k 可以表示任意整数，描述法抽象、概括.认真理解代数式的意义，以及内涵和外延．同学们应加强这方面的理解．故A B .故选B ．(2)A ＝{x |(x －a )2＜1}＝{x ||x －a |＜1}＝{x |a －1＜x ＜a ＋1}．因为2∈A,3∉A－1＜2，＋1＞2，＋1≤3，解得1＜a ≤2.故实数a 的取值范围是(1,2]．故答案为(1,2]．求解与集合中元素有关问题的关键点(1)用描述法表示集合，首先要搞清楚集合中代表元素的含义，再看元素的限制条件，明白集合的类型，是数集、点集还是其他类型的集合．(2)集合元素的三个特性中的互异性对解题的影响较大，特别是含有字母的集合，在求出字母的值后，要注意检验集合中的元素是否满足互异性．对点练1(1)已知集合A ＝{(x ，y )|x 2＋y 2≤3，x ∈Z ，y ∈Z }，则A 中元素的个数为()A ．9B ．8C ．5D ．4(2)(2024·湖南长沙月考)如果集合A ＝{x |ax 2＋4x ＋1＝0}中只有一个元素，则实数a 的值是()A ．0B ．4C ．0或4D ．不能确定解析：(1)因为A ＝{(x ，y )|x 2＋y 2≤3，x ∈Z ，y ∈Z }＝{(－1，－1)，(－1,0)，(－1,1)，(0，－1)，(0,0)，(0,1)，(1，－1)，(1,0)，(1,1)}，故选A ．(2)当a ＝0时，集合A ＝{x |ax 2＋4x ＋1＝0}a ≠0时，由集合A ＝{x |ax 2＋4x ＋1＝0}中只有一个元素，可得Δ＝42－4a ＝0，解得a ＝ 4.则a 的值是0或4.故选C ．答案：(1)A(2)C题型集合基本关系的分析典例2(1)若集合A ＝{1,2}，B ＝{x |x 2＋mx ＋1＝0，x ∈R }，且B ⊆A ，每当有此条件，不可忽视B ＝∅的特殊情形.当B ＝∅时，转化为判别式Δ＜0.则实数m 的取值范围为________．(2)若集合A ＝{x |－2≤x ≤5}，B ＝{x |m ＋1≤x ≤2m －1}，若B ⊆A ，则实数m 的取值范围为________．解析：(1)若B ＝∅，则Δ＝m 2－4＜0，解得－2＜m ＜2，符合题意；若1∈B ，则12＋m ＋1＝0，解得m ＝－2，此时B ＝{1}，符合题意；若2代入求参后，回来再次确认条件B ⊆A ，这是个易错点．不符合题意．综上所述，实数m 的取值范围为[－2，2)．故答案为[－2,2)．(2)∵B ⊆A，∴若B ＝∅，则2m －1＜m ＋1，解得m ＜2；若此三个不等式，学生易错点在于第一个不等式容易遗漏.思维的完整性：既要考虑B ＝∅的情况，又要思考B≠∅时应满足的条件．解得2≤m ≤3.故实数m 的取值范围为(－∞，3]．故答案为(－∞，3]．集合间的关系问题的注意点(1)空集是任何集合的子集，在涉及集合关系问题时，必须考虑是否存在空集的情勤思考，多练习这一特殊情形．况，否则易造成漏解．(2)已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，集合的包含关系，转化为区间端点的大小关系，这是一个难点，主要是对端点值的取舍，尤其注意区别开区间和闭区间.例如：[－1,2)⊆(2a－3，a＋2]－3＜－1，＋2≥2.进而转化为参数所满足的关系，常用数轴、Venn图等来直观解决这类问题．求得参数后，可以把端点值代入进行验证，以免增解或漏解．对点练2(1)(2023·新高考全国Ⅱ卷)设集合A＝{0，－a}，B＝{1，a－2,2a－2}，若A⊆B，则a＝()A．2B．1C．23D．－1(2)设A＝{x|x2－8x＋15＝0}，B＝{x|ax－1＝0}．①若a＝15，试判定集合A与B的关系；②若B A，求实数a组成的集合C.(1)解析：若a－2＝0，解得a＝2，此时A＝{0，－2}，B＝{1,0,2}，不符合题意；若2a－2＝0，解得a＝1，此时A＝{0，－1}，B＝{1，－1,0}，符合题意．综上所述，a＝1.故选B．答案：B(2)解：①由x2－8x＋15＝0，得x＝3或x＝5，∴A＝{3,5}．若a＝15，由ax－1＝0，得15x－1＝0，即x＝5.∴B＝{5}．∴B A.②∵A＝{3,5}，又B A，故若B＝∅，则方程ax－1＝0无解，有a＝0；若B≠∅，则a≠0，由ax－1＝0，得x＝1 a .∴1a ＝3或1a ＝5，即a ＝13或a ＝15.故C ，13，题型集合基本运算的多维研讨维度1集合的基本运算典例3(1)(2023·新高考全国Ⅰ卷)已知集合M ＝{－2，－1,0,1,2}，N ＝{x |x 2－x －6≥0}，则M ∩N ＝()两集合的性质不同，M 属于离散集，N 属于连续集，高考有意这样设计．A ．{－2，－1,0,1}B ．{0,1,2}C ．{－2}D ．{2}(2)已知集合M ＝{x |y ＝lg(4－x 2)}，N |cos x ≤12则如图所示的Venn 图中阴影部分表示的集合为()A ．－π3，π3B 2，－π3∪π3，C －π3，D 2解析：(1)方法一：因为N ＝{x |x 2－x －6≥0}＝(－∞，－2]∪[3，＋∞)，而M ＝{－2，－1，0,1,2}，所以M ∩N ＝{－2}．方法二：因为M ＝{－2，－1,0,1,2}，将－2，－1,0,1,2代入不等式x 2－x －6≥0，只有－2使不等式成立，所以M ∩N ＝{－2}．故选C ．(2)由4－x 2＞0得－2＜x ＜2，所以M ＝(－2,2)．由cos x ≤12，得2k π＋π3≤x ≤2k π＋5π3(k ∈Z )，坐标系中，快速求解三角不等式：如图：可以写出cos x＞a和cos x＜a的区域角.即“大于取右边，小于取左边”．所以N＝2kπ＋π3，2kπ＋5π3(k∈Z)．k＝－1时，N＝－5π3，－π3，k＝0时，N＝π3，5π3.则M∩N －2，－π3∪π3，2所以Venn图中阴影部分表示的集合为M(M∩N)－π3，π3.故选C．集合基本运算的求解策略(1)当集合是用列举法表示的数集时，可以通过列举集合的元素进行运算，也可借助Venn图运算．(2)当集合是用不等式表示时，可运用数轴求解．对于端点处的取舍，可以单独检验．对点练3(1)(2023·全国甲卷，理)设全集U＝Z，集合M＝{x|x＝3k＋1，k∈Z}，N＝{x|x＝3k＋2，k∈Z}，则U(M∪N)＝()A．{x|x＝3k，k∈Z}B．{x|x＝3k－1，k∈Z}C．{x|x＝3k－2，k∈Z}D．∅(2)(2023·全国乙卷，理)设集合U＝R，集合M＝{x|x<1}，N＝{x|－1<x<2}，则{x|x≥2}＝()A．U(M∪N)B．N∪U MC．U(M∩N)D．M∪U N解析：(1)因为整数集Z＝{x|x＝3k，k∈Z}∪{x|x＝3k＋1，k∈Z}∪{x|x＝3k＋2，k∈Z}，U＝Z，所以U(M∪N)＝{x|x＝3k，k∈Z}．故选A．(2)由题意可得M∪N＝{x|x<2}，则U(M∪N)＝{x|x≥2}，选项A正确；U M＝{x|x≥1}，则N∪U M＝{x|x>－1}，选项B错误；M∩N＝{x|－1<x<1}，则U(M∩N)＝{x|x≤－1或x≥1}，选项C错误；U N＝{x|x≤－1或x≥2}，则M∪U N＝{x|x<1或x≥2}，选项D错误．故选A．答案：(1)A (2)A维度2利用集合的运算求参数典例4(1)已知集合A ＝{x |x 2＋x －6＞0}，B ＝{x |2a －1＜x ＜a ＋2}，若A ∩B ≠∅，则实数a 的取值范围为()A∞(1,3)B∞(0,3)C ．(－∞，－1)∪(0,3)D ．(－∞，－2)∪(0,3)(2)已知集合A ＝{x |x 2＋ax ＋1＝0}，B ＝{x |x 2＋2x －a ＝0}，C ＝{x |x 2＋2ax ＋2＝0}，若三个集合至少有一个集合不是空集，则实数a 的取值范围是________．解析：(1)由题意可得集合A ＝(－∞，－3)∪(2，＋∞)，因为A ∩B ≠∅或在B≠∅的条件下，B 的左端点落在(－∞，－3)内或者右端点落在(2，＋∞)内，仔细体会这个取并集的含义．解得a ＜－1或0＜a ＜3，所以实数a 的取值范围是(－∞，－1)∪(0,3)．故选C ．(2)假设三个集合都是空集，即三个方程均无实根，这种解法很妙，在于应用了补集思想.先计算命题的否定，即三个集合都是空集时对应a 的范围，再取其补集．1＝a 2－4<0，2＝4＋4a <0，3＝4a 2－8<0，2<a <2，<－1，－2<a <2，则－2<a <－1，∴当a ≤－2或a ≥－1时，三个方程至少有一个方程有实根，即三个集合至少有一个集合不是空集．故实数a 的取值范围为{a |a ≤－2或a ≥－1}．故答案为{a |a ≤－2或a ≥－1}．利用集合的运算求参数的值或取值范围的方法(1)与不等式有关的集合，一般利用数轴解决，要注意端点值能否取到．(2)若集合中的元素能一一列举，则一般先用观察法得到不同集合中元素之间的关系，再列方程(组)求解．(3)运用补集思想求参数取值范围的步骤．第一步：把已知的条件否定，考虑反面问题．准确理解命题的否定叙述．第二步：求解反面问题对应的参数的取值范围．第三步：求反面问题对应的参数的取值集合的补集．对点练4已知集合A＝{x|x＜－1或x≥0}，B＝{x|x≥a}，若A∪B＝R，则实数a的取值范围是() A．(－∞，－1)B．(－∞，－1]C．(－∞，0)D．(－1,0)解析：如图，在数轴上表示出集合A，若A∪B＝R，则由图易知a≤－1，所以实数a的取值范围是(－∞，－1]，故选B．答案：B维度3集合新定义问题典例5(2024·名师原创)对集合A，B，记A－B＝{x|x∈A且x∉B}，定义A△B＝(A－B)∪(B－A)为A，B的对称差集．若A＝{x，xy，lg(xy)}，B＝{0，y，|x|}，且A△B＝∅，＋…________.解析：依题意及Venn图知，图中左侧阴影部分为A－B，右侧阴影部分为B－A，两阴影部分合起来就是A△B，因为A△B＝∅，所以A＝B，根据说明A－B＝∅且B－A＝∅，故有A＝B．集合中元素的互异性，且结合集合B知，x≠0，y≠0，因为0∈B，且A＝B，所以0∈A，故只有lg(xy)＝0，从而xy＝1，而1＝xy∈A，由A＝B其中x＝y＝1与思维线路：0∈A⇒xy＝1⇒x＝y＝1或x＝y＝－1，由互异性去伪存真．集合中元素的互异性矛盾，所以x＝y＝－1，…2＋2－2＋…＋2－2＝－2.故答案为－2.解决集合新定义问题的方法(1)紧扣新定义从抽象叙述，到具体的集合运算关系．分析新定义的特点，把新定义所叙述的问题的本质弄清楚，并能够应用到具体的解题过程之中，这是解答新定义型集合问题的关键．(2)用好集合的性质集合的性质(概念、元素的性质、运算性质等)是解答集合新定义问题的基础，也是突破口，在解答时要善于从试题中发现可以使用集合性质的一些因素，在关键之处用好集合的性质．对点练5设全集U＝{1,2,3,4,5,6}，且U的子集可表示由0,1组成的6位字符串，如：{2,4}表示的是自左向右的第2个字符为1，第4个字符为1，其余字符均为0的6位字符串010100，并规定空集表示的字符串为000000.(1)若M＝{2,3,6}，则U M表示的6位字符串为________；(2)已知A＝{1,3}，B⊆U，若集合A∪B表示的字符串为101001，则满足条件的集合B的个数是________．解析：(1)由已知，得U M＝{1,4,5}，则U M表示的6位字符串为100110.(2)由题意可知A∪B＝{1,3,6}，而A＝{1,3}，B⊆U，则B可能为{6}，{1,6}，{3,6}，{1,3,6}，故满足条件的集合B的个数是4.答案：(1)100110(2)4。

高考数学讲义：集合的运算(并集)(解析版)

第5讲：集合的运算（并集）【学习目标】1．理解两个集合的并集的含义．会求两个简单集合的并集；2．能使用Venn 图表达集合的关系及运算，体会直观图示对理解抽象概念的作用．【基础知识】一、并集【考点剖析】考点一：并集的求解（基础）例1．若集合{2,1,2}M =--，集合{0,2}N =，则M N 等于（）A．{2,1,2}--B．{2,1,0,2}--C．{}2D．{2,1,0}--【答案】B 【详解】因为集合{2,1,2}M =--，集合{0,2}N =，所以{2,1,0,2}M N =-- ，故选：B变式训练1：已知集合{}2,0,1M =-，{}1,0,1,2N =-，则M N = （）A．{}2,1,0,2--B．{}2,0,1-C．{}2,0,1,2-D．{}2,1,0,1,2--【答案】D 【详解】由{}2,0,1M =-，{}1,0,1,2N =-，∴{2,1,0,1,2}M N ⋃=--.故选：D.变式训练2：已知{|7}A x x =∈<N ，{5,6,7,8}B =，则集合A B 中的元素个数为（）A．7B．8C．9D．10【答案】C 【详解】{0,1,2,3,4,5,6}A =，{0,1,2,3,4,5,6,7,8}A B = ，共9个元素．故选：C．变式训练3：已知集合A=1{1,2,}2A =，B={}2|,y y x x A =∈，A B = _______________．【答案】11{1,2,,4,}24【详解】因为B={y|y=x2，x∈A}=1144⎧⎫⎨⎬⎩⎭，，，所以A∪B=1112424⎧⎫⎨⎬⎩⎭，，，，．故答案为：1112424⎧⎫⎨⎬⎩⎭，，，，考点二：并集的求解（提升）例2．已知集合{}{}7,27A y y B x x =<=-≤≤，则A B = （）A．{}22x x -≤<B．{}7x x ≤C．{}7x x <D．{}27x x -≤<【答案】B 【详解】{}{}{}77,27A y y x x B x x =<=<=-≤≤，∴A B = {}7x x ≤，故选：B.变式训练1：若集合{0,1,2,3},{13}S T xx ==-<<∣，则S T = （）A．{|13}x x -<<B．{|13}x x -<≤C．{0,1,2}D．{|03}x x <≤【答案】B 【详解】画数轴如图：可看出并集为S T ⋃={|13}x x -<≤故选：B变式训练2：设集合{}{}21,02M x x N x x =-<<=<<，则M N = （）A．{|20}x x -<<B．{|01}x x <<C．{|02}x x <<D．{|22}x x -<<【答案】D 【详解】由{|21}M x x =-<<，{|02}N x x =<<，则{|22}M N x x =-<< 故选：D.变式训练3：设集合13{|}A x x =≤≤，{|24}B x x =<<，则A B = （）A．{|14}x x ≤<B．{|23}x x ≤≤C．{|23}x x <≤D．{|24}x x £<【答案】A 【详解】因为集合13{|}A x x =≤≤，{|24}B x x =<<，所以[13](24)[14)A B == ，，，，故选：A.考点三：并集的求解（拓展）例3．已知集合{|42}M x x =-<<，2{|60}N x x x =--<，则M N =（）A．{|43}x x -<<B．{|42}x x -<<-C．{|22}x x -<<D．{|23}x x <<【答案】A 【详解】由题意，集合2{|60}{|23}N x x x x x =--<=-<<，且{|42}M x x =-<<，根据集合并集的概念及运算，可得{|43}M N x x ⋃=-<<.故选：A.变式训练1：若集合{}2270A x x x =-<，{}3B x x =>，则A B = （）A．{}x x >B．732x x ⎧⎫<<⎨⎬⎩⎭C．702x x ⎧⎫<<⎨⎬⎩⎭D．{0x x <或}3x >【答案】A 【详解】(){}727002A x x x x x ⎧⎫=-<=<<⎨⎬⎩⎭，{}3B x x =>，{}0A B x x ∴⋃=>.故选：A.变式训练2：已知集合{}220A x R x x =∈-<，{}14B x R x =∈≤≤，则A B = （）A．{}|04x x <<B．{}04x x <≤C．{}12x x ≤<D．{}24x x <≤【答案】B 【详解】因为{}{}22002A x R x x x R x =∈-<=∈<<，{}14B x R x =∈≤≤，所以{}04A B x x =<≤ .故选：B.变式训练3：已知集合()(){}410A x x x =+-≤，{}2B x x =<，则A B = （）A．{}22x x -<<B．{}21x x -<≤C．{}24x x -<≤D．{}42x x -≤<【答案】D 【详解】由不等式()()410x x +-≤，解得41x -≤≤，即{}41A x x =-≤≤，又因为{}22B x x =-<<，所以{}42A B x x ⋃=-≤<.故选：D.考点四：已知并集求参数例4．设集合{}{}20,2,|40A B x x mx n ==-+=，，若{}0,1,2,3,4A B = ，则m n +的值是（）A．1B．3C．5D．7【答案】D 【详解】因为集合{}{}20,2,|40A B x x mx n ==-+=，，{}0,1,2,3,4A B = ，则{}1,3B =，所以，1、3是方程20x mx n -+=的两根，所以，1313mn+=⎧⎨⨯=⎩，因此，437m n +=+=.故选：D.变式训练1：已知集合{}21,A a=，{}1,0,1B =-，若A B B = ，则A 中元素的和为（）A．0B．1C．2D．1-【答案】B 【详解】A B B =Q U ，A B ∴⊆，20a ∴=，则0a =，{}1,0A ∴=，因此，集合A 中元素的和为011+=.故选：B.变式训练2：设集合{}24A x Z x =∈≤，{}1,2,B a =，且A B A = ，则实数a 的取值集合为（）A．{}2,1,0--B．{}2,1--C．{}1,0-D．{}2,1,1--由题得{}{}242,1,0,1,2A x Z x =∈≤=--，因为{}1,2,B a =，且A B A = ，所以实数a 的取值集合为{}2,1,0--.故选：A变式训练3：已知集合{}2320A x x x =-+=，{}210B x x ax a =-+-=.（1）若A B A = ，求实数a 的值；【答案】（1）2a =或3；【详解】（1）由2320x x -+=得1x =或2，所以{1,2}A =，由210x ax a -+-=得1x =或1a -，所以1,1B a B ∈-∈，因为A B A ⋃=，所以B A ⊆，所以11a -=或2，所以2a =或3；考点五：已知并集求参数范围（基础）例5．已知集合{}2430A x x x =-+<，{}B x x m =>，若{}1A B x x => ，则（）A．1m ≥B．13m ≤<C．13m <<D．13m ≤≤【答案】B 【详解】解不等式2430x x -+<可得13x <<，所以{}13A x x =<<，因为{}B x x m =>，{}1A B x x ⋃=>，所以13m ≤<.故选：B.变式训练1：已知集合{|1}A x x =≤，{|}B x x a =≥，且A B R = ，则实数a 的取值范围是（）A．1a <B．1a >C．1a ≤D．1a ≥【答案】C 【详解】解：{|1}A x x =≤ ，{|}B x x a =≥，且A B R = ，故选：C.变式训练2：已知集合{}2A x x =>，{}B x x m =<，若A B R = ，则实数m 的取值范围（）A．2m ≤B．2m <C．2m ≥D．2m >【答案】D 【详解】因为A B R = ，即集合A 与集合B 包含了所有的实数，那么m>2.故选：D.变式训练3：设集合{}240A x x =-≥，{}20B x x a =+≤，且A B R = ，则a 的取值范围是（）A．{|4}x x ≥-B．{|4}x x ≤-C．{|2}x x ≥-D．{|2}x x ≤-【答案】B 【详解】240x -≥，解得：2x ≥或2x -≤，即{2A x x =≥或2}x £-，{|}2aB x x =≤-,A B R = ,22a∴-≥，解得：4a ≤-.故选：B考点六：已知并集关系，求参数范围（提升）例6．已知集合{|25},{|121}A x x B x m x m =-<<=+≤≤-.（1）当3m =时，求A B U ；（2）若A B A = ，求实数m 的取值范围.【答案】（1）{|25}A B x x =-<≤ ；（2）3m <.【详解】（1）当3m =时，B 中不等式为45x ≤≤，即{}|45B x x =≤≤，∴{|25}A B x x =-<≤ （2）∵A B A = ，∴B A ⊆，①当B =∅时，121m m +>-，即2m <，此时B A ⊆；②当B ≠∅时，12112215m m m m +≤+⎧⎪+>-⎨⎪-<⎩，即23m ≤<，此时B A ⊆.综上m 的取值范围为3m <.变式训练1：已知集合{}2430A xx x =-+>∣，{4}B x m x m =<≤+∣，若A B R = ，则实数m 的取值范围是（）A．{|12}x x -≤<B．{|11}x x -≤<C．{|1}x x <D．{|1}x x ≥-【答案】B 【详解】因为{}2430{|1A xx x x x =-+>=<∣或3}x >，{4}B x m x m =<≤+∣，且A B R = ，所以有143m m <⎧⎨+≥⎩，解得11m -≤<，故选：B.变式训练2：已知集合{}2|3100M x x x =--≤，{}|121N x a x a =+≤≤+．（1）若M N M = ，求实数a 的取值范围．【答案】（1）{|2}m m ≤.【详解】（1）（2）,M N M N M=∴⊆ ①若N =∅，则121a a +>+，解得0a <，符合题意；②若N ≠∅，则12121512a a a a +≤+⎧⎪+≤⎨⎪+≥-⎩，解得02a ≤≤．综合可得实数a 的取值范围是{|2}m m ≤．变式训练3：已知集合{}121A x a x a =+≤≤+,{}25B x x =-≤≤.（1）若3a =，求A B ；（2）若A B B = ，求实数a 的取值范围.【答案】（1）{}27x x -≤≤；（2）2a ≤.【详解】（1）当3a =时，{}47A x x =≤≤，{}25B x x =-≤≤.∴{}27A B x x ⋃=-≤≤（2）由A B B = 得A B ⊆，当A =∅时，211a a +<+，0a <当A ≠∅时，有12215121a a a a +≥-⎧⎪+≤⎨⎪+≤+⎩，解得02a ≤≤综上a 的取值范围为：2a ≤．【过关检测】1、已知集合{3,2,1}A =---，{2,1,0}B =--，则A B = （）A．{3,2,1,0}---B．{3,2,1}---C．{2,1,0}--D．{2,1}--【答案】A 【详解】由{3,2,1}A =---，{2,1,0}B =--，则{3,2,1,0}A B ⋃=---.故选：A2、若集合{}=2,1,1M --，集合{}0,1N =，则M N 等于（）A．{}2,1,0,1--B．{}2,1,1--C．{}2,1,0--D．{}1【答案】A 【详解】因为集合{}=2,1,1M --，集合{}0,1N =，所以M N ⋃{}2,1,0,1=--，故选：A3、已知集合{}210,A x x x =-≤∈Z ，{}2,B y y x x A ==∈，则A B = （）A．{2,1,1,2}--B．{2,1,0,1,2}--C．{1,1}-D．{0}【答案】B 【详解】集合{}{}{}210,11,1,0,1A x x x x x x =-≤∈=-≤≤∈=-Z Z ，{}{}2,2,0,2B y y x x A ==∈=-，{}2,1,0,1,2A B ∴=--U ，故选：B.4、已知集合{}2,4,6A =，{}1,3,4,6B =，则A B 中元素的个数是（）A．2B．5C．6D．7【答案】B 【详解】由题意得，{}1,2,3,4,6A B = ，显然A B 中元素的个数是5.故选：B．5、若集合{1,3,}A x =，{}2,1B x =，且{1,3,}A B x = ，则满足条件的x 的个数是（）A．1B．2C．3D．4【答案】C 【详解】∵{1,3,}A B x = ，{1,3,}A x =，{}2,1B x =，∴23x =或2x x =，解得x =或1x =或0x =，1x =显然不合题意，经检验0x =或故选：C．6、已知集合{}0,1,2A ，{}21,B x x n n A ==-∈，则A B 中元素的个数为（）A．1B．3C．4D．5【答案】D【详解】解：{}0,1,2A =，{}1,1,3B =-；∴{}1,0,1,2,3A B ⋃=-；∴A B 中元素的个数为5.故选：D.7、已知集合{}1,0,1A =-，{}2|1,B y y x x A ==+∈，则集合A B 中元素的个数为（）A．4B．3C．2D．1【答案】A【详解】当1,0,1x =-，对应2,1,2y =，{}2,1B ∴=，则{}1,0,1,2A B ⋃=-，A B 中有4个元素.故选：A8、满足条件{}{},,,,a b M a b c d = 的所有集合M 的个数是（）A．1B．2C．3D．4【答案】D【详解】解:由{}{},,,,a b M a b c d ⋃=,则{},M c d ={},,M a c d =,或{},,M b c d =,或{},,,M a b c d =共4个,故选D.9、已知集合{0,1,2}M =，{}2N x x =<，则M N = （）A．{0}B．{}2x x <C．{0,1}D．{}2x x ≤【答案】D【详解】由题意，集合{0,1,2}M =，{}2N x x =<，根据集合并集的概念及运算，可得{}2M N x x ⋃=≤.故选：D.10、已知集合{}13A x x =<<，{}02B x x =<<，则A B = （）A．{}12x x <<B．{}13x x x <<C．{}02x x <<D．{}03x x <<【答案】D【详解】因为{}13A x x =<<，{}02B x x =<<，所以A B = {}03x x <<故选：D11、已知集合{1},{12}A x x B x x =>=-<<∣∣，则A B = （）A．{1}x x >-∣B．{2}x x <∣C．{11}x x -<<∣D．{12}x x <<∣【答案】A【详解】因为{1},{12}A x x B x x =>=-<<∣∣，所以A B = {1}x x >-∣，故选：A．12、已知集合{}42M x x =-<<，{}(2)(3)0N x x x =+-<，则M N = （）A．{}43x x -<<B．{}42x x -<<-C．{}22x x -<<D．{}23x x <<【答案】A【详解】解：∵{}42M x x =-<<，{}{}(2)(3)023N x x x x x =+-<=-<<，∴{}43M N x x ⋃=-<<，故选：A．13、已知集合{}2230A xx x =--<∣，1{0}2B x x =->∣，则A B = （）A．13{}22x x <<∣B．3{}2x x <∣C．1{1}2x x -<<∣D．{1}xx >-∣【答案】D【详解】解：∵集合{}2323012A xx x x x ⎧⎫=--<=-<<⎨⎩⎭∣∣，11022B x x x x ⎧⎫⎧⎫=->=>⎨⎬⎨⎬⎩⎭⎩⎭∣∣，∴{1}A B xx ⋃=>-∣．故选：D．14、已知集合{}{}2|5140,|5100A x x x B x x =--<=-<，则A B = （）A．{}|27x x -<<B．{}27x x <<C．{}|7x x <D．{}2x x >-【答案】C【详解】解不等式25140x x --<得27x -<<，所以{}27A x x =-<<；解不等式5100x -<得2x <，所以{}2B x x =<，所以{}|7A B x x ⋃=<.故选：C.15、若集合{1,2}A =-，{}240B x x x m =-+=，且{1,2,5}A B =- ，则（）A．2B∈B．5B ∉C．1B ∈D．1B-∈【答案】D【详解】依题意，5∈B ，则25200m -+=，解得5m =-，故{1,5}B =-；观察可知，1B -∈，故选：D．16、若集合{1,1}A =-，{|1}B x mx ==，且A B A = ，则m 的值为（）A．1或0B．1-或0C．1或1-或0D．1或1-或2【答案】C【详解】,A B A B A⋃=⊆ ∴B ∴=∅；{1}B =-；{1}B =当B =∅时，0m =当{1}B =-时，1m =-当{1}B =时，1m =故m 的值是0；1；1-故选：C．17、已知集合2{|20}A x x x =-≥，{|}B x x a =<，且A B = R ，则实数a 的取值范围是（）A．0a <B．0a >C．2a >D．2a ≥【答案】D【详解】由220x x -≥解得0x ≤或2x ≥，则{|0,A x x =≤或}2x ≥，又{|}B x x a =<，若A B = R ，则2a ≥.故选：D .18、已知集合{}2430A x x x =-+=，{}230B x x ax =-+=．（1）若A B B = ，求实数a 的值；【答案】（1）4；【详解】{}2430A x x x =-+=={}1,3，（1）因为A B B ⋃=，所以A B ⊆，所以1和3是230x ax -+=的两个实根，所以13a +=，即4a =.19、设集合{213}A xm x m =-+<<-+∣，{216}B x x =≤+≤∣．（1）若1m =，求A B ；（2）若A B B = ，求实数m 的取值范围．【答案】（1）{|15}A B x x =-<≤ ；（2）{|0}m m ≤．【详解】解：（1）因为{213}A xm x m =-+<<-+∣，{216}{15}B x x x x =≤+≤=≤≤∣∣，（1）若1m =，{12}A xx =-<<∣，则{|15}A B x x =-<≤ ．（2）因为A B B = ，所以A B ⊆，①当A =∅时，213m m -+≥-+，即2m ≤-；②当A ≠∅时，213,211,35,m m m m -+<-+⎧⎪-+≥⎨⎪-+≤⎩解得20m -<≤，综上，实数m 的取值范围是{|0}m m ≤．20、已知集合{}25A x x =-≤≤，{}121B x m x m =+≤≤-.（1）若A B A = ，求实数m 的取值范围；（2）当{},C x x A x Z =∈∈时，求C 的非空真子集的个数；【答案】（1）(],3-∞；（2）254.【详解】（1）A B A =Q U ，B A ∴⊆.①若B =∅，则121m m +>-，解得2m <；②若B ≠∅，则121m m +≤-，可得2m ≥.由B A ⊆可得12215m m +≥-⎧⎨-≤⎩，解得33m -≤≤，此时23m ≤≤.综上所述，实数m 的取值范围是(],3-∞；（2）{}{},2,1,0,1,2,3,4,5C x x A x Z =∈∈=-- ，集合C 中共8个元素，因此，集合C 的非空真子集个数为822254-=；21、已知集合{}13A x x =≤≤，集合{}21B x m x m =≤≤-.（1）当1m =-时，求A B ；（2）若A B B = ，求实数m 的取值范围.【答案】（1）{}23A B x x =-≤≤ ；（2）{}2m m ≤-.【详解】（1）当1m =-时,{}22B x x =-≤≤，又{}13A x x =≤≤，∴{}23A B x x ⋃=-≤≤；（2）∵A B B = ，则A B ⊆，∴B ≠∅，则有：212113m m m m <-⎧⎪≤⎨⎪-≥⎩，解之得：2m ≤-.∴实数m 的取值范围是{}2m m ≤-.。

高中必修一集合复习讲义

第一讲集合题型1．正确理解和运用集合概念理解集合的概念,正确应用集合的性质是解此类题目的关键.例1.已知集合M={y|y=x 2＋1,x∈R},N={y|y=x＋1,x∈R}，则M∩N=（）A ．（0，1），（1，2）B ．{（0，1），（1，2）}C ．{y|y=1,或y=2}D ．{y|y≥1} 例2.若P={y|y=x 2,x∈R}，Q={y|y=x 2＋1,x∈R}，则P∩Q 等于（）A ．PB ．QC ．D ．不知道例3. 若P={y|y=x 2,x∈R}，Q={(x ，y)|y=x 2,x∈R}，则必有（）A ．P∩Q=∅B ．PQ C ．P=Q D ．P Q 例4若}032|{}1|{22=--===x x x B x x A ，，则B A ⋂= （） A ．{3} B ．{1} C ．∅D ．{－1} 题型2．集合元素的互异性集合元素的互异性，是集合的重要属性，教学实践告诉我们，集合中元素的互异性常常被学生在解题中忽略，从而导致解题的失败，下面再结合例题进一步讲解以期强化对集合元素互异性的认识．例6. 已知集合A a ={}13，，，集合B a a =-+{}112，，如果B A ⊆，求a 的值例7.已知集合A={x|x 2－3x ＋2=0},B={x|x 2－a x ＋a －1=0}，且A∪B=A，则a 的值为______．题型3．要注意掌握好证明、判断两集合关系的方法集合与集合之间的关系问题，是我们解答数学问题过程中经常遇到，并且必须解决的问题，因此应予以重视．反映集合与集合关系的一系列概念，都是用元素与集合的关系来定义的．因此，在证明（判断）两集合的关系时，应回到元素与集合的关系中去．例8.设集合A={a |a =3n ＋2,n∈Z}，集合B={b|b=3k －1,k∈Z}，则集合A 、B 的关系是________．例9若A 、B 、C 为三个集合，C B B A ⋂=⋃，则一定有（）A . C A ⊆B .AC ⊆ C .C A ≠D . A =∅例10．设集合{1,2}A =,则满足{1,2,3}A B ⋃=的集合B 的个数是（）A . 1B .3C .4D . 8例11．记关于x 的不等式01x a x -<+的解集为P ，不等式11x -≤的解集为Q ．（I ）若3a =，求P ；（II ）若Q P ⊆，求正数a 的取值范围．题型4. 要注意空集的特殊性和特殊作用空集是一个特殊的重要集合，它不含任何元素，是任何集合的子集，是任何非空集合的真子集．显然，空集与任何集合的交集为空集，与任何集合的并集仍等于这个集合．当题设中隐含有空集参与的集合关系时，其特殊性很容易被忽视的，从而引发解题失误．例12. 已知A={x|x 2－3x ＋2=0},B={x|a x －2=0}且A∪B=A，则实数a 组成的集合C 是____．例13．已知集合{}|1A x x a =-≤，{}2540B x x x =-+≥．若A B ⋂=∅，则实数a 的取值范围是．例14.已知集合{}0103|2≤--=x x x A ，集合B={x|p ＋1≤x ≤2p －1}．若B A ，则实数p 的取值范围是________．题型5．要注意利用数形结合解集合问题集合问题大都比较抽象，解题时要尽可能借助文氏图、数轴或直角坐标系等工具将抽象问题直观化、形象化、明朗化，然后利用数形结合的思想方法使问题灵活直观地获解．例15.集合A={x|x2＋5x－6≤0},B={x|x2＋3x>0}，求A∪B和A∩B．例16.已知集合{}{}22=-->=++≤,且230,0A x x xB x x ax b{},34⋃=⋂=<≤，A B R A B x x求a,b的值.练习：1．设集合U＝{1,2,3,4,5}，A＝{1,2}，B＝{2,3,4}，则∁U(A∪B)等于()A．{2}B．{5}C．{1,2,3,4} D．{1,3,4,5}2．集合A＝{x|0＜x≤2}，B＝{x∈R|x2－x－2＞0}，则A∩(∁R B)＝()A ．(－1,2)B ．[－1,2]C ．(0,2)D ．(0,2]3．已知a ∈R ，集合M ＝{1，a 2}，N ＝{a ，－1}．若M ∪N 有三个元素，则M ∩N ＝( )A ．{0,1}B ．{0，－1}C ．{0}D ．{1}二、填空题7．已知集合A ＝{x |log 2x ≤2}，B ＝(－∞，a )，若A ⊆B ，则实数a 的取值范围是(c ，＋∞)，其中c ＝__________.9．若集合{x |ax 2＋2x ＋1＝0}与集合{x 2－1＝0}的元素个数相同，则实数a 的取值集合为__________．三、解答题10．已知集合A ＝{x |－1＜x ＜3}，集合B ＝⎝ ⎛⎭⎪⎫－∞，－13∪(1，＋∞)，集合C ＝{x |2x 2＋mx －8＜0}．(1)求A ∩B ，A ∪(∁R B )；2)若(A ∩B )⊆C ，求m 的取值范围．。

1集合(高考讲义)

1集合（高考讲义）专题一：普通集合的交并补运算1、[2012·辽宁卷理1] 已知全集U＝{0,1,2,3,4,5,6,7,8,9}，集合A＝{0,1,3,5,8}，集合B＝{2,4,5,6,8}，则(∁U A)∩(∁∪B)＝( B )A、{5,8}B、{7,9}C、{0,1,3}D、{2,4,6}2、[2012·广东卷理2] 设集合U＝{1,2,3,4,5,6}，M＝{1,2,4}，则∁U M＝( C )A、UB、{1,3,5}C、{3,5,6}D、{2,4,6}3、（2010•湖北）设集合M={1，2，4，8}，N={x|x是2的倍数}，则M∩N=（ C ）A、{2，4}B、{1，2，4}C、{2，4，8}D、{1，2，8}4、（2010•广东）若集合A={0，1，2，3}，B={1，2，4}，则集合A∪B=（ A ）A、{0，1，2，3，4}B、{1，2，3，4}C、{1，2}D、{0}5、（2010•辽宁）已知集合U={1，3，5，7，9}，A={1，5，7}，则C U A=（ D ）A、{1，3}B、{3，7，9}C、{3，5，9}D、{3，9}6、（2011•湖南）设全集U=M∪N=﹛1，2，3，4，5﹜，M∩C u N=﹛2，4﹜，则N=（ B ）A、{1，2，3}B、{1，3，5}C、{1，4，5}D、{2，3，4}7、（2011•湖北）已知U={1，2，3，4，5，6，7，8}，A={1，3，5，7}，B={2，4，5}则C u （A∪B）（ A ）A、{6，8}B、{5，7}C、{4，6，7}D、{1，3，5，6，8}8、[2012·浙江卷文1] 设全集U＝{1,2,3,4,5,6}，集合P＝{1,2,3,4}，Q＝{3,4,5}，则P∩(∁U Q)＝( D )A、{1,2,3,4,6}B、{1,2,3,4,5}C、{1,2,5}D、{1,2}9、（2011•安徽）集合U={1，2，3，4，5，6}，S={1，4，5}，T={2.3.4}，则S∩（∁U T）等于（ B ）A、{1，4，5，6}B、{1，5}C、{4}D、{1，2，3，4，5}10、（2009•宁夏）已知集合A={1，3，5，7，9}，B={0，3，6，9，12}，则A∩C N B=（ A ）A、{1，5，7}B、{3，5，7}C、{1，3，9}D、{1，2，3}11、[2012·山东卷理2] 已知全集U＝{0,1,2,3,4}，集合A＝{1,2,3}，B＝{2,4}，则(∁U A)∪B为( C )A、{1,2,4}B、{2,3,4}C、{0,2,4}D、{0,2,3,4}12、[2012·四川卷文1] 设集合A＝{a，b}，B＝{b，c，d}，则A∪B＝( D )A、{b}B、{b，c，d}C、{a，c，d}D、{a，b，c，d}13、[2012·江苏卷理1] 已知集合A＝{1,2,4}，B＝{2,4,6}，则A∪B＝____{1,2,4,6}____.14、[2012·四川卷理13] 设全集U＝{a，b，c，d}，集合A＝{a，b}，B＝{b，c，d}，则(∁U A)∪(∁U B)＝____{a，c，d}____.15、（2011•江苏）已知集合A={﹣1，1，2，4}，B={﹣1，0，2}，则A∩B= {﹣1，2} ．16、（2009•重庆）若U={n|n是小于9的正整数}，A={n∈U|n是奇数}，B={n∈U|n是3的倍数}，则∁U（A∪B）= {2，4，8} ．专题二：集合的包含关系1、[2012·福建卷文2] 已知集合M＝{1,2,3,4}，N＝{－2,2}，下列结论成立的是( D )A、N⊂MB、M∪N＝MC、M∩N＝ND、M∩N＝{2}2、（2010•湖南）已知集合M={1，2，3}，N={2，3，4}，则（ C ）A、M⊆NB、N⊆MC、M∩N={2，3}D、M∪N={1，4}3、（2011•江西）若全集U={1，2，3，4，5，6}，M={2，3}，N={1，4}，则集合{5，6}等于（ D ）A、M∪NB、M∩NC、（C u M）∪（C u N）D、（C u M）∩（C u N）4、（2011•浙江）若P={x|x＜1}，Q={x|x＞1}，则（ D ）A、P⊆QB、Q⊆PC、C R P⊆QD、Q⊆C R P5、（2010•浙江）设P={x|x＜4}，Q={x|x2＜4}，则（ B ）A、P⊆QB、Q⊆PC、P⊆C R QD、Q⊆C R P6、[2012·全国卷文1] 已知集合A＝{x|x是平行四边形}，B＝{x|x是矩形}，C＝{x|x是正方形}，D＝{x|x是菱形}，则( B )A、A⊆BB、C⊆BC、D⊆CD、A⊆D专题三：元素、子集、真子集个数1、[2012·江西卷理1]若集合A＝{－1,1}，B＝{0,2}，则集合{z|z＝x＋y，x∈A，y∈B}中的元素的个数为( C )A、5B、4C、3D、22、[2012·湖北卷文1]已知集合A＝{x|x2－3x＋2＝0，x∈Z}，B＝{x|0＜x<5，x∈Z}，则满足条件A⊆C⊆B的集合C的个数为( D )A、1B、2C、3D、43、*（2011•安徽）设集合A={1，2，3，4，5，6}，B={4，5，6，7，8}，则满足S⊆A且S ∩B≠∅的集合S的个数是（ B ）A、57B、56C、49D、84、*（2010•湖北）设集合A={（x，y）∣x 24+y216=1}，B={（x，y）|y=3x}，则A∩B的子集的个数是（ A ）A、4B、3C、2D、1专题四： Venn图表达集合的关系及运算1、（2010•辽宁）已知A，B均为集合U={1，3，5，7，9}的子集，且A∩B={3}，C U B∩A={9}，则A=（ D ）A、{1，3}B、{3，7，9}C、{3，5，9}D、{3，9}2、（2009•广东）已知全集U=R，集合M={x|﹣2≤x﹣1≤2}和N={x|x=2k﹣1，k=1，2，…}的关系的韦恩（Venn）图如图所示，则阴影部分所示的集合的元素共有（ B ）A、3个B、2个C、1个D、无穷多个3、（2009•广东）已知全集U=R，则正确表示集合M={﹣1，0，1}和N={x|x2+x=0}关系的韦恩（Venn）图是（ B ）A、B、C、D、4、（2011•辽宁）已知M，N为集合I的非空真子集，且M，N不相等，若N∩C1M=∅，则M∪N=（ A ）A、MB、NC、ID、∅5、（2009•江西）50名学生参加甲、乙两项体育活动，每人至少参加了一项，参加甲项的学生有30名，参加乙项的学生有25名，则仅参加了一项活动的学生人数为（ B ）A、50B、45C、40D、356、（2009•湖南）某班共30人，其中15人喜爱篮球运动，10人喜爱乒乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为12 ．*7、（2009•陕西）某班有36名同学参加数学、物理、化学课外探究小组，每名同学至多参加两个小组，已知参加数学、物理、化学小组的人数分别为26，15，13，同时参加数学和物理小组的有6人，同时参加物理和化学小组的有4人，则同时参加数学和化学小组的有8 人．专题五：集合与函数定义域及值域的综合运用1、（2010•江西）若集合A={x||x|≤1，x∈R}，B={y|y=x2，x∈R}，则A∩B=（ C ）A、{x|﹣1≤x≤1}B、{x|x≥0}C、{x|0≤x≤1}D、∅2、[2012·安徽卷文2]设集合A＝{x|－3≤2x－1≤3}，集合B为函数y＝lg(x－1)的定义域，则A∩B＝( D )A、(1,2)B、[1,2]C、[1,2)D、(1,2]|＜2，i为虚数单3、*（2011•陕西）设集合M={y|y=|cos2x﹣sin2x|，x∈R}，N={x||x﹣1i位，x∈R}，则M∩N为（ B ）A、（0，1）B、[0，1）C、（﹣1，1）D、[0，1]专题六：点集的应用1、（2011•广东）已知集合A={（x，y）|x，y为实数，且x2+y2=1}，B={（x，y）|x，y为实数，且y=x}，则A∩B的元素个数为（ C ）A、0B、1C、2D、32、（2011•广东）已知集合A={（x，y）|x，y为实数，且x2+y2=1}，B=|（x，y）|x，y为实数，且x+y=1}，则A∩B的元素个数为（ C ）A、4B、3C、2D、13、*[2012·课标全国卷理1] 已知集合A＝{1,2,3,4,5}，B＝{(x，y)|x∈A，y∈A，x－y∈A}，则B中所含元素的个数为( D )A、3B、6C、8D、104、*（2009•湖北）已知P={a|a=（1，0）+m（0，1），m∈R}，Q={b|b=（1，1）+n（﹣1，1），n∈R}是两个向量集合，则P∩Q=（ A ）A、{（1，1）}B、{（﹣1，1）}C、{（1，0）}D、{（0，1）}专题七：集合中参数取值1、（2009•山东）集合A={0，2，a}，B={1，a2}，若A∪B={0，1，2，4，16}，则a的值为（ D ）A、0B、1C、2D、42、（2011•湖南）设集合M={1，2}，N={a2}，则“a=1”是“N⊆M”的（ A ）A、充分不必要条件B、必要不充分条件C、充分必要条件D、既不充分又不必要条件3、（2011•北京）已知集合P={x|x2≤1}，M={a}．若P∪M=P，则a的取值范围是（ C ）A、（﹣∞，﹣1]B、[1，+∞）C、[﹣1，1]D、（﹣∞，﹣1]∪[1，+∞）4、[2012·全国卷理2]已知集合A＝{1,3，m}，B＝{1，m}，A∪B＝A，则m＝( B )A、0或 3B、0或3C、1或 3D、1或35、（2010•江苏）设集合A={﹣1，1，3}，B={a+2，a2+4}，A∩B={3}，则实数a= 1 ．6、（2010•湖南）已知集合A={1，2，3，}，B={2，m，4}，A∩B={2，3}，则m= 37、（2010•上海）已知集合A={1，3，m}，B={3，4}，A∪B={1，2，3，4}，则m= 2 ．8、（2010•重庆）设U={0，1，2，3}，A={x∈U|x2+mx=0}，若∁U A={1，2}，则实数m= ﹣3 ．专题八：新定义问题1、（2009•浙江）定义A﹣B={x|x∈A且x∉B}，若P={1，2，3，4}，Q={2，5}，则Q﹣P（ B ）A、PB、{5}C、{1，3，4}D、Q2、（2010•广东）在集合{a，b，c，d}上定义两种运算+和*如下那么d*（a+c）（ A ）A、aB、bC、cD、d3、*（2010•福建）设非空集合S={x|m≤x≤l}满足：当x∈S时，有x2∈S．给出如下三个命题：①若m=1，则S={1}；②若m=﹣12，则14≤l≤1；③若l=12，则﹣22≤m≤0．其中正确命题的个数是（ D ）A、0B、1C、2D、34、*（2011•广东）设S是整数集Z的非空子集，如果∀a，b∈S有ab∈S，则称S关于数的乘法是封闭的，若T，V是Z的两个不相交的非空子集，T∪V=Z，且∀a，b，c∈T，有abc ∈T；∀x，y，z∈V，有xyz∈V，则下列结论恒成立的是（ A ）A、T，V中至少有一个关于乘法是封闭的B、T，V中至多有一个关于乘法是封闭的C、T，V中有且只有一个关于乘法是封闭的D、T，V中每一个关于乘法都是封闭的5、*（2011•浙江）设a，b，c为实数，f（x）=（x+a）（x2+bx+c），g（x）=（ax+1）（cx2+bx+1）．记集合S={x|f（x）=0，x∈R}，T={x|g（x）=0，x∈R}．若{S}，{T}分别为集合S，T 的元素个数，则下列结论不可能的是（ D ）A、{S}=1且{T}=0B、{S}=1且{T}=1C、{S}=2且{T}=2D、{S}=2且{T}=36、*（2009•北京）设A是整数集的一个非空子集，对于k∈A，如果k﹣1∉A且k+1∉A，那么称k是A的一个“孤立元”，给定S={1，2，3，4，5，6，7，8}，由S的3个元素构成的所有集合中，不含“孤立元”的集合共有 6 个．。

集合的基本运算(精讲)(原卷版)--2023届初升高数学衔接专题讲义

2023年初高中衔接素养提升专题讲义第八讲集合的基本运算（精讲）（原卷版）【知识点透析】一、交集1、文字语言：对于两个给定的集合A ，B ，由属于A 又属于B 的所有元素构成的集合，叫做A ，B 的交集，记作A ∩B ，读作“A 交B ”2、符号语言：A ∩B ＝{x |x ∈A 且x ∈B }3、图形语言：阴影部分为A ∩B4、性质：A ∩B ＝B ∩A ，A ∩A ＝A ，A ∩∅＝∅∩A ＝∅，如果A ⊆B ，则A ∩B ＝A5、解题思路：单个数字交集找相同，不等式的交集画数轴，不同集合高度画不同。

二、并集1、文字语言：对于两个给定的集合A ，B ，由两个集合的所有的元素组成的集合，叫做A 与B 的并集，记作A ∪B ，读作“A 并B ”2、符号语言：A ∪B ＝{x |x ∈A 或x ∈B }3、符号语言：阴影部分为A ∪B4、性质：A ∪B ＝B ∪A ，A ∪A ＝A ，A ∪∅＝∅∪A ＝A ，如果A ⊆B ，则A ∪B ＝B .5、解题思路：两个集合所有元素集中在一起，但是重复元素只写一次，要满足集合中的互异性三、补集1、全集：在研究集合与集合之间的关系时，如果所要研究的集合都是某一给定集合的子集，那么称这个给定的集合为全集．记法：全集通常记作U .2、补集（1）文字语言：如果给定集合A 是全集U 的一个子集，由U 中不属于A 的所有元素构成的集合，叫做A 在U 中的补集，记作A C U .（2）符号语言：}|{A x U x x A C U ∉∈=且（3）符号语言：（4）性质：A ∪∁U A ＝U ；A ∩∁U A ＝∅；∁U (∁U A )＝A .【注意】并不是所有的全集都是用字母U 表示，也不是都是R，要看题目的。

四、利用交并补求参数范围的解题思路1、根据并集求参数范围：=⇒⊆ A B B A B ，若A 有参数，则需要讨论A 是否为空集；若B 有参数，则≠∅B 2、根据交集求参数范围：=⇒⊆ A B A A B若A 有参数，则需要讨论A 是否为空集；若B 有参数，则≠∅B 【知识点精讲】题型一并集、交集、补集的运算【例题1】（2022·浙江·杭十四中高一期中）设全集{}1,2,3,4,5,6U =，集合{}{}1,3,5,2,3,4,5S T ==，则S T ⋃=（）A ．{}3,5B ．{}2,4C ．{}1,2,3,4,5D ．{}1,2,3,4,5,6【例题2】（2021春•山西大同期中）设集合{|1}A x x =<，{|22}B x x =-<<，则(A B = )A ．{|21}x x -<<B ．{|2}x x <C ．{|22}x x -<<D ．{|1}x x <【例题3】．（2022·江苏·高二期末）已知集合{}1,2A =，{}21,2B a a =-+，若{}1A B ⋂=，则实数a 的值为（）A ．0B ．1C ．2D ．3【例题4】．（2022·陕西·宝鸡市陈仓高级中学高三开学考试（理））已知集合{}21A x x =-<≤，{}0B x x a =<≤，若{|23}A B x x =-<≤ ，A B = （）A ．{|20}x x -<<B ．{|01}x x <≤C ．{|13}x x <≤D ．{|23}x x -<≤【例题5】．（2021·北京昌平区·高二期末）已知全集{0,1,2,3,4,5}U =，集合{0,1,2,3}A =，{3,4}B =，则()U A B = ð___________.【例题6】．（2022·四川南充高一课时检测）已知全集{}16A x x =≤≤，集合{}15B x x =<<，则A B =ð（）．A ．{}5x x ≥B ．{1x x ≤或}5x ≥C ．{1x x =或}56x <≤D ．{1x x =或}56x ≤≤【例题7】．41．（2021·陕西商洛市·镇安中学高一期中）已知集合{}25A x x =-≤≤，{}121B x m x m =+≤≤-．（1）若4m =，求A B ；（2）若A B =∅ ，求实数m 的取值范围．【变式1】．（2022·河北邢台高二期末）若集合{}|24M x x =-<≤，{}|46N x x =≤≤，则A ．M N ⊆B ．{}4M N =C ．M N ⊇D ．{}26|M N x x =-<< 【变式2】．（2022·江苏常州高三开学考试）设集合{}11A x x =-<<，{}220B x x x =-≤，则A B ⋃=（）A ．(]1,2-B ．()1,2-C ．[)0,1D ．(]0,1【变式3】（2022·青海·海东市第一中学模拟预测（文））已知集合{}1,1,2M =-，{}2N x x x =∈=R ，则M N ⋃=（）A ．{}1B ．{}1,0-C ．{}1,0,1,2-D ．{}1,0,2-【变式4】．（2022·浙江·三模）已知集合{}{}25,36P x x Q x x =≤<=≤<，则P Q = （）A ．{}25x x ≤<B ．{}26x x ≤<C ．{}35x x ≤<D ．{}36x x ≤<题型二并集、交集、补集综合运算及性质的应用【例题8】．（2022·河南洛阳高一课时检测）已知全集U ，集合{}1,3,5,7,9A =，{}2,4,6,8U C A =，{}1,4,6,8,9U C B =，则集合B =（）A ．{}1,5,7B ．{}3,5,7,9C ．{}2,3,5,7,9D ．{}2,3,5,7【例题9】．（2022·重庆·西南大学附中模拟预测）已知集合{}|10A x ax =-=，{}*|14B x x =∈≤<N ，且A B B ⋃=，则实数a 的所有值构成的集合是（）A ．11,2⎧⎫⎨⎬⎩⎭B ．11,23⎧⎫⎨⎬⎩⎭C ．111,,23⎧⎫⎬⎭D ．110,1,,23⎧⎫⎨⎬⎩⎭【例题10】．（湖北省“宜荆荆恩”2022-2023学年高三上学期起点考试）已知集合(,1][2,)A =-∞⋃+∞，{|11}B x a x a =-<<+，若A B =R ，则实数a 的取值范围为（）A ．(1,2)B ．[1,2)C ．(1,2]D ．[1,2]【例题11】．（2022·云南昆明一中高一检测）已知A ，B 都是非空集合，(){}&A B x x A B =∈⋃且()x A B ∉ ．若{}02A x x =<<，{}0B x x =≥，则&A B =（）A ．{}0x x ≥B ．{}02x x <<C ．{0x x =或}2x <-D ．{0x x =或}2x ≥【例题12】．（2021·江苏高一专题练习）已知集合{}42A x x =-<<，{}110B x m x m m =--<<->，．（1）若A B B ⋃=，求实数m 的取值范围；（2）若A B ⋂≠∅，求实数m 的取值范围．【变式1】（2022·辽宁沈阳高一课前预习）集合{}2320A x x x =-+=，{}2220B x x ax =-+=，若A B A ⋃=，求实数a 的取值范围.【变式2】．（2023·浙江高二开学考试）已知R a ∈，设集合{}22210A x x ax a =-+-<，{}2B x x =>，（1）当2a =时，求集合A ．（2）若R A B ⊆ð，求实数a 的取值范围．【变式3】．（2022·四川乐山市高一单元测试）已知集合{}211A x a x a =-<<+，{}01B x x =≤≤．(1)在①1a =-，②0a =，③1a =这三个条件中任选一个作为已知条件，求A B ；(2)若R A B A ⋂=ð，求实数a 的取值范围．题型三Venn 图的应用【例题13】．（2021·贵州省思南中学高三月考（理））已知全集U =R ，集合{}23,A y y x x R ==+∈，{}24B x x =-<<，则图中阴影部分表示的集合为（）A ．[]2,3-B ．()2,3-C ．(]2,3-D ．[)2,3-【例题14】．（2021·全国高三其他模拟）已知全集U x y ⎧⎫=∈=⎨⎩Z ，集合{}13M x x =∈-<Z ，{}4,2,0,1,5N =--，则下列Venn 图中阴影部分表示的集合为（）A ．{}0,1B ．{}3,1,4-C ．{}1,2,3-D ．{}1,0,2,3-【例题15】．（2021·山东济南·高一期中）国庆期间，高一某班35名学生去电影院观看了《长津湖》、《我和我的父辈》这两部电影中的一部或两部.其中有23人观看了《长津湖》，有20人观看了《我和我的父辈》则同时观看了这两部电影的人数为（）A ．8B ．10C ．12D ．15【变式】．（2021·广东·广州外国语学校高一检测）某公司共有50人，此次组织参加社会公益活动，其中参加A 项公益活动的有28人，参加B 项公益活动的有33人，且A ，B 两项公益活动都不参加的人数比都参加的人数的三分之一多1人，则只参加A 项不参加B 项的有（）A ．7人B ．8人C ．9人D ．10人。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

一集合的概念集合是一个不定义的概念，集合中的元素有三个特征：1）确定性设A 是一个给定的集合，a 是某一具体对象，则a 或者是A 的元素，或者不是A 的元素，两者必居其一，即a ∈A 与a ∉A 仅有一种情况成立。

2）互异性一个给定的集合中的元素是指互不相同的对象,即同一个集合中不应出现同一个元素。

3）无序性1．下列关系式中正确的是（）(A){}Φ⊆Φ (B){}0∈Φ (C)0{}Φ= (D)0{}⊆Φ2．设{}{}24,21,,9,5,1A a a B a a =--=--,已知{}9A B = ,求实数a 的值.3．设集合A={1,,22-y x x ｝,B=｛0,y x |,|｝且A=B,求y x ,的值。

4．（全国1理）设,a b R ∈，集合{1,,}{0,,}b a b a b a+=，则b a -= A ．1 B ．1- C ．2 D ．2-5．已知全集U ＝｛2，4，1－a ｝，A ＝｛2，a 2－a ＋2｝如果{}1U A =-ð，那么a 的值为____.20102010,,{1,,}{0,,},b a b R a a b b a b a∈+=-6.若集合求的值。

二集合的表示方法主要有列举法、描述法、区间法、语言叙述法。

常用数集如：R Q Z N ,,,应熟记。

三子集、真子集及相等集（1）A ⊆⇔B A ⊂B 或A ＝B ；（2）A ⊂B ⇔A ⊆B 且A ≠B ；（3）A ＝B ⇔A ⊆B 且A ⊇B 。

1.已知集合{}1,2A =，集合B 满足{}1,2A B = ，则集合B 有个.2.已知集合{}1,2A =，集合B 满足A B A = ，集合B 与集合A 之间满足的关系是3.已知集合A 有n 个元素，则集合A 的子集个数有个，真子集个数有个4.满足条件{}{}1,21,2,3A = 的所有集合A 的个数是个四一个n 阶集合（即由个元素组成的集合）有n 2个不同的子集，其中有n 2－1个非空子集，也有n 2－1个真子集。

1．【2010〃黄岗中学八月月考】设集合22{5,log (36)}A a a =-+，集合{1,,},B a b =若{2},A B = 则集合A B 的真子集的个数是（） A ．3个 B ．7个 C ．12个 D ．15个五集合的交、并、补运算A B ={A x x ∈|且B x ∈}；A B ={A x x ∈|或B x ∈}I x x A ∈=|{且A x ∉}六有关集合的几个运算律：（1）交换律 A B ＝B A ，A B ＝B A ；（2）结合律A （B C ）＝（A B ） C ，A （BC ）＝(A B ) C ；（3）分配律 A （B C ）＝（A B ）（A C ）A （BC ）＝ (A B ) （A C ）（4）0—1律 A φ＝A ，A I ＝A ，A I ＝I ，A φ＝φ（5）等幂律 A A ＝A ，A A ＝A（6）吸收律 A (A B )＝A ，A （A B ）＝A（7）求补律 A C I A ＝I ，A C I A ＝φ（8）反演律 B A B A B A B A ==,七有限集合所含元素个数的几个简单性质（1）A B A B A B =+-（2）A B C A B C A B A C B C A B C =++---+真题：1．已知A={4|2m m Z -∈}，B={x |3}2x N +∈，则A ∩B=__________。

2．已知集合M={y |y =x 2+1，x ∈R}，N={y|y =x +1，x ∈R}，求M ∩N 。

3．若A ={(x ，y )| y =x +1},B={y |y =x 2+1},则A ∩B =_____.4．设全集 U = {1，2，3，4，5，6，7，8}，A = {3，4，5} B = {4，7，8},求：（C U A ）∩(C U B), (C U A)∪(C U B), C U (A ∪B), C U (A ∩B).5.【2010·北京文数】集合2{03},{9}P x Z x M x Z x =∈≤<=∈≤，则P M I =（）A.{1,2}B.{0,1,2}C.{1,2,3}D.{0,1,2,3}6. 如果集合A={x |ax 2＋2x ＋1=0}中只有一个元素，则a 的值是（）A ．0B ．0 或1C ．1D ．不能确定7.【上海文数】已知集合{}1,3,A m =，{}3,4B =，{}1,2,3,4A B = 则m = .8．集合{}{}2,1,1,2,1,lg --=>=∈=B x x y R y A 则下列结论正确的是（）A {2,1}AB =-- B ()(,0)RC A B =-∞ C (0,)A B =+∞D (){2,1}R C A B =--9.集合{|P x y ==，集合{|Q y y ==，则P 与Q 的关系是（）A. P ＝ QB. PQ C. P ≠⊂Q D. P ∩Q ＝∅ 10．设集合2{5,log (3)}A a =+，集合{,}B a b =，若{2}A B = ，则a b +等于（）A ．1B ．2C ．3D ．411.集合()22{,|1}416x y A x y =+=，{(,)|3}x B x y y ==，则A B ⋂的子集的个数是（） A ．4 B ．3 C ．2 D ．112.设集合{}{}A x||x-a|<1,x R ,|15,.A B B x x x R =∈=<<∈⋂=∅若，则实数a 的取值范围是（） A.{}a |0a 6≤≤ B.{}|2,a a ≤≥或a 4C.{}|0,6a a ≤≥或aD.{}|24a a ≤≤13.集合A={x |042=+x x }，B={x |01)1(222=-+++a x a x } ，A ∩B=B ，求a 的值．14. 已知A={023|2≥++x x x }, B={014|2>-+-m x mx x ,m ∈R},若A ∩B=φ, 且A ∪B=A, 求m 的取值范围.15.已知集合{}|37A x x =≤<，{}|210B x x =<<，求()R C A B ，()R C A B ，()R C A B ，()R A C B16．【2010·滦县一中第三次模拟】如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是（）A ．（M∩P）∩SB ．（M∩P）∪SC ．（M∩P）∩C I SD ．（M∩P）∪C I S17．如图，U 是全集，M 、P 、S 是U 的三个子集，则阴影部分所表示的集合是（）（A ）（M S P ⋂⋂) （B ）（M S P ⋃⋂)（C ）（M ⋂P ）⋂（C U S ）（D ）（M ⋂P ）⋃（C U S ）18、（07安徽理5）若}{2228x A x -=∈Z ≤<，{2R |log |1}B x x =∈>，则)(C R B A ⋂的元素个数为（A ）0 （B ）1 （C ）2 （D ）3 19、（07江苏2）已知全集U Z =，2{1,0,1,2},{|}A B x x x =-==，则U A C B 为（A ）A ．{1,2}-B ．{1,0}-C ．{0,1}D ．{1,2}20、（07湖北理3）设P 和Q 是两个集合，定义集合{}|P Q x x P x Q -=∈∉，且，如果{}2|log 1P x x =<，{}|21Q x x =-<，那么P Q -等于（）Ａ．{}|01x x << Ｂ．{}|01x x <≤Ｃ．{}|12x x <≤ Ｄ．{}|23x x <≤21、（07陕西理2）已知全信U ＝{1，2，3， 4，5}，集合A ＝{}23Z <-∈x x ,则集合C u A等于（）（A ）{}4,3,2,1 （B ）{}4,3,2 (C) {}5,1 (D) {}5Z 22.【2010·陕西文数】集合A={x－1≤x≤2}，B ＝｛x x ＜1｝,则A∩B=（） A.{x x ＜1} B.{x －1≤x≤2} C.{x －1≤x≤1} D.{x－1≤x＜1} 23、（07北京理12）已知集合{}|1A x x a =-≤，{}2540B x x x =-+≥．若A B =∅ ，则实数a 的取值范围是．24.【2010·重庆文数】设{}{}|10,|0A x x B x x =+>=<，则A B =____________.25.【2010·江苏卷】设集合A={-1,1,3}，B={a+2,a 2+4},A ∩B={3}，则实数a=___________.26.（08陕西卷2）已知全集{12345}U =，，，，，集合2{|320}A x x x =-+=，{|2}B x x a a A ==∈，，则集合)(B A C U 中元素的个数为（）A ．1B ．2C ．3D ．427.设集合{|32}M m m =∈-<<Z ，{|13}N n n M N =∈-=Z 则，≤≤（）A ．{}01，B ．{}101-，，C ．{}012，，D ．{}1012-，，，28.【2010·重庆八中第四次月考】设{}260,A x x x x Z =+-<∈，{}12,B x x x Z =-≤∈，则A B = （）A ．{}0,1B ．{}1,0,1-C ．{}0,1,2D ．{}1,0,1,2- 29．【2010·浙江省金华十校四月模拟】如果全集U R = ，2{|60}A x x x =+->，{||1|3}B x x =+<，()U C A B ⋃=则（）A ．{|42}x x -<≤B ．{|42}x x -<<C ．{|32}x x -≤<D ．{|32}x x -≤≤30．【2010·银川一中第三次月考】已知M={x|x 2＞4}，N ＝{x|12-x ≥1}，则C R M ∩N=（） A ．{x|1＜x ≤2} B ．{x|－2≤x ≤1} C ．{x|－2≤x ＜1} D ．{x|x ＜2} 31.已知集合{}3|0|31x M x x N x x x +⎧⎫==<=-⎨⎬-⎩⎭，≤，则集合{}|1x x ≥＝（） A ．M N B ．M NC ．)(N M C UD ．)(N M C U 32.2{|60},{|10},,M x x x N x ax M N N a =+-==-=⋂=已知集合且求实数的值。