2018新版小学五年级奥数经典30讲
小学数学奥数教程(五年级)--12

小学数学奥数基础教程(五年级)本教程共30讲最大公约数与最小公倍数(一)如果一个自然数a能被自然数b整除,那么称a为b的倍数,b为a 的约数。
如果一个自然数同时是若干个自然数的约数,那么称这个自然数是这若干个自然数的公约数。
在所有公约数中最大的一个公约数,称为这若干个自然数的最大公约数。
自然数a1,a2,…,a n的最大公约数通常用符号(a1,a2,…,a n)表示,例如,(8,12)=4,(6,9,15)=3。
如果一个自然数同时是若干个自然数的倍数,那么称这个自然数是这若干个自然数的公倍数。
在所有公倍数中最小的一个公倍数,称为这若干个自然数的最小公倍数。
自然数a1,a2,…,a n的最小公倍数通常用符号[a1,a2,…,a n]表示,例如[8,12]=24,[6,9,15]=90。
常用的求最大公约数和最小公倍数的方法是分解质因数法和短除法。
例1 用60元钱可以买一级茶叶144克,或买二级茶叶180克,或买三级茶叶240克。
现将这三种茶叶分别按整克数装袋,要求每袋的价格都相等,那么每袋的价格最低是多少元钱?分析与解:因为144克一级茶叶、180克二级茶叶、240克三级茶叶都是60元,分装后每袋的价格相等,所以144克一级茶叶、180克二级茶叶、240克三级茶叶,分装的袋数应相同,即分装的袋数应是144,180,240的公约数。
题目要求每袋的价格尽量低,所以分装的袋数应尽量多,应是144,180,240的最大公约数。
所以(144,180,240)=2×2×3=12,即每60元的茶叶分装成12袋,每袋的价格最低是60÷12=5(元)。
为节约篇幅,除必要时外,在求最大公约数和最小公倍数时,将不再写出短除式。
例2 用自然数a去除498,450,414,得到相同的余数,a最大是多少?分析与解:因为498,450,414除以a所得的余数相同,所以它们两两之差的公约数应能被a整除。
2018五年级奥数.几何.长方体与正方体表面涂色与三视图(B级).学生版
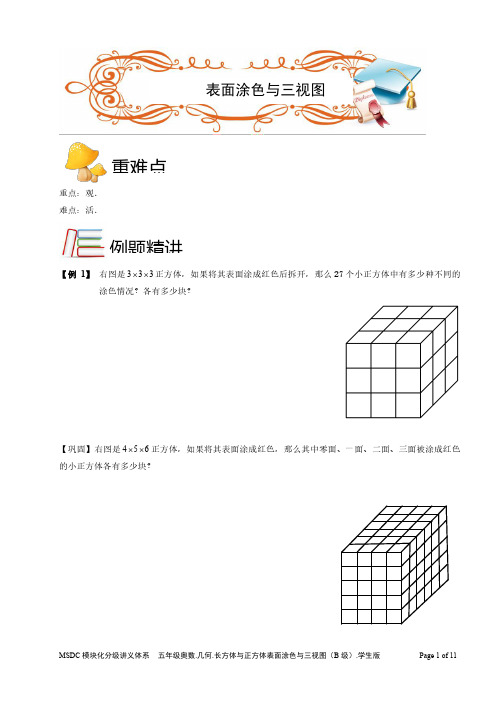
重难点重点:观.难点:活.例题精讲【例1】右图是333⨯⨯正方体,如果将其表面涂成红色后拆开,那么27个小正方体中有多少种不同的涂色情况?各有多少块?【巩固】右图是456⨯⨯正方体,如果将其表面涂成红色,那么其中零面、一面、二面、三面被涂成红色的小正方体各有多少块?表面涂色与三视图【例2】将一个表面积涂有红色的长方体分割成若干个棱长为1厘米的小正方体,其中一面都没有红色的小正方形只有3个,求原来长方体的表面积是多少平方厘米?【巩固】一个长方体,六个面均涂有红色,沿着长边等距离切5刀,沿着宽边等距离切4刀,沿着高边等距离切_______次后,要使各面上均没有红色的小方块为24块.欢迎关注:奥数轻松学余老师薇芯:69039270【例3】将长为5,宽为3,高为1的长方体木块的表面涂上漆,再切成15块棱长为1的小正方体。
则三个面涂漆的小正方体有________块。
【巩固】将8个相同的小正方体拼成一个体积为8立方厘米的长方体,表面涂上漆,然后分开,则3个面涂漆的小正方体最多有_________个,最少有________个。
【例4】将16个相同的小正方体拼成一个体积为16平方厘米的长方体,将表面涂漆,然后分开,结果,其中2面涂漆的小正方体有8个,那么3面涂漆的小正方体有__________个,4面涂漆的小正方体有__________个。
【巩固】把一个大长方体木块表面上涂满红色后,分割成若干个同样大小的小正方体,其中恰好有两个面涂上红色的小正方体恰好是100块,那么至少要把这个大长方体分割成多少个小正方体?欢迎关注:奥数轻松学余老师薇芯:69039270【例5】有一个3×4×5的长方体,先把其中相邻的两个面染红,再把它切成60个1×1×1的小正方体,请问:这些小正方体中最多有多少个是恰有一个面被染红的?【巩固】有6个相同的棱长分别是3厘米、4厘米、5厘米的长方体,把它们的某些面染上红色,使得有的长方体只有1个面是红色的,有的长方体恰有2个面是红色的,有的长方体恰有3个面是红色的,有的长方体恰有4个面是红色的,有的长方体恰有5个面是红色的,还有一个长方体6个面都是红色的,染色后把所有长方体分割成棱长为1厘米的小正方体.分割完毕后,恰有一面是红色的小正方体最多有多少个?【例6】有64个边长为1厘米的同样大小的小正方体,其中34个为白色的,30个为黑色的.现将它们拼成一个444⨯⨯的大正方体,在大正方体的表面上白色部分最多可以是多少平方厘米?欢迎关注:奥数轻松学余老师薇芯:69039270【巩固】有l25个同样大小的正方体木块,木块的每个面的面积均为1平方厘米,其中63个表面涂上白色,还有62个表面涂上蓝色。
2018年小学五年级奥数真题及答案

时间比为 4: 5 那么乙行完全程需要 10×5/4=12.5 小时 那么 AB距离 =72×12.5=900 千米 25、甲乙两人分别以每小时 4 千米和每小时 5 千米的速度从 A、 B 两地相向而 行,相遇后二人继续往前走,如果甲从相遇点到达 B 地又行 2 小时, A、 B 两地 相距多少千米? 解:甲乙的相遇时的路程比 =速度比 =4:5 那么相遇时,甲距离目的地还有全程的 5/9 所以 AB距离 =4×2/ ( 5/9 )=72/5=14.4 千米 2、一项工作,甲 5 小时先完成 4 分之 1,乙 6 小时又完成剩下任务的一半,最 后余下的工作有甲乙合作,还需要多长时间能完成? 解:甲的工作效率 =( 1/4 ) /5=1/20 乙完成( 1-1/4 )× 1/2=3/8 乙的工作效率 =(3/8 )/6=1/16 甲乙的工作效率和 =1/20+1/16=9/80 此时还有 1-1/4-3/8=3/8 没有完成 还需要( 3/8 )/ (9/80 )=10/3 小时 3、工程队 30 天完成一项工程,先由 18 人做, 12 天完成了工程的 3/1 ,如果 按时完成还要增加多少人? 解:每个人的工作效率 =(1/3 ) / (12×18) =1/648 按时完成,还需要做 30-12=18 天 按时完成需要的人员( 1-1/3 )/ (1/648 ×18) =24 人 需要增加 24-18=6 人 4、甲乙两人加工一批零件 , 甲先加工 1.5 小时 , 乙再加工 , 完成任务时 , 甲完成 这批零件的八分之五 . 已知甲乙的共效比是 3:2. 问: 甲单独加工完成着批零件需 多少小时 ? 解:甲乙工效比 =3:2 也就是工作量之比 =3:2 乙完成的是甲的 2/3 乙完成( 1-5/8 )=3/8 那么甲和乙一起工作时,完成的工作量 =( 3/8 )/ ( 2/3 )=9/16 所以甲单独完成需要 1.5/ (5/8-9/16 )=1.5/ ( 1/16 ) =24 小时 5、一项工程,甲、乙、丙三人合作需要 13 天,如果丙休息 2 天,乙要多做 4 天,或者由甲、乙合作多做 1 天。问:这项工程由甲单独做需要多少天? 解:丙做 2 天,乙要做 4 天 也就是说并做 1 天乙要做 2 天 那么丙 13 天的工作量乙要 2×13=26 天完成 乙做 4 天相当于甲乙合作 1 天 也就是乙做 3 天等于甲做 1 天 设甲单独完成需要 a 天 那么乙单独做需要 3a 天 丙单独做需要 3a/2 天 根据题意 1/a+1/3a+1/ (3a/2 )=1/13
人教版【精选】小学五年级奥数30及答案图文百度文库

人教版【精选】小学五年级奥数30及答案图文百度文库一、拓展提优试题1.(12分)甲、乙两人从A地步行去B地.乙早上6:00出发,匀速步行前往;甲早上8:00才出发,也是匀速步行.甲的速度是乙的速度的2.5倍,但甲每行进半小时都需要休息半小时.甲出发后经过分钟才能追上乙.2.(7分)爱尔兰作家刘易斯曾写过一篇反讽寓言,文中描述了一个名为尼亚特泊的野蛮国家.在这个国家里使用西巴巴数字.西巴巴数字的形状与通用的阿拉伯数字相同,但含义相反.如“0”表示“9”,“1”表示“8”,以次类推.他们写数字是从左到右,使用的运算符号也与我们使用的一样.例如,他们用62代表我们所写的37.按照尼亚特泊人的习惯,应怎样写837+742的和是419.【分析】“0”表示“9”,0+9=9,“1”表示“8”,1+8=9,由此可知西巴巴数字,表示的数字与正常数字的和都是9;由此找出837、742表示的数字,然后相加即可.3.幼儿园给小朋友派礼物,如果有2人各派4个,其余各派3个,则还剩余11个,如果4人各派3个,其余各派6个,则剩余10个,问一共有多少件礼物?4.数一数,图中有多少个正方形?5.将等边三角形纸片按图1所示步骤折叠3次(图1中的虚线是三边的中点的连线),然后沿两边的重点的边减去一角(如图2).将剩下的纸片展开、平铺,得到的图形是A6.如图,甲、乙两人按箭头方向从A点同时出发,沿正方形ABCD的边行走,正方形ABCD的边长是100米,甲的速度是乙的速度的1.5倍,两人在E 点第一次相遇,则三角形ADE的面积比三角形BCE的面积大1000平方米.7.星期天早晨,哥哥和弟弟去练习跑步,哥哥每分钟跑110米,弟弟每分钟跑80米,弟弟比哥哥多跑了半小时,结果比哥哥多跑了900米,那么,哥哥跑了米.8.如图,正方形的边长是6厘米,AE=8厘米,求OB=厘米.9.用0、1、2、3、4这五个数字可以组成个不同的三位数.10.对于自然数N,如果在1﹣9这九个自然数中至少有七个数是N的因数,则称N是一个“七星数”,则在大于2000的自然数中,最小的“七星数”是.11.将100按“加15,减12,加3,加15,减12,加3,…”的顺序不断重复运算,运算26步后,得到的结果是.(1步指每“加”或“减”一个数)12.解放军战士在洪水不断冲毁大坝的过程中要修好大坝,若10人需45分钟,20人需要20分钟,则14人修好大坝需分钟.13.(8分)如果两个质数的差恰好是2,称这两个质数为一对孪生质数.例如3和5是一对孪生质数,29和31也是一对孪生质数.在数论研究中,孪生质数是最热门的研究课题之一.华裔数学家张益唐在该课题的研究中取得了令人瞩目的成就,他的事迹激励着更多的青年学子投身数学研究.在不超过100的整数中,一共可以找到对孪生质数.14.观察下表中的数的规律,可知第8行中,从左向右第5个数是.15.某场考试共有7道题,每道题问的问题都只与这7道题的答案有关,且答案只能是1、2、3、4中的一个.已知题目如下:①有几道题的答案是4?②有几道题的答案不是2也不是3?③第⑤题和第⑥题的答案的平均数是多少?④第①题和第②题的答案的差是多少?⑤第①题和第⑦题的答案的和是多少?⑥第几题是第一个答案为2的?⑦有几种答案只是一道题的答案?那么,7道题的答案的总和是.【参考答案】一、拓展提优试题1.解:法一:假设甲一小时走5米,乙一小时走2米,列表如下:时间甲(米)乙(米)时间甲(米)乙(米)0小时043小时7.5100.5小时 2.55 3.5小时10111小时 2.564小时10121.5小时57 4.5小时12.5132小时585小时12.5142.5小时7.59 5.5小时1515观察得5.5小时恰好追上(如果这时间超过了乙,就要用具体追及公式计算追及时间)法二:也可以设甲的速度为每小时10a(甲要休息,实际每小时走5a),乙的速度为每小时4a,因此要追8a.半小时内最多追3a,可以先从要追的8a中扣除3a,因为在此之前不可能追上(之前的距离差不止3a).之后再开始按每半小时列出,若不够半小时的话,用追及公式算.前面追的5a,相当于每小时追a,可以用5a÷(5a﹣4a)=5(小时)计算.之后,甲半小时再走2a,乙再走5a,加上还差的3a,正好追上.因此,要追5.5小时,即330分钟.故答案为:330.2.解:西巴巴数字8表示阿拉伯数字9﹣8=1,西巴巴数字3表示阿拉伯数字9﹣3=6,西巴巴数字7表示阿拉伯数字9﹣7=2,西巴巴数字4表示阿拉伯数字9﹣4=5,西巴巴数字2表示阿拉伯数字9﹣2=7,所以837+742表示的正常算式为:162+257=419.故答案为:419.3.【分析】假设第一次每人都派3个,则还剩余2×(4﹣3)+11=13个,第二次如每人都派6个,同时少了4×(6﹣3)﹣10=2个,就是每人多派6﹣3=3个,则需要13+2=15个礼物,据此可求出人数,进而可求出礼物数.解:[2×(4﹣3)+11+4×(6﹣3)﹣10]÷(6﹣3)=[2×1+11+4×3﹣10]÷3=[2+11+12﹣10]÷3=15÷3=5(人)2×4+(5﹣2)×3+11=8+3×3+11=8+9+11=28(件)答:一共有28件礼物.4.解:通过有规律的数,得出:(1)边长为1的正方形有4×3=12(个);(2)边长为2的正方形有6个;(3)边长为3的正方形有2个.(4)以小正方形的对角线为边的正方形有8个;(5)以对角线的一半为边长的正方形是17个;(6)以3个对角线的一半为边长的正方形有1个.所以图中共有正方形:12+6+2+8+17+1=46(个).答:图中有46个正方形.5.解:找一剪刀与一等边三角形纸片,按题中所示步骤进行操作,最后得到的图形是A,故答案为:A.6.解:由于甲的速度是乙的速度的1.5倍所以两人速度比为:1.5:1=3:2,所以两人在E点相遇时,甲行了:(100×4)×=240(米);乙行了:400﹣240=160(米);则EC=240﹣100×2=40(米),DE=160﹣100=60(米);三角形ADE的面积比三角形BCE的面积大:60×100÷2﹣40×100÷2=3000﹣2000,=1000(平方米).故答案为:1000.7.解:设哥哥跑了X分钟,则有:(X+30)×80﹣110X=900,80x+2400﹣110x=900,2400﹣30x=900,X=50;110×50=5500(米);答:哥哥跑了5500米.故答案为:5500.8.解:6×6÷2=18(平方厘米),18×2÷8=4.5(厘米);答:OB长4.5厘米.故答案为:4.5.9.解:4×4×3,=16×3,=48(种);答:这五个数字可以组成 48个不同的三位数.故答案为:48.10.解:根据分析,在2000~2020之间排除掉奇数,剩下的偶数还可以排除掉不能被3整除的偶数,最后只剩下:2004、2010、2016,再将三个数分别分解质因数得:2004=2×2×3×167;2010=2×3×5×67;2016=2×2×2×2×2×3×3×7,显然2014和2010的质因数在1~9中不到7个,不符合题意,排除,符合题意的只有2016,此时2016的因数分别是:2、3、4、6、7、8、9.故答案是:2016.11.解:每一个计算周期运算3步,增加:15﹣12+3=6,则26÷3=8…2,所以,100+6×8+15﹣12=100+48+3=151答:得到的结果是 151.故答案为:151.12.解:假设每人每分钟修大坝1份洪水冲毁大坝速度:(10×45﹣20×20)÷(45﹣20)=(450﹣400)÷25=50÷25=2(份)大坝原有的份数45×10﹣2×45=450﹣90=360(份)14人修好大坝需要的时间360÷(14﹣2)=360÷12=30(分钟)答:14人修好大坝需30分钟.故答案为:30.13.解:在不超过100的整数中,以下8组:3,5;5,7;11,13;17,19;29,31;41,43;59,61;71,73是孪生质数.故答案为8.14.解:由图可知,第1行的数为1,第2行的最后一个数为2×2=4,第3行的最后一个数为3×3=9,…所以第7行最后一个数为7×7=49,则第8行第1个数为49+1=50,第5个数为50+4=54,故答案为:54.15.解:因为每道题的答案都是1、2、3、4的一个,所以①的答案不宜太大,不妨取1,此时②的答案其实就是7个答案中1和4的个数,显然只能取2、3、4中的一个,若取2,则意味着剩余的题目只能有一道题答案为1,这是④填1,⑦填2,⑤填3,⑥填2,而③无法填整数,与题意矛盾;所以②的答案取3,则剩余的题目答案为1和4各有1道,此时④填2,显然⑦只能填1,那么⑤填2,则4应该是⑥的答案,从而③填3,此时7道题的答案如表;它们的和是1+3+3+2+2+4+1=16.。
五年级奥数30及答案word百度文库

五年级奥数30及答案word百度文库一、拓展提优试题1.(15分)一个自然数恰有9个互不相同的约数,其中3个约数A,B,C满足:①A+B+C=79②A×A=B×C那么,这个自然数是.∆的面积等于5平方厘2.如图所示,P为平行四边形ABDC外一点。
已知PCD米,PAB∆的面积等于11平方厘米。
则平行四边形ABCD的面积是3.(7分)爱尔兰作家刘易斯曾写过一篇反讽寓言,文中描述了一个名为尼亚特泊的野蛮国家.在这个国家里使用西巴巴数字.西巴巴数字的形状与通用的阿拉伯数字相同,但含义相反.如“0”表示“9”,“1”表示“8”,以次类推.他们写数字是从左到右,使用的运算符号也与我们使用的一样.例如,他们用62代表我们所写的37.按照尼亚特泊人的习惯,应怎样写837+742的和是419.【分析】“0”表示“9”,0+9=9,“1”表示“8”,1+8=9,由此可知西巴巴数字,表示的数字与正常数字的和都是9;由此找出837、742表示的数字,然后相加即可.4.有一行数:1,1,2,3,5,8,13,21,…,从第三个数开始,每个数都是前两个数的和,问在前2007个数中,有是偶数.5.(7分)今年小翔和爸爸、妈妈的年龄分别是5岁、48岁、42岁.年后爸爸、妈妈的年龄和是小翔的6倍.6.(7分)将偶数按下图进行排列,问:2008排在第列.2 4681614121018 20 22 2432 30 28 26…7.数一数,图中有多少个正方形?8.(8分)小张有200支铅笔,小李有20支钢笔.每次小张给小李6支铅笔,小李还给小张1支钢笔.经过次这样的交换后,小张手中铅笔的数量是小李手中钢笔数量的11倍.9.(1)数一数图1中有个三角形.(2)数一数图2中有个正方形.10.如图,若每个小正方形的边长是2,则图中阴影部分的面积是.11.如果2头牛可以换42只羊,3只羊可以换26只兔,2只兔可以换3只鸡,则3头牛可以换多少只鸡?12.(15分)甲、乙两船顺流每小时行8千米,逆流每小时行4千米,若甲船顺流而下,然后返回;乙船逆流而上,然后返回,两船同时出发,经过3小时同时回到各自的出发点,在这3小时中有多长时间甲、乙两船同向航行?13.(8分)彤彤和林林分别有若干张卡片:如果彤彤拿6张给林林,林林变为彤彤的3倍;如果林林给彤彤2张,则林林变为彤彤的2倍.那么,林林原有张.14.小明准备和面包饺子,他在1.5千克面粉中加入了5千克的水,发现面和得太稀了,奶奶告诉他,包饺子的面需要按照3份面,2份水和面,于是小明分三次加入相同分量的面粉,终于将面按按要求和好了,那么他每次加入了 千克面粉.15.如图,在△ABC 中,D 、E 分别是AB 、AC 的中点,且图中两个阴影部分(甲和乙)的面积差是5.04,则S △ABC= .【参考答案】一、拓展提优试题1.解:一个自然数N 恰有9个互不相同的约数,则可得N =x 2y 2,或者N =x 8,(1)当N =x 8,则九个约数分别是:1,x ,x 2,x 3,x 4,x 5,x 6,x 7,x 8,其中有3个约数A 、B 、C 且满足A ×A =B ×C ,不可能.(2)当N =x 2y 2,则九个约数分别是:1,x ,y ,x 2,xy ,y 2,x 2y ,xy 2,x 2y 2,其中有3个约数A 、B 、C 且满足A ×A =B ×C ,①A =x ,B =1,C =x 2,则x +1+x 2=79,无解.②A =xy ,B =1,C =x 2y 2,则xy +1+x 2y 2=79,无解.③A =xy ,B =x ,C =xy 2,则xy +x +xy 2=79,无解.④A =xy ,B =x 2,C =y 2,则xy +x 2+y 2=79,解得:,则N =32×72=441.⑤A =x 2y ,B =x 2y 2,C =x 2,则x 2y +x 2y 2+x 2=79,无解.故答案为441.2.12[解答]作PF AB ⊥,由于//AB DC ,所以PF CD ⊥。
2018最新五年级奥数.数论.质数与合数(C级).学生版

知识框架一、质数与合数一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数).一个数除了1和它本身,还有别的约数,这个数叫做合数。
要特别记住:0和1不是质数,也不是合数。
常用的100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,共计25个;除了2其余的质数都是奇数;除了2和5,其余的质数个位数字只能是1,3,7或9.考点:⑴值得注意的是很多题都会以质数2的特殊性为考点.⑵除了2和5,其余质数个位数字只能是1,3,7或9.这也是很多题解题思路,需要大家注意.二、判断一个数是否为质数的方法根据定义如果能够找到一个小于p 的质数q (均为整数),使得q 能够整除p ,那么p 就不是质数,所以我们只要拿所有小于p 的质数去除p 就可以了;但是这样的计算量很大,对于不太大的p ,我们可以先找一个大于且接近p 的平方数2K ,再列出所有不大于K 的质数,用这些质数去除p ,如没有能够除尽的那么p 就为质数.例如:149很接近1441212=⨯,根据整除的性质149不能被2、3、5、7、11整除,所以149是质数.三、质因数与分解质因数(1).质因数:如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数.(2).互质数:公约数只有1的两个自然数,叫做互质数.(3).分解质因数:把一个合数用质因数相乘的形式表示出来,叫做分解质因数.例如:30235=⨯⨯.其中2、3、5叫做30的质因数.又如21222323=⨯⨯=⨯,2、3都叫做12的质因数,其中后一个式子叫做分解质因数的标准式,在求一个数约数的个数和约数的和的时候都要用到这个标准式.分解质因数往往是解数论题目的突破口,因为这样可以帮助我们分析数字的特征.质数与合数(4).分解质因数的方法:短除法例如:212263,(┖是短除法的符号)所以12223=⨯⨯;四、唯一分解定理任何一个大于1的自然数n 都可以写成质数的连乘积,即:312123k a a a a kn p p p p =⨯⨯⨯⨯ 其中为质数,12k a a a <<< 为自然数,并且这种表示是唯一的.该式称为n 的质因子分解式.例如:三个连续自然数的乘积是210,求这三个数.分析:∵210=2×3×5×7,∴可知这三个数是5、6和7.部分特殊数的分解余老师薇芯:69039270111337=⨯;100171113=⨯⨯;1111141271=⨯;1000173137=⨯;199535719=⨯⨯⨯;1998233337=⨯⨯⨯⨯;200733223=⨯⨯;2008222251=⨯⨯⨯;10101371337=⨯⨯⨯.【例1】著名的哥德巴赫猜想是:“任意一个大于4的偶数都可以表示为两个质数的和”。
2018五年级奥数.数论.数的整除、约数倍数(C级).学生版
数的整除、约数倍数“0”大约1500年前,欧洲的数学家们是不知道用“0”的。
他们使用罗马数字。
罗马数字是用几个表示数的符号,按照一定规则,把它们组合起来表示不同的数目。
在这种数字的运用里,不需要“0”这个数字。
而在当时,罗马帝国有一位学者从印度记数法里发现了“0”这个符号。
他发现,有了“0”,进行数学运算方便极了,他非常高兴,还把印度人使用“0”的方法向大家做了介绍。
过了一段时间,这件事被当时的罗马教皇知道了。
当时是欧洲的中世纪,教会的势力非常大,罗马教皇的权利更是远远超过皇帝。
教皇非常恼怒,他斥责说,神圣的数是上帝创造的,在上帝创造的数里没有“0”这个怪物,如今谁要把它给引进来,谁就是亵渎上帝!于是,教皇就下令,把这位学者抓了起来,并对他施加了酷刑,用夹子把他的十个手指头紧紧夹注,使他两手残废,让他再也不能握笔写字。
就这样,“0”被那个愚昧、残忍的罗马教皇明令禁止了。
但是,虽然“0”被禁止使用,然而罗马的数学家们还是不管禁令,在数学的研究中仍然秘密地使用“0”,仍然用“0”做出了很多数学上的贡献。
后来“0”终于在欧洲被广泛使用,而罗马数字却逐渐被淘汰了。
知识框架一、常见数字的整除判定方法:1.一个数的末位能被2或5整除,这个数就能被2或5整除;2.一个数的末两位能被4或25整除,这个数就能被4或25整除;3.一个数的末三位能被8或125整除,这个数就能被8或125整除;4.一各位数数字和能被3整除,这个数就能比9整除;5.一个数各位数数字和能被9整除,这个数就能被9整除;6.如果一个整数的奇数位上的数字之和与偶数位上的数字之和的差能被11整除,那么这个数能被11整除.7.1001特征(家有三子7、11、13)一个数除以7的余数,其末三位与前面隔开,等于末三位与前面隔出数的差除以7的余数;一个数除以11的余数,其末三位与前面隔开,等于末三位与前面隔出数的差除以11的余数;或者,其奇数位数字之和(从个位往高位数,个位为第1位,即为奇数位)减去偶数位数字之和所得的差除以11的余数;一个数除以13的余数,其末三位与前面隔开,等于末三位与前面隔出数的差(大减小)能被13整除;【备注】(以上规律仅在十进制数中成立.)二、整除性质性质1如果数a和数b都能被数c整除,那么它们的和或差也能被c整除.即如果c︱a,c︱b,那么c︱(a±b).性质2如果数a能被数b整除,b又能被数c整除,那么a也能被c整除.即如果b∣a,c∣b,那么c∣a.用同样的方法,我们还可以得出:性质3如果数a能被数b与数c的积整除,那么a也能被b或c整除.即如果bc∣a,那么b∣a,c∣a.性质4如果数a能被数b整除,也能被数c整除,且数b和数c互质,那么a一定能被b与c的乘积整除.即如果b∣a,c∣a,且(b,c)=1,那么bc∣a.例如:如果3∣12,4∣12,且(3,4)=1,那么(3×4)∣12.性质5如果数a能被数b整除,那么am也能被bm整除.如果b|a,那么bm|am(m为非0整数);性质6如果数a能被数b整除,且数c能被数d整除,那么bd也能被ac整除.如果b|a,且d|c,那么ac|bd;三、质数与合数一个数除了1和它本身,不再有别的约数,这个数叫做质数(也叫做素数).一个数除了1和它本身,还有别的约数,这个数叫做合数.要特别记住:0和1不是质数,也不是合数.常用的100以内的质数:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97,共计25个;除了2其余的质数都是奇数;除了2和5,其余的质数个位数字只能是1,3,7或9.考点:⑴值得注意的是很多题都会以质数2的特殊性为考点.⑵除了2和5,其余质数个位数字只能是1,3,7或9.这也是很多题解题思路,需要大家注意.四、质因数与分解质因数1.质因数:如果一个质数是某个数的约数,那么就说这个质数是这个数的质因数.互质数:公约数只有1的两个自然数,叫做互质数.分解质因数:把一个合数用质因数相乘的形式表示出来,叫做分解质因数.例如:30235=⨯⨯.其中2、3、5叫做30的质因数.又如21222323=⨯⨯=⨯,2、3都叫做12的质因数,其中后一个式子叫做分解质因数的标准式,在求一个数约数的个数和约数的和的时候都要用到这个标准式.分解质因数往往是解数论题目的突破口,因为这样可以帮助我们分析数字的特征.2.唯一分解定理任何一个大于1的自然数n 都可以写成质数的连乘积,即:312123k a a a a k n p p p p =⨯⨯⨯⨯ 其中为质数,12k a a a <<< 为自然数,并且这种表示是唯一的.该式称为n 的质因子分解式.例如:三个连续自然数的乘积是210,求这三个数.分析:∵210=2×3×5×7,∴可知这三个数是5、6和7.3.部分特殊数的分解111337=⨯;100171113=⨯⨯;1111141271=⨯;1000173137=⨯;199535719=⨯⨯⨯;1998233337=⨯⨯⨯⨯;200733223=⨯⨯;2008222251=⨯⨯⨯;10101371337=⨯⨯⨯.4.判断一个数是否为质数的方法根据定义如果能够找到一个小于p 的质数q(均为整数),使得q 能够整除p ,那么p 就不是质数,所以我们只要拿所有小于p 的质数去除p 就可以了;但是这样的计算量很大,对于不太大的p ,我们可以先找一个大于且接近p 的平方数2K ,再列出所有不大于K 的质数,用这些质数去除p ,如没有能够除尽的那么p 就为质数.例如:149很接近1441212=⨯,根据整除的性质149不能被2、3、5、7、11整除,所以149是质数.五、约数的概念与最大公约数0被排除在约数与倍数之外1.求最大公约数的方法①分解质因数法:先分解质因数,然后把相同的因数连乘起来.例如:2313711=⨯⨯,22252237=⨯⨯,所以(231,252)3721=⨯=;②短除法:先找出所有共有的约数,然后相乘.例如:2181239632,所以(12,18)236=⨯=;③辗转相除法:每一次都用除数和余数相除,能够整除的那个余数,就是所求的最大公约数.用辗转相除法求两个数的最大公约数的步骤如下:先用小的一个数除大的一个数,得第一个余数;再用第一个余数除小的一个数,得第二个余数;又用第二个余数除第一个余数,得第三个余数;这样逐次用后一个余数去除前一个余数,直到余数是0为止.那么,最后一个除数就是所求的最大公约数.(如果最后的除数是1,那么原来的两个数是互质的).例如,求600和1515的最大公约数:151********÷= ;6003151285÷= ;315285130÷= ;28530915÷= ;301520÷= ;所以1515和600的最大公约数是15.2.最大公约数的性质①几个数都除以它们的最大公约数,所得的几个商是互质数;②几个数的公约数,都是这几个数的最大公约数的约数;③几个数都乘以一个自然数n ,所得的积的最大公约数等于这几个数的最大公约数乘以n .3.求一组分数的最大公约数先把带分数化成假分数,其他分数不变;求出各个分数的分母的最小公倍数a ;求出各个分数的分子的最大公约数b ;b a即为所求.欢迎关注:奥数轻松学余老师薇芯:69039270六、倍数的概念与最小公倍数1.求最小公倍数的方法①分解质因数的方法;例如:2313711=⨯⨯,22252237=⨯⨯,所以[]22231,252237112772=⨯⨯⨯=;②短除法求最小公倍数;例如:2181239632,所以[]18,12233236=⨯⨯⨯=;③[,]a b a b ⨯=.2.最小公倍数的性质①两个数的任意公倍数都是它们最小公倍数的倍数.②两个互质的数的最小公倍数是这两个数的乘积.③两个数具有倍数关系,则它们的最大公约数是其中较小的数,最小公倍数是较大的数.3.求一组分数的最小公倍数方法步骤先将各个分数化为假分数;求出各个分数分子的最小公倍数a ;求出各个分数分母的最大公约数b ;b 即为所求.例如:35[3,5]15[,412(4,12)4==注意:两个最简分数的最大公约数不能是整数,最小公倍数可以是整数.例如:[]()1,414,4232,3⎡⎤==⎢⎥⎣⎦七、最大公约数与最小公倍数的常用性质1.两个自然数分别除以它们的最大公约数,所得的商互质。
2018五年级奥数.几何.勾股定理与弦图(B级)学生版
MSDC 模块化分级讲义体系
五年级奥数. 几何.勾股定理与弦图(B 级).学生版
Page 1 of 13
点评:此种解法主要利用了三角形的面积公式:底×高÷2,和梯形的面积公式:(上底+下底)×高÷2. 而在我国对于勾股定理的证明又做出了那些贡献哪? 在我国古代,把直角三角形叫做勾股形。 把 直 角 三 角 形 的 较 短 直 角 边 称 为 “勾 ”,较 长 直 角 边 为 “股 ”,斜 边 称 为 “弦 ”,所 以 把 这 个 定 理 称 为 “勾 股 定 理 ”。勾 股 定 理 揭 示 了 直 角 三 角 形 边 之 间 的 关 系 。即 :在 直 角 三 角 形 中 俩 条 直 角 边 的 平 方 和等于斜边的平方。 公元前 11 世纪的《周髀算经》中提到:故折矩,以为句广三,股修四、径修五.既方之.外半卿一矩,环而共盘. 得成三、四、五.
黄
红 绿
【巩固】三个面积都是 12 的正方形放在一个长方形的盒子里面,如图 7-15,盒中空白部分的面积已经标
出,求图中大长方形的面积?
MSDC 模块化分级讲义体系
五年级奥数. 几何.勾股定理与弦图(B 级).学生版
Page 8 of 13
【例 9】如图所示,直角三角形 PQR 的两个直角边分别为 5 厘米,9 厘米问下图中 3 个正方形面积之和比 4 个三角形面积之和大多少?
MSDC 模块化分级讲义体系
五年级奥数. 几何.勾股定理与弦图(B 级).学生版
Page 7 of 13
分之
;
【巩固】如图所示,在四边形 ABCD 中,E,F,G,H 分别是 ABCD 各边的中点,求阴影部分与四边形 PQRS 的面积之比。
【例 8】如下图所示,红、黄、绿三块大小一样的正它们方形纸片,放在一个正方形盒内,它们之间相互 叠合,已知露在外面的部分中,红色的面积是 20,黄色的面积是 14,绿色的面积是 10,那么,正方形盒 子的底面积是__________.
2018五年级上册奥数(简便方法、消去问题、分段计费)
五年级上册数学简便方法训练思路导航:在小数乘法中可以利用乘法分配律使计算简便,为了符合乘法分配律,可以把某一个乘数拆分成两个数相加。
例题:4.5x12.6-3.6x4.5+4.512.5x80.8 4.8x3.9+0.39+0.39 0.65x7.2+0.35x7.20.056x0.4x0.5 102x0.36 49.5x10.1-49.5x0.1拓展提升例2: 47.5x2.3+3.4x52.5+7.5x1.11.25x67.875+125x6.7875+1.25x53.3757.5x2.3+1.9x2.5+22.5x0.4五年级上册数学消去问题例题:3筐苹果和5筐梨共重138千克,同样的9筐苹果和4筐梨共重216千克,每筐苹果和每筐梨各重少千克?点拨:根据条件可以列出:3筐苹果+5筐梨=138千克①9筐苹果+4筐梨=216千克②巩固练习:1、小军计划买3个茶杯和4个保温杯,算好了价钱是88元,到了商店,他突然想买3个保温杯和4个茶杯,结果多出了几元钱,正好能多买一个茶杯。
保温杯的单价是多少元,茶杯的单价是多少元?2、3筐苹果和5筐梨共重138千克,同样的9筐苹果和4筐梨共重216千克,每筐苹果重多少千克?每筐梨重多少千克?3、买9支钢笔和5支圆珠笔共用891元,买同样价格的9支钢笔与8支圆珠笔共用94.5元,圆珠笔的单价是多少元?钢笔的单价是多少元?五年级上册奥数分段计费例题:在一个停车场停车一次至少要交费0.5元。
如果停车超过1小时,每多停0.5小时(不足0.5小时按0.5小时计算)要多交0.5元。
一辆汽车在离开停车场时司机交了5.5元停车费,这辆汽车最多停了几小时?巩固训练:1、某市出租车的起步价为6元(3千米以内),超过3千米的部分按1.8元/千米收费(不足1千米按1千米计算)。
明明坐出租车去爷爷家,付车费18.6元,明明家距离爷爷家最远多少千米?2、王叔叔租门店做早餐生意。
租金1年内收2.5万元,超过1年,每半年收1.5万元(不足半年按半年计算)。
2018最新五年级奥数.数论.带余除法(A级).学生版
知识框架带余除法的定义及性质1、定义:一般地,如果a 是整数,b 是整数(b ≠0),若有a ÷b =q ……r ,也就是a =b ×q +r ,0≤r <b ;我们称上面的除法算式为一个带余除法算式。
这里:(1)当0r =时:我们称a 可以被b 整除,q 称为a 除以b 的商或完全商(2)当0r ≠时:我们称a 不可以被b 整除,q 称为a 除以b 的商或不完全商一个完美的带余除法讲解模型:如图这是一堆书,共有a 本,这个a 就可以理解为被除数,现在要求按照b 本一捆打包,那么b 就是除数的角色,经过打包后共打包了c 捆,那么这个c 就是商,最后还剩余d 本,这个d 就是余数。
这个图能够让学生清晰的明白带余除法算式中4个量的关系。
并且可以看出余数一定要比除数小。
2、余数的性质⑴被除数=除数⨯商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数;⑵余数小于除数.3、解题关键理解余数性质时,要与整除性联系起来,从被除数中减掉余数,那么所得到的差就能够被除数整除了.在一些题目中因为余数的存在,不便于我们计算,去掉余数,回到我们比较熟悉的整除性问题,那么问题就会变得简单了.例题精讲带余除法【例1】某数被13除,商是9,余数是8,则某数等于。
【巩固】一个三位数除以36,得余数8,这样的三位数中,最大的是__________。
【例2】除法算式□□=208中,被除数最小等于。
【巩固】计算口÷△,结果是:商为10,余数为▲。
如果▲的值是6,那么△的最小值是_____。
【例3】71427和19的积被7除,余数是几?欢迎关注:“奥数轻松学”【巩固】在下面的空格中填上适当的数。
【例4】1013除以一个两位数,余数是12.求出符合条件的所有的两位数.【巩固】一个两位数除310,余数是37,求这样的两位数。
【例5】一个两位奇数除1477,余数是49,那么,这个两位奇数是多少?【巩固】大于35的所有数中,有多少个数除以7的余数和商相等?【例6】已知2008被一些自然数去除,所得的余数都是10,那么这样的自然数共有多少个?【巩固】写出全部除109后余数为4的两位数.【例7】甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数.【巩固】用某自然数a去除1992,得到商是46,余数是r,求a和r.【例8】当1991和1769除以某个自然数n,余数分别为2和1.那么,n最小是多少?欢迎关注:“奥数轻松学”【巩固】有三个自然数a,b,c,已知b除以a,得商3余3;c除以a,得商9余11。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018新版小学五年级奥数经典30讲
第1讲 数字迷(一)
第2讲 数字谜(二)
第3讲 定义新运算(一)
第4讲 定义新运算(二)
第5讲 数的整除性(一)
第6讲 数的整除性(二)
第7讲 奇偶性(一)
第8讲 奇偶性(二)
第9讲 奇偶性(三)
第10讲 质数与合数
第11讲 分解质因数
第12讲 最大公约数与最小公倍数(一)
第13讲 最大公约数与最小公倍数(二)
第14讲 余数问题
第15讲 孙子问题与逐步约束法
第16讲 巧算
第17讲 位置原则
第18讲 最大最小
第19讲 图形的分割与拼接
第20讲 多边形的面积
第21讲 用等量代换求面积
第22 讲 用割补法求面积
第23讲 列方程解应用题
第24讲 行程问题(一)
第25讲 行程问题(二)
第26讲 行程问题(三)
第27讲 逻辑问题(一)
第28讲 逻辑问题(二)
第29讲 抽屉原理(一)
第30讲 抽屉原理(二)
第1讲 数字谜(一)
数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。数字谜涉及的知识多,思考
性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小
数的除法竖式问题。
例1
把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式
成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解
:因为运算结果是整数,在四则运算中只有除法运算可能出
现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个
括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)
=12。
例2
将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×
□□=□□×□□=5568。
解:
将5568质因数分解为5568=26×3×29。由此容易知道,将 5568
分解为两个两位数的乘积有两种:58×96和64×87,分解为一个两位数与
一个三位数的乘积有六种:
12×464, 16×348, 24×232,
29×192, 32×174, 48×116。
显然,符合题意的只有下面一种填法:174×32=58×96=5568。
例3
在443后面添上一个三位数,使得到的六位数能被573整除。
分析与解
:先用443000除以573,通过所得的余数,可以求出应添
的三位数。由
443000÷573=773……71
推知, 443000+(573-71)=443502一定能被573整除,所以应添
502。
例4
已知六位数33□□44是89的倍数,求这个六位数。
分析与解
:因为未知的数码在中间,所以我们采用两边做除法的方法
求解。
先从右边做除法。由被除数的个位是4,推知商的个位是6;由左下式
知,十位相减后的差是1,所以商的十位是9。这时,虽然89×96=8544,
但不能认为六位数中间的两个□内是85,因为还没有考虑前面两位数。
再从左边做除法。如右上式所示,a可能是6或7,所以b只可能是7
或8。
由左、右两边做除法的商,得到商是3796或3896。由3796×
89=337844, 3896×89=346744
知,商是3796,所求六位数是337844。
例5
在左下方的加法竖式中,不同的字母代表不同的数字,相同的字
母代表相同的数字,请你用适当的数字代替字母,使加法竖式成立。
分析与解
:先看竖式的个位。由Y+N+N=Y或Y+ 10,推知N要么
是0,要么是5。如果N=5,那么要向上进位,由竖式的十位加法有
T+E+E+1=T或T+10,等号两边的奇偶性不同,所以N≠5,N=0。
此时,由竖式的十位加法T+E+E=T或T+10, E不是0就是5,但
是N=0,所以E=5。
竖式千位、万位的字母与加数的千位、万位上的字母不同,说明百位、
千位加法都要向上进位。因为N=0,所以I≠0,推知I=1,O=9,说明百
位加法向千位进2。
再看竖式的百位加法。因为十位加法向百位进1,百位加法向千位进2,
且X≠0或1,所以R+T+T+1≥22,再由R,T都不等于9知,T只能是7
或8。
若T=7,则R=8,X=3,这时只剩下数字2,4,6没有用过,而S只
比F大1,S,F不可能是2,4,6中的数,矛盾。
若T=8,则R只能取6或7。R=6时,X=3,这时只剩下2,4,7,
同上理由,出现矛盾;R=7时,X=4,剩下数字2,3,6,可取F=2,S=3,
Y=6。
所求竖式见上页右式。
