有源低通滤波器(LPF)
eeg信号的滤波方法

EEG(脑电图)信号滤波是为了从原始EEG数据中去除噪声、干扰以及不感兴趣的频率成分,以提取出所关注的脑电活动。
以下是常用的EEG信号滤波方法:低通滤波(LPF):低通滤波器用于去除高频噪声,保留低频脑电活动。
这有助于提取大脑慢速活动,如α和δ波。
常见的低通滤波器包括Butterworth、Chebyshev和Elliptic等。
高通滤波(HPF):高通滤波器用于去除低频噪声,保留高频脑电活动,如β和γ波。
高通滤波可以改善EEG信号的清晰度。
同样,常见的高通滤波器包括Butterworth、Chebyshev 和Elliptic等。
带通滤波(BPF):带通滤波器允许通过某个频率范围的信号,同时去除低于或高于该范围的频率。
这对于捕获特定频率范围内的脑电活动非常有用。
陷波滤波(Notch滤波):陷波滤波器用于去除电源线频率(如50Hz或60Hz)引起的干扰,以及其他频率噪声。
这有助于减少电源干扰对EEG信号的影响。
小波变换滤波:小波变换是一种多分辨率信号分析方法,可以同时提供时域和频域信息。
小波变换可以将EEG信号分解成不同频率的子信号,并对这些子信号进行滤波和重构。
卡尔曼滤波:卡尔曼滤波是一种递归滤波技术,可以估计信号的状态,同时对观测值和系统噪声进行优化的滤波方法,适用于动态系统。
自适应滤波:自适应滤波方法根据信号的特性自动调整滤波器参数。
这种方法可以根据不同的EEG信号特征来调整滤波参数,从而更好地去除噪声和保留感兴趣的信号。
在选择滤波方法时,需要考虑到EEG信号的频率范围、研究目的以及信号质量。
不同的滤波方法可以根据需求进行组合使用,以获得更好的结果。
同时,在滤波过程中也需要注意不会对感兴趣的脑电活动造成严重损失。
lpf滤波器计算公式

lpf滤波器计算公式LPF滤波器计算公式。
在信号处理领域中,滤波器是一种用于去除或减弱信号中特定频率成分的设备或算法。
低通滤波器(LPF)是一种常用的滤波器类型,它可以去除高于一定频率的信号成分,保留低频成分。
LPF滤波器的设计和计算是信号处理中的重要内容,本文将介绍LPF滤波器的计算公式和相关知识。
LPF滤波器的基本原理是通过将信号通过一个低通滤波器,去除高于一定频率的信号成分。
在频域中,LPF滤波器的频率响应曲线呈现出一种特定的形状,通常是在截止频率处有较大的衰减,而在截止频率以下则有较小的衰减。
LPF滤波器的设计需要考虑到截止频率、通带增益和衰减特性等因素。
LPF滤波器的设计通常需要先确定一些参数,比如截止频率、通带增益和衰减特性等。
然后根据这些参数来计算滤波器的传递函数,从而得到滤波器的频率响应曲线。
LPF滤波器的传递函数通常可以表示为以下形式:H(s) = K / (s + ωc)。
其中,H(s)表示滤波器的传递函数,K表示通带增益,s是复变量,ωc是截止频率。
这个传递函数描述了滤波器在频域中的响应特性,可以帮助我们了解滤波器的频率特性。
根据传递函数,我们可以得到滤波器的频率响应曲线。
在频率响应曲线中,截止频率处的增益通常是0dB,而在截止频率以下则有一定的增益。
这种频率响应特性可以帮助我们理解滤波器在频域中的工作原理。
除了传递函数和频率响应曲线,我们还可以通过差分方程来表示LPF滤波器的计算公式。
差分方程是一种描述离散系统的数学工具,可以帮助我们理解滤波器的时域特性。
LPF滤波器的差分方程通常可以表示为以下形式:y[n] = α x[n] + (1-α) y[n-1]其中,y[n]表示滤波器的输出信号,x[n]表示滤波器的输入信号,α是一个控制参数。
这个差分方程描述了滤波器在时域中的工作原理,可以帮助我们理解滤波器的时域特性。
通过传递函数和差分方程,我们可以计算出LPF滤波器的频率响应曲线和时域特性,从而对滤波器的性能有一个全面的了解。
lpf低通滤波器的原理

lpf低通滤波器的原理
低通滤波器(LPF)是一种电子过滤器,可以允许低频信号通过,并阻止高频信号通过。
其原理是利用电容器和电感器的特性,将输入信号分成高频和低频两个部分,只将低频部分传递到输出端口。
在LPF电路中,电容器和电感器的数值可以根据需要进行选择,以实现所需的频率截止。
当输入信号的频率很高时,电容器会充电并阻止信号通过,而电感器则会阻止电流通过。
因此,高频信号会被过滤掉,只有低频信号可以通过。
LPF常用于音频、视频和通信领域。
例如,音频LPF被用于滤除高频噪声,从而提高音频质量。
视频LPF则用于滤除高频噪声和颜色偏移,从而提高视频质量。
通信LPF则用于滤除高频噪声和干扰,从而提高通信质量和数据传输速率。
总之,LPF是一种实用的电子过滤器,可以有效地滤除高频噪声和干扰,提高信号质量和可靠性。
- 1 -。
二阶RC有源滤波器的设计

二阶R C有源滤波器的设计-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN二阶RC有源滤波器的设计摘要:滤波器是一种能够使有用频率信号通过,而同时抑制(或衰减)无用频率信号的电子电路或装置,在工程上常用它来进行信号处理、数据传送或抑制干扰等。
有源滤波器是由集成运放、R、C组成,其开环电压增益和输入阻抗都很高,输出阻抗又低,构成有源滤波电路后还具有一定的电压放大和缓冲作用,但因受运算放大器频率限制,这种滤波器主要用于低频范围。
本次毕业设计主要是在所学《模拟电子技术基础》、《集成电路》等专业知识的基础上研究和设计几种典型的二阶有源滤波电路:巴特沃斯二阶有源低通滤波器、巴特沃斯二阶有源高通滤波器、二阶有源带通滤波器,研究和设计其电路结构、传递函数,并对有关参数进行计算,再利用multisim 软件进行仿真,组装和调试各种有源滤波器,探究其幅频特性。
经过仿真和调试,本次设计的二阶RC有源滤波器各测量参数均与理论计算值相符,通频带的频率响应曲线平坦,没有起伏,而在阻频带则逐渐下降为零,衰减率可达到|-40Db/10oct|,滤波效果很理想。
关键词:有源滤波器二阶 RC 频率Abstract:Filter is a kind of can make useful frequency signal through,While suppressing ( or attenuation) useless frequency signal electronic circuit or device, commonly used in engineering to signal processing, data transfer or suppression of interference. Active power filter is composed of integrated operational amplifier, R, C composition, its open loop voltage gain and input impedance is very high, and low output impedance, an active filter circuit also has a voltage amplifying and buffering effect, but due to operational amplifier frequency limit, this filter is mainly used in low frequency graduation design is mainly in the" analog electronic technology"," integrated circuit" and other professional knowledge based on research and design of several typical two order active filter circuit: Butterworth two, Butterworth two step active low pass filter active high-pass filter, two step active band-pass filter, research and design of its circuit structure, transfer function, and the related parameters are calculated, then the use of Multisim software simulation, assembly and commissioning of various active filter, explore its amplitude frequency simulation and debugging, the design of the two order active RC filter the measurement parameters and calculation results, the pass band frequency response curve is flat, no ups and downs, and in the stop band is decreased to zero, attenuation rate can reach | - 40dB / 10oct |, filtering effect is very ideal.Key words: Active power filter Two order RC Frequency Signal第一章前言选题依据近现代,在电子工程、通信工程、自动控制、遥测控制、测量仪器、仪表和计算机等技术领域,滤波器的应用极为广泛,滤波器的优劣直接决定产品的优劣,所以,对滤波器的研究和生产历来为各国所重视。
lpf低通滤波器参数

lpf低通滤波器参数摘要:1.LPF低通滤波器简介2.LPF低通滤波器的设计方法3.LPF低通滤波器的应用4.LPF低通滤波器参数设置实例正文:LPF低通滤波器是一种广泛应用于信号处理领域的滤波器,其主要作用是去除信号中的高频成分,保留低频成分。
在matlab 中,LPF低通滤波器的设计可以通过多种方法实现,其中一种常见的方法是基于巴特沃斯(Butterworth)滤波器的设计。
LPF低通滤波器的设计方法主要包括以下几个步骤:1.确定滤波器的截止频率:滤波器的截止频率是决定滤波器性能的关键参数,需要根据信号的特性和应用需求来确定。
2.选择滤波器的阶数:滤波器的阶数决定了滤波器的性能,如通带波动、阻带衰减和过渡带宽度等。
一般来说,阶数越高,滤波器的性能越好,但同时也会增加滤波器的复杂性和计算成本。
3.设计滤波器的传递函数:根据滤波器的阶数和截止频率,可以设计出滤波器的传递函数。
4.使用matlab实现滤波器:可以使用matlab中的filter函数或其他滤波器设计工具实现LPF低通滤波器。
LPF低通滤波器的应用广泛,包括但不限于音频处理、图像处理、通信系统等。
例如,在音频处理中,LPF低通滤波器可以用于去除高频噪声,提高音频信号的质量;在图像处理中,LPF低通滤波器可以用于去除图像噪声,提高图像的清晰度。
在实际应用中,LPF低通滤波器的参数设置需要根据具体需求进行调整。
一种常见的方法是根据截止频率和滤波器的阶数来计算滤波器的参数。
此外,还可以通过仿真和实验来调整滤波器的参数,以达到最佳的性能。
总之,LPF低通滤波器是一种重要的信号处理工具,其设计方法和应用广泛。
低通滤波器-实验报告
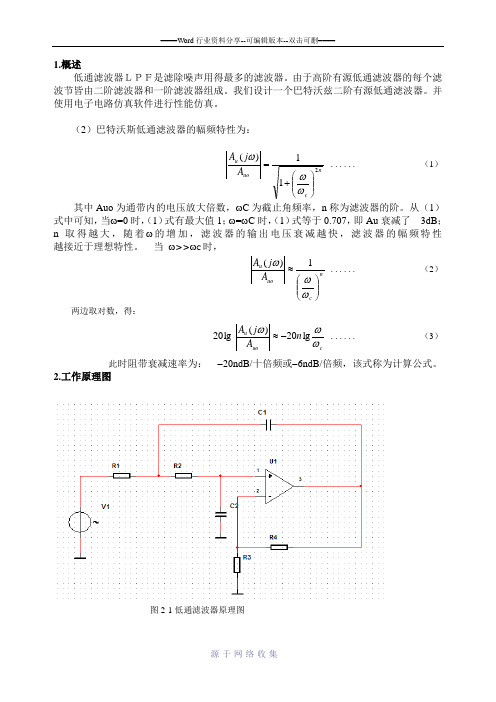
1.概述低通滤波器LPF是滤除噪声用得最多的滤波器。
由于高阶有源低通滤波器的每个滤波节皆由二阶滤波器和一阶滤波器组成。
我们设计一个巴特沃兹二阶有源低通滤波器。
并使用电子电路仿真软件进行性能仿真。
(2)巴特沃斯低通滤波器的幅频特性为:n c uo u A j A 211)(⎪⎪⎭⎫ ⎝⎛+=ωωω . . . . . . (1)其中Auo 为通带内的电压放大倍数,ωC 为截止角频率,n 称为滤波器的阶。
从(1)式中可知,当ω=0时,(1)式有最大值1;ω=ωC 时,(1)式等于0.707,即Au 衰减了 3dB ;n 取得越大,随着ω的增加,滤波器的输出电压衰减越快,滤波器的幅频特性 越接近于理想特性。
当 ω>>ωC 时, n c uo u A j A ⎪⎪⎭⎫ ⎝⎛≈ωωω1)( . . . . . . (2) 两边取对数,得:lg 20cuo u n A j A ωωωlg 20)(-≈ . . . . . . (3) 此时阻带衰减速率为: -20ndB/十倍频或-6ndB/倍频,该式称为计算公式。
2.工作原理图图2-1低通滤波器原理图2-2低通滤波器原理图工作原理:(1)滤波器是具有频率选择作用的电路或运算处理系统。
滤波处理可以利用模拟电路实现,也可以利用数字运算处理系统实现。
滤波器的工作原理是当信号与噪声分布在不同频带中时,可以在频率与域中实现信号分离。
在实际测量系统中,噪声与信号的频率往往有一定的重叠,如果重叠不严重,仍可利用滤波器有效地抑制噪声功率,提高测量精度。
任何复杂地滤波网络,可由若干简单地、相互隔离地一阶与二阶滤波电路级联等效构成。
一阶滤波电路只能构成低通和高通滤波器,而不能构成带通和带阻。
可先设计一个一阶滤波电路来熟悉电路设计思路以及器件使用要求和软件地进一步学习。
有源滤波器地设计,主要包括确定传递函数,选择电路结构,选择有源器件与计算无源元件参数四个过程。
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
二阶有源低通滤波器LPF
吴晓燕
项目四 扩音器的制作
2.1
2.2 2.3
项目描述 项目资讯
项目实施
2.4
项目评价与总结
4.1 项目描述
在大型的会议室、商场、学校里,在促销、旅游及健身等活动中, 有一种电子设备是必备的,那就是扩音器。最简易的扩音器整机电路,可 分为前置放大级、音调控制级和功率放大级三部分。其中前置放大级我们 第二个项目已经学习了,而音调控制级由低通滤波器和高通滤波器共同组 成,所以需要先从各种滤波器的特性讲述。
理论上在滤波器通带内电压放大倍数 ,上截止频率 ,用波特 图示仪测得 , 。将电路相关元件参数代入公式计 =1.592kHz, (20lg3=9.542dB),理论计算和 仿真仪器测量结果基本一致。
2. 反相输入低通滤波器电路
(a)电路 (b)幅频特性 图8-2 一阶有源反相输入低通滤波器 图8-2(a)为反相输入低通滤波器电路,电路的电压放大倍数 (20lg2=6.02dB),上截止频率 。图8-2(b)为 幅频特性,测量出放大器增益为6dB,上截止频率为1.585kHz。理论计算和仪 器测量结果基本一致。图8-2(a)中将低通滤波电路R、C原件接入负反馈电 路。虽然前后两个滤波电路不同,但R、C元件参数相同,所以幅频特性是一 样的。上述两个电路也可应用“交流分析”法测量它们的幅频特性。
任务4-1 集成运放构成的低通、高通滤波电
路的组建与测试
任务引入
•最简易的扩音器整机电路,可分为前置放大 级、音调控制级和功率放大级三部分。其中 前置放大级我们第二个项目已经学习了,而 音调控制级由低通滤波器和高通滤波器共同 组成,所以需要先从各种滤波器的特性讲述 。
相关知识
1)滤波电路的基础知识。 2)滤波电路的分类 3)有源滤波器与无源滤波器的特性差别。
信号处理电路
低通滤波器(LPF)
➢无源低通滤波器
——由无源器件(R、L、C)构成。
电压放大倍数为
Au
Uo Ui
1 1 j
f
f0
f0
1 2RC
——通带截止频率
电路缺点:
✓电压放大倍数低,带载能力很差;
✓特性不理想,边沿不陡;
有源滤波器
➢一阶低通有源滤波器
R1
RF
U o = 1+
RF R1
U
U
1 1 f
➢传输特性
u O
f (uI)
➢工作在非线性区
uo +UOPP
0
UOPP
u+ ≠u i i_ 0 ➢阈值电压UT :使输出产生跃变的输入电压。
u+-u-
过零比较器
uI
-
A
+
uO
简单过零比较器
uI < 0 uI > 0
uo = + UOPP uo = - UOPP
阈值电压UT (门限电平)
uo
+UOPP
的信号阻断。
U i
低通
高通
U o
20lg Au
低通
0
f2
f
20lg Au
0
20lg Au
高通
f1
f f2>f1
0
阻 f1
通阻 f2
f
当R2=2R,R3=R时,
Au
A uo
(3-Auo )
j(
f f0
f0 ) f
A up
1 jQ ( f f0 )
f0
1 2RC
f0 f
——中心频率
fir低通滤波器原理
fir低通滤波器原理低通滤波器原理一、什么是低通滤波器低通滤波器(LPF)是一种输入信号在指定的频率范围内阻抗为高的滤波器。
它能够有效地抑制较高频率的输入信号,从而只保留较低频率信号,增强信号低频部分的特征,例如:增强低频声音信号提取出人声信号,以及视频信号提取出高清图像。
二、低通滤波器的作用1. 降噪和抑制高频干扰。
低通滤波器可以抑制高于某一特定频率的信号,从而减少输出信号中的噪声和其他干扰,使输出信号的质量更高、更清晰。
2. 细节处理。
低通滤波器可以提取出较低频率的信号,使信号有更多的细节,从而更容易被人们理解。
3. 低频增强。
低通滤波器可以增强低频信号,使低频声音更清晰、更柔和,以及视频信号更细腻、更柔和。
三、低通滤波器的工作原理低通滤波器的工作原理是在特定的截止频率(也称为滤料频率)及其以下的频率信号被有效地通过滤波器,而该频率以上的频率信号被滤波器有效地抑制。
这意味着滤波器在特定的截止频率以上的信号,有效地降低其强度,从而使输出信号低频部分比输入信号强度更高。
四、低通滤波器的类型1. 振荡滤波器(Oscillator Filter)振荡滤波器是一种由震荡电路构成的滤波器,它的两种常见的类型是双稳态振荡滤波器(BFO)和双动态振荡滤波器(BDE)。
它们都执行同样的功能,即通过反馈电路构成的振荡电路来实现低通滤波效果,从而实现高质量的低频信号。
2. 卷积滤波器(Convolution Filters)卷积滤波器是由单独的一段信号与待处理信号的积分求和运算构成的一种滤波器。
它的特点比较灵活,支持多种不同类型的滤波器,比如:低通滤波器、带通滤波器和高通滤波器等,并且支持设计更复杂的滤波器。
3. 周期滤波器(Periodic Filters)周期滤波器是通过模拟周期滤波器的机制来实现低通滤波效果的一种滤波器。
它以用户定义的一组振幅、相位和频率为基础,创建一组周期函数,然后将待处理信号的周期性构造与之匹配,从而实现低通滤波的效果。
lpf低通滤波器参数
低通滤波器(Low-Pass Filter,LPF)是一种可以通过滤除高频信号而仅传递低频信号的滤波器。
LPF的参数可以包括截止频率、衰减特性以及滤波器的阶数等。
1. 截止频率(Cutoff Frequency):这是LPF的最重要参数之一。
截止频率指的是滤波器开始滤除高频信号的频率点。
通常用赫兹(Hz)来表示,例如100 Hz、1 kHz等。
2. 衰减特性(Attenuation characteristics):指的是LPF对于截止频率之后的高频信号的衰减程度。
常见的单位是分贝(dB)。
例如,一个LPF的衰减特性可以为-20 dB/十分之一倍(decade),代表每增加一个频率十分之一倍,信号的幅度将下降20 dB。
3. 阶数(Order):指示LPF的阶数,即滤波器电路中使用的电容和电感的数量。
阶数越高,滤波器的斜率越陡峭。
常见的LPF阶数包括一阶、二阶、三阶等。
一阶LPF具有较为温和的滤波特性,而高阶LPF可以实现更精确的滤波。
对于具体的LPF设计,你可能需要了解其滤波器类型(如巴特沃斯滤波器、切比雪夫滤波器等),以及所需的频率响应和设计指标。
根据这些参数,你可以使用相关的电路设计工具
或计算公式来获得所需的元件数值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
有源低通滤波器(LPF)
1 低通滤波器的主要技术指标
(1)通带增益Avp
通带增益是指滤波器在通频带内的电压放大倍数,如图3所示。
性能良好的LPF通带内的幅频特性曲线是平坦的,阻带内的电压放大倍数基本为零。
(2)通带截止频率fp
其定义与放大电路的上限截止频率相同,见图3。
通带与阻带之间称为过渡带,过渡带越窄,说明滤波器的选择性越好。
图3 LPF的幅频特性曲线
2 简单一阶低通有源滤波器
一阶低通滤波器的电路如图4所示,其幅频特性见图5,图中虚线为理想的情况,实线为实际的情况。
特点是电路简单,阻带衰减太慢,选择性较差。
图4 一阶LP
F
图5 一阶LPF的幅频特性曲线
当f = 0时,电容器可视为开路,通带内的增益为
一阶低通滤波器的传递函数如下
,其中
该传递函数式的样子与一节RC低通环节的增益频率表达式差不多,只是缺少通带增益Avp这一项。
3 简单二阶低通有源滤波器
为了使输出电压在高频段以更快的速率下降,以改善滤波效果,再加一节RC低通滤波环节,称为二阶有源滤波电路。
它比一阶低通滤波器的滤波效果更好。
二阶LPF的电路图如图6
所示,幅频特性曲线如图7所示。
图6 二阶LP
F
图7 二阶LPF的幅频特性曲线
(1)通带增益
当f = 0时,各电容器可视为开路,通带内的增益为
(2)二阶低通有源滤波器传递函数
根据图8-2.06可以写
出
通常有,联立求解以上三式,可得滤波器的传递函数
(3)通带截止频率
将s换成jω,令ω0=2πf0=1/(RC)可得
当f=fp 时,上式分母的模
解得截止频率:
与理想的二阶波特图相比,在超过f0以后,幅频特性以-40 dB/dec的速率下降,比一阶的下降快。
但在通带截止频率f
p→f0之间幅频特性下降的还不够快。
4 二阶压控型低通有源滤波器
(1)二阶压控型LPF
二阶压控型低通有源滤波器如图8所示。
其中的一个电容器C1原来是接地的,现在改接到输出端。
显然,C1的改接不影响通带增益。
图8 二阶压控型LP
F
图9 二阶压控型LPF的幅频特性
(2)二阶压控型LPF的传递函数
对于节点N,可以列出下列方程
联立求解以上三式,可得LPF的传递函数
上式表明,该滤波器的通带增益应小于3,才能保障电路稳定工作。
(3)频率响应
由传递函数可以写出频率响应的表达式
当f=f0时,上式可以化简为
定义有源滤波器的品质因数Q值为f=f0时的电压放大倍数的模与通带增益之比
以上两式表明,当2<Avp<3时,Q>1,在f=f0处的电压增益将大于Avp,幅频特性在f=f0处将抬高,具体请参阅图9。
当Avp≥
3时,Q=∞,有源滤波器自激。
由于将C1接到输出端,等于在高频端给LPF加了一点正反馈,所以在高频端的放大倍数有所抬高,甚至可能引起自激。
5 二阶反相型低通有源滤波器
二阶反相型LPF如图8-2.10所示,它是在反相比例积分器的输入端再加一节RC低通电路而构成。
二阶反相型LPF的改进电路如图8-2.11所示。
图10 反相型二阶LP F
图11多路反馈反相型二阶LPF
由图11可知
对于节点N,可以列出下列方程
传递函数为
频率响应为
以上各式中。
