9.19 多项式除以单项式
2019多项式除以单项式

初中数学备课组教师年级:学生日期上课时间学生情况:主课题:多项式除以单项式教学目标:1.掌握多项式除以单项式的法则,并能熟练地进行多项式除以单项式的计算;2.渗透转化思想;3.提高学生的抽象、概括能力,以及运算能力.教学重点:1.多项式除以单项式的运算法则;2.准确、熟练地运用法则进行计算。
教学难点:1.正确熟练地运用法则进行计算;考点及考试要求:教学设计【要点归纳】1.多项式除以单项式的法则多项式除以单项式,先把多项式的每一项除以单项式,再把所得的商相加。
2.进行相关的混合运算时,既要注意运算法则,又要注意运算顺序。
3.多项式除以单项式所得商的项数与这个多项式的项数相同,不要漏项。
4.运算性质是整式乘除法的基础,只要抓住这关键的一步,才能准确地进行多项式除以单项式的运算。
5.符号仍是运算中的重要问题,用多项式的每一项除以单项式时,要注意每一项的符号和单项式的符号。
一、复习引入1.计算并回答问题:34223222;(1) 4 a b c÷2a b c;(2) (- a b c) ÷3ab4提问:以上的计算是什么运算? 能否叙述这种运算的法则?2.计算并回答问题:(1) 3 x(x2- 1x+1);(2) -4 a·(3a2-a+2) ;62提问:以上的计算是什么运算? 能否叙述这种运算的法则?二、讲授新课1.提出问题对照整式乘法的学习顺序,下面我们应该研究整式除法的什么内容? (多项式除以单项式) 2.多项式除以单项式的法则引例:计算 (am+bm+cm) ÷m我们曾把多项式乘以单项式的运算转化为单项式乘以单项式的运算来进行,那么多项式除以单项式的运算是否也能进行类似的转化呢?根据“除以一个数等于乘以这个数的倒数”,有( a+b+c) ÷m1= ( a+b+c) ·m111=a·+b·+c·m m m=a÷m+b÷m+c÷m这就是多项式除以单项式的法则,你能用文字语言叙述吗?(多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加)三、应用举例例1. 计算(1) (28 a3-14a2+7a) ÷7a;(2) (36x4y3-24x3y2+3 x2y2) ÷(-6x2y);解: (1) (28a3 -14a2+7a) ÷7a=28a3÷7a-14a2÷7a+7 a÷7a2=4a -2a+1 ;(2) (36 x4y3-24x3y2 +3x2y2) ÷(-6x2y)432322 2 22=36x y ÷(-6x y)-24 x y ÷(-6x y)+3x y ÷(-6x y)2 21= -6x y +4 xy- y2第 (1) 小题由师生共同解答,教师板演,并提醒学生注意商式中“1不”可漏掉;第(2)小题由学生板演,根据学生的板演,教师强调指出:当除式的系数为负数时,商式的各项符号与被除式各项的符号相反。
沪教初一数学知识点整理

11.1 平移 1. 将图形上的所有点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为 平移 2. 图形平移后,对应点之间的距离、对应线段的长度、对应角的大小相等。图形平移后,图 形的大小、形状都不变。 3. 平移后各对应点之间的距离叫做图形平移的距离。
11.2 旋转 1. 在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的运动叫做图形的旋转。 这个定点叫做旋转中心,转动的角度叫做旋转角。 2. 图形的旋转是图形上的每一点在平面上绕着某个固定点旋转固定角度的位置移动,其中对 应点到旋转中心的距离相等,对应线段的长度、对应角的大小相等,旋转前后图形的大小 和形状没有改变。
9.5 合并同类项 1. 所含的字母相同,且相同字母的指数也相同的单项式叫做同类项。 2. 把多项式中的同类项合并成一项,叫做合并同类项。一个多项式合并后含有几项,这个多 项式就叫做几项式。 3. 把同类项的系数相加的结果作为合并后的系数,字母和字母的指数不变。 4. 多项式的同类项可以运用交换率、结合律、分配率合并。 9.6 整式的加减 1. 括号前面是“+”号,去掉“+”号和括号,括号里的各项不变号;括号前面是“-”号, 去掉“-”号和括号,括号里的各项都变号。
9.17 同底数幂的除法 1. am ÷an=am-n(m、n是正整数且m>n, a ≠0).同底数幂相除,底数不变,指数相减。 2. 任何不等于零的数的零次幂为1,即a0=1(a ≠0). 9.18 单项式除以单项式 1. 两个单项式相除,把系数、同底数幂分别相除作为商的因式,对于只在被除式里含有的自 母,则连同它的指数作为商的一个因式。 9.19 多项式除以单项式 1. 多项式除以单项式,先把多项式的每一项除以单项式,再把所得的商相加。
多项式除以单项式ppt课件
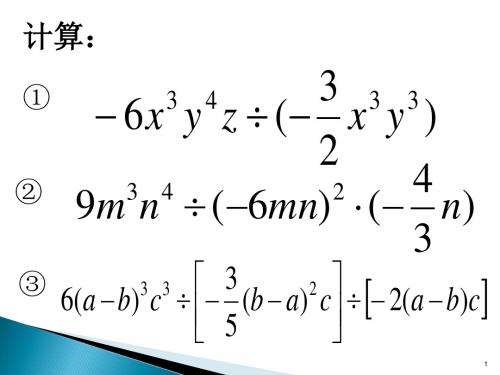
③ (8a2b 4ab2 ) 4ab;
④ (4c2d c3d 3) (2c2d ).
12
练习:
(2)计算:
① (16m3 24m2 ) (8m2 );
② (9x3 y2 21xy2 ) 7xy2 ;
③ (25x2 15x3 y 20x4 ) (5x2 ); ④ (4a2 12a2b 7a3b2 ) (4a2 ).
n 平方 加n 除以n 答案
15
n 平方 加n 除以n 答案
16
小结
1.多项式除以单项式的法则是什么? 2.运用该法则应注意什么?
正确地把多项式除以单项式问题转化 为单项式除以单项式问题。计算不可丢 项,分清“约掉”与“消掉”的区别: “约掉”对乘除法则言,不减项;“消 掉”对加减法而言,减项。
9
多项式除以单项式的法则的应用:
10
例4.计算:
[5xy2(x2-3xy)-(-3x2y)3]
÷(2xy)2
=[5x3y2-15x2y3 - (-27x6y3)]
÷4x2y
=[5x3y2-15x2y3+27x6y3)]
÷4x2y
= 5x- 15y + 27 x4y
44
4
11
练习:
(1)计算:
① (6xy 5x) x;
解:原式 28a3 7a 14a2 7a 7a 7a
4a2 2a 1
7
(2)
(36 x4 y3 24 x3 y2 3x2 y2 ) (6x2 y)
8
多项式除以单项式的法则:
例2 化简:
(2x y)2 y( y 4x) 8x 2x
多项式除以单项式注意事项

多项式除以单项式注意事项1.多项式的次数:在进行除法运算之前,需要确定多项式的次数。
多项式的次数是指多项式中各项中的最高次数。
例如,对于多项式f(x)=2x^3+3x^2+4x+5,其次数是3、这一步骤的目的是为了确定除法的次数,以及最后的商和余数的次数。
2.单项式的除数:在进行多项式除以单项式的运算中,单项式作为除数,可以是一个常数项或者含有变量的项。
例如,进行多项式f(x)=2x^3+3x^2+4x+5除以单项式g(x)=x+2的运算时,g(x)是一个一次多项式,可以作为除数。
需要注意的是,除数的系数不能为0,否则除法运算将无法进行。
3.除法运算的步骤:多项式除以单项式的运算可以通过长除法的方法进行,具体步骤如下:a)首先将除数的第一项与被除式的首项相除,得到商的第一项。
例如,将f(x)除以g(x)的第一步是将2x^3和x相除,得到商的第一项为2x^2b)将上一步得到的商的第一项与除数相乘,得到乘积项。
c)将乘积项减去被除式,得到差项。
d)重复上述步骤,将差项作为新的被除式,进行下一轮的除法运算。
e)当差项的次数小于除数的次数时,停止除法运算,此时商为所有商的项的和,余数为差项。
以上是进行多项式除以单项式的一般步骤,具体的运算过程可能因多项式或单项式的形式而有所不同。
在进行除法运算的过程中,需要注意每一步的计算准确性,确保每一步的结果都是正确的。
4.多项式系数的计算:在进行多项式除以单项式运算的过程中,需要进行多项式系数的计算。
多项式系数是指多项式中各项中变量的系数。
在计算过程中,需要进行系数的乘法和减法运算。
在进行乘法运算时,需要注意乘法规则,确保乘法的结果是正确的。
在进行减法运算时,需要注意减法的顺序,确保减法的结果是正确的。
5.结果的表达形式:多项式除以单项式的最终结果通常由两部分组成,即商和余数。
商是被除式和除数相除的结果,余数是被除式减去乘积项的结果。
这两部分的表达形式可以是多项式形式,也可以是数形式。
多项式除以单项式ppt课件

系数相除
(3)(-9x5) ÷(-3x) =-3x4 (× )
求系数的商, 应注意符号
×
(4)12a3b ÷4a2=3a ( )
只在一个被除式里含有的字母,要连同
它的指数写在商里,防) 3ab2 9ab5
(2) ( 3m3n ) (mn) 3m2
(3) (21a3bc) ( 3ac ) 7a2b
4
例2:计算
(1) (14a3 7a2 ) (7a) 解原式=(14a3 ) (7a) + (7a2 ) (7a)
= 2a2 a
(2) (15 x3 y5 10 x4 y4 20 x3 y2 ) (5 x3 y2 )
解原式= (15 x3 y5 ) (5 x3 y2 ) +(10x4 y4 ) (5 x3 y2 ) +(20x3 y2 ) (5x3 y2 )
(4) (4c3 d4- 6c2d 3 ) ÷(-3c2d)
4 cd 3 + 2d 2
3
9
练一练:填空
(1) ( 21s2t 2 + 14st 3 ) (7st 2 ) 3s + 2t
(2) ( 3a2 2ab ) (a) 3a + 2b
(3) ( 3 x + 1 7 x2 ) 2x 3x2 + 2x 7 x3
(2) (4a + 6) 2
4a 2 + 6 2
2a + 3
(3) (2a2 a) 2a
2a2 2a + a 2a
1
a + 2
3
(a + b + c) m
am+bm+cm
你能总结多项式除以单项式的法则吗?
最新沪教版数学教材目录-沪教版初中数学(初一、初二、初三)教材版本目录大纲

沪教版初中数学教材版本目录大纲七年级(上)第九章整式第1节整式的概念9.1 字母表示数9.2 代数式9.3 代数式的值9.4 整式第2节整式的加减9.5 合并同类项9.6 整式的加减第3节整式的乘法9.7 同底数幂的乘法9.9 积的乘方9.8 幂的乘方9.10 整式的乘法第4节乘法公式9.11 平方差公式9.12 完全平方公式第5节因式分解9.13 提取公因式法9.14 公式法9.15 十字相乘法9.16 分组分解法第6节整式的除法9.18 单项式除以单项式9.17 同底数幂的除法9.19 多项式除以单项式本章小结第十章分式第1节分式10.1 分式的意义10.2 分式的基本性质第2节分式的运算10.3 分式的乘除10.4 分式的加减10.5 可以化成一元一次方程的分式方程10.6 整数指数幂及其运算本章小结第十一章图形的运动第1节图形的平移11.1 平移第2节图形的旋转11.2 旋转11.3 旋转对称图形与中心对称图形11.4 中心对称第3节图形的翻折11.5 翻折与轴对称图形11.6 轴对称本章小结七年级(下)第十二章实数第1节实数的概念12.1 实数的概念第2节数的开方12.2 平方根和开平方12.3 立方根和开立方12.4 n次方根第3节实数的运算12.5 用数轴上的点表示实数12.6 实数的运算第4节分数指数幂12.7 分数指数幂第十三章相交线平行线第1节相交线13.1 邻补角、对顶角13.2 垂线13.3 同位角、内错角、同旁内角第2节平行线13.4 平行线的判定13.5 平行线的性质第十四章三角形第1节三角形的有关概念与性质14.1 三角形的有关概念14.2 三角形的内角和第2节全等三角形14.3 全等三角形的概念与性质14.4 全等三角形的判定第3节等腰三角形14.5 等腰三角形的性质14.6 等腰三角形的判定14.7 等边三角形第十五章平面直角坐标系第1节平面直角坐标系15.1 平面直角坐标系第2节直角坐标平面内点运动15.2 直角坐标平面内点运动八年级(上)第十六章二次根式第一节二次根式的概念和性质16.1 二次根式16.2 最简二次根式和同类二次根式第二节二次根式的运算16.3 二次根式的运算本章小结阅读材料二次不尽根与简单连分数第十七章一元二次方程第一节一元二次方程的概念17.1 一元二次方程的概念第二节一元二次方程的解法17.2 一元二次方程的解法17.3 一元二次方程根的判别式第三节一元二次方程的应用17.4 一元二次方程的应用本章小结阅读材料关于一元二次方程的求根公式探究活动数字世界一个“平方和”等式宝塔的构建第十八章正比例和反比例函数第一节正比例函数18.1 函数的概念18.2 正比例函数第二节反比例函数18.3 反比例函数第三节函数的表示法18.4 函数的表示法本章小结探究活动生活中的函数第十九章几何证明第一节几何证明19.1 命题和证明19.2 证明举例第二节线段的垂直平分线与角的平分线19.3 逆命题和逆定理19.4 线段的垂直平分线19.5 角的平分线19.6 轨迹第三节直角三角形19.7 直角三角形全等的判定19.8 直角三角形的性质19.9 勾股定理19.10 两点的距离公式本章小结阅读材料一《几何原本》古今谈阅读材料二勾股定理万花筒八年级(下)第二十章一次函数第一节一次函数的概念第二节一次函数的图像与性质20.2 一次函数的图像20.3 一次函数的性质第三节一次函数的应用第二十一章代数方程第一节整式方程21.1 一元整式方程21.2 二项方程第二节分式方程21.3 可化为一元二次方程的分式方程第三节无理方程第四节二元二次方程组21.5 二元二次方程和方程组21.6 二元二次方程组的解法第五节列方程(组)解应用题第二十二章四边形第一节多边形第二节平行四边形22.2 平行四边形22.3 特殊的平行四边形第三节梯形22.4 梯形22.5 等腰梯形22.6 三角形、梯形的中位线第四节平面向量及其加减运算22.7 平面向量22.8 平面向量的加法22.9 平面向量的减法第二十三章概率初步第一节事件及其发生的可能性23.1 确定事件和随机事件23.2 事件发生的可能性第二节事件的概率23.3 事件的概率23.4 概率计算举例九年级(上)第二十四章相似三角形第一节相似形24.1 放缩与相似形第二节比例线段24.2 比例线段24.3 三角形一边的平行线第三节相似三角形24.4 相似三角形的判定24.5 相似三角形的性质第四节平面向量的线性运算24.6 实数与向量相乘24.7 向量的线性运算第二十五章锐角的三角比第一节锐角的三角比25.1 锐角的三角比的意义25.2 求锐角的三角比的值第二节解直角三角形25.3 解直角三角形25.4 解直角三角形的应用第二十六章二次函数第一节二次函数的概念26.1 二次函数的概念第二节二次函数的图像26.2 特殊二次函数的图像26.3 二次函数y = ax2+bx+c的图像九年级(下)第二十七章圆与正多边形第一节圆的基本性质27.1 圆的确定27.2 圆心角、弧、弦、弦心距之间的关系27.3 垂径定理第二节直线与圆、圆与圆的位置关系27.4 直线与圆的位置关系27.5 圆与圆的位置关系第三节正多边形与圆27.6 正多边形与圆第二十八章统计初步第一节统计的意义28.1 数据整理与表示28.2 统计的意义第二节基本的统计量28.3 表示一组数据平均水平的量28.4 表示一组数据波动程度的量28.5 表示一组数据分布的量28.6 统计实习。
多项式除以单项式PPT教学课件
2.计算:
(1)[(-3xy)2•x3-2x3(3xy2)3• 1 y] 2 ÷9x4y
作业:第50页知识技能:第 1题(5)(6)(7)(8) 小题
陶渊明(约公元365年~427年),字元亮,一说名 潜,字渊明,世称靖节先生。因宅边生五棵柳树,又自号 “五柳先生”。浔阳柴桑(今江西市九江西南)人,他的祖 父,父亲均做过太守一类官职,但到了陶渊明,家境早已破 败。因为这样的家世背景,陶渊明少年时代既好读六经,有 大济苍生的宏愿,又厌恶世俗,热爱纯净的自然,他自29 岁入仕,做过祭酒、参军一类的小官。后因仕途坎坷又不耐 烦“为五斗米折腰向乡里小儿”(《宋书.隐逸传》)更愤 慨于南北仕族的兼并不厌,王恭、司马道子、桓温、刘裕等 人的篡乱相替,陶渊明于41岁毅然辞去在任仅80余日的 彭泽县令,回柴桑归隐。此后直至逝世的23年间,以耕读 自娱,未在入世。
1、厌恶官场; 2、淡泊名利; 3、热爱自然; 4、热爱田园;
5、安贫乐道
隐逸 出世
云无心以出岫,鸟倦飞而知还
单项式与多项式相乘, 就是用单项式去乘多项式
的每一项,再把所得的 积 相加 。
计算下列各式,并说说你 是怎样计算的?
(1) (am bm) m (2) (a2 ab) a (3) (4x2y 2xy2 ) 2xy
多项式除以单项式
m(a+b+c)= am+bm+cm 反之(am+bm+cm)÷m
整式的乘除
多项式除以单 项式
课前练习 1.计算: (1)3a2b3+5a2b3=8a2b3
《多项式除以单项式》 知识清单
《多项式除以单项式》知识清单在数学的学习中,多项式除以单项式是一个重要的知识点。
它不仅是代数式运算的基础,也在解决各种数学问题中有着广泛的应用。
接下来,让我们一起来详细了解一下多项式除以单项式的相关内容。
一、基本概念多项式:由有限个单项式的代数和组成的代数式叫做多项式。
在多项式中,每个单项式叫做多项式的项,不含字母的项叫做常数项。
多项式中次数最高的项的次数,叫做这个多项式的次数。
单项式:由数与字母的积组成的代数式叫做单项式,单独的一个数或一个字母也叫做单项式。
单项式中的数字因数叫做这个单项式的系数,一个单项式中,所有字母的指数的和叫做这个单项式的次数。
二、运算法则多项式除以单项式,先把这个多项式的每一项分别除以这个单项式,再把所得的商相加。
用式子表示为:$(am + bm + cm)÷m = am÷m + bm÷m +cm÷m = a + b + c$三、运算步骤1、把多项式的每一项分别除以单项式。
2、计算各项除以单项式的商。
3、将所得的商相加。
例如:计算$(6x³ 9x²+ 3x)÷3x$第一步:分别除以单项式$6x³÷3x = 2x²$$ 9x²÷3x = 3x$$3x÷3x = 1$第二步:将商相加$(6x³ 9x²+ 3x)÷3x = 2x² 3x + 1$四、注意事项1、运算时要注意符号,同号相除得正,异号相除得负。
2、不要漏项,每一项都要除以单项式。
3、注意商的次数,商的每一项的次数都应该小于等于原来多项式中对应项的次数。
五、实际应用多项式除以单项式在解决实际问题中经常用到,比如在几何图形的面积计算、工程问题中的工作量计算等方面。
例如:一个长方形的面积为$(6x²+ 9x)平方米$,宽为 3x 米,求长方形的长。
【可编辑全文】沪教版七年级数学上册目录
可编辑修改精选全文完整版
七年级上册数学目录
第九章整式
第一节整式的概念
9.1字母表示数
9.2代数式
9.3代数式的值
9.4整式
第二节整式的加减
9.5合并同类项
9.6整式的加减
第三节整式的乘法
9.7同底数幂的乘法
9.8积的乘方
9.9幂的乘方
9.10整式的乘法
第四节乘法公式
9.11平方差公式
9.12完全平方公式
第五节因式分解
9.13提取公因式法
9.14公式法
9.15十字相乘法
9.16分组分解法
第六节整式的除法
9.17单项式除以单项式
9.18同底数幂的除法
9.19多项式除以单项式
第十章分式
第一节分式
10.1分式的意义
10.2分式的基本性质
第二节分式的运算
10.3分式的乘除
10.4分式的加减
10.5可化为一元一次方程的分式方程
10.6整数指数幂及其运算
第十一章图形的运动
第一节图形的平移
11.1 平移
第二节图形的旋转
11.2旋转
11.3旋转对称图形与中心对称图形
11.4中心对称
第三节图形的翻折
11.5翻折与轴对称图形
11.6轴对称。
