第一节 n维欧氏空间 - 欢迎来到重庆邮电大学理学院首页
第二章 矩阵与线性变换

证 我们仅给出证明的思路, 细节见习题 3. 设 dim U = s, dim W = t, dim (U ∩ W ) = r. 任取 U ∩ W 的一组基 α1 , α2 , · · · , αr . 由于 U ∩ W 是 U 与 W 的公共子空间, 故 U ∩ W 的基 是 U 与 W 的线性无关的向量组, 因此可以扩充成 U 或 W 的基. 设 α1 , α2 , · · · , αr , βr+1 , βr+2 , · · · , βs 与 α1 , α2 , · · · , αr , γr+1 , γr+2 , · · · , γt 分别是 U 与 W 的基. 则 α1 , α2 , · · · , αr , βr+1 , βr+2 , · · · , βs , γr+1 , γr+2 , · · · , γt 是 U + W 的一组基. (为此只需证明该向量组线性无关, 且 U + W 的任何向量均可由这些向量 线性表示.) 由维数定理可知, 欲使子空间 U + W 的维数最大, 必要且只要 U ∩ W = 0, 亦即 U 与 W 重 合的部分最小. 这时我们称和 U + W 是直 直和, 记为 U ⊕ W . 因此 dim (U ⊕ W ) = dim U +dim W . 例 2.1.4 二维平面 R2 是 x 轴与 y 轴 (均是 1 维子空间) 的直和. 类似地, R3 是 x 轴, yoz 平面 (这是一个 2 维子空间) 的直和. 例 2.1.5 只含奇 (偶) 次项的多项式称为奇 (偶) 多项式. 0 多项式既是奇多项式也是偶 多项式. 全体奇 (偶) 多项式作成多项式空间的子空间, 称为奇 (偶) 多项式子空间. 多项式空间 是奇多项式子空间与偶多项式子空间的直和. 例 2.1.6 n 阶矩阵空间 Mn (F ) 是纯量矩阵子空间 {A ∈ Mn |A = λI, λ ∈ F } 与迹 0 子空 间 {A ∈ Mn |trA = 0} 的直和. 定 理 2.1.3 (直和的判定) 设 U 与 W 是线性空间 V 的两个子空间, 则下列命题等价: (1) U + W 是直和 (即 U ∩ W = 0); (2) 对任意 α ∈ U + W , 分解式 α = u + w, 其中 u ∈ U, w ∈ W 是唯一的, 即若还 有 α=u +w, 则 u=u, w =w; (3) 零向量的分解式唯一; 即若 0 = u + w, u ∈ U, w ∈ W , 则 u = w = 0; (4) dim (U + W ) = dim U + dim W . 注: 经常将 定理 2.1.3(3) 作为直和的定义. 31
安徽大学研究生各学院课表培养方案(DOC)
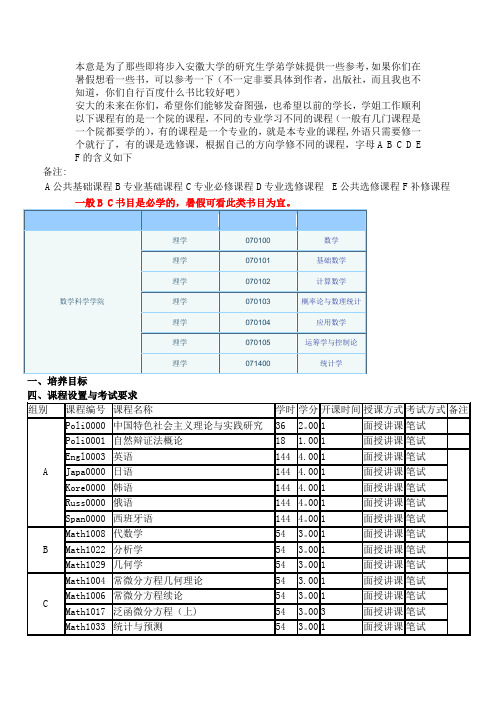
本意是为了那些即将步入安徽大学的研究生学弟学妹提供一些参考,如果你们在暑假想看一些书,可以参考一下(不一定非要具体到作者,出版社,而且我也不知道,你们自行百度什么书比较好吧)安大的未来在你们,希望你们能够发奋图强,也希望以前的学长,学姐工作顺利以下课程有的是一个院的课程,不同的专业学习不同的课程(一般有几门课程是一个院都要学的),有的课程是一个专业的,就是本专业的课程,外语只需要修一个就行了,有的课是选修课,根据自己的方向学修不同的课程,字母A B C D EF的含义如下备注:A公共基础课程B专业基础课程C专业必修课程D专业选修课程E公共选修课程F补修课程四、课程设置与考试要求一、培养目标一、培养目标备注:七、必读书目1、《结构与物性》,周公度,高等教育出版社,19932、《材料科学导论》,冯端等,化学工业出版社 20023、《固体表面物理化学若干研究前沿》,万惠霖等,厦门大学出版社,20064、《Atkins Physical Chemistry》(Seventh Edition), Atkins,P。
等,高等教育出版社,20065、《材料表面与界面》,胡福增等,华东理工大学出版社,20086、《固体材料界面研究的物理基础》,闻立时,科学出版社,20117、《先进材料表面处理和测试技术》,刘勇,等,科学出版社,20088、《纳米材料表面电子结构分析》,曹立礼,清华大学出版社,20109、《环境光催化材料与光催化净化技术》,蔡伟民等,上海交通大学出2001备注:(二级学科代码:080902 二级学科名称:电路与系统)一、培养目标三、研究方向1。
超大规模集成电路与系统设计 2.微纳电子器件模拟与建模 3.网络与智能信息系统 4.非线性电子系统分析与设计 5.嵌入式系统与应用四、课程设置与考试要求二级学科代码:080903 二级学科名称:微电子学与固体电子学)一、培养目标三、研究方向1、微纳电子器件模拟与建模2、高压功器件与电路3、集成电路与系统的结构话设计。
泛函分析讲义(中文版-武汉大学).

则称 d 是 X 上的度量(距离)函数,称 X 为度量(距离)空间.有时为了明确,记为 ( X , d ) .
度量空间的子集合 E ,仍以 d 为 E 上度量构成的度量空间称为 ( X , d ) 的子空间.
例 1 对于 n 维空间Φ n 中的点 x = (x1, , xn ) 和 y = ( y1, , yn ) ,定义
利用 Zorn 引理可以证明: 任一线性空间必存在极大线性无关集合,这一集合即是 X 的 Hamel 基.换句话说,任一线性空间必存在 Hamel 基.
凸集和子空间是线性空间中时常用到的子集. X 的子集 E 称为是凸的,若 ∀x, y ∈ E ,
0 ≤ r ≤ 1 , rx + (1 − r) y ∈ E .对于任一集合 E ⊂ X ,记
容易验证 X 是线性空间. 今后对于有限维空间,无穷序列空间和函数空间将分别采用以上规定的线性运算.许多
在经典分析、代数、复变、实变、微分方程中遇到的空间都是线性空间。 注意:定义 1 与线性代数中关于线性空间的叙述是一致的,但是其内涵要比线性代数中
广泛得多。因为在线性代数中限定所考虑的对象为 n 数组。这一点很重要,例如在线性代数 中有一个结论:任何 n +1 个向量必线性相关。对于现在的空间,这一结论却不必成立。
实际上在Φ
n
上还可以定义其他度量,例如
d1 ( x,
y)
=
max
1≤i≤n
xi
−
yi
,此时 (Φ n , d1) 仍是度
量空间.但须注意应把 (Φ n , d1) 与 (Φ n , d ) 视为不同的度量空间.此外注意今后当说到Φ n 是
度量空间时,总意味着它带有欧氏度量.
MIT公开课-线性代数笔记

目录方程组的几何解释 (2)矩阵消元 (3)乘法和逆矩阵 (4)A的LU分解 (6)转置-置换-向量空间R (8)求解AX=0:主变量,特解 (9)求解AX=b:可解性和解的解构 (10)线性相关性、基、维数 (11)四个基本子空间 (12)矩阵空间、秩1矩阵和小世界图 (13)图和网络 (14)正交向量与子空间 (15)子空间投影 (18)投影矩阵与最小二乘 (20)正交矩阵和Gram-Schmidt正交化 (21)特征值与特征向量 (27)对角化和A的幂 (28)微分方程和exp(At)(待处理) (29)对称矩阵与正定性 (29)正定矩阵与最小值 (31)相似矩阵和若尔当型(未完成) (32)奇异值分解(SVD) (33)线性变换及对应矩阵 (34)基变换和图像压缩 (36)NOTATIONp:projection vectorP:projection matrixe:error vectorP:permutation matrixT:transport signC(A):column spaceN(A):null spaceU:upper triangularL:lower triangularE:elimination matrixQ:orthogonal matrix, which means the column vectors are orthogonalE:elementary/elimination matrix, which always appears in the elimination of matrix N:null space matrix, the “solution matrix” of AX=0R:reduced matrix, which always appears in the triangular matrix, “IF00”I:identity matrixS:eigenvector matrixΛ:eigenvalue matrixC:cofactor matrix关于LINER ALGEBA名垂青史的分析方法:由具象到抽象,由二维到高维。
第二章内积空间

定理4:设 ε1 , ε 2 ,L, ε n 与 η1 ,η 2 ,L,η n 为n维酉空间V的基,它们 定理4 维酉空间V的基, 的度量矩阵为A和B,,C是 ε1 , ε 2 ,L, ε n 到 η1 ,η 2 ,L,η n 的过渡 的度量矩阵为A ,,C
(α ,α )
.
∀α ≠ 0 ∈ V ,
称
α α
为α 的规范化单位向量
定义 α , β 的距离为 d (α , β ) = α − β 2、向量长度的性质
(1) α ≥ 0, 当且仅当 α = 0时等式成立; 时等式成立; (2) kα = k α ;
引理(Chauchy不等式) 引理(Chauchy不等式)设V是酉(欧氏)空间, ∀α , β ∈ V , 不等式 是酉(欧氏)空间, 向量的长度满足 证明: 证明:
y1 n n y2 (α , β ) = ∑∑ xi y j (α i ,α j ) = (x1 , x2 ,L, xn )A = xT Ay M i =1 j =1 y n
则
即抽象的向量的内积可通过他们在基下的坐标及度量矩阵 的双线性函数来计算。 的双线性函数来计算。 定理2:设 ε1 , ε 2 ,L, ε n 与 η1 ,η 2 ,L,η n 为n维欧氏空间V的基,它们 定理2 维欧氏空间V的基, 的度量矩阵为A ,,C 的度量矩阵为A和B,,C是 ε1 , ε 2 ,L, ε n 到 η1 ,η 2 ,L,η n 的过渡 证明详见P26-27) (证明详见 ) 矩阵,则 B = C AC 矩阵, 即同一欧氏空间不同基的度量矩阵是相合矩阵。 欧氏空间不同基的度量矩阵是相合矩阵 即同一欧氏空间不同基的度量矩阵是相合矩阵。
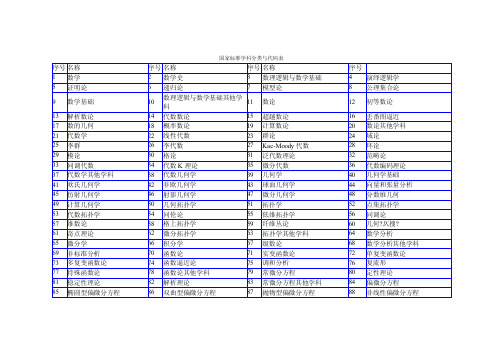
国家标准学科分类与代码表
207 弹性力学
208
210 蠕变
211 界面力学与表面力学
212
214 断裂力学
215 散体力学
216
218 结构力学
219 计算固体力学
220
222 振动与波
223 线性振动力学
224
226 随机振动力学
227 振动控制理论
228
230 振动与波其他学科
231 流体力学
232
234 气体动力学
235 空气动力学
236
238 粘性流体力学
239 多相流体力学
240
242 等离子体动力学
243 电磁流体力学
244
246 野生动物保护与管理
247 防护林学
248
250 园林植物学
251 风景园林工程
252
254 林业工程
255 森林采运学
256
258 木材学
259 木材加工与人造板工艺学 260
262 林业工程其他学科
35 微分代数 39 几何学
42 非欧几何学
43 球面几何学
46 射影几何学
47 微分几何学
50 几何拓扑学
51 拓扑学
54 同伦论 58 格上拓扑学
55 低维拓扑学 59 纤维丛论
62 微分拓扑学
63 拓扑学其他学科
66 积分学
67 级数论
70 函数论
71 实变函数论
74 函数逼近论 78 函数论其他学科
469 环境医学
470 职业病学
471 地方病学
473 卫生检验学
474 食品卫生学
475 儿少卫生学
477 环境卫生学
一类拟线性抛物方程解的爆破
对 问题 B 作假设 : I) 力上 ( ,( 连续且 h , ( 在 )h ) ( )>0 (I / R × × “ R连续且满足 ; I) “ R R 一
)以  ̄ u 条件 : 存在常数 >0 c>0 , 使得 , , u u )≥ ( 一1 ∑ n ( O )
应 用分 部积分 法 得 :
n
t )=
1
i
) 一( 1~ ) xL ,, )( 考 L 一 毒 ̄ + l1 3 n - x ) _ K d n v
= L g舢 - ( )l 1 舢
:
其 中,o为 a d" 力上的面积元素, 利用问题 B中的边界条件 , 得:
于是 问题 A变为 问题 B:
收稿 日期 :0"一 1— 4 修 回 日期 :0"一 3—2 . 20 O 0 : / 20 0 / 4 作者简 介: 雷澜 (9 3一) 女 , 17 , 重庆市沙 坪坝人 , 硕士 , 讲师 , 主要从事应用 数学研究.
维普资讯
20 0 7年 8月
Au . 0 7 g20
文章 编 号 :6 2— 5 X(0 7)5一o 6 0 17 0 8 20 0 4 4— 3
一
类 拟 线 性 抛 物 方 程解 的爆 破
雷 澜 田 1
( 重庆工商大学 理学院 , 重庆 4 06 ) 0 0 7
摘 要: 讨论 了拟线性抛物方程具有 第 3类非线性边界条件混合 问题解的爆破 , 究 了其 研 古典 解 , 对混合 问题 中的 和 g作 出适 当假 设 的前提 下 , 明 了上 述混 合 问题 的解在 有 限 时刻 在 证
爆破 . 结论 放 宽 了对 假设 条件 的 限制 . 该 关键词 : 线性抛 物 方程 ; 拟 混合 问题 ; 爆破
2016年苏州大学物理与光电
物理学 102856211305888 物理学 102856211305899 物理学 102856211305974 物理学 102856211305870 物理学 102856211305913 物理学 102856211305953 物理学 102856211305862 物理学 102856211305978 物理学 102856211305941 物理学 102856211305973 物理学 102856211305955 物理学 102856211305970 材料物理 102516210000 与化学 662 材料物理 102856211306174 与化学 材料物理 102856211306173 与化学 材料物理 102856211306180 与化学 检测与自 102856211306189 动化装置 检测与自 102856211306186 动化装置 检测与自 102856211306183 动化装置 检测与自 102856211306187 动化装置 检测与自 102856211306185 动化装置 新能源科 102856102850256 学与工程 新能源科 102856211305991 学与工程 新能源科 102856211305992 学与工程 新能源科 102856211305994 学与工程 新能源科 102856211305982 学与工程 新能源科 102856211305997 学与工程 新能源科 102856211305985 学与工程 新能源科 102856211305988 学与工程 新能源科 102856211306002 学与工程 新能源科 102856211305995 学与工程 新能源科 102856211306005 学与工程 新能源科 102856211305989 学与工程 新能源科 102856211306000 学与工程 新能源科 102856211305990 学与工程
大学数学《实变函数》电子教案
《实变函数》电子教案(重庆邮电大学数理学院邓志颖)课程名称:实变函数学时/学分:48/3.0教材名称:实变函数与泛函分析基础(第三版)出版社:高等教育出版社编著者:程其襄等适用专业:数学与应用数学专业(大三上学期)序言: 实变函数简介微积分发展的三个阶段:•创立(17世纪):Newton (力学)Leibniz (几何)(无穷小)•严格化(19世纪): Cauchy, Riemann, Weierstrass(极限理论(ε-N, ε-δ语言),实数理论)•外微分形式(20世纪初):Grassmann, Poincare, Cartan (微积分基本定理如何在高维空间得到体现)微积分继续发展的三个方向:•外微分形式 (整体微分几何)(微积分基本定理如何在高维空间得到体现)•复数域上的微积分(复变函数)•微积分的深化和拓展(实变函数)1.Riemann 积分回顾:(1) Riemann 积分的定义||||01()()lim()nbiiaT i R f x dx f x ξ→==∆∑⎰ 其中11,ii i i i i xx x x x ξ--∆=-≤≤积分与分割、介点集的取法无关.几何意义(非负函数):函数图象下方图形的面积。
(2) Riemann 可积的充要条件()f x 在[,]a b 上Riemann 可积||||01()limnbiiaT i f x dx M x →=⇔=∆∑⎰||||01lim ()nbiiaT i m x f x dx →==∆=∑⎰其中:11sup{():}inf{():}i i i i i i M f x x x x m f x x x x --=≤≤=≤≤0,ε⇔∀>∃分划T ,使得1ni i i x ωε=∆≤∑0,εη⇔∀>∃,分划T ,使得所有振幅i ωη≥的小区间i ∆的总长度不超过ε.例:Dirichlet 函数不Riemann 可积.1[0,1]()0[0,1]x QD x x Q∈⋂⎧=⎨∈-⎩ 因为上积分为||||01()lim1nbiiaT i f x dx M x→==∆=∑⎰下积分为||||01()lim0nbiiaT i f x dx m x→==∆=∑⎰所以对于∀分划T ,有11niii xω=∆=∑所以Dirichlet 函数不Riemann 可积. (3)Riemann 积分的局限性)a 微积分基本定理定理:若'()F x 在[,]a b 上连续,则()'()()()xaR F t dt F x F a =-⎰1881年Volterra 作出一可微函数,导函数有界但不Riemann 可积;)b 积分与极限交换次序(一般要求一致收敛)例:设{}n r 为[0,1]中全体有理数(因为其为可数集,故可把它排成序列),作[0,1]上的函数列1231231{,,,,}()1,2,3,0[0,1]{,,,,}n n n x r r r r f x n x r r r r ∈⎧==⎨∈-⎩则{()}n f x 在[,]a b 上Riemann 可积,但1[0,1]lim ()()0[0,1]n n x Qf x D x x Q →∞∈⋂⎧==⎨∈-⎩不Riemann 可积. 故对一般收敛函数列,在Riemann 积分意义下极限运算与积分运算不一定可交换次序,即:lim ()lim ()bbn n aan n f x dx f x dx →∞→∞=⎰⎰不一定成立.2.Lebesgue 积分思想简介:为使()f x 在[,]a b 上Riemann 可积,按Riemann 积分思想,必须使得分划后在多数小区间上的振幅足够小,这迫使在较多地方振动的函数不可积.Lebesgue 提出,不从分割定义域入手,而从分割值域入手;即采取对值域作分划,相应得到对定义域的分划(每一块不一定是区间),使得在每一块上的振幅都很小,即按函数值的大小对定义域的点加以归类对此Lebesgue 自己曾经作过一个比喻,他说:● 假如我欠人家一笔钱,现在要还,此时按钞票的面值的大小分类,然后计算每一类的面额总值,再相加,这就是Lebesgue 积分思想;● 如不按面额大小分类,而是按从钱袋取出的先后次序来计算总数,那就是Riemann积分思想 即:0,δ∀> 作分划012n m y y y y M =<<<<=其中1,()i i y y m f x M δ--<≤<作点集1{:()}i i i E x y f x y -=≤<()f x 在i E 上的振幅不会大于δ. 作和:1ni ii s mEξ==∑i mE 表示i E 的“长度,1i i i y y ξ-≤<取极限:[,]1()()lim ni i a b i L f x dx mE δξ→==∑⎰3.Lebesgue 积分构思产生的问题:● (1) 先介绍集合i E (第一章集合,第二章点集) ● (2) 集合i E 的“长度”如何定义(第三章 测度论); ● (3) 怎样的函数可使i E 都有“长度”(第四章 可测函数);● (4) 定义Lebesgue 积分并研究其性质(第五章 积分论);● (5) 将牛顿—莱布尼兹公式加以推广(第六章 微分与不定积分)● 教材:实变函数论与泛函分析基础(第三版),程其襄等编, 高等教育出版社,2010年6月.参考文献:● 实变函数论(第二版),江泽坚,吴智泉编, 高等教育出版社,2003年7月. ● 周民强,实变函数(论),北京大学出版社,1995.6(2001) ● 周性伟,实变函数,科学出版社,1998.9 ● 胡适耕,实变函数,高等教育出版社,1999.7● 徐森林,实变函数论,中国科学技术大学出版社,2002● 郑维行等,实变函数论与泛函分析概要,高等教育出版社,1987 ● 夏道行等,实变函数论与泛函分析,高等教育出版社,1983.2 ● Halmos ,测度论(Measure theory)● Rudin , 实分析与复分析(Real and complex analysis).教时安排:第一章 集合 6学时,第二章 点集 6学时,第三章 测度论 8学时,第四章 可测函数 10学时,第四章 积分论 12学时,第六章 微分与不定积分 6学时,共六章 48学时。
理学院简介学院代码306
理学院简介(学院代码306)理学院承担物理学、材料科学与技术、数学和系统科学等4个一级学科的学科建设任务,在数学、物理学、系统科学等3个一级学科、15个二级学科招收硕士研究生。
拥有1个重庆市重点学科,3个中央与地方共建实验室,1个重庆市高校创新团队,1个重庆高校市级重点实验室;2个校级研究平台、3个校级科研机构和3个校级科研团队。
学院师资力量雄厚,教授27人(含海外特聘教授2人),副教授34人,具有博士学位教师49人;重庆市“百人计划”3人,“巴渝海外引智计划”2人,“高端外国专家项目”1人,“巴渝学者特聘教授”2人,“重庆市名师”1人,重庆市高等学校优秀人才支持计划获得者2人,重庆市中青年骨干教师4名;重庆邮电大学“十佳师德标兵”4人,“十佳优秀青年教师”5人。
近年来,学院承担了包括国家“973”项目子项目、国家自然科学基金面上项目和青年基金项目、重庆市科委重点项目等省部级及以上科研项目160余项;获重庆市自然科学奖一等奖2项、二等奖4项;发表SCI、EI期刊论文400余篇,在包括物理学、材料科学与技术、数学和系统科学顶级刊物Light: Science & Applications、Physical Review Letters、Nano Letters、Journal of the American Ceramic Society、Advanced Functional Materials、J Differ Equations、Fuzzy Sets and Systems、IEEE Transactions on Automatic Control、Automatica、中国科学(数学)、数学学报在内的国内外重要学术期刊上发表论文近150篇,其中ESI高被引论文在库17篇;出版专著8部。
近年来学院邀请了菲尔兹奖获得者丘成桐、美国德州农工大学陈鞏、美国纽约大学姜钟平、中科院半导体所常凯、中科院长春光学精密机械与物理研究所张家骅、塞尔维亚贝尔格莱德大学Miroslav、爱沙尼亚塔尔图大学物理所Mikhail Brik教授等一批国内外著名专家学者到学院为学生做学术报告,并多次成功举办国际国内学术会议,与台湾理论科学中心物理组、波兰科学院物理所签订了学术交流合作协议,启动了彼此间在科研人员互访、学术资源共享、学生交换与联合培养等方面的合作与交流计划。
