常用GeoGebra指令—10.脚本
动态数学软件GeoGebra使用教程

动态数学软件GeoGebra使用教程GeoGebra是一款功能强大的动态数学软件,它结合了几何、代数、微积分和统计等数学学科,使得学生能够以直观的方式探索和理解数学概念。
在本教程中,我将向您介绍如何使用GeoGebra进行基本操作和创建动态数学模型。
让我们从一个简单的示例开始。
在几何视图中,点击工具栏中的"点"按钮,然后在绘图区域中点击两次以创建两个点A和B。
接下来,点击"线段"按钮,并依次选择点A和点B,以创建连接它们的线段。
现在,我们可以使用代数视图来探索这个线段。
在输入栏中输入“AB”的名称,并按Enter键。
您将在代数视图中看到一个名为“AB”的对象,它代表了线段AB的长度和位置。
要添加一些更复杂的功能,我们可以使用GeoGebra的命令语言。
在输入栏中输入“Midpoint[A, B]”,然后按Enter键。
这将创建一个表示线段AB中点的对象。
您可以在代数视图中看到新创建的对象。
除了几何对象,GeoGebra还支持函数和方程。
在输入栏中输入“f(x) = x^2”,然后按Enter键。
这将创建一个二次函数的图像。
您可以使用工具栏中的放大和缩小按钮来调整视图。
另一个强大的功能是GeoGebra的动画功能。
您可以使用动画工具栏上的按钮来创建动画。
例如,您可以选择一个点并使用动画工具栏上的按钮来使其沿着一条线移动。
这样,您可以模拟一个物体在平面上的运动。
除了这些基本操作,GeoGebra还提供了许多高级功能,如计算导数、积分和解方程等。
您可以使用工具栏上的不同按钮来访问这些功能。
总结一下,在本教程中,我们介绍了GeoGebra的基本操作和创建动态数学模型的方法。
您可以使用工具栏上的各种按钮来创建几何对象、函数和方程。
您还可以使用动画工具栏来创建动画效果。
希望这个教程能够帮助您开始使用GeoGebra并探索数学的乐趣!。
常用GeoGebra指令—09.几何变换
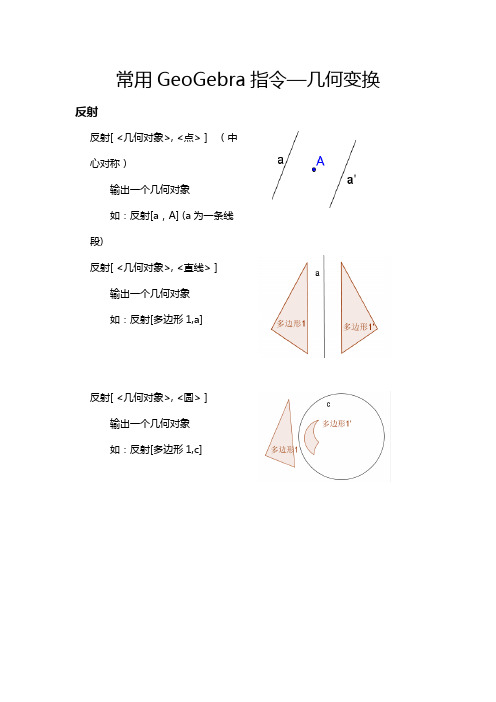
常用GeoGebra指令—几何变换反射反射[ <几何对象>, <点> ] (中心对称)输出一个几何对象如:反射[a,A] (a为一条线段)反射[ <几何对象>, <直线> ]输出一个几何对象如:反射[多边形1,a]反射[ <几何对象>, <圆> ]输出一个几何对象如:反射[多边形1,c]平移平移[ <几何对象>, <向量> ]输出一个几何对象 如:平移[多边形1,u]平移[ <向量>, <起点> ]输出一个向量 如:平移[u,A]切变切变[ <几何对象>, <直线|射线|线段>, <比> ]输出几何对象 如:切变[多边形1,a]伸压伸压[ <几何对象>, <向量> ]输出一个几何对象 如:伸压[多边形1,u]伸压[ <几何对象>, <直线|射线|线段>, <比> ]输出一个几何对象如:伸压[多边形1,a , 0.1]缩放缩放[ <几何对象>, <缩放比例> ]输出一个几何对象 如:缩放[多边形1,0.5]O 为原点,该指令的缩放中心为原点缩放[ <几何对象>, <缩放比例>, <缩放中心点> ]输出一个几何对象 如:缩放[多边形1,0.5,A]旋转旋转[ <几何对象>, <角度> ]输出一个几何对象 如:旋转[多边形1,60°]O 为原点,该指令的旋转中心为原点旋转[ <几何对象>, <角度> ,<旋转中心>]输出一个几何对象 如:旋转[多边形1,90°,D]以上内容主要结合官网介绍和4.4版的软件实际检验,如有问题请及时反馈。
GeoGebra学习交流群:217440999作者:云南师大-小孟Q Q:319774699E-mail:****************。
GeoGebra+manual

GeoGebra 使用說明官方版使用說明3.0Markus Hohenwarter and Judith Preiner, June 2007GeoGebra 3.0 使用說明GeoGebra Website: Last modified: June 4, 2007作者Markus Hohenwarter, mhohen@Judith Preiner, jpreiner@翻譯志工黃福坤,國立台灣師範大學物理系,hwang@.tw羅驥韡,台北市立陽明高中數學科,pegasusroe@陳禾凱,台北縣立錦和高中數學科,jojoba0326@林螢婕,linchuenhui@GeoGebra 說明搜尋•線上: GeoGebra Help Search•PDF檔: Press Ctrl + Shift + F in Adobe Acrobat ReaderContents翻譯志工 (2)GeoGebra 說明搜尋 (2)Contents (3)1: GeoGebra是什麼? (7)2: 範例 (8)2.1 三角形 (8)2.2 線性方程式y = m x + b (8)2.3 三點A, B, C 的重心 (9)2.4 將線段以7 : 3 的比例分割 (9)1.1 二元一次聯立方程組 (10)2.5 函數的切線 (10)2.6 探討多項式函數 (11)2.7 積分 (11)3: 幾何輸入 (12)3.1 一般須知 (12)3.1.1滑鼠右鍵功能表 (12)3.1.2顯示與隱藏 (12)3.1.3痕跡 (12)3.1.4放大縮小繪圖區 (13)3.1.5座標軸比例 (13)3.1.6 作圖過程 (13)3.1.7 「前進後退」按鈕 (13)3.1.8 重新定義 (14)3.1.9 屬性對話方塊 (15)3.2模組 (15)3.2.1 一般模組 (16)3.2.2 點 (17)3.2.3 向量 (18)3.2.4 線段 (18)3.2.6 多邊形 (19)3.2.7 直線 (19)3.2.8 圓錐曲線 (20)3.2.9 圓弧與扇形 (21)3.2.10 數值與角度 (21)3.2.11 顯示或隱藏物件群組 (22)3.2.12 軌跡 (23)3.2.13 幾何變換 (23)3.2.14 文字 (24)3.2.15 圖片 (25)3.2.16 圖片的屬性 (25)4: 輸入代數式 (27)4.1 一般須知 (27)4.1.1 改變代表值 (27)4.1.2 動畫 (27)4.2 直接輸入 (28)4.2.1 數值和角度 (28)4.2.2點和向量 (29)4.2.3 直線 (29)4.2.4圓錐曲線 (29)4.2.5函數 (30)4.2.6 物件集合 (31)4.2.7 數學運算 (31)4.2.8 布林變數 (32)4.2.9 布林運算 (33)4.3指令 (33)4.3.1 一般指令 (33)4.3.2布林指令 (34)4.3.3 數值指令 (34)4.3.4 角度 (36)4.3.5 點 (37)4.3.6 向量 (38)4.3.8 射線 (39)4.3.9 多邊形 (40)4.3.10 直線 (40)4.3.11 圓錐曲線 (41)4.3.12 函數 (42)4.3.13 參數曲線 (43)4.3.14 圓弧和扇形 (43)4.3.15 圖片 (44)4.3.16 軌跡 (44)4.3.17 序列 (45)4.3.18 幾何轉換 (45)5: 列印和輸出 (48)5.1 列印 (48)5.1.1 繪圖區 (48)5.1.2 作圖過程 (48)5.2 繪圖區以圖檔輸出 (48)5.3繪圖區複製到剪貼簿 (49)5.4作圖過程以網頁輸出 (50)5.5動態工作底稿以網頁輸出 (50)6: 選項 (52)6.1 點的吸附功能 (52)6.2角度單位 (52)6.3小數位數 (52)6.4 連續性 (52)6.5 點的類型 (52)6.6 直角的類型 (52)6.7 座標軸 (53)6.8 標籤 (53)6.9 字體大小 (53)6.10 語言 (53)6.11 繪圖區 (53)6.12 儲存設定 (53)7: 工具與工具列 (54)7.1 使用者自訂工具 (54)7.2 自訂工具列 (54)8: JavaScript 介面 (56)1:GeoGebra是什麼?GeoGebra 是一套結合幾何、代數和微積分的數學軟體, 由任教於Florida Atlantic 大學的Markus Hohenwarter 為學校數學教育所研發的。
动态数学软件GeoGebra使用教程

. GeoGebra使用入门数字式的坐标平面系统目录安装 (3)基本概念.............................................5跨系统、跨平台........................................5使用者接口............................................5输出..................................................6重要的网络资源. (7)基础操作 (8)1-新点、交点、中心点 (8)2-直线、线段、向量 (10)3-垂直线、并行线、角平分线、切线、轨迹 (13)4-多边形、正多边形 (20)5-圆形、扇形、圆弧 (22)6-角、斜率 (26)7-对称、平移、旋转 (28)8-数值滑杆、文字 (34)9-对象的属性设定 (37)进阶操作X例 (38)1-直线方程式、函数 (38)2-动态文字处理、代数式定义处理:if语法的应用 (39)3-参数曲面(Curve) (41)4-序列物件(Sequence) (42)5-自订工具列管理 (45)附录:以代数式建立对象之指令速查表 (47)GeoGebr a使用入门安装Windows接口下的安装请先到GeoGebra的:/cms/(若要阅读中文画面,请将下拉式选单切换到Chinese。
)这画面中包含大部分的资源,如「Help」、「中文讨论区」等。
从「WebStart」画面中进行安装,可以保证安装到目前最新的版本,而「下载」页面,则列出目前最稳定的版本。
本说明建议读者可以「WebStart」方式进行安装,点选「启用GeoGebra」这个连结,画面会导向到「WebStart」页面,步骤如下页:按下「GeoGebraWebStart」按钮后,因为GeoGebra是在「Java」环境下执行的软件,若您的计算机没有安装「Java」环境,则画面会自动导向到「Java」安装网页,若您的计算机没有「Java」环境,且浏览器没有导向到「Java」安装网页,您可以自行输入网址:java./zh_TW/,来进行在线安装,该上有详细的安装说明。
GeoGebra使用手册

GeoGebra使用手册欢迎使用GeoGebra,这是一个功能强大且易于使用的数学软件。
本手册将为您提供详细的指导,帮助您了解并熟练使用GeoGebra的各项功能。
请按照以下步骤进行操作:第一步:下载与安装GeoGebra1. 打开您的浏览器,搜索“GeoGebra官方网站”。
2. 进入官方网站后,在主页上找到“下载”或“Download”按钮。
3. 点击按钮选择适用于您的操作系统的版本,并开始下载。
4. 下载完成后,双击该文件并按照提示进行安装。
第二步:GeoGebra的主要界面1. 当您首次打开GeoGebra时,会看到主界面。
主界面由三个主要区域组成:代数视图、几何视图和计算视图。
2. 代数视图用于处理和展示代数表达式和方程。
3. 几何视图用于构建和探索几何图形。
4. 计算视图用于进行符号计算和数值计算。
第三步:基本功能与工具栏1. 工具栏位于GeoGebra主界面的顶部,包含各种常用功能按钮。
2. 点击“点工具”按钮,可以创建和操作点。
3. 点击“线段工具”按钮,可以绘制线段和直线。
4. 点击“圆工具”按钮,可以绘制圆和弧。
5. 点击“平移工具”按钮,可以平移几何图形。
6. 点击“旋转工具”按钮,可以旋转几何图形等。
第四步:创建几何图形1. 在几何视图中,使用工具栏上的按钮来创建各种几何图形,例如点、线段、圆等。
2. 您可以使用鼠标进行交互,拖动点、拉伸线段或改变图形的属性。
3. 如果需要输入特定的数值或公式,请使用代数视图。
第五步:功能扩展与自定义1. GeoGebra提供了丰富的扩展功能,您可以通过访问菜单栏中的“视图”或“工具”来获取更多选项。
2. 您还可以通过创建自定义命令和工具栏来定制自己的GeoGebra环境。
3. 扩展功能和自定义选项可以根据您的需求进行灵活设置,以便更高效地使用GeoGebra。
第六步:数学运算与分析1. 在GeoGebra中,您可以进行各种数学运算,例如求解方程、计算函数的导数和极限等。
geogebra的使用方法

geogebra的使用方法Geogebra是一款强大的数学软件,它能够帮助学生和教师进行数学建模、图形绘制、计算和数据分析。
本文将介绍如何使用Geogebra,包括创建图形、绘制函数、进行几何建模、进行统计分析以及如何在Gegebra社区中分享你的成果。
1.创建图形:- 打开Geogebra软件,你将看到一个空白的工作区。
-在工具栏上选择不同的工具来创建图形,如点、线、圆等。
-点击工作区中的点或线,然后拖动它们来移动或改变形状。
2.绘制函数:-在工具栏上选择函数工具,如直线、抛物线、正弦函数等。
- 点击工作区来确定函数的起点和终点,Geogebra将自动生成函数图形。
-可以通过调整函数方程式或改变函数属性来修改图形。
3.进行几何建模:-可以使用点、线、圆等工具来进行几何建模。
-选择工具,然后点击工作区创建相应的几何元素。
-可以根据需要进行移动、旋转和缩放等操作。
4.进行统计分析:- 使用Geogebra的统计工具可以进行各种统计分析。
-创建一个数据集,并输入数据。
-在工具栏中选择统计工具,如直方图、箱线图等。
- Geogebra将生成对应的统计图表。
5. 在Geogebra社区中分享成果:- 在工具栏中选择"分享"选项,然后选择"上传到Geogebra社区"。
- 创建一个Geogebra账号,如果还没有的话。
- 根据提示将你的图形或模型上传到Geogebra社区。
6.组织和管理工作:- 使用Geogebra的"视图"菜单可以打开或关闭各个功能面板。
- 使用"文件"菜单可以保存和打开Geogebra文件。
- 使用"选项"菜单可以调整Geogebra的设置和显示风格。
7. 自定义Geogebra:-在工具栏上右键单击,可以选择添加新工具或修改工具。
-在工具栏上点击"选项",然后选择"自定义工具栏"可以添加自定义的工具。
geogebra描点指令

geogebra描点指令摘要:1.引言2.FPGA 与脉冲同步技术的关系3.如何使用FPGA 实现脉冲信号载波频率同步环4.结论正文:1.引言FPGA(现场可编程门阵列)是一种集成电路,可以由用户编程和配置,以实现特定的功能。
在电子设计领域,FPGA 被广泛应用,例如在数字信号处理、通信和雷达系统中。
在这些应用中,脉冲同步技术起到了关键作用。
本文将讨论如何使用FPGA 实现脉冲信号载波频率同步环。
2.FPGA 与脉冲同步技术的关系FPGA 作为一种可编程硬件平台,可以实现各种数字信号处理算法,如数字滤波、频率估计和同步等。
在脉冲信号处理中,同步技术是最重要的环节之一。
通过同步,可以提取脉冲信号中的有用信息,如载波频率、脉冲周期等。
因此,FPGA 在脉冲同步技术中具有重要作用。
3.如何使用FPGA 实现脉冲信号载波频率同步环为了实现脉冲信号载波频率同步环,可以采用以下步骤:(1)使用改进的相位差分频率估计算法进行快速载波频率粗估计。
这种算法的信噪比阚值低于kay 法,即使在信噪比较低的情况下,也能达到cramer-rao 界。
(2)应用数字下变频技术和kay 算法实现载波频率的精确估计。
数字下变频技术可以将高频信号转换为低频信号,从而降低信号处理难度。
kay 算法是一种基于矩阵求逆的频率估计方法,具有较高的精度和稳定性。
(3)设计并实现同步环路。
同步环路包括相位差分频率估计算法、数字下变频技术和kay 算法。
通过仿真验证,该环路可以在短时间内实现高精度的载波频率同步。
4.结论FPGA 在脉冲同步技术中具有重要作用,可以通过实现同步环路来提取脉冲信号中的载波频率信息。
使用改进的相位差分频率估计算法、数字下变频技术和kay 算法可以实现高精度、高稳定性的载波频率同步。
geogebra制作高中物理动画课件必修二6-10

2.6飞机投弹5.41.添加变量isStart,用于判断开始还是暂停计时isStart=false2.添加变量dt,表示时间间隔dt=0.023.添加变量t,表示时间t=04.添加滑动条speed,1∼10,增量为1,控制动画速度5.添加滑动条N,1∼1,增量1,计时用,速度用滑动条speed控制dtSetValue(t,t+dt)6.添加《on/off》按钮,用于控制开始或暂停,添加脚本SetValue(isStart,!isStart)StartAnimation(N,isStart)SetCaption(button1,if(isStart,"off","on"))7.添加《reset》按钮,用于重置。
添加脚本SetValue(isStart,false)StartAnimation(N,isStart)SetCaption(button1,"on")SetValue(t,0)8.添加变量h,表示高度h=109.添加滑动条theta,0°∼45°表示地面的倾角theta=0°10.添加射线,表示地面ray((0,0),(1;theta))11.添加变量dt1,表示投弹间隔dt1=0.312.添加变量h0,表示投弹时间间隔内地面上升的高度h0=v0dt1tan(theta)13.添加变量g,表示重力加速度g=1014.添加变量v0,表示飞机速度v0=515.添加点A,表示飞机A=(v0t,h)16.添加列表,表示飞机形状{ellipse(A+(-sqrt(0.4^2-0.2^2),0),A+(sqrt(0.4^2-0.2^2),0),0.4), polyline(A+(-0.4,0),A+(-0.6,0),A+(-0.8,0.2))}17.添加列表lsttm,表示落地时间,因为地面倾斜时的时间不同。
公式h−ih0−12gt2v0t=tanθlsttm=sequence((-v0tan(theta)+sqrt((v0tan(theta))^2-2g(i h0-h)))/g,i,1,floor(t/dt1))18.添加序列,表示炸弹Sequence((v0i dt1+v0If(t-i dt1<lsttm(i),t-i dt1,lsttm(i)),h-0.5g If(t-i dt1<lsttm(i),t-i dt1,lsttm(i))^2),i,1,floor(t/dt1))19.添加序列,表示轨迹Sequence(Curve(v0i dt1+v0j,h-0.5g j^2,j,0,If(t-i dt1<lsttm(i),t-i dt1,lsttm(i))),i,1,floor(t/dt1))20.添加复选框,显示/隐藏轨迹21.添加变量xm,表示斜面与飞行线的交点水平坐标xm=if(theta!=0°,h/tan(theta))22.N中添加脚本,防止飞机与斜面碰撞if(theta!=0°&&v0t>=xm-1,Execute({"StartAnimation(N,false)","SetVisibleInView(button1,1,false)"}))23.在<reset>中添加脚本SetVisibleInView(button1,1,true)24.添加序列l4,计算点间距离l4=sequence((v0(dt1+lsttm(i+1)-lsttm(i)))/cos(theta),i,1,length(lsttm)-1)25.添加复选框b,目的是显示/隐藏落点间距。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
常用GeoGebra指令—脚本按钮按钮[ ]新建一个空白按钮如:按钮[]按钮[ "<标题>" ]新建一个特定标题按钮如:按钮[“开始”]背景色背景色[ <对象>, "<颜色>" ]更改文字和电子表格中的对象的背景颜色如:背景色[文字1,Cyan](颜色对照表)更多的颜色列表:/en/Reference:Colors 背景色[ <对象>, <红>, <绿>, <蓝> ]更改文字和电子表格中的对象的背景颜色如:背景色[文字1,255,0,255]红绿蓝三色用0-255之间的数字输入就可以了,大于255的取余转化标签模式标签模式[ <对象>, <0_名称|1 _名称+数值| 2_数值| 3_标题> ] 改变对象的标签模式如:标签模式[A,2]标题标题[ <对象>, "<标题>" ]改变对象的标题如:标题[A,“圆心”]标题在标签模式选择标题时才会显示播放声音播放声音[ <文件> ]播放一个电脑上的mid文件如:播放声音[“光辉岁月.mid”]播放声音[“C:\Users\mengbaoxing\Downloads\光辉岁月.mid”] 相对路径:将MID文件与GGB文件放在同一文件夹下;绝对路径:文件可以放在任意文件夹下,只是需要写上复杂的路径。
播放声音[ <是否播放?> ]播放和暂停声音如:播放声音[true] 播放声音[false]播放声音[ <音符组合>, <乐器> ]播放由特定乐器演奏的一串音符如:播放声音["V0 A3q B3q C3q B3q V1 A2h C2h", 0]音符组合,请看音符输入规则乐器,请看乐器对照表播放声音[ <音符>, <持续时间>, <乐器> ] 播放一个音符如:播放声音[1,1,1]音符,请看音符对照表音符输入规则乐器对照表音符对照表播放声音[ <函数>, <最小值>, <最大值> ]通过函数播放一个声音如:播放声音[sin(x),0,1]播放声音[ <函数>, <最小值>, <最大值>, <采样率>, <样本深度> ] 通过函数播放一个声音如:播放声音[sin(x),0,1,44100,16]采样率值:8000, 11025, 16000, 22050, 44100样本深度:8 或16.参数参数[ <最小值>, <最大值>, <增量>, <速度>, <宽度(px)>, <true | false(角度)>, <true | false(水平)>, <true | false(开启动画)>, <true | false(随机)> ] 新建一个参数如:参数[0,10,1,1,200,false,true,false,true]新建参数一般用工具相比较工具更好用些点径点径[ <点>, <数值1+> ]更改点对象的大小如:[A,9]数值越大,点越大,不受参数设置中的限制点型点型[ <点>, <数值> ]更改点对象的形状如:[A,0]数值含义:0_圆点|1_叉形|2_空心点|3_十字|4_菱形|5_空心菱形|6_上三角|7_下三角|8_左三角|9_右三角动态颜色动态颜色[ <对象>, <红>, <绿>, <蓝> ]改变对象的颜色如:动态颜色[A,1,1,1]三种颜色取值范围均为0-1动态颜色[ <对象>, <红>, <绿>, <蓝>, <透明程度> ]改变对象的颜色和透明度如:动态颜色[A,1,1,1,1]透明度取值范围是0-1放大放大[ <缩放因子> ]放大绘图区如:放大[0.5]放大画面,能够看到的内容会减少这里如果缩放因子取值为0-1,起到的是缩小效果放大[ <缩放因子>, <中心点)> ]保持中心点在画面上的位置不变,放大绘图区如:放大[0.5,A]放大[ <x最小值>, <y最小值>, <x最大值>, <y最大值> ] 放大绘图区到特定的范围如:放大[0,0,2,2]复选框复选框[ ]新建一个无标题的空白复选框(真假值)如:复选框[]空白复选框指没有标题,默认显示名称复选框[ "<标题>" ]新建一个有标题的空白复选框-如:复选框[“正误”]有标题的复选框默认显示标题复选框[ <集合> ]新建一个无标题的集合复选框-如:复选框[{A, B, C, D}]集合复选框可以直接控制集合内所有对象的显示,自身显示为名称复选框[ "<标题>", <集合> ]新建一个有标题的集合复选框-如:复选框[{A, B, C, D},“点集”]集合复选框可以直接控制集合内所有对象的显示,自身显示为标题如果两次复选框包括了相同的对象,那么这个对象只受后面新建的复选框控制。
复制到视图复制到视图[ <对象>, <视图0|1|2> ]新建一个对象副本到特定的绘图区如:复制到视图[A,2]视图参数的意义:0:副本出现在绘图区,跟随画面缩放变化,跟随对象移动;1:副本出现在绘图区,不跟随画面缩放变化,只跟随对象移动;2:副本出现在绘图区2,不跟随画面缩放变化,只跟随对象移动。
复制到视图[ <对象>, <视图0|1|2>, <点1>, <点2>, <屏幕点1>, <屏幕点2> ]新建一个对象副本到特定的绘图区如:复制到视图[A,2,(0,0),(10,-10),(0,0),(100,100)]视图参数的意义:0:在原对象位置复制出对象,复制出的对象的大小和位置跟随原对象,后面的对应关系无作用。
1:在正确的位置复制出对象,复制出的对象的大小不会缩放,位置跟随原对象。
2:在偏移了一个正确的位置的地方复制出对象,复制出的对象的大小会缩放,位置跟随原对象。
后面四个点的意义:<点1>, <点2>, <屏幕点1>, <屏幕点2>表示的是一种对应关系。
其中点1与屏幕点1对应,点2与屏幕点2对应。
屏幕点的坐标系是以视图的左上角为坐标原点,向右是x轴正方向,向上是y轴正方向,单位是像素。
恰当的对应关系例如(0,0),(10,-10),(0,0),(100,100)对象向上复制对象也向上,对象向右复制对象跟随向右。
如果对应关系直接写为(0,0),(10,10),(0,0),(100,100)对象向上复制对象也向下,对象向右复制对象跟随向右。
对应关系中尽量不使用点对象(例如A),那样对应关系会变得非常复杂。
复制自由对象复制自由对象[<自由对象> ]复制出一个自由对象如:复制自由对象[ A ]需要注意这里需输入的是自由对象,如果输入派生对象,这里会出现异常如:复制自由对象[ 多边形1 ] 会得到一个数值(大小等于多边形面积)复制自由对象[a] 会得到一条线段所在的直线无论输入时选择的是否是自由对象,得到的对象都可是自由对象,可改变定义;得到的对象也和原对象不再相关。
更新作图更新作图[ ]重新计算所有对象(主要用于随机数和随机元素的更新)如:更新作图[ ]工具提示模式工具提示模式[ <对象>, <数值> ]设置每一个对象的提示模式如:工具提示模式[E,2]数值: 0_自动| 1_开启| 2_关闭| 3_标题| 4_下一单元格4:对象必须是从表格新建出的对象,下一个单元格是右边的单元格激活绘图区激活绘图区[1/2]设置活动绘图区如:激活绘图区[2]活动绘图区是通过指令输入新建的对象存在的绘图区;默认的活动绘图区是绘图区1;当绘图区2打开并输入”激活绘图区[2]”指令后,绘图区2才会成为活动绘图区,否则活动绘图区一直是绘图区1。
解析到数解析到数[ <数值>, <字符串> ]将文字中数值解析出来如:解析到数[a , 文字1] (a的原来数值被改为解析出来的数值)解析到数[1, 文字1] (新建数值为解析出来的数值)解析到数中用到的数值与结果无任何关系,用到的数值对象会被改变,用到的文字必须是全数值文字,否则结果为未定义。
解析函数解析函数[ <函数>, <字符串> ]将文字中函数解析出来如:解析函数[ f, 文字1] (f的原来函数被改为解析出来的函数)解析函数[2x, 文字1] (新建函数为解析出来的函数)解析函数中用到的函数与结果无任何关系,用到的函数对象会被改变,用到的文字必须是全函数文字(x的多项式或f(x)=x的多项式),否则结果为未定义。
开启动画开启动画[ ]开启动画如:开启动画[ ]开启设置过动画的点和参数的动画开启动画[ <true | false> ]开启/关闭动画如:开启动画[ false]开启/关闭设置过动画的点和参数的动画开启动画[ <参数|点>, <参数|点>, ... ]开启动画如:开启动画[ A ]开启特定点或参数的动画开启动画[ <参数|点>, <参数|点>, ..., <true | false> ] 开启动画如:开启动画[ A ,false]开启/关闭特定点或参数的动画平移视图平移视图[ <横向移动的像素量>, <纵向移动的像素量> ] 平移绘图区如:平移视图[10,10]删除删除[ <对象> ]删除某一对象如:删除[A]删除可直接使用Delete设定值设定值[ <复选框>, <0|1> ]设置复选框(真假值)的状态如:设定值[a,1]0/false表示假,1/true表示真。
设定值[ <对象1>, <对象2> ]设置已有对象的值如:设定值[A,B] (A,B均为已有的点)设定值[A,(0,0)]设定值[a,线段[A,B]]该指令中虽然要求后面是对象,但是也可以直接输入数值(定义)只要保证对象的类型不发生改变,发生改变的定义会被提示错误设定值[ <集合>, <数值>, <对象> ] (其中<数值>可理解为<元素位置>)设置某集合中特定元素的值如:设定值[集合1,1,2] (集合1为数集)设定值[集合1,1,B] (集合1为点集)元素位置的值必须保证能够找到对应元素。
