同济大学钢结构基本原理(第二版)习题参考解答第五章
钢结构设计原理第五章.ppt

抗弯强度的计算
抗弯强度的计算
根据局部稳定要求,当梁受压翼缘的自由外伸宽度与
其厚度之比大于
但不超过
时,塑性
发展对翼缘局部稳定会有不利影响,应取 x =1.0。
对于需要计算疲劳的梁,因为有塑性区深入的截面,
塑性区钢材易发生硬化,促使疲劳断裂提前发生,宜取 x= y =1.0。
控制梁的刚度通过对标准荷载下的最大挠度加以限制实现。根据公
式:
w≤[w]
(5-13)
w——标准荷载下梁的最大挠度;
[w]——受弯构件的挠度限值,按表5-3规定采用。
梁的最大挠度可用材料力学、结构力学方法计算。
均布荷载下等 截面简支梁 集中荷载下等 截面简支梁
w 5qL4 5 MxL2 38E4xI 48ExI
w PL3 MxL2 4梁8整E体Ix稳定的1概2E念 Ix
式中, IMx—x———跨跨中中毛截截面面弯惯矩性矩
梁整体稳定的概念
梁整体稳定的概念
梁整体稳定的概念
梁可以看做是受拉构件和受压构件的组合体。 1 Y 1
受压翼缘其弱轴为1 -1轴,但由于有腹板作连 X X
续支承,(下翼缘和腹板下部均受拉,可以提
变形等); 按承载能力极限状态和正常使用极限状态进行设计。
受弯构件设计内容
受弯构件设计内容
强度
整体稳定 受
(承载能力极限状态)
弯
局部稳定
构
件
刚度 (正常使用极限状态)
应用
应用
梁在钢结构中是应用较广泛的一种基本构件。例如房屋建 筑中的楼盖梁、墙梁、檩条、吊车梁和工作平台梁,水工 钢闸门中的梁和采油平台梁等。
第5章 钢结构例题..

【解】(B)。 纵向加劲肋应配置在受压区而不是受拉区;横向 加劲肋不应与下翼缘焊牢,应在距下翼缘50~100mm处 断开
1500
160 160 z
20
z 180
16
20
1450
20
【例5.3】一钢梁端部支承加劲肋设计采用突缘加劲板,尺 寸如图所示,支座反力F=682.5kN,钢材采用Q235B,试验算该 加劲肋。
x 1200/ 14.5 83 [ ] 200
【例5.5】设计一支承波形石棉瓦屋面的檩条,屋面坡 度为1/2.5,无雪荷载和积灰荷载。檩条跨度为6m,水 平间距为0.79m(沿屋面坡向间距为0.851m),跨中设置 一道拉条,采用槽钢截面[图(b)],材料Q235B。
(b)
【解】 波形石棉瓦自重约为0.20kN/㎡(坡向),预估檩
(a)
【解】 压型钢板屋面自重约为0.15kN/㎡(坡向)。檩条自重 假设为0.5kN/m。 檩条受荷水平投影面积为5×12=60㎡,为超过60㎡, 故屋面均布活荷载取0.5kN/㎡,大于雪荷载,故不考虑 雪荷载。 檩条线荷载为[对轻屋面,只考虑式(1.29)可变荷载 效应控制的组合]: 标准值:
由于试选截面时,整体稳定系数是参考普通工字钢假 定的,对H型钢应按附录3附式(3.1)进行计算: lt 5000 11 11 0.898 b1h 175 350 b 0.69 0.13 0.898 0.807 500 y 127 3.93
y t1 235 4320 Ah b b 2 1 y Wx fy 4.4h 0.807 4320 63.66 35 127 1.1 1 0.83 0.6 2 127 782 4.4 35
同济大学钢结构基本原理课后习题答案完全

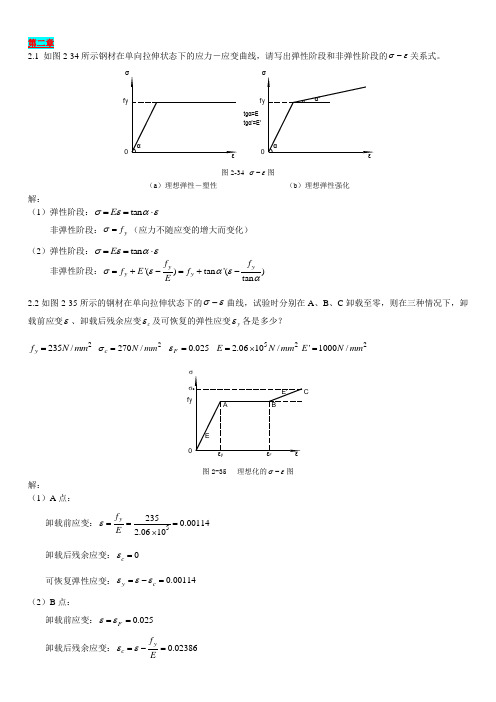
第二章如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少? 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本原理课后习题与答案完全版

第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线,请写出弹性阶段和非弹性阶段的解:(1)A 点:卸载后残余应变: 关系式。
解:(1弹性阶段:非弹性阶段: (2)弹性阶段:非弹性阶段:(b)理想弹性强化tan(应力不随应变的增大而变化)tanE'(y―)f y tan '( tan2.2如图2-35所示的钢材在单向拉伸状态下的曲线,试验时分别在载前应变、卸载后残余应变c及可恢复的弹性应变y各是多少?f y 235N/mm2270N/mm20.025 E 5 22.06 105N/mm2A、B、C卸载至零,则在三种情况下,卸2E' 1000N/mm2卸载前应变: fyE23552.06 1050.00114可恢复弹性应变: c 0.00114 (2)B 点:卸载前应变: 0.025图图图2-35 理想化的卸载后残余应变:可恢复弹性应变:2.3试述钢材在单轴反复应力作用下,钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材曲线与反复应力大小和作用时间关系:当构件反复力|| f y时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材曲线基本无变化;当| | f y时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢材曲线会相对更高而更短。
另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材曲线也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低。
2.4试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,可能会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
钢结构原理与设计第2版__课后答案

4-1解:kN N N N QK Q GK G 420315324.1315312.1=⨯⨯+⨯⨯=+=γγ焊缝质量为三级,用引弧板施焊。
查表得E43焊条的2/185mm N f W t =,Q235钢的2/215mm N f =。
mm bf N t W t 35.11185200104203=⨯⨯=≥ 故取mm t 12=。
4-2解:k k k QK Q GK G N N N N N N 36.18.04.12.02.1=⨯+⨯=+=γγ焊缝质量为二级,2/215mm N f W t =未用引弧板施焊mm l W 376122400=⨯-=tl Nf W W t =,k W W t N t l f N 36.1== kN t l f N W W t k 3.71336.11237621536.1=⨯⨯==4-4解: 1)焊脚尺寸f h背部尺寸⎪⎩⎪⎨⎧=⨯=≤=⨯=≥mmt h mmt h f f 6.982.12.174.4105.15.1min 1max 1趾部尺寸()()⎪⎩⎪⎨⎧=-=-≤=⨯=≥mm t h mmt h f f 7~62~182~174.4105.15.1min2max 2为方便备料,取mm h h h f f f 621===,满足上述要求。
2)轴心力N 的设计值kN N N N QK Q GK G 4.2481809.04.11801.02.1=⨯⨯+⨯⨯=+=γγ按角钢背与趾部侧面角焊缝内力分配系数可知:等边角钢内力分配系数3.01=b e 7.02=be对角钢趾部取力矩平衡得: 21Ne b N =kN N N be N 52.744.2483.03.021=⨯===kN N N N N 88.1734.2487.07.012=⨯==-=3)焊缝长度。
当构件截面为一只角钢时,考虑角钢与节点板单面连接所引起的偏心影响, W t f 应乘以折减系数0-85。
角钢趾:mm h mm f h N l f W f f W 48813016085.067.01052.7485.07.0311=>=⨯⨯⨯⨯=⋅≥取mm l 1401= (mm h f 1422130=+,取10mm 的整数倍) 角钢背:mm h mm f h N l f W f f W 3606030416085.067.01088.17385.07.0322=<=⨯⨯⨯⨯=⋅≥ 取mm l 3202= (mm h f 3162304=+,取10mm 的整数)4-5解:腹板受到轴心拉力k N 作用kN N N N QK Q GK G 4.5984408.04.14402.02.1=⨯⨯+⨯⨯=+=γγ焊脚尺寸f hmmt h f 6.55.1max =≥,mmt h f 9~8)2~1(min =-≤取mm h f 6=时,mm h mm f h N l f Wf f W 360602.44516067.02104.5987.023=>=⨯⨯⨯⨯=⨯≥ 不可行;取mm h f 7=时,mm l w 6.381≥,mm h l f w 42060=≤ 可行,mm h l f 6.39526.381=+=,取mm l 400= 取mm h f 9=时,mm l w 8.296≥,mm h l f w 54060=< 可行,mm h l f 8.31428.296=+=,取mm l 320=故最小的焊脚尺寸可取mm 7,钢板搭接长度为mm 400 最大的焊脚尺寸可取mm 9,钢板搭接长度为mm 3204-7解:(1)直接计算法m kN Nl M ⋅=⨯==102.0502262/1.148862407.0101067.0mm N h h l h M ff W f f =⨯⨯==σ23/6.2972407.010507.0mm N h h l h N ff W f f =⨯⨯==τW f f ff f ≤+⎪⎪⎭⎫⎝⎛22τβσ 1606.29722.11.148822≤⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛f f h h 解得:mm h f 85.7= 采用()mmt mmt mmh f 9~82~136.6185.15.18min max =-≤=⨯=≥=,可(2)试算法()⎩⎨⎧=-≤=⨯=≥mm t mm t h f 9~82~136.6185.15.1min max取mm h f 8=2134424087.07.0mm l h l h A W f W e W =⨯⨯=== 3225376024087.06161mm l h W W e W =⨯⨯⨯==2262/0.186624087.0101067.0mm N l h M W f f =⨯⨯⨯==σ 23/2.3724087.010507.0mm N l h N W f f =⨯⨯⨯==τ222222/160/9.1562.3722.1186mm N f mm N W f f ff =≤=+⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛τβσ,可 故mm h f 8=4-8解:kN R R R k k 405%754.1%252.1=⨯+⨯=mm l 300= mm l h 701080=-=取焊脚尺寸mm h f 6= mm h h f e 2.47.0== (1)几何关系水平焊缝计算长度mm h l l f h Wh 64670=-=-= 全部焊缝计算长度mm l l l Wh W 4286423002=⨯+=+= 全部焊缝有效截面W e W l h A = 形心位置cm h h A l l h x e e WWhWh e 96.08.4224.64.6222=⨯⨯⨯⨯=⋅=略去3e h 项423236.21542304.642.02123042.02212cm l l h l h I Wh e e x =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⋅+=42232238.4796.04.642.096.024.64.642.0124.642.022122cm x l h x l l h l h I Wh e Wh Wh e Wh e y =⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯+⨯⨯=+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+= 焊缝有效截面对形心O 的极惯性矩404.22028.476.2154cm I I I y x =+=+=(2)强度验算kN RV 5.2022== mm x a 4.7080=-= m kN Ra T ⋅=⨯⨯==-3.142104.7040523 mm x l x Wh 4.546.9641=-=-= mm ly 15021==↑=⨯⨯⨯==24601/3.35104.22024.54103.14mm N I Tx Tfσ ←=⨯⨯⨯==2461/4.97104.2202150103.14mm N I Ty Tfτ↑=⨯⨯==23/7.1124282.4105.202mm N A V V fσ剪力和扭矩共同作用下的强度条件()222222/160/6.1554.9722.17.1123.35mmN f mm N W f Tf f Vf Tf =≤=+⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫⎝⎛+τβσσ,可5-1解:QK Q GK G N N N γγ+=则:N N k 8.772560%904.1560%102.1=⨯⨯+⨯⨯=查表,得:钢板螺栓孔壁承压承载力设计值:2/405mm N f b c = 螺栓的强度设计值为:2/190mm N f b v =)(32.1191019044002432kN f d n N bv e vbv =⨯⨯⨯⨯==-ππ)(1621040520203kN tf d N bc b c =⨯⨯⨯=∑=-取)(32.119},min{kN N N N b c b v b == 需要的螺栓数目:48.632.1198.772===b N N n 最少采用7=n试取螺栓距mm mm d p o 655.613≈== 端距mm mm d a o 45412≈== 边距mm mm d c o 3575.305.1≈==因为板宽mm b 250=,若边距为mm 35则不满足间距不大于mm t 12012=要求,故最外排每列螺栓应设3个,取螺栓横向间距为mm 90,端距为mm 45,螺栓数增加为8个。
钢结构基本原理课后习题与答案完全版电子教案

钢结构基本原理课后习题与答案完全版2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
同济大学钢结构设计原理题库及答案.doc

一、填空1.承受动力荷载作用的钢结构,应选用综合性能好的钢材。
2.冷作硬化会改变钢材的性能,将使钢材的强度提高,塑性、韧性降低。
3.钢材五项机械性能指标是屈服强度、抗拉强度、延伸率、冷弯性能、冲击韧性。
4.钢材中氧的含量过多,将使钢材出现热脆现象。
5.钢材含硫量过多,高温下会发生热脆,含磷量过多,低温下会发生冷脆。
6.时效硬化会改变钢材的性能,将使钢材的强度提高,塑性、韧性降低。
7.钢材在250oC度附近有强度提高塑性、韧性降低现象,称之为蓝脆现象。
8.钢材的冲击韧性值越大,表示钢材抵抗脆性断裂的能力越强。
9.钢材牌号Q235-BF,其中235表示屈服强度 ,B表示质量等级为B 级 ,F表示沸腾钢。
10.钢材的三脆是指热脆、冷脆、蓝脆。
11.钢材在250oC度附近有强度提高塑性、韧性降低现象,称之为蓝脆现象。
12.焊接结构选用焊条的原则是,计算焊缝金属强度宜与母材强度相适应,一般采用等强度原则。
13.钢材中含有C、P、N、S、O、Cu、Si、Mn、V等元素,其中 N、O为有害的杂质元素。
14.衡量钢材塑性性能的主要指标是伸长率。
15..结构的可靠指标β越大,其失效概率越小。
16.承重结构的钢材应具有抗拉强度、屈服点、伸长率和硫、磷极限含量的合格保证,对焊接结构尚应具有碳极限含量的合格保证;对于重级工作制和起重量对于或大于50 t中级工作制焊接吊车梁、吊车桁架或类似结构的钢材,应具有冷弯试验的的合格保证。
17.冷弯性能合格是鉴定钢材在弯曲状态下塑性应变能力和钢材质量的综合指标。
18.冷弯性能是判别钢材塑性变形能力和钢材质量的综合指标。
19.薄板的强度比厚板略高。
20.采用手工电弧焊焊接Q345钢材时应采用 E50 焊条。
21.焊接残余应力不影响构件的强度。
22.角焊缝的最小计算长度不得小于和焊件厚度。
23.承受静力荷载的侧面角焊缝的最大计算长度是。
2.在螺栓连接中,最小端距 22.在螺栓连接中,最小栓距 32.普通螺栓连当板叠厚度5 (-螺栓直)连接可能栓杆受破坏2单个普通螺栓承压承载力设计,式表受力方承压构件总厚度的较小值2.普通螺栓连接螺栓传递剪力;摩擦型高强度螺栓连接摩传递剪力30手工焊焊Q23钢,一般采 E43型焊条31焊接结构在焊缝附近形成热影响该区材存在缺32侧面角焊缝连接或正面角焊缝的计算长度不33承压型高强度螺栓仅用承受非动力荷结构的连接中34采用手工电弧焊焊Q34钢材时应采 E50焊条35承受动力荷载的侧面角焊缝的最大计算长度3.轴心受压构件的承载能力极限状态强稳定3.格构式轴心受压构件的等稳定性的条绕虚轴与绕实轴的长细比3.双轴对称的工字型截面轴压构件失稳时的屈曲形式弯屈曲39. 单轴对称截面的轴心受压构件,当构件绕对称轴失稳时发生弯扭屈曲。
钢结构基本原理课后习题标准答案完全版
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σ图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386yc f E εε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-= 可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑?5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载.如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm === 柱子两端较接, 1.0x y μμ== 故柱子长细比为 1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x y λλ<,故对于Q235钢相对长细比为137.61.48λπ=== 钢柱轧制, /0.8b h ≤.对y 轴查P106表5-4(a)知为不b 类截面。
故由式5-34b得()223212ϕααλλλ⎡=++⎢⎣ ()2210.9650.300 1.48 1.482 1.48⎡=+⨯+⎢⎣⨯ 0.354=(或计算137.6λ=,再由附表4-4查得0.354ϕ=)故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kN ϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=。
由式5-34b 计算得0.257ϕ= (或由166.7λ=,查表得0.257ϕ=)故稳定临界荷载为20.25726.1110310208.0crd d N Af kN ϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN (包括自重).如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5解答:截面特性计算: 对a)截面:32394112(5002020500260)8500 1.436101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 3384112205005008 4.167101212y I mm =⨯⨯⨯+⨯⨯=⨯ 2250020500824000A mm =⨯⨯+⨯=244.6x i mm ==131.8y i mm==对b)截面:32384112(4002540025212.5)104009.575101212x I mm =⨯⨯⨯+⨯⨯+⨯⨯=⨯ 33841122540040010 2.667101212y I mm =⨯⨯⨯+⨯⨯=⨯ 24002524001024000A mm =⨯⨯+⨯=199.7x i mm ==105.4y i mm==整体稳定系数的计算:钢柱两端铰接,计算长度10000ox oy l l mm == 对a)截面: 1000040.88244.6ox x x l i λ=== 1000075.87131.8ox y y l i λ=== 对b)截面: 1000050.08199.7kx x x l i λ=== 1000094.88105.4ox y y l i λ=== 根据题意,查P106表5-4(a),知钢柱对x 轴为b 类截面,对y 轴为c 类截面.对a)截面:对x 轴:40.880.440x λπ===()223212x x x x ϕααλλλ⎡=++⎢⎣()2210.9650.30.440.4420.44⎡=⨯+⨯+-⎢⨯⎣0.895=(或计算40.88λ=,再由附表4-4查得0.896xϕ)对y 轴:25.870.816y λπ===()223212y y y y ϕααλλλ⎡=++⎢⎣()2210.9060.5950.8160.81620.816⎡=⨯+⨯+⎢⨯⎣0.604=(或计算75.87λ=,再由附表4-5查得0.604yϕ)故取该柱的整体稳定系数为0.604ϕ=对b)截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ= 整体稳定验算:对a)截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足。
对b)截面 0.489240002052405.88 3000 crd N kN kN =⨯⨯=<不满足。
5.6 一轴心受压实腹柱,截面见图5-27.求轴心压力设计值.计算长度08x l m =,04y l m =(x 轴为强轴).截面采用焊接组合工字形,翼缘采用I28a 型钢.钢材为Q345,强度设计值2310/d f N mm =.5.7 一轴心受压缀条柱,柱肢采用工字型钢,如图5-28所示.求轴心压力设计值.计算长度030x l m =,015y l m =(x 轴为虚轴),材料为Q235, 2205/d f N mm =.图5-28 题5.7解答:截面及构件几何性质计算截面面积:2286.07172.14A cm =⨯=I40a 单肢惯性矩: 41659.9I cm =绕虚轴惯性矩: 241102[659.986.07()]522043.32x I cm =⨯+⨯= 绕实轴惯性矩: 422171443428y I cm =⨯= 回转半径: 55.07x i cm === 15.88y i cm = 长细比: 300054.4855.07ox x x l i λ=== 150094.4615.88oy y y l i λ=== 缀条用L75⨯6,前后两平面缀条总面积2128.79717.594x A cm =⨯=由P111表5-5得:56.85ox λ=== 构件相对长细比,因ox y λλ<,只需计算y λ:94.461.014y λπ=== 查P106表5-4(a)可知应采用b 类截面:()2210.9650.32ϕλλλ⎡=++-⎢⎣0.591=(或计算94.46λ=,再由附表4-4查得0.591ϕ=) 故轴的压力设计值为20.591172.14102052085.6crd d N Af kN ϕ==⨯⨯⨯=5.8 验算一轴心受压缀板柱.柱肢采用工字型钢,如图5-29所示.已知轴心压力设计值2000N kN =(包括自重),计算长度020x l m =,010y l m =(x 轴为虚轴),材料为Q235, 2205/d f N mm =,2125/vd f N mm =.图5-29 题5.8解答:一、整体稳定验算截面及构件几何性质计算:截面面积:2286.07172.14A cm =⨯=I40a 单肢惯性矩: 41659.9I cm =绕虚轴惯性矩: 241102[659.986.07()]522043.32x I cm =⨯+⨯= 绕实轴惯性矩: 422171443428y I cm =⨯= 回转半径: 55.07x i cm === 15.88y i cm = 长细比: 200036.3255.07ox x x l i λ=== 100062.9715.88oy y y l i λ=== 缀板采用303001100mm ⨯⨯。
计算知1/6b K K >,由P111表5-5得46.40ox λ===(其中18028.882.77λ==) 构件相对长细比: 因ox y λλ<,只需计算y λ:62.970.677y λπ===查P106表5-4(a)可知应采用b 类截面()2210.9650.30.7912ϕλλλ⎡=++=⎢⎣(或计算62.97λ=,再由附表4-4查得0.791ϕ=) 故20.791172.14102052791.34crd d N Af kN ϕ==⨯⨯⨯=,满足。
二、局部稳定验算:1)单肢截面板件的局部稳定单肢采用型钢,板件不会发生局部失稳.2)受压构件单肢自身稳定 单肢回转半径 1 2.77i cm = 长细比满足:01max 18028.880.50.562.9731.492.77a i λλ===<=⨯=,且满足140λ< 故单肢自身稳定满足要求.3)缀板的稳定轴心受压构件的最大剪力: 2max 172.14102054151685V N ⨯⨯=== 缀板剪力: 14151611002075821100a T V N c ==⨯= 缀板弯矩: 714151611001.14210222a M V N mm ==⨯=⨯缀板厚度满足: 11003027.5 40b t mm =≥=,故只作强度验算:72221.1421025.4/ 205/303006dM N mm f N mm Wσ⨯===<=⨯ 22207581.51.5 3.5/ 125/30030vd b T N mm f N mm bt τ==⨯=<=⨯ 故由以上整体稳定验算和局部稳定验算可知,该缀板柱满足要求.5.9 有一拔杆,采用Q235钢, 2215/d f N mm =,如图5-30所示,缀条采用斜杆式体系.设考虑起吊物时的动力作用等,应将起重量乘以1.25,并设平面内、外计算长度相等.问60θ=︒时,拔杆最大起重量设计值为多少?。
